The role of water co-adsorption on the modification of ZnO nanowires using acetic acid

Abstract

Density functional theory (DFT) and Car–Parinello molecular dynamic simulations were employed to investigate the interaction of acetic acid with non-polar facets of ultra-thin ZnO nanowires. We consider both a dry and a water environment as well as different molecule coverages for the hydrated system. Our calculations reveal that the fully-covered nanowire is energetically favored in the aqueous environment at room temperature. We also identified a minor influence of liquid water on the denticity of the ligands for the fully modified system. However, a monodentate adsorption is expected for a half-covered nanowire due to strong ligand–water interactions.

---

1 Introduction

Due to the increasing demand for developing a sustainable and green nano-technology, the fabrication of nanostructure-based devices with high integration densities has gained importance as it requires less source material than conventional layer-based approaches. Nanostructured materials have large surface-to-volume ratios which offer a unique possibility of enhancing sensitivity and selectivity. Chemical species introduced onto the surface of such nanostructures could then be employed to create novel hybrid functional devices. Charge accumulation or depletion in one-dimensional nanostructures can take place in the bulk region of the structure, which gives rise to large changes in their electrical properties. Such a feature is particularly desirable for efficient charge injection in solar cells. In particular, one-dimensional nanostructures such as nanowires are preferable, since they naturally provide a direct path for electrical transport. Experiments reveal that electron transport can be up to two orders of magnitude faster in nanowire-based dye-sensitized solar cells (DSSC) than in nanoparticle DSSCs.^1–3

Currently, hybrid organic–inorganic solar cells have a relatively low efficiency (below 10%) and limited stability. These factors strongly depend on the structural details of the organic–inorganic interface which includes binding mechanisms, band offsets and electron injection. Due to the complexity of the interface an explicit theoretical understanding at the atomistic level can help in unveiling the limiting factors and consequently enhancing the device performance.

In DSSCs the organic dye molecules usually attach to the oxide surface via one or several functional groups. The nature of the exposed surface planes of the oxide and the mode of interaction with the organic molecule is the first important information to understand. For example, in the adsorption of the N3 dye on TiO₂ anatase (101) surfaces, the sensitizer binds through two of the four carboxyl groups (–COOH), at least one of them being anchored via a bidentate configuration bridging two adjacent titanium sites.⁴ However, there are still controversies on how the geometry of these molecules on the oxide surfaces and the character of this interaction (physisorption versus chemisorption) affect the electronic and optical properties of the hybrid material.^5–7

Although TiO₂ has become the semiconductor material of choice for the preparation of DSSCs, ZnO-based solar cells have been increasingly investigated.^2,8–15 ZnO represents an appealing alternative to TiO₂ due to its promising transport properties and the possibility of fabrication of an ample variety of ZnO nanostructures. However, the highest efficiencies accomplished with ZnO-based DSSCs are still considerably smaller than for TiO₂-based cells.^16,17 In this sense, a better understanding of the dye–ZnO interface and in particular, the interaction of ZnO with the employed anchoring groups, may be crucial for the design of solar cells with improved efficiency.

Among the compounds employed for the functionalization of ZnO surfaces and nanostructures, carboxylic acids have emerged as one of the most promising choices.^5,18–25 However, there seems to be a general discrepancy regarding the success of –COOH as an anchor group for this metal oxide. Whereas some measurements suggest a favorable covalent binding of the functional group on ZnO nanostructures,^5,23,24,26 other studies indicate surface etching under certain experimental circumstances.²⁷ Especially, pH conditions must be carefully controlled to prevent the ZnO structures from undergoing unwanted reactions in the presence of carboxylic acid. Theoretical investigations have demonstrated the stability of the –COOH group on ZnO surfaces in the gas phase.^28–30 In a previous work²⁹ we pointed out that the stability of acetic acid (AcOH) [employed as the prototype adsorbate to study the interaction of –COOH with ZnO] on non-polar ZnO surfaces remains even in a water environment for moderate concentrations of the ligand. This conclusion was drawn from purely thermodynamic considerations. The explicit inclusion of water in the hybrid system is however fundamental to gain more insight into these phenomena.

In this paper we investigate the adsorption of AcOH on the surfaces of ZnO nanowires under both dry and aqueous conditions by employing Density functional theory (DFT) and Car–Parinello molecular dynamic simulations. The aqueous case is simulated by specific addition of bulk water in our model.

2 Model and computational details

The bare nanowires have been modeled by cutting a hexagonal prism out of a ZnO wurzite structure in such a way that their growth direction is oriented along the c-axis and they exhibit non-polar (101̲0) and (12̲10) facets as shown in Fig. 1. For all systems we considered a tetragonal supercell with a dimension of 30 × 30 × 5.41 ų, containing 48 atoms and a large vacuum region so that no spurious interaction with the nanowire replicas takes place. The lattice parameter c for the bare structure was optimized and kept fixed for every subsequent calculation. We define the molecular coverage on the nanowire θ as the number of AcOH molecules adsorbed per surface Zn–O pair. For the AcOH-covered nanowire in a dry environment, we consider adsorption of the molecules on every available binding site, which corresponds to θ = 1. This amounts to 12 molecules per supercell.

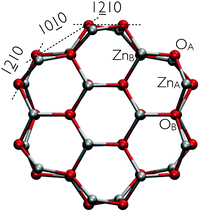Fig. 1 Cross-sectional view of the optimized structure of the bare ZnO nanowire. Zinc (oxygen) atoms are displayed as silver (red) spheres.

The initial molecular geometries correspond to the preferred configurations found in a previous investigation on the adsorption of AcOH on non-polar surfaces.²⁹ It should be noticed that the (101̲0) surface is invariant under a reflection about a perpendicular (12̲10) plane containing the zinc binding sites (Zn_A in Fig. 1). Additionally, as AcOH is an achiral compound, bend molecular configurations with orientations to one or the other direction along the normal to the (12̲10) plane are equivalent. We chose alternate orientations of the molecules in such a way that on a same (101̲0) facet they look in the same direction whereas the orientation is switched in the neighboring (101̲0) facets. 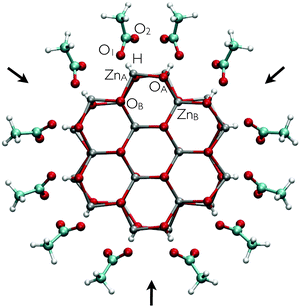This in turn implies that at the (12̲10) facets they are either oriented towards or opposing each other. In this way, every second (12̲10) facet displays a ligand-free region which has been explicitly flagged with black arrows in Fig. 2. We will come back to this point later. It is obviously possible to build up a system with all molecules oriented toward the same direction. However, the chosen model allows us to study two possible scenarios regarding the ligand adsorption while considering a single adduct configuration.

Fig. 2 Cross-sectional view of the optimized structure of the AcOH-modified ZnO nanowire. Zinc, oxygen, hydrogen and carbon atoms are displayed as silver, red, white and cyan spheres, respectively. The black arrows indicate ligand-free regions on the nanowire facets.

For the geometry optimization, DFT calculations were performed as implemented in the Vienna ab initio Simulation Package (VASP) code.^31–34 The Kohn–Sham equations were solved using the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) form for the exchange–correlation functional.^35,36 Plane wave basis sets with a cutoff energy of 300 eV as well as the projector-augmented wave (PAW) method^37,38 have been employed. For the integration in the Brillouin zone, a (1 × 1 × 4) Monkhorst–Pack k-point sampling^39,40 was conducted. During the calculations, all atoms were allowed to move till the interatomic forces were smaller than 10⁻² eV Å⁻¹.

Molecular Dynamic (MD) simulations were performed using Car–Parinello MD as implemented in the CPMD code.⁴¹ We used ab initio ultrasoft-pseudopotentials to describe the atomic potentials.⁴² The plane wave cutoff energy was set to 30 Ryd (300 Ryd) for the electronic wavefunctions (charge density). For all MD simulations the Brillouin zone integration was performed using the Γ-point only. The equations of motion were integrated using a timestep of 5 a.u. and an electron mass of 300 a.u. All systems were heated up to 300 K using a Nose–Hoover thermostat applying a heating figure in which the temperature is held constant at values of 40, 70, 120, and 200 K for 500 integration steps.⁴³ The region between the periodically repeated nanowires was filled with water molecules up to a density of about 1 g cm⁻³ which corresponds to 124 water molecules per supercell. Molecular coverages of θ = 0, 0.5 and 1 were considered.

3 Results

3.1 Geometry and binding energies under dry conditions

Previous results show that AcOH dissociates on ZnO non-polar surfaces as one hydrogen atom migrates from the –COOH group to the surface oxygen site.^28,29 Our results regarding the adsorption on the nanowire support this dissociative regime. The molecule was also found to relax to a bidentate chelating mode in a similar manner as reported for the surface, as seen in Fig. 2. To gain insight into the strength of the adsorbate–substrate interaction and compare it with previous results for the surface, we calculated the absorption energy per ligand. This quantity is defined aswhere E_T is the total energy of the modified nanowire, E_bare is the total energy of the bare nanowire, E_AcOH is the energy of an isolated neutral AcOH molecule in the gas phase and n is the number of molecules absorbed on the nanowire. The obtained adsorption energy of AcOH on the ZnO nanowire is −1.31 eV, which compares well with the adsorption energy of AcOH on the surface which is −1.39 eV.²⁹

The relaxation of nanowire facets upon adsorption of AcOH also resembles that observed for the ZnO surfaces. The surface Zn atoms relax outwards, thus enlarging the bond length of Zn_A–O_A surface pairs. In this case, the bond length goes from 1.90 Å for the bare nanowire to 2.04–2.12 Å for the modified nanostructure, for a relative elongation of up to 12%. This value is slightly greater than the 9% enlargement found for the two-dimensional model. At the same time, the bond lengths between the four-fold coordinated Zn_B and the O_A atoms in the modified nanowire experience a reduction of around 6% with respect to the bare wire. Hydrogen bonds with one of the –COOH oxygens have bond lengths of 1.66 Å. Previous DFT-based tight-binding calculations for the interaction of AcOH with the (101̲0) ZnO surface reported a somewhat larger value of 1.74 Å.²⁸ The C–O bond lengths of the –COOH group vary from 1.31 to 1.27 Å. This is in agreement with the findings for the (101̲0) surface.

3.2 Geometry and adsorption energies in an aqueous environment

Our discussion has so far been limited to the adsorption of AcOH in a dry environment. We now turn to a more realistic model by including bulk water in the AcOH–ZnO system. This model is suitable as a first approximation to investigate the stability of the modified nanowire in a wet environment. The optimized structure for the adsorption in the dry environment was chosen as the initial configuration of the adsorbate. To analyze the influence of the aqueous media on the ligand adsorption, an eight-picoseconds (ps) MD run was performed. To verify if the considered supercell is large enough to sample a bulk water regime, we calculated the radial water density surrounding the nanowire during the MD run. Our results yield the standard water density of 1 g cm⁻³ (data not shown), thus showing that the dimensions of the supercell are indeed appropriate.

A snapshot of the corresponding trajectory at 8 ps is depicted in Fig. 3. In order to describe the dynamics of the adsorbates, the Zn_A–O₁ and Zn_A–O₂ bond lengths, as well as the H–O₁ hydrogen bond length are evaluated over time. The latter is shown in Fig. 4 for every AcOH molecule in the supercell. The employed color code corresponds to that used in the snapshot of the trajectory (Fig. 3) and the hydrogen bond lengths are plotted clockwise starting from the –COOH group with the gray-dyed carbon atom. The curves shown in Fig. 4 can be split into two different groups according to the stability of the corresponding hydrogen bond. The first group comprises the plots in the first two columns (corresponding to adsorbates marked with colors gray, orange, green, black, purple and ochre), which yield very stable hydrogen bonds with an average length ranging approximately from 1.65 Å to 1.75 Å. The hydrogen bond lengths for the second group of adsorbates (third and fourth columns in Fig. 4) exhibit a stronger overall fluctuation. For the red-dyed ligand the fluctuations are especially large; the corresponding hydrogen bond length reaches values greater than 2.5 Å. The large fluctuations for the second group of ligands can be explained by their positions on the nanowire. They adsorb right next to the ligand-free region indicated with black arrows in Fig. 3. Our results indicate that these ligand-free regions allow bulk water to approach the surface. These water molecules then interact with the carboxyl groups of the second group of adsorbates via formation of hydrogen bonds. From the analysis of the hydrogen bond lengths, it is therefore straightforward to identify a first influence of the bulk water on the adsorption of AcOH on the nanowires.

Fig. 3 The snapshot of the molecular dynamics run at 8 ps for the fully-covered ZnO nanowire in aqueous medium. To distinguish between the twelve identical adsorbates, the carbon atom of the carboxylic group is shown in different colors. Zinc, oxygen and hydrogen atoms are displayed as silver, red and white spheres, respectively whereas the carbon atoms of the methyl groups have been represented by cyan spheres. For ease of viewing the bulk water is displayed transparent. The black arrows indicate the sites where bulk water is able to settle in.

Fig. 4 Hydrogen bond lengths between one of the oxygen atoms of the carboxyl group and the hydrogen atom transferred to the surface for the fully-covered ZnO nanowire during the simulation time. The color code corresponds to the one used in Fig. 3.

Similarly to the dry case, under wet conditions the –COOH group adsorbs in a bidentate mode as inferred from the analysis of the Zn–O bond length depicted in Fig. 5. A common feature among the twelve plots is the formation of a bond between the surface Zn atom and one oxygen of the carboxyl group with an average bond length of about 2 Å. The distance between the second carboxyl oxygen and the Zn_A site shows, however, strong fluctuations ranging from 2.2 to 3.2 Å. In general, the oxygen atom forming the stable Zn–O bond is not fixed during the MD run. In this sense the roles of the two oxygens are interchangeable. Thus, we can conclude that the AcOH–ZnO interaction is dominated by a bond between one of the carboxyl oxygens and the Zn site with a bond length similar to that for Zn–O bonds in bulk ZnO. Analysis of the trajectory suggests that this tendency for a monodentate adsorption in the hydrated system is not mainly because of the interaction with water but rather due to the thermal fluctuations. Our results indicate, therefore, that the presence of bulk water appears to play only a minor role in the adsorption mode of the ligands for the fully covered ZnO nanowire.

Fig. 5 Bond lengths between the oxygen atoms of the carboxyl group, O₁ and O₂, and the surface zinc atoms, Zn_A, for the fully-covered ZnO nanowire during the simulation time. The color code corresponds to the one used in Fig. 3 and the atom notation to the one employed in Fig. 2.

To inspect if these results depend on the ligand coverage, we considered a second model where the nanowire is capped with a one-half monolayer of AcOH (θ = 0.5) in a bulk water environment. There are, doubtlessly, numerous ways to model the semi-covered ZnO nanowire, but as just the interaction between neighboring ligands is of interest here, we chose a configuration in which every second ligand was removed from the surface. The evaluation of the trajectory regarding the O₁–H, Zn_A–O₁ and Zn_A–O₂ bonds is shown in Fig. 6. The results for the hydrogen bond length exhibit strong fluctuations, especially for the molecules marked with the gray and yellow-dyed carbon, where the O₁–H distances reach values greater than 3 Å. Analysis of the corresponding trajectory shows that the bulk water is able to settle in between every neighboring AcOH molecule due to the newly available adsorption sites on the surface. These water molecules are able to form hydrogen bonds with the oxygen atoms of the carboxyl group. This interaction competes with the formation of hydrogen bonds between the molecule and the surface H atom. This finding is evinced from the analysis of the Zn–O bond lengths over time. Only the carboxyl oxygens of the pink- and green-dyed molecules alternately bind to the Zn_A site. For all other molecules the surface Zn atoms remain attached to the same molecular oxygen during the simulation. These results indicate that the adsorption of the ligands occurs in a monodentate mode. This reveals that the presence of water leads to an important stabilization of the anchor groups through formation of hydrogen bonds.

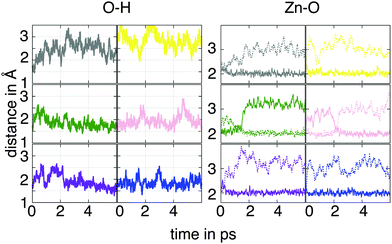Fig. 6 O₁–H hydrogen bond lengths (left) and Zn_A–O₁ and Zn_A–O₂ bond lengths (right) for the half-covered ZnO nanowire during the simulation time. The color code corresponds to the one used in Fig. 3 and the atom notation to the one employed in Fig. 2. Only the data for the adsorbed molecules are shown.

We finally consider a system in which all AcOH molecules are detached from the nanowire facets at the beginning of the simulation. This case corresponds to θ = 0. The potential energy versus time for the three investigated coverages is shown in Fig. 7. The energy of the system with θ = 0 was set to the zero of energy. The energy plots corresponding to θ = 1 and 0.5 show a similar trend and exhibit some overlap over nearly all time regimes. For θ = 0 the energy converges to a higher value during the MD run. To determine the adsorption energies for the considered systems we evaluated the energies obtained during the MD simulations in an approach similar to the one employed in a previous work on the adsorption of small molecules on TiO₂ surfaces.⁴³ A Gaussian curve was fitted to the energy distribution obtained in the last picosecond of the simulation. The binding energies are then estimated as the difference between the Gaussian maxima of the investigated system and the system with θ = 0. This leads to a total binding energy of −8.84 eV for θ = 1, which corresponds to an adsorption energy per ligand of −0.74 eV. For θ = 0.5 we find a binding energy of 6.84 eV and an adsorption energy per adsorbate of −1.14 eV. Thus, for both coverages the adsorption energies are smaller than for the system in the dry environment. Our results indicate that the fully-covered ZnO nanowire is the most stable system. This suggests that the modified nanostructure is stable against adsorption of liquid water under ligand-rich conditions. This is in agreement with recent experiments, which have demonstrated the successful functionalization of ZnO nanotips by immersing them in solutions of AcOH diluted to 2 mM per liter.⁵ However, it should be borne in mind that an energy barrier needs to be overcome to replace molecules from the first water layer by AcOH. Investigation on energy barriers is out of the scope of this paper.

Fig. 7 Energy distribution over the last picosecond of the simulation time obtained for the ZnO nanowire with the three considered coverages: full coverage (θ = 1), half-coverage (θ = 0.5) and total ligand desorption (θ = 0). The energy of the ligand-free nanowire was set to the zero of energy. The inset shows the course of the energy over the entire simulation time.

4 Conclusions

We have investigated the adsorption of acetic acid on the facets of ZnO nanowires under dry conditions and in aqueous medium. For the former case, the geometry optimization of the adduct at 0 K indicated a strong bidentate adsorption of the ligand via two asymmetric O–Zn bonds. MD simulations of the system at 300 K and under wet conditions show small fluctuations of the bond length between one oxygen atom of the carboxyl group and the surface Zn atom around its optimized value at 0 K. In contrast, the distance from the other carboxylic oxygen to the Zn binding site was found to fluctuate considerably around larger values, thus indicating that this second attachment is weaker. This tendency for a monodenticity of the anchor groups is better seen for a system with half-covered nanowires. In this case, water occupies the now available binding sites and interacts with the adsorbed AcOH via H bonds, thus weakening one of the O–Zn bonds. The absolute value of the adsorption energy per adsorbate decreases considerably for the fully-covered nanowire under wet conditions compared to the dry case. Our results suggest that ZnO nanowires modified with acetic acid are still stable in aqueous solution at room temperature, as we have previously suggested in a more simplified model. Finally, we believe that our results motivate the investigation of a migration barrier for the substitution of adsorbed water by AcOH which could help understand better the adsorption of functional groups and organic molecules on oxide surfaces in a wet environment.

Acknowledgements

This work was supported by the Deutsche Forschungsgemeinschaft under the program FOR1616. The Northern Germany supercomputing facility (HLRN) is acknowledged for computational resources.

References

1. G. K. Mor, K. Shankar, M. Paulose, O. Varghese and C. Grimes, Nano Lett., 2006, 6, 215.
2. E. Galoppini, J. Rochford, H. Chen, G. Saraf, Y. Lu, A. Hagfeldt and G. Boschloo, J. Phys. Chem. B, 2006, 110, 16159–16161.
3. K. Zhu, N. R. Neale, A. Miedaner and A. J. Frank, Nano Lett., 2007, 7, 69.
4. G. Benkö, J. Kallioinen, J. E. I. Korppi-Tommola, A. P. Yartsev and V. Sundström, J. Am. Chem. Soc, 2002, 489.
5. O. Taratula, E. Galoppini, D. Wang, D. Chu, Z. Zhang, H. Chen, G. Saraf and Y. Lu, J. Phys. Chem. B, 2006, 110, 6506.
6. S. Blumstegel, H. Glowatzki, S. Sadofev, N. Koch, S. Kowarik, J. P. Rabe and F. Hanneberger, Phys. Chem. Chem. Phys., 2010, 12, 11642.
7. S. Rani, P. K. Shishodia and R. M. Mehra, J. Renewable Sustainable Energy, 2010, 2, 043103.
8. K. Keis, J. Lindgren, S.-E. Lindquist and A. Hagfeldt, Langmuir, 2000, 16, 4688–4694.
9. K. Keis, E. Magnusson, H. Lindström, S.-E. Lindquist and A. Hagfeldt, Sol. Energy Mater. Sol. Cells, 2002, 73, 51–58.
10. T. Dentani, K. ichi Nagasaka, K. Funabiki, J.-Y. Jin, T. Yoshida, H. Minoura and M. Matsui, Dyes Pigm., 2008, 77, 59–69.
11. H. Gao, G. Fang, M. Wang, N. Liu, L. Yuan, C. Li, L. Ai, J. Zhang, C. Zhou, S. Wu and X. Zhao, Mater. Res. Bull., 2008, 43, 3345–3351.
12. I. Gonzalez-Valls and M. Lira-Cantu, Energy Environ. Sci., 2009, 2, 19–34.
13. E. Guillén, C. Fernández-Lorenzo, R. Alcántara, J. Martín-Calleja and J. Anta, Sol. Energy Mater. Sol. Cells, 2009, 93, 1846–1852.
14. W.-H. Chiu, C.-H. Lee, H.-M. Cheng, H.-F. Lin, S.-C. Liao, J.-M. Wu and W.-F. Hsieh, Energy Environ. Sci., 2009, 2, 694–698.
15. N. M. Gómez-Ortíz, J. Idígoras, E. Guillén, A. Hernández, A. Sastre-Santos, F. Fernández-Lázaro, J. Anta and G. Oskam, J. Photochem. Photobiol., A, 2013, 264, 26–33.
16. M. Saito and S. Fujuhara, Energy Environ. Sci., 2008, 1, 280–283.
17. N. Koide, R. Yamanaka and H. Katayama, MRS Online Proc. Libr., 2009, 1211, R12–R22.
18. S. Kuehn, S. Friede, S. Sadofev, S. Blumstengel, F. Henneberger and T. Elsaesser, Appl. Phys. Lett., 2013, 103, 191909.
19. Y. Cao, E. Galoppini, P. I. Reyes and Y. Lu, Langmuir, 2013, 29, 7768–7775.
20. K. Yao, L. Chen, Y. Chen, F. Li and P. Wang, J. Phys. Chem. C, 2012, 116, 3486–3491.
21. S. K. Hau, Y.-J. Cheng, H.-L. Yip, Y. Zhang, H. Ma and A. K.-Y. Jen, ACS Appl. Mater. Interfaces, 2010, 2, 1892–1902.
22. X. Tian, J. Xu and W. Xie, J. Phys. Chem. C, 2010, 114, 3973–3980.
23. A. Lenz, L. Selegård, F. Soderlind, A. Larsson, P. O. Holtz, K. Uvdal, L. Ojamae and P.-O. Kall, J. Phys. Chem. C, 2009, 113, 17332–17341.
24. O. Taratula, E. Galoppini, R. Mendelsohn, P. I. Reyes, Z. Zhang, Z. Duan, J. Zhong and Y. Lu, Langmuir, 2009, 25, 2107–2113.
25. A. Gupta, B. C. Kim, E. Edwards, C. Brantley and P. Ruffin, Adv. Mater. Res., 2012, 567, 228–231.
26. G. J. Ehlert and H. A. Sodano, ACS Appl. Mater. Interfaces, 2009, 1, 1827–1833.
27. J. Chen, R. E. Ruther, Y. Tan, L. M. Bishop and R. J. Hamers, Langmuir, 2012, 28, 10437–10445.
28. N. H. Moreira, A. L. da Rosa and T. Frauenheim, Appl. Phys. Lett., 2009, 94, 193109.
29. N. H. Moreira, A. Dominguez, T. Frauenheim and A. L. da Rosa, Phys. Chem. Chem. Phys., 2012, 14, 15445–15451.
30. A. Dominguez, N. H. Moreira, G. Dolgonos, A. L. Rosa and T. Frauenheim, J. Phys. Chem. C, 2011, 115, 6491–6495.
31. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
32. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
33. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
34. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
35. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
36. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
37. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
38. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
39. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
40. J. D. Pack and H. J. Monkhorst, Phys. Rev. B: Condens. Matter Mater. Phys., 1977, 16, 1748–1749.
41. CPMD, http://www.cpmd.org/, Copyright IBM Corp 1990–2008, Copyright MPI für Festkörperforschung, Stuttgart 1997–2001.
42. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
43. S. Koppen, O. Bronkalla and W. Langel, J. Phys. Chem. C, 2008, 112, 13600–13606.

---

Footnote

† These authors contributed equally to this work.

---