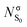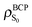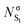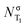Open Access Article
Open Access ArticleBeyond the molecular orbital conception of electronically excited states through the quantum theory of atoms in molecules†
David
Ferro-Costas
a,
Ángel Martín
Pendás
b,
Leticia
González
c and
Ricardo A.
Mosquera
*a
aDepartamento de Química Física, Universidade de Vigo, Facultade de Química, Lagoas-Marcosende s/n, 36310 Vigo, Spain. E-mail: mosquera@uvigo.es
bDepartamento de Química Física y Analítica, Facultad de Química, Universidad de Oviedo, 33006-Oviedo, Spain
cInstitute of Theoretical Chemistry, University of Vienna, Währinger Str. 17, 1090 Vienna, Austria
First published on 17th March 2014
Abstract
We show that the use of the quantum theory of atoms in molecules (QTAIM) in electronically excited states allows expanding the knowledge that the molecular orbital (MO) framework provides about electronic rearrangements. Despite that historical prejudice seemed to preclude the use of QTAIM beyond the electronic ground state, this paper evidences that QTAIM is versatile enough to deal with excited states. As an example, the paradigmatic n → π* electronic transition of formaldehyde is analyzed. Using QTAIM, an energy partition of excited state energies into atomic and diatomic energies is carried out for the first time. This partition shows that upon electronic excitation the atoms of the CO bond experience a stabilization in their net energies, accompanied by a destabilization in their interaction, a fact which is in accordance with the idea of populating an antibonding π* MO. The associated C–O bond elongation in the nπ* state does not involve a change in the π atomic populations – as one would expect from a π* orbital – but in the σ ones. Moreover, it is also found that the nπ* state is characterized by a weaker C–O interaction energy in comparison to that in the electronic ground state. In order to strengthen this interaction, the electron–electron repulsion between C and O is reduced via a symmetry-breaking of the electron density, causing the C pyramidalization. A topological analysis based on the Laplacian of the electron density and on the electron localization function (ELF) reveals that the n → π* transition can be visualized as a rotation of 90° of the oxygen lone pairs.
1 Introduction
Understanding the nature of electronically excited states is fundamental to disciplines ranging from basic synthetic organic and inorganic chemistry to nanotechnology and biology. Photoinduced processes are basic to life itself through photosynthesis, and it has become increasingly clear that many biologically important molecules have been subjected to strong natural selection favoring their photostability.1 A theoretical approach to these problems has traditionally been hindered due to difficulties in solving the time-independent Schrödinger equation for states different from the ground state. However, computational advances in the last decade have started reverting the situation and, with the introduction of multireference methods and the developments in linear scaling techniques,2ab initio predictability in excited states for moderately sized systems can be reached.3Conspicuously, despite the increasing wide black-box availability of computational methods to aid practicing chemists, most experiments are designed and/or interpreted in terms of a set of rules that were introduced to understand chemical bonding in electronic ground states. Some of these rules are based on the one-electron approximation inherent to one-determinant descriptions as, for example, the use of molecular orbital (MO) arguments to understand reactivity pathways. Unfortunately, this approximation is sometimes poor, especially in the case of electronic excited states. It is for this reason that a working framework to understand chemical bonding in excited states still needs to be appropriately developed.
Any chemical bonding paradigm for excited states must be able to tackle multireference systems and, as a consequence, it cannot rely on a fixed set of one-electron functions (orbitals). Mainstream ground state chemical bonding theory is still dominated by MO thinking (an intrinsically one-electron scheme). As such, more than often, it offers results strongly dependent on the method used to obtain the approximated wave function because MOs are not invariant under orbital transformations. One textbook example is the description of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond in ethylene. While the Pipek–Mezey localization method4 provides a representation based on one σ MO and one π orbital, the Boys localization method5,6 describes the bond by two equivalent banana bond orbitals. Such a situation could be, in a certain way, confusing for some practicing chemists. A possible way out to this ambivalence is to rewrite chemical bonding theory in terms of orbital invariant quantities. These objects can be obtained in terms of reduced density matrices (RDMs), either in position or momentum space. As the chemist's language is developed in the physical space, most of the implementations proposed so far are based on r dependent RDMs, and these methods are collectively known as real space theories of chemical bonding.
C double bond in ethylene. While the Pipek–Mezey localization method4 provides a representation based on one σ MO and one π orbital, the Boys localization method5,6 describes the bond by two equivalent banana bond orbitals. Such a situation could be, in a certain way, confusing for some practicing chemists. A possible way out to this ambivalence is to rewrite chemical bonding theory in terms of orbital invariant quantities. These objects can be obtained in terms of reduced density matrices (RDMs), either in position or momentum space. As the chemist's language is developed in the physical space, most of the implementations proposed so far are based on r dependent RDMs, and these methods are collectively known as real space theories of chemical bonding.
RDMs depend on spin-spatial coordinates and lack atomic information intrinsic to orbitals. Fortunately, Richard F. W. Bader paved the road by showing how atomic, and in general, chemically meaningful regions may be extracted from the RDMs7,8 by examining the topology induced by the electron density, ρ. This, so-called Quantum Theory of Atoms in Molecules (QTAIM), has provided deep insights into the nature of the chemical bond for over thirty years, and its methods have been widely generalized to develop what is called Quantum Chemical Topology (QCT).9 QTAIM thinking satisfies all of the requirements previously commented: it is invariant under orbital transformations, all of its descriptors are equally defined and obtained for one determinant or correlated wave functions (thus providing a smooth procedure to understand how correlation affects bonding), and it includes an exact energy partitioning into atomic and interatomic contributions.10
Traditionally, QTAIM is thought of as a theory of ground state molecules. This historical prejudice roots to the difficulties of the topological procedure to properly define atoms in simple excited states, like the 2s H atom, for which each attraction basin of ρ, i.e. each of its local maxima, defines a quantum atom in the theory. A similar situation is found in the ground state of some molecules, e.g. in Li2, which displays a non-nuclear maximum of the electron density at the internuclear midpoint.11 However, the controversy on ground state non-nuclear maxima is now over, their existence related to important concepts like F-centers in ionic solids.12 Despite that a large class of chemically important molecules do not show excited states with non-nuclear attractors, the use of QTAIM to aid understanding of excited state processes is scarce.13–17
To our knowledge, this paper is the first in performing an energetic partition scheme based on QTAIM regions that allows us to understand physically the evolution of the charge density and geometry of a molecule upon excitation. This type of analysis can be extremely helpful to explain, in an orbital invariant language, photophysical and photochemical phenomena. As a practical example, a paradigmatic process in photochemistry, the n → π* electronic transition, has been selected. A simple but very well studied molecule, formaldehyde, is chosen to illustrate how QTAIM can explain the molecular changes that take place after the electronic excitation. Three electronic states will be analyzed: the ground state S0 and the first singlet S1 and triplet T1 states. In the traditional MO language, S1 and T1 are understood as one-electron excitations from a non-bonding MO centered at the oxygen atom (the n lone pair) to the C–O antibonding π* orbital. According to textbook MO machinery, populating the π* MO weakens the C–O double bond and this manifests as a lengthening of the bond. Concurrently, the hybridization of the C atom changes from sp2-like to sp3 leading to a C pyramidalization in any of the two S1 and T1 excited states.18 In this work we shall show the ability of the QTAIM to cope with excited states and we will carefully monitor the QTAIM interpretation against the traditional MO explanation, to correlate both views as much as possible.
2 Methodology
2.1 Basic descriptors of the quantum theory of atoms in molecules
Bader and coworkers showed that the topology induced by the electron density, ρ(r), comes from generalizing the quantum mechanics to subsystems in![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3. These subsystems (Ω) are associated with the atoms in the molecule and they are referred as “atomic basins”. In the following, the QTAIM descriptors employed in this paper are briefly revised. Further information can be found in ref. 7, 8 and 19.
3. These subsystems (Ω) are associated with the atoms in the molecule and they are referred as “atomic basins”. In the following, the QTAIM descriptors employed in this paper are briefly revised. Further information can be found in ref. 7, 8 and 19.
Some elements of chemical structure can be identified with critical points of ρ(r). For example, critical points exhibiting three negative curvatures are called nuclear critical points (NCPs), as they are normally placed at, or close to, the position of the nuclei. Critical points with two negative curvatures (and one positive) are called bond critical points (BCPs). The line of locally maximum density linking two NCPs define what is known as the bond path and its presence implies that the corresponding atoms are bonded to one another. The interaction between a given pair of atoms bonded is characterized according to the properties of the electron and energy densities at the BCP.
Two interesting descriptors are defined at the BCP. One is the electron density at that point, ρBCP, and it is related to the strength of the bonding. The second is the ellipticity, ε, which measures the extent to which density is preferentially accumulated in a given plane containing the bond path, and it is defined as follows
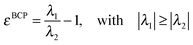 | (1) |
The average number of electrons associated with the atomic basin Ω, N(Ω), can be obtained by
 | (2) |
| q(Ω) = Z − N(Ω) | (3) |
 | (4) |
The term λΩ is associated exclusively to Ω and is called localization index. The terms related to the pair of basins, δΩ,Ω′, are called delocalization indices and measure the number of electrons shared between Ω and Ω′.
2.2 Energy partition
Within the Born–Oppenheimer approximation, the expected value for the molecular electronic energy, E, is given by:| E = 〈Ψ|Ĥ|Ψ〉 = T + Vne + Vee + Vnn | (5) |
All these quantities can be written in terms of the electron density of the system, ρ(r):
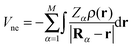 | (6) |
 | (7) |
 | (8) |
 | (9) |
| Vee = Vcoul + Vxc | (10) |
As QTAIM provides a partition of the three-dimensional space into atomic basins, the electron density is also susceptible of partitioning into atomic contributions:
 | (11) |
 | (12) |
Likewise, the RDMs can be also partitioned as
 | (13) |
 | (14) |
 | (15) |
Similarly, through eqn (11), Vne is given by
 | (16) |
Finally, the electron–electron repulsion results in:
 | (17) |
 | (18) |
 | (19) |
 | (20) |
 | (21) |
Once the partition of all the energetic terms associated with the operators comprising the Hamiltonian of the system is done, different terms can be grouped. The collection of all the terms that takes place exclusively in one atomic basin results in the definition of the net energy for that atom, Enet,
| Enet(Ω) = T(Ω) + Vne(ω,Ω) + Vee(Ω,Ω) | (22) |
| Vint(Ω,Ω′) = Vnn(ω,ω′) + Vne(ω,Ω′) + Vne(ω′,Ω) + Vee(Ω,Ω′) | (23) |
 | (24) |
According to this equation, a molecular system can be analysed in terms of its constituent elements (atoms or even groups of them) and their interactions. This point of view resembles the traditional conception of chemistry before the introduction of quantum mechanics and it does not invoke orbital definitions.
2.3 Computational details
All the geometries have been optimized using the Complete Active Space Self Consistent Field (CASSCF) procedure20 with an active space of 12 electrons distributed in 10 MOs. The active space is depicted in Fig. 1 and comprises three σ, σ* pairs, the πCO, πCO* orbital pair, and two lone pairs of electrons of the oxygen atom. For computational sake, the IQA scheme10 has been performed using the wave function corresponding to a more modest CASSCF(4,3) method (restricted to the most relevant lone pair of O and the π, π* pair of MOs – see Fig. 1). The energies of each state are computed state-specific. An analysis of the electronic wavefunctions obtained with the (12,10) and (4,3) active spaces reveals that the main configurations contributing to the state are the same. In all cases, the basis set employed is the cc-pVTZ.21 All the geometries and energies were obtained using the MOLCAS 7.8 program.22The Molden2AIM23 software has been used for the generation of wfn files, needed to carry out the QTAIM analysis of the electron density. This analysis has been done using the AIMPAC package of programs,24 as well as using the PROMOLDEN code,10 developed by the Quantum Chemistry group of Oviedo University. Additionally, the MULTIWFN software25 was used to obtain the Laplacian of the ρ function (∇2ρ) and the Electron Localization Function (ELF).26
3 Results
3.1 Geometries
In order to study the evolution of the S1 and T1 excited states step by step, a total of five geometries, associated with critical points in different potential energy surfaces (PES), have been considered. Fig. 2 shows the equilibrium geometry in the electronic ground state S0 (denoted as min S0) and the optimized S1 (min S1) and T1 (min T1) minima. As it can be seen, the optimized S1 and T1 minima show pyramidalized C atoms and C–O bonds elongated with respect to the ground state by ca. 0.14 Å. To separate the effect of elongation and pyramidalization, constrained planar optimizations have also been performed in each electronic excited state (planar S1 and planar T1). The latter C2v geometries correspond to structures with an imaginary vibration frequency associated with the loss of planarity. The relative energy of each critical point in each PES is collected in Table 1. As expected the energy of T1 is smaller than that of S1 for each geometry. | ||
| Fig. 2 Equilibrium geometries of formaldehyde in the S0, S1 and T1 electronic states, as well as planar structures in the S1 and T1 excited states. Bond distances in Å and the H–C–H angle in degrees. | ||
3.2 QTAIM analysis in the excited state
To understand which processes are taking place upon excitation, it is illustrative to analyse the charge density separately in (a) the vertical electronic excitation, (b) the lengthening of the C–O and (c) C pyramidalization steps.Fig. 4a shows the reorganization of the atomic electron populations in the vertical excitation. As expected, the most important change takes place in the C–O moiety, where the oxygen transfers 0.293 electrons to the carbon basin.
The electron density can be also expanded in terms of the natural MO χi:
 | (25) |
 | (26) |
 | (27) |
It should be emphasized that Nσ and Nπ come from the MO framework and thus they are not physical observables. However, their analysis may still be useful in chemical bonding theory. Moreover, it is interesting to analyze them if we want to find the parallelism between QTAIM results and MO concepts. The σ–π partitioning of the atomic population in the S0 state is shown in Table 2, together with their variations, ΔN, upon vertical excitation. Overall, one “σ electron” is converted into one “π electron” in the electronic excitation. While O loses 0.759 au from its σ distribution, both C and O increase their π electronic population to 0.484 and 0.466, respectively (i.e. larger at the C, as expected from the antibonding character of the MO). This means that around 60% of the oxygen electronic population involved in the electronic transition still belongs to its basin. Similarly, it can be seen that around 40% of the electronic population gained by the C comes from the H atoms, indicating that the transition is not completely described by an nO → πCO* transition.
Also interesting is to follow the change in the electron density and the ellipticity at the bond critical points7 (Table 3). The nO → π* electronic transition produces an increase of the electron density in the C basin, implying a larger electronic repulsion to its environment. As a consequence, the electron density at the BCP of different bonds in which the carbon is involved decreases. Important to note is that although ρBCP decreases in the three bonds, only the C–O bond distance increases after excitation (see Fig. 2), clearly illustrating that the ΔρBCP between two electronic states is not enough to predict the geometric reorganization taking place upon excitation. In passing we note that correlations between ρBCP and the bond length should only be done within the same kind of chemical bonds and an electronic excitation does not assure that bonds in different electronic states share the same chemical nature.
The ellipticity increases in both C–O and C–H bonds, in agreement with the fact that the electron density is accumulated at both sides of the molecular plane over the C atom, implying that the electron density distribution along the bonds is less cylindrical. This is also a clear example where the association of the ellipticity (or, in general, properties emerging from the electron density) with the bond order (or concepts related to the orbital conception) can be dangerous.
The results of the energy partition following the IQA scheme are collected in Table 4. The first column refers to the change in energies for the vertical excitation. Accordingly, in the S1 excited state the net energies of C and O decrease whereas the interaction between them, ΔVint(C,O), becomes very much repulsive (1131 kJ mol−1). As O is negatively charged in the ground state (charge qO = −1.118 au), the withdrawal of electron density from its basins upon excitation stabilizes the atom through the reduction of the electron–electron repulsion in its basin. At the same time, the C in S0 is positively charged (qC = +1.150 au) and the increment of its atomic electron population increases its nucleus–electron attraction.‡ However, this redistribution of the electron density also intensifies the electron–electron repulsion between both basins (C–O), destabilizing the interaction between them. It can be also of interest to sum up all the inter-atomic interaction energies depending on ρ(r) in what we call a classical potential, Vclas, defined as Vint − Vxc (recall eqn (21) and (23)). The variation of Vclas for the CO pair (998.9 kJ mol−1) is pretty close to the one obtained by employing a point-charge model (around 877 kJ mol−1). The same agreement is obtained for the C–H bond (35.1 kJ mol−1vs. ca. 65 kJ mol−1). Moreover, a ΔVxc(C,O) of 132.5 kJ mol−1 after vertical excitation (see Table S1 in the ESI†) indicates that an important part of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond breaks. In summary, it can be seen that the stabilization of the individual atoms comprised in the bond and destabilization of the interaction, making the bond strength weaker, is in line with the idea of populating an antibonding MO.
O double bond breaks. In summary, it can be seen that the stabilization of the individual atoms comprised in the bond and destabilization of the interaction, making the bond strength weaker, is in line with the idea of populating an antibonding MO.
Using the CASSCF(4,3) wave function employed in the IQA scheme, localization and delocalization indices7 can be obtained (Table 5).§ In the ground state, the most important differences, comparing the expected values of the ideal Lewis structure for the formaldehyde, are found in C and O atoms (λC, λO, and δC,O). These differences can be basically justified considering the other resonance form of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond (C+–O−). Upon excitation, the localization indices (λ) follow the total basin electron populations (cf.Table 2). Since oxygen suffers a loss of electron density, it becomes less prone to share it, decreasing δC,O. This behavior is again the one expected according to the orbital interpretation because the π* MO should entail a reduction in the bond order. Indeed, δC,O = 1.098 au for S1 is close to the expected value for a single bond. Therefore, the evolution of λ and δ values could be taken as an indication of the partial heterolytic cleavage of the π bond upon vertical electronic excitation. As shown in Table 5, the electrons delocalized in the bond now become localized in one of the two atoms (C).
O bond (C+–O−). Upon excitation, the localization indices (λ) follow the total basin electron populations (cf.Table 2). Since oxygen suffers a loss of electron density, it becomes less prone to share it, decreasing δC,O. This behavior is again the one expected according to the orbital interpretation because the π* MO should entail a reduction in the bond order. Indeed, δC,O = 1.098 au for S1 is close to the expected value for a single bond. Therefore, the evolution of λ and δ values could be taken as an indication of the partial heterolytic cleavage of the π bond upon vertical electronic excitation. As shown in Table 5, the electrons delocalized in the bond now become localized in one of the two atoms (C).
| λ Ω & δΩ,Ω′ | C | O | H1 | H2 | |
|---|---|---|---|---|---|
| S0 Lewis | C | 4.000 | |||
| O | 2.000 | 7.000 | |||
| H1 | 1.000 | 0.000 | 0.500 | ||
| H2 | 1.000 | 0.000 | 0.000 | 0.500 | |
| S0 at min S0 | C | 3.305 | |||
| O | 1.297 | 8.389 | |||
| H1 | 0.908 | 0.112 | 0.458 | ||
| H2 | 0.908 | 0.112 | 0.051 | 0.458 | |
| S0 → S1 at min S0 | C | 0.559 | |||
| O | −0.199 | −0.222 | |||
| H1 | 0.022 | 0.007 | −0.088 | ||
| H2 | 0.022 | 0.007 | −0.019 | −0.088 | |
| min S0 → planar S1 in the S1 state | C | 0.147 | |||
| O | −0.103 | −0.033 | |||
| H1 | 0.029 | −0.036 | 0.001 | ||
| H2 | 0.029 | −0.036 | 0.000 | 0.001 | |
| planar S1 → min S1 in the S1 state | C | −0.064 | |||
| O | −0.016 | 0.006 | |||
| H1 | −0.006 | 0.010 | 0.032 | ||
| H2 | −0.006 | 0.010 | 0.002 | 0.032 | |
As it has been previously reported,28 a change in δΩ,Ω′ accompanying vertical excitation may be used, in general, to predict the evolution of the corresponding bond length. Thus, δC,O decreases (−0.199 au) and δC,H increases (0.022 au) upon electronic excitation, facts which can be directly related to a stretch and a shrink of the C–O and C–H bonds, respectively (Fig. 2).
The atomic electron population reorganizations that occur in the C–O elongation process are shown in Fig. 4b. The oxygen transfers the electron density to the C basin (as expected when the C–O bond is breaking, since at an infinite C–O distance O should be neutral). A detailed analysis of the σ and π populations reveals that the nature of the electronic reorganization is practically σ (Table 6). Delocalization indices (Table 5) indicate that, in this process, the C–O bond order is reduced to a value of 0.995 au. Thus, elongation breaks the double bond, homolytically in the π distribution, as no significant changes are observed in π populations, and partially heterolytically in the σ one.
During the C–O bond elongation process, important changes in the values of ρBCP and εBCP are not observed, with the exception of the electron density in the C–O bond, which obviously decreases as a consequence of the C–O bond cleavage (Table 3).
In the IQA scheme (Table 4) the same trends found in the excitation process are observed: stabilization of C and O net energies and destabilization in their interaction energies. This is again in agreement with the fact that the antibonding character of the π* MO is responsible for the elongation. However, our analysis indicates that the lengthening of the C–O bond is not accompanied by a transfer of the π electron density, but a σ one.
The IQA energy partition (Table 4) for pyramidalization does not show any remarkable stabilization. The most important term arises from the C–O interaction, which behaves oppositely to the excitation and C–O bond elongation processes. This stabilization, however, is in line with a deformation of the C electron density to reach a sp3-like hybridisation that occurs to make the bond stronger. In terms of IQA energies this is reflected as a destabilization in Enet and a stabilization in Vint.
In order to understand why the C pyramidalises, it is useful to look at the terms that define Vint (recall eqn (17) and (23)) which are collected in Table S3 of the ESI.† As it can be seen, the origin of the C–O stabilization is due to the reduction in the electron–electron repulsion between both atomic basins. Thus, the driving force of the pyramidalization seems to be the reduction of the initial electron–electron repulsion introduced by the vertical excitation (Table S1, ESI†). This repulsion has its origin (see above) from the π contribution of the electron density (see Fig. 3).
For the sake of simplicity, let us consider the ideal spherical out-of-plane π electron densities shown in Fig. 5. Taking into consideration only the large interatomic interactions (that is, interactions between spheres in the same side of the plane) depicted as double red arrows, we find that: (i) the ρ with π-symmetry in the planar conformation (II) gives rise to Vπee ∝ 2nm between C and O bonds (being n and m the electronic charge of the spheres); (ii) after distortion of the π distribution, upon transferring certain a and b amounts of electron density (with a,b ≥ 0) across the plane (as indicated in the imaginary state III), repulsion decreases, since Vπee ∝ 2(nm − ab);¶ and (iii) due to the distortion, the local geometric environment of the atoms is modified, causing the pyramidalization of the atom (IV). In plain English, a symmetry-breaking in the electron density reduces the electron–electron repulsion.
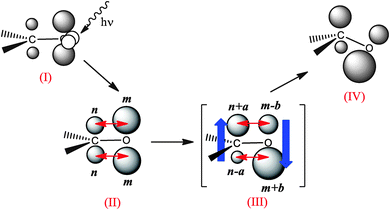 | ||
| Fig. 5 Scheme of the pyramidalization of the carbonyl carbon. This process takes place in order to reduce the repulsion between the out-of-plane electron densities at C and O. | ||
In addition, Vclas and Vxc values for the C–O pair (−71 kJ mol−1 and 8.8 kJ mol−1, respectively) indicate that this process is governed by classical energy terms.
3.3 Comparison between S1 and T1
In the previous section, an analysis of the changes undergone by formaldehyde after excitation from S0 to S1 has been done. A similar study can be done for the T1 state, at the planar T1 and min T1 geometries, and the results obtained are very similar (Table S4, ESI†).In Fig. 6, the Δρ(r) function between the T1 and S1 states is shown at planar S1 geometry. The triplet state is characterized by a larger population at the C basin, which has mainly π character (Table 7). This means that the π population of C and O basins are more “alike” in the triplet state than in the singlet (0.964 and 1.967 au vs. 1.006 and 1.920 au, for C and O basins, Table 7). According to the mechanism described in Fig. 5, larger repulsions between C and O are expected in T1 and the pyramidalization in the triplet state should be slightly larger. Indeed, the HHOC dihedral angle for min S1 is 22.8 degrees while it is 26.9 degrees for min T1.
 | ||
| Fig. 6 ρ T1 − ρS1 at the planar S1 geometry. Isosurfaces of ±0.002 and ±0.0007 au and isolines of ±0.0001, ±0.0002, ±0.0004, ±0.0008, and ±0.001 au are shown (positive in green and negative in red.) | ||
Differences in IQA energetic terms (at planar S1 geometry) are all smaller than 5.0 kJ mol−1 in absolute value (Table S5, ESI†), with the exception of the Enet(C), whose change is −18.1 kJ mol−1. This is due to the increase in the nucleus–electron attraction in the C basin.
3.4 Laplacian of the electron density in the excited states
In QTAIM, the Laplacian of the electron density, ∇2ρ(r), is typically used to recover the main features of the Lewis and Valence-Shell Electron-Pair Repulsion (VSEPR) models.29 Similarly, the electron localization function (ELF)26 is known for its ability to analyze the distribution of electron pairs in the molecule. However, the usual formulation of the ELF is only well defined for monodeterminatal wave functions, while ∇2ρ(r) can be obtained at any level of theory.Isosurfaces of the Laplacian of the electron density of S0 at min S0 and of S1 at min S0 and min S1 (Fig. 7) show two interesting facts. First, upon vertical electronic excitation, the ∇2ρ < 0 region typically associated with the O lone pairs rotates 90 degrees around the C–O bond. And second, during the pyramidalization, a ∇2ρ < 0 region (not associated with any bond) appears in the surroundings of the C atom. The isosurfaces of T1 at min S0 and min T1 are identical to those of S1 and therefore not shown.
In order to visualize the ELF not only in the S0 state but also in the excited state of formaldehyde, we analyzed the T1 state, which can be described with one Slater determinant in an unrestricted Hartree–Fock (UHF) formulation. This is in this case justified because the S1 and T1 states exhibit similar properties and thus, the ELF analysis may be extended “mutatis mutandis” to describe also the S1 state. Interestingly, the two facts observed with ∇2ρ(r) are also reproduced by the topology of the ELF,30 as observed in Fig. 8.
 | ||
| Fig. 8 0.85 au ELF isosurface for the the S0 (at min S0) and T1 (at min S0 and min T1) states. The ELF was obtained at the UHF/cc-pVTZ level of theory. | ||
It is of importance to point that according to the traditional nomenclature of the S0 → S1 transition (n → π*), it is expected that the electron density of the lone pairs is transformed into that of a π* MO. As it is shown here, the topological analysis of ρ (both QTAIM or ELF) enriches this description, showing that this conversion is caused by a rotation of the ρ associated with the O lone pairs, what could be interpreted as that the “σ” lone pairs become “π” lone pairs and this triggers a concomitant weakening of the C–O double bond.
The rotation of the O lone pairs is very relevant, as it appears in a huge number of photophysical processes. It seems reasonable that the O lone pairs are in a σ disposition due to the presence of the C–O double bond in the S0 state, even if it maximizes the repulsion between C–H bonding pairs and the O lone pairs. In the S1 electronic arrangement, the repulsion between the O lone pairs and the C–H bonding pairs is minimized.
4 Conclusions
The main conclusions may be summarized as follows:• The QTAIM has proved to be versatile enough to be applied to systems in their electronic excited states, generating results that are in line with firmly-established chemical facts and interpretations. Moreover, QTAIM results have not only been useful as those coming from MO concepts, but even capable of adding details of electronic rearrangements that are not easily deduced from the MO framework.
• Excitation to the singlet nπ* state is accompanied by the stabilization of the individual atoms of the carbonyl bond but with a destabilization of the interaction between them. This fact is in accordance with the idea of populating a π* MO, being also an indication that the nature of the C–O bond has changed.
• The energy partitions associated with the vertical excitation and the lengthening of the carbonyl bond show the same trend, which could be also ascribed to the antibonding character of the πC–O* MO. However, the C–O bond lengthening does not involve a change in the π contribution of the atomic populations, but in the σ one.
• The pyramidalization of the C atom can be understood as a breaking of the symmetry of the electron density in order to reduce the electron–electron repulsion between C and O basins.
• The analysis of the electron density (through QTAIM and ELF) reveals that the n → π* transition may be also understood as a rotation of the oxygen lone pairs to a π disposition, accompanied by a synchronous weakening of the C–O double bond.
Acknowledgements
D.F-C. and R.A.M. thank Spanish Ministry of Economy for the project CTQ2010-21500 and A.M.P. for project CTQ2012-31174. D. F-C. also thanks Spanish Ministry of Education for an FPU fellowship and the University of Vigo for the “Estadía en centros de investigación” grant.References
- M. Klessinger and J. Michl, Excited States and Photochemistry of Organic Molecules, VH Publishers, Inc., Toronto, 1995 Search PubMed.
- F. Weigend, M. Kattannek and R. Ahlrichs, J. Chem. Phys., 2009, 130, 164106 CrossRef PubMed.
- L. González, D. Escudero and L. Serrano-Andrés, ChemPhysChem, 2012, 13, 28–51 CrossRef PubMed.
- J. Pipek and P. G. Mezey, J. Chem. Phys., 1989, 90, 4916–4926 CrossRef CAS PubMed.
- J. M. Foster and S. F. Boys, Rev. Mod. Phys., 1960, 32, 300–302 CrossRef CAS.
- D. A. Kleier, T. A. Halgren, J. H. Hall Jr and W. N. Lipscomb, J. Chem. Phys., 1974, 61, 3905–3919 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, Oxford, 1995 Search PubMed.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- P. L. A. Popelier, Struct. Bonding, 2005, 115, 1–56 CrossRef CAS.
- M. A. Blanco, A. M. Pendás and E. Francisco, J. Chem. Theory Comput., 2005, 1, 1096–1109 CrossRef CAS.
- J. Cioslowski, J. Phys. Chem., 1990, 94, 5496–5498 CrossRef CAS.
- P. Mori-Sanchez, J. Recio, B. Silvi, C. Sousa, A. M. Pendas, V. Luaña and F. Illas, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 075103 CrossRef.
- R. F. W. Bader, D. Bayles and G. L. Heard, J. Chem. Phys., 2000, 112, 10095 CrossRef CAS PubMed.
- Y.-G. Wang, K. B. Wiberg and N. H. Werstiuk, J. Phys. Chem. A, 2007, 111, 3592 CrossRef CAS PubMed.
- P. B. Coto, D. Roca-Sanjuán, L. Serrano-Andrés, A. M. Pendás, S. Martí and J. Andrés, J. Chem. Theory Comput., 2009, 5, 3032 CrossRef CAS.
- R. Chávez-Calvillo and J. Hernández-Trujillo, J. Phys. Chem. A, 2011, 115, 13036–13044 CrossRef PubMed.
- V. Tognetti and L. Joubert, Chem. Phys. Lett., 2013, 557, 150–153 CrossRef CAS PubMed.
- N. J. Turro, Modern molecular photochemistry, The Benjamin Cummings, Menlo Park, California, 1978 Search PubMed.
- C. F. Matta and R. J. Boyd, The Quantum Theory of Atoms in Molecules: From Solids State to DNA and Drug Design, Wiley-VCH, 2007 Search PubMed.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS PubMed.
- F. Aquilante, L. De Vico, N. Ferré, G. Ghigo, P. Malmqvist, P. Neogrády, T. B. Pedersen, M. Pitoñák, M. Reiher, B. O. Roos, L. Serrano-Andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224–247 CrossRef CAS PubMed.
- W. Zou, Molden2AIM, http://people.smu.edu/wzou/program/index.html Search PubMed.
- R. Biegler-Knig, R. Bader and T.-H. Tang, J. Comput. Chem., 1982, 13, 317 CrossRef PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS PubMed.
- A. M. Pendás, M. A. Blanco and E. Francisco, J. Comput. Chem., 2006, 28, 161–184 CrossRef PubMed.
- A. M. Pendás, M. Blanco and E. Francisco, J. Comput. Chem., 2009, 30, 98–109 CrossRef PubMed.
- R. J. Gillespie and P. L. A. Popelier, Chemical Bonding and Molecular Geometry, Oxford University Press, 2001 Search PubMed.
- I. Fourré, B. Silvi, P. Chaquin and A. Sevin, J. Comput. Chem., 1999, 20, 897–910 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp00431k |
| ‡ The variation experienced by Enet(C) in this vertical electronic excitation may be basically assigned to a charge transfer term. Thus, ΔEnet roughly corresponds to −IP(C)·ΔN(C), where IP(C) is the ionization potential of the isolated atom. For example, using the IP experimental value for C (11.26 eV), we get an estimated ΔEnet(C) value of −523 kJ mol−1, which satisfactorily compares with our computed value shown in Table 4 (−606 kJ mol−1). This approximation also holds for processes (b) and (c); however, it does not provide good estimations for negatively charged atoms (using electron affinities), where the deformation of the basin plays a more significant role. More details can be found in ref. 27. |
| § The active space used in these calculations introduces correlation basically in the CO moiety, which is the most important one for our purposes. This means, δC,O is smaller than the one from Hartree–Fock (HF), while δH,H and δC,H are very close to those obtained from HF description. Then, the value of 1.297 au for CO is clearly a polarized double bond with correlation, whereas 0.908 au is a single C–H bond without correlation. |
| ¶ In this situation, Vπee is proportional to (n + a)(m − b) + (n − a)(m + b). |
| This journal is © the Owner Societies 2014 |