Open Access Article
Open Access ArticleCorrelated fluorine diffusion and ionic conduction in the nanocrystalline F− solid electrolyte Ba0.6La0.4F2.4—19F T1(ρ) NMR relaxation vs. conductivity measurements
F.
Preishuber-Pflügl
*ab,
P.
Bottke
a,
V.
Pregartner
a,
B.
Bitschnau
c and
M.
Wilkening
*ab
aInstitute for Chemistry and Technology of Materials, and Christian Doppler Laboratory for Lithium Batteries, Graz University of Technology, Stremayrgasse 9, 8010 Graz, Austria. E-mail: preishuber-pfluegl@tugraz.at
bDFG Priority Program (SPP) 1415, Graz University of Technology, Stremayrgasse 9, 8010 Graz, Austria. E-mail: wilkening@tugraz.at
cInstitute of Physical and Theoretical Chemistry, Graz University of Technology, Stremayrgasse 9, 8010 Graz, Austria
First published on 31st March 2014
Abstract
Chemical reactions induced by mechanical treatment may give access to new compounds whose properties are governed by chemical metastability, defects introduced and the size effects present. Their interplay may lead to nanocrystalline ceramics with enhanced transport properties being useful to act as solid electrolytes. Here, the introduction of large amounts of La into the cubic structure of BaF2 served as such an example. The ion transport properties in terms of dc-conductivity values of the F− anion conductor Ba1−xLaxF2+x (here with x = 0.4) considerably exceed those of pure, nanocrystalline BaF2. So far, there is only little knowledge about activation energies and jump rates of the elementary hopping processes. Here, we took advantage of both impedance spectroscopy and 19F NMR relaxometry to get to the bottom of ion jump diffusion proceeding on short-range and long-range length scales in Ba0.6La0.4F2.4. While macroscopic transport is governed by an activation energy of 0.55 to 0.59 eV, the elementary steps of hopping seen by NMR are characterised by much smaller activation energies. Fortunately, we were able to deduce an F− self-diffusion coefficient by the application of spin-locking NMR relaxometry.
I. Introduction
Studying ion dynamics in solids is one of the most vital topics in modern solid-state chemistry.1–3 The development of advanced sensors or energy storage systems requires careful examining of the correlation of ion transport over long distances and local ion hopping between neighbouring sites within a rigid lattice structure. Such studies are directly linked with the development of advanced solid electrolytes,1–5 urgently needed for future all-solid-state rechargeable batteries.In particular, highly conducting and electrochemically stable fluorides5–9 are necessary components to bring all-solid-state fluorine-ion batteries8 alive. Regarding particular applications they might serve as alternatives to those relying on lithium2 and sodium4 as ionic charge carriers. Quite recently, solid solutions of nanocrystalline fluorite-type Ba1−xLaxF2+x prepared by high-energy ball milling have been introduced as a promising solid F− electrolyte.9 First measurements of its electrochemical stability10 encouraged us to study F dynamics in detail. As presented by Fichtner and co-workers,9 ionic transport properties of a series of mechanochemically synthesized nanocrystalline samples with x ranging from x = 0 to x = 0.55 have been studied by impedance spectroscopy recently, and the data have been analysed with respect to macroscopic ion transport. Overall conductivity is anticipated to be fully governed by F anions, i.e., the transference number is assumed to be close to one and, thus, no electronic contributions play a role practically. The highest ion conductivity was found for samples with x = 0.3 and x = 0.4.9
In the present study, we take advantage of 19F nuclear magnetic resonance (NMR) relaxation measurements,11,12 carried out under static conditions, to collect information on the elementary steps of ion hopping in structurally disordered Ba0.6La0.4F2.4. NMR can be a powerful tool and has extensive applications in the field of fast (nanocrystalline) ion conductors, in particular.13–22 It is worth noting that nanocrystalline Ba1−xLaxF2+x is not stable in its nanostructured form at high temperatures; this restricts the temperature range, and thus also the number of available methods to probe diffusion parameters from an atomic scale point of view. NMR, however, offers quite a large set of techniques that are sensitive to both slow and fast (translational) ion dynamics. Here, with the use of SLR measurements, carried out in both (i) the rotating frame and (ii) the laboratory frame of reference,11,23,24 F dynamics with jump rates ranging from the kHz to the MHz range can be probed. Their combination gives access to a quite large dynamic window.25 Spin–spin relaxation measurements20 and line shape studies,26 which do probe even slower F motions, complement the set of time-domain resonance techniques applied.
Considering fast ion conductors with a large number fraction of highly mobile ions, correlation effects27–30 are expected to influence the movement of the charge carriers. Besides the possibility of quantifying F anion dynamics, as has been excellently presented by Chadwick and Strange,31 NMR is also highly useful in distinguishing correlated from independent hopping.18,26,32–35 In conjunction with conductivity spectroscopy,28,36,37 complementary information of translational ion dynamics can be collected. Therefore, the present investigation is also aimed at contributing to the question32,33,38 how results from various time domain NMR methods, viz. F migration activation energies and jump rates compare with those obtained from ac impedance spectroscopy, i.e., probed on different length- and time scales. For this reason, impedance data have also been recorded over the whole temperature range covered by NMR, i.e., including also temperatures well below ambient. In particular, the study presents impedance data recorded at frequencies as high as 3 GHz.
One major advantage of NMR is that it can often provide a direct estimate of the F− jump rate25,32 provided diffusion-induced contributions can be well separated from those being largely affected by so-called background relaxation. In the present case, with the spin-lock NMR technique, see, e.g., ref. 39, it was indeed possible to record a diffusion-induced rate peak from which the self-diffusion coefficient D could be deduced. Our estimation uses the relaxation model of Bloembergen, Purcell and Pound40 which was developed for three-dimensional (isotropic) motions of spin-1/2 nuclei moving in an uncorrelated manner. Finally, the NMR self-diffusion coefficient can be compared with solid-state diffusion coefficients extracted via the Nernst–Einstein equation from dc conductivity data.
II. Experiment
The Ba1−xLaxF2+x sample with x = 0.4 has been prepared by high-energy ball milling41–46 making use of a planetary mill (Fritsch, Pulverisette 7). The starting materials, powders of BaF2 and LaF3 with μm-sized crystallites, were purchased with high purity (99.99%) from Alfa Aesar and Sigma Aldrich, respectively. To synthesize several g of Ba0.6La0.4F2.4, the binary fluorides were mixed under an Ar atmosphere according to the stoichiometric ratio needed. We used a beaker made of ZrO2 (Fritsch) or tungsten carbide (Fritsch) equipped with 180 or 140 balls (5 mm in diameter) of the same material to treat the mixtures at 600 rpm under dry conditions. The ball-to-powder ratio was 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. We carefully avoided any contact with moisture; thus, the beakers were airtight filled with BaF2:LaF3 in a glove box with dry Ar atmosphere. Later on, i.e., after milling periods ranging from 6 h to 10 h, they were also opened in the glove box.
1. We carefully avoided any contact with moisture; thus, the beakers were airtight filled with BaF2:LaF3 in a glove box with dry Ar atmosphere. Later on, i.e., after milling periods ranging from 6 h to 10 h, they were also opened in the glove box.
Structural analysis of the prepared nanocrystalline powders was carried out using X-ray powder diffraction (XRPD) and magic angle spinning (MAS) NMR spectroscopy. The powder diffraction patterns, shown in Fig. 1, were recorded on a Bruker D8 Advance diffractometer with Bragg Brentano geometry using Cu Kα radiation (10–100° 2θ, step size 0.02° 2θ, step time 1 s). Rietveld refinement was carried out with X-PertHighScorePlus (PANalytical). 19F MAS NMR experiments were recorded on a Bruker Avance III spectrometer operating at 470.5 MHz. We used a 2.5 mm-MAS probe (Bruker) with the ability to reach a spinning frequency of 30 kHz; spectra were recorded by non-selective excitation using a short pulse with a length of approximately 1.6 μs.
To prepare dense pellets for impedance measurements the powder samples were cold-pressed by applying an uniaxial pressure of 0.13 GPa. Our press sets allow the fabrication of pellets with, e.g., diameters of 5 mm, 8 mm and 10 mm (sample 3, see below). Pt electrodes (ca. 100 nm in thickness) were applied using a sputter coater (Leica). The thicknesses of the pellet pressed were measured with appropriate gauges. The impedance measurements were carried out using a Novocontrol Concept 80 broadband analyser (Alpha-AN, Novocontrol) being connected to a BDS 1200 cell in combination with an active ZGS cell interface (Novocontrol) allowing temperature-variable 2-electrode (dielectric) measurements. The temperature is automatically controlled by means of a QUATRO cryosystem (Novocontrol) making use of a heating element which builds up a specified pressure in a liquid nitrogen dewar in order to create a highly constant N2 gas flow. After being heated by a gas jet, the freshly evaporated N2 flows directly through the sample cell that is mounted in a cryostat. This setup allows very stable system operation with an accuracy of ±0.01 °C. In summary, the whole setup is able to record the complex impedance (Ẑ) and the permittivity (![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) ) at frequencies ranging from few μHz up to 20 MHz (110–570 K). For impedance measurements up to 3 GHz we used an Agilent E4991 A high-frequency analyser connected to a high frequency cell (Novocontrol).
) at frequencies ranging from few μHz up to 20 MHz (110–570 K). For impedance measurements up to 3 GHz we used an Agilent E4991 A high-frequency analyser connected to a high frequency cell (Novocontrol).
For the NMR measurements the fluoride was sealed in glass ampoules, ca. 4 cm in length and 5 mm in diameter, to protect the nano-crystalline samples with their large surface area permanently from any influence of humidity. NMR lines and relaxation rates were measured using an Avance III spectrometer connected to a shimmed cryomagnet with nominal magnetic fields of 7 T. This field corresponds to a 19F Larmor frequency of ω0/2π = 282 MHz. We used a home-built (high-temperature) NMR probe capable of recording NMR signals under static, i.e., non-rotating conditions up to temperatures as high as 550 K. The π/2 pulse length was approximately 1 μs at 200 W. A Eurotherm temperature controller in combination with a type T thermocouple was used to control and monitor the temperature in the probe's sample chamber.
19F NMR spin-lattice relaxation (SLR) rates 1/T1 were acquired with the saturation recovery pulse sequence 10 × π/2–td–π/2–acquisition (acq.)47,48 The pulse sequence works as follows: an initial pulse train, consisting of ten π/2 pulses separated by 40 μs, was used to destroy any longitudinal magnetization Mz prior to recording its temperature-dependent recovery as a function of the delay time td. Rotating-frame 19F NMR SLRϱ rates 1/T1ϱ were recorded with the spin-lock technique, π/2 p(tlock)−acq.39,47,49–53 With our probe we were able to make use of a locking frequency ω1 of approximately 62.5 kHz. The corresponding locking pulse tlock was varied from 40 μs to 400 ms. Note that the recycle delay for the SLRϱ experiments was set to at least 5 × T1 in order to guarantee full longitudinal relaxation between each scan. 1/T1(2) and 1/T1ϱ rates were obtained by parameterizing the magnetic transients Mz(td) and Mϱ(tlock), respectively, by stretched exponentials: Mz(td) ∝ 1 − exp(−(t/T1)γ) and Mϱ(tlock) ∝ exp(−(tlock/T1ϱ)γϱ), respectively (cf.Fig. 2).
 | ||
| Fig. 2 Left: 19F NMR transversal decay of the spin-locked magnetization recorded at the various temperatures indicated. The locking frequency was 62.5 kHz. Note the logarithmic scale of the x-axis. Solid line represent fits according to stretched exponentials yielding T1ρ−1 and γ1ρ. Right: 19F NMR spin–spin relaxation transients. From the fits (stretched exponentials, solid lines) the rates T2−1 and stretching factors γ2 shown in the upper part of the Arrhenius plot of Fig. 3 can be obtained. The corresponding T1-transients do almost follow an exponential time behaviour. | ||
In addition, temperature-variable 19F NMR spin–spin relaxation (SSR) rates 1/T2 were recorded by taking advantage of a (two-pulse) solid-echo pulse sequence:47 π/2–techo–π/2–acq. techo denotes the variable interpulse delay. The transients obtained were fitted with stretched exponentials. Static 19F NMR spectra were either obtained after Fourier transformation (FT) of the free induction decay, which were recorded by non-selective irradiation with a single π/2 pulse, or by FT of the solid echo beginning from the top of the signal.
III. Results and discussion
A. Characterization by X-ray diffraction
Phase purity of the mechanochemical preparation of nanocrystalline Ba0.6La0.4F2.4 was checked by powder X-ray diffraction carried out at room temperature and in air atmosphere. In Fig. 1 the diffractograms of several samples, which have been differently prepared, are shown. While sample 1, which was prepared in a tungsten carbide (WC) vial (tmill = 6 h), does not reveal any binary fluorides left, sample 2, which was synthesized under slightly different milling conditions (ZrO2 vial, tmill = 6 h), shows residual LaF3. According to Rietveld refinement, phase pure Ba0.6La0.4F2.4 is formed in the ZrO2 beaker, when the milling time tmill to prepare the ternary fluoride is increased from 6 h to 10 h (sample 3). The vertical bars in Fig. 1 represent positions and intensities of the reflexes of the two starting materials. The systematic shift of the diffraction angle 2θ towards larger values points to lattice contraction due to the incorporation of the smaller La ions into the fluorite structure of BaF2.9From the broadening of the reflexes we estimated an average crystallite size of approximately 10 nm (Scherrer equation). Such a value is typically found for mechanosynthesized ceramics treated in high-energy ball mills. The X-ray powder patterns show a low and straight-line background and, therefore, no indications for notable amounts of the amorphous material present. Sample 1 has been used for 19F NMR and impedance measurements up to 20 MHz. From sample 3 a larger pellet with a diameter of 10 mm was pressed for high-frequency impedance measurements carried out up to 3 GHz.
B. NMR measurements
Compared to the recently published study of Rongeat et al.,9 which mainly focusses on the investigation of F ion transport in Ba1−xLaxF2+x by impedance spectroscopy, we emphasized on static 19F NMR relaxometry to point out the differences between short- and long-range F diffusivity. To that end, the present study centres upon a single mechanosynthesized sample with x = 0.4 which is the composition leading to the highest conductivity observed.9 In the Arrhenius plot of Fig. 3(a) an overview of the NMR relaxation rates measured is shown. The figure presents the temperature-dependent relaxation rates 1/T1, 1/T1ρ, and 1/T2 together with the stretching exponents γi (i = 1, 1ρ, 2) obtained by parameterizing the underlying magnetization transients (see Fig. 2) with appropriate fitting functions;34 in our case stretched exponentials were used (see above). For comparison, on the right-hand side of Fig. 3 a couple of temperature-variable 19F NMR spectra of mechanosynthesized Ba0.6La0.4F2.4 are shown.Starting the discussion with the 19F NMR spectra, which were recorded under non-rotating conditions, it is evident that at the lowest temperature, being accessible with the probe used here, the overall NMR signal is composed of several components. Owing to both structural disorder and cation mixing introduced during milling, the shape of the low-T spectrum likely reveals a superposition of many NMR intensities that reflect magnetically different F species. These species result from a broad distribution of locally distinct environments. For comparison, it is known for pure nanocrystalline BaF2, even if severely treated in shaker or planetary mills, that the corresponding 19F NMR signal is much less broadened than it is found in the present case.43
Here, the overall shape of the NMR spectra recorded at low T results from the mixing effect of Ba and La ions; this alters the 19F chemical shifts. Similarly, this has also been reported by Fichtner and co-workers using magic angle spinning (MAS) 19F NMR on samples with varying La-content.9 For comparison, in cation-mixed mechanosynthesized (Ba,Ca)F2, as well as in mixed fluorides with Sr and Ca ions, the individual F environments could be well resolved due to relatively sharp resonance lines and the application of high-speed MAS NMR.44
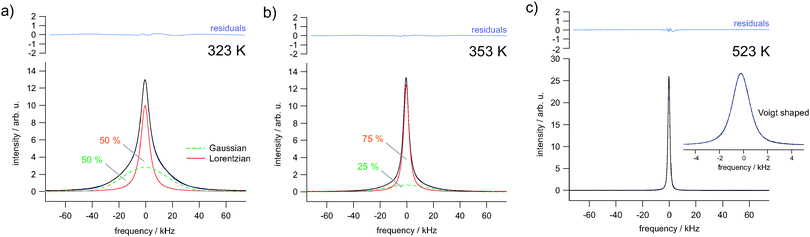
As it becomes obvious from Fig. 3(b), with increasing temperature a narrowed NMR line emerges which is due to both averaging of dipole–dipole26 and local chemical shift interactions of the various magnetically inequivalent F ions. At sufficiently high temperatures the mean exchange rate becomes much faster than the spectral width of the NMR line. This slows down spin–spin relaxation and leads to a single NMR line being fully narrowed by motional averaging; see the spectrum recorded at 523 K, which is the upper temperature we used for our study. Compared to the initial situation, the line width (full width at half maximum) has been decreased from ca. 50 kHz down to 1.7 kHz; in the regime of extreme averaging it is mainly governed by inhomogeneities of the external magnetic field. From motional averaging it is evident that the jump rate τ−1 (523 K) is much larger than 50 kHz × 2π, i.e., the rate should be in the order of 105 s−1 to 106 s−1.
In Fig. 4 selected 19F NMR spectra are shown which were deconvoluted by using a Gaussian and a Lorentzian line (see the solid and dashed lines of the spectra recorded at 323 K and 353 K, respectively). At higher temperatures, i.e., in the regime of full averaging, viz. at 523 K, the NMR line can be best represented by a single Voigt profile. In general, such heterogeneous motional narrowing can be linked with a distribution of F− jump rates. Cation mixing44 and local structural disorder in nanocrystalline Ba0.6La0.4F2.4 prepared by mechanical treatment supports this idea. Thus, the rate estimated above should be regarded as a mean value.
According to a mean jump rate in the order of or even larger than 104 s−1, the 19F NMR spin–spin and spin–lattice relaxation rates are expected to be greatly, if not solely, influenced by F self-diffusion. F dynamics lead to fluctuations of the local dipolar fields and induce longitudinal magnetization recovery as well as affect transversal NMR relaxation. Starting the analysis with the laboratory-frame SLR rates, we observe a weaker-than-activated temperature dependence below 225 K (see Fig. 3(a)). In this low-T regime, which is characterised by ω0τc ⋘ 1 where τc is the motional correlation time, T1−1 is mainly driven by non-diffusive relaxation sources such as lattice vibrations and coupling of the spins with paramagnetic impurities. With increasing temperature, however, the rate T1−1 increases; at T > 370 K it has already reached the low-T flank (ω0τc ≪ 1) of the diffusion-induced rate peak, which is expected to show up at higher T. It should be noted that temperatures well above 550 K are not accessible with the NMR setup available in our laboratory. Moreover, the onset of grain growth may represent a natural limit to investigate F diffusion parameters in nanocrystalline (metastable) fluorides.
In order to carefully separate non-diffusive background relaxation from purely diffusion-induced contributions, we parameterized the low-T rates with an appropriate power law T1 ∝ Tβ and extrapolated the rates obtained to higher temperatures (see the dashed line in Fig. 3(a)). Subsequent subtraction from the overall rates measured resulted in background-corrected SLR rates which are represented in Fig. 3 by unfilled symbols. As a result, we observe a stepwise increase in the diffusion-induced T1−1 rates: starting from low T an activation energy of Ea′′ = 0.16 eV can be deduced, while an Arrhenius fit of the flank showing up at higher temperatures yields Ea,low = 0.44 eV.
The first value nicely agrees with the one obtained from spin–spin-relaxation measurements which are also shown in Fig. 3. In the limit T → 0 K, which is the rigid lattice, T2−1 is approximately given by 105 s−1 ≡ T20−1. The rate T2−1 starts to deviate from T20−1 at 330 K and then follows an Arrhenius law characterised by an activation energy of only Ea′ = 0.19 eV. According to the simple behaviour expected from the relaxation model of Bloembergen, Purcell and Pound (BPP), which had been introduced for 3D (isotropic) uncorrelated motion,40 one would expect the T2−1 flank to coincide with the high-T flank (ω0τc ≫ 1) of the T1−1 rate peak leading to Ea′ = Ea,high with Ea,high being the activation energy in the regime ω0τc ≫ 1. It should be noted that Ea,high cannot be determined via T1−1 measurements in the present case because of temperature restrictions and limitations in our experimental setup (see above).
The various models developed for correlated motions do predict asymmetric NMR rate peaks.14,17,30 Indeed, such shapes are observed in general; the corresponding peaks are characterised by Ea,low being smaller than Ea,high and Ea′ = Ea,high, respectively. Ea,high is often compared with the corresponding value from dc conductivity measurements (see Fig. 5 and the following section).32 In our case, however, these general characteristics for correlated 3D jump diffusion seem to be not fulfilled and an anomaly is observed as will be outlined in detail in the following.
To shed further light on this situation, we recorded 19F T1ρ NMR SLR rates in the rotating frame of reference at locking frequencies much smaller than the Larmor frequency used for our T1 measurements. Compared to NMR relaxometry in the lab frame, T1ρ−1 is per se sensitive to F motions taking place on a longer length (and time) scale.17 As expected, we were able to partly reach the high-T flank of the corresponding T1ρ−1(1/T) peak; compared to T1−1(1/T) it is shifted towards lower T. The peak itself spans a rather broad T range; even after appropriate background correction, as it was done for T1, the high-T flank cannot be clearly separated. The broadened peak might be the result of superimposing rate peaks reflecting the distribution of migration processes in the disordered Ba0.6La0.4F2.4 phase. Irrespective of its overall shape, the activation energy in the limit ω1τc ≪ 1 lies in the range 0.25–0.35 eV. The resulting value depends on the quality of the correction procedure applied, i.e., the β chosen, and the number of data points taking into account for the Arrhenius fit. Most importantly, these values are even smaller than Ea,low deduced from T1−1(1/T) in the limit ω0τc ≪ 1. This points to a second anomaly observed via NMR relaxation. Frequency-dependent conductivity measurements might help understand the complex results found by NMR relaxometry.
C. Impedance and dielectric measurements
Quite recently, impedance spectra, that is the real part σ′ of the complex conductivity (![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) ) plotted vs. frequency ν, have been reported by Fichtner and co-workers;9 conductivity data were discussed in terms of contributions from bulk and grain boundaries of mechanosynthesized Ba1−xLaxF2+x. To compare our results from NMR, recorded at lower temperatures and resonance frequencies in the kHz and MHz range, the samples have been investigated at temperatures down to 173 K and at frequencies as high as 3 GHz. In Fig. 5–7 selected conductivity as well as permittivity spectra are shown.
) plotted vs. frequency ν, have been reported by Fichtner and co-workers;9 conductivity data were discussed in terms of contributions from bulk and grain boundaries of mechanosynthesized Ba1−xLaxF2+x. To compare our results from NMR, recorded at lower temperatures and resonance frequencies in the kHz and MHz range, the samples have been investigated at temperatures down to 173 K and at frequencies as high as 3 GHz. In Fig. 5–7 selected conductivity as well as permittivity spectra are shown.
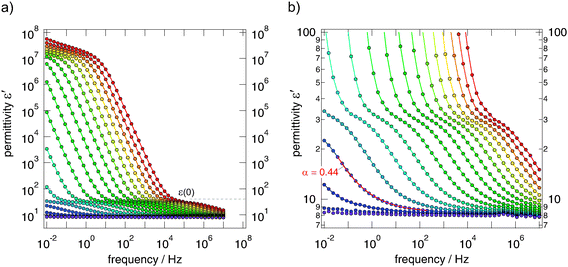
The isotherms (sample 1) shown in Fig. 5(a) reveal the typical characteristics of impedance spectra of structurally disordered materials usually showing a distribution of jump rates and activation energies. If not perturbed by electrode polarisation (EP) effects, dominating impedance response at high temperatures and low frequencies, the spectra are composed of a dc-plateau and a Jonscher-type dispersive region, which can be approximated with a power law according to σ′ = σDC = Aσνκ. As has been shown by many previous studies on other ion conductors, the exponent κ takes values ranging from 0.5 to 0.8. In our case we found κ = 0.56 almost independent of T. κ ≠ f(T) means that the isotherms have the same shape and can be collapsed into a single so-called master curve after appropriate scaling has been carried out. This behaviour indicates that impedance spectroscopy, when carried out at different temperatures (>193 K) and frequencies with values as high as 1 MHz, is sensitive to the same motional process in Ba0.6La0.4F2.4.
At the lowest temperatures, that is, at temperatures lower than 173 K, the dc-plateau has been mainly shifted towards lower frequencies and a ν0.89-dependence shows up. The increase of κ towards larger values might be related to the presence of strictly localized F motions governing the isotherms at sufficiently low T. κ being close to 1 would correspond to the (nearly) constant loss (NCL) phenomenon which is frequently related to such caged dynamics, see, e.g., ref. 28 for a brief overview on this topic.
In order to quantify thermal activation of long-range F transport, DC conductivity values (σDCT) have been plotted in Fig. 5(b)vs. 1000/T. The solid line represents a linear fit and yields an activation energy Ea,dc of 0.59 eV. This result is in very good agreement with the value found by Rongeat et al.9 (0.58 eV) and with those reported for F− ion transport in single crystals.54–56 Moreover, it is comparable with the activation energy when electrical relaxation times τM′ are analysed, which can be deduced from modulus peaks M′′(ν). These are less sensitive to an electrical response determined by large capacities such as the response from grain boundaries. Hence, we may assume that σDC mainly reflects the bulk response and that grain boundaries seem to play a less prominent role in blocking long-range transport. As has been pointed out by Rongeat et al.,9 the activation energy obtained from σDCT vs. 1/T mainly reflects the migration enthalpy rather than contributions from forming F vacancies. The authors already have pointed out that activation energies ranging from 0.5 to 0.6 eV would correspond to those being characteristic for vacancy migration in microcrystalline BaF2 (and its single crystals).31,57 In a structurally disordered material, particularly when prepared by mechanical treatment, also other point defects such as F interstitials have to be considered – especially in the case of La-doped BaF2. In such a case, specifying a primary point defect, if there is any, is very difficult. Most likely, the situation has to be described by a complex interplay of different kinds of defects, including not only point defects.
To judge which capacities and permittivities are associated with the impedance spectra and dc-plateaus obtained, we plotted ε′ as a function of ν (see Fig. 6). Starting with ε′(∞) ≈ 8 at low temperatures and high frequencies, at intermediate temperatures a plateau is reached indicating that ε′(0) is approximately 35 (see the magnification in Fig. 6(b)). The corresponding capacity takes a value of approximately 9 pF (Fig. 7). In our opinion these values corroborate the anticipation that σDC is predominantly determined by the bulk response. The further increase of ε′ observed is due to polarisation effects of the ion blocking electrodes applied. In Fig. 7 the real and imaginary parts of ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) and
and ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) are compared. The curves reveal the well-known features of impedance spectroscopy and show an almost ‘ideal’ frequency dependence that is expected for a non-Debye impedance response. This is also expressed as follows. If ε′ is given by ε′(ν) = ε′(∞) + Aεν−p an AC storage-to-loss ratio of one is obtained if p + κ = 1. Indeed, our data fulfill this relation; we have κ = 0.56 and p = 0.44 (see Fig. 6(b)).
are compared. The curves reveal the well-known features of impedance spectroscopy and show an almost ‘ideal’ frequency dependence that is expected for a non-Debye impedance response. This is also expressed as follows. If ε′ is given by ε′(ν) = ε′(∞) + Aεν−p an AC storage-to-loss ratio of one is obtained if p + κ = 1. Indeed, our data fulfill this relation; we have κ = 0.56 and p = 0.44 (see Fig. 6(b)).
 | ||
Fig. 7 (a) The frequency dependence of ε′ and ε′′ recorded at 413 K. (b) Frequency dependence of σ′ and (−1)·σ′′ recorded at 413 K. According to the Kramers–Kronig relation and ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (ω) =iωε0 (ω) =iωε0![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) (ω) (here, we have ω/2π = ν, i2 = −1 and ε0 being the permeability under vacuum) the plateau σ′ ∝ Aσν0 corresponds to ε′′ ∝ Aεν−1. The local minimum of ε′′ (see arrow) is expressed as a change in slope in the EP region of σ′, see also Fig. 5. The slopes given for ε′ indicate electrode polarisation. (ω) (here, we have ω/2π = ν, i2 = −1 and ε0 being the permeability under vacuum) the plateau σ′ ∝ Aσν0 corresponds to ε′′ ∝ Aεν−1. The local minimum of ε′′ (see arrow) is expressed as a change in slope in the EP region of σ′, see also Fig. 5. The slopes given for ε′ indicate electrode polarisation. | ||
At this stage let us start comparing the results from impedance spectroscopy with those from NMR relaxometry. Even if Ea,dc represents bulk properties, it cannot be expected to fully match Ea,low from NMR. The two methods are sensitive to anion motions taking place on quite different time scales and they have to be described by distinct motional correlation functions. If at all, Ea,dc is expected to coincide with Ea,high;17 the latter is per se sensitive to long-range ion motion at least. In contrast to Ea,high, the low-T flank of a given T1−1 rate peak is affected by correlation effects such as structural disorder and Coulomb interactions.27,29 Such interactions lead to the aforementioned asymmetry of an NMR rate peak.
If we, however, readout conductivities at higher frequencies instead of determining dc-values at ν → 0, lower activation energies should result.26,32 Indeed, this is the case when the Arrhenius plot of Fig. 5 is considered. The unfilled symbols represent σ′T measured at 56 kHz and 1 MHz. Although, as expected, the values coincide with σDCT at sufficiently high temperatures, the deviations at lower T hint to smaller activation energies being responsible for anion hopping if shorter length scales are regarded. Typically, Ea,ac = 0.35 eV is obtained here, that is, however, smaller than Ea,low from 19F NMR. Instead, good agreement has been found between Ea,low and Ea,ac in the case of nanocrystalline LiTaO3 analysed in a similar manner. Such an agreement is proposed by the coupling concept introduced by Ngai32 and has been documented for a number of ion dynamics in glassy systems, in particular.
Although Ea,ac, irrespective of being determined at 56 kHz or 1 MHz, might be interpreted as an activation energy that is comparable with that of the low-T flank of the T1ρ−1-peak, the discrepancy between Ea,ac = 0.35 eV and Ea,low = 0.44 eV is apparent. To answer the question whether this changes the frequency regime that is identical with the Larmor frequency of 282 MHz, we performed conductivity measurements up to the GHz range. In Fig. 8 some of the impedance data of sample 3 are shown. The conductivities recorded span a dynamic range of eleven decades. The data points recorded in the GHz regime perfectly match those collected with the Alpha-analyser working up to 20 MHz. As a side note, the high-frequency data reveal a change in the slope of the isotherms recorded at low temperatures. This might be an indication of a high-frequency plateau increasingly affecting conductivity data.
At high temperatures, ac conductivities σ′ determined at 282 MHz, which equates the NMR Larmor frequency, do also follow an Arrhenius law with an activation energy of 0.35 eV (see Fig. 8). Of course, at lower temperatures the influence of an NCL-type contribution increases and σ′(T) reveals only a weak dependence on T. Let us identify the ac activation energy of 0.35 eV with that of short-range ion motion affected by correlated forward–backward jumps and Ea,dc with that of long-range translational ion hopping. If we do so, the difference Ea,dc − Ea,ac ≈ 0.22 eV could be interpreted in terms of the jump relaxation model as an activation energy needed for the surrounding lattice to relax towards a new equilibrium state accommodating the ion just jumped to a vacant site.58
Lastly, in order to compare the response of conductivity spectroscopy with that of NMR, within an extra experiment we recorded σ′ (and ε′) at a single frequency but varied the temperature. In Fig. 9 the real part of the complex resistivity, which is given by ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) = 1/
= 1/![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) and related to the complex modulus according to
and related to the complex modulus according to ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) = 1/
= 1/![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) via
via ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) =
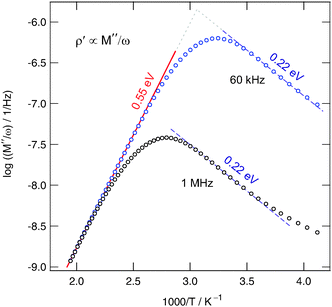
= ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) /(iωe0), is plotted vs. the inverse temperature. ρ′ passes through distinct maxima. If recorded at 60 kHz the peak shows up at T ≈ 335 K; this result is in good agreement with the position of the corresponding 1/T1ρ(1/T)-peak, see Fig. 3. As expected, the ρ′(1/T)-peak shifts towards higher T with increasing frequency. The slope of the high temperature flank yields Ea,ρ = 0.55 eV (≈Ea,dc) (see the solid line drawn).
/(iωe0), is plotted vs. the inverse temperature. ρ′ passes through distinct maxima. If recorded at 60 kHz the peak shows up at T ≈ 335 K; this result is in good agreement with the position of the corresponding 1/T1ρ(1/T)-peak, see Fig. 3. As expected, the ρ′(1/T)-peak shifts towards higher T with increasing frequency. The slope of the high temperature flank yields Ea,ρ = 0.55 eV (≈Ea,dc) (see the solid line drawn).
The pronounced asymmetry of the peaks is in agreement with that commonly found for glassy or at least structurally disordered ion conductors, see ref. 59, in particular. Important to note, the rather broad shape of the maximum resembles that of the 1/T1ρ(1/T) peak. It is an indication of a broad distribution of different relaxation mechanisms present. Before we finally compare the various activation energies obtained, we will contrast the self-diffusion coefficient obtained from the 1/T1ρ(1/T) peak with that which can be deduced from σdc. According to the NMR maximum conditions in the rotating frame of reference ω1τ ≈ 0.5, the jump rate is in the order of 7.85 × 105 s−1. With the Einstein–Smoluchowski equation Dsd = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 2/(6τ) for 3D diffusion60 this translates into a self diffusion coefficient Dsd of 1.2 × 10−14 m2 s−1 at 380 K if we assume a jump distance
2/(6τ) for 3D diffusion60 this translates into a self diffusion coefficient Dsd of 1.2 × 10−14 m2 s−1 at 380 K if we assume a jump distance ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) of approximately 3 Å. Reducing
of approximately 3 Å. Reducing ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) to 2 Å, Dsd decreases to 5.2 × 10−15 m2 s−1.
to 2 Å, Dsd decreases to 5.2 × 10−15 m2 s−1.
However, the Nernst–Einstein equation relates σdc with a solid-state diffusion coefficient D′.60 According to our conductivity values, diffusion coefficients of D′(373 K) ≈ 3.0 × 10−15 m2 s−1 and D′(393 K) ≈ 7.6 × 10−15 m2 s−1 are obtained. While D′ is related to the tracer diffusion coefficient via Dtr = HRD′ with the Haven ratio HR; Dsd given by Dtr = fDsd and f denotes the correlation factor ranging from 0 to 1. Altogether this leads to Dsd = (HR/f)D′. Assuming that the quotient HR/f is in the order of unity, good agreement between σdc and the appearance of the 1/T1ρ(1/T) rate peak is obtained. The high-temperature flank of the NMR peak is expected to be governed by an activation energy being similar to that found by dc conductivity measurements.
D. Final discussion and comparison of activation energies
To sum up, in Table 1, the activation energies probed by both impedance and NMR spectroscopy are listed. Disregarding fully NCL-type caged dynamics (see above), the different regimes of activation energies probed illustrate the transition from short-range motions (I and II) to long-range ion transport (IV).| Method | E a (eV) | Type | T-range, frequency |
|---|---|---|---|
| a Low-T flank of the 1/T1(1/T)-peak. | |||
| T 1 | 0.16(2) | I | 220–330 K, 116 MHz |
| T 2 | 0.19(1) | I | 350–550 K, 116 MHz |
| ρ′ | 0.22(2) | I | Low-T flank of (M′′/ω)-peaks |
| σ′ ac | 0.35(3) | II | 250–500 K, 56 kHz–282 MHz |
| T 1ρ | 0.25–0.35 | II | 250–330 K, 56 kHz |
| T 1 | 0.44(1)a | III | 400–530 K, 116 MHz |
| τ M′′ | 0.55(1) | IV | 220–400 K, modulus peaks |
| ρ′ | 0.55(1) | IV | High-T flank of (M′′/ω)-peaks |
| σ′ dc | 0.57(1) | IV | 200–500 K (sample 3) |
| σ′ dc | 0.59(1) | IV | 200–500 K (sample 1) |
The data clearly illustrate that the final result for the activation energy is determined by the method chosen and its sensitivity to a specific time and length scale. Only in structurally ordered and (macroscopic) homogeneous materials with a perfectly regular energy landscape one might expect a single value for the activation energy Ea.
While the activation energy of type I might point to localized dynamics, group II could be identified with the (mean) activation energy describing the elementary jump processes in nanocrystalline Ba0.6La0.4F2.4. The relatively large value probed by T1 NMR seems to reflect an anomaly coupled with the different jump mechanisms leading to long-range ion transport. It is worth noting that the latter result does not depend on the integration range of the underlying NMR free induction decays. This means that it does not play a role whether parts of the free induction decays or the whole integral over the transient signal is analysed in terms of a saturation recovery experiment to extract the T1 rates. In all cases the same magnetization recovery curve is obtained which follows a pure exponential containing a single T1−1 rate. Hence, from the point of view of SLR NMR the spin ensemble appears as a dynamically uniform system. Even if there are any microscopic spin regions acting differentially, fast spin-diffusion, i.e., so-called spin flip-flop processes without mass transfer, results in a homogeneous 19F NMR spin system characterised by a single spin temperature.
IV. Conclusions
Up to a certain concentration the mechanochemical introduction of La ions into BaF2 leads to solid solutions of Ba1−xLaxF2+x crystallizing with a fluorite-type structure.9 Structural disorder and strain owing to the socialization of two cations with largely different radii, see also ref. 44, is anticipated to severely affect overall ion transport of F−. The relatively high ion conductivity of Ba1−xLaxF2+x with x = 0.4 at elevated temperatures makes the cation-mixed material a promising solid electrolyte in modern energy storage systems with F− ions as charge carriers. Preliminary solid-state cyclovoltammetry measurements10 encouragingly show a sufficiently good electrochemical stability over a relatively large potential window.Here, we could show, by using both atomic-scale NMR relaxometry and (high-frequency) broadband impedance spectroscopy, that F− ion transport in the ternary fluoride is governed by multiple hopping processes. Depending on the time scale the particular technique is sensitive to, we could distinguish between short-range and long-range translational dynamics. This manifests in a broad range of activation energies found spanning the range from localized hopping (0.16 eV) to macroscopic ion transport (0.55 eV). Interestingly, an anomaly is found when activation energies obtained from ac conductivity spectroscopy (0.35 eV) are compared with that deduced from diffusion-induced T1−1 19F NMR performed at 282 MHz. This might be explained by the fact that the two methods, even if applied in the same frequency window, do probe different motional correlation functions. Structural heterogeneities, such as the formation of F− clusters,9,54,55,61 or size effects such as the influence of space charge zones62,63 in materials with a large surface area might also be considered to discuss the results found. To this end, detailed structural information is needed to correlate them with the dynamic properties studied here.
Unfortunately, due to the heat sensitivity of the sample we could not probe the high-temperature flank of the corresponding 19F NMR peak in the rotating frame of reference. Fortunately, via the shallow maximum detected at approximately 380 K the F self-diffusion coefficient Dsd could be determined. A value of 7.85 × 105 s−1 is in line with that which can be estimated from dc conductivity results. This is consistent with the agreement between activation energies from ac conductivity and the low-T flank of the T1ρ−1 NMR peak.
Author contributions
The authors were equally involved in experimental work, data analysis and project planning. All authors have given approval to the final version of the manuscript.Acknowledgements
We thank our colleagues at the TU Graz and the University of Hannover, especially A. Düvel, for valuable discussions concerning sample preparation and characterisation. Financial support by the Deutsche Forschungsgemeinschaft (DFG), SPP 1415, the Austrian Federal Ministry of Economy, Family and Youth, and the Austrian National Foundation for Research, Technology and Development is greatly appreciated. Furthermore, we thank the DFG for access to the NMR and impedance spectrometers of the DFG Research Unit 1277, grant no. WI3600/2-1 and 4-1.References
- K. Funke, Sci. Technol. Adv. Mater., 2013, 14, 043502 CrossRef.
- P. Knauth, Solid State Ionics, 2009, 180, 911 CrossRef CAS PubMed.
- Nanocomposites: Ionic Conducting Materials and Structural Spectroscopies, ed. P. Knauth and J. Schoonman, Springer, Berlin, 2008 Search PubMed.
- A. Hayashi, K. Noi, A. Sakuda and M. Tatsumisago, Nat. Commun., 2012, 3, 856 CrossRef PubMed.
- L. N. Patro and K. Hariharan, Solid State Ionics, 2013, 239, 41 CrossRef CAS PubMed.
- J. Schoonman, K. Wapenaar, G. Oversluizen and G. Dirksen, J. Electrochem. Soc., 1979, 126, 709 CrossRef CAS PubMed.
- J. Schoonman and A. Wolfert, J. Electrochem. Soc., 1981, 128, 1522 CrossRef CAS PubMed.
- M. A. Reddy and M. Fichtner, J. Mater. Chem., 2011, 21, 17059 RSC.
- C. Rongeat, M. A. Reddy, R. Witter and M. Fichtner, J. Phys. Chem. C, 2013, 117, 4943 CAS.
- I. Hanzu, A. Düvel, F. Preishuber-Pflügl, P. Heitjans and M. Wilkening, 2013, to be published.
- V. Epp, z. Gün, H.-J. Deiseroth and M. Wilkening, J. Phys. Chem. Lett., 2013, 4, 2118 CrossRef CAS.
- A. Kuhn, S. Narayanan, L. Spencer, G. R. Goward, V. Thangadurai and M. Wilkening, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 94302 CrossRef.
- P. M. Richards, in Topics in Current Physics, ed. M. B. Salamon, Springer, Berlin, 1979, vol. 15 Search PubMed.
- P. Heitjans, A. Schirmer and S. Indris, in Diffusion in Condensed Matter – Methods, Materials, Models, ed. P. Heitjans and J. Kärger, Springer, Berlin, 2nd edn, 2005, ch. 9, pp. 369–415 Search PubMed.
- D. Brinkmann, Prog. Nucl. Magn. Reson. Spectrosc., 1992, 24, 527 CrossRef CAS.
- R. Böhmer, K. Jeffrey and M. Vogel, Prog. Nucl. Magn. Reson. Spectrosc., 2007, 50, 87 CrossRef PubMed.
- M. Wilkening and P. Heitjans, ChemPhysChem, 2012, 13, 53 CrossRef CAS PubMed.
- M. Wilkening and P. Heitjans, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 024311 CrossRef.
- H. Buschmann, J. Dölle, S. Berendts, A. Kuhn, P. Bottke, M. Wilkening, P. Heitjans, A. Senyshyn, H. Ehrenberg and A. Lotnyk, et al. , Phys. Chem. Chem. Phys., 2011, 13, 19378 RSC.
- J. Langer, V. Epp, P. Heitjans, F. A. Mautner and M. Wilkening, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 094304 CrossRef.
- P. Heitjans and M. Wilkening, Mater. Res. Bull., 2009, 34, 915 CrossRef CAS.
- P. Heitjans, E. Tobschall and M. Wilkening, Eur. Phys. J.: Spec. Top., 2008, 161, 97 CrossRef.
- A. Kuhn, M. Kunze, P. Sreeraj, H. D. Wiemhöfer, V. Thangadurai, M. Wilkening and P. Heitjans, Solid State Nucl. Magn. Reson., 2012, 42, 2 CrossRef CAS PubMed.
- A. Kuhn, P. Sreeraj, R. Pöttgen, H.-D. Wiemhöfer, M. Wilkening and P. Heitjans, J. Am. Chem. Soc., 2011, 133, 11018 CrossRef CAS PubMed.
- M. Wilkening, W. Küchler and P. Heitjans, Phys. Rev. Lett., 2006, 97, 065901 CrossRef CAS.
- M. Wilkening, V. Epp, A. Feldhoff and P. Heitjans, J. Phys. Chem. C, 2008, 112, 9291 CAS.
- K. Funke, Prog. Solid State Chem., 1993, 22, 111 CrossRef CAS.
- K. Funke, C. Cramer and D. Wilmer, in Diffusion in Condensed Matter – Methods, Materials, Models, ed. P. Heitjans and J. Kärger, Springer, Berlin, 2nd edn, 2005, ch. 21, pp. 857–893 Search PubMed.
- M. Meyer, P. Maass and A. Bunde, Phys. Rev. Lett., 1993, 71, 573 CrossRef CAS.
- A. Bunde, W. Dieterich, P. Maass and M. Meyer, in Diffusion in Condensed Matter – Methods, Materials, Models, ed. P. Heitjans and J. Kärger, Springer, Berlin, 2nd edn, 2005ch. 20, pp. 813–856 Search PubMed.
- D. R. Figueroa, A. V. Chadwick and J. H. Strange, J. Phys. C: Solid State Phys., 1978, 11, 55 CrossRef CAS.
- O. Kanert, R. Küchler, K. L. Ngai and H. Jain, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 76 CrossRef CAS.
- K. Ngai, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13481 CrossRef CAS.
- V. Epp, O. Gün, H.-J. Deiseroth and M. Wilkening, Phys. Chem. Chem. Phys., 2013, 15, 7123 RSC.
- K. L. Ngai, Relaxation and Diffusion in Complex Systems, Springer, New York, 2011 Search PubMed.
- D. L. Sidebottom, Rev. Mod. Phys., 2009, 81, 999 CrossRef.
- J. R. Macdonald, J. Appl. Phys., 1998, 84, 812 CrossRef CAS PubMed.
- K. Ngai and C. León, J. Non-Cryst. Solids, 2003, 315, 124 CrossRef CAS.
- D. Ailion and C. P. Slichter, Phys. Rev. Lett., 1964, 12, 168 CrossRef CAS.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679 CrossRef CAS.
- V. Šepelák, A. Düvel, M. Wilkening, K.-D. Becker and P. Heitjans, Chem. Soc. Rev., 2013, 42, 7507 RSC.
- B. Ruprecht, M. Wilkening, S. Steuernagel and P. Heitjans, J. Mater. Chem., 2008, 18, 5412 RSC.
- B. Ruprecht, M. Wilkening, A. Feldhoff, S. Steuernagel and P. Heitjans, Phys. Chem. Chem. Phys., 2009, 11, 3071 RSC.
- A. Düvel, B. Ruprecht, P. Heitjans and M. Wilkening, J. Phys. Chem. C, 2011, 115, 23784 Search PubMed.
- A. Düvel, M. Wilkening, R. Uecker, S. Wegner, V. Šepelák and P. Heitjans, Phys. Chem. Chem. Phys., 2010, 12, 11251 RSC.
- A. Düvel, S. Wegner, K. Efimov, A. Feldhoff, P. Heitjans and M. Wilkening, J. Mater. Chem., 2011, 21, 6238 RSC.
- E. Fukushima and S. B. W. Roeder, Experimental Pulse NMR: A Nuts and Bolts Approach, Addison-Wesley Pub. Co., Advanced Book Program, Reading, Mass., 1981 Search PubMed.
- P. Heitjans, A. Schirmer and S. Indris, in Diffusion in Condensed Matter, ed. P. Heitjans and J. Kärger, Springer, 2005, ch. 9, p. 367 Search PubMed.
- C. P. Slichter and D. Ailion, Phys. Rev., 1964, 135, A1099 CrossRef.
- D. C. Ailion and C. P. Slichter, Phys. Rev., 1965, 137, A235 CrossRef.
- D. C. Look and I. J. Lowe, J. Chem. Phys., 1966, 44, 2995 CrossRef CAS PubMed.
- T. J. Rowland and F. Y. Fradin, Phys. Rev., 1969, 182, 760 CrossRef CAS.
- D. Wolf, Phys. Rev. B: Solid State, 1974, 10, 2724 CrossRef CAS.
- K. E. D. Wapenaar, J. L. Van Koesveld and J. Schoonman, Solid State Ionics, 1981, 2, 145 CrossRef CAS.
- A. K. Ivanov-Shits, N. I. Sorokin, P. P. Fedorov and B. P. Sobolev, Solid State Ionics, 1989, 31, 269 CrossRef CAS.
- N. I. Sorokin and M. W. Breiter, Solid State Ionics, 1997, 99, 241 CrossRef CAS.
- E. Barsis and A. Taylor, J. Phys. Chem., 1968, 48, 4357 CrossRef CAS PubMed.
- K. Funke and R. D. Banhatti, J. Mater. Sci., 2007, 42, 1942–1947 CrossRef CAS PubMed.
- B. Munro, M. Schrader and P. Heitjans, Ber. Bunsenges. Phys. Chem., 1992, 96, 1718 CrossRef CAS.
- H. Mehrer, Diffusion in Solids, Springer, Berlin, 2006 Search PubMed.
- F. Wang and C. P. Grey, Chem. Mater., 1998, 10, 3081 CrossRef CAS.
- J. Maier, Prog. Solid State Chem., 1995, 23, 171 CrossRef CAS.
- W. Puin, S. Rodewald, R. Ramlau, P. Heitjans and J. Maier, Solid State Ionics, 2000, 131, 159 CrossRef CAS.
| This journal is © the Owner Societies 2014 |