Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Conformational changes of globular proteins upon adsorption on a hydrophobic surface
Yevgeny
Moskovitz
a and
Simcha
Srebnik
*b
aDepartment of Chemistry, Scientific Computing Research Unit, University of Cape Town, Rondebosch 7701, Western Cape, South Africa
bDepartment of Chemical Engineering, Technion – Israel Institute of Technology, Haifa 32000, Israel. E-mail: simchas@technion.ac.il; klw54cp@gmail.com
First published on 16th April 2014
Abstract
This paper presents a study of protein adsorption and denaturation using coarse-grained Monte Carlo simulations with simulated annealing. Intermolecular interactions are modeled using the Miyazawa–Jernigan (MJ) knowledge-based potential for an implicit solvent. Three different hydrophobicity scales are tested for adsorption of fibronectin on a hydrophobic surface. The hydrophobic scale BULDG was chosen for further analysis due to its greater stability during heating and its partial regenerative ability upon slow cooling. Differences between helical and sheet structures are observed upon denaturation – α-helices undergo spreading of their native helical order to an elliptical perturbed shape, while β-sheets transform into random coils and other more structured conformations. Electronic calculations carried out on rebuilt all-atom coordinates of adsorbed lysozymes revealed consistent destabilization of helices, while beta sheets show a greater variety of trends.
1. Introduction
When a protein is placed outside its natural medium, its structure and function are usually affected.1 Near a solid surface, proteins tend to adsorb, and depending on the protein and surface properties, they may undergo partial or significant conformational changes. Many modern medical devices rely on the direct contact between bodily fluids and artificial surfaces, and their use is often complicated by immunological reactions induced by adsorption of proteins on the artificial interface.2 In addition, many biomimetic devices3 are based on catalytic and reception functions of immobilized proteins, such as biosensors, bioreactors, and artificial organs, which also suffer from the problem of adsorption and consequent denaturation of bioactive materials. Proteins tend to adhere more strongly to nonpolar than to polar substrates since the nonpolar environment destabilizes the protein and thereby facilitates a conformational rearrangement that leads to strong protein–surface hydrophobic interactions.4Protein adsorption and denaturation is a common but very complicated phenomenon, and to date there has been inadequate understanding of the adsorption process.5 It is driven largely by an entropy gain arising from the release of surface adsorbed water molecules in addition to the structural rearrangement of the protein. It is possible to define three basic levels of events: (1) microscale that analyzes events at the atomic level, (2) motions of macromolecular clusters like alpha helices and beta sheets which can be of significance in phase transition processes, and (3) macroscale events that take into account forces acting on the whole protein, for example, hydrodynamics of a viscous fluid.1,6 Some structural information can be obtained from experimental techniques,1,3,7,8 such as circular dichroism (CD), Fourier-transform infrared (FTIR) spectroscopy, scanning angle reflectometry (SAR), and atomic force microscopy (AFM) imaging. These techniques provide evidence for structural transitions of proteins in adsorbed states5 such as β-sheets to α-helices transitions. The dynamics of single-molecule adsorption and denaturation can now be measured using Förster resonance energy transfer.9
Adsorption of globular proteins follows 2-step kinetics that lead to partial denaturation of the protein, exposing the hydrophobic residues to the surface.10 For ambient conditions relevant to biological solutions, proteins most generally approach the surface in their native state, and the initial adsorption is followed by a slow structural rearrangement, corresponding to a relaxation process with macroscopically observable effects including an altered secondary structure.6 AFM experiments point to conformational changes of the adsorbed proteins that occur over periods extending to minutes or hours.3,11 This kind of 2-step adsorption kinetics is a manifestation of frustrated macromolecules whose conformational space is restricted to a small number of most stable conformations.12,13 Notably, cooperative adsorption and protein aggregation in solution and on the surface may influence the adsorption kinetics as well as the resulting protein layer structure,4,14,15 though, it has recently been shown that protein–protein interactions have little influence on the structure of the lyz on highly hydrophobic surfaces.16
During the last decade, the role of computational modeling in structural biology has increased substantially.17 Since protein adsorption is associated with complex molecular events beyond the nanosecond timescale, fully atomistic models require biasing techniques to overcome free energy minima to allow for denaturation.18 One of the most promising tools is the coarse-grained (CG) approaches, as they demand much less computational effort than all-atom models, and therefore allow for longer time scales of molecular events. A common CG model of proteins represents each amino acid as having two interacting sites (α-carbon and side chains). CG models of proteins provide good representation of the conformational space of proteins near the folded state region,19,20 as well as those adsorbed onto a hydrophobic surface.21 A recent model developed by Wei et al.22 revealed the power of such parametrized coarse-grained models in predicting protein adsorption behavior.
The problem of protein adsorption deals with a highly complex energetic landscape that is characterized by a large number of local minima, for which standard simulation algorithms result in trapping at local minima for long periods. Following the work in ref. 23, we use simulated annealing to predict the structure of the denatured protein upon adsorption. In this method, we search for equilibrium states of the system through heating followed by slow cooling, in order to surmount local minima that kinetically prevent the system from reaching energetically favorable states at short simulation times. We have previously determined the thermal limits of stability of proteins in the bulk and on the surface,24 which are used in the design of annealing schedules used in this work. The MC algorithm is based on the coarse-grained model developed by Haliloglu et al.25 using the Miyazawa–Jernigan knowledge-based potential for residue–residue interactions.26 The specific surface–amino acid interactions are modeled using different hydrophobicity (hb) scales for fibronectin (fn), lysozyme (lyz), and a small helical peptide. Lysozyme CG coordinates are converted to all-atom presentation and evaluation of intramolecular interactions at secondary structure elements at the B3LYP level of theory is performed.
2. Methods
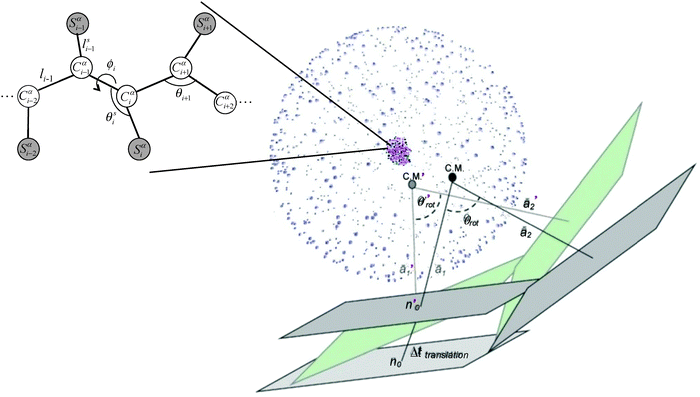
We base our model on the work of Jernigan and coworkers19,20 developed for the investigation of conformational dynamics of several globular proteins. In this model, each amino acid residue i is represented by two principal interacting sites, an α-carbon (Cα) atom and a sidechain center Si, as is depicted in Fig. 1.In this model, the energy of a given conformation Φ is a sum over all non-bonded interactions (EL) between non-neighboring residue pairs and bonded interactions (ES),
| E{Φ} = EL{Φ} + ES{Φ} | (1) |
These interactions are given by a potential of mean force discretized by intervals of 0.4 Å in the range 2.0 ≤ rij ≤ 12.4 Å, where rij is the distance between interacting sites, and 10° for the angle-dependent bonded potentials. The simulation proceeds through perturbations of all dihedral angles and spatial perturbations of backbone monomers.
The surface potential is taken to be an integrated form of the Lennard-Jones 6–12 potential in cylindrical coordinates,
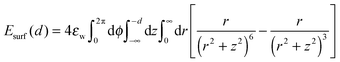 | (2) |
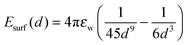 | (3) |
The effective range of Esurf is set equal to the range of long-range interactions, and its value is normalized according to the most hydrophobic residue. Hydrophobic surfaces possess a significant water depletion zone and hence the hydrophilic reference near the surface is not optimal. Future work will aim at improving the chosen force field by introducing a distance-dependent MJ potential with water as a reference.
Fig. 2 depicts the proteins that were chosen for our analysis: lysozyme (lyz) for its prevalence of α-helices, fibronectin (fn) for its prevalence of β-sheets, and a short single helix-containing peptide. Since realistic timescales of protein adsorption27 are beyond computational capabilities of molecular models, we use simulated annealing to overcome local energy minima. We carried out simulations in the reduced temperature (T* = kT/εw) range of 1.0–5.0, which corresponds to 300–400 K, and covers the most characteristic thermal transitions that result in total denaturation of tertiary and secondary structural elements of these proteins.28T* = 1 is assigned to the crystallographic temperature of the protein and T* = 0 corresponds to 273 K, with the following conversion for other temperatures: T (Kelvin) = T (reduced) × [T (crystallographic) − 273)] + 273. Each simulation begins with equilibration of the protein in the absence of the surface under standard conditions for 105 MC steps. Isothermal adsorption and equilibration on the surface follows for additional 105 MC steps. Non-periodic boundaries with unlimited box dimensions are used to model infinitely dilute solution conditions. We have previously shown24 that the force field and MC method cannot predict denaturation under isothermal conditions, and have analyzed the thermal limits of denaturation of three proteins under annealing. Accordingly, simulated annealing simulations with maximal reduced temperatures of 2.5, 3.5 and 5.05 were carried out in this work for lyz, fn, and the peptide, respectively. A combination of rotation, translation and angle perturbations was used to achieve equilibrium conformations. Several independent runs were carried out for each of the annealing simulations. For each run, 105 MC steps were performed at each temperature, of which 7 × 104 MC equilibration steps were followed by 3 × 104 MC steps of sampling every 102 steps.
 | ||
| Fig. 2 Cartoon depiction of lysozyme (left), fibronectin (center) and single-helix peptide (right). PDB structures of 1JSF, 1FBR, and 1MEQ, respectively. | ||
3. Results and discussion
Hydrophobicity scales define the relative hydrophobicity of amino acid residues, where the more hydrophobic residues have higher positive values. Out of 37 hb scales examined by Cornette et al.,29 three (BULDG,19,20,30 ABODR21,31 and MIJER32) were deemed to be most relevant for residue surface interactions, and were tested in adsorption simulations of fibronectin. The BULDG scale is based on the effect of varying concentrations of each amino acid on the surface tension of water. The ABODR scale measures the mobility of the amino acids on chromatography paper and might therefore be appropriate for adsorption processes. The MIJER scale is based on contact energies between amino acids within proteins taken from crystallographic data, and is the basis of the knowledge-based potential set used in this simulation. Most of the remaining hb scales are based on measures of the accessibility of the amino acids or energy of transfers between water and alcohols. The values of the three selected hydrophobicity indices of different amino acids normalized according to the work of ref. 29 are compared in Fig. 3. The hydrophobic residues (Met, Val, Trp, Tyr, Ile, Phe, and Leu) appear to be in much better agreement among the three scales than the hydrophilic residues. But generally the statistical MIJER hb scale assigns more positive indices than the experimental hb scales.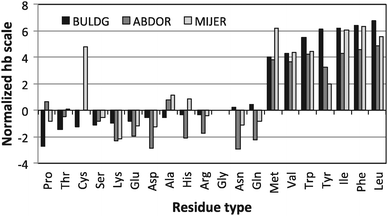 | ||
| Fig. 3 Value of the hb indexes of BLUDG, ABDOR, and MIJER hb scales normalized according to the work of ref. 29. | ||
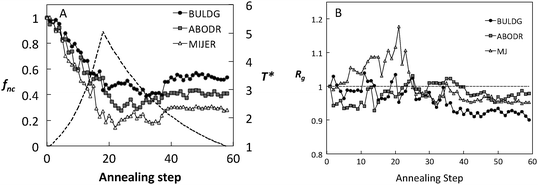
The impact of the hb scale on the average fraction of native contacts, fnc, and the radius of gyration (Rg) is shown in Fig. 4 for fibronectin. Both fnc and Rg reveal significant differences among the hb scales during the course of the simulation. For each scale, fluctuations in these measures seem to stabilize for T* < 3.0 during the cooling cycle. This temperature corresponds to the sharp decrease in the perpendicular component of Rg (Fig. 5B), beyond which the local structural rearrangement occurs. Rg under the ABDOR hp scale seems to be least affected by the variation in temperature and MIJER is the most affected, especially during heating. The MIJER scale also reveals the least stable native contacts. The BULDG scale leads to the greatest reduction in Rg on the one hand, while retaining the most number of native contacts upon heating. Moreover, the BULDG scale shows the greatest ability for regeneration of native contacts for the adsorbed protein upon cooling. The BULDG scale has a high amphipathic index, which encompasses both hydrophobic and hydrophilic elements of native amphipathic α-helices.29 It is likely that there is a close similarity between intermediate folding stages when secondary structural elements are formed in solution and advanced stages of protein adsorption when secondary structures begin to denature. Hence, we concentrate on the BULDG hb scale below.
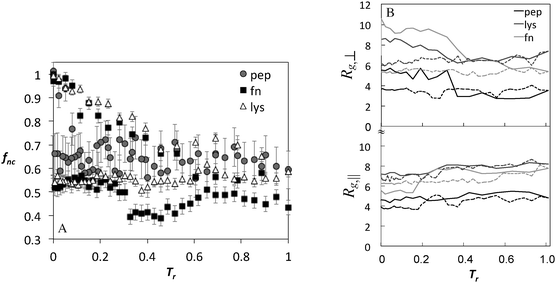
The fraction of native contacts and the components of the radius of gyration as a function of annealing temperature for BULDG scale are plotted in Fig. 5 for the peptide, lyz, and fn, and the changes in Rg are summarized in Table 1. Both the fraction of native contacts and the radius of gyration change significantly during the course of annealing. The adsorbed proteins settle at a conformational landscape characterized by 30–50% reduction in native contacts around T* = 3.0, following the collapse of the perpendicular component of Rg and expansion in the parallel direction. These values are retained in the cooling cycle, suggesting that we are sampling a characteristic conformational landscape of the adsorbed protein. AFM data reveal high statistical variability in the dimensions of the adsorbed proteins,33 but the detected shape that has been most commonly reported is ellipsoidal with an aspect ratio ar (the ratio of lateral to transverse radii components with respect to the surface) ranging from 0.6–0.8, which is somewhat lower that what we observe in our simulation.
| Fibronectin (Rg = 12.5 Å) | Lysozyme (Rg = 12.8 Å) | Peptide (Rg = 7.6 Å) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Adsorption | Heating | Annealing | Adsorption | Heating | Annealing | Adsorption | Heating | Annealing | |
| R g | 1.0 | 1.19 | 0.90 | 0.98 | 1.15 | 0.98 | 1.0 | 1.03 | 0.99 |
| R g,par | 0.88 | 1.09 | 0.87 | 1.04 | 1.27 | 0.98 | 1.08 | 1.17 | 0.90 |
| R g,per | 1.22 | 1.11 | 0.74 | 0.98 | 0.87 | 0.82 | 1.13 | 0.56 | 0.82 |
| a r | 1.39 | 1.02 | 0.85 | 0.94 | 0.69 | 0.84 | 1.05 | 0.48 | 0.91 |
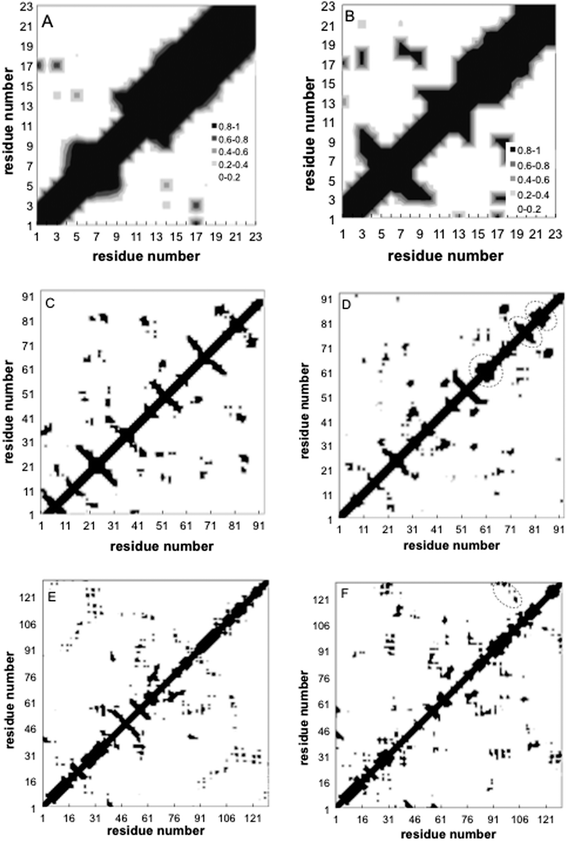
Contact maps showing the average contact probability between different residues before and after annealing, are shown in Fig. 6. For the peptide, the helix persists throughout adsorption, but the internal helical morphology is altered at residues 12–15, where most of the hydrophobic elements are located (Fig. 6A and B). Alteration of the native helical structure causes the appearance of some non-native tertiary contacts as well (between monomers 7–9 and 17–19). For fn, we observe significant denaturation and appearance of several secondary structure elements (Fig. 6C and D). Beta structures 1, 5 and 6 denature completely while 3 new secondary order clusters appear from monomers 65 to 90, one with a characteristic signature of the β sheet. Beta structure 4 undergoes significant perturbations as well, but retains its initial position. In contrast, the contact maps of lyz reveal a more robust protein where most secondary alpha structures and the beta 2 sheet sustain the annealing process, whereas beta 1 completely denatures (Fig. 6E and F). Still, the shape and the area of tertiary contacts on the final map are altered and a new tertiary contact α 6-7,8 appears.
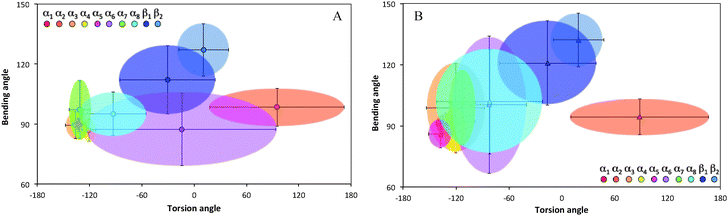
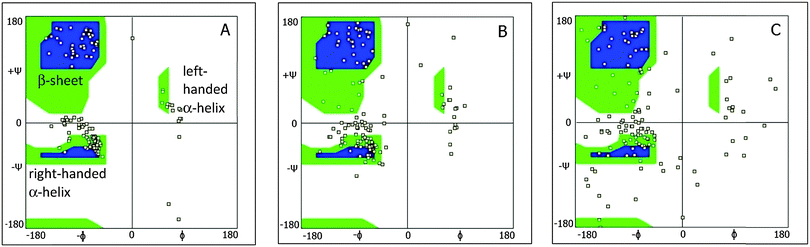
Ramachandran plots allow further examination of the morphological alterations of the internal secondary structures, which are not fully traceable by contact maps. In these plots, the distributions of torsional angles for secondary structure elements are mapped.34 In the coarse-grained model, we cannot use such plots since each residue is represented by two sites, alpha carbon and side chain. Alternatively, we consider the bending-torsion distribution upon annealing, shown in Fig. 7–9. The spread of most secondary structures shifts and widens either in the bending or torsion dimensions, or both. β2 is the most stable element, maintaining nearly the same contour before and after annealing, as was also apparent from the contact maps (Fig. 7). For lysozymes, on the other hand, we observe that the helical elements are still confined to their characteristic regions on the torsion–bending plot, but undergo a significant stretching of the bending angles. β1 completely shifts while β2 remains relatively unchanged. The conformational transformations during annealing of all α-helices in lysozymes as well as the single long peptide α-helix demonstrate consistent deformation upon reduction of the average torsion angle and an increase in the average bending angle. The same pattern of helical deformations that all α-helices share suggests opening and radial stretching. As the hydrophobic residues approach the surface, the helices tend to be more ellipsoidal with different curvatures. The β-sheets of fibronectin demonstrate higher structural variation during annealing than its helices. However, the degree of deformation does not depend on the average hydrophobicity of the lyz helix or change in the surface potential during annealing. In addition to its characteristic length, the decisive factor in defining helical spreading is its stabilization within the protein structure by long-range interactions with nearest neighbor elements. Similar to the helical elements of the lysozyme, the peptide helix undergoes partial denaturation upon adsorption, characterized by significant torsional untwisting.
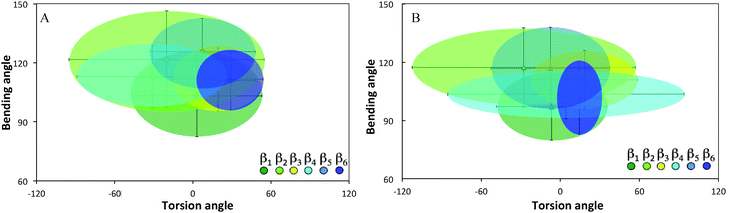 | ||
| Fig. 7 Torsion–bending plots of fibronectin (A) before (native conformation) and (B) after annealing for each of the 6 native beta sheets. | ||
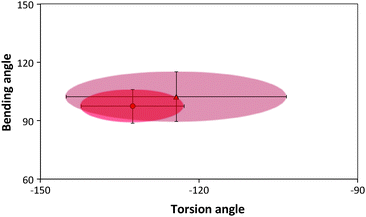 | ||
| Fig. 9 Torsion–bending plots of the peptide before (darker oval) before and after annealing (lighter oval). | ||
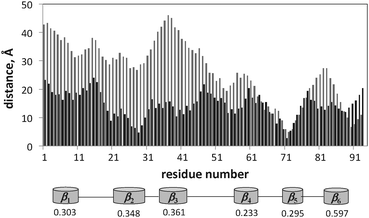
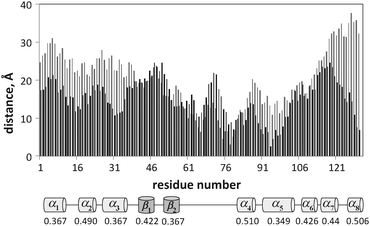
The changes in the average distance from the surface 〈D〉 of the residues for the proteins and peptide are shown in Fig. 10–12. After adsorption, lyz monomers are on average 43% closer to the surface relative to the initial distances, while fn monomers are on average 57% closer. However, the final average distance of the monomers is similar for the two proteins (〈D〉lyz = 17.5 Å and 〈D〉fn = 16.7 Å), indicating greater structural rearrangement of fn. But a correlation between the hb index of the secondary structure elements and the decrease in the average distance during annealing could not be determined. Fig. 11 reveals that lyz residues in the approximate range of 50–100 are closer to the surface than others. This range corresponds to the coiled region and the nearby helices and sheets. There is theoretical evidence that this portion of the protein corresponds to the weaker portion of the protein35 and denatures first upon adsorption.22
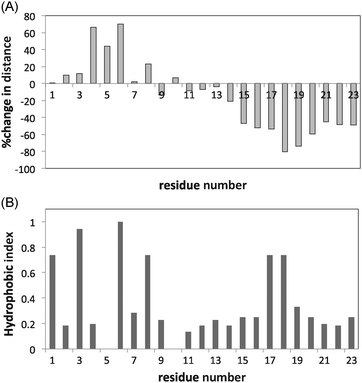
There appears to be a relationship between the total decrease in the distance (%) and the hb indices of the monomers for the peptide (Fig. 12). It is clearly seen that the hydrophobic amino acids 17–19 (VAL and VAL respectively) approach the surface. Since no such relationship is noticeable for the proteins, this strengthens the notion that the conformational complexity of the protein, which is absent in peptides, determines adsorption and denaturation. For proteins, the long-range monomer–monomer interactions compensate for the surface hydrophobic potential.
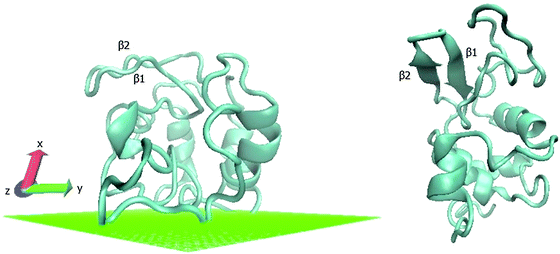
Structural changes in the protein upon absorption may crucially affect the activity of the protein. Enzymatic activity is highly affected by the reorganization of the electronic structure of those atoms involved in the reaction. We obtained a rough indication of the potential effects on enzymatic activity due to structural changes upon adsorption by reconstructing the atomistic coordinates of the protein followed by analysis of the electronic properties of the helices and sheets. We used the program PULCHRA36 for rebuilding the atomic coordinates of the adsorbed lysozyme, averaged over equilibrated annealed conformations, as described by Rotkiewicz and Skolnick.37 Lysozyme coordinates 1JSF listed in the RCSB Protein Data Bank PDB38,39 were used as reference. The α-carbons of the final annealing step were submitted as PULCHRA input for generating atomic coordinates of the adsorbed protein, while the α-carbons of the original PDB conformation were used for rebuilding the protein in solution. The 3-dimensional presentations of optimized adsorbed and native conformation, shown in Fig. 13 are plotted with the Structural Identification algorithm (STRIDE40) incorporated in the VMD package.41,42
Ramachandran plots of the absorbed protein and the rebuilt protein in solution versus original PDB conformation are shown in Fig. 14. The plot of the protein obtained from PDB coordinates show a smaller angle distribution than the rebuilt conformations. Rebuilding combined with MM optimization leads to a more relaxed structure. This is also due in part to the reduced water content in the protein structures obtained from crystallographic data.37 The observed distortion of helical secondary elements and dissolution of two beta-sheets during the adsorption process are consistent with torsion–bending angle distributions (Fig. 8).
We further analyzed the conformational changes upon adsorption using first principle studies. Single Point Energy (SPE) calculations have been performed using the Jaguar 7.9 tool of the Schrödinger package43,44 in the gas phase at the B3LYP/6-31G* hybrid DFT level of theory using 6D functions at fully analytic accuracy for the regenerated atomistic coordinates. The dimensionless energy data listed in Table 2 have been calculated according to e* = f* (Ei,surf − Ei,bulk)/|Epdb − Ebulk| where f* is the normalized average fraction of the energy term, and the quantity |Epdb − Ebulk| represents the noise inherent to the rebuilding procedure. The surface potential was neglected during these calculations. From Table 2, we observe that most of the helical structures show a clear decrease in repulsive contributions to the Hamiltonian upon adsorption and an overall increase in the internal energy for these secondary elements, suggesting destabilization of the adsorbed structures. Beta sheet 1, in contrast, shows the opposite trend. Indeed, adsorption of lysozyme on hydrophobic surfaces reveals the appearance of beta sheets as well as a decrease in helical content.7
| Energy term, dimensionless | α1 | α2 | α3 | α4 | β1 | β2 |
|---|---|---|---|---|---|---|
| Nuclear repulsion | −22 | −13 | −1.3 | −16 | +9.7 | −8.6 |
| Total one-electron terms | +51 | +37 | +3.7 | +45 | −26.1 | +25.2 |
| Total two-electron terms | −18.8 | −16.1 | −1.6 | −19.6 | +10.8 | −11.3 |
| Coulomb | −18.9 | −16.0 | −1.6 | −19.6 | +10.7 | −11.4 |
| Exchange + correlation | −1.0 | +0.025 | −0.0050 | −0.00035 | −0.012 | −0.0022 |
| Electronic energy | +30 | +18 | +1.9 | +23 | −14 | +12 |
| Total energy | +9.3 | +8.1 | +0.79 | +9.6 | −5.7 | +5.2 |
The number of hydrogen bonds, determined using the Maestro tool of the Schrödinger package, is listed in Table 3 for the secondary structures and for the entire protein. Hydrogen bonding within the secondary structures follows a similar trend to that observed in the angle distribution of the adsorbed protein (Fig. 7–9). A significant decrease in the total number of hydrogen bonds in the adsorbed protein corresponds to the observed distortion of the secondary structures of the proteins upon adsorption. The difference in amount of hydrogen bonds is 6% between native PDB conformation and the rebuilt one, giving an indication of the rebuilding efficiency.
| Conformation | α1 | α2 | α3 | α4 | β1 | β2 | Total |
|---|---|---|---|---|---|---|---|
| Original PDB | 5 | 5 | 6 | 4 | 0 | 1 | 148 |
| Rebuilt PDB (bulk) | 10 | 4 | 7 | 4 | 3 | 3 | 139 |
| Rebuilt adsorbed (surf) | 9 | 5 | 7 | 2 | 3 | 2 | 118 |
4. Conclusions
In our previous work we analyzed adsorption of globular proteins at constant temperature using a coarse-grained model. Our analysis revealed minor conformational changes for single proteins adsorbed on a hydrophobic surface under the MJ force field. In this work, we performed simulated annealing to obtain the equilibrium adsorbed conformation that would otherwise require unmanageable computational timescales under realistic conditions. We carried out a detailed analysis of protein adsorption on a hydrophobic surface using three different hb scales, and chose to concentrate on the BULDG due to the greater stability of native contacts of this hb scale. A correlation between the hb indices and the distance of the monomers from the surface upon adsorption could not be found. The observed decrease in energy following adsorption was in the 35–75% range and depends on conformational stiffness of the native protein. Differences in the behavior of secondary structures were apparent, in particular, α-helices undergo spreading as the hydrophobic residues approach the hydrophobic surface while the β-sheets lose their structure due to their higher hydrophobicity compared with α helices.Contributions to the intramolecular interactions were analyzed using all-atom rebuilding of the adsorbed CG model. Dissimilarities in the behavior of helices and sheets were characterized at the DFT level of theory pointing to the appearance of more dense and stabilized beta sheets with a higher hb index. These calculations confirm that secondary structures are destabilized by adsorption. Such a multiscale approach applied to the active site of, e.g., immobilized proteins may potentially be used to predict their functional properties as well as be applied for modeling, e.g., biosensors and bioreactors.
Acknowledgements
YM thanks Prof. Turkan Haliloglu for providing the original coarse-grained Monte Carlo code, Irena Yungerman for MPI computing, and Dr Chris Barnett for fruitful discussions and his advice on electronic structure analysis. This research was supported, in part, by the Israel Science Foundation.References
- L. Shang, Y. Wang, J. Jiang and S. Dong, Langmuir, 2007, 23, 2714–2721 CrossRef CAS PubMed.
- S. Franz, S. Rammelt, D. Scharnweber and J. C. Simon, Biomaterials, 2011, 32, 6692–6709 CrossRef CAS PubMed.
- T. Horbett, in Biopolymers at Interfaces, ed. M. Malmsten, CRC Press, 2003 Search PubMed.
- G. Anand, S. Sharma, A. K. Dutta, S. K. Kumar and G. Belfort, Langmuir, 2010, 26, 10803–10811 CrossRef CAS PubMed.
- M. Rabe, D. Verdes and S. Seeger, Adv. Colloid Interface Sci., 2011, 162, 87–106 CrossRef CAS PubMed.
- D. Barthes-Biesel, Microhydrodynamics and Complex Fluids, CRC Press, 2012 Search PubMed.
- A. Sethuraman and G. Belfort, Biophys. J., 2005, 88, 1322–1333 CrossRef CAS PubMed.
- D. T. Kim, H. W. Blanch and C. J. Radke, Langmuir, 2002, 18, 5841–5850 CrossRef CAS.
- S. Y. McLoughlin, M. Kastantin, D. K. Schwartz and J. L. Kaar, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 19396–19401 CrossRef CAS PubMed.
- H. Pan, M. Qin, W. Meng, Y. Cao and W. Wang, Langmuir, 2012, 28, 12779–12787 CrossRef CAS PubMed.
- R. L. Baldwin, Nature, 1994, 369, 183–184 CrossRef CAS PubMed.
- S. Srebnik, A. K. Chakraborty and E. I. Shakhnovich, Phys. Rev. Lett., 1996, 77, 3157–3160 CrossRef CAS.
- S. Srebnik, A. K. Chakraborty and D. Bratko, J. Chem. Phys., 1998, 109, 6415–6419 CrossRef CAS PubMed.
- L. Haggerty and A. M. Lenhoff, Biophys. J., 1993, 64, 886–895 CrossRef CAS.
- Y. Schmitt, H. Hähl, C. Gilow, H. Mantz, K. Jacobs, O. Leidinger, M. Bellion and L. Santen, Biomicrofluidics, 2010, 4, 32201 CrossRef CAS PubMed.
- Y. Wei, A. A. Thyparambil and R. A. Latour, Colloids Surf., B, 2013, 110, 363–371 CrossRef CAS PubMed.
- L. M. Szott and T. A. Horbett, Curr. Opin. Chem. Biol., 2011, 15, 683–689 CrossRef CAS PubMed.
- C. Mücksch and H. M. Urbassek, PLoS One, 2013, 8, e64883 Search PubMed.
- I. Bahar, B. Erman, T. Haliloglu and R. L. Jernigan, Biophys. J., 1997, 36, 13512–13523 CAS.
- I. Bahar and R. L. Jernigan, J. Mol. Biol., 1997, 266, 195–214 CrossRef CAS PubMed.
- A. M. Al-Mekhnaqi, M. S. Mayeed and G. M. Newaz, Mol. Simul., 2009, 35, 292–300 CrossRef CAS.
- S. Wei and T. A. Knotts, J. Chem. Phys., 2013, 139, 095102 CrossRef PubMed.
- Y. Okamoto, Comput. Phys. Commun., 2001, 142, 55–63 CrossRef CAS.
- Y. Moskovitz and S. Srebnik, Phys. Chem. Chem. Phys., 2012, 14, 8013–8022 RSC.
- T. Haliloglu and I. Bahar, Proteins: Struct., Funct., Genet., 1998, 31, 271–281 CrossRef CAS.
- S. Miyazawa and R. L. Jernigan, J. Mol. Biol., 1996, 256, 623–644 CrossRef CAS PubMed.
- J. J. Gray, Curr. Opin. Struct. Biol., 2004, 14, 110–115 CrossRef CAS PubMed.
- D. F. Nicoli and G. B. Benedek, Biopolymers, 1976, 15, 2421–2437 CrossRef CAS PubMed.
- J. L. Cornette, K. B. Cease, H. Margalit, J. L. Spouge, J. A. Berzofsky and C. DeLisi, J. Mol. Biol., 1987, 195, 659–685 CrossRef CAS.
- H. B. Bull and K. Breese, Arch. Biochem. Biophys., 1973, 156, 604–612 CrossRef CAS.
- A. A. Aboderin, Int. J. Biochem., 1971, 2, 537–544 CrossRef CAS.
- S. Miyazawa and R. L. Jernigan, Macromolecules, 1985, 18, 534–552 CrossRef CAS.
- A. Ikai, R. Afrin and H. Sekiguchi, Curr. Nanosci., 2007, 3, 17–29 CrossRef CAS.
- G. N. Ramachandran, C. Ramakrishnan and V. Sasisekharan, J. Mol. Biol., 1963, 7, 95–99 CrossRef CAS.
- S. Wei and T. A. Knotts IV, J. Chem. Phys., 2011, 134, 185101 CrossRef PubMed.
- P. Rotkiewicz and J. Skolnick, http://cssb.biology.gatech.edu.
- P. Rotkiewicz and J. Skolnick, J. Comput. Chem., 2008, 29, 1460–1465 CrossRef CAS PubMed.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS PubMed.
- http://rcsb.org .
- D. Frishman and P. Argos, Proteins: Struct., Funct., Genet., 1995, 23, 566–579 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- http://ks.uiuc.edu .
- A. D. Bochevarov, E. Harder and T. F. Hughes, Int. J. Quantum Chem., 2013, 113, 2110–2142 CrossRef CAS.
- http://schr http://ö http://dinger.com .
| This journal is © the Owner Societies 2014 |