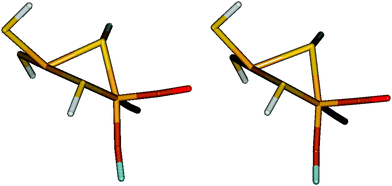Accurate calculations of geometries and singlet–triplet energy differences for active-site models of [NiFe] hydrogenase

Abstract

We have studied the geometry and singlet–triplet energy difference of two mono-nuclear Ni²⁺ models related to the active site in [NiFe] hydrogenase. Multiconfigurational second-order perturbation theory based on a complete active-space wavefunction with an active space of 12 electrons in 12 orbitals, CASPT2(12,12), reproduces experimental bond lengths to within 1 pm. Calculated singlet–triplet energy differences agree with those obtained from coupled-cluster calculations with single, double and (perturbatively treated) triple excitations (CCSD(T)) to within 12 kJ mol⁻¹. For a bimetallic model of the active site of [NiFe] hydrogenase, the CASPT2(12,12) results were compared with the results obtained with an extended active space of 22 electrons in 22 orbitals. This is so large that we need to use restricted active-space theory (RASPT2). The calculations predict that the singlet state is 48–57 kJ mol⁻¹ more stable than the triplet state for this model of the Ni–SI_a state. However, in the [NiFe] hydrogenase protein, the structure around the Ni ion is far from the square-planar structure preferred by the singlet state. This destabilises the singlet state so that it is only ∼24 kJ mol⁻¹ more stable than the triplet state. Finally, we have studied how various density functional theory methods compare to the experimental, CCSD(T), CASPT2, and RASPT2 results. Semi-local functionals predict the best singlet–triplet energy differences, with BP86, TPSS, and PBE giving mean unsigned errors of 12–13 kJ mol⁻¹ (maximum errors of 25–31 kJ mol⁻¹) compared to CCSD(T). For bond lengths, several methods give good results, e.g. TPSS, BP86, and M06, with mean unsigned errors of 2 pm for the bond lengths if relativistic effects are considered.

---

1 Introduction

The hydrogenases are a group of enzymes that catalyse the reversible conversion of H₂ to protons and electrons. In nature, three types of hydrogenases are known, depending on the constitution of the active site, [Fe], [FeFe], and [NiFe] hydrogenases.¹ The active site of the [NiFe] hydrogenases contains a Ni ion that is coordinated to four cysteine side chains^1,2 as can be seen in Fig. 1. Two of these bridge to the Fe ion, which also has one CO and two CN⁻ ligands.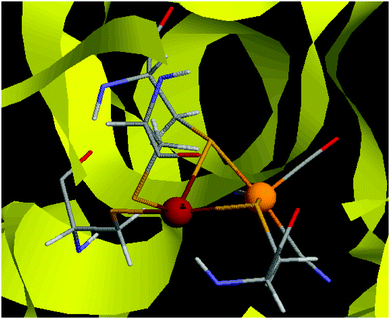

Fig. 1 The active site of [NiFe] hydrogenase.⁶⁵ The Ni ion is to the left, the Fe ion to the right.

The [NiFe] hydrogenases have been extensively studied by both experimental and theoretical methods.^1–6 Several distinct states of the enzyme have been characterised, depending on the oxidation state of the metal ions and the coordination of extraneous ligands to the bimetal site.¹ The current consensus is that the Fe ion remains in the low-spin Fe²⁺ state throughout the catalytic cycle, whereas the Ni ion cycles between the Ni²⁺ and Ni³⁺ states, although the Ni⁺ state may also be involved.

However, the spin state of the Ni²⁺ ion is not clear. In small inorganic complexes, low-spin Ni²⁺ (which is d⁸) normally forms square-planar complexes owing to the Jahn–Teller effect.^7,8 However, with bulky ligands, high-spin tetrahedral complexes can be obtained.⁹ Crystal structures of [NiFe] hydrogenases show a Ni structure that is intermediate between square planar and tetrahedral with S–Ni–S angles of 70°–170° and a twist angle between the planes formed by the Ni ion and the two bridging cysteine sulphur atoms or the Ni ion and the two terminal cysteine sulphur atoms (ϕ) of ∼70° (ϕ = 0° for a perfect square-planar structure and 90° for a tetrahedral structure).^2,10 Several experimental studies have been performed, but they give varying results for the spin state of the Ni ion: magnetic circular dichroism (MCD) spectroscopy,¹¹ electron paramagnetic resonance (EPR) spectroscopy¹² and magnetic saturation techniques¹³ suggest a low-spin state, whereas L-edge X-ray absorption spectroscopy¹⁴ indicates a high-spin state.

The situation is similar in theoretical calculations: various flavours of density functional theory (DFT) give different ground states. For example, hybrid functionals like B3LYP suggest a high-spin state, whereas pure functionals like BP86 favour the low-spin state.^10,15–19 This is a major obstacle for theoretical studies of the [NiFe] hydrogenases and there is an urgent need to assess the quality of the various functionals. Multiconfigurational methods are promising candidates for such an application.^20,21

A few years ago, Jayapal et al. compared the BP86 and B3LYP DFT functionals to multireference Møller–Plesset second-order perturbation theory (MRMP2²²) calculations of the Ni–SI_a state of [NiFe] hydrogenase and concluded that BP86 is the best functional to describe such systems.¹⁸ Unfortunately, they used only small active spaces (four or six active orbitals) for their MRMP2 calculation, which may make the results unreliable.

To check this possibility, we present in this paper multiconfigurational calculations on three different models of the [NiFe] hydrogenase with appropriate active spaces, according to the experience gained from other transition-metal complexes.^23,24 We also study how well different DFT functionals reproduce the obtained geometries and the singlet–triplet energy difference. When available, experimental data, as well as accurate coupled-cluster calculations with single, double and (perturbatively treated) triple excitations (CCSD(T)), are also used to confirm the quality of the calculations.

2 Methods

Three small models were studied, which are shown in Fig. 2. The first two models contain only a Ni²⁺ site: [Ni(SH)₄]²⁻ and [Ni(edt)₂]²⁻ (where edt = ethane 1,2-dithiolate, [SCH₂CH₂S]²⁻), the latter being an experimentally characterised complex.²⁵ The third model is a more realistic bimetallic model of the [NiFe] hydrogenase active site in the catalytically active Ni–SI_a state, [(SH)₂Ni(SH)₂Fe(CO)(CN)₂]²⁻, hereafter called the NiFe model. It is essentially the same model as that Jayapal et al. used¹⁸ except that the methyl groups are replaced by hydrogen atoms. [Ni(SH)₄]²⁻ was studied in C₂ symmetry for both the singlet and triplet states. The [Ni(edt)₂]²⁻ complex was studied in D₂ and C₂ symmetry for the singlet and triplet geometries, respectively, whereas the NiFe model was studied in C_s symmetry for both states.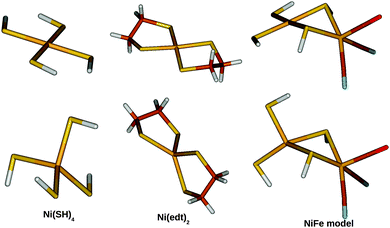

Fig. 2 The three model systems used in this study: [Ni(SH)₄]²⁻ (left), [Ni(edt)₂]²⁻ (middle), and the NiFe model (right). Singlet structures are shown at the top and triplet structures at the bottom.

Calculations were performed with second-order multiconfigurational perturbation theory on a complete active-space wavefunction (CASPT2) or on a restricted active-space wavefunction (RASPT2). ANO-RCC basis sets²⁶ of three different sizes were employed, as described in Table 1. BS1 was used for the geometry optimizations, whereas all three basis sets were used for energy calculations. Scalar relativistic effects were included using the Douglas–Kroll–Hess approach to second order.^27,28 Cholesky-derived auxiliary basis sets acCD²⁹ with a default threshold of 10⁻⁴ a.u. was used for the geometries whereas the full Cholesky approach with a threshold of 10⁻⁶ a.u. was used for energies, to speed-up the calculations without sacrificing the accuracy.^30,31 A parallel implementation of the CASPT2/RASPT2 method was used to further speed-up the largest calculations.³²

Table 1 Contractions used for the three ANO-RCC basis sets used in this investigation

Name	Ni	S	C	H
BS1	[6s5p3d2f1g]	[5s4p2d1f]	[4s3p2d1f]	[3s2p1d]
BS2	[7s6p4d3f2g1h]	[5s4p2d1f]	[4s3p2d1f]	[3s1p]
BS3	[7s6p4d3f2g1h]	[6s5p3d2f1g]	[5s4p3d2f1g]	[4s3p2d1f]

---

For the [Ni(SH)₄]²⁻ and [Ni(edt)₂]²⁻ models, the active space consisted of 12 electrons in 12 orbitals, CAS(12,12). This active space contains all Ni 3d orbitals and a second set of correlating d orbitals (which is often referred to as 3d′) to account for the so-called double-shell effect.³³ In addition, two bonding orbitals between Ni and the ligands were included. In the triplet state, there are two bonding orbitals (corresponding to the two singly occupied Ni 3d orbitals) that may be involved in covalent metal–ligand bonding (in particular in the tetrahedral structure), whereas in the singlet structure there is only one such orbital, i.e. the one corresponding to the unoccupied Ni 3d orbital. Including an extra bonding orbital in the calculation of the singlet state is not straightforward, because this orbital tends to rotate out of the active space in favour of some other orbital, e.g. a core orbital. This problem was solved by first calculating the triplet state (at the singlet structure) with CAS(12,12), and then keeping the concerned bonding orbital fixed (with the supsym option) in the active space when calculating the singlet state. It should be noted that the CASPT2(12,12) energy obtained in this way for the singlet state matches the CASPT2 energy obtained for the same state with a CAS(10,11) reference wavefunction (i.e. with the extra bonding orbitals kept inactive) to within a few tenths of a kJ mol⁻¹. This proves that the extra bonding active orbital is completely unimportant for the singlet state. However, this additional orbital has a significant effect on the CASPT2 energy of the triplet state, affecting the singlet–triplet energy difference by up to 10 kJ mol⁻¹.

For the larger NiFe model, the CASPT2(12,12) calculations were compared to calculations with a larger active space, in which ten orbitals arising from the Fe centre were added, viz. the five Fe 3d orbitals, three Fe 3d′ orbitals (i.e. only for the occupied 3d orbitals) and two bonding ligand orbitals corresponding to the unoccupied Fe 3d orbitals. This gives a total of 22 electrons in 22 orbitals, which is intractable with current CASSCF/CASPT2 technology. Therefore, RASSCF/RASPT2 was used instead. For the singlet state, the second bonding orbital on Ni was left out of the active space (making use of the experience from the calculations on the two smaller models, showing that including the second ligand orbital does not alter the CASPT2 energy of the singlet state to any significant extent), thus giving a global RAS(20,21) space. The global active space of the RASSCF calculations was further subdivided as RAS(20,4,4;9,2,10) for the singlet versus RAS(22,4,4;8,4,10) for the triplet state, i.e. with the empty or singly occupied Ni 3d orbitals as well as their bonding ligand counterpart in the RAS2 space. In these RASSCF calculations, up to quadruple excitations were allowed out of RAS1 and into RAS3. This is essential to describe the combined double-shell effect on both metal centres.^34,35 A plot of the active orbitals obtained from the RAS(20,4,4;9,2,10) calculation on the NiFe singlet state is provided in Fig. 3. Similar plots for the other models and states are included in Fig. S1–S3 in the ESI.†

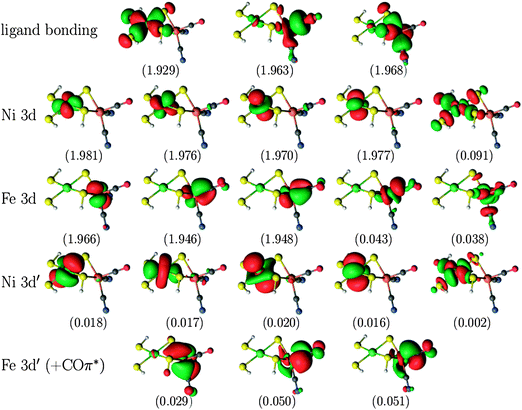Fig. 3 Active natural orbitals and their occupation numbers resulting from the RAS(20,4,4;9,2,10) calculation on the singlet state of the NiFe model.

For all three models, CCSD(T)³⁶ calculations were also performed on structures optimised with the CASPT2 ([Ni(SH)₄]²⁻ and [Ni(edt)₂]²⁻) or M06 (NiFe model) methods, using the ANO-RCC basis sets BS1 and BS2.

Moreover, the results were compared to calculations with DFT methods. Four DFT methods were studied with the BS1 basis set: B3LYP³⁷ and BP86,^38,39 as in the studies by Jayapal and Bruschi,^17,18 as well as the M06 and M06-L functionals,⁴⁰ which have been specifically parametrised for transition metal complexes.

In the CASPT2, RASPT2, and CCSD(T) calculations, all valence electrons were correlated, including the Ni and Fe 3s and 3p electrons. The CASPT2 calculations were performed with the standard IPEA (0.25-)shifted zeroth-order Hamiltonian⁴¹ and an imaginary level shift of 0.1 a.u. The CCSD(T) calculations on the triplet state were performed starting from a ROHF wavefunction, and with restrictions on the amplitudes, such that the linear part of the wavefunction becomes a spin eigenfunction.⁴² The CASPT2 and RASPT2 calculations, as well as the DFT calculations with basis set BS1, were performed using the MOLCAS⁴³ program package, whereas for the CCSD(T) calculations we used the MOLPRO software.⁴⁴

For the [Ni(SH)₄]²⁻ and [Ni(edt)₂]²⁻ models, full geometry optimizations were performed with all methods (except CCSD(T), which employed the CASPT2 structures) and the BS1 basis set. The CASPT2 optimisation employed numerical gradients. However, a geometry optimization of the NiFe model at the RASPT2 level was too costly. Therefore, based on the results for the other two models, the RASPT2 and CCSD(T) calculations were performed on a structure optimised with the M06 functional.

In addition, ten DFT functionals were tested using the Turbomole software⁴⁵ and the def2-TZVP basis set⁴⁶ (always with fully optimised structures): SVWN,^47,48 BP86,^38,39 BLYP,^38,49 PBE,⁵⁰ TPSS,⁵¹ B97-D,⁵² TPSSH,⁵³ B3LYP,³⁷ PBE0,⁵⁴ and BHLYP.⁵⁵ The def2-TZVP basis set has been shown to give singlet–triplet energy differences within 1 kJ mol⁻¹ of those obtained with the larger cc-pVQZ basis set.¹⁰ The calculations with the semi-local functionals were sped up by expansion of the Coulomb interactions in auxiliary basis sets, the resolution-of-identity (RI) approximation.^56,57 For three of the methods (BP86-D, B3LYP-D, and B97) we also tested to include the DFT-D2 empirical dispersion correction in the calculations (both for geometries and energies).^58,59

Finally, we also studied some models with relevance to the protein structure. First, we employed singlet and triplet structures of the Ni–SI_a state in [NiFe] hydrogenase from Desulfovibrio fructosovorans, obtained with quantum refinement (X-ray crystallographic refinement supplemented by combined QM and molecular mechanics, QM/MM, calculations^60,61).⁶² From these, we cut out either the normal NiFe model, or the larger [(SCH₃)₂Ni(SCH₃)₂Fe(CO)(CN)₂]²⁻ model. Second, we calculated standard QM/MM structures (without restraints to the X-ray structure) for the singlet and triplet structures of the Ni–SI_a, using the ComQum software.^63,64 They were based on the same crystal structure of [NiFe] hydrogenase from Desulfovibrio fructosovorans,⁶⁵ after addition of protons and solvation water molecules, and after a molecular dynamics equilibration of the whole structure.⁶⁶ The QM/MM calculations employed the def2-SV(P) basis set,⁴⁶ the Amber 99SB force field,⁶⁷ and either the TPSS or BP86 functionals. In these calculations, the QM system consisted of the [(SCH₃)₂Ni(SCH₃)₂Fe(CO)(CN)₂]²⁻ model, enhanced by a protonated (neutral) acetate group, as a model of Glu-25, which forms a hydrogen bond to the Cys-543 ligand, and a protonated (positively charged) imidazole group as a model of His-79, which forms a hydrogen bond to the Cys-546 ligand, in total 46 atoms.⁶² In one set of TPSS calculations, this QM system was enlarged to 763 atoms (single-point energy) by including all atoms within 4.5 Å of the central [(SCH₃)₂Ni(SCH₃)₂Fe(CO)(CN)₂]²⁻ model, all buried charged groups connected to the active site, and moving any cut bonds at least three residues away from the active site.^66,68

3 Results and discussion

In this paper, we study three simple Ni complexes (shown in Fig. 2) related to the active site in [NiFe] hydrogenase with three accurate wavefunction methods, CASPT2, RASPT2, and CCSD(T). We also compare the results with those obtained with DFT methods. We start by discussing geometries, especially those of the [Ni(edt)₂]²⁻ complex, for which accurate experimental data are available for the singlet state.²⁵ Then, we compare the singlet–triplet energy difference, which is expected to be even more sensitive to the level of theory.^10,17

3.1 Geometries

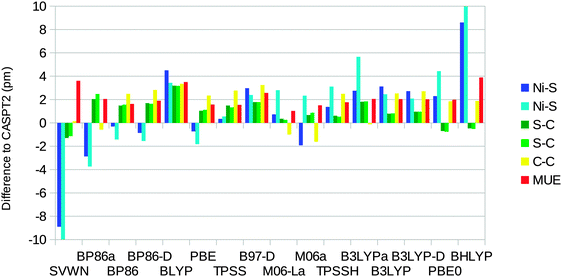
The optimised structures of the singlet state of the [Ni(edt)₂]²⁻ complex have D₂ symmetry (even when started from an asymmetric structure and optimised without symmetry constraints). Therefore, there is only one distance of each kind. On the other hand, the experimental structure²⁵ has two slightly different Ni–S bonds (219.1 and 219.8 pm). The uncertainties in the experimental distances are 0.1, 0.6, and 0.8 pm for the Ni–S, S–C, and C–C bond lengths respectively.

Fig. 4 shows how well the optimised structures reproduce the experimental data. It can be seen that the CASPT2 method reproduces the experimental geometry excellently, with errors of only ∼1 pm for all three distances. Among the DFT functionals, all methods except SVWN overestimate the bond lengths, by up to 9 pm. The BP86 and B3LYP calculations performed using the MOLCAS software and the BS1 basis set give slightly better results than the corresponding Turbomole calculations. This is caused by differences in the basis set: turning off the Douglas–Kroll–Hess treatment of the relativistic effects changes the bond lengths by only 0.3 pm (for B3LYP), whereas shifting to the ANO-L basis set of equal size changes the three distances by 0.3–2.8 pm, increasing the mean unsigned error (MUE) from the experimental structure to 4.5 pm, i.e. close to the results obtained with Turbomole. However, the only difference between the ANO-L and ANO-RCC basis sets is that the latter was designed for relativity, so in the end, the difference is caused by relativistic effects.

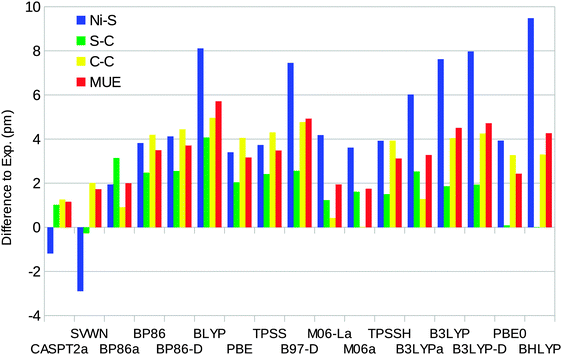Fig. 4 Errors of CASPT2 and the various DFT methods compared to experiments for the singlet-state geometry of the [Ni(edt)₂]²⁻ model (a negative sign indicates that the calculated distance is too short). Calculations with methods ending with “a” were performed using the MOLCAS software and the BS1 basis set. MUE is the mean unsigned error. The experimental results are 219.5, 181.5, and 147.8 pm for the Ni–S, S–C, and C–C bonds, respectively (after correction of a puckering disorder of the Ni–S–C–C–S five-rings¹⁷).²⁵

The DFT-D2 dispersion correction gives very small changes (up to 0.3 pm), which do not improve the results. The SVWN and M06 methods give results closest to experiments, with MUEs of 1.7 pm. BLYP gives the largest MUE of 6 pm and BHLYP gives the largest individual difference of 9 pm for the Ni–S distance.

For the triplet state, no experimental results are available. Based on the results for the singlet, we use the CASPT2 results as the reference instead. The optimised triplet state has C₂ symmetry, so there are two distinct instances of each distance. For the triplet, the DFT methods give more varying results, with errors in the Ni–S distances from −10 pm for SVWN to 10 pm for BHLYP (Fig. 5). TPSS gives the smallest errors, less than 1 pm for both Ni–S distances. For the S–C and C–C distances, the variation is much smaller, up to 3 pm. However, for the C–C distance, all Turbomole calculations, except that with SVWN, give too long bonds of 2–3 pm. On average, the M06-L method gives the smallest errors with a MUE of 1 pm. The SVWN and BHLYP methods give the largest MUE of 4 pm.

Fig. 5 Errors of the various DFT methods with respect to the CASPT2 geometry for the triplet state of the [Ni(edt)₂]²⁻ model. Calculations with methods ending with “a” were performed using the MOLCAS software and the BS1 basis set. With all methods, the two C–C distances are equal. The CASPT2 results were 230.6 and 231.7 pm for the Ni–S distances, 182.5 and 183.2 pm for the S–C distances, and 150.0 pm for the C–C distances.

Finally, we note that the DFT results for both spin states are somewhat different from those found by Bruschi et al.¹⁷ (our Ni–S bonds are ∼4 pm shorter). The reason for this is that we use slightly different basis sets (although both are of triple-zeta quality).

We have also optimised the structure of the [Ni(SH)₄]²⁻ model with the CASPT2 method and the various DFT methods in the singlet and triplet states. Both structures have C₂ symmetry, so there are two distinct Ni–S and two S–H distances, although for the singlet, the difference is less than 0.02 pm. The results are presented in Table S1 in the ESI.† As for the [Ni(edt)₂]²⁻ model, SVWN gives the best structure for the singlet state with a MUE of 2 pm compared to the CASPT2 structure. BLYP and BHLYP give the largest MUEs of 6 pm and a maximum error of 11 pm for the Ni–S distance. For the triplet state, M06 gives bond lengths that all agree with CASPT2 within 1 pm. DFT calculations using MOLCAS give significantly smaller errors than the Turbomole calculations, which all give errors of 5–12 pm for at least one Ni–S distance. As usual, SVWN and BHLYP give the largest errors.

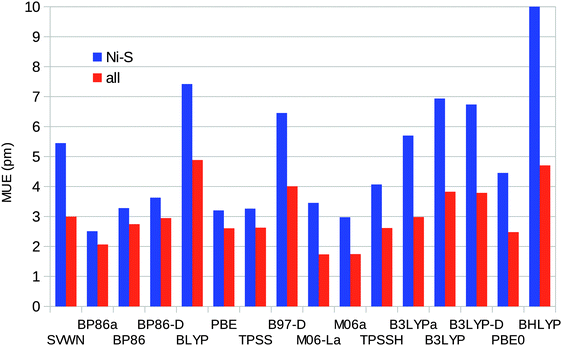
Taking all four complexes together, BP86 calculated using MOLCAS gives the smallest error in the Ni–S distances (MUE = 2.5 pm) and also the smallest maximum error of 4 pm. M06 and M06-L give the smallest average error for all bonds (MUE = 2 pm), as can be seen in Fig. 6. Among the Turbomole calculations, TPSS gives the best Ni–S distances (MUE = 3.2 pm) and also the smallest maximum error (5 pm). PBE0 gives the smallest average error for all bonds (MUE = 2.5 pm), but several other methods have similar MUEs, e.g. TPSS, BLYP, and TPSSH with MUEs of 2.6 pm. BP86, which gives the best results with MOLCAS, has a slightly larger MUE of 2.9 pm.

Fig. 6 Mean unsigned errors of the various DFT methods for the Ni–S or all distances in the [Ni(SH)₄]²⁻ and [Ni(edt)₂]²⁻ models, both singlet and triplet states, with respect to the experimental (the [Ni(SH)₄]²⁻ model in the singlet state) or CASPT2 geometry (other models). Calculations with methods ending with “a” were performed using the MOLCAS software and the BS1 basis set.

Bond lengths for the NiFe model (for which we do not have any reliable reference structures) are presented in Table S2 (ESI†).

3.2 Singlet–triplet energy difference

Next, we looked at the energy difference between the lowest singlet and triplet states (ΔE_ST = E_triplet − E_singlet). We calculated this energy difference both vertically (for the singlet geometry) and adiabatically (for the optimum geometries of the singlet and triplet states, respectively). Table 2 shows the results for the [Ni(SH)₄]²⁻ model obtained with CASPT2 and CCSD(T) with three different basis sets (BS1, BS2, and BS3, described in Table 1).

Table 2 Singlet–triplet energy difference for the [Ni(SH)₄]²⁻ complex in kJ mol⁻¹. The singlet state is ¹A_g in C_2h symmetry, whereas the triplet state is ³A_g for the vertical transition and ³B₃ in its optimum geometry (D₂ symmetry)

Basis set	CASPT2(12,12)	CCSD(T)
At singlet geometry
BS1	86	95
BS2	91	100
BS3	90	99
Adiabatic
BS1	0	−4
BS2	9	5
BS3	12	7

---

It can be seen that the basis-set dependence is modest. The vertical ΔE_ST changes by only ∼4 kJ mol⁻¹ and the adiabatic energies change by 11–12 kJ mol⁻¹ when going from the triple-ζ BS1 to the quadruple-ζ BS3. In particular, the mixed BS2 basis set reproduces the BS3 results within 3 kJ mol⁻¹.

Our best estimates of the adiabatic ΔE_ST for the [Ni(SH)₄]²⁻ model are 12 kJ mol⁻¹ for CASPT2 and 7 kJ mol⁻¹ with CCSD(T), which is a reasonable agreement. For the vertical energy, the results are somewhat more different, 90 and 99 kJ mol⁻¹, respectively. Most importantly, both sets of calculations indicate that the [Ni(SH)₄]²⁻ model has a singlet ground state.

The results for the [Ni(edt)₂]²⁻ model are similar, as can be seen in Table 3. The basis-set dependence is modest: when the basis set is improved, ΔE_ST increases by 4–10 kJ mol⁻¹. In particular, the results obtained with BS2 and BS3 agree within 2 kJ mol⁻¹, which is appropriate because for this larger model, we could not perform the CCSD(T) calculation with the BS3 basis set. Both the CASPT2 and CCSD(T) methods conclusively predict a singlet ground state for this model, in agreement with experiments.²⁵ The two methods give ΔE_ST energies that agree within 9–12 kJ mol⁻¹. As for the [Ni(SH)₄]²⁻ model, CCSD(T) gives a larger difference for the vertical energy and a smaller difference for the adiabatic energy, compared to CASPT2.

Table 3 Singlet–triplet energy difference for the [Ni(edt)₂]²⁻ complex in kJ mol⁻¹. The singlet state is ¹A in D₂ symmetry, whereas the triplet state is ³B₃ for the vertical transition and ³B in its optimum geometry (C₂ symmetry)

Basis set	CASPT2	RASPT2(SD)	RASPT2(SDTQ)	CCSD(T)
At singlet geometry
BS1	114			122
BS2	119	106	113	128
BS3	118
Adiabatic
BS1	52			40
BS2	62	45	56	50
BS3	61

---

In order to check the accuracy of the RASPT2 approach (which will be used for the NiFe model), test calculations with this method were performed for [Ni(edt)₂]²⁻ with the BS2 basis set. We used a RAS2 composition of two orbitals for the singlet and four orbitals for the triplet state (cf. the Methods section) and allowed for either up to double (SD) or quadruple (SDTQ) excitations out of RAS1 and into RAS3. As can be seen from Table 3, ΔE_ST is considerably smaller with RASPT2(SD) than with CASPT2 (by up to 17 kJ mol). With RASPT2(SDTQ) ΔE_ST is significantly increased, but it remains smaller than CASPT2 by 6 kJ mol⁻¹. One may therefore expect a similar underestimation of ΔE_ST with RASPT2 for the NiFe model.

Finally, we also studied the binuclear NiFe model. For this model, both CASPT2 and RASPT2 calculations were performed. For the CASPT2 calculations, the same active space was used as for the Ni-only models, i.e. not including any orbitals centred on Fe. In the RASPT2 calculations, a set of ten orbitals (with ten electrons) on the Fe centre was added to the active space. The subdivision of the RASPT2 active space was the same as that for the [Ni(edt)₂]²⁻ mode and is detailed in the Methods section.

The results of these calculations are listed in Table 4. As before, the basis-set dependence is small and the BS2 basis set gives results that agree with those of the BS3 basis set to within 2 kJ mol⁻¹. All three methods conclusively predict a singlet ground state for the NiFe model, by 61 (CASPT2), 48 (RASPT2), and 57 kJ mol⁻¹ (CCSD(T)). Somewhat strikingly, the CASPT2 results agree more closely with CCSD(T) than the RASPT2 results. In fact, a similar agreement between CASPT2 and CCSD(T) is found as for the smaller complexes, with CASPT2 predicting a slightly smaller vertical ΔE_ST and a slightly larger adiabatic ΔE_ST than CCSD(T). On the other hand, the RASPT2 results are systematically lower than CASPT2 (by 11–13 kJ mol⁻¹). Given that RASPT2 was found to underestimate ΔE_ST also for the [Ni(edt)₂]²⁻ complex, the CASPT2 results in Table 4 might be considered to be more accurate than the RASPT2 results. Apparently, non-dynamical correlation effects on the Fe centre are similar for the singlet and the triplet state, so that the quality of their treatment (in the active space or in the perturbational step) does not significantly affect the relative energy of the two states. This is related to the fact that the singlet–triplet transition is essentially located on the Ni-centre.

Table 4 Singlet–triplet energy difference for the NiFe model in kJ mol⁻¹. The singlet state is ¹A′ in C_s symmetry, whereas the triplet state is ³A′′

Basis set	CASPT2	RASPT2(SDTQ)	CCSD(T)
At singlet geometry
BS1	112	101	124
BS2	117	106	129
BS3	115	104
Adiabatic
BS1	53	41	50
BS2	60	48	57
BS3	61	48

---

The fact that the difference between RASPT2 and CASPT2 is larger for the NiFe model, ∼12 kJ mol⁻¹, than for the [Ni(edt)₂]²⁻ complex, 6 kJ mol⁻¹, might be related to the fact that with two metal centres, a higher-than-four excitation level might be necessary in RASPT2 to obtain the same degree of accuracy compared to the RASPT2(SDTQ) calculation of the Ni-only complex. Therefore, we performed a RASPT2 calculation on the NiFe complex with BS2, in which the excitation level in the RASSCF wavefunction was increased to five. ΔE_ST obtained from this RASPT2(SDTQ5) calculation is 50 kJ mol⁻¹, i.e. 2 kJ mol⁻¹ higher than from the corresponding RASPT2(SDTQ) calculation. A slight further increase might be expected from the inclusion of sextuple and higher excitations in the RASSCF reference wavefunction.

3.3 Multiconfigurational character of the models

An important question when interpreting the results is how large the multiconfigurational character is for these models. Looking at the [Ni(edt)₂]²⁻ model as an example (with the BS2 basis set), we find that at the Hartree–Fock level, the triplet state (at its optimum structure) lies below the singlet state by 266 kJ mol⁻¹, whereas at the correlated level their relative energies are reversed and the triplet energy becomes higher than the singlet energy by 50–60 kJ mol⁻¹. This means that there is a huge correlation effect on ΔE_ST, >300 kJ mol⁻¹. The fact that CCSD(T) and CASPT2 differ in their description of this correlation energy by ∼10 kJ mol⁻¹ is therefore not surprising, nor is the fact that very large basis sets are needed to accurately describe the relative correlation energy of both states.

At the CASSCF(12,12) level, the triplet state still lies below the singlet state by 147 kJ mol⁻¹. An important part of the relative correlation energy may therefore be captured by a multiconfigurational wavefunction including just a limited number of orbitals and configurations. This would indicate that this is indeed a multiconfigurational problem. Other signs are that MP2 completely breaks down, that the effect of triples on the coupled-cluster results is substantial (at the CCSD level, ΔE_ST = −8 kJ mol⁻¹), and that the effect of spin correction on the CCSD(T) energy of the triplet state is substantial. Starting from an appropriate triplet ROHF wavefunction, the difference between the UCCSD(T) and RCCSD(T) energy of the [Ni(edt)₂]²⁻ complex (BS2) amounts to 12 kJ mol⁻¹.

On the other hand, it is likely that this kind of multiconfigurational problem can be properly treated by CCSD(T). For both states, the occupation numbers of the natural orbitals resulting from the CASSCF calculations remain rather close to either zero or two (within 0.09; cf.Fig. 3 and Fig. S1–S3, ESI†). This is also supported by the fact that CASPT2 and CCSD(T) give results that agree to within 3–12 kJ mol⁻¹ in all cases, which is reasonable given the huge correlation energy difference that needs to be captured.

Criteria to judge the multiconfigurational character, and hence the accuracy to be expected from CCSD(T) for transition-metal-containing molecules were recently proposed by Jiang et al.⁶⁹ The following diagnostic criteria were proposed for the computation of reliable d-block energetic and spectroscopic properties using single-reference-based model chemistries: T₁ < 0.05, D₁ < 0.15, and |%TAE| < 10. Here, T₁ and D₁ represent the Frobenius norm and matrix 2-norm of the coupled-cluster amplitudes for single excitations, respectively, whereas |%TAE| stands for the percentage of the (T) contribution to the total atomization energy. A too high |%TAE| value indicates that the effect of the triple correction to the CC results is substantial and hence that CCSD(T) may fail.

The values of T₁, D₁ and |%TAE| obtained from the CC calculations are shown in Table 5. For the two small models, [Ni(SH)₄]²⁻ and [Ni(edt)₂]²⁻, one might safely conclude that non-dynamical correlation effects are limited, even though the D₁ diagnostics are rather large. This indicates that the CCSD(T) results for these two complexes should be reliable. On the other hand, for the NiFe model, both the D₁ and T₁ diagnostics are above the limits although the values of |%TAE| are still below 10%. This shows that non-dynamical correlation effects become more important in the bimetal complex, putting some doubt on the CCSD(T) results. However, this is not necessarily problematic, because the extra non-dynamical correlation effects in the NiFe complex are in fact situated on the Fe centre, and have been shown (in the discussion of CASPT2 versus RASPT2 above) not to significantly affect the relative energy of the singlet–triplet transition, which is essentially localised on the Ni centre.

Table 5 T ₁, D₁ and |%TAE| diagnostics in the RCCSD(T) calculations, as well as the weight of the leading CSF in the C(R)ASSCF wavefunction, computed with the BS2 basis set

State	T 1	D 1	%TAE[(T)]	C 0 ^2
a Adiabatic. b At singlet geometry.
[Ni(SH)4]^2−
^1Ag	0.047	0.278	5.0	91.6
^3B3^a	0.027	0.113	2.5	90.5
^3Ag^b	0.032	0.161	3.6	93.8
[Ni(edt)4]^2−
^1A	0.041	0.277	3.0	91.7
^3B^a	0.026	0.137	2.1	94.8
^3B3^b	0.029	0.163	2.5	94.0
NiFe model, optimised geometries
^1A′	0.053	0.296	7.4	77.5
^3A′′^a	0.044	0.199	6.6	79.7
^3A′′^b	0.045	0.197	7.0	78.9
NiFe model, protein geometry
^1A	0.058	0.365		76.5
^3A^a	0.046	0.200		79.7

---

3.4 Comparison with DFT results

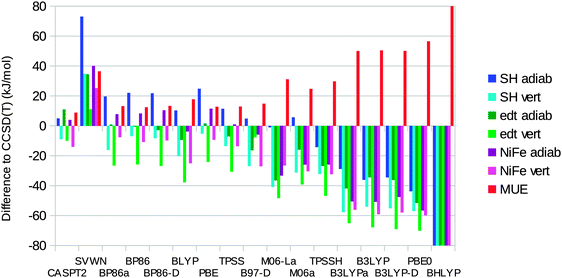
We have also calculated ΔE_ST for the three complexes with 14 different DFT methods (always on geometries optimised with the same method). The results are presented in Fig. 7 and they are presented as differences with respect to the best CCSD(T) results.

Fig. 7 Errors in ΔE_ST for CASPT2 and the various DFT methods compared to the CCSD(T) results for the three model complexes (adiabatic or vertical energies). Calculations with DFT methods ending with “a” were performed using the MOLCAS software and the BS1 basis set. Note that the BHLYP results are out of the scale of the figure (to emphasize the differences of the other methods); the actual errors are −136, −139, −140, −161, −165, −149, and 148 kJ mol⁻¹ for the seven entries in the legend, respectively.

It can be seen that SVWN always overestimates the stability of the singlet state, by 11–73 kJ mol⁻¹. On the other hand, the hybrid functionals overestimate the stability of the triplet state by 14–165 kJ mol⁻¹. The error is roughly proportional to the amount of Hartree–Fock exchange in the functional (10% for TPSSH, 20% for B3LYP, 25% for PBE0, and 50% for BHLYP). The only exception is M06, which contains 27% exact exchange but gives a MUE of only 25 kJ mol⁻¹ and actually gives a too high adiabatic ΔE_ST for the [Ni(SH)₄]²⁻ model. However, all the semi-local functionals (except M06-L) give lower errors, with MUEs of 12–18 kJ mol⁻¹. All these methods give varying signs of the errors for the six energies, although they always overestimate the stability of the triplet state in the singlet geometry. The best results are obtained for the BP86, TPSS, and PBE functionals, which have MUEs of 12–13 kJ mol⁻¹. TPSS gives the smallest MUE for the adiabatic energies (7 kJ mol⁻¹), whereas PBE gives the smallest MUE for the vertical energies (19 kJ mol⁻¹) and also the smallest maximum error (25 kJ mol⁻¹; the other semi-local functionals have maximum errors of 26–38 kJ mol⁻¹).

The dispersion correction has a minimal effect (up to 3 kJ mol⁻¹) for both BP86 and B3LYP. The MOLCAS calculations with the larger BS1 basis set give results similar to those of the Turbomole calculations, with differences of up to 9 kJ mol⁻¹. The MUEs agree within 1 kJ mol⁻¹.

Using instead the best CASPT2/RASPT2 results as the reference, we obtain similar results: TPSS, BP86, and PBE still give the best results with MUEs of 9–10 kJ mol⁻¹ and maximum errors of 17–21 kJ mol⁻¹. The semi-local functionals except M06-L (MUEs of 9–14 kJ mol⁻¹) are better than the hybrid functionals (21–146 kJ mol⁻¹) and SVWN (39 kJ mol⁻¹). CASPT2/RASPT2 differs from CCSD(T) by 4–15 kJ mol⁻¹ (9 kJ mol⁻¹ on average).

Our results agree with those of the previous study by Bruschi et al.¹⁷ in that the BP86 functional favours the singlet state and that B3LYP favours the triplet state for the adiabatic energies. However, even with B3LYP, we find a singlet ground state for all three model complexes, in contrast to the previous prediction that the triplet state should be 4 kJ mol⁻¹ more stable than the singlet state for the [Ni(edt)₂]²⁻ model. In our study, only the PBE0 and BHLYP functionals give a triplet ground state for this complex (in disagreement with the experimental data²⁵). Only the BHLYP method gives a triplet ground state for the NiFe complex, whereas all hybrid functionals except M06 predict a triplet ground state for [Ni(SH)₄]²⁻.

3.5 The spin state in the protein

We have also performed calculations on the NiFe model in the geometry observed inside the protein, employing structures from quantum-refinement calculations (X-ray crystallographic refinement supplemented by QM/MM calculations^60,61) for [NiFe] hydrogenase from Desulfovibrio fructosovorans.⁶² Owing to the restraints from the crystallographic raw data, both the singlet and triplet structures are far from square planar around the Ni ion, as can be seen in Fig. 8 (the ϕ twist angle is 68 and 71° in the two states, respectively). Consequently, the singlet state is strongly destabilised with respect to the triplet state in these structures.

Fig. 8 Protein geometry of the NiFe model in the singlet (left) and triplet (right) states.

Table 6 shows ΔE_ST for these structures, calculated with CASPT2, RASPT2, and CCSD(T). It can be seen that in all cases, the triplet state is the most stable by 5 (CCSD(T)) to 28 (RASPT2) kJ mol⁻¹. TPSS gives a result close to that of CCSD(T), 9 kJ mol⁻¹ in favour of the triplet state.

Table 6 Adiabatic ΔE_ST for the NiFe and [(SCH₃)₂Ni(SCH₃)₂Fe(CO)(CN)₂]²⁻ models, in kJ mol⁻¹, making use of structures optimised inside the protein (C₁ symmetry)

Basis set	CASPT2	RASPT2(SDTQ)	CCSD(T)
NiFe model
BS1	−26	−34	−11
BS2	−20	−29	−5
BS3	−22	−28
[(SCH3)2Ni(SCH3)2Fe(CO)(CN)2]^2−
BS1	−7	−14
BS2	0	−8

---

Next, we also tested the slightly larger (and more realistic) [(SCH₃)₂Ni(SCH₃)₂Fe(CO)(CN)₂]²⁻ model, with methyl groups on the four sulphur ligands. The results for these calculations (only CASPT2 and RASPT2) are also included in Table 6 and show that these methyl groups stabilise the singlet state by ∼20 kJ mol⁻¹. Consequently, CASPT2 predicts that the two states are degenerate and by extrapolation towards the CCSD(T) results (which could not be calculated), we would predict that the complex in the protein should have a singlet ground state by ∼15 kJ mol⁻¹. TPSS calculations give ΔE_ST = 4 kJ mol⁻¹.

These structures were obtained with a crystal structure of an oxidised form of the enzyme.⁶⁵ Unfortunately, most hydrogenase structures have problems with oxidations and photoreduction, giving structures that are a mixture of various spectrometric states.⁶² Therefore, we have also studied structures optimised by combined quantum mechanics and molecular mechanics (QM/MM) for the Ni–SI_a state.⁶⁶ These structures are still far from square planar, but they are less tetrahedral around the Ni ion with ϕ twist angles of 58 and 65°–68°, respectively. However, they do not change the relative stability of the two states very much. At the TPSS level and using a 46-atom QM system (with methyl groups on the sulphur ligands and including a protonated acetate group and a protonated imidazole group, forming hydrogen bonds with two of the sulphur ligands), ΔE_ST = 9 kJ mol⁻¹ for structures optimised with the BP86 functional, but −3 kJ mol⁻¹ for structures optimised with the TPSS functional (Table 7). If a point-charge model of the surrounding protein is included in the QM calculation, the singlet state is stabilised by 3–7 kJ mol⁻¹, but if also the MM terms are added, yielding a full QM/MM energy, ΔE_ST = 5 or −4 kJ mol⁻¹, respectively.

Table 7 Adiabatic ΔE_ST for the QM/MM models of [NiFe] hydrogenase. The structures were optimised with either the BP86 or TPSS functionals (and the def2-SV(P) basis set). Single-point energies were calculated with the TPSS functional and either the def2-SV(P) or def2-TZVP basis sets. They were calculated with either the 46-atom QM system used also in the QM/MM optimisation or with a 763-atom QM system. Moreover, they were calculated with QM/MM, with QM and a point-charge model of the surroundings, or for an isolated QM system

Method	#QM	Basis	BP86	TPSS
QM/MM	46	SV(P)	5	−4
QM + ptch	46	SV(P)	12	4
QM	46	SV(P)	9	−3
QM	46	TZVP	18	11
QM	763	SV(P)	11	6

---

All these energies were obtained with the smaller def2-SV(P) basis set. If we instead use the larger def2-TZVP basis set (used in the other DFT calculations in this article), the singlet state is stabilised by 9–14 kJ mol⁻¹. Finally, we calculated ΔE_ST for a very large 763-atom QM system, including all atoms within 4.5 Å of the central [(SCH₃)₂Ni(SCH₃)₂Fe(CO)(CN)₂]²⁻ model, all buried charged groups connected to the active site, and moving any cut bonds at least three residues away from the active site, and including a point-charge model of the surrounding protein and solvent.^66,68 This gave ΔE_ST = 6–11 kJ mol⁻¹, which should include all important effects from the QM/MM calculation. Therefore, we arrive at our final estimate ΔE_ST = 24 kJ mol⁻¹ for both structures by adding the correction for going from the def2-SV(P) to the def2-TZVP basis set and the difference between TPSS and CCSD(T) for the NiFe model in the crystallographic structure. This indicates that the active site is most likely in the singlet state in the protein, but the energy difference is so small that the conclusion is still somewhat uncertain.

Jayapal et al. also studied the [(SCH₃)₂Ni(SCH₃)₂Fe(CO)(CN)₂]²⁻ model with the MRMP2 method and found that the singlet state was 60–99 kJ mol⁻¹ more stable than the triplet state for structures optimised in vacuum,¹⁸i.e. similar to our results, considering that their model included methyl groups on the thiolate ligands. They used a much smaller active space than in our calculations with only four orbitals: a pair of bonding and antibonding orbitals between a Ni 3d orbital and the four surrounding sulphur atoms, an essentially pure Ni 3d orbital, and a diffuse orbital that is the correlating 3d′ orbital of the latter (they also performed a test calculation with six active orbitals, selected according to the occupation numbers from an unrestricted Kohn–Sham calculation). CASPT2 calculations with such a (4,4) active space on the NiFe model (with BS2) gave vertical and adiabatic ΔE_ST of 98 and 43 kJ mol⁻¹, respectively, i.e. 17–19 kJ mol⁻¹ lower than the corresponding CASPT2(12,12) calculations shown in Table 4, and 31 or 14 kJ mol⁻¹ lower than the corresponding CCSD(T) results. This shows that the current results are more accurate.

4 Conclusions

In this article, we have studied the accuracy of the CASPT2 and RASPT2 methods, as well as of 14 DFT functionals, for three models of the [NiFe] hydrogenase active site (shown in Fig. 2). The CASPT2 and RASPT2 approaches with appropriate active spaces and large basis sets accurately reproduce experimental and CCSD(T) results (bond lengths within 1 pm, singlet–triplet energy differences within 15 kJ mol⁻¹). Therefore, the CASPT2 and RASPT2 methods can be used as a suitable reference when there are no experimental data and when CCSD(T) calculations become intractable or unreliable because of strong non-dynamical correlation.

Concerning the DFT methods, we have confirmed previous observations that B3LYP gives too long metal–ligand bonds.^17,70 Moreover, our results illustrate the usual tendency of semi-local functionals to over-stabilise the low-spin state and of hybrid functionals to over-stabilise the high-spin state.^17,71 The BP86, TPSS, and PBE methods give singlet–triplet energy differences in best agreement with the CCSD(T) results (MUEs of 12–13 kJ mol⁻¹ and maximum errors of 19–29 kJ mol⁻¹). TPSS also gives the most accurate Ni–S bond lengths and, together with PBE, BLYP, TPSSH, and PBE0, the best results for all bond lengths in the Turbomole calculations with the def2-TZVP basis set, so it seems to be the method of choice for this type of systems. The geometries from the DFT calculations seem to improve if relativistic effects are considered, but ΔE_ST is not significantly changed.

Our results suggest a singlet ground state of Ni–SI_a in [NiFe] hydrogenase, in agreement with previous BP86 studies,^17,18 but in contrast to B3LYP results.^15,16 For vacuum-optimised structures, ΔE_ST is so large (57 kJ mol⁻¹ for the NiFe model and ∼20 kJ mol⁻¹ larger for the [(SCH₃)₂Ni(SCH₃)₂Fe(CO)(CN)₂]²⁻ model) and the methods so advanced that we strongly believe that this result can be trusted. However, the geometry observed in the protein strongly disfavours the singlet state and with this geometry, the singlet state is predicted to be only ∼24 kJ mol⁻¹ more stable than the triplet state, which is on the limit of the accuracy of the methods used. Apparently, it seems that the protein has selected a structure of the active site for which the singlet and triplet states have similar energies, as has also been suggested in a recent study, showing that the minimal energy crossing point between the singlet and triplet energy surfaces is close to the structure observed in the protein.¹⁰ In future publications, we will investigate how this selection is obtained and what mechanistic advantages it gives.

Acknowledgements

This investigation has been supported by grants from the Swedish research council (projects 2010-5025 and 2012-3910) and by research grants from the Flemish Science Foundation (FWO). The computations were performed on computer resources provided by the Swedish National Infrastructure for Computing (SNIC) at Lunarc at Lund University. QMP and SV thank the FWO for a pre- and postdoctoral fellowship, respectively.

References

1. J. C. Fontecilla-Camps, A. Volbeda, C. Cavazza and Y. Nicolet, Chem. Rev., 2007, 107, 4273.
2. A. Volbeda and J. C. Fontecilla-Camps, Coord. Chem. Rev., 2005, 249, 1609.
3. A. L. D. Lacey, V. M. Fernández, M. Rousset and R. Cammack, Chem. Rev., 2007, 107, 4304.
4. W. Lubitz, E. Reijerse and M. van Gastel, Chem. Rev., 2007, 107, 4331.
5. K. A. Vicent, A. Parkin and F. A. Armstrong, Chem. Rev., 2007, 107, 4366.
6. P. E. M. Siegbahn, J. W. Tye and M. B. Hall, Chem. Rev., 2007, 107, 4414.
7. D. Sellmann and J. Sutter, Acc. Chem. Res., 1997, 30, 460.
8. D. Sellmann, F. Geipel and M. Moll, Angew. Chem., Int. Ed., 2000, 39, 561.
9. M. A. Halcrow and G. Christou, Chem. Rev., 1994, 94, 2421.
10. R. L. Yson, J. L. Gilgor, B. A. Guberman and S. A. Varganov, Chem. Phys. Lett., 2013, 577, 138.
11. A. T. Kowal, I. C. Zambrano, I. Moura, J. J. G. Moura, J. LeGall and M. K. Johnson, Inorg. Chem., 1988, 27, 1162.
12. F. Dole, A. Fournel, V. Magro, E. C. Hatchikian, P. Bertrand and B. Guigliarelli, Biochemistry, 1997, 36, 7847.
13. C.-P. Wangs, R. Franco, J. G. Moura, I. Moura and E. P. Day, J. Biol. Chem., 1992, 267, 7378.
14. H. Wang, C. Y. Ralston, D. S. Patil, R. M. Jones, W. Gu, M. Verhagen, M. Adams, P. Ge, C. Riordan, C. A. Marganian, P. Mascharak, J. Kovacs, C. G. Miller, T. J. Collins, S. Brooker, P. D. Croucher, K. Wang, E. I. Stiefel and S. P. Cramer, J. Am. Chem. Soc., 2000, 122, 10544.
15. H. J. Fan and M. B. Hall, J. Am. Chem. Soc., 2002, 124, 394.
16. A. Pardo, A. L. D. Lacey, V. M. Fernández, H.-J. Fan, Y. Fan and M. B. Hall, JBIC, J. Biol. Inorg. Chem., 2006, 11, 286.
17. M. Bruschi, L. De Gioia, G. Zampella, M. Reiher, P. Fantucci and M. Stein, JBIC, J. Biol. Inorg. Chem., 2004, 9, 873.
18. P. Jayapal, D. Robinson, M. Sundararajan, I. H. Hillier and J. J. W. McDouall, Phys. Chem. Chem. Phys., 2008, 10, 1734.
19. S. P. de Visser, M. G. Quesne, B. Martin, P. Comba and U. Ryde, Chem. Commun., 2014, 50, 262.
20. K. Pierloot and S. Vancoillie, J. Chem. Phys., 2008, 128, 034104.
21. S. Vancoillie, H. Zhao, M. Radoń and K. Pierloot, J. Chem. Theory Comput., 2010, 6, 576.
22. K. Hirao, Chem. Phys. Lett., 1992, 196, 397.
23. K. Pierloot, Mol. Phys., 2003, 101, 2083.
24. S. Vancoillie, H. Zhao, V. Tan Tran, M. F. A. Hendrickx and K. Pierloot, J. Chem. Theory Comput., 2011, 7, 3961.
25. T. Yamamura, H. Kurihara, N. Nakamura, R. Kuroda and K. Asakura, Chem. Lett., 1990, 101.
26. B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2005, 109, 6575.
27. M. Reiher and A. Wolf, J. Chem. Phys., 2004, 121, 2037.
28. M. Reiher and A. Wolf, J. Chem. Phys., 2004, 121, 10945.
29. F. Aquilante, L. Gagliardi, T. B. Pedersen and R. Lindh, J. Chem. Phys., 2009, 130, 154107.
30. J. Boström, F. Aquilante, T. B. Pedersen and R. Lindh, J. Chem. Theory Comput., 2009, 5, 1545.
31. J. Boström, M. G. Delcey, F. Aquilante, L. Serrano-Andrés, T. B. Pedersen and R. Lindh, J. Chem. Theory Comput., 2010, 6, 747.
32. S. Vancoillie, M. G. Delcey, R. Lindh, V. Vysotskiy, P.-Å. Malmqvist and V. Veryazov, J. Comput. Chem., 2013, 34, 1937–1948.
33. K. Andersson and B. O. Roos, Chem. Phys. Lett., 1992, 191, 507.
34. P. Å. Malmqvist, K. Pierloot, A. R. M. Shahi, C. J. Cramer and L. Gagliardi, J. Chem. Phys., 2008, 128, 204109.
35. V. Sauri, L. Serrano-Andrés, A. R. M. Shahi, L. Gagliardi, S. Vancoillie and K. Pierloot, J. Chem. Theory Comput., 2011, 7, 153.
36. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479.
37. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
38. A. Becke, Phys. Rev. A, 1988, 38, 3098.
39. J. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822.
40. Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
41. G. Ghigo, B. Roos and P.-Å. Malmqvist, Chem. Phys. Lett., 2004, 396, 142.
42. P. J. Knowles, C. Hampel and H.-J. Werner, J. Chem. Phys., 1993, 99, 5219.
43. F. Aquilante, L. de Vico, N. Ferré, G. Ghigo, P.-Å. Malmqvist, P. Neogrády, T. B. Pedersen, M. Pitoňák, M. Reiher, B. O. Roos, L. Serrano-Andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224.
44. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2012.1, a package of ab initio programs, 2012, see http://www.molpro.net.
45. TURBOMOLE V6.1 2009, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com.
46. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
47. J. C. Slater, Phys. Rev., 1951, 81, 385.
48. S. H. Vosko, L. Wilk and J. C. Nusair, Can. J. Phys., 1980, 58, 1200.
49. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
50. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
51. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
52. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
53. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129.
54. J. P. Perdew, M. Ernzerhof and K. J. Burke, Chem. Phys., 1996, 105, 9982.
55. A. D. Becke, J. Chem. Phys., 1993, 98, 1372.
56. K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283.
57. K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119.
58. M. Elstner, P. Hobza, T. Frauenheim, S. Suhai and E. Kaxiras, J. Chem. Phys., 2001, 114, 5149.
59. S. Grimme, J. Comput. Chem., 2004, 25, 1463.
60. U. Ryde, L. Olsen and K. Nilsson, J. Comput. Chem., 2002, 23, 1058.
61. U. Ryde and K. Nilsson, J. Am. Chem. Soc., 2003, 125, 14232.
62. P. Söderhjelm and U. Ryde, J. Mol. Struct.: THEOCHEM, 2006, 770, 199.
63. U. Ryde, J. Comput. Aided Mol. Des., 1996, 10, 153.
64. U. Ryde and M. H. M. Olsson, Int. J. Quantum Chem., 2001, 81, 335.
65. A. Volbeda, Y. Montet, X. Vernede, E. C. Hatchikian and J. C. Fontecilla-Camps, Int. J. Hydrogen Energy, 2002, 27, 1449.
66. L.-H. Hu, P. Söderhjelm and U. Ryde, J. Chem. Theory Comput., 2013, 9, 640.
67. V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins, 2006, 65, 712.
68. S. Sumner, P. Söderhjelm and U. Ryde, J. Chem. Theory Comput., 2013, 9, 4205.
69. W. Jiang, N. J. DeYonker and A. K. Wilson, J. Chem. Theory Comput., 2012, 8, 460.
70. F. Neese, JBIC, J. Biol. Inorg. Chem., 2006, 11, 702.
71. M. Reiher, O. Salomon and B. A. Hess, Theor. Chem. Acc., 2001, 107, 48.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp00253a

---