Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecules in the mirror: how SERS backgrounds arise from the quantum method of images†
Stephen M.
Barnett
a,
Nadine
Harris
b and
Jeremy J.
Baumberg
*b
aSchool of Physics and Astronomy, University of Glasgow, Glasgow G12 8QQ, UK
bCavendish Laboratory, Department of Physics, University of Cambridge, Cambridge, CB30HE, UK. E-mail: jjb12@cam.ac.uk
First published on 20th February 2014
Abstract
The Raman coupling of light to molecular vibrations is strongly modified when they are placed near a plasmonic metal surface, with the appearance of a strong broad continuum background in addition to the normal surface-enhanced Raman scattering (SERS) peaks. Using a quantum method of images approach, we produce a simple but quantitative explanation of the inevitable presence of the background, due to the resistive damping of the image molecule. This model thus suggests new strategies for enhancing the SERS peak to background ratio.
The coupling of light to molecules is a key aspect of both fundamental and applied spectroscopy, and widely used as the basis of diagnostics, biological sensing, chemical analysis, as well as much of surface science.1–5 When molecules are placed on metal surfaces their interaction with light of wavelength λ is modified from a variety of effects. Firstly, absorption and emission are suppressed by the null in the optical field at the metal surface caused by interference with the out-of-phase reflection. As the molecule is lifted above the metal surface, however, absorption and emission are enhanced for heights of ∼λ/4.6 Secondly, for certain (notably coinage) metals, plasmonic resonances exist on the surface with a high density of states, into which molecules can emit light very efficiently, so that when molecules approach the surface they feel the enhanced electric field, E, produced by these resonances. This has the effect of increasing their emission rates, although once the molecule is closer than ∼10 nm, quenching of emission occurs.6 Luminescence, Rayleigh and SERS (which is the focus here) are all strongly enhanced by the presence of plasmonic metal surfaces.
SERS is a more than thirty year old technique for enhancing the Raman scattering of molecules.7 The recent availability of a variety of nanostructured plasmonic particles and substrates, with large numbers of ‘hot-spots’, increases the average overall E field and allows dramatic enhancement of the SERS signal.8 This has given rise to a huge interest in SERS spectroscopies. Over the years, however, there have been strong debates over the origin of the SERS signals and a variety of mechanisms for this effect have been proposed.9–12 While it is well established that the enhancement (scaling as |E|4)7 is due to the excitation of the plasmonic resonance at the surface, there is discussion of the extent to which the pure electromagnetic enhancement is supplemented by a chemical contribution, and experiments suggest that the electronic structure of the molecules is actually modified in some SERS experiments.1,13,14 More puzzling still is that SERS vibrational Raman peaks are always accompanied by a spectrally broad background, which is increased by a similar factor to the SERS itself. It is this increased broad background that interests us here. The origin of this background has been the subject of much debate, and little consensus exists.10,11,15 Recently we established that on quantitatively reproducible substrates, (i) the SERS background requires both molecules and plasmons, (ii) is sensitive to the chemical nature of the surface, and (iii) is not seen for the anti-Stokes emission.16
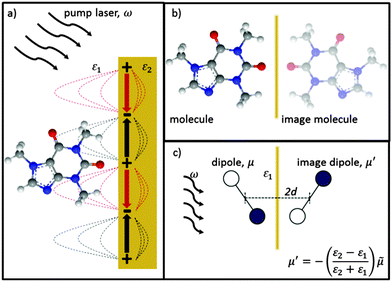
Here we use the method of images technique17 to develop a new model for the coupling of light to molecules on plasmonically-active metal nanostructures which explains the presence of the broad SERS background.17 Using this approach the interaction between the molecule and the nearby plasmonic surface (Fig. 1a) is treated as if there were no surface at all, but the molecule is accompanied by an image molecule (Fig. 1b), the properties of which are designed to take account of the required boundary conditions. The two molecules (real and its image) then interact with the exponentially localized surface plasmon resonance to produce the Raman spectrum. The physical picture can be thought of as two oscillators (vibrating at the frequency of their excited molecular vibrational modes, ν), coupled by the dipole–dipole interaction. The molecular image dipole is strongly damped from its excited vibrational state to its vibrational ground state at a rate, Γ, by resistive effects inside the metal while the real molecule is damped between these two states at a rate, γ, by the metal surface. Note that accounting for the electric field boundary conditions at the metal surface using the images does not on its own produce the contact interaction between the image molecule and the electronic modes in the metal, which separately introduces the higher damping rate Γ. The method of images technique works well at low frequencies (ν ≪ ωp), with ωp being the plasma frequency, below which the metal is a good reflector. This well-established technique can account for the force of attraction between a charge and an uncharged dielectric medium, Van der Waals interactions between molecules and surfaces, quantum electrodynamical effects such as modified spontaneous emission rates18 and the Casimir–Polder force.19
To begin with we consider a single point charge, q placed in a medium of relative permittivity, ε1 at a distance, d from a plane interface (defined by the x–y-plane) with a second medium of relative permittivity, ε2. The field in medium 1 can be obtained if we replace the plane interface by an image charge with magnitude
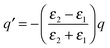 | (1) |
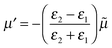 | (2) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) is the mirror image of the original dipole. In this way we can introduce an image of the real molecule situated inside the metal.
is the mirror image of the original dipole. In this way we can introduce an image of the real molecule situated inside the metal.
We require one additional feature before we can apply the method of images to SERS and this is to allow the dipole to oscillate with an angular frequency, ω. If we write the time-dependent dipole as the real part of the complex dipole moment μe−iωt then the associated complex image dipole will be
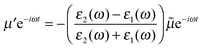 | (3) |
The probability amplitude for making a Raman transition from the electronic ground-state and vibrational state, ν to the electronic ground-state and vibrational state, ν′ is proportional to the molecular tensor,
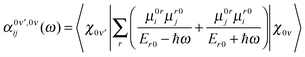 | (4) |
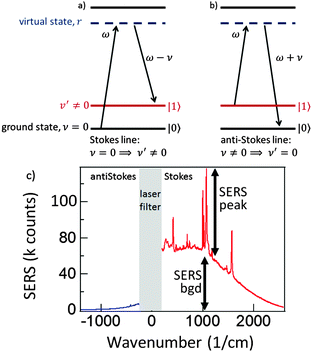
A Raman transition in a molecule proceeds via the resonance excitation to a virtual excited state through the absorption of a photon of frequency ω from the pump laser. Then a Raman photon of frequency ω′ is emitted, so as to conserve energy, leaving the molecule in either its original vibrational ground state ν = 0 or in a different vibrational ground state ν′. If the state ν′ has a higher energy than the initial vibrational ground state ν, then the emitted Raman photon will be of lower frequency than the laser frequency ω and a Stokes line is produced (ν = 0 ⇒ ν′ ≠ 0) (Fig. 2a). If, however the state ν′ has a lower energy than the initial vibrational ground state ν then the emitted Raman photon will be of higher frequency than the laser frequency ω and an anti-Stokes line is produced (ν ≠ 0 ⇒ ν′ = 0) (Fig. 2b). A typical SERS spectrum for both Stokes and anti-Stokes scattering is seen in Fig. 2c, with similar enhancements for both the vibrational peaks, and the ever present background.
Both the real molecule and its image molecule contribute to this Raman transition process and, for the Stokes line, the result is the superposition of two Lorentzian functions which produce a line shape of the form
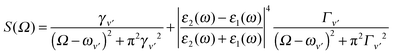 | (5) |
The first term in eqn (5) is the Lorentzian associated with the decay of the real molecule from the excited vibrational state ν′ ≠ 0 to the vibrational ground state ν = 0. Its characteristic line will be a sharp, narrow peak because typically the damping, γν′ of the real molecule by the metal surface will be rather small; these are the normal SERS vibrational peaks. The second term is the Lorentzian associated with the decay of the image molecule from the excited vibrational state ν′ ≠ 0 to the vibrational ground state ν = 0. In this case however, the charges in the metal will tend to oscillate in sympathy with the image molecule producing heavy resistive damping, Γν′ (associated with the imaginary part of the metal permittivity) until such time when the excited vibrational state will eventually decohere into the vibrational ground state. This heavy damping means that Γν′ ≫ γν′ which will have the effect of producing a large broad continuum background, much broader than the first Lorentzian term giving the normal SERS peak. Crucially, the background continuum is only visible due to the enhancement factor 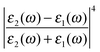 associated with the large magnitude of the image dipole, μ′, oscillating at the surface-plasmon frequency. It is this factor that explains why the SERS background is only evident when there is interaction between both molecules and plasmons.16 The fourth power arises because the transition probability depends on the fourth power of the dipole moment. The modeled Stokes spectrum from eqn (5), depicting a narrow Raman line on a broad background, is shown in Fig. 3 based on conditions that give
associated with the large magnitude of the image dipole, μ′, oscillating at the surface-plasmon frequency. It is this factor that explains why the SERS background is only evident when there is interaction between both molecules and plasmons.16 The fourth power arises because the transition probability depends on the fourth power of the dipole moment. The modeled Stokes spectrum from eqn (5), depicting a narrow Raman line on a broad background, is shown in Fig. 3 based on conditions that give 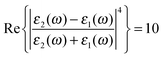 , γν′ = 1 cm−1 and Γν′ = 100 cm−1 (where Re{χ} denotes the real part of χ).
, γν′ = 1 cm−1 and Γν′ = 100 cm−1 (where Re{χ} denotes the real part of χ).
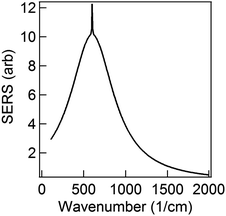 | ||
Fig. 3 Modeled spectrum Stokes spectrum of a broad background peak under a weaker and narrow Raman line, from (5) with 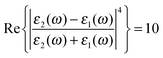 , γν′ = 1 cm−1 and Γν′ = 100 cm−1. , γν′ = 1 cm−1 and Γν′ = 100 cm−1. | ||
To examine the dependence of the Raman peak on γν′ we fix all other variables constant (to the values of Fig. 3) and vary γν′ from 0.01 cm−1 to >1 cm−1. When γν′ = 0.01 cm−1 the Raman peak is initially very narrow, with a very large amplitude (due to γν′ in the denominator of the first term in (5)) (Fig. 4a). This amplitude decreases as γν′ is increased beyond 1 cm−1 (Fig. 4b), and disappears into the broad background when γν′ = Γν′ = 10 cm−1 (Fig. 4c).
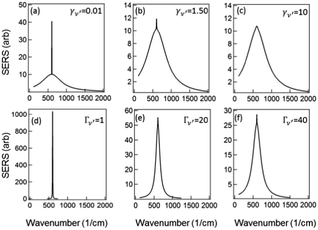 | ||
Fig. 4 Modeled Stokes spectra from eqn (5) with varying values of γν′ and Γν′ using 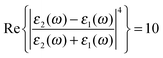 held constant, for (a–c) Γν′ = 100 cm−1 and (a) γν′ = 0.01 cm−1, (b) γν′ = 1.5 cm−1, (c) γν′ = 10 cm−1. (d and e) γν′ = 1 cm−1 and (d) Γν′ = 1 cm−1, (e) Γν′ = 20 cm−1, (f) Γν′ = 40 cm−1. held constant, for (a–c) Γν′ = 100 cm−1 and (a) γν′ = 0.01 cm−1, (b) γν′ = 1.5 cm−1, (c) γν′ = 10 cm−1. (d and e) γν′ = 1 cm−1 and (d) Γν′ = 1 cm−1, (e) Γν′ = 20 cm−1, (f) Γν′ = 40 cm−1. | ||
Similarly if all other variables are held constant and we vary Γν′ from 1 cm−1 to 100 cm−1 we see that there is a very narrow peak, similar to the narrow Raman spectrum (but not in magnitude due to the 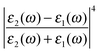 term) when Γν′ = γν′ = 1 cm−1 (Fig. 4d). The broad background starts to become evident as we increase the damping Γν′ to values roughly 20× that of γν′ (Γν′ = 20 cm−1) (Fig. 4e). Both the narrow Raman peak and the broader background are fully evident in the Stokes spectrum when Γν′ > 40 cm−1 (Fig. 4f). The combination of the many different Lorentzian background components for each molecule leads to the overall background observed in experiment, with a resulting shape that reflects only the density of possible Raman transitions.
term) when Γν′ = γν′ = 1 cm−1 (Fig. 4d). The broad background starts to become evident as we increase the damping Γν′ to values roughly 20× that of γν′ (Γν′ = 20 cm−1) (Fig. 4e). Both the narrow Raman peak and the broader background are fully evident in the Stokes spectrum when Γν′ > 40 cm−1 (Fig. 4f). The combination of the many different Lorentzian background components for each molecule leads to the overall background observed in experiment, with a resulting shape that reflects only the density of possible Raman transitions.
Let us now turn our attention to the anti-Stokes region of the spectrum. An anti-Stokes line is at a higher frequency than that of the pump laser, ω and corresponds to a transition from a higher to a lower vibrational state (ν ≠ 0 ⇒ ν′ = 0) (Fig. 2b). At first sight we might expect both a narrow line corresponding to emission from the molecule and a background emitted by the image molecule. The fact that there is no broad background, however, is a further consequence of the same rapid resistive damping, Γν′, that is responsible for the broad background on the Stokes side of the spectrum. A vibrational excitation in the image molecule dissipates very rapidly and hence Raman transitions occur only from the vibrational ground state (ν = 0) for the image. Therefore energy conservation dictates that such transitions can give rise only to Stokes lines.16 This consideration thus produces a spectrum resembling that from experiment as seen in Fig. 2c.
We should ask if there is any interference between the Stokes emission of the molecule and the image molecule. To see there is none, we can appeal to quantum mechanics. After the emission of a Stokes photon we could, at least in principle, examine the real molecule to see if it is in the excited vibrational state, ν′. If it is then the emission must have come from the real molecule but if it is in its vibrational ground state, (ν = 0) then the emission must have come from the image molecule. The existence of this “which-way” information suffices to tell us that there cannot be any interference in this case, which is indeed reproduced by the exact calculations.
Finally let us discuss the coupling, V between the molecule and its image. The molecular dipole excited by the pump laser and its image molecule can couple to each other by means of the dipole–dipole interaction familiar from electrostatics.19 Let the metal surface define the x–y plane so that the molecular dipole lies on the z axis at a distance d from the surface as in Fig. 1c. The complex molecular and image dipoles are related by eqn (3). The cycle-averaged potential energy associated with this interaction has the simple form
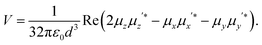 | (6) |
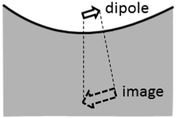
The ratio between the SERS peaks and background is thus set by a number of factors. Experimentally we find SERS peak linewidths are of order γ = 1 cm−1, which reduces as the molecules are further distanced from the surface towards the unperturbed Raman linewidths. Typical backgrounds observed have linewidths exceeding Γ = 100 cm−1, since the backgrounds from different vibrational lines are always blurred together. Moreover we assume here the simplest case in which the Raman selection rules are identical for real and image molecules, however this may not always be the case. For instance the rapid decay of plasmonic fields inside the metal can lead to a significant gradient in field strength along a normally Raman-inactive vibrational bond, and thus making background transitions visible without any large corresponding SERS peak from the real molecule. As the molecule is moved away from the surface, the strength of both SERS peaks and backgrounds will decrease as the local field exciting the dipoles reduces. However the ratio between these SERS contributions will be modified if the metallic surface is not flat as assumed throughout here, but has some curvature on the scale of the separation involved. For instance a concave surface of negative radius of curvature R leads to further magnification of the image dipole by a factor [1 − d/R]−3 (Fig. 5). This for instance can enhance the background contribution to SERS by 50% for only R = 10 nm scale roughness with molecules at d = 1.2 nm above the surface. We thus expect the ratio of peak to background SERS to be highly sensitive to the nanoscale morphology of the surfaces, which is indeed found experimentally,16 but needs further careful work to verify directly. However it suggests that to reduce the ratio of the SERS background for improving the signal to noise in SERS sensing, target molecules should be close to sharply convex nano-patterned surfaces, matching more recent observations on nanoparticles and etched nanostructures.
Various criticisms can be levelled at the simplicity of the model adopted here. Image charge models have a long history in SERS, and are known to possess various limitations.7,12,23 We indeed noted already that the distance dependence of molecule to surface of the SERS is not explicitly included (it scales with the plasmon field intensity at the molecule), but we are concerned here only with the ratio of background to SERS peaks. We explicitly postulated that the image and molecule have different damping to their environments, but this is the aspect that is normally left out of image charge models. However our model does agree with experiments that show the background observed does always scale with the SERS peak strength. Additional spectral variation in the background observed can arise from spectral filtering by the finite width of plasmonic resonance used to enhance the Raman, and this is only implicitly included here. The reason continuum backgrounds are not seen for molecules on completely flat surfaces is that in this case no external coupling is possible to the plasmons which are bound to the surface, and these are needed to provide the enhanced field used to get SERS, and to couple the scattering plasmons back into far field photons. Finally the image model is not suited to higher level precise descriptions of the SERS effects, as it does not include retardation sufficiently well, nor can it simply account for polarization selection rules. However the basic simplicity of the model to solve the long running question of the origin of the continuum background is strongly in its favour.
Conclusions
In summary we have shown that the method of images approach can be used to explain the spectra associated with a system of a vibrating SERS molecule interacting with a resonant, plasmonic metal surface. By replacing the molecular–surface interaction with a molecular–image interaction we derive an equation for the Stokes line combining two Lorentzian terms. The first Lorentzian term produces a narrow sharp peak associated with a normal SERS line, due to the relatively small amount of damping between the molecule and the plasmonic surface. The second Lorentzian term produces a large continuum spectrum, referred to as the SERS background, from the dissipative, resistive damping of the image molecule due to the imaginary part of the metal refractive index. Such an intuitive model is of crucial importance in developing spectroscopies with improved signal to noise (not just enhanced signal) as needed for ultra-sensitive sensing.We gratefully acknowledge data and stimulating discussions provided by Sumeet Mahajan and Phil Bartlett. This work was supported by UK EPSRC EP/C511786/1, EP/F011393, ERC 320503 LINASS, EU CUBIHOLES, 3M, the Royal Society and the Wolfson Foundation.
Notes and references
- K. A. Willets and R. P. Van Duyne, Annu. Rev. Phys. Chem., 2007, 58, 267–297 CrossRef CAS PubMed.
- X. Qian, X.-H. Peng, D. O. Ansari, Q. Yin-Goen, G. Z. Chen, D. M. Shin, L. Yang, A. N. Young, M. D. Wang and S. Nie, Nat. Biotechnol., 2008, 26, 83–90 CrossRef CAS PubMed.
- K. Kneipp, Y. Wang, H. Kneipp, L. Perelman, I. Itzkan, R. Dasari and M. Feld, Phys. Rev. Lett., 1997, 78, 1667–1670 CrossRef CAS.
- M. D. Porter, R. J. Lipert, L. M. Siperko, G. Wang and R. Narayanan, Chem. Soc. Rev., 2008, 37, 1001–1011 RSC.
- D. A. Stuart, A. J. Haes, C. R. Yonzon, E. M. Hicks and R. P. Duyne, Van IEEE Proc.-Nanobiotech., 2005, 152, 13–32 CrossRef CAS.
- R. M. Amos and W. L. Barnes, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 7249–7254 CrossRef CAS.
- M. Moskovits, J. Raman Spectrosc., 2005, 36, 485–496 CrossRef CAS; M. Moskovits, Rev. Mod. Phys., 1985, 57, 783–826 CrossRef.
- K. D. Osberg, M. Rycenga, N. Harris, A. L. Schmucker, M. R. Langille, G. C. Schatz and C. A. Mirkin, Nano Lett., 2012, 12, 3828–3832 CrossRef CAS PubMed.
- A. Bagchi, R. G. Barrera and B. B. Dasgupta, Phys. Rev. Lett., 1980, 44, 1475–1478 CrossRef CAS.
- E. Burstein, Y. J. Chen, S. Lundquist and E. Tosatti, Solid State Commun., 1979, 29, 567–570 CrossRef CAS.
- J. I. Gersten, R. L. Birke and J. B. Lombardi, Phys. Rev. Lett., 1979, 43, 147–150 CrossRef CAS.
- W. H. Weber and G. W. Ford, Phys. Rev. Lett., 1980, 4, 1774–1777 CrossRef.
- A. Campion, P. Kambhampati and C. Harris, Chem. Soc. Rev., 1998, 27, 241–250 RSC.
- D. Cunningham, R. E. Littleford, W. E. Smith, P. J. Lundahl, I. Khan, D. W. McComb, D. Graham and N. Laforest, Faraday Discuss., 2006, 132, 135–145 RSC.
- T. E. Furtak and J. Reyes, Solid State Commun., 1980, 93, 351–382 CAS.
- S. Mahajan, R. M. Cole, J. D. Speed, S. H. Pelfrey, A. E. Russell, P. N. Bartlett, S. M. Barnett and J. J. Baumberg, J. Phys. Chem. C, 2010, 114, 7242–7250 CAS.
- J. D. Jackson, Classical Electrodynamics, John Wiley & Sons, Inc., 3rd edn, 1998 Search PubMed.
- P. W. Milonni and P. L. Knight, Opt. Commun., 1973, 9, 119–122 CrossRef.
- S. M. Barnett, A. Aspect and P. W. Milonni, J. Phys. B: At., Mol. Opt. Phys., 2000, 33, L143–L149 CrossRef CAS.
- O. Madelung, Introduction to Solid State Theory, Springer, Berlin, 1996 Search PubMed.
- T. Forster, Modern Quantum Chemistry, Academic Press, New York, 1965, pp. 93–137 Search PubMed.
- P. Wu and L. Brand, Anal. Biochem., 1994, 218, 1–13 CrossRef CAS.
- F. W. King, R. P. Van Duyne and G. C. Schatz, J. Chem. Phys., 1978, 69, 4472 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional derivation of eqn (5). See DOI: 10.1039/c4cp00093e |
| This journal is © the Owner Societies 2014 |