Vibrational density of states of triphenylene based discotic liquid crystals: dependence on the length of the alkyl chain

Abstract

The vibrational density of states of a series of homologous triphenylene-based discotic liquid crystals HATn (n = 5, 6, 8, 10, 12) depending on the length of the aliphatic side chain is investigated by means of inelastic neutron scattering. All studied materials have a plastic crystalline phase at low temperatures, followed by a hexagonally ordered liquid crystalline phase at higher temperatures and a quasi isotropic phase at the highest temperatures. The X-ray scattering pattern for the plastic crystalline phase of all materials shows a sharp Bragg reflection corresponding to the intercolumnar distance in the lower q-range and a peak at circa 17 nm⁻¹ related to intracolumnar distances between the cores perpendicular to the columns as well as a broad amorphous halo related to the disordered structure of the methylene groups in the side chains in the higher q-range. The intercolumnar distance increases linearly with increasing chain length for the hexagonal columnar ordered liquid crystalline phase. A similar behaviour is assumed for the plastic crystalline phase. Besides n = 8 all materials under study exhibit a Boson peak. With increasing chain length, the frequency of the Boson peak decreases and its intensity increases. This can be explained by a self-organized confinement model. The peaks for n = 10, 12 are much narrower than for n = 5, 6 which might imply the transformation from a rigid system to a softer one with increasing chain length. Moreover the results can also be discussed in the framework of a transition from an uncorrelated to a correlated disorder with increasing n where n = 8 might be speculatively considered as a transitional state.

---

Introduction

In contrast to crystalline materials where it is expected that the vibrational density of states (VDOS) g(ω) follows the Debye model of sound waves g(ω) ∼ ω², amorphous materials exhibit an excess contribution in the frequency range of ω = 0.2–1 THz (energy range 1–5 meV). In the reduced representation g(ω)/ω²versus frequency a peak is observed for these materials, which is commonly called the Boson peak (BP).¹ The Boson peak is a universal but controversially discussed feature of glasses and other materials with a complete or partial disorder. Moreover the BP corresponds to the excess contributions commonly found for glasses in the specific heat and in the thermal conductivity at low temperatures. As a matter of fact many systems which show a BP also exhibit a glass transition characterized for instance by the glass transition temperature T_g. Until today the glass transition phenomenon has been a topical problem of condensed matter physics.^2–4 Despite the different time scales of the thermal glass transition (∼100 s at T_g), and the BP (terahertz range), there are strong indications of a relevance of the BP for the glass transition. Within the concept of the fragility of glasses⁵ the BP is well pronounced for materials which are classified as “strong glasses”, the BP is weak primarily for “fragile ones”.⁶ It is further known that the Boson peak is more or less independent of temperature.⁷

The origin of the BP is still unclear and the different existing theoretical approaches can be divided into two classes:

(1) The modes of the BP are different from sound waves and originate from (quasi) localized modes^8–10 which are due to peculiarities of the interatomic forces in the material (e.g. group of atoms subject to a soft potential).

(2) The BP of the amorphous system is a broadened version of the Van Hove singularity which is a well-known phenomenon in crystalline systems:¹¹ for a linear chain as a model system the frequency is proportional to the sine of the wave vector, which is why frequencies close to the maximum are more numerous than low sound frequencies. It is assumed that this singularity exists also in amorphous materials to a given extent. This means that the VDOS of an amorphous material is just a modification of the VDOS of the corresponding crystalline system due to random fluctuations of force constants.¹²

To elucidate the controversy on the BP several studies have been carried out by means of Fourier transform infrared spectroscopy, inelastic X-ray scattering, neutron scattering, Mössbauer spectroscopy, low frequency Raman spectroscopy and light scattering on conventional glass formers such as low molecular weight liquids and polymers.^13–20 This concerns also biologically active systems such as proteins²¹ which are also considered to undergo a glass transition. As discussed above a detailed theoretical description of the boson peak is not developed untill now, the connection of the Boson peak to fluctuations of elastic constants has been demonstrated in ref. 22. In detail sound waves were considered in a disordered environment where the local elastic constants are subjected to fluctuations. The spatial correlation of these fluctuations is described by a correlation length. Sokolov et al. investigated the correlation between the dynamic heterogeneity length scale ξ of glasses estimated from the boson peak and the activation volume for the dynamic glass transition ΔV^# in a number of molecular, hydrogen bond and polymeric glass formers. They observed that ξ³(T_g) ∼ ΔV^#(T_g) holds regardless of chemical structure, molecular weight and pressure (density) of the studied materials.²³

Embedding materials into nanostructures can also be helpful to discriminate between the two theoretical approaches where both surface effects and the confinement size play a role. Confinement can be classified into two categories, hard and soft confinement. For organic glass-forming systems impregnated in a hard confinement like nanopores the high frequency range remains more or less unaffected, while the low frequency wing is suppressed with decreasing confinement size. Therefore the BP becomes sharper and is shifted to higher frequencies. These results were obtained for conventional low molecular weight (salol) and polymeric glass-forming systems (poly(dimethyl siloxane), poly(phenylmethyl siloxane), poly(propylene glycol)) under confinement.^13,24–26 These findings might support the hypothesis of a collective nature of the BP.²⁷ The same effect was also observed for a glass forming liquid crystal confined to the pores of a molecular sieve.²⁸ The effect of soft confinement was investigated by enclosing propylene glycol to microemulsion droplets. In contrast to what is found for hard confinement, the boson peak of the bulk material is completely washed out under the soft confinement.²⁹

Besides for low molecular weight glass formers and polymers a boson peak was detected also for plastic crystals, by means of THz dielectric spectroscopy.^30,31 This indicates that these materials can also undergo a glass transition as it is discussed in ref. 5 and 32 where Seki and Suga³³ observed a glass transition in plastic crystals for the first time. Our contribution focuses on discotic liquid crystals (DLCs). DLCs are self-assembled materials where self-assembly is driven by noncovalent intermolecular interactions.³⁴ The molecules consist of a flat and rigid aromatic core substituted by flexible aliphatic side chains.^35,36 The former is responsible for the π-stacking and the latter for the increased solubility, processability, and rich thermotropic behaviour.³⁷ At low temperatures discotic liquid crystals exhibit a plastic crystalline phase. This phase can be followed by a hexagonal columnar mesophase where the disc-shaped molecules organize into columns that further assemble into two-dimensional arrays with a hexagonal mesophase. The alkyl chains fill the intercolumnar space giving so rise to a nanophase separated state. This can also be considered as a confinement of the alkyl chains in between the columns. Besides hexagonal mesophases also nematic structures can appear.²⁸ At even higher temperatures discotic liquid crystals undergo a phase transition to a more or less isotropic, disordered liquid. Hence these soft matter materials combine aspects both of a conventional fluid and a solid crystal. The isotropization temperature and the temperature range of the hexagonal columnar mesophase depend besides the nature of the core on both the length and specific structure of the side chains. Furthermore confinement can influence these properties, e.g. result in a decrease of the phase transition temperatures and a rise of additional new phases as found in a study on a pyrene-based liquid crystal confined to self-ordered alumina oxide membranes with different pore sizes.³⁸ With their ordered structure, discotic liquid crystals look very promising in the field of organic electronics³⁹ and to fulfill today's dire need for effective, low cost, portable and disposable elements such as tunable organic light-emitting diodes,⁴⁰ thin film field-effect transistors or photovoltaic chips: they outperform many photoconductive polymers (e.g. in terms of charge transport or short-lived excitonic response).⁴¹ Several studies have been carried out on the electronic properties and the self assembly of typical discotics such as triphenylene and hexa-peri-hexabenzocoronene (HBC) derivatives.^34,42,43 Besides applications, the counterplay between order and molecular mobility offers the unique possibility to address fundamental questions about the glass transition and the underlying molecular dynamics. Currently it is an open question whether discotic liquid crystals exhibit glassy dynamics in general or not. Glassy dynamics were found for a pyrene-based⁴⁴ and claimed for a triphenylene-based³¹ discotic liquid crystal as well as for several other similar materials.^45–47 However it is not clear if this is a common behaviour for this class of material. Considering the possible relevance of the BP for glassy dynamics an investigation of the vibrational density of states for these soft mater materials might contribute to solve this question and to gain a better understanding of the molecular origin of the Boson peak.

In this study differential scanning calorimetry, X-ray Scattering, and inelastic neutron scattering are employed to investigate a homologous series of triphenylene based discotic liquid crystals with varying length of the side chain in the bulk state. The general aim is to ascertain the existence of a boson peak for these materials and to investigate the influence of the length of the alkyl chains on its position and shape. The X-ray study provides detailed structural information to discuss the inelastic neutron scattering data.

Materials

The considered homologous series of hexakis(n-alkyloxy)triphenylene (HATn) DLCs is based on an aromatic triphenylene core where the length of the side chain n is varied from 5 to 12. All materials were purchased from Synthon Chemicals (Bitterfeld, Germany) and used as received. Their chemical structure is shown in Fig. 1. The chemical structure of the obtained materials was confirmed by MALDI-TOF mass spectrometry. As an example Fig. 2 shows the MALDI-TOF MS spectrum of HAT6. Pronounced peaks were observed in the theoretical molar mass range of 828 g mol⁻¹ of HAT6 considering only the mass of ¹²C. The detection of different peaks is due to the fact that carbon has different stable and unstable isotopes where the most common are ¹²C, ¹³C, and ¹⁴C. The mass difference between the different peaks is as expected 1 Da. Considering the natural occurrence of the isotopes this leads to a molar mass of HAT6 of 829.24 g mol⁻¹. For the other materials corresponding results are obtained.

Fig. 1 Chemical structure of hexakis(n-alkyloxy)triphenylene HATn. The length n of the side chains is varied: n = 5, 6, 8, 10, 12.

Fig. 2 MALDI-TOF MS spectrum of HAT6 (C₅₄H₈₄O₆). The spectra were collected employing a Bruker Autoflex III (Bruker Daltonik GmbH, Bremen, Germany) spectrometer equipped with a Smartbeam™ laser (356 nm, frequency 200 Hz).

Experimental techniques

1. Differential scanning calorimetry

Conventional Differential Scanning Calorimetry (DSC) was carried out using a Seiko DSC 7020. The sample (∼10 mg) was measured from 173 K to 283 K at a heating and cooling rate of 10 K min⁻¹. Nitrogen was used as a protection gas.

2. X-ray scattering

For the X-ray scattering experiments, the sample was filled into borosilicate glass capillaries (WJM-Glas Glastechnik & Konstruktion, Germany) with a diameter of 0.3 mm. The measurements were carried out on the synchrotron micro focus beamline μSpot (BESSY II of the Helmholtz Centre Berlin for Materials and Energy). With a divergence of less than 1 mrad (horizontally and vertically), the focusing scheme of the beamline is designed to provide a beam diameter of 100 μm at a flux of 1 × 10⁹ photons s⁻¹ at a ring current of 100 mÅ. The experiments were carried out applying a wavelength of 1.03358 Å using a double crystal monochromator (Si 111). Scattered intensities were collected 820 mm behind the sample position using a two dimensional X-ray detector (MarMosaic, CCD 3072 × 3072 pixel with a point spread function width of about 100 μm). A more detailed description of the beamline is given in ref. 48. The obtained scattering images were processed, converted into diagrams of scattered intensities versus scattering vector q where q is defined in terms of the scattering angle 2θ and the wavelength λ_X of the radiation, thus q = 4π/λ_X sin θ, and employing an algorithm of the computer program FIT2D.⁴⁹ The materials were heated at a heating rate of 10 K min⁻¹ in order to be consistent with the DSC measurements.

3. Neutron scattering

Neutron scattering measurements are carried out at the time focusing time-of-flight spectrometer IN6 at the Institut Laue Langevin in Grenoble, France.⁵⁰ The instrument was used with an incident wavelength of λ_n = 5.12 Å resulting in a resolution of 100 μeV (full width at half maximum). The raw data were corrected following the usual procedure using the program INX⁵¹ for background and absorption. Different detectors have been interpolated to obtain constant q values. The maximal accessible elastic scattering vector in this configuration is q = 2.05 Å⁻¹. The VDOS is measured at 80 K. This makes sure that the inelastic scattering due to the vibrations is not overlaid by quasielastic scattering caused by molecular motions. The resolution of the instrument was obtained by measuring the sample under investigation at 2 K where all molecular motion and vibrations are frozen. Absolute values of S(q,ω) were obtained also by INX.

Results

DSC measurements were carried out to determine the phase transition temperatures of the discotic liquid crystals. Fig. 3 gives the DSC thermograms of HAT6 for heating and cooling. For the other materials corresponding DSC traces are obtained.

Fig. 3 DSC thermogram of HAT6 during cooling (dashed line) and heating (solid line). Inset: DSC thermogram for cooling in the temperature range between 180 and 220 K, the temperature where a glass transition is observed in ref. 31.

The phase transition temperatures between the plastic crystalline and the liquid crystalline phase (T_cry,colh) and between liquid crystalline and isotropic phase (T_colh,iso) were estimated from the maximum positions of the peaks in the heat flow. A hysteresis between heating and cooling is observed, especially for the phase transition between the plastic crystalline and the liquid crystalline phase. The inset enlarges the heat flow in the temperature range from 180 K to 220 K, the temperature where a glass transition is observed in ref. 31. A tiny step-like change of the heat capacity was observed during cooling which might indicate a glass transition. In contrast to what was found by Wübbenhorst et al.,³¹ in this study the step-like change in the heat flow is much weaker and hard to observe (see the inset of Fig. 3). A step-like change in the heat flow is also observed for HAT5, HAT8 and HAT10. First of all this seems to indicate that this small change in the heat flow is a real effect. With increasing n the step height decreases. For the heating scans no step-like change is observed for any material under study. In contradiction a more detailed investigation by means of Temperature Modulated Differential Scanning Calorimetry during heating does also not evidence a glass transition.^52–54

The phase transition temperatures depending on the length of the side chains n for cooling and the second heating are shown in Fig. 4 and summarized in Table 1. Similar results were found for a series of HATn (n = 5, 6, 7, 8, 9, 10) with only slight deviations for n = 10 (HAT10; ΔT_colh,iso = 4 K) in ref. 55. All discotic liquid crystals under study show a hysteresis as demonstrated for HAT6. While the phase transition temperature for the phase transition between the plastic crystalline and the liquid crystalline phase is more or less independent of the length of the aliphatic side chain, the phase transition temperature for the transition between the liquid crystalline and the isotropic phase decreases with increasing n. This results in a narrowed temperature range ΔT of the liquid crystalline mesophase with increasing n as it can be seen from the inset of Fig. 4. Fig. 5 presents the transition enthalpy depending on the chain length for both phase transitions. For the phase transition between the plastic crystalline and the liquid crystalline phase, the transition enthalpy first increases with n until it reaches a maximum enthalpy for n = 8 after which it decreases again. For the phase transition between the liquid crystalline and the isotropic phase the transition enthalpy decreases slightly with n until a small increase for the longest side chain n = 12 is observed.

Fig. 4 Transition temperatures for the phase transitions between plastic crystalline and liquid crystalline phase T_cry,colh and between liquid crystalline and isotropic phase T_colh,iso of the HATn materials depending on the length of the side chains n for heating (circles) and cooling (down triangles). Pentagons and stars indicate phase transition temperatures given in the literature.⁵⁵ Inset: size of the temperature range of the liquid crystalline mesophase ΔT depending on the length of the side chains n.

Fig. 5 Transition enthalpies for the transition from the plastic crystalline to the liquid crystalline phase (squares) and for the transition from the liquid crystalline to the isotropic phase (circles) depending on the length n of the side chains. Lines are guides for the eyes. The errors for the transition enthalpies for the phase transition from the liquid crystalline to the isotropic phase are smaller than the size of the symbols with regard to the scale of the y-axis.

Table 1 Phase transition temperatures from the plastic crystalline to the hexagonal columnar mesophase T_cry,col and from the hexagonal columnar mesophase to the isotropic phase T_col,iso during the second heating at a heating rate of 10 K min⁻¹

HATn	T cry,col (K)	T col,iso (K)
HAT5	341.7 ± 1.5	396.1 ± 1.5
HAT6	342.0 ± 1.5	372.3 ± 1.5
HAT8	338.6 ± 1.5	357.4 ± 1.5
HAT10	332.5 ± 1.5	346.0 ± 1.5
HAT12	331.7 ± 1.5	335.0 ± 1.5

---

Fig. 6 gives the X-ray diffractograms of HAT6 for the different phases. The diffractogram corresponding to the plastic crystalline phase (see Fig. 6a) appears complex with numerous reflections in the whole q range with the most prominent peak at q = 3.5 nm⁻¹. First of all, this indicates a more or less crystalline structure. Secondly, in the q-range from ca. 10 nm⁻¹ to 20 nm⁻¹ a kind of amorphous halo is observed. Such an amorphous halo is typical for semi-crystalline polymers consisting of amorphous and crystalline regions where the amorphous halo is related to the amorphous parts of the material.⁵⁶ Therefore the existence of an amorphous halo also for the HATn materials implies the existence of some disorder in the system. The inset of Fig. 6a compares the X-ray scattering pattern of HAT6 and semicrystalline polyethylene in the q-range between 10 nm⁻¹ and 25 nm⁻¹ (PE, degree of crystallization ca. 38%). Data are taken from ref. 57. Although the X-ray pattern of HAT6 exhibits more detailed reflections than that of PE, both spectra show also close similarities. This concerns especially the amorphous halo. Keeping in mind that the side chains of HATn consist also of CH₂ groups like PE one might discuss that the amorphous halo for HAT6 is related to a disordered structure of the methylene groups in-between the columns. This disordered structure on a larger length scale does not exclude local short range correlations. This was discussed for liquid hydro carbons as short translatorial chain–chain correlations.^58,59 A similar structure was confirmed for the comparable amorphous polymer polybutadiene by coherent neutron diffraction⁶⁰ which is also in agreement with detailed molecular simulation.⁶¹ For all lengths n of the side chains a comparable behavior of the amorphous halo is observed. Several efforts have been made to ascertain also the single crystal structure and the lattice type of triphenylene derivatives in the plastic crystal state but with only limited success.⁶² This might be due to the low scattering lengths of the C, H, O and N-atoms and the difficulty to prepare large enough single crystals for X-ray single crystal diffraction experiments. Moreover the existence of an inherent disordered amorphous structure indicated by the amorphous halo might impede the determination of a single crystal structure of HATn for higher values of n in general. The single crystal structure of the triphenylene-HAT2-NO₂ and other triphenylene-based discotic molecules with shorter side chains could be obtained by using sublimation or recrystallization of the ethylacetate for the sample preparation.^63,64 In several cases columns of the discotic core with separated side chains are found for the plastic crystalline phase. Therefore and also because of the incompatibility of the aromatic cores and aliphatic side chains here we assume for the plastic crystalline phase also columns of the core structure where the distance of the columns increases with increasing n. The X-ray spectrum corresponding to the hexagonally ordered liquid crystalline mesophase is depicted in Fig. 6b. The Bragg reflection at q_max = 3.5 nm⁻¹ corresponds to the core–core distance of the triphenylene cores.³⁶ The hexagonal ordering is confirmed by higher order reflections at q values 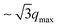(see the inset in Fig. 6b). The peak at q = 17.5 nm⁻¹ is related to the horizontal distance of the triphenylene cores within a column.^36,65 Moreover a broad amorphous halo is observed linked to the disordered structure of the methylene groups of the side chains in between the columns of the triphenylene cores. Compared to the plastic crystalline phase the amorphous halo is slightly shifted to lower q values. However, its appearance in both phases affirms further the disordered structure of the alkyl chains in the plastic crystalline phase. In the isotropic phase (see Fig. 6c) again the amorphous halo is observed in a q-value range which is similar to that for the hexagonal ordered liquid crystalline and the plastic crystal phase. Moreover a reflection at q = 3.65 nm⁻¹ indicates a column-like ordering also deeply in the “isotropic state”. Compared to the hexagonal liquid crystalline phase the peak is essential broader implying a more disordered structure of the columns with smaller column lengths. Therefore the peak due to the disc–disc distance is expected to be also quite broad and is probably hidden under the amorphous halo. For all investigated materials a similar behavior is found. Fig. 7 compares the X-ray diffractograms of the HATn materials in the columnar hexagonal phase. All materials show a pronounced reflection at scattering vectors smaller than 5 nm⁻¹. With increasing n this peak position shifts to lower q values. Taking the maximum position q_max the core–core distance d is calculated according to^36,65

Fig. 6 (a) X-ray spectra of HAT6 in the crystalline phase. Inset: diffractogram of plastic crystalline HAT6 (dashed line) and semi-crystalline polyethylene (solid line) in the q-range between 10 nm⁻¹ and 25 nm⁻¹. (b) X-ray spectra of HAT6 in the liquid-crystalline phase. Inset: X-ray diffractogramm of liquid crystalline HAT6 between q = 5 nm⁻¹ and q = 10 nm⁻¹. (c) X-ray spectra of HAT6 at T = 423 K where the material is supposed to be in the isotropic phase.

Fig. 7 X-ray diffractogram of the HATn materials at a temperature corresponding to the columnar hexagonal mesophase: T = 353 K for n = 5, T = 351 K for n = 6, 8, T = 341 K for n = 10. For n = 12 the temperature range of the mesophase is very narrow and due to the high heating rate, the curve here taken at T = 335 K is already in the isotropic phase. The curves are shifted on the y-scale for the sake of clearness.

The results are shown in Fig. 8 depending on the number of C-atoms in the side chain. As expected, with increasing lengths of the side chain the core–core distance increases more or less linearly as well as for the hexagonal columnar liquid crystalline and the isotropic phase with a similar slope. To prove this in more detail the data for the DLCs are compared with the length of a single alkyl chain in all conformation depending on n in Fig. 8.⁶⁷ Both the experimental data for the DLC and the theoretical values for a single alkyl chain have a similar slope with regard to n. This evidences that the distance between the columns is mainly due to the lengths of the alkyl chains. The d values for the DLCs are larger because more sides are involved than for one alkyl chain in all trans conformation. In Fig. 8 the obtained data are also compared to a pyrene-based discotic DLC with a shorter side chain⁴⁴ which fits well to the data of the HATn materials. Comparison is also made to the size of alkyl group rich nanodomains found in nanophase separated poly(n-alkylmetharylates)^66,67 In this case, the distance increases as well linearly with regard to n with a similar slope.

Fig. 8 Distance versus number of C-atoms for HATn: circles – the columnar hexagonal phase; squares – isotropic “phase”. Error bars were given for the distances in the liquid crystalline phase. For the distances in the isotropic state the error is similar. The dashed and dashed dotted lines are linear fits to the corresponding data. Data for triangles – poly(n-alkyl metharylates) and star – pyrene-1,3,6,8-tetracaroxylictetra (2-ethylhexyl)ester are taken from ref. 44 and 66. The straight line corresponds to data for a single alkyl chain in all trans conformation.⁶⁶ Non integer numbers for the poly(n-alkyl metharylates) refer to mixtures of polymers with different lengths of the side chain.

Inelastic neutron scattering is related to the molecular motions and vibrations of atoms or molecules on a microscopic length and time scale.⁶⁸ The momentum and energy exchanged during the experiment between neutrons and the sample give information on space and time, respectively. The essential quantity is the double differential cross section defined as

where k_i and k_f are the incident and final wave vectors of the neutron beam, q the scattering vector, ω the angular frequency related to the energy transfer ΔE/ℏ, Ω the solid angle of detection, S(q,ω) are the so-called coherent and incoherent scattering functions (dynamic structure factor) and σ the scattering cross-sections for coherent and incoherent scattering. The materials under study consist of hydrogen (H), carbon (C) and oxygen (O). The corresponding incoherent scattering cross sections σ_inc for these atoms are: σ_inc,H = 80.27(6) barn, σ_inc,C = 0 barn, σ_inc,O = 0 barn. Because of the fact that hydrogen is a strong incoherent scatterer and the coherent scattering cross sections are much smaller for all nuclei (σ_co,H = 1.7568(10) barn, σ_co,C = 5.551(2) barn, σ_co,O = 4.232(6) barn), mainly the scattering due to the hydrogen nuclei is monitored and as a result of the H-distribution in the molecule, at least for long alkyl chains, mainly the hydrogen in the alkyl chains. Therefore the observed scattering or dynamics can be assigned predominantly to the intercolumnar space. Fig. 9 gives spectra as measured by IN6 at 80 K normalized to the height of the elastic peak. The data show a weak Boson peak around an energy transfer of 1 meV. The comparison with the resolution of the instrument measured at 2 K reveals that a considerable amount of the scattering at 80 K is due to the resolution broadening of the elastic line. In order to separate the parts from the resolution and from the low-energy vibrations the standard expression for the one-phonon scattering function is applied:⁶⁹where e^−2W(q) is the Debye–Waller factor and m̄ the average mass of an atom. k_B is the Boltzmann constant. The observed scattering law is the convolution of eqn (3) with the resolution function of the instrument R(q,ω). The convolution effect on the inelastic term can be omitted because the boson peak is a broad feature when compared to the resolution. Therefore it holds:⁷⁰

Fig. 9 IN6 spectra of HAT10 normalized to the height of the elastic peak (corresponding to a q range of 1.1–2.0 Å⁻¹ for elastic scattering): filled circles at T = 80 K; open circles correspond to a measurement at 2 K representing the instrumental resolution. The black solid line is a guide for the eyes. The data were averaged over the detector range 54–108° which is the range from which the VDOS was evaluated.

When applied to spectra at two different temperatures (here 2 K and 80 K), eqn (4) gives a system of two linear equations from which the vibrational density of states g(ω) and the resolution R(q,ω) can be calculated. Fig. 10 gives the vibrational density of states (VDOS) for HAT5 in the frequency range of the Boson peak normalized to the VDOS expected from the Debye theory of sound waves which gives g(ω) ∼ ω². A BP is observed for this discotic liquid crystal in the plastic crystalline state. As already discussed above, as a BP seems to be characteristic of a glassy behaviour one can conclude that this class of discotic liquid crystals in the plastic crystalline state resembles features of a glass although only a weak (HAT5, HAT6) or non (HAT10, HAT12) step-like change in the heat flow indicating a thermal glass transition is observed. Moreover because of the fact that the observed scattering is mainly due to the hydrogen atoms located in the intercolumnar regions and it was evidenced by the X-ray investigation that the alkyl chains have a more or less disordered structure (amorphous halo), one can further conclude that these glassy features are related to the intercolumnar regions. Fig. 11 compares the Boson peak of HAT5 with the vibrational density of states of “amorphous” polyethylene (PE) given by Kanaya.¹⁷ In this context one has to note that the term “amorphous” here means that the VDOS was estimated for the amorphous regions of the semicrystalline polyethylene constraint by or within the crystalline regions. It does not represent the VDOS for a purely (hypothetical) amorphous PE. Because no absolute values for g(ω)/ω² are given in ref. 17 the data for PE were scaled to collapse at the high frequency side with the HAT5 data. Fig. 11 shows that the Boson peak of HAT5 approximately agrees roughly with regard to both its position and its shape with the data estimated for PE. This indicates that the vibrational density of states measured for the methylene groups in the intercolumnar regions of HAT5 corresponds well to that for the CH₂ groups in the constraint amorphous regions of semicrystalline polyethylene. The inset of Fig. 10 compares the Boson peak of the amorphous polymeric glass poly(methyl phenyl siloxane) (PMPS) and the nematic glass of the liquid crystalline mixture E7 with the BP of HAT5. First of all, compared to the other two materials the Boson peak of HAT5 is weak. Secondly, the degree of molecular order increases from PMPS over E7 to HAT5 (amorphous glass, nematic glass, plastic crystal). With the increase of the molecular order the BP decreases in intensity and its position shifts to higher frequencies. So one might speculate that the intensity of the Boson peak of a material decreases with the amount of order involved in the material. In addition the position of the BP shifts to higher frequencies with increasing order of the material under study. This might be related to the fact that with an increasingly better ordered structure the material becomes stiffer. In agreement with the line of arguments given in ref. 21 and 22 the Boson peak should shift to lower frequencies for softer materials. The inset of Fig. 12 compares the Boson peak of HAT5 with that of HAT6. One might imagine that the “soft” and flexible alkyl chains are confined between the “hard” (stiff), ordered columns built up by the cores of the molecules. Therefore we could compare this case from a phenomenological point of view with the case of molecules confined in hard confining matrices. As mentioned already, in such cases it is observed that the BP decreases in intensity mainly at its low frequency side and that the peak shifts to higher frequencies. The behavior of HAT6 is just opposite: compared to HAT5 the BP of HAT6 is increased in its intensity and shifted to lower frequencies. Keeping in mind that the distance between the columns for HAT6 is larger than for HAT5 one might consider the increase in the intensity and the shift to lower frequencies of the BP for HAT6 compared to HAT5 as a partial release of the self-organized confinement imposed by the columns of the aromatic cores onto the methylene groups in the intercolumnar space. Fig. 12 shows the reduced density of states g(ω)/ω² for HATn (n = 5, 10, 12) in the frequency range of the BP. All discotic liquid crystals considered here show a weak but well developed Boson peak (for HAT6 see the inset of Fig. 12). With an increasing number of methylene groups in the side chain the BP shifts to lower frequencies and gains in intensity. This is in agreement with the phenomenological self-organized confinement release hypothesis as discussed above. The columns generate a self-organized confinement with regard to the intercolumnar space and therefore also the side chains. As a result the side chains are stiffly organized in between these columns. The intercolumnar distance increases with n which leads to a release and weakening of the confinement. Fig. 13 shows how the Boson peak maximum shifts to lower frequencies with an increasing number n of side chain carbons. The line of arguments discussed in ref. 22 and 21 that with increasing length of the side chain the systems transform from a stiff system to a softer one is in full agreement with the release of the self-organized confinement model discussed above. Moreover the peaks for n = 10, 12 are much narrower than for n = 5, 6 which might be related to the transition from a rigid to a soft system. A comparison of HAT5, HAT6 with HAT10, HAT12 allows for another interesting comparison with the Schirmacher model.²² For HAT5, 6 the peak is quite broad while for HAT10, 12 the BP is much narrower. One might be tempted to relate this to the two limiting cases which were calculated in ref. 22 for different spatial correlations of the elastic constants. In analogy it might be deduced that the elastic constants for the longer side chains (HAT10, 12) are stronger correlated compared to the shorter ones. As longer chains tend to explore a wider space and should interact more with the neighbors, this seems to be logical. In light of this approach the behavior observed for HAT5 and HAT6 corresponds to an uncorrelated disorder where the data measured for HAT10 and HAT12 would indicate a correlated disorder. For low values of n (n = 5, 6) the structure of the CH₂ groups is mainly dominated and constrained by the columns where for HAT10, 12 the CH₂ groups are more free to organize by themselves and a certain correlation between the methylene groups can be established. These considerations are in agreement with the self-organized confinement model developed above. Fig. 14 compares the VDOS reduced by ω² for HAT8 with the data of HAT5 and HAT12. For HAT8 unexpectedly no pronounced Boson peak is observed. Till now the reason for that behavior has been quite unclear and has to be further investigated by other methods. Nevertheless the line of the arguments of the transition from an uncorrelated to a correlated disorder (with increasing n) one might speculate that n = 8 corresponds to transitional state between the two kinds of disorder. In ref. 22 it was also mentioned that for a critical value of the disorder parameter for the uncorrelated state the calculations becomes unstable. This might be a possible explanation for the absence of a Boson peak in HAT8. This argument is supported by the fact that for high frequencies the data for HAT8 coincide with those for HAT5 and HAT6.

Fig. 10 Vibrational density of states (VDOS) of HAT5. Inset: vibrational density of states of HAT5 – circles, the nematic mixture E7²⁸ – stars and for polymeric glass poly(methyl phenyl siloxane) (PMPS) – upward triangles.²⁴ The data for the different materials were not normalized.

Fig. 11 Vibrational density of states of HAT5 (empty circles) and of “amorphous” polyethylene (PE) (filled circles) given by Kanaya in ref. 17. The data for PE are scaled to collapse at the high frequency side with the HAT5 data.

Fig. 12 VDOS at T = 80 K of HATn for the different lengths of the alkyl chains: circles – HAT5, stars – HAT10, diamonds – HAT12. Inset: Boson peak for HAT5 – circles and HAT6 – squares. Lines are guides for the eyes.

Fig. 13 Frequency of the Boson peak ω_BPversus the number of carbon atom in the side chains.

Fig. 14 VDOS of HATn with different lengths of the side chains: diamonds – HAT12, triangles – HAT8, circles – HAT5.

Conclusions

A series of triphenylene based discotic liquid crystals (HATn, n = 5, 6, 8, 10, 12) is investigated by differential scanning calorimetry, X-ray scattering and neutron scattering. In the liquid crystalline phase, the scattering pattern of all materials shows a sharp Bragg-reflection corresponding to the intercolumnar distance in the lower q-range. In the higher q-range, a reflection corresponding to the stacking of the cores within one column and a broad amorphous halo linked to the disordered structure of the methylene groups in the side chains are observed. In the plastic crystalline phase a similar structural arrangement is assumed, these alkyl chains form a nanophase separated state between the columns. Besides HAT8, all other materials under study exhibit a boson peak (BP). With increasing lengths n of the side chains the BP shifts to lower frequencies and gains in intensity. This can be discussed employing a self-organized confinement model, where the confinement is generated by the highly ordered columns to the intercolumnar space, where with increasing n the confinement is weakened. Furthermore for the longer chain lengths n = 10, 12, the Boson peak is considerably narrower than for the smaller chain lengths n = 5, 6. This might indicate the transformation from a stiff to a soft system. Moreover these results can also be discussed in the framework of a transition from an uncorrelated to a correlated disorder with increasing n. In this approach n = 8 might be considered as a transitional state.

Acknowledgements

D. Neubert and S. Rolf are thanked for experimental help. The financial support from the German Science foundation (DFG SCHO 470/21-1 and HU 850/3-1) is gratefully acknowledged. The Institut Laue-Langevin and the Helmholtz Centre Berlin for Materials and Energy are thanked for enabling the neutron and X-ray scattering experiments.

Notes and references

1. R. Zallen, The physics of amorphous solids, Wiley, New York, 1983.
2. P. W. Anderson, Science, 1995, 267, 1615.
3. C. A. Angell, Science, 1995, 267, 1924.
4. P. G. Debenedetti and F. H. Stillinger, Nature, 2001, 410, 259.
5. C. A. Angell, J. Res. Natl. Inst. Stand. Technol., 1997, 102, 171.
6. A. P. Sokolov, R. Calemczuk, B. Salce, A. Kisliuk, D. Quitmann and E. Duval, Phys. Rev. Lett., 1997, 78, 2405.
7. R. Zorn, A. Arbe, J. Colmenero, B. Frick, D. Richter and U. Buchenau, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 781.
8. V. K. Malinovski, V. N. Novikov and A. P. Sokolov, J. Non-Cryst. Solids, 1987, 90, 485.
9. U. Buchenau, Y. M. Galperin, V. L. Gurevich, D. A. Parshin, M. A. Ramos and H. R. Schober, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 2798.
10. B. B. Laird and H. R. Schober, Phys. Rev. Lett., 1991, 66, 636.
11. S. N. Taraskin, Y. L. Loh, G. Natarajan and S. R. Elliott, Phys. Rev. Lett., 2001, 86, 1255.
12. W. Schirmacher, G. Diezemann and C. Ganter, Phys. Rev. Lett., 1998, 81, 136.
13. R. Zorn, M. Mayorova, D. Richter, A. Schönhals, L. Hartmann, F. Kremer and B. Frick, AIP Conf. Proc., 2008, 982, 79.
14. R. Zorn, B. Frick, L. Hartmann, F. Kremer, A. Schönhals and D. Richter, Physica B, 2004, 350, e1115.
15. E. Duval, A. Mermet and L. Saviot, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 024201.
16. V. K. Malinovsky and N. V. Surovtsev, Phys. Status Solidi C, 2004, 1, 2900–2903.
17. T. Kanaya, K. Kaji, S. Ikeda and K. Inoue, Chem. Phys. Lett., 1988, 150, 334–338.
18. A. Mermet, N. V. Surovtsev, E. Duval, J. F. Jal, J. Dupuy-Philon and A. J. Dianoux, EPL, 1996, 36, 277.
19. A. Mermet, E. Duval, S. Etienne and C. G'Sell, J. Non-Cryst. Solids, 1996, 196, 227–232.
20. R. Inoue, T. Kanaya, K. Nishida, I. Tsukushi and K. Shibata, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 021801.
21. M. T. Cicerone and C. L. Soles, Biophys. J., 2004, 86, 3836.
22. W. Schirmacher, B. Schmid, C. Tomaras, G. Viliani, G. Baldi, G. Ruocco and T. Scopigno, Phys. Status Solidi C, 2008, 5, 862.
23. L. Hong, V. N. Novikov and A. P. Sokolov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 061508.
24. T. Asthalter, M. Bauer, U. van Bürck, I. Sergueev, H. Franz and A. I. Chumakov, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 12, S9.
25. A. Schönhals, B. Frick and R. Zorn, in preparation.
26. A. Schönhals, H. Goering, C. Schick, B. Frick and R. Zorn, Colloid Polym. Sci., 2004, 282, 882.
27. R. Zorn, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 054208.
28. A. Schönhals, S. Frunza, L. Frunza, T. Unruh, B. Frick and R. Zorn, Eur. Phys. J.: Spec. Top., 2010, 189, 251.
29. R. Zorn, M. Mayorova, D. Richter and B. Frick, Soft Matter, 2008, 4, 522.
30. P. Lunkenheimer and A. Loidl, J. Non-Cryst. Solids, 2006, 352(42–49), 4556.
31. Z. Yildirim, M. Wübbenhorst, E. Mendes, S. J. Picken, I. Paraschiv, A. T. M. Marcelis, H. Zuilhof and E. J. R. Sudhölter, J. Non-Cryst. Solids, 2005, 351, 2622.
32. C. A. Angell, J. Non-Cryst. Solids, 1991, 131–133, 13.
33. H. Suga and S. Seki, J. Non-Cryst. Solids, 1974, 16, 171.
34. J. Wu, W. Pisula and K. Müllen, Chem. Rev., 2007, 107, 718.
35. Handbook of Liquid Crystals, ed. D. Demus, J. Goodby, G. W. Gray, H. W. Spiess and V. Vill, Wiley-VCH, Weinheim, 1998.
36. S. Laschat, A. Baro, N. Steinke, F. Giesselmann, C. Hägele, G. Scalia, R. Judele, E. Kapatsina, S. Sauer, A. Schreivogel and T. Tosoni, Angew. Chem., 2007, 119, 4916.
37. C. Grigoriadis, N. Haase, H. J. Butt, K. Müllen and G. Floudas, Adv. Mater., 2010, 22, 1403.
38. C. Krause and A. Schönhals, J. Phys. Chem. C, 2013, 117, 19712.
39. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197.
40. J. H. Wendorff, T. Christ, B. Glüsen, A. Greiner, A. Kettner, R. Sander, V. Stümpflen and V. V. Tsukruk, Adv. Mater., 1997, 9, 48–52.
41. S. Sergeyev, W. Pisula and Y.-H. Geerts, Chem. Soc. Rev., 2007, 36, 1902.
42. L. Schmidt-Mende, A. Fechtenkötter, K. Müllen, E. Moons, R. H. Friend and J. D. MacKenzie, Science, 2001, 293, 1119.
43. S. Ito, M. Wehmeier, J. D. Brand, C. Kübel, R. Epsch, J. P. Rabe and K. Müllen, Chem.–Eur. J., 2000, 6, 4327.
44. C. Krause, H. Yin, C. Cerclier, D. Morineau, A. Wurm, C. Schick, F. Emmerling and A. Schönhals, Soft Matter, 2012, 8, 11115.
45. M. M. Elmahdy, X. Dou, M. Mondeshki, G. Floudas, H. J. Butt, H. W. Spiess and K. Müllen, J. Am. Chem. Soc., 2008, 130, 5311.
46. M. M. Elmahdy, G. Floudas, M. Mondeshki, H. W. Spiess, X. Dou and K. Müllen, Phys. Rev. Lett., 2008, 100, 107801.
47. N. Tasios, C. Grigoriadis, M. R. Hansen, H. Wonneberger, C. Li, H. W. Spiess, K. Müllen and G. Floudas, J. Am. Chem. Soc., 2010, 132, 7478.
48. O. Paris, C. Li, S. Siegel, G. Weseloh, F. Emmerling, H. Riesemeier, A. Erko and P. Fratzl, J. Appl. Crystallogr., 2007, 40, S466.
49. A. P. Hammersley, S. O. Svensson, M. Hanfland, A. N. Fitch and D. Hausermann, High Pressure Res., 1996, 14, 235.
50. http://www.ill.eu/instruments-support/instruments-groups/instruments/in6/ .
51. http://www.ill.eu/instruments-support/computing-for-science/cs-software/all-software/tofhr/inx/ .
52. C. Krause, A. Schönhals, A. Wurm and C. Schick, unpublished results.
53. H. Huth, A. A. Minakov and C. Schick, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 2996.
54. H. Gobrecht, K. Hamann and G. Willers, J. Phys. E: Sci. Instrum., 1971, 4, 21.
55. C. Destrade, M. C. Mondon and J. Malthete, J. Phys., Colloq., 1979, 40, C3–C17.
56. G. R. Strobl, The Physics of Polymers-Concepts for Understanding Their Structures and Behavior, Springer, 2007.
57. P. J. Purohit, D. Y. Wang, F. Emmerling, A. F. Thünemann, G. Heinrich and A. Schönhals, Polymer, 2012, 53, 2245.
58. A. Spaar and T. Salditt, Biophys. J., 2003, 85, 1576.
59. B. E. Warren, Phys. Rev., 1933, 44, 969.
60. B. Frick, D. Richter and C. Ritter, Europhys. Lett., 1998, 9, 557.
61. A. Narros, A. Arbe, F. Alvarez, J. Colmenero, R. Zorn, W. Schweika and D. Richter, Macromolecules, 2005, 38, 9847.
62. T. Wang, D. Yan, J. Luo, E. Zhou, O. Karthaus and H. Ringsdorf, Liq. Cryst., 1997, 23, 869.
63. R. J. Bushby, N. Boden, C. A. Kilner, O. R. Lozman, Z. Lu, Q. Liu and M. A. Thornton-Pett, J. Mater. Chem., 2003, 13, 470–474.
64. T. L. Andresen, F. C. Krebs, N. Thorup and K. Bechgaard, Chem. Mater., 2000, 12, 2428.
65. E. Grelet, S. Dardel, H. Bock, M. Goldmann, E. Lacaze and F. Nallet, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 31, 343.
66. M. Beiner, K. Schröter, E. Hempel, S. Reissig and E. Donth, Macromolecules, 1999, 32, 6278.
67. M. Beiner and H. Huth, Nat. Mater., 2003, 2, 595.
68. M. Bée, Quasielastic neutron scattering. Principles and applications in solid state chemistry, biology and materials science, Adam Hilger, 1988.
69. S. W. Lovesey, Theory of Neutron Scattering from Condensed Matter, Oxford University, New York, 1987, vol. 1, p. 121.
70. R. Zorn, L. Hartmann, B. Frick, D. Richter and F. Kremer, J. Non-Cryst. Solids, 2002, 307, 547.

---