Manipulating the excitation transfer in Photosystem I using a Fabry–Perot metal resonator with optical subwavelength dimensions

Abstract

We demonstrate controlled modification of the fluorescence and energy transfer properties of Photosystem I (PSI) – one of the most important light harvesting systems – by using a newly developed approach to produce optical subwavelength microcavities for cryogenic temperature issues. The experiments were carried out on PSI from the cyanobacterium Arthrospira platensis as it shows a broad and structured fluorescence emission. By changing the distance between the cavity forming mirrors, the electromagnetic field mode structure around PSI is varied affecting the emission and energy transfer properties, which allows us to selectively enhance signals of resonant emitters and suppress off-resonant emission. By comparing the experimental data with simulations, we are able to show how excitation transfer within PSI is affected by the microcavity. The ability to control the energy transfer within such efficient energy converters as photosynthetic proteins can establish the opportunity for enhancing the efficiencies of bio-solar applications. The defined control of the resonance conditions by microcavities makes them a preferable tool to study the effects of additional electromagnetic modes on the energy transfer in any coupled multi-chromophore system. The resonator geometry excludes the direct contact of the proteins with any surface. Possible quenching or denaturation of the complexes close to metal surfaces is still an insuperable obstacle for studies with proteins and nanostructures, which can be avoided by resonators.

---

1 Introduction

Optical microcavities are efficient tools to tailor the fluorescence of embedded emitters to a narrow spectral range.¹ Placing an emitter within a confined geometry of a resonator modifies its emission properties,² in particular, the spectral, spatial and temporal distributions. According to Fermi's golden rule, the spontaneous emission lifetime of a dipole emitter depends on both the transition dipole moment and the density of modes of the electromagnetic field.³ Inside cavities, the density of modes coupling to the dipole emitter is changed with respect to free space and hence the emission rate of the emitter. This effect – first described by Purcell² – can be used to enhance and shape the fluorescence emission down to the single particle/molecule level.^4–7 One type of such cavities is realized by Fabry–Perot like microresonators, which are emerging devices for manipulating optical properties of fluorophores.⁶ In the last few years, experimental studies on cavity-controlled photo-luminescence have been carried out on model systems such as single quantum dots,⁸ molecules,⁴ atoms,⁹ nitrogen-vacancy centers in diamonds¹⁰ and simple energy transfer systems.^11,12 In this article, we demonstrate first optical experiments of a prominent and complex energy transfer coupled protein system confined in an optical resonator at cryogenic temperatures (1.6 K). We selectively tune the fluorescence of emitting pools in Photosystem I (PSI) by a subwavelength microcavity and describe the consequent modifications in the exciton transfer dynamics.

PSI is one of the key proteins of the photosynthetic apparatus and a promising candidate for bio-solar applications.^13–15 Especially, interactions with electric fields created by plasmonic nanostructures have attracted a lot of attention during the last few years.^{13,14,16–22} The attractiveness of PSI relies partially on its simple function, which is capturing and converting solar energy into electric energy. For this purpose around 100 chlorophyll molecules per monomer are involved in efficient light-harvesting and excitation energy transfer leading to light induced charge separation in the reaction center and a subsequent transfer of an electron (Fig. 1a–d).²³ An intriguing feature of the PSI core antenna of cyanobacteria is the presence of several chlorophyll (Chl) molecules absorbing at lower energy than the reaction center at 700 nm (P700). These Chls have a pronounced effect on the excitation energy transfer within the whole antenna system (Fig. 1c–f).²⁷ These red-shifted Chls are often referred to as “red-most” Chls or long-wavelength Chls (for details see ref. 25 and 28). At low temperatures, these long-wavelength Chls act as traps for excitons, partially releasing this excitation energy as fluorescence (Fig. 1e–f).²³ The fluorescence emission of PSI is a composition of several spectroscopically discernible contributions from different long-wavelength Chls.²⁵ The high quality of the protein preparations, the large absorption cross section, the red-shifted emission and its prominence makes PSI a perfect system to analyze the influence of external fields on the optical properties and excitation energy transfer dynamics of coupled multi-chromophoric systems.^{16–18,22,29}

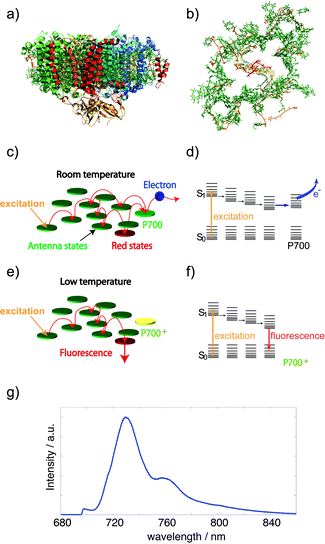Fig. 1 Photosystem I from oxygenic photosynthesis. (a) Side view of PSI from cyanobacteria (protein data bank (PDB) entry: 1JB0).²⁴ (b) Top view of PSI without the protein backbone. In each monomer about 100 chlorophyll molecules (green) absorb excitation energy and transfer it to a chlorophyll dimer (red) in the reaction center²³ which absorbs at 700 nm (P700). (c and d) Illustration of excitation-energy transfer pathways at ambient temperatures and an energy-level scheme. Upon excitation of P700 a charge-separated state across the membrane is formed.²³ Interestingly, red chlorophyll states (red) with lower excitation energies than P700 are also involved in energy transfer. (e and f) At low temperatures the transfer from the red chlorophylls towards P700 is partially blocked, as a consequence these chlorophylls become fluorescent. (g) The low temperature fluorescence emission of PSI trimers (blue) is composed of several contributions having different wavelength positions, width and intensity (for further details, see ref. 25 and 26).

The modifications of the excitation energy transfer in PSI embedded in a subwavelength microcavity result in altered fluorescence spectra which are observed using a confocal microscope. Revealing these altered exciton transfer dynamics is achieved by comparing the experimental spectra with simulated spectra of uncoupled chromophores. The resonance wavelength and with that the cavity length can be measured and modified by scanning the position of the focal spot (confocal volume) over the microcavity as shown in Fig. 2. This approach enables the collection of transmission and fluorescence spectra of PSI complexes exposed to different electromagnetic field mode structures. Production and application of the microresonators at cryogenic temperatures are described in the ESI.† Altering transfer efficiencies in transfer coupled systems embedded in resonators by modifying their optical properties has already been shown by Andrew et al.¹² or Schleifenbaum et al.¹¹ who used model systems at room temperature. It has been shown for such coupled systems that microcavities enable the enhancement and characterization of luminescence bands which are suppressed in free space. Addressing individual fluorescent pools in PSI is hampered by large lifetime variations,^30,31 overlapping of spectral bands, potentially hidden quenched pools and spectral diffusion even at cryogenic temperatures. In this article we report on the selective control of the energy transfer in a complex and one of the most important protein systems in nature for the first time. We can also confirm previously reported^22,25,32 approaches addressing fluorescent Chl pools by measurements and the used model for interpretation. With our new approach for low temperature Fabry–Perot resonators any biological sample can be prepared and frozen in standard solutions like water–glycerol-mixtures. Contrary to experiments with nanostructures, we can also exclude any chemical interaction of the proteins at metal surfaces due to a large cavity mode volume and a glass spacing layer on the silver mirrors. Conformational changes or denaturation induced by nearby metal surfaces is a severe problem for observing native protein states. The defined control of light-harvesting and energy-transfer coupled system is one prerequisite for developing or improving bio-solar devices.

Fig. 2 Simplified scheme showing the scanning of the focal spot over a λ/2 microcavity. The curved shape of one of the mirrors results in a continuous change of the resonance conditions as indicated by the rainbow colors inside the cavity. The cavity is illuminated by a white light source to determine the cavity properties at the focal spot; only the components fulfilling the resonance conditions pass the cavity. This light is collected by an objective yielding the transmission spectrum (on top). The resonance wavelength of the resonator is changed simply, by changing the position of the focal spot in relation to the cavity (right). For detailed information concerning the setup and manufacturing of the cavities, see also the ESI.†

2 Results and discussion

In the first order of interference of the cavity (λ/2 region), several positions with different resonance conditions were selected as illustrated in Fig. 2. At these positions, the white light transmission spectrum of the cavity and the fluorescence emission of PSI were recorded one after the other. For each position, the cavity length was determined from the white light transmission spectrum (as shown in the ESI†). The λ/2 region contains only one matching order of resonator modes in the wavelength range of the absorption and emission of PSI. This gives the opportunity to control the mode density with high precision over a large spectral range. The excited photosystems in the resonator are forced to enhanced decoherence resulting in changed lifetimes and restricted energy distribution.

Several fluorescence spectral series with tuned resonance frequencies of the resonator covering the whole wavelength range of the fluorescence emission of PSI were collected. Fig. 3a shows four emission spectra (blue curves) out of one series together with the corresponding Lorentzian fits of the white light transmission spectra (black curves). For comparison, the spectrum on top shows the free space emission spectrum of PSI trimers from A. platensis (blue curve). The same spectrum is also displayed in Fig. 3b described by a multiple Gaussian fit (see also Table 1). The four measured spectra at selected resonance wavelengths differ extremely from the free-space spectrum but also from each other. Mostly emission around the white light transmission maximum is enhanced and emission on the long wavelength side inhibited. On the short wavelength side angular distribution modes are still able to couple with emitters to enhance their radiative rate, visible in Fig. 3c by the shown Purcell factor distribution.³³ We claim that the influences on PSI resulting in the shown spectra are on the one hand determined by the spectral shaping of the Purcell factor and on the other hand by altered transfer dynamics, depending on changed population/depopulation rates.

Fig. 3 (a) Four measured (blue curves) and calculated (red curves) fluorescence spectra of PSI placed inside the microresonator at different cavity lengths. The white light transmission (black curves) shows their resonance wavelengths at 702, 712, 730, and 759 nm. On top, the free-space fluorescence spectrum of PSI trimers from A. platensis is given (the drop down of the intensity at <695 nm is due to the longpass filter used). (b) The free space spectrum of PSI from A. platensis (blue curve) together with a fit (green dotted curve) based on six individual Gaussian functions (red dotted curves), the details are given in the text and in Table 1. (c) One selected set of measured (blue curves) and calculated spectrum (red curves) in combination with the Purcell factor (green curve) as given in ref. 33 and the ESI.†

Table 1 Comparison of parameters resulting from a fit of the free-space emission spectrum of PSI trimers from A. platensis with wavelength positions of fluorescent pools reported in the literature

Gaussian	Wavelength/nm	Width/nm	Pool
1	697	21	F699^32
2	715	12	F714^26
3	727	20	F726^25,26
4	737	20	F731^25
5	759	39	F760^26
6	798	62	—

---

To highlight the pure contribution caused by modifications within the transfer dynamics we simulated the emission spectrum of PSI inside the cavity without assuming any coupling between the emitting pools and compared these simulations with the experiment. The method for simulating the cavity influenced spectra is based on ref. 7. The main concept is grounded on the assumption that the spectral band and its overall intensity are proportional to the fluorescence quantum yield and the population probability of its corresponding emitter. In a cavity, the radiative rate is altered leading to a changed intensity of the band. Also the shape of the spectral band is changed due to the spectral shape of the cavity mode distribution. Therefore, the characteristic spectral distribution of the Purcell factor enables enhancing or suppressing and addressing of single emitting bands inside a composite spectrum. For this purpose the single spectral bands of the free-space PSI spectrum are characterized by Gaussian fits (see Fig. 3b). Five Gaussian contributions, centered at 697, 715, 727, 737 and 760 nm, are used with wavelength positions and widths in agreement with the recently reported positions of the red-emitting states, for details, see ref. 25, 26 and 32. A sixth contribution at 798 nm is not reported for PSI in the literature up to now, but the contribution is necessary to reconstruct the emission profile properly. The spectral position and the width of all six contributions together with the assigned red Chls are summarized in Table 1.

Each Gaussian is overlapped with the corresponding Purcell factor distribution for each corresponding resonance wavelengths. The spectral distribution of the Purcell factors was calculated by using ref. 33. Finally the six single shaped Gaussians were summed up again and scaled to same integral intensity as the corresponding measured spectrum to make their comparison feasible. A more detailed description is given in the ESI.†

Fig. 3a and c show experimental (blue) and simulated spectra (red) at various resonance wavelengths. Each experimental spectrum differs from its corresponding simulation with various degrees within various spectral regions, indicating the additional effect of disturbed transfer pathways inside PSI. Fig. 4a and b show the complete fluorescence spectral series of experimental (a) and calculated (b) spectra for resonance wavelengths between 697 and 850 nm (white circles). Comparing (a) and (b) it can be seen that the simulations of the uncoupled system differ slightly for specific wavelength ranges from the experiment. To highlight these specific differences between coupled and uncoupled systems the simulated series was subtracted from the experimental series, whose result is shown in Fig. 4c. This series now shows the fluorescence enhancement/inhibition (violet/red), depending on wavelengths and cavity lengths, of the coupled system compared to the uncoupled system. Red colors show less fluorescence to the simulation, meaning a lowered population of these emitting pools, while violet and blue show more fluorescence, meaning an increased population of these emitting pools. Positive values can be observed for the first five spectra in the region at ∼690 nm and for spectra with number 3–10 close to their resonance wavelengths. Negative values are observed for almost all spectra in the wavelength range close to the emission maximum of PSI.

Fig. 4 (a) Contour plot of a fluorescence spectral series of experimental data taken from a scan of the resonance wavelength of the resonator over the emission profile of PSI from A. platensis. The resonance wavelength of the resonator is given by white dots; it varies between 697 nm and 850 nm. (b) Contour plot of a fluorescence spectral series of the calculated spectra based on the conditions given in (a) and without respect to coupling between the emitters. (c) Contour plot showing the difference between the plots given in (a) and (b) revealing the cavity induced modifications in the energy transfer dynamics. Violet means more emission, red less emission of the coupled to the uncoupled system.

The specific effects of alterations of the process rates in PSI can be seen in Fig. 4 and are schematically visualized in Fig. 5. Spectra with resonances <720 nm show increased intensity at wavelengths around 690 nm. This enhanced fluorescence indicates a deactivation of states, which show virtually no fluorescence emission in the absence of the resonator. This can be explained by an increased residence time of excitons at these emitters and therefore an inhibited transfer to chromophores with lower energies. Also the off-resonant (longer wavelengths than transmission maximum) emitters are inhibited in their radiative deactivation leading to increased saturation than to free space. The spectra with resonances >750 nm show lowered intensity for all emitting pools, mostly for Chls emitting at around 730 nm. This can be explained by the enhanced deactivation of all fluorescent Chls because of the flattened flank of the Purcell factor to short wavelengths. Therefore a lowered excitonic population probability of these emitters induced by the resonator compared with the simulations can be assumed.

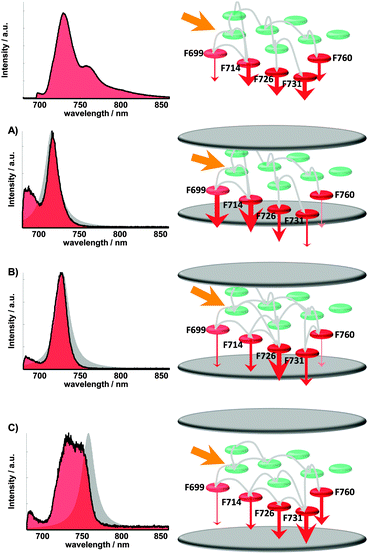Fig. 5 Visualization of altered excitation energy transfer pathways in Photosystem I (exaggerated and simplified). From (A) to (C) the cavity length increases, noticeable by the spectral position of the white light transmission (grey area). The set of radiative transition rates and the population of the red states are modified by the additional mode density depending on mirror spacing. Changing the radiative rate (to free space) as a depopulation channel of a certain luminescent chlorophyll containing pool also alters the population dynamics of its corresponding transferring and receiving pools. The observed spectrum is a superposition of every single pool emission (see Table 1), depending on its population amount, the wavelength dependent resonator emission pattern and the radiative rate enhancement/inhibition. The altered spectrum enables therefore statements on the relative population probability of every luminescent pool. The altered occupations, indicated by Fig. 4, are visualized exemplarily on the right side by the thickness of the red arrows illustrating the emission intensity, together with the corresponding spectra (left, red area).

The most striking effects are found in the wavelength areas of the pools F699, F726 and F731 (see Table 1). In Fig. 5 this behavior is sketched for three different mirror spacings. On the left the modified spectra are shown (red) with the corresponding transmission spectra (gray) below the free-space spectrum on top. On the right the arrangement of the Chl, the emitting pools (see Table 1) and their deactivation rates are sketched by red arrows.

The specific arrangement and coupling of the chromophores in PSI is optimized for efficient excitation transfer to the reaction center.³⁴ The energy transfer efficiency between chromophores depends on the spectral overlap, distance, and orientation,^34,35 the individual relaxation properties and saturation effects of long-living states. This means, each Chl within the transfer chain features a characteristic time and probability of accepting, containing and transferring an exciton. By changing one or more Chl relaxation rates within PSI all other relaxation properties are influenced. Such cavity enhanced transfer efficiency changes have been shown already for two simple systems under ambient conditions: a two-chromophore model system¹² and the fluorescent protein DsRed.^6,11

As a consequence, the field in the microresonator can change the specific and controllable exciton distribution within PSI by involving additional chromophores in excitation energy transfer^19,22,29 or by changing the evolution inside the energy transfer pathways by enhanced/inhibited population/depopulation of excited states. Fig. 4 also supports the assignment of the fluorescent pools according to Table 1. Obvious deviations between experiment and simulation are only found in wavelength regions corresponding to reported Chl pools.

Comparable effects on the fluorescence emission of different photosynthetic complexes were recently observed in the vicinity of plasmonic nanostructures.^20,22,29 Such effects on optical properties of chromophores are induced by the optical near-field of the nanostructures.^36,37 The interaction between pigments and the electric near-field of plasmonic nanostructures shows a strong distance- and orientation-dependence.^36,37 A fluorophore coupled to an Au nanosphere of 100 nm diameter shows within 13 nm a change from quenching to maximum enhancement,³⁶ this value is even smaller than the diameter of a PSI trimer (∼20 nm). As a consequence, the effect of a plasmonic near field on the different Chls in one single protein complex can vary between quenching and maximal enhancement.^20,22,29 If one aims to control the optical properties of a protein complex by plasmonic nanostructures a precise positioning in the sub-nanometer regime is required and in addition, the relative orientations must be controlled. As a consequence, studies to investigate the interaction of the electromagnetic fields produced by plasmonic nanostructures are hindered by these constraints. Optical microcavities, however, exhibit several advantages. The field distribution within a Fabry–Perot resonator is well defined by the distance between the mirrors and it changes only slightly over the dimension of a single protein (λ/2 vs. 20 nm for PSI); therefore the mode structure of the electric field at the position of the proteins can be determined directly from the transmission spectrum. This approach simplifies theoretical modeling of the decoherence induced by the mode structure and provides further insights into coherent or incoherent parts of the transfer. Another advantage compared to metallic nanostructures lies in the possibility to exclude chemical interactions with the protein complexes. The protein structure can be altered or even denaturized upon direct contact with metal surfaces.^38,39 Thus, in experiments with proteins close to metal surfaces or structures one can never be sure to gather information on native states. The volume of the microcavity is comparably large and a spacing layer of SiO₂ covering the silver surfaces prevents interactions completely. Therefore, chemical interactions by the field enhancing geometry on luminescent proteins can be excluded in the reported experiments. In principle, all pigment–proteins can be investigated by the resonator production and sample transfer⁴⁰ method presented here.

3 Experimental section

A schematic along with a detailed description of the manufacturing process of low temperature cavities and the confocal microscope used for efficient excitation and detection of the emission of PSI in the microresonator are given in the ESI.†

In short, the microcavity consists of two silver mirrors one being planar and one being slightly curved such that the gap between the mirrors slowly increases with increasing distance from the center, shown in Fig. 2. The cavity mirrors were fabricated by coating quartz substrates with several layers. The first layer is made of 1 nm chromium, followed by a silver layer (60 nm bottom and 30 nm top mirror), a 1 nm gold layer that is finally covered by a 30 nm SiO₂ layer, which acts as a spacer between the proteins and the silver surface. Their reflectivity was determined by transmission spectroscopy to be 0.95 (bottom) and 0.90 (top) @ 700 nm.

On one of the coated glass substrates less than 1 μL of the PSI containing sample solution was placed and then covered by a second coated glass substrate. This sandwich was transferred to the sample holder designed for our low temperature setup (for details see ref. 40). The sample holder is fixed on a stage for squeezing the mirrors together yielding a Fabry–Perot resonator showing concentric Newton rings in transmission indicating variable mirror distances and resonance conditions. The whole squeezer (including the sample holder and the sample) is then transferred into a Dewar flask filled with liquid nitrogen. The frozen sample solution acts as a glue holding the squeezed mirrors in position. A home-built sample transfer system⁴⁰ enables us to transfer the squeezed resonator into the cold cryostat (4.2 K) without temperature increase during handling and transfer. After mounting the sample inside the cryostat, the temperature is lowered to 1.6 K.

The wavelength of the cavity mode perpendicular to the mirror surfaces was determined from the white light transmission spectrum (see Fig. S2 and S4 in the ESI†). The design of our low temperature microresonator results in a quality factor of ∼60 (fwhm ∼ 15 nm in the transmission spectrum at 1.6 K), which is several times smaller than the full width at half maximum of the emission spectrum of PSI trimers from A. platensis. All fluorescence measurements were done with cw-excitation at 665 nm.

4 Conclusion

In conclusion, our experiments show an altered fluorescence emission of PSI in an optical microresonator with subwavelength dimensions. Comparing the experimental data with simulations assuming uncoupled emitters provides the intensity changes caused by altered energy transfer pathways. Particularly chlorophyll molecules with site-energies close to that of the reaction center undergo much stronger deactivation through fluorescence emission as the uncoupled model, indicating an increased presence probability of excitons. We suppose that altered responses can generally be expected for multichromophore coupled systems in any resonate optical structure. The mode density can be changed by microcavities in a defined manner in a very simple way. Any structural distortion or denaturation of the proteins by the metallic surfaces in our experiments can be ruled out. Therefore, optical microresonators are superior to plasmonic nanostructures for studying the influence of optical fields on any kind of luminescent particles.

Acknowledgements

Financial support from the German Research Council (DFG) for ME1600/13-1 and Heisenberg-Programm (BR 4102/1-1 and BR 4102/2-1), the Russian Academy of Sciences, program MCB and RFBR (Grant 14-04-00148a, to N.V.K.) is gratefully acknowledged.

References

1. K. J. Vahala, Nature, 2003, 424, 839–846.
2. E. M. Purcell, Phys. Rev., 1946, 69, 681.
3. E. Fermi, Rev. Mod. Phys., 1932, 4, 88–132.
4. M. Steiner, F. Schleifenbaum, C. Stupperich, A. V. Failla, A. Hartschuh and A. J. Meixner, J. Lumin., 2006, 119, 167–172.
5. M. Steiner, A. V. Failla, A. Hartschuh, F. Schleifenbaum, C. Stupperich and A. J. Meixner, New J. Phys., 2008, 10, 123017.
6. S. Bar, A. Chizhik, R. Gutbrod, F. Schleifenbaum, A. Chizhik and A. J. Meixner, Anal. Bioanal. Chem., 2010, 396, 3–14.
7. A. I. Chizhik, A. M. Chizhik, A. M. Kern, T. Schmidt, K. Potrick, F. Huisken and A. J. Meixner, Phys. Rev. Lett., 2012, 109, 223902.
8. D. Englund, D. Fattal, E. Waks, G. Solomon, B. Zhang, T. Nakaoka, Y. Arakawa, Y. Yamamoto and J. Vuckovic, Phys. Rev. Lett., 2005, 95, 013904.
9. T. Aoki, B. Dayan, E. Wilcut, W. P. Bowen, A. S. Parkins, T. J. Kippenberg, K. J. Vahala and H. J. Kimble, Nature, 2006, 443, 671–674.
10. S. Schietinger, T. Schroder and O. Benson, Nano Lett., 2008, 8, 3911–3915.
11. F. Schleifenbaum, K. Elgass, M. Steiner, J. Enderlein, S. Peter and A. Meixner, Proc. SPIE, 2009, 7185, 718504.
12. P. Andrew and W. L. Barnes, Science, 2000, 290, 785–788.
13. R. A. Grimme, C. E. Lubner, D. A. Bryant and J. H. Golbeck, J. Am. Chem. Soc., 2008, 130, 6308–6309.
14. C. E. Lubner, R. Grimme, D. A. Bryant and J. H. Golbeck, Biochemistry, 2010, 49, 404–414.
15. A. Mershin, K. Matsumoto, L. Kaiser, D. Yu, M. Vaughn, M. K. Nazeeruddin, B. D. Bruce, M. Graetzel and S. Zhang, Sci. Rep., 2012, 2, 234.
16. L. Frolov, Y. Rosenwaks, C. Carmeli and I. Carmeli, Adv. Mater., 2005, 17, 2434–2437.
17. A. O. Govorov and I. Carmeli, Nano Lett., 2007, 7, 620–625.
18. I. Carmeli, I. Lieberman, L. Kraversky, Z. Fan, A. O. Govorov, G. Markovich and S. Richter, Nano Lett., 2010, 10, 2069–2074.
19. J. B. Nieder, PhD thesis, Freie Universitaet Berlin, Germany, 2011.
20. S. R. Beyer, S. Ullrich, S. Kudera, A. T. Gardiner, R. J. Cogdell and J. Koehler, Nano Lett., 2011, 11, 4897–4901.
21. H. Toporik, I. Carmeli, I. Volotsenko, M. Molotskii, Y. Rosenwaks, C. Carmeli and N. Nelson, Adv. Mater., 2012, 24, 2988–2991.
22. M. Brecht, M. Hussels, J. B. Nieder, H. Fang and C. Elsässer, Chem. Phys., 2012, 406, 15–20.
23. B. Gobets and R. van Grondelle, Biochim. Biophys. Acta, 2001, 1507, 80–99.
24. P. Fromme, P. Jordan and N. Krauss, Biochim. Biophys. Acta, Bioenerg., 2001, 1507, 5–31.
25. E. Schlodder, M. Hussels, M. Cetin, N. V. Karapetyan and M. Brecht, Biochim. Biophys. Acta, 2011, 1807, 1423–1431.
26. M. Brecht, M. Hussels, E. Schlodder and N. V. Karapetyan, Biochim. Biophys. Acta, Bioenerg., 2012, 1817, 445–452.
27. A. N. Melkozernov, Photosynth. Res., 2001, 70, 129–153.
28. N. V. Karapetyan, E. Schlodder, R. van Grondelle and J. P. Dekker, Photosystem I: The Light-Driven Plastocyanin: Ferredoxin Oxidoreductase, Advances in Photosynthesis and Respiration, Springer, 2006, vol. 24.
29. J. B. Nieder, R. Bittl and M. Brecht, Angew. Chem., Int. Ed., 2010, 49, 10217–10220.
30. B. Gobets, I. H. M. van Stokkum, M. Rogner, J. Kruip, E. Schlodder, N. V. Karapetyan, J. P. Dekker and R. van Grondelle, Biophys. J., 2001, 81, 407–424.
31. B. Gobets, I. H. M. van Stokkum, F. van Mourik, J. P. Dekker and R. van Grondelle, Biophys. J., 2003, 85, 3883–3898.
32. M. Brecht, V. Radics, J. B. Nieder, H. Studier and R. Bittl, Biochemistry, 2008, 47, 5536–5543.
33. G. Bjork, IEEE J. Quantum Electron., 1994, 30, 2314–2318.
34. M. Byrdin, P. Jordan, N. Krauss, P. Fromme, D. Stehlik and E. Schlodder, Biophys. J., 2002, 83, 433–457.
35. M. Yang, A. Damjanovic, H. M. Vaswani and G. R. Fleming, Biophys. J., 2003, 85, 140–158.
36. P. Anger, P. Bharadwaj and L. Novotny, Phys. Rev. Lett., 2006, 96, 113002.
37. A. M. Kern, A. J. Meixner and O. J. F. Martin, ACS Nano, 2012, 6, 9828–9836.
38. L. Shang, Y. Z. Wang, J. G. Jiang and S. J. Dong, Langmuir, 2007, 23, 2714–2721.
39. S. Chah, M. R. Hammond and R. N. Zare, Chem. Biol., 2005, 12, 323–328.
40. M. Hussels, A. Konrad and M. Brecht, Rev. Sci. Instrum., 2012, 83, 123706.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c3cp55195d

---