The influence of the ΔK280 mutation and N- or C-terminal extensions on the structure, dynamics, and fibril morphology of the tau R2 repeat

Abstract

Tau is a microtubule-associated protein and is involved in microtubule assembly and stabilization. It consists of four repeats that bind to the microtubule. The ΔK280 deletion mutation in the tau R2 repeat region is directly associated with the development of the frontotemporal dementia parkinsonism linked to chromosome 17 (FTDP-17). This deletion mutation is known to accelerate tau R2 repeat aggregation. However, the secondary and the tertiary structures of the self-assembled ΔK280 tau R2 repeat mutant aggregates are still controversial. Moreover, it is unclear whether extensions by one residue in the N- or the C-terminus of this mutant can influence the secondary or the tertiary structure. Herein, we combine solid-state NMR, atomic force microscopy, electron microscopy and all-atom explicit molecular dynamics simulations to investigate the effects of the deletion mutation and the N- and the C-terminal extension of this mutant on the structure. Our main findings show that the deletion mutation induces the formation of small aggregates, such as oligomers, and reduces the formation of fibrils. However, the extensions in the N- or the C-terminus revealed more fibril formation than small aggregates. Further, in the deletion mutation only one structure is preferred, while the N- and the C-terminal extensions strongly lead to polymorphic states. Finally, our broad and combined experimental and computational techniques provide direct structural information regarding ΔK280 tau R2 repeat mutant aggregates and their extensions in the N- and C-terminii by one residue.

---

Introduction

The microtubule associated protein tau is essential for the development and maintenance of the nervous system. Tau dysfunction is associated with classic, age-related neurodegenerative diseases called taupathies, among which progressive supranuclear palsy (PSP), corticobasal degeneration (CBD), Pick's disease, argyrophilic grain disease and frontotemporal dementia parkinsonism linked to chromosome 17 (FTDP-17) are known. The importance of tau in neurodegeneration has been verified by the discovery of the single gene MAPT (located in chromosome 17q21)¹ mutations in families with FTDP-17.^2–4 Several mutations within tau in the FTDP-17 are known to enhance neurofibrillary deposits.^5–8 These mutations include G279K, P301L, ΔK280, the silent mutation L284L and R406W.⁹In vivo and in vitro studies have suggested that particularly mutants P301L and ΔK280 have a much stronger tendency to aggregate.⁸ Mandelkow and coworkers have shown that the repeat domains of tau contain regions of β-structures, which have the tendency to serve as seeds for aggregation.¹⁰ Recently, Yu et al.¹¹ reported the conformations of K18 and K19 tau protein isoforms and demonstrated that the formation of stable R2 and R3 is critical for K18 and K19 aggregation. Daebel et al.¹² showed that the β-structure-rich region in the K19 tau protein isoform is important for tau aggregation. Miller et al.¹³ demonstrated that the repeat domains in the tau protein, particularly repeat R2 domain (V275-P301), can interact with Aβ via interactions between common β-strands of these two proteins. While R2 tau–Aβ complex illustrates a structurally stable β-structure, the R2 tau repeat shows a relatively unstable β-structure.¹³ Previously, it has been observed experimentally that ΔK280 deletion in the tau protein promotes aggregation.⁶ A recent study¹⁴ investigated the conformation of a monomer and a dimer of a short fragment of ΔK280 tau repeat R2 (G273-L284). Yet, so far, the structure of the ΔK280 in the full-length tau R2 repeat aggregates is illusive at the molecular level.

Herein, applying all-atom molecular dynamics (MD) simulations, we predict and examine several ΔK280 tau repeat models, based on the wild-type (WT) R2 repeat tau model that has been previously proposed by Miller et al.¹³ We examine several models to reveal the wild-type (WT) and the most stable ΔK280 tau R2 repeat model, while considering both conformational energy and structural stability. We employed solid-state nuclear magnetic resonance (ssNMR), time-resolved atomic force microscopy (AFM) and transmission electron microscopy (TEM) measurements and compared the experimental results with predictions from the computational models of the WT and the ΔK280 tau R2 repeat.

Taken together, the broad methodological background of this work confirms that the structure and the dynamics are strongly influenced by the ΔK280 tau R2 repeat mutation and by the N- and C-terminal extensions. The mutation and the extensions in the N- and the C-terminii of the investigated mutated tau peptides induce formation of fibrils and lead to polymorphism. Furthermore, the simulations and the experiments show good agreement with the secondary structures of the self-assembled peptides.

Results and discussion

Constructions of models

To construct the ΔK280 repeat R2 oligomers, we applied the previously constructed model of the tau repeat R2 oligomer¹³ and the ΔK280 repeat R2 oligomers,¹⁵ (Fig. 1) in which the backbone hairpins were based on the Lührs ssNMR model of Aβ_17–42.¹⁶ The highest propensity for β-structure content in the tau protein also appears in repeat R2. It is known that the tau R2 repeat is involved in abnormal aggregation of tau.¹⁷ Moreover, it is known that the high propensity of β-structures in this repeat is also essential for paired helical filaments.^6,10 In addition to the β-structure in the repeat R2, we also considered other similar structural properties between Aβ and repeat R2.¹³ Two possible models were constructed to form the mutated tau ΔK280 tau repeat R2 oligomers on the basis of the wild-type tau repeat R2: models M1 and M2 (Fig. 1). In the first model, designated M1, the deletion mutation was obtained by ‘shifting’ the sequence from the C-terminal end towards the ΔK280 deletion site, while in the second model, M2, the deletion mutation was obtained by ‘shifting’ the N-terminal sequence towards the ΔK280 mutation site. Model M1 is characterized by hydrophobic contacts (between I277 and I297 and between L284 and V287) in the core domain of the oligomer. In contrast, model M2 is characterized by salt-bridges (between K281, D283, and K290) in the core domain of the oligomer.

Fig. 1 Schematic representations of the initial structural models of wild-type (WT), and the two structural models of the mutated ΔK280 tau repeat R2: models M1 and M2. In M1, the deletion mutation was obtained by ‘shifting’ the C-terminal sequence towards K280. This model is stabilized by hydrophobic interactions in the core domain. In M2, the deletion mutation was obtained by ‘shifting’ the N-terminal sequence towards K280. This model is stabilized by salt-bridges in the core domain. These three models were constructed as hexamers. The colors in the primary sequence of tau R2 repeat (proposed by Mukrasch et al.¹⁷) highlight the secondary structure: β-structure (red), turn structure (blue) and disordered structure (green).

We further constructed four ΔK280 mutants' models (Fig. 2): models M31 and M32, which represent an extension of the tau sequence of models M1 and M2, respectively, by one residue in the C-terminus (P301), and models M41 and M42, which extend the models M1 and M2, respectively, by one residue in the N-terminus (K274).

Fig. 2 Initially constructed models of mutated ΔK280 tau R2 repeat R2: models M31 and M32 are extensions of the tau sequence by one residue (P301) of models M1 and M2, respectively. Models M41 and M42 represent extensions of the tau sequence by one residue (K274) of models M1 and M2, respectively. All models were constructed as hexamers.

The influence of the ΔK280 mutation on the secondary and the tertiary structures of the tau R2 repeat

Previously,^6,18 TEM and AFM techniques revealed the formation of the wild-type tau R2 repeat aggregates (fibrils and oligomers) and the ΔK280 mutated tau R2 repeat aggregates. However, so far the structural differences at the molecular level between the wild-type tau R2 repeat aggregates and the mutated tau R2 repeat aggregates remain elusive.

The predicted structure of the wild-type tau R2 repeat oligomers was based on the proposed secondary structure by Mukrasch et al.¹⁷ One can see that the secondary structure of our simulated WT tau R2 repeat is in agreement with that suggested by Mukrasch et al. (Fig. S1, ESI†). Further, our constructed model also shows a few residues with β-strand structures: D283, N286, and V287, S289 and K290. This was confirmed experimentally by ¹³C magic-angle spinning (MAS). ssNMR chemical shift measurements of the labeled D283, V287 and K290 revealed that these residues have the β-sheet structure (Table S1 and Fig. S2, ESI†).

So far, the secondary structure of the mutated ΔK280 tau R2 repeat had not been investigated experimentally. Our simulated model M1 demonstrates a secondary structure similar to the WT, particularly from the N-terminus towards the mutation and the simulated model M2 also shows a similar secondary structure, particularly from the C-terminus towards the mutation (Fig. S3, ESI†). The assignment of the secondary structure from the ssNMR chemical shifts revealed that the labeled residues D283, V287, and K290 show the β-sheet structure for the ΔK280 mutated tau R2 repeat M1/M2 (Table S1, ESI†).¹⁹ The simulated models M1, V286 and K290 show the β-sheet structure, while the simulated models M2, D283 and V287 show the β-sheet structure.

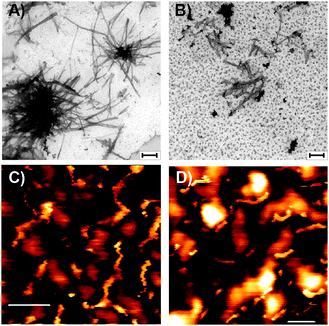
The constructed mutant model M1 illustrates a relatively well-packed structure compared with the WT and the mutant model M2 (Table S2 and Fig. S4–S6, ESI†). Due to the hydrophobic contacts in the core domain in M1, the relatively small RMSDs, the relatively short Cα backbone–backbone distance, and the relatively high percentage of hydrogen bonds between the monomers in M2 demonstrate a well-packed structural oligomer/fibril-like compared with the WT and model M1. Moreover, analysis of the backbone solvation illustrated that most of the residues in M1 are less solvated compared to those in the WT and model M2 (Fig. S7, ESI†). Comparison of the relative conformational energies and the populations of models M1 and M2 shows that model M1 is more stable and strongly preferred over model M2 (Table S3, ESI†). Therefore, we propose that the higher populations of the self-assembled ΔK280 tau R2 repeat aggregates (oligomers and fibrils) are organized as the model M1. Furthermore, we propose that this mutation is strongly stabilizing the structure of the aggregates compared to the wild-type (as shown in the TEM, Fig. 3).

Fig. 3 TEM images of (A) WT tau R2 repeat aggregates and (B) ΔK280 mutated tau R2 repeat aggregates. (C) and (D): AFM height images of WT and M1 fibrils (color scale black 0–1.5 nm white, scale bars 50 nm).

We further measured and computed segmental C–H order parameters (OPs) of the labeled residues of the WT and models M1 and M2 (Fig. 4 and Table S4, ESI†) to investigate fluctuations in the fibrils. The backbones of residues D283, V287, and L290 are rather rigid, as indicated by the high order parameter values, while the G292 and the side chains of the former residues are more flexible, as shown by lower order parameters. One can see that there is relatively good agreement of the computed OP values with the experimental OPs values for all atoms, except for D283(Cβ), possibly due to the polarity of the side chain of this residue.

Fig. 4 Experimental and computational segmental ¹³C–¹H order parameters for WT tau R2 repeat aggregates and ΔK280 mutated tau R2 repeat aggregates.

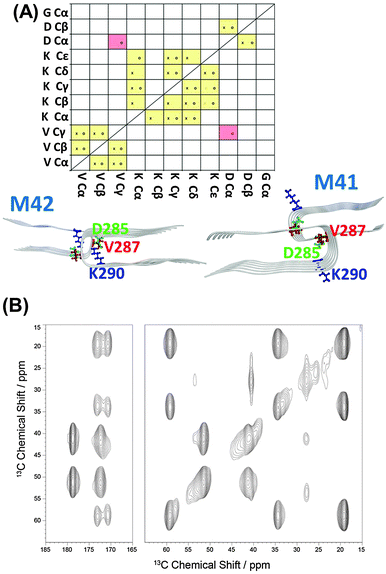
Finally, we investigated the tertiary structure of the WT tau R2 repeat and the ΔK280 mutated tau R2 repeat structures. In the two-dimensional ¹³C MAS NMR proton driven spin diffusion (PDSD) experiments, all peaks could be assigned and correlations between molecular segments in close proximity were measured (Fig. S8, ESI†). Crosspeak intensity, which indicates a proximity between segments of less than ∼6 Å, depends on the mixing time. For short mixing times of 50 ms, only crosspeaks within one amino acid over one or two bonds should be visible. For longer mixing times of 600 ms, interresidual crosspeaks are also detectable between differently labeled amino acids. The crosspeak patterns that are observed in this preparation are indicated in the yellow boxes in Fig. 5. While mostly intraresidual interactions are observed, some interresidual contacts between V287 and K290 are also detected.

Fig. 5 Overview of the intraresidual (yellow boxes) and interresidual (red boxes) crosspeaks of the WT tau R2 repeat found experimentally in the PDSD studies. (A) Crosspeaks that are found in experiments with a mixing time of 50 ms are shown as crosses, those that are found at longer mixing times (600 ms) are shown as circles. The interactions between residues are seen in the constructed WT model. (B) ¹³C–¹³C proton driven spin diffusion spectrum of WT at a MAS frequency of 7 kHz and a temperature of 30 °C. The mixing time is 600 ms.

In the TEM image for the WT, one can see that semiquantitatively most aggregates formed are fibrils and only a small portion of the aggregates are in the form of oligomers (as seen in Fig. S9, ESI†). Our constructed WT model demonstrates oligomer/fibril-like forms. We suggest that the crosspeaks that are seen in the two-dimensional ¹³C NMR spectra are related to the “cross-link” between fibrils or between longer oligomers, as seen in Fig. 3. We, therefore, suggest that for the WT the crosspeaks could be assigned as the interactions between long oligomers or fibrils, as seen in Fig. 5.

For the ΔK280 mutated tau R2 repeat aggregates, one can see that one crosspeak is assigned to the interactions between two residues (D283-K290) in the oligomeric size of model M2 (Fig. 6). We monitored the distance Cα D285–Cε K290 for the specific crosspeak along the last 5 ns of the MD simulations for M2 and revealed that almost 60% of the snapshots demonstrate a distance of 5–6 Å (Fig. S10, ESI†). The other two crosspeaks may be assigned to the interactions between oligomers or fibrils, as seen for model M1 (Fig. 6) and in model M2. The TEM images revealed more oligomers than fibrils for this mutant (Fig. S11, ESI†). The large number of the oligomers may support our interpretation of ‘cross-links’ between oligomers. These large number of oligomers may increase the chances of ‘cross-links’ between oligomers. One can argue, whether these ‘cross-links’ increase or decrease the toxicity. However, since more oligomers are formed, we hypothesize that the ‘cross-links’ that are formed may induce toxicity.

Fig. 6 Overview of the intraresidual (yellow boxes) and interresidual (red boxes) crosspeaks of the ΔK280 mutated tau R2 repeat found experimentally in the PDSD studies. (A) Crosspeaks that are found in experiments with a mixing time of 50 ms are shown as cross, those that are found at longer mixing times (600 ms) are shown as circle. The interactions between residues are seen in the constructed models M1 and M2. (B) ¹³C–¹³C proton driven spin diffusion spectrum of M1/M2 at a MAS frequency of 7 kHz and a temperature of 30 °C. The mixing time is 600 ms.

The influence of the extension of one residue in the ends of the tau R2 repeat oligomer sequence of the ΔK280 mutation

One of the main challenging issues in amyloid research is to determine the relationship between the sequence of the peptide and its effect on the mechanisms of the aggregation. Here, we examined the effect of the sequence of the ΔK280 mutated tau R2 repeat by adding one residue of the tau sequence P301 in the C-terminus and by adding the residue of the tau sequence K274 in the N-terminus. We constructed two models for the extension of the C-terminus, termed M31 and M32, which are based on models M1 and M2, respectively, and two models for the extension in the N-terminus, termed M41 and M42, based on the same M1 and M2 models.

Interestingly, while in the non-extended sequence of the mutated tau R2 oligomers show high preference for model M1 versus model M2, in the extended sequence one can see some polymorphism. Model M31 and M32 have similar conformational energies and similar populations, and similarly for models M41 and M42 (Table S5, ESI†). Therefore, we suggest that an extension of one residue in the C-terminus or in the N-terminus lead to more polymorphic aggregates.

It is interesting to examine the effect of the extension of only one terminal residue on the morphology of the aggregates. To this end, we monitored the Cα backbone–backbone distances, the hydrogen bonds between the β-strands and the RMSDs (Table S6 and Fig. S12–S14, ESI†). One can see that extension of one residue increases the Cα backbone–backbone distance for all models compared to models M1 and M2. We further estimated the solvation of the backbone for all residues of each model. The analysis demonstrates that many residues in models M31 and M41 are more exposed to water compared to model M1, and similar results are obtained for models M2, M32 and M42 (Fig. S15 and S16, ESI†). These extensions also increase the RMSDs for models M31 and M41, which are derived from model M1 compared to model M1. The RMSDs for models M32 and M42, which are derived from model M2, are similar to model M2. Finally, the percentage of hydrogen bonds between the β-strands for models M31 and M41 is similar to model M1 and for models M32 and M31 to model M2.

To examine the effect of the one residue extension in the N- or the C-terminus of the mutated tau R2 repeat on the secondary structure, we estimated the ψ and Φ dihedral angles (Fig. S17, ESI†). One can see that these extensions do not dramatically affect the secondary structure.

We further computed the OPs of the constructed models and compared them with the experimental values (Tables S7 and S8, ESI†). One can see that most of the computed OPs for both M31 and M32 are in agreement with those of the experiment. Interestingly, the OPs of most of the labeled amino acids in M31 reveal similar OPs as those of M32. A similar phenomenon was also seen in M41 and M42.

TEM measurements revealed more fibrils than small aggregates for M3 and M4 (Fig. S18 and S19, ESI†). We propose that the network of the fibrilar states of both M3 and M4 may exhibit interactions between small aggregates or long fibrils and thus may give insight into the crosspeaks that are seen in the two-dimensional NMR spectra (Fig. 7 and 8).

Fig. 7 Overview of the intraresidual (yellow boxes) and interresidual (red boxes) crosspeaks of the extended of ΔK280 mutated tau R2 repeat by one residue (P301) in the C-terminus of tau. (A) Crosspeaks that are found in experiments with a mixing time of 50 ms are shown as crosses, those that are found at longer mixing times (600 ms) are shown as circles. The interactions between residues are seen in the constructed model M31. (B) ¹³C–¹³C proton driven spin diffusion spectrum of M3 at a MAS frequency of 7 kHz and a temperature of 30 °C. The mixing time is 600 ms.

Fig. 8 Overview of the intraresidual (yellow boxes) and interresidual (red boxes) crosspeaks of the extended of ΔK280 mutated tau R2 repeat by one residue (K274) in the N-terminus of tau. (A) Crosspeaks that are found in experiments with a mixing time of 50 ms are shown as crosses, those that are found at longer mixing times (600 ms) are shown as circles. The interactions between residues are seen in the constructed models M41 and M42. (B) ¹³C–¹³C proton driven spin diffusion spectrum of M4 at a MAS frequency of 7 kHz and a temperature of 30 °C. The mixing time is 600 ms.

Conclusions

The effect of the ΔK280 mutation on tau R2 repeat aggregation and the effect of a single residue extension on either end of the peptide were investigated by ssNMR, TEM, AFM, and all-atom explicit MD simulations. We propose the three-dimensional models of the self-assembled aggregates of WT tau R2 repeat, of the ΔK280 tau R2 repeat mutants and the aggregates that feature an extension of one residue either on the N- or the C-terminus. Three main conclusions can be drawn from this study: first, the ΔK280 mutation in the R2 repeat increases the formation of small aggregates (perhaps oligomers) and relatively to the WT, fewer fibrils are formed. Mandelkow and coworkers⁶ also illustrated similar results for the WT R2 repeat. Moreover, they showed that the ΔK280 mutation in the R2 repeat increases the formation of small aggregates, similarly to our results. However, it is important to note that for larger fragments of the tau protein, such as in the case of K18 (which consists of all four repeats R1–R4) the results may be different. For example, Mandelkow and coworkers demonstrated that the ΔK280 mutation in K18 exhibits a better β-structure with the typical twisted morphology than the WT K18 fibrils. From our results for the ΔK280 R2 repeat, one can speculate that this mutation may lead to more toxic species than the WT, since it is known that oligomeric states are toxic, while the fibrils are not the toxic species.²⁰ Second, an extension of this mutant by one residue of the original tau sequence in the N- or the C-terminus revealed more fibril formation than small aggregates. It is important to note that extension by more than one residue of the original tau sequence may lead to more oligomer formation and thus to more toxicity or to more fibril formation and less toxicity. We therefore suggest that the formation of fibrils or oligomers is due to the sequence of the tau protein. Finally, while for the ΔK280 mutant tau R2 oligomer only one structure is preferred, upon making an extension by one residue in the N-terminus or in the C-terminus in this mutant it leads to polymorphism.

Material and methods

Molecular dynamics simulations protocol

We constructed a model of the WT repeat R2 oligomer and six models of mutated tau ΔK280 tau repeat R2 oligomers. MD simulations of the solvated oligomers were performed in the NPT ensemble using NAMD²¹ with the CHARMM27 force-field.^22,23 The oligomers were energy minimized and explicitly solvated in a TIP3P water box^24,25 with a minimum distance of 15 Å from each edge of the box. Each water molecule within 2.5 Å of the oligomers was removed. Counter ions were added at random locations to neutralize the charge on the oligomers. The Langevin piston method^21,26,27 with a decay period of 100 fs and a damping time of 50 fs was used to maintain a constant pressure of 1 atm. A temperature of 330 K was controlled by a Langevin thermostat with a damping coefficient of 10 ps⁻¹.²¹ The short-range van der Waals interactions were calculated using the switching function, with a twin range cut-off of 10.0 and 12.0 Å. Long-range electrostatic interactions were calculated using the particle mesh Ewald method with a cutoff of 12.0 Å.^28,29 The equations of motion were integrated using the leapfrog integrator with a step of 1 fs. The solvated systems were energy minimized for 2000 conjugated gradient steps, where the hydrogen bonding distance between the β-sheet in each oligomer was fixed in the range 2.2–2.5 Å. The counter ions and water molecules were allowed to move. The hydrogen atoms were constrained to the equilibrium bond using the SHAKE algorithm.³⁰ The minimized solvated systems were energy minimized for 5000 additional conjugate gradient steps and 20 000 heating steps at 250 K, with all atoms being allowed to move. Then, the system was heated from 250 K to 330 K for 300 ps and equilibrated at 330 K for 300 ps. All simulations were run for 30 ns at 330 K.

Generalized born method with molecular volume (GBMV)

The relative conformational energies can be compared only for models that have the same sequence and number of peptides; thus the relative conformational energies have been computed for models M1 and M2, for models M31 and M32, and for models M41 and M42. To obtain the relative conformational energies of the ΔK280 repeat R2 oligomers, the oligomer trajectories of the last 5 ns were first extracted from the explicit MD simulations excluding the water molecules – a total of 500 conformations for each oligomer. The solvation energies of all conformations were calculated using the GMBV. In the GBMV calculations, the dielectric constant of water was set to 80. The hydrophobic solvent-accessible surface area (SASA) term factor was set to 0.00592 kcal mol⁻¹ Å⁻¹. Each conformation was minimized using 1000 cycles, and the conformational energy was evaluated by grid-based GBMV.

A total of 1000 conformations (500 for each of the 2 models, i.e. M1 and M2, M31 and M32, and M41 and M42) were used to construct the energy landscape of the ΔK280 repeat R2 oligomers and to evaluate the conformer probabilities by using Monte Carlo (MC) simulations. In the first step, one conformation of conformer i and one conformation of conformer j were randomly selected. Then, the Boltzmann factor was computed as e^{−(E_j–E_i)/kT}, where E_i and E_j are the conformational energies evaluated using the GBMV calculations for conformations i and j, respectively, k is the Boltzmann constant and T is the absolute temperature (298 K used here). If the value of the Boltzmann factor was larger than the random number, then the move from conformation i to conformation j was allowed. After 1 million steps, the conformations ‘visited’ for each conformer were counted. Finally, the relative probability of model n (M1 or M2) was evaluate as P_n = N_n/N_total, where P_n is the population of model n, N_n is the total number of conformations visited for model n, and N_total is the total steps. The advantages of using MC simulations to estimate conformer probability lie in their good numerical stability and the control that they allow of transition probabilities among several conformers.

Using models M1 and M2 (or M31 and M32; or M41 and M42) and 1000 conformations (500 for each model) generated from the MD simulations, we estimated the overall stability and populations for each conformer based on the MD simulations, with the energy landscape being computed with GBMV for these two models. For the complex kinetics of amyloid formation, the group of these two models is likely to present only a very small percentage of the ensemble. Nevertheless, the carefully selected models cover the most likely structures.

Structural and dynamical analysis

We examined the structural stability of the studied oligomers by following the changes in the number of hydrogen bonds between β-strands, with the hydrogen bond cut-off being set to 2.5 Å. This examination was performed by following the root-mean square deviations (RMSDs) and by monitoring the changes in the inter-sheet distance (Cα backbone–backbone distance) in the core domain of all of oligomers. In the wild-type model, the core domain was defined as the distance between residue K280 and residue S293, and that for the mutants between residue K281 and residue S293. We further measured distances between atoms of residues and computed the dihedral angles ψ and Φ for each residue for each model studied. Finally, we investigated the average number of water molecules around each side-chain Cβ carbon within 4 Å for the studied oligomers.

The order parameters (OPs) for various C–H bonds were calculated from the MD trajectories as detailed by Vogel et al.³¹ In short, the OPs are computed for each residue from the tensor of dipolar interaction averaged over all MD simulation frames.

Experimental procedures

Peptide synthesis, fibrillation and morphology characterization by AFM.

The four tau repeats (Table S9, ESI†) were synthesized using standard Fmoc solid-phase synthesis. Each peptide contained uniformly ¹³C/¹⁵N labelled amino acids in positions D283, V287, K290, G292.

Fibril formation

Fibril formation took place under ambient conditions in buffer solution (1 mg peptide per 1 ml of deionized water, 0.01 M phosphate pH 7.0, 0.1 M NaCl) within 4 hours.

The morphology of the grown fibrils was investigated using transmission electron microscopy (TEM). Fibril solutions were diluted 1 : 20 with pure water and 1 μl droplets of this solution were applied on 200 mesh copper grids, allowed to dry for about 2 hours and negatively stained with 1% uranyl acetate. Transmission electron micrographs were recorded with a Zeiss EM 900 (Zeiss NTS, Oberkochen, Germany).

1 μl droplets of the fibril solution were deposited on freshly cleaved mica (muscovite, V1 grade) and dried in an exsiccator. Atomic force microscopy measurements were performed on the JPK NanoWizard® II system with silicon cantilevers (ACTA, spring constant 40 N m⁻¹) in intermittent contact mode. The height resolution was ±200 pm, and the lateral resolution was tip size limited (∼10 nm). Height images were analyzed to interpret the structure of protein aggregates, and phase lag images were used to confirm the distinction between the mica surface signal and substance deposited on mica.

Solid-state NMR

For NMR measurements, fibril solutions were ultracentrifuged (86 000g, 1 h, 4 °C). The pellets were lyophilized, rehydrated with 50 wt% H₂O, homogenized by freezing the sample in liquid nitrogen and thawing at 37 °C and centrifuged into MAS rotors.

MAS NMR spectra were acquired on a Bruker 600 Avance III Spectrometer (Bruker BioSpin GmbH, Rheinstetten, Germany) at a resonance frequency of 600.1 MHz for ¹H and 150.9 MHz for ¹³C using a 4 mm MAS probe at a temperature of 303 K. The ¹H and ¹³C 90° pulses had lengths of 4 μs and 5 μs, respectively. Standard ¹³C CPMAS were acquired at a MAS frequency of 7 kHz and Spinal64 decoupling at a decoupling field of 62.5 kHz.

For the peak assignment, two dimensional ¹³C–¹³C proton driven spin diffusion spectra³² with mixing times of 50 ms and 600 ms were acquired using 80 to 100 increments in the indirect dimension. ¹H–¹³C dipolar couplings were measured using the DIPSHIFT experiment³³ at an MAS frequency of 5 kHz with homonuclear FSLG decoupling³⁴ at a decoupling field of 80 kHz. Order parameters were calculated as the ratio of the measured motionally averaged and full dipolar coupling as described in the literature.³⁵

Acknowledgements

This project is supported by the FP7-PEOPLE-2011-CIG, research grant no. 303741 and by the Deutsche Forschungsgemeinschaft through the SFB-TR102, Projects A6 and B1. All simulations were performed using the high-performance computational facilities of the Miller lab in the BGU HPC computational center. The support of the BGU HPC computational center staff is greatly appreciated.

Notes and references

1. R. L. Neve, P. Harris, K. S. Kosik, D. M. Kurnit and T. A. Donlon, Mol. Brain Res., 1986, 1, 271.
2. M. S. Wolfe, J. Biol. Chem., 2009, 284, 6021.
3. J. van Swieten and M. G. Spillantini, Brain Pathol., 2007, 17, 63.
4. V. M. Y. Lee, M. Goedert and J. Q. Trojanowski, Annu. Rev. Neurosci., 2001, 24, 1121.
5. P. Nacharaju, J. Lewis, C. Easson, S. Yen, J. Hackett, M. Hutton and S. H. Yen, FEBS Lett., 1999, 447, 195.
6. M. von Bergen, S. Barghorn, L. Li, A. Marx, J. Biernat, E. M. Mandelkow and E. Mandelkow, J. Biol. Chem., 2001, 276, 48165.
7. D. Fischer, M. D. Mukrasch, M. von Bergen, A. Klos-Witkowska, J. Biernat, C. Griesinger, E. Mandelkow and M. Zweckstetter, Biochemistry, 2007, 46, 2574.
8. S. Barghorn, Q. Zheng-Fischhofer, M. Ackmann, J. Biernat, M. von Bergen, E. M. Mandelkow and E. Mandelkow, Biochemistry, 2000, 39, 11714.
9. M. G. Spillantini and M. Goedert, Brain, 2000, 123(Pt 5), 857.
10. M. von Bergen, P. Friedhoff, J. Biernat, J. Heberle, E. M. Mandelkow and E. Mandelkow, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 5129.
11. X. Yu, Y. Luo, P. Dinkel, J. Zheng, G. Wei, M. Margittai, R. Nussinov and B. Ma, J. Biol. Chem., 2012, 287, 14950.
12. V. Daebel, S. Chinnathambi, J. Biernat, M. Schwalbe, B. Habenstein, A. Loquet, E. Akoury, K. Tepper, H. Muller, M. Baldus, C. Griesinger, M. Zweckstetter, E. Mandelkow, V. Vijayan and A. Lange, J. Am. Chem. Soc., 2012, 134, 13982.
13. Y. Miller, B. Ma and R. Nussinov, Biochemistry, 2011, 50, 5172.
14. L. Larini, M. M. Gessel, N. E. LaPointe, T. D. Do, M. T. Bowers, S. C. Feinstein and J.-E. Shea, Phys. Chem. Chem. Phys., 2013, 15, 8916.
15. Y. Raz and Y. Miller, PLoS One, 2013, 8, e73303.
16. T. Lührs, C. Ritter, M. Adrian, D. Riek-Loher, B. Bohrmann, H. Dobeli, D. Schubert and R. Riek, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 17342.
17. M. D. Mukrasch, S. Bibow, J. Korukottu, S. Jeganathan, J. Biernat, C. Griesinger, E. Mandelkow and M. Zweckstetter, PLoS Biol., 2009, 7, e34.
18. S. Wegmann, Y. J. Jung, S. Chinnathambi, E. M. Mandelkow, E. Mandelkow and D. J. Muller, J. Biol. Chem., 2010, 285, 27302.
19. D. S. Wishart and B. D. Sykes, Methods Enzymol., 1994, 239, 363.
20. C. A. Lasagna-Reeves, D. L. Castillo-Carranza, U. Sengupta, A. L. Clos, G. R. Jackson and R. Kayed, Mol. Neurodegener., 2011, 6, 39.
21. L. Kale, R. Skeel, M. Bhandarkar, R. Brunner, A. Gursoy, N. Krawetz, J. Phillips, A. Shinozaki, K. Varadarajan and K. Schulten, J. Comput. Phys., 1999, 151, 283.
22. B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan and M. Karplus, J. Comput. Chem., 1983, 4, 187.
23. A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586.
24. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926.
25. M. W. Mahoney and W. L. Jorgensen, J. Chem. Phys., 2000, 112, 8910.
26. S. E. Feller, Y. Zhang, R. W. Pastor and B. R. Brooks, J. Chem. Phys., 1995, 103, 4613.
27. K. Tu, D. J. Tobias and M. L. Klein, Biophys. J., 1995, 69, 2558.
28. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089.
29. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577.
30. J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327.
31. A. Vogel, G. Reuther, M. B. Roark, K. T. Tan, H. Waldmann, S. E. Feller and D. Huster, Biochim. Biophys. Acta, 2010, 1798, 275.
32. N. M. Szeverenyi, M. J. Sullivan and G. E. Maciel, J. Magn. Reson., 1982, 47, 462.
33. M. G. Munowitz, R. G. Griffin, G. Bodenhausen and T. H. Huang, J. Am. Chem. Soc., 1981, 103, 2529.
34. A. Bielecki, A. C. Kolbert and M. H. Levitt, Chem. Phys. Lett., 1989, 155, 341.
35. H. A. Scheidt, I. Morgado, S. Rothemund and D. Huster, J. Biol. Chem., 2012, 287, 2017.

---

Footnote

† Electronic supplementary information (ESI) available: Proton decoupled ¹³C MAS NMR spectra, structural analysis, solvation analysis, TEM images of the studied peptides are illustrated in Figures. In addition, ¹³C chemical shift values, averaged structural values, conformational energies, experimental and computational order parameters values are detailed in Tables. See DOI: 10.1039/c3cp54890b

---