Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Advanced magnetic resonance strategies for the elucidation of nanostructured soft matter
R.
Graf
a,
M. R.
Hansen
ab,
D.
Hinderberger
ac,
K.
Muennemann
a and
H. W.
Spiess
*a
aMax Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: spiess@mpip-mainz.mnpg.de
bInterdisciplinary Nanoscience Center (iNANO) and Department of Chemistry, Aarhus University, Gustav Wieds Vej 14, DK-8000 Aarhus C, Denmark
cMartin-Luther-Universität Halle-Wittenberg, Institute of Chemistry, Von-Danckelmann-Platz 4, 06120 Halle (Saale), Germany
First published on 18th December 2013
Abstract
An overview is given on advanced magnetic resonance strategies and techniques, both nuclear magnetic resonance (NMR) and electron paramagnetic resonance (EPR), as applied to nanostructured soft matter. In addition, the combination of the two forms of spectroscopy to enhance signal intensity in NMR by means of dynamic nuclear polarization (DNP) is described. It is shown how these techniques can provide unique information on the structure of soft matter as well as the local dynamics of the constituents. Examples of recent applications are described, including dendronized and thermoresponsive polymers, hydrogels, synthetic and bio-inspired polymers, as well as polypeptides and biopolymers.
1 Introduction
The function of complex synthetic as well as natural systems is often achieved by separating regions of order and disorder.1 Examples are semi-crystalline synthetic polymers or polymer systems composed of different repeat units, i.e. polymer blends or copolymers. Likewise biomacromolecules, such as proteins, are often composed of well-ordered regions with α-helices or β-sheets, interlinked by conformationally disordered chain segments.2 Moreover, incompatibility of building blocks, e.g., backbone and side groups in macromolecules, or non-covalent interactions, such as hydrogen bonds, ionic forces or π–π-interactions lead to self-organization.3 In all these structures the different units are spatially separated and, therefore, can display vastly different dynamics.Even if highly ordered on a local scale, such systems often do not crystallize. Therefore, their atomic resolution structures cannot be determined by conventional X-ray or neutron scattering techniques.4 In order to provide insight into the organization of such materials to further understand their function, advanced methods of characterization are needed to probe both structure and dynamics simultaneously.5
If structural information on a molecular level is sought, site-selectivity is required. Moreover, for macroscopic organization, mechanical properties, and transport of ions or charges in highly viscous materials or even solids, ‘slow’ dynamics on time scales longer than nano- or microseconds are particularly relevant. While several techniques meet one or the other requirement for elucidating structure and dynamics, nuclear magnetic resonance (NMR) spectroscopy6,7 meets all needs and rapid development of NMR methods is still ongoing.8 Likewise, electron paramagnetic resonance (EPR) spectroscopy of spin labels and spin probes in synthetic and biomacromolecules is enjoying a remarkable revival, due to improved microwave technology.9,10 These advances now allow routine applications of pulsed EPR methods and high-field EPR with similar improvements as in high-field NMR. However, no single technique can provide the required information. Instead, a combination of complementary methods is required as sketched in Fig. 1. This also includes the combination of experimental techniques and computer simulations. Remarkably, recent developments in magnetic resonance have been recognized by a large number of papers in Physical Chemistry Chemical Physics, e.g., see ref. 11–14.
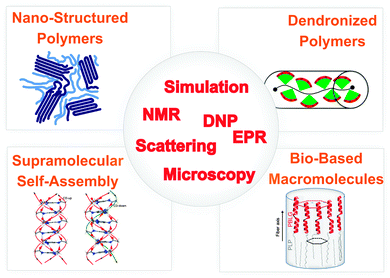 | ||
| Fig. 1 Overview of systems, phenomena and techniques for elucidating the interplay between structure and dynamics in nanostructured soft matter. | ||
Despite the wealth of information NMR spectroscopy provides, it suffers from its inherently low signal intensity due to the low magnetic moment of nuclei. In contrast, the magnetic moment of electrons is almost three orders of magnitude higher. This can be exploited, i.e., by combining NMR and EPR, transferring magnetization from electrons to nuclei. This possibility was realized early on and was called dynamic nuclear polarization (DNP).15,16 Similar to EPR itself, DNP has experienced a remarkable revival in recent years and is now applied to biopolymers in both solution and the solid state.17
In this Perspective Article we briefly introduce magnetic resonance in general, followed by a more detailed description of specific examples, which demonstrate the application of such techniques to study bio-inspired synthetic macromolecules and biopolymers, mostly taken from our own recent work.
1.1 Solid state NMR and pulsed EPR techniques for analyzing structure and dynamics
NMR spectroscopy today is an indispensable tool in chemistry, physics and life sciences. The introduction of Fourier transform NMR and its extension to two- and higher dimensions made it possible to perform in addition to 1H NMR, highly informative spectroscopy of rare nuclei, such as 13C or 15N despite their formidably low sensitivity.6 These techniques are now mainly applied to study biomacromolecules in solution,18 but increasingly also in the solid state.19 In the latter case multidimensional NMR techniques were actually developed for synthetic polymers first.7 Advances in solid state NMR under fast Magic Angle Spinning (MAS) offered an attractive way to elucidate the packing and local dynamics of the building blocks in supramolecular assemblies; for a review of the early examples, see ref. 20.In the early days of magnetic resonance, NMR and EPR spectroscopy were developed in parallel and often by the same people.21,22 Later on the two techniques largely separated, but as mentioned above, recent developments in microwave technology have allowed spectroscopists to use pulse methods in EPR as well and it is rewarding to see the two ‘sister spectroscopies’ merge again. In fact, the current revival of EPR (ESR) spectroscopy in macromolecular science is largely due to the development of pulsed methods in groups active in both solid state NMR and EPR.23,24 Together with site directed spin labeling,25 the structure of biomacromolecules and supramolecular assemblies can now be probed on the nanometer scale,26 which nicely augments the sub-nm information provided by NMR. A singular advantage of MR methods is the fact that structure determination does not require single crystals needed for X-ray, or neutron scattering. Therefore, MR can be applied to condensed matter in all forms, including liquids, crystalline solids, disordered solids, liquid crystals and even gases.27
Signals originating from hydrogen-bonded protons are well separated in 1H MAS NMR spectra, typically resonating between 8 and 20 ppm.28 Hence, the 1H chemical shift provides semiquantitative information about the strength of hydrogen bonds.29 In addition, the 1H chemical shift is also a sensitive probe of so-called ring currents associated with aromatic moieties. These are observed as a low field shift compared to the corresponding liquid state NMR signal and may thereby serve as a direct indicator of π–π interactions. Likewise, the low field shift can be simply related to the crystal packing via so-called Nucleus Independent Chemical Shift (NICS) maps.30 This augments the well-known sensitivity of 13C NMR chemical shifts to local conformation, manifested, e.g., by the γ-gauche effect.31 Detailed packing information is obtained from distance measurements between specific proton sites at adjacent building blocks via high resolution double quantum (DQ) solid state NMR under MAS.20,32,33 This is particularly important for supramolecular assemblies involving aromatic groups and functional polymers for organic electronics.34
Solid state NMR, however, is probably even more powerful for probing the time scale and amplitude of rotational motions.7,35 For instance, disk shaped aromatics often stack into columnar structures as part of discotic liquid crystals (DLC),36 which are of great interest because of their function in organic electronics.37,38 In the liquid crystalline phase the disks rotate around the column axis.35 A particularly simple way of characterizing such restricted molecular dynamics is provided by the dynamic order parameter, 0 ≤ S ≤ 1. It is defined as the ratio between the motionally averaged and the static anisotropic NMR interaction, e.g., dipole–dipole coupling, anisotropic chemical shift, or quadrupole coupling. For the rotation of disks in a perfectly packed column, S = 0.5 for 13C–1H dipole–dipole coupling, or 2H quadrupole coupling, probing the C–H (C–D) bond direction.35 Imperfections of the packing in the liquid crystalline phase, where disks can be tilted towards the column axis, lead to reduction of S below 0.5 and values as low as 0.15 have been found.39 Thus, S provides both dynamic and structural information. In general, solid state NMR yields site selective information about the amplitudes and time scales of molecular motions over broad ranges of length and time; for a recent review see ref. 35.
The information about structure and dynamics of soft matter that EPR can provide is very similar.9,10 For synthetic polymers, biopolymers, and supramolecular assemblies, nitroxide spin probes and spin labels are particularly useful.40 In solution, their EPR spectra are governed by the g-factor and the hyperfine splitting (denoted as a) due to the 14N nucleus of the NO group. In solution, the former determines the frequency of the center of the triplet arising from the hyperfine coupling. Both parameters are sensitive to the electronic environment. In the solid state, the anisotropy of the g-tensor leads to broad characteristic EPR line shapes, similar to those in solid state NMR. EPR spectra are averaged by rotational motions, yet on the ns timescale rather than the μs scale that is relevant in NMR.7,9 This motional averaging has been exploited extensively in macromolecular science, due to the pioneering work of J. Freed.41 Moreover, similar to NMR, the dipole–dipole couplings between electron and nuclear spins can be exploited to determine intermolecular distances below one nm. The much stronger couplings between two electron spins can be used to probe distances up to about 8–10 nm. These types of measurements are achieved by pulsed electron-nuclear (ENDOR) or double electron-electron resonance (DEER) techniques, respectively.23,24
2 EPR studies of dendronized polymers in solution and in the solid state
2.1 Identifying molecular objects by EPR spectroscopy
Synthetic nanostructured systems are intricately connected with high precision through chemical synthesis. Dendrimers can be viewed as early examples of complex yet highly precise supramolecular structures.42 Dendronized polymers (denpols), highly precise polymers with dendronized side chains on every repeat unit, are an exciting new class of materials.43 Denpols combine the possibility to create large, polymeric structures with the precision and versatility of dendrimers, which distinguishes them from, e.g. hyperbranched polymers.44 Recently, continuous wave (CW) EPR has been shown to be an extremely versatile tool to study the nanoscale of thermoresponsive denpols and polymers in general.45,46 Distinct from responsive polymers, dendronized polymers can be considered as molecular objects, i.e., nanostructured objects exhibiting a persistent shape, independent of their immediate environment, and having a well-defined envelope.43To qualify as a molecular object, the solution structure of a chemical entity should not differ significantly from that in the solid state. For most macromolecules marked differences between liquid and solid state structures are observed, even for biomacromolecules. For instance, by double electron electron resonance (DEER) spectroscopy we have recently shown that even for the well-folded protein human serum albumin (HSA), the solution structure differs significantly from the crystal structure.47–49 The entry points of fatty acids into HSA are distributed highly symmetrically over the surface of the protein in solution to optimize fatty acid uptake, while an asymmetric distribution is observed in the crystal structure. Remarkably, the solution structure of the highly related bovine serum albumin was in good agreement with the crystal structure.48,49
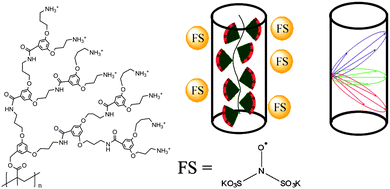
Among other advantages, denpols have tunable thicknesses and high persistence lengths.43 From the structural point of view, they are linear polymers whose repeat units all carry dendrons of variable generation (the number of branching units, n; here, the number of terminal groups is 2n) and termination (the end groups of the outer shell). We have studied denpols that are based on poly(methacrylate) and carry positively charged ammonium groups at their peripheral end groups, see Fig. 2.50–52 The densely packed dendrons around the backbone render the polymer's shape cylindrical and provide it with variable stiffness and diameter. Recently, a generation 5 species has been reported that can be considered as a molecular object due to its considerable stiffness (persistence length lp ≈ 30 nm) and the fact that it largely maintains its cross-section geometry when deposited on a solid substrate.
To study the shape and size of dendronized polymers in solution, we have used DEER spectroscopy, measuring the dipolar coupling between two or more electron spins, which depends on the interspin distance, r.52 In practice, distance distributions ranging from approximately 1.5 to 8 nm can be obtained. In this way, we determined the size (thickness) of different generations of cylindrical denpols in solution. The claim that any conventional polymer is rendered into a molecular object by attaching high generation dendrons to each of its main chain repeat units was then substantiated by showing that the difference between the solid state radius and the solution size decreases with each successive generation. Furthermore, the DEER-based characterization of dianionic spin probes that self-assemble close to the surface of cationic denpols is an indirect yet precise method to determine the effective spatial constitution and diameter of large, charged objects in solution.
Modern EPR spectroscopy, in particular for structural elucidation of proteins, heavily relies on covalent attachment by site-directed spin labeling (SDSL).53 Instead of chemically labeling the denpols, here one can elegantly rely on the self-assembly of the doubly negatively charged spin probe Fremy's salt (FS, potassium nitrosodisulfonate, also shown in Fig. 2) at the denpol ammonium surface layer of high positive charge density. The electrostatic attachment of FS spin probes to the denpols of varying generation (de-PG1 to de-PG4) was verified by CW EPR, as observed before for polyelectrolytes.54 This allows us to use this approach for nanoscale distance measurements by DEER.
2.2 Data analysis and comparison with other methods
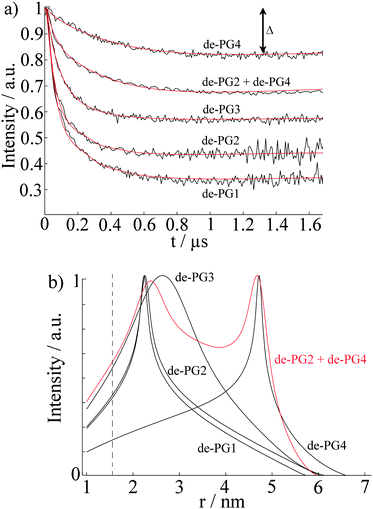
Previous AFM studies indicate that in the solid state the diameter of the denpols PG1-4 grows with increasing generation; PG-1 is approx. 0.8 nm thick and PG-4 about 4 nm. Since one can assess distances between approx. 1.5 and 8 nm with DEER, one may determine the solution diameter of the denpols, which might be difficult or would require substantial effort (e.g., SANS) to access by other means. Fig. 3a depicts the time traces of the dipolar evolution for FS ions in the presence of denpols of different generations. We also show fits (red traces) based on a physical model assuming a uniform distribution of the probes on the surface of a cylinder, described in detail elsewhere.50Given the highly constrained molecular shapes of dendronized polymers, we assumed that the spin probes are distributed independently and uniformly on the lateral surface of circular cylinders. For this geometry an analytic expression for the distance distribution P(r) was derived.50 Fits of DEER time traces to this analytical expression are shown in Fig. 3a. They yield the distance distribution of FS on the cylindrical surface shown in Fig. 3b. The most probable inter-probe distance RDEER, after correction for the finite size of the probe and its thermal motion, corresponds to the diameter of the effective cylinder and, hence, the approximate thickness of the nanoscopic objects. The denpol radii obtained via DEER are graphically depicted in Fig. 4 together with the radii determined on the basis of the AFM tapping heights (RAFM) for the denpols with protected terminal amines on mica.43 The latter can be considered to correspond to the radii of the neutral denpol-analogues in the solid state, since the samples are dried on a mica surface during the preparation process. When comparing the results deduced from AFM and DEER, the following aspects have to be taken into account: (i) AFM is known to underestimate heights of objects on surfaces; (ii) DEER measurements have a lower limit of ∼1.5 nm and are based on the electrostatic self-assembly of FS, for which the surface distribution through thermal motion has to be corrected.50 The corrected radii so obtained are shown in Fig. 4, while the distribution functions in Fig. 3 are plotted as a function of the unscaled radii.
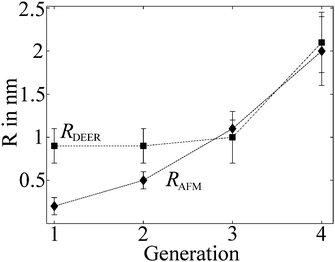 | ||
| Fig. 4 Radii of the different generations of dendronized polymers determined from solution and solid state measurements plotted versus denpol generation. Values marked RDEER stem from analysis of the data presented in Fig. 3 and are representative for the size of the molecules in solution (filled squares). Values marked RAFM stem from AFM tapping of the protected denpols PG1-4 heights published before and are representative for the size in the solid state (filled diamonds). Reprinted with permission of the American Chemical Society. | ||
This approach of fitting DEER time domain data to analytical solutions of cylindrical spin probe distributions was also checked by performing DEER experiments on mixtures of de-PG2 and de-PG4. The data were fitted with a bimodal distribution based on two cylinders. The time-trace is also shown in Fig. 3a, while the respective distance distribution is shown in red in Fig. 3b. Analysis of the mixed sample supports the picture of two individual, significantly different generations of denpols which can be described by the cylindrical shell model.
In summary, these studies show that DEER is a fast and precise method to determine the size of nanoscopic objects in solution. In the case presented here, a simple geometrical model was sufficient to determine the thickness of a cylindrical nano-sized object in solution and supports the idea that dendronized polymers (even of generation as low as 3) can be considered as molecular objects with an environment-independent, persistent shape. In particular, it was found that the size of the ammonium-terminated denpols in solution becomes similar to the size in the solid state as the generation grows. In the particular case of ammonium-terminated denpols addressed here, Fremy's salt could be applied as a negatively charged spin probe, although a correction accounting for the thermal motion of the probe in the electrostatic potential is necessary. This provides a simple alternative to the more difficult method of spin labeling the periphery of a molecular object.
In follow-up studies it could furthermore be shown how amphiphilic molecules (e.g., fatty acids) are taken up into these charged denpols, and by combining two spin probes (FS on the surface and spin-labeled fatty acids inside the denpols), it could even be shown how many molecules are taken up into denpols and how these are oriented within the large polymeric scaffold.51 Also, in a combined TEM/EPR study the use of charged denpols as carriers for small molecules and the formation of structures in the ten to hundred nm scale could be elucidated.52
Finally, the strategy to determine shapes and sizes of macromolecules with EPR methods may be expanded to other complex self-assembled supramolecular systems, since e.g. attraction of spin-probes to large macromolecules due to hydrophobicity/hydrophilicity is well documented.
3 NMR studies of structure and dynamics in synthetic and bio-based polymers
One of the key challenges for the future sustainable use of polymers is to make the production of these independent of oil resources. This has inspired researchers to employ plant oils and other biomass-derived chemicals as feedstock for the production of bio-based polymers.55–58 Another important strategy is to take advantage of enzymatic reactions that facilitate a green chemistry route to such polymeric materials.59 However, a concern remains whether the chemical and physical properties of bio-based polymers match those synthesized from petrochemical sources.From a structural point-of-view this encompasses the influence of the bio-based groups on (i) how the polymer material crystallizes to form nano-structured domains,61 utilizing non-covalent interactions such as hydrogen-bonding and π–π-stacking,62–64 (ii) crystallinity and chain conformations,65 and (iii) whether the bio-based groups themselves are conformationally stable when built into a polymeric structure. Such structural properties can influence the melting point and lead to potentially stiffer or more flexible materials.
3.1 Influence of ester groups on the physical properties of polyolefins
In a recent study focusing on the incorporation of ester groups in polyethylene, forming aliphatic long-chain polyesters (ALCPEs) via ring-opening metathesis polymerization (ROMP) of cyclic olefins,66–68 we have characterized the crystalline and amorphous domains of a polymer with the aim of quantifying the partitioning of the ester groups.60Fig. 5a displays the melting temperatures of a series of ALCPEs plotted as a function of the methylene-to-ester ratio (M/E). This plot clearly shows that an increase of the number of methylene units between the ester groups causes a gradual increase in the melting temperature, converging toward the melting temperature of HDPE. Such a behavior is similar to that found on incorporating aliphatic side groups in polyethylene at well-defined positions.69,70 To investigate the partitioning of the ester groups over the crystal and amorphous phases, we have employed a combination of variable-temperature (VT) solid state 13C{1H} CP/MAS NMR and quantitative 13C MAS NMR as summarized in Fig. 5b, and solid state 13C{1H} INEPT NMR together with liquid-state 13C NMR (see Fig. S7 and S8 in ref. 60). This allows us to differentiate between rigid and flexible parts of the polymer material.7 The two main 13C resonances at 30.8 and 32.8 ppm are assigned to the non-crystalline and the crystalline all-trans methylene conformations, respectively.71 The α-methoxy carbons also display two signals: one at 64.3 ppm, identified via13C{1H} INEPT NMR as arising from the more flexible fraction in gauche conformation, and a second peak at 65.7 ppm from the crystalline part that gradually decreases upon heating. On the basis of these 13C signals it is possible to quantify the partitioning of ester groups between the crystalline and amorphous phase as illustrated in Fig. 5c, using quantitative single-pulse 13C MAS NMR. A deconvolution of both regions leads to ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.14 and 1
1.14 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.18 for the α-methoxy and methylene groups, respectively. Thus, the solid state NMR results demonstrate that the ester groups are uniformly distributed over the crystalline and amorphous phases in line with results from DSC and X-ray diffraction experiments.60
1.18 for the α-methoxy and methylene groups, respectively. Thus, the solid state NMR results demonstrate that the ester groups are uniformly distributed over the crystalline and amorphous phases in line with results from DSC and X-ray diffraction experiments.60
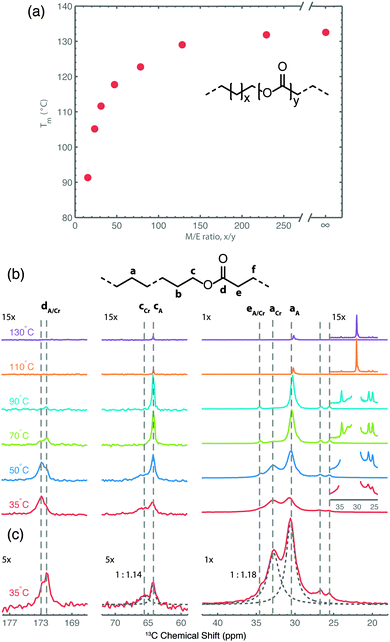 | ||
| Fig. 5 (a) Plot of the melting temperature for ALCPEs as a function of the methylene-to-ester ratio (M/E) synthesized via ROMP using a first-generation Grubbs catalyst. (b) Variable-temperature 13C{1H} CP/MAS NMR spectra of an ALCPE with a M/E ratio of 31 (ME31) recorded from 35 to 130 °C. (c) Quantitative 13C MAS NMR spectrum of ME31 illustrating the deconvolution into crystalline (Cr) and amorphous (A) fractions (dashed lines) for the methylene and α-methoxy carbon groups. Reprinted with permission from ref. 60. Copyright 2013, American Chemical Society. | ||
3.2 Bio-based polyamides
Polyamides belong to one of the most important groups of step-growth polymers due to their favorable and controllable physicochemical and mechanical properties.72 For this reason they are extensively used in industry for injection molding, extrusion, and film or fiber applications. Recently, we have focused on bio-based polyamides created by incorporation of carbohydrate-derived 1,4:3,6-dianhydrohexitols (isohexides), since these are suitable building blocks for step-growth polymerization.73–75Isohexides are secondary diols derived from C6-sugars, which can be obtained from starch or cellulose via a few (bio-)organic transformations.76 Three isohexide isomers exist where the major conformer for each isomer is shown in Fig. 6a. These give rise to quite different 13C chemical shifts (Fig. 6b) obtained from gas phase quantum chemical calculations (MP2/6-311G**).75
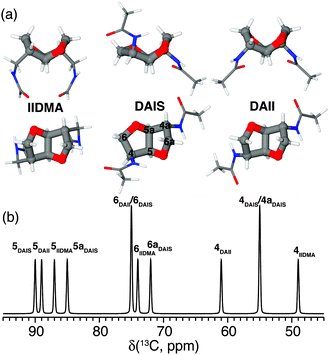 | ||
| Fig. 6 (a) Top and side views of the most stable conformers for the primary diamines isoidide-2,5-dimethyleneamine (IIDMA, endo–endo), diaminoisosorbide (DAIS, exo–endo), and diaminoisoidide (DAII, exo–exo) found via gas phase MP2/6-311G** calculations. (b) Graphical representation of the calculated 13C chemical shifts for all three conformers assigned using the nomenclature shown for DAIS in (a). Reprinted with permission from ref. 75. Copyright 2012, American Chemical Society. | ||
Variable-temperature solid state 13C{1H} CP/MAS NMR experiments were performed to determine the solid state behavior and stability of these isomers.73–75 As reported by Gitsas et al.,77 the dynamic changes of the local chain mobility of a polymer result in the reduction of the effective nuclear dipole–dipole couplings and thereby a lower CP efficiency at higher temperatures. Thus, by affecting the hydrogen bonding of the nano-structured polyamide chain fragments, the intensity of the signals originating from the crystalline phase will be affected more rapidly as a function of temperature compared with signals from the amorphous domains. As an example of the isohexide-based polyamides, Fig. 7a displays a series of VT solid state 13C{1H} CP/MAS NMR spectra for diaminoisosorbide (DAIS) when built into a regular polyamide structure based on sebacic acid monomers. These spectra include well-resolved 13C resonances originating from the C4 and C4a positions attached to the exo and endo oriented amide groups of DAIS. This suggests that the polymerization process does not affect the stereo configuration of the DAIS groups. Moreover, the resonances C5, C5a, and the amide C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O at 174.6 ppm exhibit lower intensities and shift to higher frequencies upon heating, while C5, C5a, C6, and C6a display significant changes in their intensities close to the melting point. The coexistence of these signals, albeit with different intensities close to the melting point, reflects the distribution of DAIS residues over the crystalline and amorphous domains of the sample. More significant intensity changes of the C5, C6, and C4 signals are observed above 100 °C, emphasizing the distribution of DAIS residues in both phases of the semi-crystalline polymer sample.
O at 174.6 ppm exhibit lower intensities and shift to higher frequencies upon heating, while C5, C5a, C6, and C6a display significant changes in their intensities close to the melting point. The coexistence of these signals, albeit with different intensities close to the melting point, reflects the distribution of DAIS residues over the crystalline and amorphous domains of the sample. More significant intensity changes of the C5, C6, and C4 signals are observed above 100 °C, emphasizing the distribution of DAIS residues in both phases of the semi-crystalline polymer sample.
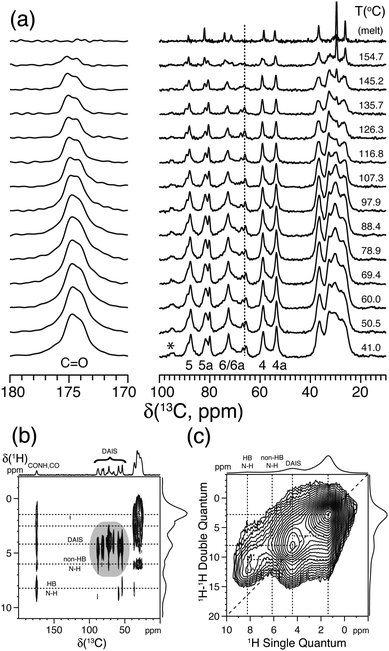 | ||
| Fig. 7 (a) Variable-temperature solid state 13C{1H} CP/MAS NMR spectra of bio-based polyamide synthesized from sebacic acid and diaminoisosorbide (DAIS). (b) 2D 13C{1H} FSLG-HETCOR spectrum acquired using 2.0 ms CP. (c) 2D 1H–1H DQ-SQ spectrum recorded using a Back-to-Back (BaBa) recoupling/reconversion period of 67.2 μs. The dashed lines in (b) and (c) illustrate selected cross-peaks and autocorrelation peaks, including hydrogen-bonded (HB) and non-hydrogen-bonded (non-HB) amide fragments. Assignment is performed according to the scheme given in Fig. 6a. The asterisk indicates the position of a spinning sideband from the carbonyl resonance. Reprinted with permission from ref. 74, copyright 2012, American Chemical Society. | ||
Further information about the molecular packing and hydrogen bonding of the DAIS-based polyamide can be derived from 2D 13C{1H} FSLG-HETCOR and 1H–1H DQ-SQ correlation experiments as shown in Fig. 7b and c. These spectra show that the DAIS-based polyamide includes two different types of amide groups which, based on the chemical shift difference and their position, are related to hydrogen-bonded (8.3 ppm) and non-hydrogen-bonded groups (6.0 ppm). The existence of two different hydrogen-bonding environments is also visible in Fig. 7a, where a doubling of the carbonyl resonance is observed. The two different hydrogen-bonding environments are most likely related to the non-crystalline and crystalline regions of the sample; however, no clear evidence for this behavior can be derived from the VT 13C{1H} CP/MAS NMR spectra in Fig. 7a, where both carbonyl signals show the same intensity decay as a function of temperature. Finally, the 2D 1H–1H DQ-SQ correlation spectrum reveals that the hydrogen-bonding environments are spatially separated (no cross-peak detected) and that the missing autocorrelation between the hydrogen-bonded amide groups points to a chain-folded structure, where these groups are not in close contact.
Thus, the above structural insights into the nano-structured ordering of isohexide-based polyamides from solid state NMR experiments combined with WAXD and DSC analysis show that the crystallinity, and hence the physical properties of the investigated compositions, can be tailored by the content of the bicyclic diamine in the backbone of the polyamides.73–75
3.3 Self-assembly and dynamics of polypeptides
Local chain conformations also play a vital role in the organization of polypeptides, i.e., macromolecules composed of amino acids. Resembling biomacromolecules they have been considered for use in drug delivery and gene therapy and thus have been subject of intensive studies.78,79 In addition, it is known that the superb performance of biological polypeptide-based materials such as hair or spiders' silk is due to a hierarchical superstructure over several length scales, where structure control is exerted at every level of hierarchy.80The two most common local conformations of polypeptides, known as secondary structures, are the α-helix and the β-sheet, both stabilized by intramolecular hydrogen bonds. These secondary structures can be probed directly by solid state NMR33 and their packing can be obtained by X-rays.4 Over the years, we have studied various polypeptides by different NMR techniques, X-ray scattering, and dielectric spectroscopy in order to unravel their hierarchical self-assembly and dynamics as depicted in Fig. 8. The concerted application of these techniques shed light onto the origin of the glass transition, the persistence of the α-helical peptide secondary motif and the effects of topology and packing on the type and persistence of secondary structures.81 Protein function and applications often depend on these issues. Using poly(γ-benzyl-L-glutamate), PBLG, as an example, it was shown that helices are objects of rather low persistence in the bulk as well as in concentrated solutions in helicogenic solvents.
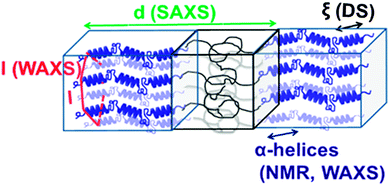 | ||
| Fig. 8 Assembly of a lamellar forming polypeptide-coil diblock copolymer depicting the main techniques employed in our studies. Small-angle X-ray scattering (SAXS) is employed for the domain spacing, d. 13C NMR and wide-angle X-ray scattering (WAXS) are employed to identify the type of the peptide secondary structure (α-helical in the schematic). WAXS is further employed to specify the lateral self-assembly of α-helices within the polypeptide domain (a hexagonal lattice is indicated in the schematic). Dielectric spectroscopy (DS) and site-specific NMR techniques are employed for the dynamics, taken from ref. 81. | ||
Copolypeptides, on the other hand, with their inherent nanometer length scale of phase separation, provide means of manipulating both the type and persistence of peptide secondary structures. As examples we refer to the partial annihilation of α-helical structural defects due to chain stretching, to the induced chain folding of β-sheets in block copolypeptides with incommensurate dimensions, and to the destabilization of β-sheets in peptidic blocks having both secondary motifs.77,82 These effects should be taken into account when such peptides are going to be employed e.g. in drug delivery.
Proline residues are of exceptional significance in protein conformation and protein folding as proline is the only amino acid where the nitrogen bears no amide hydrogen, preventing hydrogen bonding. Furthermore, the bulky pyrrolidine ring restricts the available conformations. Therefore, polypeptides with proline residues offer a unique possibility to unravel the interplay between hydrogen bonding and geometric packing effects. In a recent multitechnique study of diblock copolymers of PBLG and poly(L-proline) (PLP) their hierarchical self-assembly was investigated.83 Both blocks possess helices stabilized either by hydrogen bonds (PBLG) or by steric hindrance (PLP) and are packed in two hexagonal cells of different dimensions. An intriguing trans/cis conformational change of PLP upon confinement was observed that mimics the isomerization of isolated proline residues in proteins. These cis PLP conformations reside primarily at the PLP/PBLG interface, alleviate the packing frustration as shown in Fig. 9, and permit for PBLG and PLP helices to pack with the bulk.
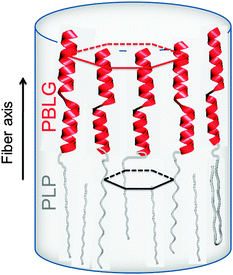 | ||
| Fig. 9 Highly schematic representation of the copolymer self-assembly showing PBLG and PLP α-helices (NMR, WAXS) that are packed (WAXS) with significantly differently sized hexagons. The respective unit cells are indicated with red and black lines. The black arrow indicates the fiber axis, adopted from ref. 83. | ||
Another important aspect of such systems that solid state NMR can tackle is the local chain dynamics, which might also be different for the two building blocks. Thermal analysis by differential scanning calorimetry (DSC), however, displayed a PBLG glass temperature in the copolymers without the indication of a second (PLP) glass temperature.83 Information on the rigidity/dynamics of both polypeptides can be obtained from 13C MAS NMR spectra recorded as a function of temperature.77,81 Such spectra are depicted in Fig. 10 for PBLG-b-PLP over the interesting spectral regions.83 Evidently, the PLP Cδ and PBLG amide C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O resonances show distinctly different T-dependences. The former resonance loses about 40% of its integrated intensity in the T-range from 300 to 400 K, whereas the latter is reduced to a level that cannot be distinguished from the background noise. These intensity losses occur because the local peptide dynamics interfere with frequencies related to magic angle spinning, cross polarization, and dipolar decoupling all of the order of 20 kHz. Hence, the intensity corresponding to the δ3 ∼ 172 ppm and the δ4 ∼ 176 ppm resonances of PBLG is minimized at ∼400 K, suggesting that the underlying motional rates are about 20 kHz. This intensity drop for PBLG indicates low amplitude backbone motions of α-helical segments. However, within the same T-range, the PLP resonances are less affected. These results thus show a mobile PBLG backbone and a relatively rigid PLP backbone at the frequencies of the NMR experiment over the investigated T-range. This is consistent with the pronounced phase separation of the two polypeptides, where PBLG has a lower glass temperature and further indicates a much higher glass temperature for PLP.
O resonances show distinctly different T-dependences. The former resonance loses about 40% of its integrated intensity in the T-range from 300 to 400 K, whereas the latter is reduced to a level that cannot be distinguished from the background noise. These intensity losses occur because the local peptide dynamics interfere with frequencies related to magic angle spinning, cross polarization, and dipolar decoupling all of the order of 20 kHz. Hence, the intensity corresponding to the δ3 ∼ 172 ppm and the δ4 ∼ 176 ppm resonances of PBLG is minimized at ∼400 K, suggesting that the underlying motional rates are about 20 kHz. This intensity drop for PBLG indicates low amplitude backbone motions of α-helical segments. However, within the same T-range, the PLP resonances are less affected. These results thus show a mobile PBLG backbone and a relatively rigid PLP backbone at the frequencies of the NMR experiment over the investigated T-range. This is consistent with the pronounced phase separation of the two polypeptides, where PBLG has a lower glass temperature and further indicates a much higher glass temperature for PLP.
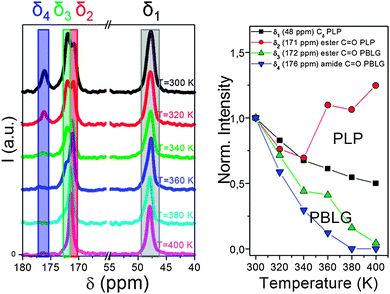 | ||
| Fig. 10 (left) 13C MAS NMR spectra of PBLG73-b-PLP plotted as a function of temperature. Resonances at δ1 ∼ 48 ppm, δ2 ∼ 171 ppm, δ3 ∼ 172 ppm and δ4 ∼ 176 ppm correspond to the PLP Cδ, the PLP ester and to the PBLG side-group ester and amide carbons, respectively. (right) Temperature-dependence of the peak intensities corresponding to the above resonances. Notice the faster intensity drop for the PBLG resonances revealing a mobile PBLG backbone and a relatively rigid PLP backbone at the relevant parameters of the NMR experiment in the range of 20 kHz, adopted from ref. 83. | ||
4 Dynamic nuclear polarization involving macromolecules
Dynamic nuclear polarization (DNP) is a versatile technique used for NMR signal enhancement (commonly called hyperpolarization) thereby enabling new applications of this important method in natural sciences and medicine. As noted in the introduction, DNP relies on the transfer of the large equilibrium polarization from an electron spin ensemble to a nuclear spin ensemble and can thus be viewed as a ‘marriage’ of NMR and EPR. In soft matter, it usually requires the admixture of stable radicals to the sample and microwave irradiation at the frequency of the corresponding electron spin transitions. DNP can facilitate the NMR detection of nuclei with low natural abundance and/or low magnetogyric ratio, even in dilute solutions or for very small sample amounts.84–86 Furthermore, it can dramatically reduce NMR measurement times, for example for multidimensional experiments on low natural abundance nuclei,87 for the study of proteins,17,88 or it can provide surface enhanced detection.89 Last, but not least, DNP can be combined with ultrafast 2D spectroscopy.90DNP experiments can be performed in the solid and in the liquid state. For the analysis of soft matter the combination of MAS NMR and solid state DNP is especially useful yet technically demanding.91 However, during the last two decades a lot of progress has been made in this area culminating in the development of a commercially available solid state dynamic nuclear polarization-enhanced NMR spectrometer.92 The milestones of this development were the implementation of high frequency microwave sources (gyrotrons93), low temperature MAS probes permitting in situ microwave irradiation of the samples94 and biradical polarizing agents95 drastically increasing the solid state DNP efficiency. However, DNP can also be applied in the liquid state for the investigation of dissolved macromolecules. In the liquid phase, the transfer of polarization from electron to nuclear spins is governed by the Overhauser effect, which is mediated via cross relaxation mechanisms.96
In situ Overhauser DNP was realized decades ago at magnetic fields ranging from around 0.1 mT97 up to 2.1 T.98 Nowadays it can also be performed at magnetic fields up to 9.2 T99 thus exploiting the excellent spectral resolution of modern high field NMR spectrometers. The DNP enhancement depends on the electron-nuclear coupling factor,96 which in general reflects the dynamics and type of the molecular motions modulating the interaction between nuclear and electron spins. Its magnetic field dependence leads to slightly lower enhancements in Overhauser DNP at high magnetic fields.100 High-field DNP also involves significant expense and technical effort, including gyrotron microwave sources and specialized cavity designs. Moreover, macromolecules exhibit considerably longer correlation times of molecular motion than solvents of low viscosity thereby further reducing the DNP coupling factor at higher magnetic fields.96 Therefore, Overhauser DNP at moderate or low magnetic fields is obviously attractive, as for these magnetic fields affordable microwave sources, amplifiers and components are readily available and site selectivity can be provided by measuring different nuclei101 or by using the spin-labeling techniques typical for EPR.
4.1 DNP enhancement of a hyperbranched polymer
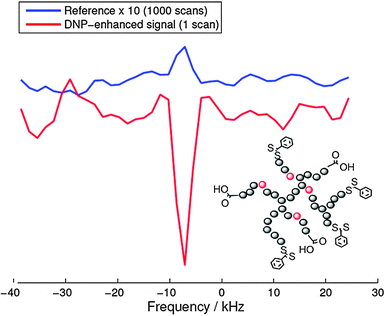
As a recent example of this strategy we report on the 19F-DNP enhancement of a biocompatible hyperbranched polymer102 which has been used for molecular medical imaging employing 19F MRI.102 For these Overhauser DNP experiments we used an electromagnet (adjusted to 0.345 T) and an ENDOR probe, both manufactured by Bruker (Karlsruhe Germany). TEMPOL radicals (20 mM) were added to the 19F containing hyperbranched polymers dissolved in water as a source of unpaired electron spins. Fig. 11 shows a 19F DNP enhancement of −37, which equals an acquisition time saving of 1400 for 19F NMR measurements. Indeed, as shown in Fig. 11 the DNP-enhanced spectrum (single shot) showed a slightly better signal-to-noise ratio than the reference spectrum acquired with 1000 scans.The fluorine atoms are located at the inner parts of the hyperbranched molecule which hinders the direct radical-19F contact, which in turn significantly lowers the DNP coupling factor. This explains the reduced enhancement as compared to water protons (−110) under comparable conditions.103 Nevertheless, this result opens up new possibilities for designing dual-mode MR imaging agents for medicine for measuring relatively fast biological processes with an additional imaging mechanism, where the DNP enhancement can overcome the less sensitive 19F MRI.
4.2 Spin-labeled macromolecules as DNP polarizing agents
DNP with polymers offers a route to improved detection of such macromolecules.104 Moreover, spin-labeling of macromolecules themselves can provide a new type of DNP polarizing agent. An interesting example of this strategy is the use of spin-labeled heparins105,106 as biocompatible DNP polarizing agents. We have demonstrated how spin-labeling of macromolecules can lead to significantly higher DNP enhancements than free TEMPOL in the low-concentration regime.107 This notably includes the absence of Heisenberg spin exchange and electron nuclear-spin relaxation (T1ne), mixing the EPR hyperfine states due to collision of the radicals and relaxation of a coupled nuclear spin, respectively. Such behavior is of interest for the investigation of biomolecules at physiological temperatures where only small sample amounts can be provided and where high radical concentration leads to NMR-line broadening and fast nuclear T1 relaxation. The chemical binding of the nitroxides to the heparin backbone is sketched in Fig. 12. It leads to a heterogeneous distribution and to an increased local concentration of electron spins as well as to reduced mobility. However, due to the stretched conformation of the heparin backbone the distance of closest approach between water molecules and spin-labels is almost unchanged as compared to free TEMPOL molecules. Therefore, the spin-labeled heparins exhibit almost the same coupling factor as free TEMPOL.107 The electron spin-electron spin relaxation time T2e on the other hand is decreased due to residual dipolar couplings and reduced mobility, resulting in broad EPR lines as shown in Fig. 12. Usually, for free radicals, broad EPR lines lead to low achievable DNP enhancement factors, because of incomplete saturation of the EPR lines. This, however, is not the case for the spin-labeled heparins where the achieved enhancement of E = −110 (see Fig. 12) proves directly that it is possible to effectively saturate more than one EPR hyperfine line. Moreover, the decreased electron spin–spin relaxation time could be identified as the reason for the high effective saturation even for small radical concentrations. Thus, despite being heterogeneously distributed, radicals attached to biomacromolecules can be used for DNP in cases where only small sample amounts are available.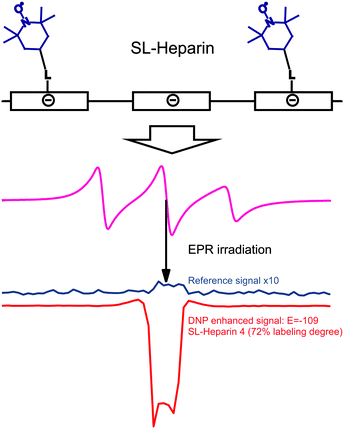 | ||
| Fig. 12 Top row: schematic representation of the polyelectrolytic heparin with attached spin labels. Middle row: CW EPR spectrum of heparin with 72% of the monomer units labelled with TEMPOL dissolved in water. Bottom row: corresponding reference and DNP spectrum of the same sample.108 | ||
4.3 Thermoresponsive, spin-labeled, hydrophilic polymer networks as separable DNP polarizing agents
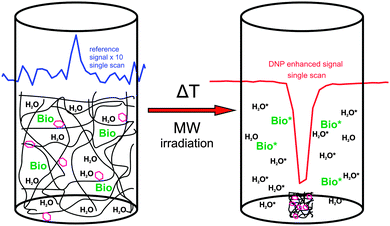
In NMR even small amounts of radicals can disturb the measurements because the radicals lead to increased NMR linewidths and/or decreased T1. Therefore, methods for reliable, complete and fast radical removal after DNP hyperpolarization are sought. This would improve the applicability of DNP substantially and is particularly important for medical applications like metabolic imaging109 of hyperpolarized substances because of the toxicity of certain radicals and the reduced lifetime of the accomplished hyperpolarization during the transport from the DNP polarizer to the MRI scanner. With these important aspects in mind we have introduced the application of thermoresponsive, spin-labeled hydrophilic polymer networks (SL-hydrogels) for DNP,108 and demonstrated that they allow fast and simple radical–solute separation as depicted in Fig. 13. Heating the swollen hydrogel to a critical temperature TC (63 °C) induces a reversible, fast (≤1s) and dramatic volume decrease (≥500 volume%) thereby expelling hyperpolarized water and other target molecules from the radical-bearing polymer network.The SL-hydrogels used provided a maximum NMR signal enhancement for water of up to E = −26.6 ± 1.3 (at 5 °C) at an incident microwave (mw) power of 2 W. For mw powers exceeding 2 W, we always observed a decline of the enhancement for all adjusted temperatures.108 This indicates that the applied mw irradiation on the sample can induce a partial thermal collapse of the thermoresponsive SL-hydrogel due to local heating of the water even in a cooled system. The resulting spatial separation of the radicals, solvent and solute (resembling a micro-phase separation) leads to a diminished coupling factor before the sample is completely saturated, explaining the small DNP enhancement factors. The thermal collapse of our system limits the achievable DNP, but it provides the possibility of combining the saturation of the EPR lines and the separation of hyperpolarized target molecules and radicals in a single step. In addition, by the spatial separation after the thermal collapse, the spin–lattice relaxation time of the hyperpolarized molecules is prolonged up to T1 values in the absence of radicals (T1 = 2100 ms at 25 °C measured in water expelled from the hydrogel). For Overhauser DNP applications, the SL-hydrogels have to be further optimized to yield maximum DNP enhancement at room temperature. However, the specified features make SL-hydrogels very promising candidates for dissolution DNP110 where the DNP polarization is accomplished at 1 K. The obvious benefits are the prolonged T1 after the dissolution step, the radical-free and non-toxic solute containing the hyperpolarized biomolecules, allowing for biomedical applications. Furthermore, the severe heating effects, which occur at room temperature, should be overcome at lower temperatures, allowing for full saturation and maximum DNP enhancement of the sample.
5 Outlook and conclusions
This Perspective Article describes just a few examples of the application of advanced magnetic resonance spectroscopy to nanostructured soft matter. We feel that today's EPR spectroscopy combined with exploiting non-covalent self-assembly of spin probes bears great potential to reveal unusual properties of synthetic and disordered biological macromolecular systems.Conformational studies of bio-based polymers and macromolecular systems by NMR will benefit strongly from the increased sensitivity offered by DNP and other hyperpolarizing methods. This will eventually allow studies of small sample volumes, such as thin films. With ever increasing MAS spinning frequencies, merging of liquid- and solid state NMR techniques for studying structure and dynamics emerge.
Indeed, as pointed out recently by L. Emsley in an editorial8 ‘Recent advances in magnetic resonance allow the study of more and more complex molecular or materials problems, with a clear shift toward the study of systems in situ and toward real-time spectroscopy. Spectacular examples are appearing in the studies of human metabolism, the surface chemistry of catalysis or materials for energy, and the biological function of large assemblies. It is no coincidence that these are some of the most dynamics areas of chemistry today.’ The examples provided in this Perspective Article should be taken as just a few examples along these lines.
Acknowledgements
Part of this work was supported by the Deutsche Forschungsgemeinschaft (DFG) under grant number HI 1094/2-1 and the Dutch Polymer Institute (DPI, project number 685). D.H. acknowledges support by the Max Planck Graduate Center with the University of Mainz (MPGC). M. R. H. acknowledges financial support from the Villum Foundation under the Young Investigator Programme. We thank D. L. Bryce for carefully checking the manuscript.Notes and references
- K. Matyjaszewski and M. Möller, Polymer Science: A Comprehensive Reference, Elsevier, 2012 Search PubMed.
- H. J. Dyson and P. E. Wright, Nat. Rev. Mol. Cell Biol., 2005, 6, 197–208 CrossRef CAS PubMed.
- J. M. Lehn, Angew. Chem., Int. Ed. Engl., 1988, 27, 89–112 CrossRef.
- B. E. Warren, X-ray Diffraction, Dover Publications, 1969 Search PubMed.
- H. W. Spiess, Macromolecules, 2010, 43, 5479–5491 CrossRef CAS.
- R. R. Ernst, G. Bodenhausen and A. Wokaun, Principles of Nuclear Magnetic Resonance in One and Two Dimensions, Clarendon Press, 1987 Search PubMed.
- K. Schmidt-Rohr and H. W. Spiess, Multidimensional Solid-state NMR and Polymers, Academic Press, 1994 Search PubMed.
- L. Emsley, J. Am. Chem. Soc., 2013, 135, 8089–8091 CrossRef CAS.
- A. Schweiger and G. Jeschke, Principles of Pulse Electron Paramagnetic Resonance, Oxford University Press, 2001 Search PubMed.
- G. Jeschke, Annu. Rev. Phys. Chem., 2012, 63, 419–446 CrossRef CAS PubMed.
- J. R. Yates, S. E. Dobbins, C. J. Pickard, F. Mauri, P. Y. Ghi and R. K. Harris, Phys. Chem. Chem. Phys., 2005, 7, 1402–1407 RSC.
- G. Buntkowsky, H. Breitzke, A. Adamczyk, F. Roelofs, T. Emmler, E. Gedat, B. Grunberg, Y. P. Xu, H. H. Limbach, I. Shenderovich, A. Vyalikh and G. Findenegg, Phys. Chem. Chem. Phys., 2007, 9, 4843–4853 RSC.
- M. C. D. Tayler and M. H. Levitt, Phys. Chem. Chem. Phys., 2011, 13, 5556–5560 RSC.
- K. Möbius, A. Savitsky, A. Schnegg, M. Plato and M. Fuchs, Phys. Chem. Chem. Phys., 2005, 7, 19–42 RSC.
- A. Abragam and W. G. Proctor, C. R. Hebd. Seances Acad. Sci., 1958, 246, 2253–2256 CAS.
- G. T. Debelouchina, M. J. Bayro, P. C. A. van der Wel, M. A. Caporini, A. B. Barnes, M. Rosay, W. E. Maas and R. G. Griffin, Phys. Chem. Chem. Phys., 2010, 12, 5911–5919 RSC.
- M. J. Bayro, G. T. Debelouchina, M. T. Eddy, N. R. Birkett, C. E. MacPhee, M. Rosay, W. E. Maas, C. M. Dobson and R. G. Griffin, J. Am. Chem. Soc., 2011, 133, 13967–13974 CrossRef CAS PubMed.
- K. Wuthrich, Angew. Chem., Int. Ed., 2003, 42, 3340–3363 CrossRef PubMed.
- M. Hong and K. Schmidt-Rohr, Acc. Chem. Res., 2013, 46, 2154–2163 CrossRef CAS PubMed.
- S. P. Brown and H. W. Spiess, Chem. Rev., 2001, 101, 4125–4155 CrossRef CAS PubMed.
- A. Abragam, The Principles of Nuclear Magnetism, Clarendon Press, 1961 Search PubMed.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, 1970 Search PubMed.
- P. Höfer, A. Grupp, H. Nebenfuhr and M. Mehring, Chem. Phys. Lett., 1986, 132, 279–282 CrossRef.
- M. Pannier, S. Veit, A. Godt, G. Jeschke and H. W. Spiess, J. Magn. Reson., 2000, 142, 331–340 CrossRef CAS PubMed.
- W. L. Hubbell, D. S. Cafiso and C. Altenbach, Nat. Struct. Biol., 2000, 7, 735–739 CrossRef CAS PubMed.
- G. Jeschke and Y. Polyhach, Phys. Chem. Chem. Phys., 2007, 9, 1895–1910 RSC.
- R. H. Acosta, P. Blümler, K. Munnemann and H. W. Spiess, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 66, 40–69 CrossRef CAS PubMed.
- J. Schmidt, A. Hoffmann, H. W. Spiess and D. Sebastiani, J. Phys. Chem. B, 2006, 110, 23204–23210 CrossRef CAS PubMed.
- S. P. Brown, Solid State Nucl. Magn. Reson., 2012, 41, 1–27 CrossRef CAS PubMed.
- D. Sebastiani, ChemPhysChem, 2006, 7, 164–175 CrossRef CAS PubMed.
- A. E. Tonelli and F. C. Schilling, Acc. Chem. Res., 1981, 14, 233–238 CrossRef CAS.
- S. P. Brown, I. Schnell, J. D. Brand, K. Müllen and H. W. Spiess, Phys. Chem. Chem. Phys., 2000, 2, 1735–1745 RSC.
- S. P. Brown, Prog. Nucl. Magn. Reson. Spectrosc., 2007, 50, 199–251 CrossRef CAS PubMed . This article provides a comprehensive introduction to proton-proton correlation techniques in solid state NMR.
- K. Müllen and J. P. Rabe, Acc. Chem. Res., 2008, 41, 511–520 CrossRef PubMed.
- M. R. Hansen, R. Graf and H. W. Spiess, Acc. Chem. Res., 2013, 46, 1996–2007 CrossRef CAS PubMed.
- D. Demus, J. W. Goodby, G. W. Gray, H. W. Spiess and V. Vill, Handbook of Liquid Crystals, Wiley, 1998 Search PubMed.
- X. Feng, V. Marcon, W. Pisula, M. R. Hansen, J. Kirkpatrick, F. Grozema, D. Andrienko, K. Kremer and K. Muellen, Nat. Mater., 2009, 8, 421–426 CrossRef CAS PubMed.
- D. Adam, P. Schuhmacher, J. Simmerer, L. Haussling, K. Siemensmeyer, K. H. Etzbach, H. Ringsdorf and D. Haarer, Nature, 1994, 371, 141–143 CrossRef CAS.
- M. R. Hansen, X. Feng, V. Macho, K. Müllen, H. W. Spiess and G. Floudas, Phys. Rev. Lett., 2011, 107, 257801 CrossRef CAS.
- L. J. Berliner, Spin Labeling: Theory and Applications, Academic Press, 1979 Search PubMed.
- S. A. Goldman, G. V. Bruno, C. F. Polnaszek and J. H. Freed, J. Chem. Phys., 1972, 56, 716–735 CrossRef CAS PubMed.
- O. A. Matthews, A. N. Shipway and J. F. Stoddart, Prog. Polym. Sci., 1998, 23, 1–56 CrossRef CAS.
- B. Z. Zhang, R. Wepf, K. Fischer, M. Schmidt, S. Besse, P. Lindner, B. T. King, R. Sigel, P. Schurtenberger, Y. Talmon, Y. Ding, M. Kroger, A. Halperin and A. D. Schluter, Angew. Chem., Int. Ed., 2011, 50, 737–740 CrossRef CAS PubMed.
- A. Sunder, R. Hanselmann, H. Frey and R. Mülhaupt, Macromolecules, 1999, 32, 4240–4246 CrossRef CAS.
- M. J. N. Junk, W. Li, A. D. Schluter, G. Wegner, H. W. Spiess, A. Zhang and D. Hinderberger, Macromol. Chem. Phys., 2011, 212, 1229–1235 CrossRef CAS.
- D. Kurzbach, M. J. N. Junk and D. Hinderberger, Macromol. Rapid Commun., 2013, 34, 119–134 CrossRef CAS PubMed.
- M. J. N. Junk, H. W. Spiess and D. Hinderberger, Angew. Chem., Int. Ed., 2010, 49, 8755–8759 CrossRef CAS PubMed.
- Y. Akdogan, J. Reichenwallner and D. Hinderberger, PLoS One, 2012, 7, e45681 CAS.
- J. Reichenwallner and D. Hinderberger, Biochim. Biophys. Acta, Gen. Subj., 2013, 1830, 5382–5393 CrossRef CAS PubMed.
- D. Kurzbach, D. R. Kattnig, B. Z. Zhang, A. D. Schluter and D. Hinderberger, J. Phys. Chem. Lett., 2011, 2, 1583–1587 CrossRef CAS.
- D. Kurzbach, D. R. Kattnig, B. Z. Zhang, A. D. Schluter and D. Hinderberger, Chem. Sci., 2012, 3, 2550–2558 RSC.
- D. Kurzbach, X. Q. Zhang, B. Z. Zhang, P. Arnold and D. Hinderberger, Chem.–Eur. J., 2013, 19, 5602–5608 CrossRef CAS PubMed.
- G. H. Bird, S. Pornsuwan, S. Saxena and C. E. Schafmeister, ACS Nano, 2008, 2, 1857–1864 CrossRef CAS PubMed.
- D. Hinderberger, H. W. Spiess and G. Jeschke, Appl. Magn. Reson., 2010, 37, 657–683 CrossRef.
- M. A. R. Meier, J. O. Metzger and U. S. Schubert, Chem. Soc. Rev., 2007, 36, 1788–1802 RSC.
- F. Fenouillot, A. Rousseau, G. Colomines, R. Saint-Loup and J. P. Pascault, Prog. Polym. Sci., 2010, 35, 578–622 CrossRef CAS PubMed.
- P. Gallezot, Chem. Soc. Rev., 2012, 41, 1538–1558 RSC.
- H. Mutlu, R. Hofsäβ, R. E. Montenegro and M. A. R. Meier, RSC Adv., 2013, 3, 4927–4934 RSC.
- N. Q. Ran, L. S. Zhao, Z. M. Chen and J. H. Tao, Green Chem., 2008, 10, 361–372 RSC.
- M. P. F. Pepels, M. R. Hansen, H. Goossens and R. Duchateau, Macromolecules, 2013, 46, 7668–7677 CrossRef CAS.
- H. M. Konig and A. F. M. Kilbinger, Angew. Chem., Int. Ed., 2007, 46, 8334–8340 CrossRef PubMed.
- A. Bohle, G. Brunklaus, M. R. Hansen, T. W. Schleuss, A. F. M. Kilbinger, J. Seltmann and H. W. Spiess, Macromolecules, 2010, 43, 4978–4985 CrossRef CAS.
- M. Wegner, D. Dudenko, D. Sebastiani, A. R. A. Palmans, T. F. A. de Greef, R. Graf and H. W. Spiess, Chem. Sci., 2011, 2, 2040–2049 RSC.
- J. Shu, D. Dudenko, M. Esmaeili, J. H. Park, S. R. Puniredd, J. Y. Chang, D. W. Breiby, W. Pisula and M. R. Hansen, J. Am. Chem. Soc., 2013, 135, 11075–11086 CrossRef CAS PubMed.
- J. Lu, P. A. Mirau and A. E. Tonelli, Prog. Polym. Sci., 2002, 27, 357–401 CrossRef CAS.
- R. H. Grubbs, Angew. Chem., Int. Ed., 2006, 45, 3760–3765 CrossRef CAS PubMed.
- M. Kamigaito, T. Ando and M. Sawamoto, Chem. Rev., 2001, 101, 3689–3745 CrossRef CAS PubMed.
- S. Monsaert, A. L. Vila, R. Drozdzak, P. Van Der Voort and F. Verpoort, Chem. Soc. Rev., 2009, 38, 3360–3372 RSC.
- T. W. Baughman and K. B. Wagener, in Metathesis Polymerization, ed. M. R. Buchmeiser, 2005, vol. 176, pp. 1–42 Search PubMed.
- Y. Y. Wei, R. Graf, J. C. Sworen, C. Y. Cheng, C. R. Bowers, K. B. Wagener and H. W. Spiess, Angew. Chem., Int. Ed., 2009, 48, 4617–4620 CrossRef CAS PubMed.
- R. G. Alamo, K. Jeon, R. L. Smith, E. Boz, K. B. Wagener and M. R. Bockstaller, Macromolecules, 2008, 41, 7141–7151 CrossRef CAS.
- C. J. Luo, S. D. Stoyanov, E. Stride, E. Pelan and M. Edirisinghe, Chem. Soc. Rev., 2012, 41, 4708–4735 RSC.
- L. Jasinska-Walc, M. Villani, D. Dudenko, O. van Asselen, E. Klop, S. Rastogi, M. R. Hansen and C. E. Koning, Macromolecules, 2012, 45, 2796–2808 CrossRef CAS.
- L. Jasinska-Walc, D. Dudenko, A. Rozanski, S. Thiyagarajan, P. Sowinski, D. van Es, J. Shu, M. R. Hansen and C. E. Koning, Macromolecules, 2012, 45, 5653–5666 CrossRef CAS.
- J. Wu, L. Jasinska-Walc, D. Dudenko, A. Rozanski, M. R. Hansen, D. van Es and C. E. Koning, Macromolecules, 2012, 45, 9333–9346 CrossRef CAS.
- G. Flèche and M. Huchette, Starch/Stärke, 1986, 38, 26–30 CrossRef.
- A. Gitsas, G. Floudas, M. Mondeshki, I. Lieberwirth, H. W. Spiess, H. Iatrou, N. Hadjichristidis and A. Hirao, Macromolecules, 2010, 43, 1874–1881 CrossRef CAS.
- H. A. Klok and S. Lecommandoux, in Peptide Hybrid Polymers, ed. H. A. Klok and H. Schlaad, Springer-Verlag Berlin, Berlin, 2006, vol. 202, pp. 75–111 Search PubMed.
- J. R. McDaniel, D. J. Callahan and A. Chilkoti, Adv. Drug Delivery Rev., 2010, 62, 1456–1467 CrossRef CAS PubMed.
- R. Tycko, Annu. Rev. Phys. Chem., 2001, 52, 575–606 CrossRef CAS PubMed.
- G. Floudas and H. W. Spiess, Macromol. Rapid Commun., 2009, 30, 278–298 CrossRef CAS PubMed.
- T. Aliferis, H. Iatrou and N. Hadjichristidis, Biomacromolecules, 2004, 5, 1653–1656 CrossRef CAS PubMed.
- R. Graf, H. W. Spiess, G. Floudas, H. J. Butt, M. Gkikas and H. Iatrou, Macromolecules, 2012, 45, 9326–9332 CrossRef CAS.
- F. Blanc, L. Sperrin, D. A. Jefferson, S. Pawsey, M. Rosay and C. P. Grey, J. Am. Chem. Soc., 2013, 135, 2975–2978 CrossRef CAS PubMed.
- O. Ouari, T. Phan, F. Ziarelli, G. Casano, F. Aussenac, P. Thureau, D. Gigmes, P. Tordo and S. Viel, ACS Macro Lett., 2013, 2, 715–719 CrossRef CAS.
- R. G. Griffin and T. F. Prisner, Phys. Chem. Chem. Phys., 2010, 12, 5737–5740 RSC.
- H. Takahashi, D. Lee, L. Dubois, M. Bardet, S. Hediger and G. De Paepe, Angew. Chem., Int. Ed., 2012, 51, 11766–11769 CrossRef CAS PubMed.
- E. Ravera, B. Corzilius, V. K. Michaelis, C. Rosa, R. G. Griffin, C. Luchinat and I. Bertini, J. Am. Chem. Soc., 2013, 135, 1641–1644 CrossRef CAS PubMed.
- A. Lesage, M. Lelli, D. Gajan, M. A. Caporini, V. Vitzthum, P. Mieville, J. Alauzun, A. Roussey, C. Thieuleux, A. Mehdi, G. Bodenhausen, C. Coperet and L. Emsley, J. Am. Chem. Soc., 2010, 132, 15459–15461 CrossRef CAS PubMed.
- L. Frydman and D. Blazina, Nat. Phys., 2007, 3, 415–419 CrossRef CAS.
- Q. Z. Ni, E. Daviso, T. V. Can, E. Markhasin, S. K. Jawla, T. M. Swager, R. J. Temkin, J. Herzfeld and R. G. Griffin, Acc. Chem. Res., 2013, 46, 1933–1941 CrossRef CAS PubMed.
- http://www.bruker.com/products/mr/nmr/dnp-nmr/overview.html .
- V. S. Bajaj, M. K. Hornstein, K. E. Kreischer, J. R. Sirigiri, P. P. Woskov, M. L. Mak-Jurkauskas, J. Herzfeld, R. J. Temkin and R. G. Griffin, J. Magn. Reson., 2007, 189, 251–279 CrossRef CAS PubMed.
- A. B. Barnes, E. A. Nanni, J. Herzfeld, R. G. Griffin and R. J. Temkin, J. Magn. Reson., 2012, 221, 147–153 CrossRef CAS PubMed.
- C. Song, K.-N. Hu, C.-G. Joo, T. M. Swager and R. G. Griffin, J. Am. Chem. Soc., 2006, 128, 11385–11390 CrossRef CAS PubMed.
- K. H. Hausser and D. Stehlik, Adv. Magn. Reson., 1968, 3, 79–139 CAS.
- E. H. Poindexter, J. A. Potenza, D. D. Thompson, N. Vannghia and R. H. Webb, Mol. Phys., 1968, 14, 385–391 CrossRef CAS.
- H. Brunner and K. H. Hausser, J. Magn. Reson., 1972, 6, 605–611 CAS.
- V. P. Denysenkov, M. J. Prandolini, A. Krahn, M. Gafurov, B. Endeward and T. F. Prisner, Appl. Magn. Reson., 2008, 34, 289–299 CrossRef CAS.
- N. M. Loening, M. Rosay, V. Weis and R. G. Griffin, J. Am. Chem. Soc., 2002, 124, 8808–8809 CrossRef CAS PubMed.
- O. Neudert, C. Mattea, H. W. Spiess, S. Stapf and K. Muennemann, Phys. Chem. Chem. Phys., 2013, 15, 20717–20726 RSC.
- K. J. Thurecht, I. Blakey, H. Peng, O. Squires, S. Hsu, C. Alexander and A. K. Whittaker, J. Am. Chem. Soc., 2010, 132, 5336–5337 CrossRef CAS PubMed.
- M.-T. Turke and M. Bennati, Phys. Chem. Chem. Phys., 2011, 13, 3630–3633 RSC.
- V. Vitzthum, F. Borcard, S. Jannin, M. Morin, P. Mieville, M. A. Caporini, A. Sienkiewicz, S. Gerber-Lemaire and G. Bodenhausen, ChemPhysChem, 2011, 12, 2929–2932 CrossRef CAS PubMed.
- A. L. Kleschyov, V. Sen, V. Golubev, K. Munnemann, D. Hinderberger, K. J. Lackner, S. Weber, M. Terekhov, L. M. Schreiber and T. Munzel, Eur. J. Med. Chem., 2012, 58, 265–271 CrossRef CAS PubMed.
- R. Lever, B. Mulloy and C. P. Page, Heparin - A Century of Progress, Springer, 2012 Search PubMed.
- B. C. Dollmann, A. L. Kleschyov, V. Sen, V. Golubev, L. M. Schreiber, H. W. Spiess, K. Munnemann and D. Hinderberger, ChemPhysChem, 2010, 11, 3656–3663 CrossRef CAS PubMed.
- B. C. Dollmann, M. J. N. Junk, M. Drechsler, H. W. Spiess, D. Hinderberger and K. Munnemann, Phys. Chem. Chem. Phys., 2010, 12, 5879–5882 RSC.
- K. Golman, R. Zandt, M. Lerche, R. Pehrson and J. H. Ardenkjaer-Larsen, Cancer Res., 2006, 66, 10855–10860 CrossRef CAS PubMed.
- J. H. Ardenkjaer-Larsen, B. Fridlund, A. Gram, G. Hansson, L. Hansson, M. H. Lerche, R. Servin, M. Thaning and K. Golman, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10158–10163 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2014 |