Li ion dynamics in TiO₂ anode materials with an ordered hierarchical pore structure – insights from ex situ NMR

Abstract

Ex situ Nuclear Magnetic Resonance (NMR) measurements were carried out to study lithium ion dynamics in lithium intercalated mesoporous anatase (Li_xTiO₂) serving as an anode material for rechargeable lithium-ion batteries. As has been shown recently, hierarchically ordered TiO₂ shows excellent cycling performance and ensures a high lithium storage capacity. ⁷Li spin–lattice relaxation NMR and stimulated echo NMR serve as a powerful combination to shed light on the Li hopping processes from an atomic-scale point of view. To determine atomic Li jump rates and microscopic activation energies temperature-variable SLR NMR measurements, in both the laboratory and rotating frame of reference, as well as mixing-time dependent spin-alignment echo NMR measurements were carried out. The results point to moderate Li diffusivities; however, in a lithium-ion cell this is compensated for by taking advantage of nm-structured materials with greatly reduced diffusion lengths. Importantly, although a phase transition from tetragonal symmetry to orthorhombic symmetry takes place at increased states of charge, the diffusion parameters and activation energies probed (0.4 to 0.5 eV) do depend weaker on Li content x than expected. Thus, despite the increased value of x, the evolution of the orthorhombic phase seems to support Li diffusivity rather than to affect the transport properties in a negative way. This interesting feature might be highly beneficial for the excellent cycling behavior observed recently.

---

1 Introduction

The development of new electrode materials for lithium-ion batteries is a vital topic in materials science.^1–6 Currently, materials with nm-sized dimensions,⁷i.e., those being characterized by large surface areas, are strongly considered to act as powerful anode and cathode materials significantly improving the performance of today's lithium ion batteries.^1,8–13 Combined with an ordered 3D pore structure¹⁴ such materials ensure high storage capacities and facile Li insertion and removal. This is inter alia related to short diffusion lengths of the nm-sized materials¹ as well as to the involvement of Li surface storage⁸ (or even pseudo-capacitive faradaic processes^15,16) due to the large volume fraction of interfacial regions.

Quite recently, excellent cycling behavior of a lithium-ion battery was achieved when mesoporous TiO₂ with a 3D hierarchical pore structure served as an anode material.¹⁴ Even after extensive charging and discharging of the battery, the hierarchical pore structure is preserved throughout clearly illustrating the high stability of the anode material.¹⁴ Initially, TiO₂ crystallizes with tetragonal symmetry. However, upon Li insertion the crystal structure transforms into an orthorhombic one,¹⁴ see also analogous studies where NMR has been used to monitor these changes.^17–19 Besides kinetic effects also Li diffusion properties are anticipated to govern the insertion and removal rates. So far, only a few studies can be found in the literature being concerned with the atomic-scale measurement of Li self-diffusion parameters of TiO₂-based anode materials with different states of charges.^17,20–23 The present study aims at the question if and to which extent Li self-diffusion changes as a function of Li content x in Li_xTiO₂. Since Li_xTiO₂ is a mixed conductor, that is, electrons and lithium ions contribute to the overall conductivity, those methods which are able to solely probe Li ion dynamics, such as NMR, represent favorable techniques for this purpose.^17,20,22

Therefore, we used complementary ⁷Li NMR techniques^20,24,25 to study the Li⁺ self-diffusion parameters such as microscopic activation energies and jump rates. The techniques applied are sensitive to Li motional processes on quite different time scales.²⁶ In particular, while ⁷Li spin-alignment echo (SAE) NMR^27–30 is useful to probe rather slow Li motions with correlation rates lower than 10⁴ Hz, ⁷Li NMR spin–lattice relaxation (SLR) measurements, in both the laboratory (SLR_L) and rotating frame of reference (SLR_ρ),^26,31,32 are applicable to detect hopping processes with rates ranging from 10⁵ Hz to 10⁹ Hz. Interestingly, considering x and the reversible phase transformation mentioned above, the dynamic parameters deduced from NMR, if identified with bulk processes, turned out to be less influenced by the Li content than expected,³³ see also ref. 34. In contrast, the orthorhombic structure seems to facilitate Li migration which seems to be beneficial for the performance of the battery.

2 Experimental

Synthesis and characterization of mesoporous anatase are described elsewhere in detail, see ref. 14. Mesoporous anatase was prepared using the silica KIT-6 as a hard template¹⁴ and lithium intercalation was carried out electrochemically at a rate of 10 mA g⁻¹. Electrochemical cells were constructed by mixing the active material and Super S carbon (MMM) in the weight ratio of 8 : 1 and pressed into a pellet. After drying at 80 °C under vacuum for 8 hours, the electrodes were assembled into cells with a Li anode and an LP 30 electrolyte (Merck; 1 M LiPF₆ in 1 : 1 v/v ethylene carbonate/dimethyl carbonate).

The cells were constructed and handled in an Ar-filled MBraun glovebox. The cells were cycled at 10 mA g⁻¹ (C/33). The first discharge was used to prepare the three different samples with overall capacities of 30 mA h g⁻¹, 117 mA h g⁻¹, and 248 mA h g⁻¹ at certain cut-off potentials. This corresponds to Li_x=0.09TiO₂, Li_0.35TiO₂, and Li_0.74TiO₂ respectively (see Fig. 1). After that the electrodes were rinsed with a small amount of dry solvent (dimethyl carbonate) to remove the residual electrolyte. They were then left under dynamic vacuum overnight to ensure that all solvent had evaporated. Prior to the temperature-variable NMR measurements, the samples were fire-sealed in glass ampoules to protect them permanently from any traces of moisture.

Fig. 1 First cycle load curve of mesoporous anatase at a rate of 10 mA g⁻¹.

⁷Li NMR data were recorded at temperatures ranging from 153 K to 453 K on MSL 100 and MSL 400 solid-state NMR spectrometers (Bruker). While the MSL 100 (Bruker) is connected to a Kalmus amplifier (400 W) and a field-variable Oxford cryo-magnet with 4.7 T, the MSL 400 (in standard configuration, Bruker) was used in combination with a shimmed Oxford cryo-magnet with a nominal magnetic field of 9.4 T. The corresponding resonance frequencies ω₀/2π were 78 and 155 MHz, respectively. Mostly, commercial probes were used to record static NMR line shapes, SLR rates and SAE NMR decay rates as a function of temperature. Typically, 90° pulse lengths were in the order of 4 to 6 μs. The temperature in the sample chamber was monitored using a Ni–CrNi thermocouple connected to an Oxford ITC. The accuracy of temperature adjustment was approximately ±2 K. Temperatures below room temperature were reached by heating a stream of freshly evaporated nitrogen gas. Above room temperature heated air was used to achieve the desired temperatures.

NMR spectra, recorded at 155 MHz, were used to determine the line width (fwhm, full widths at half maximum) for the analysis of so-called motional narrowing curves. The corresponding free induction decays were recorded with the help of a single pulse sequence using a delay of 5 × T₁ between each scan to ensure full longitudinal relaxation; T₁ denotes the spin–lattice relaxation time. In the case of Li_x=0.09TiO₂ up to 64 scans were accumulated to compensate for the weak signal-to-noise ratio.

The classical saturation recovery pulse sequence³⁵ has served to determine ⁷Li SLR_L NMR rates. We used a comb of 10 closely spaced 90° pulses to destroy any longitudinal magnetization M_z(t). The subsequent recovery of M_z(t) was then recorded with a 90° detection pulse as a function of delay time and temperature. The transients follow non-exponential time behavior and have been parameterized with stretched exponentials.

Slower Li diffusion processes were measured via the spin-lock technique introduced by Ailion and Slichter:^36–38 90°−spin-lock pulse−acquisition (acq.) at angular locking frequencies ω₁/2π in the kHz range. Our locking pulses varied from t_lock = 1 μs to t_lock = 100 ms. As in the case of SLR_L the transients M_ρ(t_lock) of SLR_ρ NMR can only be described by stretched exponentials. Finally, mixing-time (t_m) dependent SAE NMR decay curves were recorded with the help of the Jeener–Broekaert^39,40 three-pulse sequence: (90°)_X − t_p − (45°)_Y − t_m − 45° − acq. We used a fixed preparation time t_p of 10 μs to acquire two-time single-spin (sin–sin) correlation functions. The mixing time was varied from 100 μs up to several seconds, i.e., spanning a time window of many decades. A 32-fold phase cycle^39,41 was employed to suppress unwanted coherences and to eliminate dipolar contributions to the echo showing up after the reading pulse. Fourier transformation of the spin-alignment echo, starting from the top of the signal, results in SAE NMR spectra useful to highlight quadrupole intensities due to the interaction of the quadrupole moment of ⁷Li (spin-3/2 nucleus) and non-vanishing electric field gradients (see below).

3 Results and discussion

Temperature-variable NMR line shape measurements give first insights into the microscopic jump processes of Li ions in solids.⁴² At low temperature (see Fig. 2), that is, at temperatures for which the mean Li jump rate is much lower than the spectral line width, both the shape and the width of an NMR line are determined by rigid dipolar interactions of the Li spins. With increasing T, however, homonuclear dipole–dipole interactions predominantly governing the line width are increasingly averaged due to Li translational motion on a sufficiently large length scale.⁴³ As a result, the NMR line undergoes a pronounced narrowing process. In many cases, the initial Gaussian shape of the NMR central line turns into a Lorentzian one determining the spectra in the regime of extreme narrowing. This is also observed for the sample with x = 0.74. The spectra shown in Fig. 2 were obtained by analyzing free induction decays. Thus, quadrupolar intensities are largely suppressed. These can be made visible by the use of spin-alignment echo NMR, for example. The technique is briefly described at the end of this section when SAE NMR decay curves are discussed. With SAE NMR, and with the solid echo technique as well, it is possible to overcome receiver dead-time effects and to increase the intensity of electric quadrupolar contributions to the overall NMR spectrum. A typical one is shown in Fig. 3 for x = 0.74, i.e., the orthorhombic form. Besides the central transition, a broad quadrupole powder pattern is visible which can be approximated with a Gaussian line. The full width at half maximum is approximately 62 kHz. Assuming an axially oriented electric field gradient, this corresponds to a coupling constant of 124 kHz. For comparison, this value is smaller than that roughly calculated and probed for microcrystalline lithium titanate (160 kHz) by Wagemaker et al.¹⁷ For x = 0.09 a coupling constant of 140 kHz can be estimated in the rigid lattice regime of mesoporous Li_xTiO₂.

Fig. 2 Selected ⁷Li NMR spectra of Li_xTiO₂ recorded at the temperatures indicated. Data were recorded at 155 MHz; x = 0.74 (fully orthorhombic) and x = 0.09 (crystallizing predominantly with the anatase structure). The lines were each centred to their individual resonance frequency ν₀ in order to better illustrate the shape and the widths of the selected lines.

Fig. 3 ⁷Li spin-alignment echo NMR spectrum recorded at 155 MHz (top). The spectrum can be deconvoluted into a broad Gaussian-shaped quadrupolar part with a full width of half maximum of ca. 62 kHz. The dashed line represents the central transition, see also Fig. 2.

Coming back to the NMR central lines shown in Fig. 2, it is worth mentioning that in the present case, no indications could be found which would significantly point to a so-called heterogeneous line narrowing, that is, the emergence of a pronounced two-component line shape with a broad and narrow contribution to the overall signal. Such a feature is thought to be diagnostic for a heterogeneous dynamics owing to two magnetically decoupled (and spatially separated) spin reservoirs of fast and slowly diffusing spins.^44,45

In Fig. 4 the ⁷Li NMR line width, deduced from the central transition, is plotted vs. temperature for the three different samples studied. Starting with a rigid line width Δν_rl of 5.8 kHz for the sample with x = 0.09, Δν_rl increases to 6.7 kHz (x = 0.35) until, for the sample with x = 0.74, a significantly broadened line characterized by Δν_rl = 7.9 kHz is detected (see also Fig. 2). Generally, the rigid-lattice line width is directly proportional to the intensity of dipolar homonuclear Li–Li interactions; those scale with the mean interatomic Li–Li distance r which, for simple geometries, can be calculated via van Vleck's formula.⁴³ An estimation of large x values, taking into account Li–Li coupling only, leads to approximately 8 kHz.¹⁷ Note that this estimation disregards the coupling of Li spins with strictly paramagnetic Ti³⁺ centers expected to be generated during Li insertion.

Fig. 4 ⁷Li NMR line widths (fwhm: full width at half maximum) of Li_xTiO₂ as a function of temperature. Data were recorded at 155 MHz. x was varied from 0.09 to 0.74. Note that the data points of the sample with x = 0.09 are shown twice. For a better comparison with the data of sample Li_0.74TiO₂, the circles in grey were offset by 2.32 kHz.

The beginning of motional narrowing is expected when the mean correlation time, that is approximately the residence time between two successful Li jumps, reaches the order of the inverse rigid lattice line width Δν_rl. For example, at x = 0.09 line narrowing starts well below room temperature. The corresponding jump rate is then expected to range from 10³ to 10⁴ jumps per second. Most interestingly, although x has been increased from 0.09 to 0.74, that is, by a factor of eight, no drastic shift of the onset of motional narrowing towards higher temperatures is observed. At first glance, one would expect that the Δν_rl becomes larger and the more the lithium ions occupy sites within the TiO₂ matrix, the more the Li diffusion is slowed down. In the present case, however, something seems to (over-)compensate for the decrease expected. To our opinion, the reason should be looked for in the anatase-to-orthorhombic phase transition the TiO₂ anode material undergoes during Li uptake. Recently, this phase transition has been studied by ex situ X-ray powder diffraction and in situ Raman microscopy.¹⁴ It has also been reported by ⁷Li magic angle spinning (MAS) NMR spectroscopy.^17,18

By analyzing ⁷Li NMR spin–spin relaxation rates of a μm-sized powder sample showing a two-phase morphology Wagemaker et al. deduced that Li diffusivity in orthorhombic lithium titanate is enhanced compared to ion mobility in anatase. The NMR signal of Li in microcrystalline anatase (Li_0.12TiO₂) is reported to be 1.35 kHz in the rigid lattice while that of Li in lithium titanate is given by 11.8 kHz. Considering the shape of the rigid-lattice NMR spectrum of mesoporous Li_0.09TiO₂ shown in Fig. 2, which tends to be more peaked even at lower T compared to the situation in Li_0.74TiO₂, one might speculate that whether this sample is already a mixture of anatase and orthorhombic TiO₂. While X-ray diffraction, which is being more sensitive to long-range order, does not reveal a distinct sign of a second phase in mesoporous Li_xTiO₂ until the composition of x = 0.25.¹⁴ Raman microscopy, instead, points to the formation of nuclei of the orthorhombic phase already at x = 0.05.¹⁴ However, as powder X-ray diffraction has shown,¹⁴ up to x = 0.1 Li intercalation into the tetragonal phase continues. Regarding the spectra shown in Fig. 2, in the case of nanostructured TiO₂ a deconvolution is hardly possible. Since Li ions are also expected to reside in the interfacial regions, the spectra may also be understood as a complex distribution of NMR intensities rather than a scenario of only two structurally distinct phases. Moreover, even for Li ions diffusing in a structurally well-defined single phase, a complex, heterogeneous motional narrowing may be found. Therefore, the static (ex situ) NMR measurements presented here reflect the overall Li diffusivity in Li_xTiO₂. Interestingly, even preliminary ⁶Li MAS NMR measurements recorded at spinning frequencies of up to 30 kHz did not allow a reliable deconvolution of the NMR signals. Further high-resolution NMR measurements are currently underway in our lab.

To prove the above-mentioned assumption of an increase of ion diffusivity in Li-rich Li_xTiO₂ (with x = 0.35 and 0.74) against Li_x=0.09TiO₂ the application of diffusion-induced SLR NMR^46–48 and SAE NMR^25,28,30 as well is helpful to quantify Li dynamics in terms of decay rates and microscopic activation energies. As a preliminary point, it is important to note that ⁷Li NMR relaxation transients, especially those recorded in the rotating frame of reference, may show a strongly non-exponential decay behavior even in those cases where a single spin reservoir is present. This is due to the spin-3/2 nature of ⁷Li which is exposed to both dipolar and quadrupolar interactions. From the outset, this hinders a separation of the transients into, e.g., two sub-transients. Additionally, in our case spin-relaxation phenomena taking place in the bulk may largely be different from those in the relatively large volume fraction of interfacial regions. Therefore, we analyzed the underlying magnetization transients in terms of stretched exponentials (as illustrated below) yielding a single relaxation rate which reflects the overall NMR spin relaxation.

In the lower part of Fig. 5 the temperature dependence of the ⁷Li NMR SLR rates measured is illustrated. Below 300 K the rates are governed by non-diffusive background relaxation due to coupling of the Li spins with the Ti³⁺ centers, lattice vibrations and/or other paramagnetic impurities. Expectedly, the absolute value of the background rates increases with increasing x pointing, e.g., to a larger number of Ti³⁺centers generated or to an increased coupling of Li spins with electrons in the conduction band, see the rates measured at a Larmor frequency of 155 MHz (Fig. 5). Sometimes these interactions can be extremely large hindering the detection of diffusion-induced contributions. In such cases other NMR techniques, as for instance mixing-time dependent SAE NMR (see below), can alternatively be used to study Li dynamics in solids.

Fig. 5 Arrhenius plot of the ⁷Li NMR SLR rates measured in the laboratory and rotating frame of reference. If not stated otherwise, data were recorded at 78 MHz. The rates 1/T₁ and 1/T_1ρ are shown as a function of inverse temperature 1/T. Note that, for a better comparison, the rates 1/T₁ of Li_0.09TiO₂ are multiplied with a factor of 4. As in the case of Li_0.74TiO₂ the diffusion-induced rates on the low-T flank reveal a relatively weak frequency (sub-linear) dependence and show non-BPP behaviour for which 1/T₁ ∝ ω⁻² is expected.⁴⁹

Fortunately, above room temperature the 1/T₁ NMR rates shown in Fig. 5 are increasingly influenced by diffusive Li⁺ hopping. This is in contrast to the study reported by Wagemaker et al., who did not observe a dependence of 1/T₁ on temperature for μm-sized crystallites up to ca. 500 K.¹⁷ Here, the rates increase with temperature and follow the low-T flank of a diffusion-induced NMR relaxation rate peak. At even higher temperatures the rates are expected to pass through the maximum on a log(1/T₁) vs. 1/T plot. However, to prevent grain growth and to conserve the nanostructure of the materials, we restricted our measurements to 500 K. Therefore, the analysis of SLR NMR data is limited to the low-temperature limit characterized by ω₀τ ≫ 1, which means that the mean correlation rate accessible is smaller than the Larmor frequency applied. In the case of Li_0.74TiO₂ the rates recorded at 78 MHz and at the highest temperature already indicate the appearance of a relatively broad 1/T₁ peak. Note that at the rate maximum of such a peak the correlation time is expected to be in the order of the inverse Larmor frequency, i.e., the relation ω₀τ ≈ 1 holds. This corresponds to Li jump rates with values in the MHz range. In the present case this is expected to be fulfilled at ca. 500 K.

The solid lines in the lower part of Fig. 5 represent fits with an Arrhenius law. The fits include only those data points recorded well above 330 K. From the slope the activation energy for short-range Li hopping can be deduced. As in the case of line narrowing, very similar activation energies are found. Interestingly, for x = 0.74 the value of E_a = 0.32(2) eV is somewhat smaller (0.37(2) eV) than that found for the sample with x = 0.09. This underpins the results from motional narrowing presented above. It is worth noting that correction procedures, taking into account the non-diffusive background rates, do not change those results much since the background rates turn out to be almost independent of temperature below T = 220 K (see also Fig. 5). Let us note that the activation energies probed here are much larger than those reported by Wagemaker et al. (0.2 eV and 0.09 eV)¹⁷ for Li diffusion in anatase and lithium titanate on the basis of spin–spin-relaxation NMR measurements.

In a more striking way the differences between the three samples probed here are illustrated by the rotating-frame SLR NMR rates of Li_0.09TiO₂ and Li_0.74TiO₂, which are exemplarily shown in the upper part of Fig. 5. The underlying magnetization transients M_ρ are shown in Fig. 6; their analysis with stretched exponentials (see above) leads to the rates plotted in Fig. 5. Starting with a weaker-than-activated background relaxation, the NMR relaxation rates of Li_0.74TiO₂ pass into the low-T flank at a slightly lower temperature than it is the case for the sample with x = 0.09. This also holds when the background rates were approximated with a power-law function, extrapolated to higher T and subtracted from the overall rates measured. At high temperatures the rates measured at a locking frequency of 14 kHz do not follow a simply shaped rate peak. Instead, they merge into a relatively broad plateau which is an indication of complex, non-BPP⁴⁹ lithium ion dynamics presumably additionally owing to the interplay with binders and carbon black present. Irrespective of that, the deviation of the SLR rates from the Arrhenius line drawn, which takes place at 420 K, points to correlation rates ranging from 10⁵ to 10⁶ jumps per second.

Fig. 6 ⁷Li NMR magnetization transients M_ρ(t_lock) of Li_0.74TiO₂ and Li_0.09TiO₂ recorded at the temperatures indicated and at ω₀/2π = 78 MHz and ω₁/2π = 14 kHz. Dashed and solid lines represent fits according to stretched exponentials M_ρ(t_lock) ∝ exp(−(t_lock/T₁)^γ) where the stretching exponent γ ranges from 0.45 at the lowest temperatures to 0.65 at the highest T.

Lastly, the activation energy obtained from rotating-frame NMR data (ca. 0.53 eV (Fig. 4), note that a similar value is found for the sample with x = 0.09) is clearly larger than that deduced from NMR measurements performed in the laboratory frame of reference. In contrast to SLR NMR in the lab frame, being sensitive to jump processes in the MHz range, data recorded with the spin-locking technique are able to probe ion motions on a longer length and time scale being defined by locking frequencies ω₁/2π in the kHz range. Additionally, the rather large activation energy probed is comparable with those usually found for long-range ion transport probed via dc conductivity. Thus, the SLR_ρ NMR rates on the low-T flank seem to be less influenced by correlation effects^50–52 usually affecting SLR_L NMR rates in this limit characterized by ω₀τ ≫ 1. Such effects may arise from repulsive Coulomb interactions and irregular formed energy landscapes the ions are subjected to, i.e., structural disorder.⁵² They are known to reduce the slope on the low-T flank of SLR NMR rate peaks.

Since the maxima of the SLR_ρ NMR rate peaks could not be resolved, we used Jeener–Broekaert⁴⁰ echoes to study spin-alignment echo (SAE) decay rates by recording single-spin motional correlation functions. Such measurements turned out to be useful to confirm the long-range nature of the activation energies probed via SLR_ρ NMR. Echo damping was recorded by using a three-pulse sequence; echo amplitudes were measured as a function of mixing time t_m but fixed preparation time of 10 μs. The principle of SAE NMR is very similar to that of exchange NMR.^25,30,53 The intensity of the echo generated after the first two pulses decreases if the jumping ions visit sites characterized by different electric field gradients (EFGs); other effects caused by (quadrupolar) spin–lattice relaxation or spin-diffusion may also contribute to the damping. A non-vanishing EFG is produced by the electric charge distribution in the direct neighborhood of the nucleus under investigation.⁴³ The interaction of the quadrupole moment of the nucleus with an EFG alters the Zeeman levels by a certain amount of energy which is determined by the quadrupole frequency ω_q. Thus, in the ideal case SAE NMR is directly sensitive to temporal changes of the site-specific quadrupole frequencies ω_q,i (i = 1…n) the ions sense during hopping. Then, the decay curve represents a correlation function reflecting the probability to find an ion initially marked by ω_q,1 at a site with the same ω_q,1 at a later time.

In Fig. 7 typical two-time ⁷Li SAE NMR decay curves are shown for the samples with x = 0.09 and x = 0.74. Such curves are obtained when the intensity of the echo S₂ is plotted vs. t_m using a logarithmic abscissa. At very low temperatures the curves depend only weakly on temperature; presumably, in this T range echo damping is caused by spin-diffusion rather than by translational diffusion.⁵⁴ Stretched exponentials with a stretching factor γ ranging from 0.32 to 0.49 are best suited to describe the dependency on mixing time t_m in this non-diffusive temperature regime. In general, stretching factors deviating from γ = 1 reveal a non-Debye motional process. For example, such deviations can arise from motions in confined dimensions⁵⁵ leading to a motional correlation function whose decay slows down with increasing time.

Fig. 7 ⁷Li SAE NMR decay curves of Li_xTiO₂ samples with x = 0.09 (left) and x = 0.74 (right). Decay curves follow stretched exponentials (0.3 < γ < 0.5) which are shown as solid lines. Data have been recorded at a Larmor frequency of 155 MHz. See the text for further details. The inset shows the T dependence of the stretching factors.

It is common to all samples that with increasing T the inflexion point of the echo decay curves shifts towards shorter t_m. Concomitantly, γ steadily decreases until values of, for example, 0.32 (x = 0.09) are reached. Moreover, at a sufficiently long mixing time the curves S₂(t_p = const., t_m) reach S_2,∞ = 0 which either indicates a rather large number of quadrupole frequencies involved or which points to the influence of dipolarly coupled spins, see ref. 41 for details of spin-alignment final state amplitudes S_2,∞.

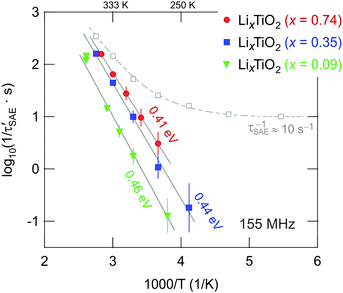
The decay rates 1/τ_SAE of the fitting functions, which were used to describe the two-time correlation functions S₂(t_p = const., t_m), are exemplarily shown for x = 0.35 in Fig. 8 (grey squares). At temperatures below 200 K the rate 1/τ_SAE amounts to about 10 s⁻¹ and can be identified with 1/τ_SAE,SD which is primarily influenced by spin diffusion (SD);^20,54 the dashed line in Fig. 8 is to guide the eye. Above 250 K the SAE NMR rates increase due to translational Li hopping. To correct the rates 1/τ_SAE for any non-diffusive background contribution, we calculated the difference 1/τ′_SAE = 1/τ_SAE – 1/τ_SAE,SD. The resulting rates 1/τ′_SAE (x = 0.35) follow an Arrhenius law with an activation energy of E_a,SAE = 0.44(2) eV (see Fig. 8). The same procedure is applied to those data obtained for x = 0.09 and x = 0.74. Starting from x = 0.09, the activation energy decreases from 0.46 eV to 0.41 eV (see Fig. 8). This is consistent with the fact that the lowest rates were obtained for the sample with x = 0.09. Activation energies from SAE NMR are somewhat lower than those determined from SLR NMR in the rotating frame of reference, while the lowest values were found by SLR NMR performed in the laboratory frame of reference. These differences illustrate that there are different types of hopping motion that each experiment type is sensitive to. Usually, the low-T flank of SLR NMR in the lab frame is sensitive to short-range Li dynamics rather than to long-range ion motion. The latter seems to be better probed by rotating frame methods carried out at much lower (effective) resonance frequencies (14 kHz, see above).

Fig. 8 Arrhenius plot of the ⁷Li SAE NMR decay rates 1/τ′_SAE, which have been corrected for any non-diffusive background contributions to S₂ (see dotted line). Solid lines represent linear fits; the values given indicate the activation energies obtained for each sample.

Although the differences in 1/τ′_SAE (and E_a,SAE) found are small for the three samples investigated, they particularly underpin the trend obtained from SLR_ρ NMR. Thus, with the increase of x, which initiates the above mentioned phase transformation, Li diffusion is slightly increased rather than decreased. Besides other advantages of the mesoporous anode material this effect is highly desirable because it is expected to contribute to the excellent rate performance documented.¹⁴

4 Summary and outlook

The present study represents one of the very first examples that takes advantage of solid-state NMR to keep track of Li dynamics during charging a (mixed conducting) TiO₂-based anode in a lithium-ion battery. The diffusion parameters extracted from the various NMR methods applied point to Li dynamics being almost independent of the amount of Li inserted into the transition metal oxide. In fact, Li bulk diffusivity, which might also be influenced by surface diffusivity, seems to increase rather than to decrease with increasing x in Li_xTiO₂. This behavior might directly be related to the phase transformation which takes place during charging. The anode material, which initially crystallizes mainly with the anatase structure, gradually transforms into orthorhombic Li_xTiO₂ upon Li insertion.

In particular, results from SAE NMR, being sensitive to relatively slow but long-range, translational ion dynamics underline this behavior. The corresponding activation energies obtained from relaxation NMR in the rotating frame of reference and SAE NMR, respectively, range from 0.41 eV to 0.53 eV. Such relatively large values are expected for Li⁺ ion transport proceeding on a longer length scale within the TiO₂ matrix. Besides NMR and a few other techniques, in the case of lithium such values are otherwise only obtainable by dc conductivity measurements. However, when dealing with mixed conductors, impedance spectroscopy needs special setups and careful sample preparation to separate ionic from electronic contributions. NMR, however, is a contactless method with no requirement for special sample (post-)preparation.

Finally, both the stretching of the two-time SAE NMR correlation functions and the lower activation energy found by SLR NMR performed in the laboratory frame of reference point to a complex Li dynamics present. This manifests in activation energies which depend on the time scale the method applied is sensitive to. Further experiments, especially those using ⁶Li (SAE) NMR techniques might be useful to shed light on the deviation from simple Debye behavior observed.

Further notes

The authors declare no competing financial interest.

Acknowledgements

Financial support from the Deutsche Forschungsgemeinschaft (DFG FOR 1277, project 7 “Li diffusion in nanostructured materials”) is highly appreciated. M.W. thanks the Leibniz University Hannover for further financial support (grant “Wege in die Forschung II”). P.G. Bruce is grateful to the EPSRC including SUPERGEN and the program grant “Nanoionics” for financial support.

References

1. P. G. Bruce, B. Scrosati and J.-M. Tarascon, Angew. Chem., Int. Ed., 2008, 47, 2930.
2. J. M. Tarascon and M. Armand, Nature, 2001, 414, 359.
3. M. S. Whittingham, Chem. Rev., 2004, 104, 4271.
4. J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587.
5. M. V. Reddy, G. V Subba Rao and B. V. R. Chowdari, Chem. Rev., 2013, 113, 5364.
6. R. Marom, S. F. Amalraj, N. Leifer, D. Jacob and D. Aurbach, J. Mater. Chem., 2011, 21, 9938.
7. J. Maier, Nat. Mater., 2005, 4, 805.
8. M. Wagemaker and F. M. Mulder, Acc. Chem. Res., 2012, 46, 1206.
9. Y. Wang and G. Cao, Adv. Mater., 2008, 20, 2251.
10. D. Deng, M. G. Kim, J. Y. Lee and J. Cho, Energy Environ. Sci., 2009, 2, 818.
11. H.-K. Song, K. Lee, M. G. Kim, L. F. Nazar and J. Cho, Adv. Funct. Mater., 2010, 20, 3818.
12. A. Vu, Y. Qian and A. Stein, Adv. Energy Mater., 2012, 2, 1056.
13. Y. Ren, Z. Ma and P. G. Bruce, Chem. Soc. Rev., 2012, 41, 4909.
14. Y. Ren, L. J. Hardwick and P. G. Bruce, Angew. Chem., Int. Ed., 2010, 49, 2570.
15. M. Zukalová, M. Kalbáč, L. Kavan, I. Exnar and M. Graetzel, Chem. Mater., 2005, 17, 1248.
16. G. Sudan, E. Baudrin, D. Larcher and J.-M. Tarascon, J. Mater. Chem., 2005, 15, 1263.
17. M. Wagemaker, R. van de Krol, A. P. M. Ken gens, A. A. van Well and F. M. Mulder, J. Am. Chem. Soc., 2001, 123, 11454.
18. V. Luca, L. Hanley, N. K. Robers and R. F. Howe, Chem. Mater., 1999, 11, 2089.
19. M. Vijayakumar, S. Kerisi, C. Wang, Z. Nie, K. M. Rosso, Z. Yang, G. Graff, J. Liu and J. Hu, J. Phys. Chem. C, 2009, 113, 14567.
20. M. Wilkening, C. Lyness, A. R. Armstrong and P. G. Bruce, J. Phys. Chem. C, 2009, 113, 4741.
21. M. Wilkening, R. Amade, W. Iwaniak and P. Heitjans, Phys. Chem. Chem. Phys., 2007, 9, 1239.
22. M. Wagemaker, A. P. M. Kentgens and F. M. Mulder, Nature, 2002, 418, 397.
23. M. Wagemaker, W. J. H. Borghols, E. R. H. van Eck, A. P. M. Kentgens, G. J. Kearley and F. M. Mulder, Chem.–Eur. J., 2007, 13, 2023.
24. M. Wilkening, W. Küchler and P. Heitjans, Phys. Rev. Lett., 2006, 97, 065901.
25. M. Wilkening and P. Heitjans, ChemPhysChem, 2012, 13, 53.
26. M. Wilkening, A. Kuhn and P. Heitjans, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 054303.
27. F. Qi, G. Hinze, R. Böhmer, H. Sillescu and H. Zimmermann, Chem. Phys. Lett., 2000, 328, 257.
28. R. Böhmer and F. Qi, Solid State Nucl. Magn. Reson., 2007, 31, 28.
29. M. Wilkening and P. Heitjans, J. Phys.: Condens. Matter, 2006, 18, 9849.
30. R. Böhmer, K. Jeffrey and M. Vogel, Prog. Nucl. Magn. Reson. Spectrosc., 2007, 50, 87.
31. M. Wilkening, W. Iwaniak, J. Heine, V. Epp, A. Kleiner, M. Behrens, G. Nuspl, W. Bensch and P. Heitjans, Phys. Chem. Chem. Phys., 2007, 9, 6199.
32. V. Epp, S. Nakhal, M. Lerch and M. Wilkening, J. Phys.: Condens. Matter, 2013, 25, 195402.
33. A. Van der Ven, J. Bhattacharya and A. A. Belak, Acc. Chem. Res., 2013, 46, 1216.
34. M. Wilkening, J. Heine, C. Lyness, A. Armstrong and P. Bruce, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 064302.
35. E. Fukushima and S. B. W. Roeder, Experimental Pulse NMR: A Nuts and Bolts Approach, New Ed., Westview Press, Boulder, 1993.
36. D. Ailion and C. Slichter, Phys. Rev. Lett., 1964, 12, 168.
37. C. Slichter and D. Ailion, Phys. Rev. A: At., Mol., Opt. Phys., 1964, 135, 1099.
38. D. Ailion and C. Slichter, Phys. Rev. A: At., Mol., Opt. Phys., 1965, 137, 235.
39. R. Böhmer, J. Magn. Reson., 2000, 147, 78.
40. J. Jeener and P. Broekaert, Phys. Rev., 1967, 157, 232.
41. F. Qi, G. Diezemann, H. Böhm, J. Lamber and R. Böhmer, J. Magn. Reson., 2004, 169, 225.
42. M. Wilkening, V. Epp, A. Feldhoff and P. Heitjans, J. Phys. Chem. C, 2008, 112, 9291.
43. A. Abragam, The Principles of Nuclear Magnetism, Clarendon, Oxford, 1961.
44. S. Indris and P. Heitjans, J. Non-Cryst. Solids, 2002, 307–310, 555.
45. M. Wilkening, S. Indris and P. Heitjans, Phys. Chem. Chem. Phys., 2003, 5, 2225.
46. H. Buschmann, J. Dölle, S. Berendts, A. Kuhn, P. Bottke, M. Wilkening, P. Heitjans, A. Senyshyn, H. Ehrenberg, A. Lotnyk, V. Duppel, L. Kienle and J. Janek, Phys. Chem. Chem. Phys., 2011, 13, 19378.
47. A. Kuhn, M. Kunze, P. Sreeraj, H. D. Wiemhöfer, V. Thangadurai, M. Wilkening and P. Heitjans, Solid State Nucl. Magn. Reson., 2012, 42, 2.
48. A. Kuhn, P. Sreeraj, R. Pöttgen, H.-D. Wiemhöfer, M. Wilkening and P. Heitjans, J. Am. Chem. Soc., 2011, 133, 11018.
49. N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679.
50. K. Funke, Prog. Solid State Chem., 1993, 22, 111.
51. M. Meyer, P. Maass and A. Bunde, Phys. Rev. Lett., 1993, 71, 573.
52. A. Bunde, W. Dieterich, P. Maass and M. Meyer, in Diffus. Condens. Matter – Methods, Mater. Model, ed. P. Heitjans and J. Kärger, Springer, Berlin, 2005, p. 813.
53. B. Koch and M. Vogel, Solid State Nucl. Magn. Reson., 2008, 34, 37.
54. C. Brinkmann, S. Faske, B. Koch and M. Vogel, Z. Phys. Chem., 2010, 224, 1535.
55. M. Wilkening and P. Heitjans, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 24311.

---