Phycocyanobilin in solution – a solvent triggered molecular switch

Abstract

We present a computational investigation of the conformational response of phycocyanobilin (PCB) to the ability of solvents to form hydrogen bonds. PCB is the chromophore of several proteins in light harvesting complexes. We determine the conformational distributions in different solvents (methanol and hexamethylphosphoramide HMPT) by means of ab initio molecular dynamics simulations and characterize them via ab initio calculations of NMR chemical shift patterns. The computed trajectories and spectroscopic fingerprints illustrate that the energy landscape is very complex and exhibits various conformations of similar energy. We elucidate the strong influence of the solvent characteristics on the structural and spectroscopic parameters. Specifically, we predict a cis–trans isomerization of phycocyanobilin upon switching from the aprotic to the protic solvent, which explains an experimentally observed change in the NMR patterns. In the context of technological molecular recognition, solvent induced conformational switching can be considered a precursor mechanism to the recognition of single molecules.

---

1 Introduction

Phycocyanobilin (PCB) is an open chain tetrapyrrole chromophore that can be found in the biliproteins allophycocyanin and phycocyanin. Similar open tetrapyrroles can be found in a vast variety of phytochrome photoreceptors as well as in phycobiliproteins that are found in various plants as well as in different bacteria and fungi. The general function of those photoreceptors is the reaction to light with the goal of collecting energy or triggering further processes in larger biological systems. The process is initialized by isomerization of the chromophore, which then starts the propagation of the absorbed energy toward the photocenter or triggers the systems' structural response to the excitation. While the exact microscopic processes of the latter two steps are still under discussion, the structure of the phytochromes as well as the isomerization process is well documented by different experimental and theoretical investigations. On the experimental side, structural analysis has been performed based on X-ray spectroscopy and neutron scattering experiments. Spectroscopic properties as well as the dynamics during the photocycle have been investigated using various techniques, among them ultrafast mid infrared spectroscopy^1–3 as well as Raman and NMR^4–6 spectroscopy. Theoretical investigations have been performed on a wide range of aspects employing various theoretical approaches ranging from classical molecular dynamics simulations, as well as QM/MM hybrid approaches. Additionally, various theoretical spectroscopic approaches have been used, including Raman,⁷ UV/VIS via TDDFT^8–11 as well as NMR simulations,¹²i.e. giving insights into the different chromophore conformations of the single states during the photocycle. In many cases, only the isolated chromophore has been considered, modeling the missing protein structure either by PCM models or ignoring it completely.

In addition to the investigations on the whole protein or photosystem, both experimental and theoretical investigations have also been performed on the isolated chromophore. Naturally, the conformational distribution of the chromophore alone is difficult to assess using diffraction techniques. However, magnetic resonance methods, in particular NMR, are highly sensitive to small changes in structural parameters such as dihedral angles.

The conformational space of a chromophore embedded in the binding pocket of a protein framework is highly restricted. In contrast to that, an isolated chromophore in solution can adopt any configuration, which often leads to an extended distribution of structures. Here, a computational analysis provides a thermodynamically weighted ensemble of geometries from the molecular phase space; this ensemble can subsequently be validated by calculations of spectroscopic observables which can be compared to experimental data.^13–19

Previous theoretical investigations on the conformational behavior of isolated similar chromophores have been performed employing Monte Carlo conformational sampling methods²⁰ as well as direct dihedral scanning.²¹

In a recent experimental NMR study on the isolated chromophore, performed by M. Röben et al.,²² two fully assigned spectra of the isolated PCB in two different solvents have been obtained. In both 2D ¹H–¹⁵N spectra, we can observe typical patterns. The B and C rings chemical shifts are in close proximity in both chemical shift directions, while the A and D ring shifts maintain their relative distances of around 1 ppm in the hydrogen and 30 ppm in the nitrogen direction. When changing the solvent from the aprotic HMPT to the protic methanol, a general small downfield shift for the hydrogen chemical shifts can be observed. Additionally, the B and C ring nitrogen chemical shifts are strongly shifted downfield. At the first look, the hydrogen chemical shifts seem to indicate stronger hydrogen bonding for the HMPT solvent, while actually stronger hydrogen bonding can be anticipated for methanol. The nitrogen chemical shifts suggest specific conformational changes, which at the first look also cannot be predicted from a solvent change.

The possible conformational changes as a response to the presence of specific molecules in the direct environment are specific forms of molecular recognition. In our case, it is not a specific key-lock mechanism, but rather a modification of the average hydrogen bonding patterns. Nevertheless, this mechanism can be considered a special variant of molecular recognition.^23–26

We investigate the said system by a combination of free energy, molecular dynamics simulations and ab initio NMR chemical shift calculations to gain insight into the microscopic origin of these at the first look contradictory findings.

Since the nature of the system allows for a huge variety of different conformations and possible hydrogen bonding patterns, in the first step the underlying energy surface in regard to the characteristic geometric variables of the system has to be explored. In the next step, we will perform molecular dynamics simulations based on the previously identified most important conformations to finally compute ensemble averaged NMR chemical shifts of the chromophore. Using experimental data as the benchmark, we will identify the preferred conformations, molecular structure and hydrogen bonding networks depending on the local surroundings of the chromophore.

2 Computational details

Well tempered 2D metadynamics simulations^27,28 have been employed using the 3 dihedral pairs (1,2), (3,4) and (5,6). The simulation was based on a DFTB²⁹ approach including dispersion correction. The timestep was set to 0.5 fs. A canonical ensemble has been used, utilizing the canonical velocity rescaling (CSVR) thermostat.³⁰ Gaussian hills with a width of 20 degrees and an initial height of 0.001 Ha have been spawned every 200 timesteps. The temperature of the tempering algorithm was set to 3000 K.

The metadynamics algorithm allows the scanning of collective variables, which is performed by modifying the underlying potential energy while running a molecular dynamics simulation. This modification is achieved by depositing Gaussian hills at regular time intervals. By this, frequently visited regions of the collective variable energy surface are less likely to be visited again in the simulation, energy basins are slowly filled, enabling the molecular dynamics simulation to escape minima and explore regions of the energy surface that could otherwise not be reached in the limited simulation time and temperature. The energy surface can then be reconstructed from the deposited Gaussians.

For the additional sampling of the various minima found, 75 ps DFTB molecular dynamics simulations with dispersion correction³¹ have been performed with a timestep of 0.5 fs and employing a canonical ensemble using the Nosé–Hoover³² thermostat. The same settings have been used for the calculations including the explicit solvent molecules. Here 212 methanol molecules have been added in a fully periodic system with a box size of 25 Å.

We employed a combined gaussian plane wave method (GPW)³³ using the BLYP functional^34,35 with additional van der Waals dispersion³⁶ for performing the ab initio molecular dynamics simulations, in order to incorporate hydrogen bonding effects as accurately as possible. We used a time step of 0.4 fs for the integration of the equations of motion, in combination with a Nosé–Hoover thermostat. All MD and metadynamics simulations have been performed using the CP2K program package.

QM/MM molecular dynamics simulations have been performed on two selected conformations, based on a BLYP/ForceField mixed approach. The coupling of the two regions has been done within the gaussian expansion of the electrostatic potential (GEEP).³⁷

NMR chemical shift averages have been calulated based on regular snapshots (50 snapshots per trajectory) from the molecular dynamics simulations. All calculations have been performed using the ORCA program³⁸ within the IGLO approach.³⁹ The PBE0⁴⁰ functional as well as the optimized IGLO-III⁴¹ basis set have been used. For the explicit solvent calculations, solvent molecules residing within 3 Å of the chromophore have been considered.

3 Results and discussion

3.1 Free energy surface and preferred conformations

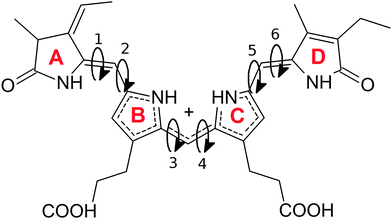
The overall structure of phycocyanobilin can be described by means of the dihedral pairs connecting the four pyrrole rings A to D (see Fig. 1). The determination of the equilibrium conformation for a given surrounding solvent thus requires a careful sampling of this conformational space. Since the energy barriers of the partly double bonded and possibly conjugated electronic systems are considerable, the molecule will cross them only rarely. Hence, the application of straight molecular dynamics simulations would result in an insufficient sampling or even in stable conformations for the entire simulation. A wealth of methods has been developed to overcome such sampling problems, and have proven to effectively escape local minima. Among them are the parallel tempering algorithm,⁴² transition path sampling,^43,44 various basin hopping methods,^45–47 minima hopping^48,49 and different tabu search based strategies.^50,51 Other algorithms have been inspired from selective mechanisms found in nature, such as artificial bee colony algorithms,^52–54 evolutionary algorithms⁵⁵ and genetic algorithms.⁵⁶

Fig. 1 Structure of the fully protonated (charge +1) phycocyanobilin with the 4 pyrrole rings labeled A to D, connected by 6 dihedrals labeled 1 to 6. The conformation is described by the three double (cis/trans) and three single (syn/anti) bonds between the pyrrole rings.

Recent studies on a different hydrogenation state of the PCB used Monte Carlo sampling,²⁰ while others generated conformations by changing all degrees of the molecule dihedral angles²¹ to tackle this problem. In this work, we used the technique of metadynamics simulations, which is an alternative approach that allows the explicit representation of the free energy hypersurface with regards to selected collective variables. This in turn enables us to detect local minima and the corresponding energy barriers between physically meaningful conformations.

We first performed three independent 2D metadynamics simulations of the chromophore in vacuo, each using one of the three pairs of dihedral angles connecting the rings A/B, B/C and C/D as collective variables. For all three calculations, a linear (ZEZsss) conformation has been used to initialize the simulation. During the simulations for each dihedral pair, all doubly bonded dihedral angles not driven by the metadynamics remained stable throughout the simulation. Thus, the resulting energy landscape is only valid for the given conformation of the unbiased dihedral angles. However, the perturbance of the energy landscape by changes in the electronic structure in distant parts of the chromophore will only have a minor influence.

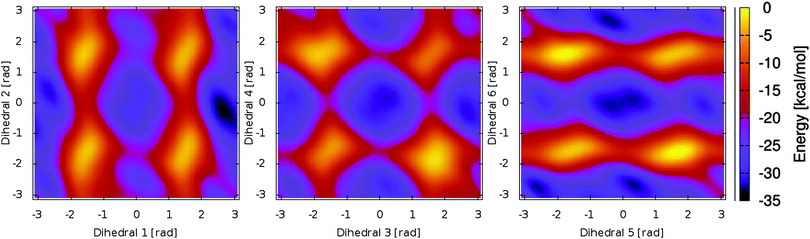
The resulting free energy surfaces are illustrated in Fig. 2 for the three metadynamics simulations sampling the dihedral angles between A/B, B/C and C/D. In the resulting energy surfaces, four minima for each dihedral pair are located at (0,0), (0,π), (π,0) and (π,π). All four minima appear twofold degenerate; this effect can be traced back to steric hindering of the amide hydrogen atoms and the pyrrole ring sidegroups. The actual depth of the energy minima however cannot be explained as easily and delicately depending on possible steric repulsion, hydrogen bonding and dihedral energies.

Fig. 2 Energy surface for the three dihedral pairs (1,2) to (5,6) connecting the pyrrole rings A to D. Twofold degenerate minima are visible for planar conformations, while the overall depth of the minima and height of the energy barriers vary to a great extent.

Examining the energy hypersurface of the dihedral pair (1,2) connecting rings A and B, the previously described twofold degenerate minima can be observed at all four conformations leading to planar arrangement of the rings. The minima are separated by two clearly distinguishable energy barriers, a small barrier of approximately 10 kcal mol⁻¹ in the direction of 2 located at 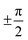and a larger barrier of 30 kcal mol⁻¹ in the direction of dihedral 1 at a similar position. This result clearly shows the different bond characteristics, resembling a double bond character for the central bond of dihedral 1 and single bond characteristics for dihedral 2.

For the two central dihedral angles 3 and 4 connecting the rings B and C, again we can see four distinctive minimum energy conformations that again correspond to the planar conformations. Again, the local maxima within the energy basins are caused by the proximity of different groups and sidechains of the B and C rings. Compared to the previous dihedral pair, however, a clear distinction in the bond character and rotational energy barriers for the two dihedrals cannot be made. The height of the energy barriers lies in-between those of the rigid dihedral 1 and the rotatable dihedral 2. With a height of approximately 12 kcal mol⁻¹, the barrier is small enough to be overcome in the time-limit of actual experiments, resulting in a delicate equilibrium for the two lowest minima of similar energy ((0,0) and (0,π)) with the actual population ratio critically depending on the exact energy difference and external influences.

The remaining two dihedral angles behave similar to the dihedrals connecting rings A and B. The dihedral 5 can rotate easily, while in the direction of dihedral 6 a high rotational barrier can be seen. However, here the energy barrier is even higher than in the first case. Also we see a clear energetic preference for a value of 0 deg for dihedral 6, with the lowest possible energy being found at (0,0).

As a main result from our metadynamics simulations, we see similar energetic properties for the different configurations of the (3,4) dihedral pair. The (π,π) and (−π,−π) states however are less favorable due to strong steric hindering. For the dihedral pair (1,2), a preference for the (π,0) conformation can be seen, while for the (5,6) pair the (0,0) state is energetically favorable. This information already heavily reduces the number of needed conformations for a sufficient sampling of the conformational space using molecular dynamics simulations. Additionally, induced by the delicate equilibrium between the two lowest energy minima, the central dihedral pair (3,4) can be expected to react strongly to small changes in the chromophore and its surroundings.

3.2 Unbiased molecular dynamics simulations

Based on the energy surfaces of our metadynamics simulations, unbiased molecular dynamics simulations of the PCB have been employed to allow for a sampling of the unperturbed system. Based on the same DFTB level of theory, we performed simulations for a broad selection of energetically favorable conformations. In 75 ps of simulation time, a good sampling of the relevant regions in the energy surface can be achieved, i.e. positions in both sides twofold degenerate minima are visited, while the general conformation does not change during the simulation. This behavior can be observed for all other conformations and dihedral pairs. As a result, a multitude of differently initialized molecular dynamics simulations is needed to calculate the properties of the system. When evaluating the dihedral distributions during the simulation, the bond characteristics found in the metadynamics simulations can be confirmed (cp. Fig. 3). While the outer dihedral angles 1 and 6 show a narrow double bond like distribution, the neighboring bonds 2 and 5 exhibit a broad distribution indicating a single bond like behavior. The width of the central dihedrals 3 and 4 lies in between the previous ones, pointing towards a conjugated electronic system. While the semi-empirical level of theory allows for the needed sampling, intramolecular hydrogen bonding however is underestimated; the rarely emerging hydrogen bonds remain stable only for parts of picoseconds.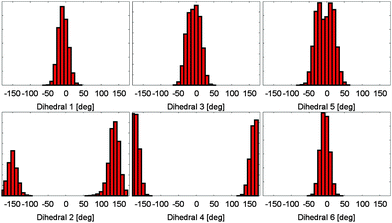

Fig. 3 Dihedral angle distributions during a molecular dynamics simulation. All dihedral angles remain stable at the simulation time of 75 ps. The different bond characteristics are clearly visible.

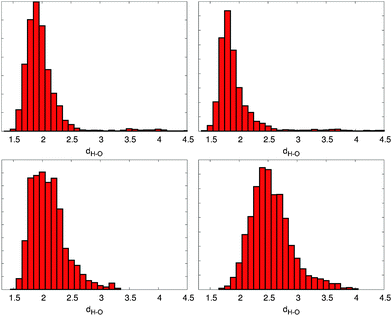
In the next step, a proper description of the hydrogen bonds needs to be achieved. Here a BLYP with the VdW correction level of theory has been used, which strongly improves the description of the intramolecular hydrogen bonds. Maximally hydrogen bonded conformers can be found in the ZZZsas and ZEZsss conformations, enabling the formation of 6 stable hydrogen bonds (cp. Fig. 4) between the B and C rings carboxyl groups and the C and D or A and B ring NH and oxygens.

Fig. 4 Distribution of the four possible hydrogen bonds between the NH groups and the carboxylic group lone oxygens, taken from a 10 ps BLYP-D trajectory of the ZEZsss conformation. Top left: ring A, right: ring B; bottom left: ring C, right: ring D.

3.3 Explicit solvent calculations

For the conformational distribution of a solute in an aprotic solvent with only weak specific intermolecular interactions, the gas phase can usually be considered a very good first approximation. For other solvents, in particular hydrogen-bonding liquids such as water or alcohols, an explicit representation of the solvent molecules is normally the method of choice in order to reproduce the sensitive equilibrium of intra- and intermolecular interactions. Hence, we have considered the solvent molecules explicitly in our unbiased molecular dynamics simulations.

The higher complexity of explicit solvent models would result in considerably higher computational costs for metadynamics simulations which require several nanoseconds of simulation time even for an approximate convergence. An additional side effect is caused by the inertia of the explicitly moving solvent, which slows down the effective response time of conformational changes in the solute. This in turn requires a more conservative choice of specific metadynamics parameters (in particular either the amplitude and width of the spawned potential energy hills or the deposition rate). Again, this issue would result in longer simulation times.

When looking at the overall dynamical behavior of the chromophore, again no conformational change can be observed on the computationally accessible timescales. Judging from the dihedral angle distribution, there are no strong changes in the structure of the energy surface. Also the bond lengths suggest no strong changes in the electronic structure.

When analyzing the overall potential energy, however, we see a clear change in lower energies for the closed compared to the open conformation. This behavior can be explained by the formation of intermolecular hydrogen bonds between the chromophore and the surrounding solvent molecules. While the closed conformations in vacuo showed no intramolecular hydrogen bonds during the 75 ps simulation time, we now observe an average of two to four intermolecular bonds to the solvent for the different conformations. In contrast, the open conformation was able to form two to six intramolecular hydrogen bonds in the in vacuo simulation, while in methanol the possible hydrogen bonding sites are blocked by intermolecular hydrogen bonding partners. Thus, in a solvent that forms strong hydrogen bonds, the energetic advantage of the open conformation vanishes.

In a conclusion we can assume a different probability for the open and closed classes of conformations, depending on the polarity of the surrounding solvent molecules. The higher the polarity of the solvent, the more intermolecular hydrogen bonds will counter the energy advantage of intramolecular hydrogen bonds.

3.4 NMR chemical shifts

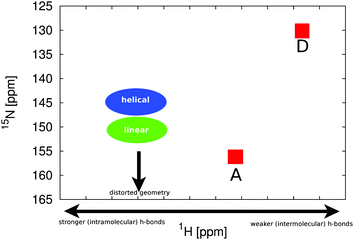
In comparison to the recent NMR chemical shift measurements mentioned in the introduction, we perform ensemble averaged NMR chemical shift calculations on the different low energy conformations obtained from the metadynamics simulations.

In the experiment, a full assignment of PCB NMR chemical shifts in the HMPT solvent has been achieved.²² Additionally, a 2D NMR spectrum of the PCB in methanol has been provided by the group of P. Schmieder. While the spectra show a similar shape and ordering, at the first look contradictory changes can be identified. When taking the actual values of the changes between the two different solvents (see Fig. 5) into account, we see that the A and D rings δN change by 2 ppm, the δH by 0.6 ppm. For the B and C rings, we see changes of δN by 10 ppm and δH by 1.2 ppm. Assuming that the change is mainly induced by hydrogen bonds and exhibits a linear behavior, i.e. upon change in hydrogen bond strength the chemical shift values move on a straight line in the 2D spectrum, an additional change in the δN by around 6 ppm has to be explained.

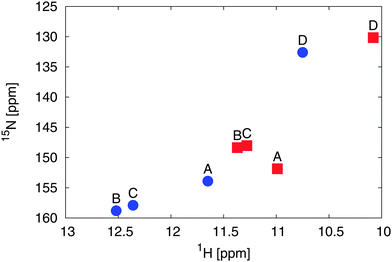Fig. 5 Experimental 2D ¹H and ¹⁵N NMR spectral different solvents: HMPT²² (blue dots) and methanol⁵⁷ (red squares) of the amine groups of rings A to D.

Based again on the most promising conformations taken from our metadynamics calculations, we perform ensemble averaged ¹⁵N as well as ¹H NMR chemical shift calculations (see Table 1). When looking at the ¹⁵N chemical shifts of the outer rings A and D, we can see that the shifts vary only within a range of 5 ppm for all energetically favorable conformations, indicating only a minor distortion in the local electronic structure upon conformational changes. Generally, the chemical shift of ring D is the lowest, A the highest, while those of rings B and C are always within a range of 5–10 ppm to each other. This overall behavior already is in good agreement with experiments not only in solvent but also with previous experiments on the whole protein. Since the experimental nitrogen shifts are similar even for hugely different systems or more specifically different surrounding hydrogen bonding networks, one can suspect the main influence on the nitrogen shifts to be the conformation of the system, while the hydrogens on the other hand are well known to be strongly influenced by hydrogen bonds.

Table 1 ¹H and ¹⁵N NMR chemical shift values for a series of characteristic conformations. ¹H referenced to benchmark calculations of TMS, ¹⁵N referenced to match the PCB D ring in methanol

Conformation	N A	N B	N C	N D	H A	H B	H C	H D
EZZaas	163.8	151.8	160.6	131.1	8.2	10.5	9.6	7.0
EEZsss	163.2	155.8	161.4	131.5	8.1	12.7	9.7	7.6
ZEZass	163.0	150.0	159.7	131.7	8.2	10.1	9.9	7.5
ZZZass	164.1	145.4	149.9	130.4	8.4	9.4	10.6	7.7
EZZsss	164.1	144.4	145.4	129.2	8.0	11.8	10.5	7.6
ZZZasa	162.4	142.9	148.4	139.4	8.4	8.9	9.3	7.7

---

When changing the conformation by moving between the two lowest energy basins of the dihedrals 3 and 4, we see a change in the rings B and C ¹⁵N chemical shifts by approximately 10 ppm. When we look at changes in the chemical shifts induced by rotation around the outer double and singlebonds, we observe a number of small changes in the range of 5 ppm in different directions for the chemical shifts of the central rings B and C (Fig. 6).

Fig. 6 Overview of the different influences on the ¹H and ¹⁵N chemical shifts of PCB. A conformational change in the central dihedral pair of rings B and C causes a change in the positions of the signals of ring B and C as indicated by the green and blue areas. The remaining signals A and D remain stable. Changes in hydrogen bonding strength mainly cause the hydrogen chemical shifts to change.

By a combination of all these possible permutations, a multitude of different within the sampling accuracy not clearly distinguishable distributions of chemical shifts arises. This quite ambiguous result however can be refined by using the previously attained information about the underlying energy surface and considering only the spectra of the energetically most probable conformations, as well as by comparing the large influence of the central dihedrals on the experimental data.

When considering explicit methanol solvent molecules on the same level of theory, we again see the pattern and changes upon change in the conformation known from the in vacuo calculations. The B and C ring nitrogen chemical shifts are in close proximity and move by approximately 10 ppm upon change in the central dihedrals, while the A and D ring positions remain stable. As a result from the hydrogen bonding to the solvent, the hydrogen chemical shifts slightly move downfield. However, on the DFTB level of theory combined with the range cutoff in the NMR calculations, these interactions are weakened, resulting in a lower hydrogen chemcial shift than expected. As the main result we notice that the influence of the surrounding explicit solvent can mainly be seen in the hydrogen chemical shifts, while the nitrogen shifts stay close to the in vacuo results, however, within their usual broad distribution and thus higher possible error from low sampling rates. In no case an influence of the same strength as that of the change in the central dihedral angles on the nitrogen chemical shifts can be observed.

3.5 Effect of hydrogen bonding

To properly include hydrogen bonding effects in the suspected main conformations for the HMPT case, BLYP calculations with VdW correction have been performed. In each of those simulations the system has been prepared in a maximally hydrogen bonded state. Here, the hydrogen bonds of the carboxilic groups of the ring B to the C and D rings and C to the A and B rings remained stable during the simulation. While the experimentally observed spectrum cannot be reproduced by one of those conformations, the influences of the single conformations can be attributed to different parts of the spectrum. Combining all of them finally gives an explanation of the experimentally observed chemical shifts.

A “sufficient” sampling of the dihedral energy surface would require long trajectories in the range of 50 to 100 ps which is not unfeasible with present-day computational resources, but appears unnecessary in view of the required computational cost. On the other hand, examining short trajectories of different hydrogen bonding patterns can also give insights into the resulting spectra and possible origins of the different characteristics for the two solvents.

One low energy conformation is the EEEsss configuration. Here however, for geometric reasons only one stable intramolecular hydrogen bond can be observed. The resulting 2D NMR spectrum shows NH positions similar to the non-hydrogen bonded case with exception of the C ring, that is strongly hydrogen bonded to the B ring carboxyle group. The appearance of a hydrogen bond increases the hydrogen chemical shift to around 13 ppm, while the nitrogen chemical shift moves to approximately 158 ppm.

For the maximally hydrogen bonded ZEZsss conformation, we see a strong change in almost all ring positions in the spectrum. However, with exception of the only weakly hydrogen bonded B ring, the alignment of the chemical shifts is similar to the non-hydrogen bonded case with only the hydrogen chemical shifts moving downfield by approx. 2 ppm. Most importantly, the non- or weakly hydrogen bonded B ring nitrogen chemical shift is strongly shifted downfield. This shows clearly that the position of the nitrogen chemical shift is not induced by the hydrogen bonding, but has instead to be caused by conformational effects and deviation from the energy minima of the dihedral distributions found in the metadynamics simulations.

4 Conclusions

We have quantified the dependence of the conformation of a tetrapyrrole chromophore (phycocyanobilin) on the character of its chemical environment, specifically the solvent type. By means of semiempirical metadynamics simulations, we have sampled the free energy hypersurface of the chromophore, resulting in the identification of the geometric equilibrium structures at ambient temperatures as a function of the solvent. In particular, our simulations show a delicate equilibrium between helical and linear conformations that reacts very sensitively on the solvent characteristics. Based on ab initio molecular dynamics simulations, we have computed the two-dimensional NMR pattern of ¹⁵N and ¹H NMR chemical shifts at the ab initio level of theory.

The experimentally observed solvent shifts exhibit a counterintuitive trend (towards higher ¹H NMR chemical shifts for HMPT which is expected to form fewer hydrogen bonds than methanol). Our ab initio molecular dynamics simulations have resolved this puzzling situation, which could be traced back to stronger intramolecular hydrogen bonding of the chromophore. These hydrogen bonds are broken in methanol due to the better electrostatic screening and the stronger intermolecular interactions with the solvent.

A striking secondary effect of the change in hydrogen bonding pattern is the isomerization of the chromophore which is equally visible in experimental as well as computed chemical shift pattern. This solvent-induced structural transition represents a mechanical switching function on the molecular scale. With a suitable chemical functionalization, this transition might be exploited for applications in the field of molecular sensors, molecular recognition or even externally triggered drug delivery.

Acknowledgements

We would like to gratefully acknowledge financial support from the Deutsche Forschungsgemeinschaft (DFG) within the SFB/TRR 102, as well as computing time provided by the HLRS.

References

1. J. J. V. Thor, K. L. Ronayne and M. Towrie, J. Am. Chem. Soc., 2007, 129, 126–132.
2. K. C. Toh, E. A. Stojkovi, A. B. Rupenyan, I. H. M. V. Stokkum, M. Salumbides, M.-L. Groot, K. Moffat and J. T. M. Kennis, J. Phys. Chem. A, 2010, 115, 3778–3786.
3. L. J. G. W. V. Wilderen, I. P. Clark, M. Towrie and J. J. V. Thor, J. Phys. Chem. B, 2009, 113, 16354–16364.
4. J. J. V. Thor, M. Mackeen, I. Kuprov, R. A. Dwek and M. R. Wormald, Biophys. J., 2006, 91, 1811–1822.
5. S. Kaminski and M. A. Mroginski, J. Phys. Chem. B, 2010, 114, 16677–16686.
6. T. Rohmer, H. Strauss, J. Hughes, H. de Groot, W. Gärtner, P. Schmieder and J. Matysik, J. Phys. Chem. B, 2006, 110, 20580–20585.
7. M. A. Mroginski, F. Mark, W. Thiel and P. Hildebrandt, Biophys. J., 2007, 93, 1885–1894.
8. R. A. Matute, R. Contreras and L. Gonzalez, J. Phys. Chem. B, 2008, 112, 16253–16256.
9. R. A. Matute, R. Contreras and L. Gonzalez, J. Phys. Chem. Lett., 2010, 1, 796–801.
10. J. Wan, X. Xu, Y. Ren and G. Yang, J. Phys. Chem. B, 2005, 109, 11088–11090.
11. C. Zazza, N. Sanna and M. Aschi, J. Phys. Chem. B, 2007, 5596–5601.
12. H. Elgabarty, P. Schmieder and D. Sebastiani, Chem. Sci., 2013, 4, 755.
13. U. F. Rohrig and D. Sebastiani, J. Phys. Chem. B, 2008, 112, 1267–1274.
14. J. Schmidt, A. Hoffmann, H. W. Spiess and D. Sebastiani, J. Phys. Chem. B, 2006, 110, 23204–23210.
15. C. Allolio and D. Sebastiani, Phys. Chem. Chem. Phys., 2011, 13, 16395–16403.
16. D. Banyai, T. Murakhtina and D. Sebastiani, Magn. Reson. Chem., 2010, 48, S56–S60.
17. C. Schiffmann and D. Sebastiani, Phys. Status Solidi B, 2012, 249, 368–375.
18. D. Sebastiani and M. Parrinello, ChemPhysChem, 2002, 3, 675.
19. C. Allolio, M. Sajadi, N. P. Ernsting and D. Sebastiani, Angew. Chem., Int. Ed., 2013, 52, 1813–1816.
20. P.-h. Tu, Y.-h. Yao, Y.-l. Li and B. Liu, THEOCHEM, 2009, 894, 9–13.
21. A. H. Göller, D. Strehlow and G. Hermann, ChemPhysChem, 2001, 2, 665–671.
22. M. Röben and P. Schmieder, Magn. Reson. Chem., 2011, 49, 543–548.
23. M. M. Boyle, R. A. Smaldone, A. C. Whalley, M. W. Ambrogio, Y. Y. Botros and J. F. Stoddart, Chem. Sci., 2011, 2, 204–210.
24. C. A. Bortolotti, L. Paltrinieri, S. Monari, A. Ranieri, M. Borsari, G. Battistuzzi and M. Sola, Chem. Sci., 2012, 3, 807–810.
25. J. M. Spruell and C. J. Hawker, Chem. Sci., 2011, 2, 18–26.
26. K. Xu, M. Qiang, W. Gao, R. Su, N. Li, Y. Gao, Y. Xie, F. Kong and B. Tang, Chem. Sci., 2013, 4, 1079–1086.
27. A. Laio and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12562–12566.
28. A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 1–4.
29. G. Seifert, J. Phys. Chem. A, 2007, 111, 5609–5613.
30. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
31. M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268.
32. S. Nosé, Mol. Phys., 1984, 5, 255.
33. J. V. Vondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
34. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098.
35. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
36. S. Grimme and M. Parac, ChemPhysChem, 2003, 3, 292–295.
37. T. Laino, F. Mohamed, A. Laio and M. Parrinello, J. Chem. Theory Comput., 2005, 1, 1176–1184.
38. F. Neese, ORCA – an ab initio, Density Functional and Semiempirical program package version 2.7.0, University of Bonn, 2009.
39. W. Kutzelnigg, Isr. J. Chem., 1980, 19, 193.
40. J. Perdew, K. Burke and M. Ernzerhof, J. Phys. Chem., 1996, 105, 9982–9985.
41. W. Kutzelnigg, U. Fleischer and M. Schindler, NMR: Basic Princ. Prog., 1990, 23, 165.
42. U. H. Hansmann, Chem. Phys. Lett., 1997, 281, 140–150.
43. P. G. Bolhuis, D. Chandler, C. Dellago and P. L. Geissler, Annu. Rev. Phys. Chem., 2002, 53, 291–318.
44. M. Christen and W. F. van Gunsteren, J. Comput. Chem., 2008, 29, 157–166.
45. R. Gehrke and K. Reuter, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 085412(10).
46. C. Grebner, J. Becker, S. Stepanenko and B. Engels, J. Comput. Chem., 2011, 32, 2245–2253.
47. D. J. Wales and H. A. Scheraga, Science, 1999, 285, 1368–1372.
48. S. Goedecker, J. Chem. Phys., 2004, 120, 9911–9917.
49. M. Sicher, S. Mohr and S. Goedecker, J. Chem. Phys., 2011, 134, 044106.
50. S. Stepanenko and B. Engels, J. Comput. Chem., 2008, 29, 768–780.
51. S. Stepanenko and B. Engels, J. Phys. Chem. A, 2009, 113, 11699–11705.
52. D. Karaboga, B. Gorkemli, C. Ozturk and N. Karaboga, Artif. Intell. Rev., 2012, 1–37.
53. W. Gao and S. Liu, Comput. Oper. Res., 2012, 39, 687–697.
54. C. Schiffmann and D. Sebastiani, J. Chem. Theory Comput., 2011, 7, 1307–1315.
55. S. E. Schönborn, S. Goedecker, S. Roy and A. R. Oganov, J. Chem. Phys., 2009, 130, 144108.
56. Z. E. Brain and M. A. Addicoat, J. Chem. Phys., 2011, 135, 174106.
57. M. Röben, NMR-spektroskopische Untersuchungen des an Cph1-, Agp1-gebundenen und des freien Chromophors zur Aufklärung des Phytochrom Photozyklus, PhD thesis, 2011.

---