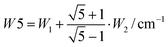Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The Raman spectrum of isolated water clusters†
Katharina E.
Otto
,
Zhifeng
Xue
,
Philipp
Zielke
and
Martin A.
Suhm
*
Institut für Physikalische Chemie, Georg-August-Universität Göttingen, Tammannstraße 6, 37077 Göttingen, Germany. E-mail: msuhm@gwdg.de; Fax: +49 551 3933117; Tel: +49 551 3933112
First published on 7th January 2014
Abstract
Cold water oligomers (H2O)n and (D2O)n with n = 2–5 are assigned in spontaneous Raman scattering spectra of seeded rare gas expansions for the first time. Comparison with infrared spectra provides direct experimental insights into the hydrogen bond-mediated excitonic OH oscillator coupling, which is responsible for ultrafast energy transfer between water molecules, usually suppressed by isotopic dilution in femtosecond experiments for the condensed phase. The experimental coupling constants are compared to those in state-of-the-art full-dimensional water potential energy hypersurfaces, leaving room for improvement in the description of the coupled dynamics in water. Evidence for intensified Fermi resonance between OH stretching and OH bending motion beyond water trimers is collected.
1 Introduction
The vibrational dynamics of water is of fundamental interest.1 It is mediated by a network of intermolecular hydrogen bonds, which can be introduced step by step in the popular cluster approach.2,3 While matrix isolation4,5 and chromophore labeling6,7 have proven useful in this context, the study of unperturbed, isolated water clusters is particularly attractive due to the close contact with theory8 and the large amplitude motion in these systems. Direct infrared2,9–11 and microwave12 studies have become available in recent years and have provided detailed information on nuclear quantum effects and electronic cooperativity, in particular when combined with theoretical predictions. Although the Raman selection rules provide essential complementary information on concerted motions, only a pioneering coherent anti-Stokes Raman spectroscopy (CARS) investigation of isolated water clusters has so far been published13 and discussed controversially.14,15 The nonlinearity of the CARS experiment rendered a firm assignment of cluster sizes difficult. Therefore, the characteristic coupling between neighboring OH oscillators in water assemblies, which controls energy flow after local excitation, has remained largely in the dark.This is where the present contribution sets in. By generating isolated, internally cold, small water clusters in slit jet expansions of an atomic carrier gas into vacuum and probing them by an intense visible laser, sufficient numbers of spontaneously Raman-scattered photons are generated to detect OH stretching modes which show negligible infrared intensity and have thus remained unassigned in the gas phase to date. The strong hydrogen bond cooperativity ensures a sufficient spread of the signals on the wavenumber axis for a reliable cluster size separation and size assignment based on stagnation pressure, nozzle temperature, polarization dependence16 and water concentration dependence up to at least five water units. Further support for the vibrational and size assignment comes from equivalent experiments with D2O. This compensates for the lack of rigorous size selection.3,17 The combination with corresponding IR data10,18 then leads to an effective approach to the oscillator coupling within a simple framework of Hückel-like coupling matrices,7 as exemplified in the case of cyclic methanol clusters.19 The energy splitting of the degenerate monomer oscillators into symmetric and asymmetric linear combinations in a cyclic cluster is caused by coupling through space or through the connecting hydrogen bonds.
These coupled modes are observable as a mode pattern in the frequency domain,20 but their importance is better visualized in the time domain. Excitation of a local OH stretching mode by a suitable ultrashort laser pulse would lead to a rapid delocalization of the excitation energy among the coupled oscillators as a function of time. In a finite cluster and in the absence of other redistribution mechanisms, this is a periodic process which ultimately leads to a refocussing of the energy in the original oscillator. In liquid or solid water, the energy is dissipated irreversibly. Although the detailed quantum dynamics can be complex, there is a reciprocal relationship between the magnitude of the excitonic splitting and the lifetime of the localized state. The larger the spectral splitting, the faster the energy dissipation. Therefore, the size of the coupling constant between OH stretching modes in a water cluster is of prime importance for the femtosecond dynamics of these high frequency oscillators.16,21,22 Because the ultrafast exciton dynamics among degenerate oscillators leads to rapid anisotropy decay, most femtosecond experiments and simulations on liquid water are carried out in isotopic dilution to focus on slower processes.1,23,24 In liquid water, the effective excitonic coupling constant has been estimated25 to be around 12 cm−1. In cold ring-like clusters, it is modelled to be of the same order of magnitude for the bonded OH stretch mode.26 This is significantly smaller than in the related alcohol clusters19 (20–30 cm−1), which feature the same hydrogen bonded ring topology.27 We will argue in this contribution that the experimental coupling constants in ring-like water clusters are indeed larger than analytically modelled and more in line with those observed in methanol clusters. The associated concerted stretching modes of water ring clusters are particularly interesting and important because they represent a low energy window of the potential energy hypersurface where water molecules lose their integrity and start to undergo isotope exchange.28 These modes are also predicted to have exceptionally fast IVR rates.29
One important aspect has to be considered in the OH stretch coupling of small water clusters. In isolated water molecules, the OH bending overtone is located more than 500 cm−1 below the symmetric stretching fundamental30 but it comes into resonance for cooperatively weakened OH bonds. As we will argue based on Raman spectroscopic evidence, this hydrogen bond-tuned Fermi resonance becomes increasingly important when moving from the trimer to the pentamer, opening up another energy flow channel in particular for symmetric and thus Raman-active excitation. The corresponding normal modes are visualized for the pentamer case in Fig. 1.
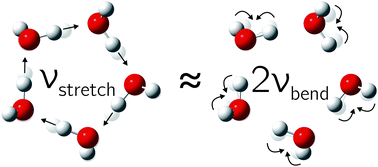 | ||
| Fig. 1 The in-phase hydrogen-bonded OH stretching fundamental is closely resonant with the overtone of the highest frequency bending mode in the water pentamer (and less so in the tetramer). | ||
While the focus of this contribution is on cyclic trimers, tetramers and pentamers with their low microwave visibility12 but well-characterized low-frequency dynamics,2,31 we also present the first Raman spectra for isolated water dimers, for which some transitions have previously been observed in He nanodroplets.32 Finally, we provide circumstantial evidence for the topologically versatile hexamer.2,12,33–36
After a brief description of the experimental setup, the spontaneous Raman spectra will be presented and assigned. The discussion of excitonic patterns in the cyclic clusters will start with the most clearcut tetramer case and extend to the trimer and pentamer, followed by preliminary assignments of non-cyclic hexamer bands.
2 Experimental setup
Gas mixtures of water with He, Ne/He or Ar/He were expanded via a 4 × 0.15 mm2 or 8 × 0.05 mm2 heatable slit nozzle into an aluminium chamber, pumped using two Roots pumps (500 m3 h−1 and 250 m3 h−1) and one rotary vane pump (100 m3 h−1). The beam of a frequency doubled cw NdYVO4-Laser (Coherent Verdi V18, 18 W, λ = 532 nm) was focused onto the expansion at 2 mm distance from the nozzle exit. The scattered light was collected perpendicular to the expansion and to the incident laser beam and collimated using a fast camera lens (50 mm Nikon, f/1.2). It was then focused onto the entrance slit of the monochromator (McPherson Model 2051 f/8.6, f = 1000 mm, grating 1200 grooves per mm or McPherson Model 205f f/3.2, f = 500 mm, grating 600 gr per mm) using an achromatic planoconvex lens (Edmund Optics, ∅ = 50 mm, f/7 for McPherson Model 2051 and Edmund Optics, ∅ = 50 mm, f/4 for McPherson Model 205f). Suppression of the Rayleigh scattered light was achieved using a Raman edge filter (L.O.T., ∅ = 25 mm, OD 6.0, T > 90%, 535.4–1200 nm). A back-illuminated CCD camera (PI Acton, Spec-10: 400 B/LN, 1340 × 400 pixels, cooled by liquid N2) served for detection in a vertical binning mode.19 Count rates refer to the full 400-pixel columns. The wavelength calibration of the spectra was carried out using the lines of a Ne I emission light source and H2O monomer Raman transitions.30,37 Cosmic ray signals were removed by the comparison of block-averaged spectra. Polarization experiments were performed by rotating the laser beam via a λ/2-plate.The Stokes scattering was probed from 80 to 8000 cm−1, but here we concentrate on the by far strongest38 Raman cluster signals between 3000 and 4000 cm−1, in the region of the OH stretching fundamentals and the OH bending overtones.
3 Results and discussion
3.1 Spectral survey
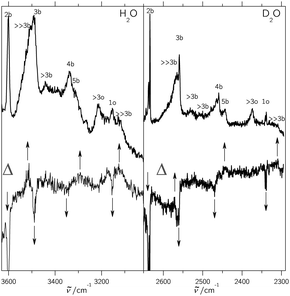
In supersonic jet expansions, different molecular degrees of freedom may have different effective temperatures or even non-thermal distributions. We obtained monomer rotational temperatures of 30–50 K based on the relative intensities of Stokes and anti-Stokes transitions (see ESI† for details). These are in qualitative agreement with recent results for cluster-free expansions of water in helium, considering the large differences in expansion conditions.37 Vibrational temperatures are probably higher and lead to relatively broad band contours with occasional hot band features, marked with * in the following spectra. The temperatures can be lowered by variation of the stagnation conditions and carrier gas.Fig. 2 and 3 contain a collection of Raman supersonic jet spectra for H2O and D2O expansions in different carrier gases and under varying conditions (described in detail in the ESI†). Their spectral windows have been matched by D2O wavenumber axis stretching (×1.508) and monomer symmetric stretch band center alignment. The correspondence between the isotopologues is indeed very close. Studies of the carrier gas dependence and of the depolarization ratio are provided in the ESI.†Table 1 provides peak positions and explains the labels of the Raman spectral features. Also shown in the upper right traces and in Table 1 are corresponding FTIR supersonic jet spectra,10 which agree with earlier laser spectroscopy observations.18,39
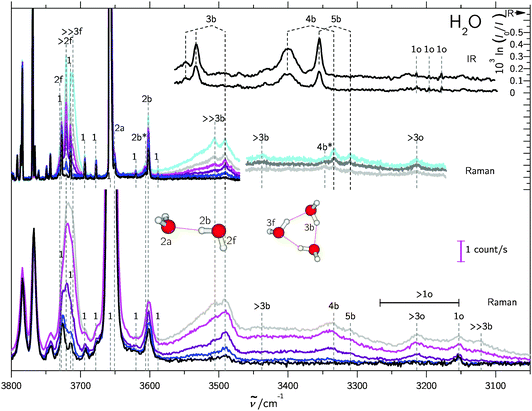 | ||
| Fig. 2 Raman and IR10 spectra of mixed H2O/rare gas expansions. Raman spectra were scaled to the same monomer scattering intensity at the point of measurement in the respective blocks. The labels are defined in the text and in Table 1. Detailed information on the measurement conditions, such as nozzle temperature ϑn, saturator temperature ϑs and stagnation pressure ps can be found in Table SI in the ESI.† Lower part: Raman spectra recorded using a 0.5 m monochromator. Basically, the clustering extent increases from bottom to top. Upper part: similar conditions but recorded using a 1 m monochromator. Again, the clustering extent increases from bottom to top. | ||
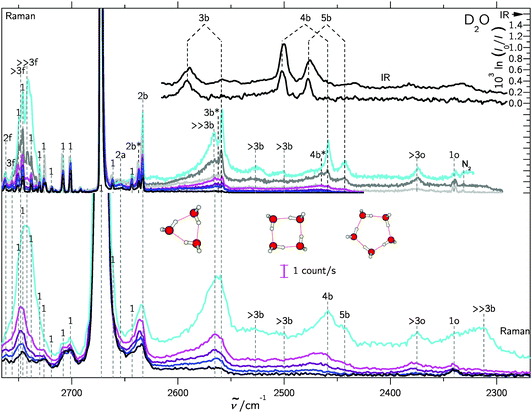 | ||
| Fig. 3 Like Fig. 2, but for D2O/rare gas expansions, also showing trimer to pentamer structures. For detailed information see Table SII in the ESI.† | ||
| Peak position/cm−1 | Assignment | |
|---|---|---|
| H2O | D2O | |
| 3730 | 2762 | 2f |
| 3721 | — | >2f |
| — | 2756 | 3f |
| — | 2748 | >3f |
| 3711 | 2742 | ≫3f |
| 3657 | 2672 | 1 |
| 3651 | 2654 | 2a |
| 3606 | 2637 | 2b* |
| 3602 | 2633 | 2b |
| 3548 | — | 3b(IR-w) |
| 3533 | 2591 | 3b(IR) |
| 3506 | 2566 | ≫3b |
| — | 2562 | 3b* |
| 3491 | 2559 | 3b |
| 3438 | 2527 | >3b(4b?) |
| 3401 | 2502 | 4b(IR) |
| — | 2500 | >3b(5b?) |
| 3355 | 2477 | 5b(IR) |
| 3347 | 2465 | 4b* |
| 3334 | 2459 | 4b |
| 3310 | 2443 | 5b |
| 3214 | 2375 | >3o |
| 3215 | — | 1o(IR) (212) ← (101) |
| 3196 | — | 1o(IR) (111) ← (000) |
| 3178 | — | 1o(IR) (110) ← (101) |
| 3153 | 2340 | 1o(n0n) ← (n0n) |
| 3121 | 2312 | ≫3b |
The high degree of complementarity for trimers (3b), tetramers (4b) and pentamers (5b) is a consequence of their ring topology. The Raman spectra are dominated by the sharp symmetric OH stretching transitions of the monomer, some of which are labeled (1). Between the symmetric and antisymmetric water monomer bands, a structured scattering signal from dangling (free) OH groups is found. Contributions from dimers (2f), trimers (3f, >2f), larger (>3f) and significantly larger (≫3f) clusters can be partially separated, but their discussion will be postponed. They are also summarized in Table 1 for both light and heavy water.
A general feature of the warmer Raman spectra is the asymmetric slope of the hydrogen-bonded stretching bands due to thermal excitation. This reflects the sensitivity of the OH stretching wavenumber to the strength of the hydrogen bond, so important in fs bulk water experiments1 and in the room temperature detection of water clusters.40,41 The colder spectra using heavier carrier gases (see ESI†) are substantially more narrow, but show larger contributions from clusters with a hydrogen bond network (n > 5), which are beyond the safe size resolution of our Raman technique.
In the following, we therefore concentrate on the cyclic trimer, tetramer and pentamer Raman features and their interpretation in terms of intermolecular and intramolecular couplings.
3.2 Water tetramer
The cyclic tetramer is particularly well suited for an analysis of the OH coupling patterns derived from the combined IR and Raman spectra19 because it has four equivalent hydrogen bonds arranged on the sides of a square. Each OH group has the same zeroth order wavenumber and couples directly to its hydrogen bond acceptor partner and either along two hydrogen bonds or across the diagonal to its next-nearest neighbor. The direct coupling is described by W1 and the weaker diagonal coupling by W2. A Hückel-like analysis19 of the combined action of all couplings leads to the determinant equation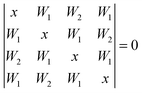 | (1) |
| x1 = −2W1 − W2 (A) |
| x2,3 = W2 (E) |
| x4 = 2W1 − W2 (B) | (2) |
The symmetry labels A, E, B derive from the S4 point group. The degenerate pair of E transitions, which is predominantly IR-active, is thus separated by W2 from the center of the coupling pattern, whereas the predominantly Raman-active A transition is below the center, by 2W1 + W2. This A level was recently predicted to have an intracluster energy redistribution rate of 0.4 ps.29 The observed width of the Raman transition of 10 cm−1 is qualitatively still compatible with this rate in the limit of a dense manifold of coupling states, but actually more narrow than the corresponding IR mode. The B-transition is expected to have a weak intensity in both types of spectra. The splitting between the IR-active and dominant Raman active bands (E/A) is thus 2W1 + 2W2. Between the weaker Raman-active and the IR-active bands (B/E) it is 2W1 − 2W2, and between the two Raman active bands (B/A) 4W1. As the assignment of the second Raman active band is less certain, we define a composite coupling constant W4 = W1 + W2 which only depends on the strong Raman and IR transitions (corresponding to one half of the E/A separation) and allows for a safer comparison between theory and experiment. The experimental error of W4 may be conservatively estimated to be around ±2 cm−1 as one half of the sum of the Raman calibration error of ±1 cm−1 and possible differences between band centers and band maxima in the IR and Raman spectra of up to 3 cm−1, which should however largely cancel in the spectral difference.
Depending on the spectral assignments, there are three different ways to analyze the coupling multiplet in the water tetramer. If one neglects couplings beyond the nearest neighbors (W2), the direct coupling constant based on the most active A-symmetric (Raman) and E-symmetric (IR) vibrations is W4 ≈ W1 = 34 cm−1, which is to be compared to 12–13 cm−1 from the most recent and otherwise fairly accurate analytical potential hypersurface.42 One could argue that the discrepancy stems from the neglect of next-nearest neighbor coupling. Indeed, inclusion of the weakly Raman-active B-transition at 3438 cm−1 reduces the experimental nearest-neighbor coupling to W1 = 26 cm−1 by compensating with a distant coupling term across the ring of W2 = 8 cm−1. This does not improve the agreement with theory, because such a second-nearest neighbor interaction is essentially absent from the most recent analytical potential energy hypersurfaces. In contrast, even simple harmonic ab initio calculations yield largely correct orders of magnitude, also in line with experiments for methanol tetramers.19 If one does not want to rely on the less certain position of the B-band, one evaluates the sum W1 + W2, defined above as the B-invariant tetramer coupling W4, which corresponds to one half of the IR/Raman band splitting. It is equivalent to W1 only if the diagonal coupling W2 is negligible. Table 2 summarizes the experimental findings for the different assumptions and isotopologues and compares them to the methanol findings. Dependent on the isotopic composition and analysis method, the methanol coupling is seen to be 10–60% larger than the water coupling, in line with qualitative expectations on the strength of the hydrogen bond and susceptible to some perturbations in the CH3OD case.19 Upon deuteration, the coupling constants shrink by 30–40%, as in methanol.19
| Method | Variant | Electronic structure | W 1/cm−1 | W 2/cm−1 | (W1 + W2)/cm−1 |
|---|---|---|---|---|---|
| Harmonic43 | B3LYP/d-aug-cc-pVTZ | 32 | 13 | 45 | |
| Harmonic44 | BSSE-corrected | MP2/6-311+G(2d,2p) | 25 | 10 | 35 |
| Vibrational CI44 | BSSE-corrected | MP2/6-311+G(2d,2p) | 21 | 11 | 32 |
| Vibrational CI44 | With BSSE | MP2/6-311+G(2d,2p) | 52 | 30 | 82 |
| Harmonic42 | CCSD(T)/aug-cc-pVDZ | 28 | 12 | 40 | |
| Harmonic42 | LCCSD(T)/aug-cc-pVDZ | 20 | 7 | 26 | |
| Harmonic42 | LCCSD(T)/aug-cc-pVTZ | 23 | 9 | 32 | |
| Harmonic42 | No 4-body terms | PES(1,2,3) | 13 | 5 | 18 |
| Harmonic26 | Full-dimensional | WHBB-surface | 13 | 1 | 13 |
| Harmonic26 | LMon-βfull | WHBB-surface | 13 | 0 | 13 |
| Anharmonic26 | LMon-βfull | WHBB-surface | 12 | 0 | 12 |
| Anharmonic45 | MP2 VPT2 est. | CCSD(T)/aug-cc-pVDZ | 21 | 7 | 28 |
| Experiment H2O | IR + Raman | Non-Born–Oppenheimer | 26 | 8 | 34 |
| Experiment D2O | IR + Raman | Non-Born–Oppenheimer | 17 | 5 | 22 |
| Experiment CH3OH19 | IR + Raman | Non-Born–Oppenheimer | 29 | 11 | 40 |
| Experiment CH3OD19 | IR + Raman | Non-Born–Oppenheimer | 23 | ≈8 | ≈31 |
In view of the involved simplifications, the agreement between experiment and harmonic ab initio calculations is remarkably good for the (H2O)4 coupling constants. While the B3LYP calculations43 somewhat overestimate the coupling, available BSSE-corrected MP2 and higher level electron correlation treatments42,46 agree with experiment within the uncertainties of the latter and vibrational CI treatment does not change the values substantially.46 This contrasts with the performance of analytical potential energy surfaces derived from these highly correlated calculations,26,42 independent of whether the latter include higher than three-body terms and whether they are evaluated harmonically or within anharmonic approximations.26 Clearly, the OH mode coupling in the most accurate analytical water potentials is underestimated, possibly at the level of specific coupling terms in the analytical many-body expansion.
We emphasize that the experimental data are quite robust, at least concerning W4, which only relies on the dominant transitions of each spectroscopic technique. It appears that coupling among the OH oscillators, and thus resonant energy flow along the OH stretching modes, is underestimated by at least a factor of two in the most accurate analytical fits. Since the multidimensional fits are truly challenging and the investigated quantity is relatively subtle, this is not an unexpected performance, but the present experiments for the first time provide solid evidence and incentive to improve the flexibility of this particular coordinate coupling. However, in order to exclude a coincidental mismatch, it is necessary to turn to the more difficult trimer case.
3.3 Water trimer
For the cyclic trimer (ref. 4 and 47 and references cited therein) one has to distinguish between a C3 symmetric aggregate (simple Hückel model) where coupling constants between the three oscillators are equal and an asymmetric coupling case where the H-bonds differ in strength.19 For the first case the solutions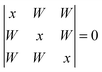 | (3) |
| x1 = −2W1 (A) |
| x2,3 = W (E) | (4) |
Therefore the coupling constant W corresponds to the splitting between the Raman and IR active levels divided by 3.
In the latter case one obtains two different coupling constants W1, W2 and the determinant equation
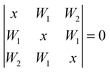 | (5) |
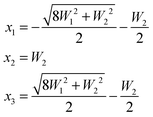 | (6) |
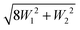 and the inner level is separated from the center of the multiplet by W2.
and the inner level is separated from the center of the multiplet by W2.
The experimental infrared OH stretching spectrum of the water trimer has been studied in different environments.4,10,33,48,49 It consists of a main band and a satellite, which is often, but not always located at higher frequency. Upon deuteration, this satellite peak disappears, hinting at a possible tunneling origin. Fig. S8 in the ESI† discusses the phenomenological situation in comparison to the tetramer. Comparison between experiment and theory depends on whether one interprets the weak satellite in the IR as one of the near-degenerate OH stretching modes or not. The maximum spread of the OH stretching modes is either 57 cm−1 or else ≈42 cm−1. A more likely value is in between, if one interprets the center of gravity of the two IR bands as the proper reference. On the theoretical side, two fit variants of the three body potential yield a spread of the bound OH stretching modes of 50 vs. 29 cm−1 for the water trimer.50 Matrix isolation IR studies4 find a large sensitivity of the trimer stretching spectra and their intensities to the environment. The Ne matrix isolation value for the exciton splitting5 of 57 cm−1 is consistent with our gas phase findings, in particular considering actual matrix-shifts of 15–19 cm−1 in this case.
The non-equivalence of the three hydrogen bonds in the trimer can be included in the analysis and adds further to the uncertainty. In Table 3, we list the experimentally derived trimer coupling constants according to the symmetric (W = W3) and the asymmetric models (W1, W2). For the regular hydrogen isotope, we distinguish between the interpretation of the main IR peak as the quasidegenerate E band (case 3A) and the interpretation of both observed peaks as the components of the E band despite their different intensities and large splitting (less likely case 3B). Despite the assignment uncertainty, one can see that the W coupling constants show the expected trend with deuteration (decrease) and methyl group substitution (increase), as in the case of the tetramer. When comparing to theory, we always interpret the (now equally intense and more closely spaced) IR doublet in the sense of model 3B, when extracting a symmetric coupling constant W. The performance of harmonically predicted coupling constants is again remarkable, quite independent of the level of computation, as Table 3 shows. The coupling pattern appears to be rather robust, as expected for a transition dipole or hydrogen bond mediated interaction. This is also the case for one of the analytical WHBB (Wang/Huang/Braams/Bowman) fits to the high level ab initio data, namely the variant 3b6 for the three body contribution.50 On the other hand, the 3b5 fit only recovers about half of the coupling. As this parametrization appears to have been used for the tetramer predictions,26,51 this may contribute to the discrepancies discussed in the previous section.
| Method | Variant | Electronic structure | W/cm−1 | W 1/cm−1 | W 2/cm−1 |
|---|---|---|---|---|---|
| Harmonic44 | BSSE-corrected | MP2/6-311+G(2d,2p) | 17 | 19 | 13 |
| Vibrational CI44 | BSSE-corrected | MP2/6-311+G(2d,2p) | 19 | 21 | 16 |
| Vibrational CI44 | With BSSE | MP2/6-311+G(2d,2p) | 24 | 26 | 20 |
| Harmonic42 | PES(1,2,3) | 11 | 13 | 7 | |
| Harmonic42 | CCSD(T)/aug-cc-pVTZ | 20 | 22 | 16 | |
| Harmonic42 | CP-CCSD(T)/aug-cc-pVTZ | 18 | 20 | 14 | |
| Harmonic42 | LCCSD(T)/aug-cc-pVTZ | 15 | 16 | 11 | |
| Harmonic50 | LCCSD(T)/aug-cc-pVQZ | 21 | 23 | 17 | |
| Harmonic50 | 3b5 fit | WHBB-surface | 8 | 10 | 4 |
| Harmonic50 | 3b6 fit | WHBB-surface | 15 | 17 | 10 |
| Harmonic45 | CCSD(T)/aug-cc-pVDZ | 18 | 20 | 15 | |
| Anharmonic45 | MP2 VPT2 est. | CCSD(T)/aug-cc-pVDZ | 15 | 17 | 9 |
| Experiment H2O (3A) | IR + Raman | Non-Born–Oppenheimer | 14 | 14 | 14 |
| Experiment H2O (3B) | IR + Raman | Non-Born–Oppenheimer | 17 | 20 | 9 |
| Experiment D2O | IR + Raman | Non-Born–Oppenheimer | 11 | 11 | 11 |
| Experiment CH3OH19 | IR + Raman | Non-Born–Oppenheimer | 20 | 21 | 17 |
| Experiment CH3OD19 | IR + Raman | Non-Born–Oppenheimer | 13 | 14 | 11 |
3.4 Tentative pentamer analysis
For the cyclic water pentamer, the absence of symmetry52 complicates the coupling analysis and several assumptions are necessary to analyze the experimental coupling pattern. We assume an averaged effective C5h symmetry, instead of the puckered non-planar ring. Based on simple connectivity considerations, the nearest and next-nearest neighbor excitonic splittings are determined from the following equation: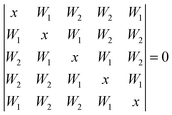 | (7) |
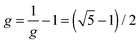 as the golden ratio):
as the golden ratio):| x1 = −2W1 − W2 (A′) |
| x2,3 = −gW1 + W2/g (E1′) |
| x4,5 = W1/g − gW2 (E2′) | (8) |
The splitting between the dominant IR band (E1′) and the dominant Raman band (A′) is thus (2 − g)W1 + (3 + g)W2, whereas the splitting between the two Raman active bands is (3 + g)W1 + (2 − g)W2. In a puckered ring, the degenerate states will be further split by a small amount. Because the highest frequency transition is not predicted to be strong in either IR or Raman spectra, it is desirable to have a linear combination of coupling constants W5 which does not depend on its assignment. This is given by 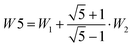 which we therefore use as a robust measure for pentameric exciton coupling. As in the case of W4, W5 corresponds to the nearest neighbor coupling W1 if more distant couplings are neglected. The experimental error in W5 is less than ±3 cm−1, if we assume a conservative error in the IR/Raman-splitting of 4 cm−1.
which we therefore use as a robust measure for pentameric exciton coupling. As in the case of W4, W5 corresponds to the nearest neighbor coupling W1 if more distant couplings are neglected. The experimental error in W5 is less than ±3 cm−1, if we assume a conservative error in the IR/Raman-splitting of 4 cm−1.
Turning now to the experimental spectra, the dominant IR/Raman water pentamer signals (Fig. 2 and 3) are closer together than the tetramer peaks, despite a reduced ring strain and enhanced cooperativity in the cyclic hydrogen bond pattern. Only the deuterated water spectra offer an assignment of all three bands, if the band at 2500 cm−1 marked >3b is tentatively interpreted as the transition to E2′. One then obtains W1 = 14 cm−1 and W2 = 4 cm−1, which may be compared with the corresponding tetramer values of 17 and 5 cm−1, respectively. The coupling parameter W5, which only depends on the strong IR and Raman features, is also systematically smaller than for the theoretical harmonic predictions, even at levels that were shown to be quite successful for tetramers and trimers (see Table 4). We think that the explanation is of an anharmonic nature. For this, the region around 3200 cm−1 (2400 cm−1 for D2O) must be addressed.34 Blue-shifted to the Raman transitions of the first monomer OH bending overtone (1o), there is a polarized signal (>3o) near 3214 cm−1 which has an intensity evolution typical for a mix of ring tetramers and pentamers. This is illustrated in Fig. 4. Its IR counterparts are weak and somewhat shifted (see Fig. 2 and 3),39 supporting a dominant ring cluster contribution. In Ne matrices, a blue-shifted53 trimer bending overtone has been reported5 at 3190 cm−1. Normally, one would expect much less Raman intensity for such a cluster transition, due to the dominance of monomers in the expansions. Furthermore, a coincidence of tetramer and pentamer signals is unlikely in an unperturbed picture.43 The progressively smaller energy gap between the OH stretching fundamentals (4b, 5b) and the OH bending overtone (>3o) explains both anomalies by an increasing extent of Fermi resonance between the two states (see Fig. 1), relative to the trimer. The pentamer may have a somewhat higher bending overtone visibility and experience a reduced overtone frequency due to this anharmonic interaction. That is particularly true for the highest frequency concerted bending modes, which are expected to couple most to the Raman active concerted OH stretching modes (Fig. 1).
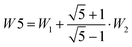 in the last column does not depend on the uncertain assignment of the weakly Raman active transition E2′ and is therefore most reliable
in the last column does not depend on the uncertain assignment of the weakly Raman active transition E2′ and is therefore most reliable
| Method | Variant | Electronic structure | W 1/cm−1 | W 2/cm−1 | |
|---|---|---|---|---|---|
| Harmonic52 | MP2/aug-cc-pVDZ | 35 | 9 | 58 | |
| Harmonic43 | Scaled | B3LYP/d-aug-cc-pVDZ | 34 | 10 | 60 |
| Harmonic44 | BSSE-corrected | MP2/6-311+G(2d,2p) | 26 | 7 | 45 |
| Vibrational CI44 | BSSE-corrected | MP2/6-311+G(2d,2p) | 26 | 6 | 42 |
| Vibrational CI44 | With BSSE | MP2/6-311+G(2d,2p) | 43 | 34 | 133 |
| Harmonic26 | Full-dimensional | WHBB | 14 | 0 | 13 |
| Harmonic26 | LMon-βdimer | WHBB | 14 | 0 | 14 |
| Anharmonic26 | LMon-βdimer | WHBB | 15 | 0 | 14 |
| Harmonic45 | CCSD(T)/aug-cc-pVDZ | 30 | 9 | 53 | |
| Anharmonic45 | MP2 VPT2 est. | CCSD(T)/aug-cc-pVDZ | 36 | 21 | 90 |
| Experiment H2O | IR + Raman | Non-Born–Oppenheimer | — | — | 33 |
| Harmonic52 D2O | MP2/aug-cc-pVDZ | 24 | 8 | 44 | |
| Experiment D2O | IR + Raman | Non-Born–Oppenheimer | 14 | 4 | 25 |
As a consequence, the latter are shifted to higher frequency, more so in the pentamer than in the tetramer. Indeed, simple model calculations show that the energy coincidence is close in the pentamer. This is illustrated in Table 5, which uses published density functional data43 to predict the energy coincidence between the experimental stretching fundamental nb and the anharmonic bend overtones. The latter are estimated from the experimental monomer bend overtone and the calculated complexation shift in the fundamental region. Fermi resonance is more likely if the depolarization ratio is low (like in the lowest frequency OH stretching fundamental) and the gap Δ(b − o) is small. One can conclude that the Raman active pentamer vibration 5b is most likely to undergo strong Fermi resonance with a bending overtone 5o. The two highest frequency bending modes indeed have the smallest depolarization ratios and the smallest gaps. This explains the apparently small pentamer OH stretch excitonic coupling in a qualitative way. We estimate 20–50 cm−1 for the order of magnitude of the Fermi resonance coupling parameter (smaller in the D2O case), but the multidimensional nature of the coupling precludes a firm experimentally derived statement. The close vicinity of the bending overtone is also responsible for the short predicted energy redistribution lifetime29 for the tetramer after Raman-active OH stretch excitation. As has been pointed out before,35 inclusion of such anharmonic interactions is crucial for a correct modeling and the present experimental data can provide valuable constraints. While there are numerous vibrational predictions for water clusters in the literature, few of them include Raman intensities43 or anharmonic effects.35 It is hoped that anharmonic calculations including Raman intensities will be carried out in the future to compare more accurately with the present experimental spectra.
| Cluster size | B3LYP/d-aug-cc-pVDZ43 | ||
|---|---|---|---|
| ω bend n /cm−1 | ρ | Δ(b − o)/cm−1 | |
| 1 | 1622 | 0.68 | 504 |
| 3 | 1658 | 0.39 | 266 |
| 1634 | 0.64 | 314 | |
| 1631 | 0.75 | 320 | |
| 4 | 1681 | 0.25 | 63 |
| 1651 | 0.75 | 123 | |
| 1636 | 0.75 | 153 | |
| 5 | 1689 | 0.17 | 23 |
| 1681 | 0.05 | 39 | |
| 1660 | 0.74 | 81 | |
| 1652 | 0.62 | 97 | |
| 1640 | 0.73 | 121 | |
3.5 Water hexamer
For the water hexamer, our Raman spectra provide polarized band evidence above 3100 cm−1 and 3500 cm−1 (≫3b, see also Fig. 4), but the lack of size-selectivity54 does not allow for an unambiguous assignment. A ring structure can be excluded based on the comparison with He droplet spectra33 and a dominant book isomer based on theoretical predictions.35 The stable prism and cage structures12 are both reasonably consistent with our Raman spectra43 with a strong signal above 3100 cm−1 (2300 cm−1 for D2O) and a second pile-up of Raman intensity around the trimer band. Weaker Raman signals predicted between the dominant trimer and tetramer bands are consistent with our spectra, but they overlap with n = 4, 5 bands.4 Conclusions
The first spontaneous Raman scattering spectra of small water clusters offer quantitative insights into the coherent energy hopping of localized OH stretching excitations from one molecule to another, when compared to existing IR spectra. This is related to the non-coincidence effect,55 which can be spectrally resolved in the case of cold clusters.23Table 6 summarizes the robust OH and OD oscillator coupling constants for the water trimer (W3), the tetramer (W4) and the pentamer (W5). The deuteration and methylation19 effects are systematic and expected. The ring size dependence is unusually weak beyond the tetramer, which we explain by the growing importance of stretch-bend Fermi resonance for the symmetric modes. Effects of intra-monomer coupling should be smaller in the case of cyclic water clusters, because the strong hydrogen bonds decouple the free and the bound OH stretching modes quite effectively.| M | W3/cm−1 | W4/cm−1 | W5/cm−1 |
|---|---|---|---|
| H2O | 14–17 | 34 | 33 |
| D2O | 11 | 22 | 25 |
| CH3OH19 | 20 | 40 |
The excitonic coupling constants obtained in this experimental study for cyclic water clusters provide valuable constraints on harmonic,20 anharmonic26,44 and empirical46 models for the vibrational dynamics in hydrogen-bonded systems and water in particular. In a somewhat model-dependent way, they can be interpreted within a time-dependent framework. Already for the trimer, the splittings are consistent with a drop of any local excitation to 1/e within about 0.3 ps.19,27 For tetramers and pentamers, the coherent transfer to neighboring modes will be even faster. In an extended network such as liquid water, this decay becomes irreversible and it qualitatively explains the ultrafast energy flow observed in fs-experiments,22,36,56 even without having to invoke Fermi resonance with the bending overtone and other relaxation channels. The latter mechanisms will follow, in particular for cluster sizes beyond the trimer, and ultimately dissipate the energy into low frequency modes.29 However, the primary step seems to be explainable in a harmonic picture57 of mode couplings and this is consistent with the present obervation that harmonically determined coupling constants agree quite well with experiment up to the tetramer. Water potentials used for the modeling of fs dynamics in water8,26,50 should thus be tested for their ability to predict the IR/Raman splitting observed in water clusters in this work. This hydrogen bond-induced excitonic splitting is a subtle, yet crucial ingredient for multidimensional cluster potential energy surfaces, in particular for the smallest clusters of the most important molecule on earth.
Acknowledgements
This project has been funded by the DFG project Su 121/2. We also thank the Fonds der Chemischen Industrie and the DFG research training group 782 (www.pcgg.de) for support, N. Lüttschwager for developing the heated nozzle setup which was used to vary the cluster concentrations, and S. Montero for valuable early advice on Raman jet spectroscopy.References
- H. J. Bakker and J. L. Skinner, Chem. Rev., 2010, 110, 1498–1517 CrossRef CAS PubMed.
- F. N. Keutsch and R. J. Saykally, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 10533–10540 CrossRef CAS PubMed.
- U. Buck and F. Huisken, Chem. Rev., 2000, 100, 3863–3890 CrossRef CAS PubMed.
- J. Ceponkus, P. Uvdal and B. Nelander, J. Chem. Phys., 2011, 134, 064309 CrossRef CAS PubMed.
- B. Tremblay, B. Madebène, M. Alikhani and J. Perchard, Chem. Phys., 2010, 378, 27–36 CrossRef CAS PubMed.
- C. C. Pradzynski, R. M. Forck, T. Zeuch, P. Slavícek and U. Buck, Science, 2012, 337, 1529–1532 CrossRef CAS PubMed.
- S. Y. Fredericks, J. M. Pedulla, K. D. Jordan and T. S. Zwier, Theor. Chem. Acc., 1997, 96, 51–55 CrossRef CAS.
- G. C. Groenenboom, E. M. Mas, R. Bukowski, K. Szalewicz, P. E. S. Wormer and A. van der Avoird, Phys. Rev. Lett., 2000, 84, 4072–4075 CrossRef CAS.
- L. M. Goss, S. W. Sharpe, T. A. Blake, V. Vaida and J. W. Brault, J. Phys. Chem. A, 1999, 103, 8620–8624 CrossRef CAS.
- D. J. Nesbitt, T. Häber and M. A. Suhm, Faraday Discuss., 2001, 118, 305–306 Search PubMed.
- A. Moudens, R. Georges, M. Goubet, J. Makarewicz and S. E. Lokshtanov, J. Chem. Phys., 2009, 131, 204312 CrossRef CAS PubMed.
- C. Pérez, M. T. Muckle, D. P. Zaleski, N. A. Seifert, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Science, 2012, 336, 897–901 CrossRef PubMed.
- S. Wuelfert, D. Herren and S. Leutwyler, J. Chem. Phys., 1987, 86, 3751–3753 CrossRef CAS PubMed.
- B. Nelander, J. Chem. Phys., 1988, 88, 5254–5256 CrossRef CAS PubMed.
- S. Wuelfert, D. Herren and S. Leutwyler, J. Chem. Phys., 1988, 88, 5256–5257 CrossRef CAS PubMed.
- T. I. C. Jansen, B. M. Auer, M. Yang and J. L. Skinner, J. Chem. Phys., 2010, 132, 224503 CrossRef CAS PubMed.
- U. Buck, I. Ettischer, M. Melzer, V. Buch and J. Sadlej, Phys. Rev. Lett., 1998, 80, 2578–2581 CrossRef CAS.
- J. B. Paul, C. P. Collier, R. J. Saykally, J. J. Scherer and A. O'Keefe, J. Phys. Chem. A, 1997, 101, 5211–5214 CrossRef CAS.
- R. W. Larsen, P. Zielke and M. A. Suhm, J. Chem. Phys., 2007, 126, 194307 CrossRef PubMed.
- G. Firanescu, D. Luckhaus and R. Signorell, J. Chem. Phys., 2008, 128, 184301 CrossRef PubMed.
- M. L. Cowan, B. D. Bruner, N. Huse, J. R. Dwyer, B. Chugh, E. T. J. Nibbering, T. Elsaesser and R. J. D. Miller, Nature, 2005, 434, 199–202 CrossRef CAS PubMed.
- H. Torii, J. Phys. Chem. A, 2006, 110, 9469–9477 CrossRef CAS PubMed.
- C. J. Tainter, Y. Ni, L. Shi and J. L. Skinner, J. Phys. Chem. Lett., 2013, 4, 12–17 CrossRef CAS.
- S. Garrett-Roe and P. Hamm, Phys. Chem. Chem. Phys., 2010, 12, 11263–11266 RSC.
- A. Paarmann, T. Hayashi, S. Mukamel and R. J. D. Miller, J. Chem. Phys., 2008, 128, 191103 CrossRef CAS PubMed.
- Y. Wang and J. M. Bowman, J. Chem. Phys., 2012, 136, 144113 CrossRef PubMed.
- M. A. Suhm, Adv. Chem. Phys., 2009, 142, 1–57 CrossRef CAS.
- C. M. Tanner, M. Quack and D. Schmidiger, J. Phys. Chem. A, 2013, 117, 10105–10118 CrossRef PubMed.
- Y. Niu, R. Pang, C. Y. Zhu, M. Hayashi, Y. Fujimura, S. H. Lin and Y. R. Shen, Chem. Phys. Lett., 2013, 586, 153–158 CrossRef CAS PubMed.
- G. Avila, J. M. Fernández, G. Tejeda and S. Montero, J. Mol. Spectrosc., 2004, 228, 38–65 CrossRef CAS PubMed.
- A. van der Avoird and K. Szalewicz, J. Chem. Phys., 2008, 128, 014302 CrossRef PubMed.
- K. Kuyanov-Prozument, M. Y. Choi and A. F. Vilesov, J. Chem. Phys., 2010, 132, 014304 CrossRef PubMed.
- C. J. Burnham, S. S. Xantheas, M. A. Miller, B. E. Applegate and R. E. Miller, J. Chem. Phys., 2002, 117, 1109–1122 CrossRef CAS PubMed.
- C. Steinbach, P. Andersson, M. Melzer, J. K. Kazimirski, U. Buck and V. Buch, Phys. Chem. Chem. Phys., 2004, 6, 3320–3324 RSC.
- Y. Wang and J. M. Bowman, J. Phys. Chem. Lett., 2013, 4, 1104–1108 CrossRef CAS.
- C. J. Tainter and J. L. Skinner, J. Chem. Phys., 2012, 137, 104304 CrossRef CAS PubMed.
- G. Tejeda, M. Fernández and S. Montero, AIP Conf. Proc., 2012, 1501, 1305 CAS.
- G. E. Walrafen, J. Chem. Phys., 1964, 40, 3249–3256 CrossRef CAS PubMed.
- J. B. Paul, R. A. Provencal, C. Chapo, A. Petterson and R. J. Saykally, J. Chem. Phys., 1998, 109, 10201–10206 CrossRef CAS PubMed.
- M. A. Suhm, Science, 2004, 304, 823 CrossRef CAS PubMed.
- M. Y. Tretyakov, E. A. Serov, M. A. Koshelev, V. V. Parshin and A. F. Krupnov, Phys. Rev. Lett., 2013, 110, 093001 CrossRef.
- Y. Wang, B. C. Shepler, B. J. Braams and J. M. Bowman, J. Chem. Phys., 2009, 131, 054511 CrossRef PubMed.
- H. Cybulski and J. Sadlej, Chem. Phys., 2007, 342, 163–172 CrossRef CAS PubMed.
- Y. Watanabe, S. Maeda and K. Ohno, J. Chem. Phys., 2008, 129, 074315 CrossRef PubMed.
- E. Miliordos, E. Aprà and S. S. Xantheas, J. Chem. Phys., 2013, 139, 114302 CrossRef PubMed.
- V. Buch, S. Bauerecker, J. P. Devlin, U. Buck and J. K. Kazimirski, Int. Rev. Phys. Chem., 2004, 23, 375–433 CrossRef CAS.
- T. Salmi, E. Sälli and L. Halonen, J. Phys. Chem. A, 2012, 116, 5368–5374 CrossRef CAS PubMed.
- J. Ceponkus, G. Karlström and B. Nelander, J. Phys. Chem. A, 2005, 109, 7859–7864 CrossRef CAS PubMed.
- J. Ceponkus, P. Uvdal and B. Nelander, J. Phys. Chem. A, 2012, 116, 4842–4850 CrossRef CAS PubMed.
- Y. Wang, X. Huang, B. C. Shepler, B. J. Braams and J. M. Bowman, J. Chem. Phys., 2011, 134, 094509 CrossRef PubMed.
- Y. Wang and J. M. Bowman, J. Chem. Phys., 2011, 134, 154510 CrossRef PubMed.
- S. Graf, W. Mohr and S. Leutwyler, J. Chem. Phys., 1999, 110, 7893–7908 CrossRef CAS PubMed.
- J. B. Paul, R. A. Provencal, C. Chapo, K. Roth, R. Casaes and R. J. Saykally, J. Phys. Chem. A, 1999, 103, 2972–2974 CrossRef CAS.
- E. G. Diken, W. H. Robertson and M. A. Johnson, J. Phys. Chem. A, 2004, 108, 64–68 CrossRef CAS.
- M. Yang and J. L. Skinner, Phys. Chem. Chem. Phys., 2010, 12, 982–991 RSC.
- J. Lindner, P. Vöhringer, M. S. Pshenichnikov, D. Cringus, D. A. Wiersma and M. Mostovoy, Chem. Phys. Lett., 2006, 421, 329–333 CrossRef CAS PubMed.
- J. A. Poulsen, G. Nyman and S. Nordholm, J. Phys. Chem. A, 2003, 107, 8420–8428 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Rotational temperature analysis based on Stokes and anti-Stokes intensities; detailed descriptions of spectra and experimental conditions; depolarization analysis; matrix isolation trends; and more extensive quantum chemical compilations. See DOI: 10.1039/c3cp54272f |
| This journal is © the Owner Societies 2014 |