Open Access Article
Open Access ArticleThe substituent effect on benzene dications†‡
Marcin
Palusiak
*a,
Małgorzata
Domagała
a,
Justyna
Dominikowska
a and
F. Matthias
Bickelhaupt
*bc
aDepartment of Theoretical and Structural Chemistry, University of Łódź, Pomorska 163/165, 90-236 Łódź, Poland. E-mail: marcinp@uni.lodz.pl
bDepartment of Theoretical Chemistry and Amsterdam Center for Multiscale Modeling (ACMM), VU University Amsterdam, De Boelelaan 1083, 1081 HV Amsterdam, The Netherlands. E-mail: f.m.bickelhaupt@vu.nl
cInstitute for Molecules and Materials (IMM), Radboud University Nijmegen, Heyendaalseweg 135, 6525 AJ Nijmegen, The Netherlands
First published on 7th January 2014
Abstract
It was recently postulated that the benzene ring and its 4n + 2 π-electron analogues are resistant to the substituent effect due to the fact that such systems tend to retain their delocalized character. Therefore, the 4n π-electron dicationic form of benzene should appear to be less resistant to the substituent effect, as compared with its parent neutral molecule. For this reason the effect of substitution on the dicationic form of benzene was thoroughly investigated and the consequences of single and double substitution (of para- and meta-type) were assessed by means of several parameters, including various aromaticity indices and the Substituent Effect Stabilization Energy (SESE) parameter. It is shown that, distinct from neutral benzene, its dicationic form is much more sensitive to the substitution. However, the dicationic benzene itself, as a moiety with a significant deficit of electrons, will be considered as a strongly electron-withdrawing centre, thus interacting in a cooperative way with electron-donating substituents and in an anticooperative way with electron-withdrawing substituents. Clear differences between singlet- and triplet-state dicationic forms of benzene were also found. Triplet state structures seem to be significantly more delocalized, and as a consequence less sensitive to the substituent effect than the singlet state structures. Finally, the para- and meta-type substitution was investigated and it was found that the disubstituted dicationic benzene exhibits significantly different behaviour from that of neutral benzene. Although the difference between para- and meta-substitution can be found for dicationic benzene, the mechanism responsible for such an observation is different from that present in neutral benzene. Finally, it is shown how and why double ionization of benzene reduces its aromatic character in the singlet dication whereas aromaticity is essentially conserved in the triplet dication. The above findings highlight that in the case of charged analogues of benzene the aromaticity indices can be misleading and are to be used with great precaution.
Introduction
The substituent effect is one of the most important phenomena in general and physical organic chemistry. According to IUPAC recommendations the term substituent should be understood as an atom or a group that replaces one or more hydrogen atoms attached to a parent structure or a characteristic group.1 Thus, following the above statement the substituent effect should be understood as the set of changes in chemical and physical properties due to the replacement of the H atom (and rarely of some other atoms or groups, for example, a methyl group in the case of steric effects) by a given substituent.2 Most frequently the substituent effect is considered as a type of interaction between a given substituent and the phenyl ring or between two substituents through the phenyl ring.3 In the latter case the definition of the substituent effect involves a division of the system into three subsystems, that is, a substituent X, the ring, which plays the role of transmitting moiety, and the functional group Y, the properties of which are changed due to the substitution.4 It should be mentioned here that the interaction between the aromatic benzene ring and the substituent attached to it leads to partial localization of the π-electron system. In 2001 Krygowski et al.5 showed numerically, using several different aromaticity indices, that substitution of the benzene ring, in fact, leads to very small reduction in the π-electron delocalization, even if other consequences of substitution (such as e.g. reactivity) are much more significant. For instance, when the benzene ring is substituted with the NO2 group, which is considered to be strongly electron-withdrawing, the reduction of π-electron delocalization is lower than 1%, as measured by the HOMA index.6 This is much less than would be expected taking into account the changes in the reactivity of nitrobenzene, as compared with unsubstituted benzene. This observation allowed Krygowski et al. to postulate that a relatively stable aromatic system tends to retain its delocalized character. Later this observation and consequent conclusion were confirmed for para-substituted phenols, including p-nitrophenol, for which the reduction in π-electron delocalization of about 2% was more than double that observed earlier for nitrobenzene, but still very small comparing the changes in reactivity and other physical and chemical properties of that species.7 Thanks to the above-mentioned observations it was possible to conclude that the substituent effect and aromaticity are the two effects being competitive with each other. The consequence of such a statement would be the assumption according to which nonaromatic π-electron conjugated systems should communicate with substituents in a more effective way than their aromatic counterparts. If we consider the substituent effect as communication between two substituents interacting through the π-electron system, this communication should be stronger in the case of a conjugated, but nonaromatic π-electron system. Such an assumption may raise some doubts due to the fact that the substituent effect is most frequently considered for aromatic compounds, with benzene derivatives in the first place. However, the above postulates seem to be confirmed by a few published papers which appeared very recently. Firstly, the substituent effect on 1,4-disubstituted cyclohexa-1,3-diene and benzene was investigated by Dobrowolski et al.8 and it was shown there that cyclohexa-1,3-diene is a medium which is about ten times better in communication between substituents (as estimated with the use of the HOMA index) than its aromatic analogue, i.e. benzene. This statement is additionally important because consideration of the substituent effect does not have to be limited to aromatic compounds. For instance, it was recently shown that substituents may communicate through the π-electron structure of antiaromatic systems, e.g. cyclooctatetraene, and that communication in such a case is also more effective than that through the benzene ring.9 What is more, distinct from the aromatic species, in the case of antiaromatic systems the substituent effect leads to additional delocalization of the naturally localized system.9 If the benzene ring, being an aromatic archetype which fulfills the 4n + 2 magic Hückel rule, is much more resistant to the substituent effect than its nonaromatic counterparts (as e.g. the above-mentioned cyclohexa-1,3-diene), then it would be interesting to investigate the doubly-charged benzene ring, which still preserves its chemical classification as a close benzene derivative possessing full π-type conjugation possibilities and being planar (or at least almost planar),10 but which is a nonaromatic (or even antiaromatic) 4n Hückel-type π-electron system.10Charged analogues of aromatic compounds are very intriguing chemical species because of their close relation with their parent counterparts being of great importance in general organic chemistry,11 but also due to the fact that they are extremely reactive and, thus, difficult to investigate under standard laboratory conditions. Recently increased attention has been paid to these types of compounds, since such chemical species are supposed to be widespread in interstellar space. In 1979 Cohen et al.12 discovered the extended red emission (ERE) which is a broad emission band that begins near 540 nm and extends into the near infrared (IR) emitted by an object known as the Red Rectangle nebula. Later ERE was detected in spectral analysis of such objects as some carbon-rich planetary nebulae13 and in the interstellar medium of the Galaxy.14 The emitting medium of ERE was not determined unequivocally and among several explanations the one according to which the charged analogues of the aromatic species are responsible for the effect is considered as the most probable.10,15 However, interstellar chemistry is not reduced to observations of long distance astronomical objects. Rare and very active molecules are increasingly synthesized and investigated under laboratory conditions, mostly due to technological developments in experimental techniques.16 For instance, very recently the heptacene dication was synthesized17 and it appeared that it is more stable than its parent neutral molecule, as explained on the basis of earlier studies on that type of dicationic systems.10
In this paper we investigate the molecular systems which may be present in interstellar space, may perhaps be an interesting challenge for chemists specializing in the synthesis of rare and extremely reactive compounds, but above all which are an interesting subject of investigation from the purely cognitive point of view. We focus in particular on the series of parent systems, i.e., benzene-0/1, benzene-2/1, and benzene-2/3. The main trends emerging from our computations are interpreted in terms of molecular orbital (MO) theory and compared to earlier Kohn–Sham MO analyses of the distortive propensity of benzene's π electrons.18
Methodology
The systems investigated in the study were dicationic forms (in both singlet and triplet states) of molecules shown in Scheme 1. The graphical representation of exemplary dicationic systems is shown in Fig. 2. For comparison neutral forms of those species were also studied. Geometries of all the systems were optimized without any symmetry constraints using DFT19 methods implemented in Gaussian0920 program. The B3LYP21 functional was used in conjunction with the 6-311++G(d,p)22 basis set. The B3LYP functional was chosen since it was reported in several benchmark studies that this functional performs very well for both singlet and triplet state structures of benzene and its analogues,23 well reproduces geometry parameters24 and in general is recommended as the functional achieving acceptable accuracy for very large span of molecular systems of various characteristics.25 In order to verify if the optimized geometries correspond to stationary points, the frequency analysis at the same level of theory was performed. No imaginary frequencies were found.To describe aromaticity of systems under consideration, several aromaticity indices were applied. The first one, HOMA (Harmonic Oscillator Model of Aromaticity),6 is the geometry-based aromaticity indicator which can be defined using the following equation:
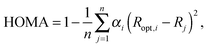 | (1) |
Other aromaticity indices used in the study, namely EL,26 PDI (Para-Delocalization Index)27 and FLU,28 are based on the electron density distribution analysed in the framework of Quantum Theory of Atoms in Molecules.29 All the properties of electron density distribution were computed using AIMAll30 program.
The EL index26 is based on ellipticities of bonds forming the ring. Ellipticity of a bond can be expressed using the following equation:29a
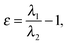 | (2) |
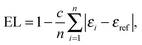 | (3) |
Two other indices, PDI27 and FLU,28 are based on electron delocalization. The delocalization index of atoms A and B can be defined using the following expression:31
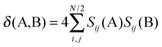 | (4) |
PDI and FLU are both the measures of cyclic electron delocalization of mobile electrons in the ring. The first one, PDI,27 is defined as a mean of all delocalization indices of para-related carbon atoms in the six-membered ring. The second one, the aromatic fluctuation index (FLU),28 can be defined using the formula:
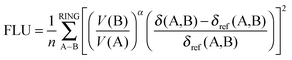 | (5) |
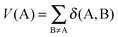 | (6) |
| α = sgn[V(B) − V(A)] | (7) |
FLU is close to zero for aromatic systems and is different from zero for non-aromatic ones.
Since the Nuclear Independent Chemical Shift (NICS) is one of the most commonly used aromaticity indices,32 we estimated values of NICS and its modified version, NICS(1).33 Nevertheless, NICS values estimated for charged systems escape any rational interpretation, which may suggest that the NICS index is perhaps not a suitable measure of π-electron delocalization in dicationic systems. This is due to the fact that in dications the significant deficit of electrons results in high nuclei deshielding and, as a consequence, difficulty in interpretation of values of chemical shifts attributed to pseudo-atoms at the centre of the ring. For this reason we give NICS and NICS(1) values in the ESI‡ and do not discuss in detail this part of numerical results. See also ref. 34a–c for some important reports on reduced applicability of the NICS index.
Since benzene and its substituted counterparts adopt in part a nonplanar conformation when they are in the dicationic state, we introduce a geometrical parameter, which quantifies the degree of planarity/nonplanarity of the given ring. This φ parameter is defined as follows:
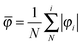 | (8) |
![[small phi variant, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d7.gif) parameter adopts the value equal to zero for ideally planar rings and drifts away from zero for nonplanar rings.
parameter adopts the value equal to zero for ideally planar rings and drifts away from zero for nonplanar rings.
A set of experimentally estimated substituent constants35 were checked against other numerical results. The following substituent constants were taken into account: σp−, F and R−. Originally substituent constants were estimated as parameters which numerically quantify mutual electron interaction between a given substituent and the para-placed reactivity center, spaced by the aromatic ring. The constants selected for these studies can be characterized as follows: the σp− is the substituent constant estimated for the para-placed reactivity centre (in respect to a given substituent), which could effectively delocalize a negative charge and which possesses lone electron pairs, e.g. the OH or NH2 group.36 The F values reflect field/inductive properties of a given substituent, while R− is the resonance constant obtained for the suitable centre of reactivity. The large positive value of a given constant implies high electron-withdrawing power by the inductive and/or resonance effect, relative to the hydrogen atom; while the large negative value of a given constant implies high electron-releasing power relative to the hydrogen atom.
Results and discussion
Benzene and its dicationic analogues
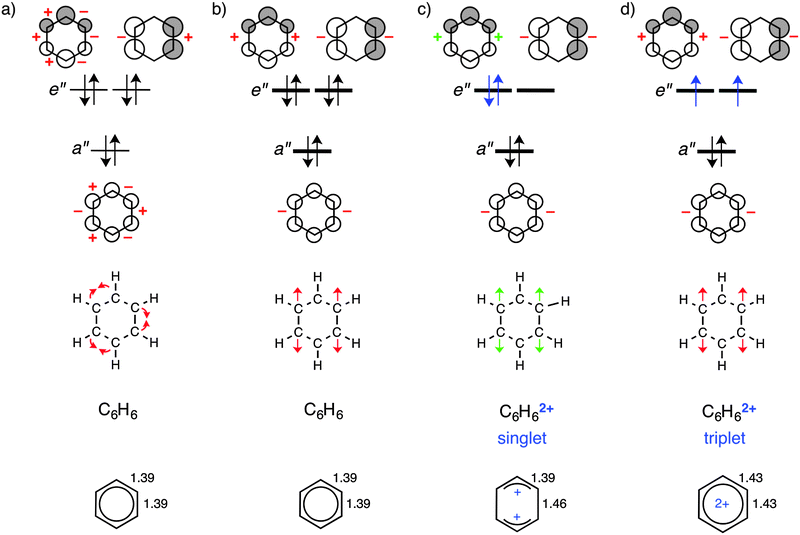
Firstly, let us discuss changes in π-electron delocalization in unsubstituted neutral benzene (benzene-0/1) and its dicationic form in singlet (benzene-2/1) and triplet (benzene-2/3) states. The structural data in Fig. 1, below, reveal that along benzene, benzene-2/1, and benzene-2/3, the geometry goes from regular with delocalized double bonds of 1.39 Å, via a structure with two elongated bonds of 1.46 Å on opposite sides of the ring, back to regular but elongated partially multiple bonds. Previously, it was shown that the π electrons in benzene have a preference for localizing the double bonds and to adopt a Kekulé-type geometry.18a This preference is a direct consequence of the fact that pπ–pπ overlap between carbon atoms assumes its maximum value of 1 at a C–C distance of 0 Å. It is the scaffold provided by the σ electrons that overrules this tendency of the π system and retains benzene in a regular C6h-symmetric structure in which all C–C bonds have equal length and a formal bond order of 1.5. The reason that the π system in benzene only has a weak bias for double-bond localization has to do with the overlap pattern of benzene π MOs. In zeroth order, this overlap pattern is subject to cancellation of stabilizing effects (i.e., increases of bonding and decreases of antibonding overlap; indicated with a red + in Fig. 1a) and destabilizing effects (i.e., decreases of bonding and increases of antibonding overlap; indicated with a red − in Fig. 1a).The overlap pattern of the π MOs in benzene also explains why this molecule does not elongate two of its bonds on opposite sides of the ring. Both the a′′ and one of the e′′ orbitals are destabilized (red − in Fig. 1b) whereas only one e′′ is stabilized (red + in Fig. 1b). These changes in the singlet dication in which two electrons are removed from the e′′ orbital oppose elongation of the two C–C bonds. The associated loss in π bonding and the remaining antibonding character of these bonds of the π electrons in the other e′′ orbital cause the observed distortion in bond lengths and planarity of the ring (green arrows in Fig. 1c, lower). This results in the formation of two allyl cation units connected by two longer C–C bonds with reduced multiple bonding character. Interestingly, an alternative deformation leading to localized double bonds on opposite sides of the ring and para localized carbocationic centers is not found in the optimization. This can be ascribed to the electrostatically unfavourable situation of two highly positively charged atomic centres as compared to a delocalized positive charge in allyl cationic centres (see Fig. 1d).
At variance, in the triplet dication, both e′′ orbitals remain occupied and therefore we conserve the tendency of the π system to resist the stretching distortion of the two bonds on opposite sides of the ring. However, π bonding is overall reduced and this translates into an overall symmetric elongation of all C–C bonds.
Aromaticity of substituted neutral and dicationic benzene
Tables 1, 2 and 4 contain the values of aromaticity indices used for estimation of the aromatic character of systems under investigation. In the first line we discuss the results obtained for singlet state systems (Tables 1 and 2). In the further part of this section the triplet states will also be investigated (Table 4). For the purpose of discussion we use the following notation:| (substituent type) − (substituent 1) − (substituent 2) − (charge/multiplicity) |
Thus, NO2-0/1 corresponds to nitrobenzene, while m-CN–N(CH3)2-2/1 corresponds to the dication of meta-cyano-N,N-dimethylamino-benzene in the singlet state. In Fig. 2a–c the graphical representation of the fully optimized geometry of the exemplary dicationic systems can be found together with the above notation. As can be seen in Table 1, the values of aromaticity indices estimated for neutral substituted benzene are very close to those of unsubstituted benzene. For instance, HOMA for neutral systems adopts values in the range of 0.94–1.00. For electron density-based indices this range is proportionally slightly larger, but still small. Additionally, the substituent effect leads to small reduction in the aromatic character of the substituted ring. This observation corroborates earlier observations made for neutral benzene and its aromatic counterparts, according to which the aromatic 4n + 2 Huckel-like systems tend to retain their π-electron structure, thus, being relatively resistant to the substituent effect.8 The situation changes dramatically when passing from neutral 4n + 2 to doubly charged 4n π-electron systems (see Table 2). First of all, for all the systems there is, as expected, a marked reduction in the aromatic character, as can be illustrated by the values of differences in aromaticity indices estimated for neutral and charged systems and collected in Table 2. This effect is accompanied by a clear distortion of the ring towards a nonplanar conformation, as shown by the ![[small phi variant, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d7.gif) parameter. For instance, the unsubstituted benzene ring loses almost a half of its aromatic character when it passes from the neutral to the doubly charged cation. What is interesting is that for substituted systems this loss of aromaticity is clearly larger (with the only exception of the CHO substituent which most probably results from the fact that due to the optimization procedure the CHO group adopted a position perpendicular to the ring, which would reduce the π-electron conjugation between the lone electron pair on the substituent and the π-electron structure within the ring). For instance in some cases the loss of aromaticity is so efficient that the ring system becomes slightly antiaromatic with negative HOMA and EL values and a nonplanar conformation. In both neutral and dicationic benzene the substituent effect leads to reduction of aromaticity, only that in the case of dicationic systems there is obviously another scale of the effect. In neutral benzene the changes were hardly noticeable, while in dications the differences between the unsubstituted and substituted systems may be of more than 0.5 of HOMA values and of more than 0.3 of EL values. Thus, already here it can be concluded that dicationic benzene is much more sensitive to the substituent effect, as compared with its neutral counterpart. Interestingly, there is a relationship between the reduction of aromaticity and the distortion from planarity of the ring. Thus, the unsubstituted benzene dication is the most nonplanar species while the introduction of substituents causes our model systems to become more planar.
parameter. For instance, the unsubstituted benzene ring loses almost a half of its aromatic character when it passes from the neutral to the doubly charged cation. What is interesting is that for substituted systems this loss of aromaticity is clearly larger (with the only exception of the CHO substituent which most probably results from the fact that due to the optimization procedure the CHO group adopted a position perpendicular to the ring, which would reduce the π-electron conjugation between the lone electron pair on the substituent and the π-electron structure within the ring). For instance in some cases the loss of aromaticity is so efficient that the ring system becomes slightly antiaromatic with negative HOMA and EL values and a nonplanar conformation. In both neutral and dicationic benzene the substituent effect leads to reduction of aromaticity, only that in the case of dicationic systems there is obviously another scale of the effect. In neutral benzene the changes were hardly noticeable, while in dications the differences between the unsubstituted and substituted systems may be of more than 0.5 of HOMA values and of more than 0.3 of EL values. Thus, already here it can be concluded that dicationic benzene is much more sensitive to the substituent effect, as compared with its neutral counterpart. Interestingly, there is a relationship between the reduction of aromaticity and the distortion from planarity of the ring. Thus, the unsubstituted benzene dication is the most nonplanar species while the introduction of substituents causes our model systems to become more planar.
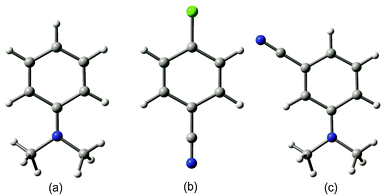 | ||
| Fig. 2 Graphical representation of exemplary dicationic systems in the singlet state: (a) N(CH3)2-2/1, (b) p-Cl–CN-2/1 and (c) m-CN–N(CH3)2-2/1. | ||
| HOMA | EL | PDI | FLU | |
|---|---|---|---|---|
| Benzene-0/1 | 0.989 | 0.100 | 0.103 | 0.000 |
| N(CH3)2-0/1 | 0.946 | 0.862 | 0.090 | 0.002 |
| NHCH3-0/1 | 0.963 | 0.842 | 0.091 | 0.002 |
| NCH2-0/1 | 0.979 | 0.902 | 0.095 | 0.001 |
| NH2-0/1 | 0.976 | 0.828 | 0.093 | 0.001 |
| OCH3-0/1 | 0.981 | 0.802 | 0.094 | 0.002 |
| OH-0/1 | 0.989 | 0.787 | 0.095 | 0.001 |
| Cl-0/1 | 0.993 | 0.870 | 0.099 | 0.000 |
| CHO-0/1 | 0.980 | 0.898 | 0.095 | 0.001 |
| NO2-0/1 | 0.993 | 0.923 | 0.095 | 0.001 |
| CN-0/1 | 0.977 | 0.928 | 0.096 | 0.001 |
![[small phi variant, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d7.gif) values (given in deg) are also collected
values (given in deg) are also collected
| HOMA | EL | PDI | FLU | ΔHOMA | ΔEL | ΔPDI | ΔFLU |
![[small phi variant, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d7.gif)
|
|
|---|---|---|---|---|---|---|---|---|---|
| Benzene-2/1 | 0.531 | 0.162 | 0.059 | 0.015 | −0.458 | −0.838 | −0.044 | 0.015 | 28.887 |
| N(CH3)2-2/1 | 0.207 | 0.098 | 0.040 | 0.032 | −0.739 | −0.764 | −0.050 | 0.030 | 0.787 |
| NHCH3-2/1 | 0.134 | 0.021 | 0.040 | 0.036 | −0.829 | −0.821 | −0.051 | 0.034 | 0.038 |
| NCH2-2/1 | 0.051 | 0.039 | 0.040 | 0.040 | −0.928 | −0.863 | −0.054 | 0.039 | 0.009 |
| NH2-2/1 | −0.074 | −0.099 | 0.040 | 0.042 | −1.050 | −0.927 | −0.053 | 0.041 | 0.025 |
| OCH3-2/1 | −0.173 | −0.058 | 0.041 | 0.047 | −1.154 | −0.860 | −0.053 | 0.046 | 0.010 |
| OH-2/1 | −0.294 | −0.152 | 0.045 | 0.051 | −1.283 | −0.939 | −0.050 | 0.050 | 0.044 |
| Cl-2/1 | −0.108 | −0.150 | 0.048 | 0.038 | −1.101 | −1.020 | −0.051 | 0.038 | 2.838 |
| CHO-2/1 | 0.716 | 0.328 | 0.059 | 0.011 | −0.264 | −0.570 | −0.036 | 0.011 | 21.184 |
| NO2-2/1 | 0.077 | −0.067 | 0.039 | 0.037 | −0.917 | −0.990 | −0.057 | 0.036 | 4.219 |
| CN-2/1 | −0.046 | 0.105 | 0.046 | 0.020 | −1.023 | −0.823 | −0.050 | 0.020 | 14.921 |
| σ p − | F | R − | |
|---|---|---|---|
| Benzene | 0 | 0 | 0 |
| N(CH3)2 | −0.12 | 0.15 | −0.27 |
| NHCH3 | — | −0.03 | — |
| NCH2 | — | — | — |
| NH2 | −0.15 | 0.08 | −0.23 |
| OCH3 | −0.26 | 0.29 | −0.55 |
| OH | −0.37 | 0.33 | −0.7 |
| Cl | 0.19 | 0.42 | −0.23 |
| CHO | 1.03 | 0.33 | 0.7 |
| NO2 | 1.27 | 0.65 | 0.62 |
| CN | 1 | 0.51 | 0.49 |
![[small phi variant, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d7.gif) values (given in deg) are also collected
values (given in deg) are also collected
| HOMA | EL | PDI | FLU | ΔHOMA | ΔEL | ΔPDI | ΔFLU |
![[small phi variant, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d7.gif)
|
|
|---|---|---|---|---|---|---|---|---|---|
| Benzene-2/3 | 0.601 | −0.298 | 0.031 | 0.005 | −0.387 | −1.298 | −0.072 | 0.005 | 10.525 |
| N(CH3)2-2/3 | 0.634 | 0.205 | 0.042 | 0.010 | −0.312 | −0.657 | −0.048 | 0.008 | 0.200 |
| NHCH3-2/3 | 0.622 | 0.122 | 0.072 | 0.013 | −0.341 | −0.720 | −0.019 | 0.011 | 0.069 |
| NCH2-2/3 | 0.592 | 0.144 | 0.071 | 0.014 | −0.387 | −0.758 | −0.023 | 0.013 | 0.014 |
| NH2-2/3 | 0.585 | 0.016 | 0.076 | 0.014 | −0.391 | −0.812 | −0.017 | 0.013 | 0.042 |
| OCH3-2/3 | 0.577 | 0.022 | 0.078 | 0.015 | −0.403 | −0.779 | −0.016 | 0.013 | 0.512 |
| OH-2/3 | 0.551 | −0.073 | 0.086 | 0.015 | −0.438 | −0.860 | −0.009 | 0.014 | 0.035 |
| Cl-2/3 | 0.606 | −0.094 | 0.034 | 0.008 | −0.387 | −0.964 | −0.065 | 0.008 | 0.003 |
| CHO-2/3 | 0.666 | 0.190 | 0.068 | 0.007 | −0.314 | −0.708 | −0.027 | 0.007 | 0.009 |
| NO2-2/3 | 0.683 | 0.090 | 0.042 | 0.007 | −0.310 | −0.833 | −0.054 | 0.006 | 2.336 |
| CN-2/3 | 0.586 | −0.129 | 0.034 | 0.008 | −0.391 | −1.057 | −0.062 | 0.007 | 0.003 |
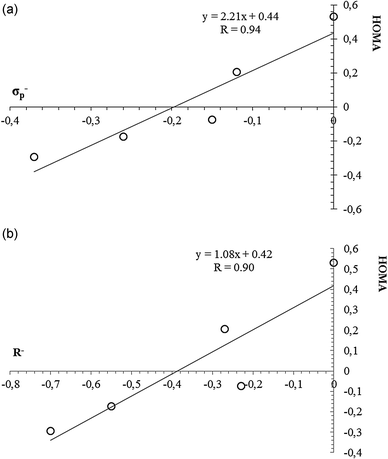
It would be interesting to check how far the changes in aromaticity due to removal of two π-electrons correlate with classic measures of the substituent effect, such as Hammett constants.36Table 3 presents the values of selected substituent constants. There is no clear correlation between e.g. HOMA or EL and any of substituent constants. For instance, there is lack of correlation between HOMA and the σp− constant when taking into account all substituents. However, if we remove all cases with positive σp− constant values, that is, when excluding all systems with electron-withdrawing substituents, the correlation is much better with cc = 0.94 (see Fig. 3a). A similar observation can be made for the R− constant (Fig. 3b). What is more, exactly the same observation can be made for the EL index, only with little worse correlation coefficients (cc of 0.87 and 0.79 for EL = f(σp−) and EL = f(R−), respectively). It is also clear that the greater loss in π-electron delocalization can be observed for stronger electron-withdrawing substituents. Thus, if we consider the F constant, which shows field/inductive properties of a given substituent, the correlations with aromaticity indices are much worse, if at all.
Therefore, it can be said that there exists some relation between aromaticity indices and substituent constants, but only for electron-donating substituents. The lack of such a relation for all sets of substituents, including electron-withdrawing ones, may have a physical background in the fact that dicationic benzene should be considered as an electron-withdrawing centre. When it interacts with electron-donating substituents, the situation is favoured and more predictable, since in such a case the substituent shares its charge with the ring which has the π-electron deficit. The situation is more complicated when the ring interacts with the electron-withdrawing substituent. In that case there is competition between electron-withdrawing power of the ring and the substituent, and due to this competitive character of interaction there is no direct linear relation between e.g. aromaticity indices and substituent constants.
All the above observations were made for singlet state systems. However, since the benzene dication itself can be more stable in the triplet state,10 we also investigated triplet states for the substituted benzene dication. On the other hand, it should be pointed out that for all investigated substituted dications the singlet states were more stable energetically, when compared with their triplet state counterparts.
Table 4 contains the values of aromaticity indices estimated for triplet state dications. At first sight it can be seen that there is a loss of aromaticity due to removal of two π-electrons, when comparing neutral (Table 1) and dicationic triplet state structures (Table 4). However, at the same time it can be said that in this case the behaviour of aromaticity indices differs from that found for singlet states. For instance, the HOMA values change due to substitution to a much lesser degree than it was observed for singlet states. For singlet state structures the maximum difference in HOMA values was of about 0.8 (even 1.0 taking into account the CHO substituent), whereas for triplet state structures this span of HOMA values is more than ten times smaller, being of about 0.05. At the same time EL changes more similarly for both singlet and triplet states (by about 0.5). What is more disturbing is that EL indicates unsubstituted benzene as the most localized (nonaromatic) system of all triplet state structures, which is in line with the fact that this system is the most nonplanar of all the triplet state structures. In the case of HOMA the situation is even more chaotic, since some substituted systems are more delocalized and some are less delocalized when compared with the unsubstituted benzene dication. Also, the triplet state structures are in general more planar than their singlet state counterparts, which is in line with the general conclusion drawn in the first section of the discussion.
Taking into account the lack of any relation between aromaticity indices and other parameters, or even between aromaticity indices themselves, we postulate that aromaticity indices (at least those used in this work) are rather unreliable measures of delocalization for triplet state systems.
Substituent effect stabilization energy
In this section we examine some selected energetic parameters of the investigated systems. Due to rather unpredictable properties of triplet state structures we firstly focus on singlet state structures, whereas triplet state structures will be discussed separately at the end of the section.The Substituent Effect Stabilization Energy (SESE)37 was originally defined as an energetic measure of the increase in stability of the system due to the interaction between X, Y and the ring. It is usually estimated as the difference between the energy of substrates and products of the isodesmic reaction shown in Scheme 2.
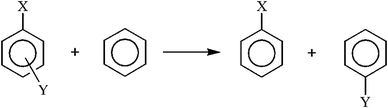 | ||
| Scheme 2 Scheme of the isodesmic reaction for calculation of Substituent Effect Stabilization Energy (SESE). | ||
The aim of this work was to estimate the energetic and structural consequences of substitution of the doubly charged benzene ring. As it was said in the previous section, the doubly charged benzene ring can be considered as a centre which may effectively delocalize negative charge, since it has a deficit of electron charge. Therefore, distinct from neutral benzene, which tends to retain its delocalized structure, thus being resistant to interaction with the substituent, the charged benzene ring itself should act as a significantly electron-withdrawing centre. Consequently, one should observe clear differences in the stabilizing–destabilizing interaction between the benzene dication and the given substituents. The character of such an interaction can be assessed using the isodesmic reaction procedure as shown in Scheme 3. Since only one substituent interacts with the benzene ring in the considered case, we use the notation SESE(1) for the parameter estimated as the energy balance of the reaction shown in Scheme 3 (in order to distinguish it from the case of two substituents interacting via the benzene ring, which we will call SESE(2) and will discuss in the next section of this paper).
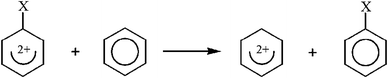 | ||
| Scheme 3 Scheme of the reaction of monosubstituted doubly charged benzene for calculation of Substituent Effect Stabilization Energy (SESE(1)). | ||
Table 5 contains SESE(1) values estimated for the reaction shown in Scheme 3. The positive value of SESE(1) indicates the stabilizing character of interaction between the given substituent and the charged benzene ring (with respect to analogous interaction with the neutral benzene ring). As can be seen, for the electron-donating substituents the SESE(1) value is positive and relatively large, which indicates a significant stabilizing character of the interaction between the substituent and the charged ring. In the case of an N(CH3)2 substituent the SESE(1) value equals over 100 kcal mol−1. For the electron-withdrawing substituents SESE(1) values are negative (the only exception is the Cl substituent, which cannot be considered as interchangeably electron-withdrawing) and systematically smaller (in absolute value) when compared with the same values estimated for the electron-donating substituents. Interestingly, when searching for some direct relation between SESE(1) and the values of aromaticity indices, there is lack of such correlation, but when we omit the electron-withdrawing substituents, a clear linear correlation can be found. Thus, some irregularity can be noticed for the electron-withdrawing substituents which interact in a competitive way with the substituted positively charged ring, but electron-donating substituents behave in a predictable way and stabilize the system via the substituent effect, in fact increasing the delocalized character of the ring itself. Fig. 4 shows a linear correlation between SESE(1) and HOMA (HOMA = f(SESE(1))) for which the correlation coefficient equals 0.99. The same parameter for the correlation between EL and SESE(1) equals 0.90. It can also be observed that for larger SESE(1) values (expressing more stabilization due to the interaction between the substituent and the ring) the ring is more delocalized. When considering triplet state structures, the SESE(1) parameter can also be estimated as the energetic balance of the reaction shown in Scheme 3. However, in this case we use energies of triplet state structures of dications only.
| Singlet | Triplet | |
|---|---|---|
| N(CH3)2 | 107.51 | 87.49 |
| NHCH3 | 94.55 | 74.63 |
| NCH2 | 82.40 | 59.96 |
| NH2 | 75.35 | 58.58 |
| OCH3 | 57.83 | 44.25 |
| OH | 36.34 | 26.73 |
| Cl | 15.74 | 12.84 |
| CHO | −1.15 | 13.78 |
| NO2 | −4.75 | −11.96 |
| CN | −13.05 | −8.88 |
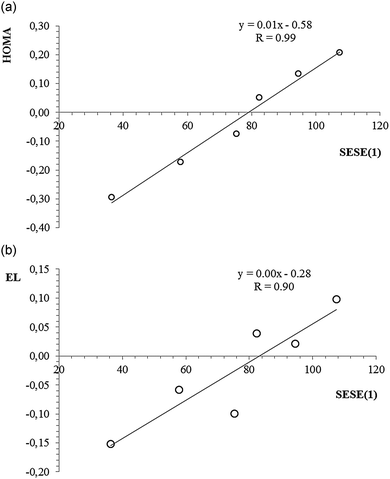 | ||
| Fig. 4 A linear correlation for HOMA index vs. SESE(1), (a), and EL index vs. SESE(1), (b), estimated for dicationic benzene substituted with electron-donating substituents in the singlet state. | ||
The SESE(1) and related data can be found in Table 5. As can be seen, the values of SESE(1) estimated for the singlet and triplet state structures are relatively similar, with slightly smaller values for triplet state structures. This observation can be illustrated by a linear correlation between both SESE(1) parameters, as shown in Fig. 5. From the slope of regression it can be concluded that the energetic effect accompanying substitution is 1.27 times more efficient in the case of singlet state benzene as compared with its triplet state counterpart. What is more, since SESE(1) values estimated for the singlet and triplet states are intercorrelated, also the relations between SESE(1) and HOMA or EL indices can be found for triplet state structures, although, again only for electron-donating substituents. In general, it can be concluded that triplet state benzene is rather less sensitive to the substituent effect, as shown earlier for aromaticity measures and now for the SESE(1) estimator.
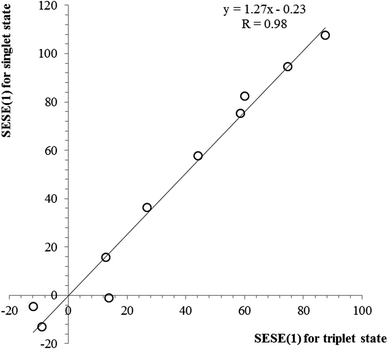 | ||
| Fig. 5 The relation between SESE(1) values (in kcal mol−1) estimated for the singlet state vs. the triplet state. | ||
para vs. meta substitution
One of the most common features of the benzene ring is its ability to act as a transferring moiety in communication between two substituents. This communication can be transferred via relatively mobile π-electrons in the delocalized ring. On the other hand, it was earlier postulated in the literature and, following that literature, in the introduction to our paper that the aromatic ring tends to retain its delocalized structure, whereas substitution leads to its partial localization, thus being the competitive effect to aromaticity. In previous sections we showed that the dicationic benzene ring may interact with the substituent in a much more effective way, since as a 4n π-electron system it is not so resistant to perturbations, its neutral parent system being the 4n + 2 π-electron system. What is also important is that in the case of neutral benzene there is a crucial difference in substitution between the meta- and para-type. It is generally known3 that in para-substituted benzene the interaction between substituents is essentially more effective than in the case of meta-type substitution. This difference between para- and meta-substitution can be obviously explained by e.g. the contribution from charge-separated canonical structures which makes it possible to separate charge and formally locate it on substituents in the case of para-substitution, but in the case of meta-substitution the formal localization of charges on substituents is possible only for doubly-charge-separated structures.38 (see Schemes S1–S3 in the ESI‡ file for the illustration of singly- and doubly-charge-separated canonical structures of benzene).However, in dicationic benzene the ring itself acts as the electron-accepting centre, and, moreover, it interacts more effectively with the (electron-donating) substituents, as was shown in the previous section. Thus, it would be interesting to find out whether or not there are some analogies between para- and meta-substitution of the benzene dication and its neutral counterpart.
Tables 6–8 contain selected numerical data obtained for doubly substituted benzene in the neutral and dicationic form. In the first line we discuss the singlet state structures. As can be seen for instance for the benzene dication disubstituted with CN (or NO2) and N(CH3)2 substituents, the para-substituted ring is slightly less delocalized than its meta-substituted counterpart. Confronting these results with the observations made for the monosubstituted benzene dication it could be postulated that in para-type substitution the consequences of substitution are slightly more efficient than in the case of meta-type substitution. However, the differences between para- and meta-substitution are rather subtle, comparing the consequences of substitution, in general, particularly in light of very small changes in π-electron delocalization in substituted neutral benzene. The most efficient loss of delocalization is observed in the case when two electron-withdrawing substituents are attached to the dicationic benzene ring, and this is true in the case of both para- and meta-substitution. A markedly different situation was found for neutral benzene, for which the most efficient loss of aromaticity was observed for para-substitution with one electron-donating and one electron-withdrawing substituent. (In such a case there is a cooperative effect of substituents, and a contribution from the quinone-like canonical structure, reflected by the most efficient loss of the aromatic character.) In dications the ring becomes less delocalized, when π-electrons are withdrawn from the ring system. Thus, distinct from neutral benzene, in singlet state dicationic benzene the ring–substituent interaction seems to predominate over the substituent–substituent interaction proceeding via the ring (as in neutral benzene derivatives).
| HOMA | EL | PDI | FLU | |
|---|---|---|---|---|
| Benzene-0/1 | 0.990 | 0.100 | 0.103 | 0.000 |
| p-CN–N(CH3)2-0/1 | 0.909 | 0.836 | 0.078 | 0.005 |
| p-NO2–N(CH3)2-0/1 | 0.911 | 0.835 | 0.074 | 0.006 |
| p-Cl–CN-0/1 | 0.980 | 0.849 | 0.091 | 0.001 |
| p-Cl–NO2-0/1 | 0.996 | 0.867 | 0.091 | 0.001 |
| m-CN–N(CH3)2-0/1 | 0.937 | 0.834 | 0.083 | 0.003 |
| m-NO2–N(CH3)2-0/1 | 0.946 | 0.850 | 0.082 | 0.003 |
| m-Cl–CN-0/1 | 0.981 | 0.844 | 0.092 | 0.001 |
| m-Cl–NO2-0/1 | 0.996 | 0.849 | 0.092 | 0.001 |
![[small phi variant, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d7.gif) values (given in deg) are also collected
values (given in deg) are also collected
| HOMA | EL | PDI | FLU | ΔHOMA | ΔEL | ΔPDI | ΔFLU |
![[small phi variant, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d7.gif)
|
|
|---|---|---|---|---|---|---|---|---|---|
| Benzene-2/1 | 0.531 | 0.162 | 0.059 | 0.015 | −0.458 | −0.838 | −0.044 | 0.015 | 28.887 |
| p-CN–N(CH3)2-2/1 | 0.188 | 0.132 | 0.037 | 0.035 | −0.721 | −0.704 | −0.041 | 0.030 | 0.778 |
| p-NO2–N(CH3)2-2/1 | 0.288 | 0.181 | 0.038 | 0.032 | −0.623 | −0.654 | −0.036 | 0.026 | 0.650 |
| p-Cl–CN-2/1 | −0.003 | −0.039 | 0.040 | 0.037 | −0.983 | −0.889 | −0.051 | 0.036 | 0.001 |
| p-Cl–NO2-2/1 | −0.036 | −0.113 | 0.030 | 0.045 | −1.031 | −0.980 | −0.061 | 0.044 | 2.487 |
| m-CN–N(CH3)2-2/1 | 0.292 | 0.157 | 0.039 | 0.029 | −0.646 | −0.677 | −0.044 | 0.026 | 0.790 |
| m-NO2–N(CH3)2-2/1 | 0.282 | 0.120 | 0.039 | 0.030 | −0.665 | −0.729 | −0.043 | 0.026 | 0.294 |
| m-Cl–CN-2/1 | −0.086 | 0.120 | 0.037 | 0.029 | −1.067 | −0.724 | −0.054 | 0.027 | 0.002 |
| m-Cl–NO2-2/1 | 0.173 | 0.091 | 0.037 | 0.029 | −0.823 | −0.758 | −0.055 | 0.028 | 4.941 |
![[small phi variant, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d7.gif) values (given in deg) are also collected
values (given in deg) are also collected
| HOMA | EL | PDI | FLU | ΔHOMA | ΔEL | ΔPDI | ΔFLU |
![[small phi variant, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d7.gif)
|
|
|---|---|---|---|---|---|---|---|---|---|
| Benzene-2/3 | 0.601 | −0.298 | 0.031 | 0.005 | −0.387 | −1.298 | −0.072 | 0.005 | 10.525 |
| p-CN–N(CH3)2-2/3 | 0.641 | 0.337 | 0.037 | 0.011 | −0.268 | −0.499 | −0.041 | 0.006 | 0.691 |
| p-NO2–N(CH3)2-2/3 | 0.754 | 0.595 | 0.050 | 0.015 | −0.156 | −0.240 | −0.024 | 0.010 | 0.601 |
| p-Cl–CN-2/3 | 0.628 | 0.041 | 0.033 | 0.009 | −0.352 | −0.808 | −0.058 | 0.008 | 0.002 |
| p-Cl–NO2-2/3 | 0.698 | 0.491 | 0.053 | 0.012 | −0.298 | −0.375 | −0.037 | 0.011 | 0.008 |
| m-CN–N(CH3)2-2/3 | 0.671 | 0.383 | 0.042 | 0.012 | −0.267 | −0.451 | −0.041 | 0.008 | 0.691 |
| m-NO2–N(CH3)2-2/3 | 0.832 | 0.545 | 0.048 | 0.009 | −0.114 | −0.305 | −0.034 | 0.006 | 0.601 |
| m-Cl–CN-2/3 | 0.641 | 0.114 | 0.038 | 0.010 | −0.340 | −0.730 | −0.054 | 0.009 | 0.001 |
| m-Cl–NO2-2/3 | 0.768 | 0.336 | 0.045 | 0.008 | −0.228 | −0.514 | −0.047 | 0.007 | 1.202 |
The situation changes significantly, when considering triplet state structures (see Table 8). In that case the disubstituted ring seems to be systematically more delocalized than the unsubstituted and monosubstituted systems. In the most extreme case corresponding to the ring meta-type substituted with N(CH3)2 and NO2 groups, the HOMA and EL adopt the values 0.83 and 0.54, respectively. These values are close to those obtained for e.g. the neutral benzene ring in a naphthalene molecule. Triplet state dications are also more planar, when compared with their singlet state counterparts. Again, such results may suggest that aromaticity indices, at least those used in the present research, may overestimate the aromatic character of the system, although it is worth pointing out that the more aromatic character of triplet state 4n benzene dications was already observed earlier for related molecular systems.10,39
As far as SESE is concerned, the energetic consequences of double substitution should be estimated as an energetic balance of the reaction shown in Scheme 4. However, in the case of charged systems there are several possibilities of construction of such a reaction, mostly resulting from the formal charge location in the right-hand and left-hand parts of the reaction equation. For instance, it would be possible to consider a reaction in which the unsubstituted benzene ring would be neutral, and then one of the products could also be neutral, so that the interaction between one of the substituents and the dicationic ring would be assessed in two situations, with the mono- and disubstituted charged ring. There are also other possibilities, however, the reaction in which all substrates and products are dications of the same (singlet) state seems to be the most consistent model for our purposes. Table 9 contains the values of the SESE(2) parameter estimated as the energetic balance of the reaction shown in Scheme 4, in which all molecular systems have the same charge and multiplicity. Thus for neutral species obviously all systems are of singlet state, whereas for charged species all systems are dications of singlet state.
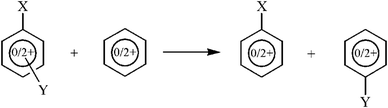 | ||
| Scheme 4 Scheme of the reaction for calculation of Substituent Effect Stabilization Energy of disubstituted neutral and doubly charged benzene (SESE(2)). | ||
| Neutral | Dication | |
|---|---|---|
| p-CN–N(CH3)2 | 2.99 | 0.21 |
| p-NO2–N(CH3)2 | 4.24 | −14.93 |
| p-Cl–CN | −0.96 | 5.80 |
| p-Cl–NO2 | −1.10 | −3.63 |
| m-CN–N(CH3)2 | 1.17 | −7.38 |
| m-NO2–N(CH3)2 | 1.56 | −18.84 |
| m-Cl–CN | −1.60 | −1.80 |
| m-Cl–NO2 | −1.93 | −14.07 |
Firstly let us compare SESE(2) values with those obtained for neutral species. The obtained SESE(2) values are in agreement with data available in the literature.38 For instance, the positive SESE(2) value obtained for the p-NO2–N(CH3)2-0/1 system indicates the left-hand situation in Scheme 1 as the one corresponding to the more energetically favourable situation. In this case the additional partial stabilization results from the cooperative character of the substituent–ring and the substituent–substituent interactions. This is a well known and well documented effect observed for para-type substitution.3 In the case of meta-substitution the energetic balance is similar, but the SESE(2) value is clearly smaller, indicating a less effective cooperative character of the interaction between two substituents being attached in positions 1 and 3 of the ring. When two substituents have uniquely electron-withdrawing properties (as for instance in the case of p-Cl–NO2-0/1, or even better for benzene substituted with two identical substituents) they both compete with each other when they interact with the ring and so the anticooperative character of the substituent–ring interaction is observed, which is revealed by negative SESE(2) values (more energetically stable is the situation on the right-hand of the reaction shown in Scheme 4).
In the case of the dicationic form of benzene the situation seems to be more complicated and the observations made for neutral benzene cannot be extrapolated directly to its dicationic form. The largest SESE(2) values were estimated for the system substituted with two N(CH3)2 groups. What is surprising is that SESE(2) not only has a large value, but is also of negative sign, suggesting that the situation where there are two monosubstituted dicationic rings (instead of the one disubstituted and the one unsubstituted ring) is energetically much more preferable. Thus, although one electron-donating substituent stabilizes dicationic benzene (as shown in the previous sections), two such substituents do not cooperate in this stabilization. In general, such a situation would be acceptable since it suggests that two monosubstituted benzene dications stabilized by single substituents are more energetically stable than one stabilized by two substituents and one unsubstituted. However, the situation is even more interesting when we look at the SESE(2) value estimated for two CN substituents (para- and meta-CN–CN-2/1 systems). In this case the situation where there is one doubly substituted ring and one unsubstituted ring is more energetically favourable, whereas the situation where two rings are monosubstituted is less energetically favourable. Thus, it seems that when the substituents stabilize the system, the situation where each substituent stabilizes separately the monosubstituted ring is more favourable. In other words, there is no cooperative effect in the case of stabilization of the ring by electron-donating substituents. This behaviour is consistently kept for destabilizing interaction between electron-withdrawing substituents and dicationic benzene. Finally, when considering substitution with one electron-donating substituent and one electron-withdrawing substituent (the well characterized case of cooperative interaction between substituents attached to neutral benzene), the effect is rather unpredictable and strongly depends on the balance in stabilizing and destabilizing interaction between individual substituents and the ring. In general, it would be postulated that although dicationic benzene is more sensitive to the substituent effect than its neutral counterpart (as shown in the previous section) the interaction between substituents through the ring is rather limited and the substituent–ring interaction is the dominant effect.
Conclusions
Our analyses of the overlap pattern of the π orbitals show that the structural aspects of aromaticity are lost if one goes from benzene to the singlet benzene dication but they are conserved in the triplet benzene dication. The latter only loses overall π stabilization.It was shown that the substituent effect can be numerically quantified, and then further interpreted not only in the case of the neutral benzene ring, but also in the case of the dicationic benzene ring, which is a 4n π-electron system showing a significantly reduced aromatic character. Although the dicationic form of benzene is the 4n π-electron system, it possesses most of the structural properties of neutral benzene and it may act as an effective medium for the substituent effect. What is more, as it is a nonaromatic species, in agreement with recent postulates8a it is much more sensitive to the substituent effect than its parent neutral system. This is revealed by very significant (about ten times larger than that in neutral benzene) reduction in delocalization due to substitution. Although the changes in delocalization due to substitution are dramatically larger when compared with neutral benzene, still similar mechanisms are responsible for the substituent effect, which is revealed by a linear correlation between the values of aromaticity indices and some Hammett constants originally estimated experimentally for neutral benzene derivatives. It should be pointed out that the above-mentioned relationships were found only for electron-donating substituents and not for electron-withdrawing ones, which was explained by the fact that the benzene dication itself should be considered as an electron-withdrawing moiety which may cooperate with electron-donating centres, but not with electron-withdrawing ones. This observation was also confirmed by SESE(1) values, which clearly indicated stabilizing interaction between dicationic benzene and the electron-donating substituents, and destabilizing interaction between the charged ring and the electron-withdrawing substituents. Finally, the para- and meta-type substitution in the dicationic ring was compared and the results were related to those observed for neutral benzene. The mechanism of interaction between the substituents and the ring evidently differs from that known for neutral disubstituted benzene. The interaction between the substituents (for both para- and meta-type substitutions) is rather limited and the primary effect is the one connected with interaction between the individual substituent and the ring.
More generally, our findings highlight that aromaticity indices can be misleading and are to be used with great precaution when charged systems are considered. The above remark is particularly true in the case of triplet state benzene dications, for which unusual values of aromaticity indices escape any rational interpretation.
Acknowledgements
MP, MD and JD acknowledge the financial support from National Science Centre of Poland (Grant no. 2011/03/B/ST4/01351). J.D. additionally acknowledges the financial support from University of Łódź Foundation (University of Łódź Foundation Award) and from the National Science Centre of Poland (Grant no. 2012/05/N/ST4/00203). F.M.B. thanks the Netherlands Organization for Scientific Research (NWO) for financial support. Calculations using the Gaussian 09 set of codes were carried out in Academic Computer Center Cyfronet AGH Kraków (http://www.cyfronet.krakow.pl) and Wrocław Center for Networking and Supercomputing (http://www.wcss.wroc.pl). Access to HPC machines and licensed software is gratefully acknowledged.References
- IUPAC. Compendium of Chemical Terminology, 2nd edn, (the “Gold Book”) compiled by A. D. McNaught and A. Wilkinson, Blackwell Scientific Publications, Oxford (1997). XML on-line corrected version: http://goldbook.iupac.org (2006) created by M. Nic, J. Jirat, B. Kosata; updates compiled by A. Jenkins. ISBN 0-9678550-9-8. DOI: 10.1351/goldbook.
- P. Muller, Glossary of terms used in physical organic chemistry, IUPAC Recommendation, 1994 Search PubMed.
- T. M. Krygowski and B. T. Stepień, Chem. Rev., 2005, 105, 3482 CrossRef CAS PubMed.
- T. M. Krygowski, K. Ejsmont, B. T. Stepień, M. K. Cyrański, J. Poatier and M. Sola, J. Org. Chem., 2004, 69, 6634 CrossRef CAS PubMed.
- T. M. Krygowski and M. K. Cyrański, Chem. Rev., 2001, 101, 1385 CrossRef CAS PubMed.
- (a) J. Kruszewski and T. M. Krygowski, Tetrahedron Lett., 1972, 13, 3839 CrossRef; (b) T. M. Krygowski, J. Chem. Inf. Comput. Sci., 1993, 33, 70 CrossRef CAS.
- T. M. Krygowski, B. T. Stepień, M. K. Cyrański and K. Ejsmont, J. Phys. Org. Chem., 2005, 18, 886 CrossRef CAS.
- (a) M. A. Dobrowolski, J. Kaniewski, T. M. Krygowski and M. K. Cyrański, Collect. Czech. Chem. Commun., 2009, 74, 115 CrossRef CAS; (b) T. M. Krygowski, M. A. Dobrowolski, M. K. Cyrański, W. P. Ozimiński and P. Bultinck, Comput. Theor. Chem., 2012, 984, 36 CrossRef CAS PubMed.
- M. Palusiak and T. M. Krygowski, New J. Chem., 2009, 33, 1753 RSC.
- J. Dominikowska and M. Palusiak, Phys. Chem. Chem. Phys., 2011, 13, 11976 RSC and references cited therein.
- (a) D. Lloyd, The chemistry of conjugated cyclic compounds: to be or not to be like benzene, Wiley, New York, 1990 Search PubMed; (b) M. B. Smith, March's Advanced Organic Chemistry: Reactions, Mechanisms, and Structure, Wiley, Hoboken, New Jersey, 7th edn, 2013 Search PubMed.
- M. Cohen, C. M. Anderson, A. Cowley, G. V. Coyne, W. Fawley, T. R. Gull, E. A. Harlan, G. H. Herbig, F. Holden and H. S. Hudson, et al , Astrophys. J., 1975, 196, 179 CrossRef CAS PubMed.
- (a) A. N. Witt, R. E. Schild and J. B. Kraiman, Astrophys. J., 1984, 281, 708 CrossRef CAS PubMed; (b) A. N. Witt and T. A. Boroson, Astrophys. J., 1990, 355, 182 CrossRef CAS PubMed; (c) D. G. Furton and A. N. Witt, Astrophys. J., 1992, 386, 587 CrossRef CAS.
- K. D. Gordon, A. N. Witt and B. C. Friedmann, Astrophys. J., 1998, 498, 522 CrossRef.
- (a) L. B. d'Hendecourt, A. Leger, G. Olofsson and W. Schmidt, Astron. Astrophys., 1986, 170, 91 CAS; (b) A. N. Witt and R. E. Schild, Astrophys. J., 1988, 325, 837 CrossRef CAS PubMed; (c) T. J. Wdowiak, B. Donn, J. A. Nuth, E. Chappelle and M. Moore, Astrophys. J., 1989, 336, 838 CrossRef CAS PubMed; (d) A. P. Jones, W. W. Duley and D. A. Williams, Q. J. R. Astron. Soc., 1990, 31, 567 CrossRef CAS; (e) A. N. Witt, K. D. Gordon and D. G. Furton, Astrophys. J., 1998, 501, 111 CrossRef; (f) S. S. Seahra and W. W. Duley, Astrophys. J., 1999, 520, 719 CrossRef CAS; (g) M. Hammonds, A. Pathak and P. J. Sarre, Phys. Chem. Chem. Phys., 2009, 11, 4458 RSC; (h) X. Chillier, P. Boulet, H. Chermette, F. Salama and J. Weber, J. Chem. Phys., 2001, 115, 1769 CrossRef CAS PubMed; (i) Y. M. Rhee, T. J. Lee, M. S. Gudipati, L. J. Allamandola and M. Head-Gordon, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 5274 CrossRef CAS PubMed.
- Interstellar molecules – their laboratory and interstellar habitat, ed.K. M. T. Yamada and G. Winnewisser, Springer, 2011 Search PubMed.
- R. Einholz and H. F. Bettinger, Angew. Chem., Int. Ed., 2013, 52, 9818 CrossRef CAS PubMed.
- (a) S. C. A. H. Pierrefixe and F. M. Bickelhaupt, Chem.–Eur. J., 2007, 13, 6321 CrossRef CAS PubMed; (b) S. C. A. H. Pierrefixe and F. M. Bickelhaupt, J. Phys. Chem. A, 2008, 112, 12816 CrossRef CAS PubMed; (c) S. C. A. H. Pierrefixe and F. M. Bickelhaupt, Aust. J. Chem., 2008, 61, 209 CrossRef CAS.
- (a) P. Hohenberg and W. Kohn, Phys. Rev. B: Solid State, 1964, 136, 864 Search PubMed; (b) W. Kohn and L. J. Sham, Phys. Rev. A, 1965, 140, 1133 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS PubMed; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS; (c) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS; (d) B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650 CrossRef CAS PubMed.
- S. Rayne and K. Forest, Comput. Theor. Chem., 2011, 976, 105 CrossRef CAS PubMed.
- N. X. Wang and A. K. Wilson, J. Chem. Phys., 2004, 121, 7632 CrossRef CAS PubMed.
- (a) L. A. Curtiss, K. Raghavachari, P. C. Redfern and J. A. Pople, J. Chem. Phys., 2000, 112, 7374 CrossRef CAS PubMed; (b) A. J. Cohen, P. Mori-Sanchez and W. Yang, Chem. Rev., 2012, 112, 289 CrossRef CAS PubMed; (c) S. F. Sousa, P. A. Fernandes and M. J. Ramos, J. Phys. Chem. A, 2007, 111, 10439 CrossRef CAS PubMed.
- J. Dominikowska and M. Palusiak, Struct. Chem., 2012, 23, 1173 CrossRef CAS.
- J. Poater, X. Fradera, M. Duran and M. Sola, Chem.–Eur. J., 2003, 9, 400 CrossRef CAS PubMed.
- (a) E. Matito, M. Duran and M. Sola, J. Chem. Phys., 2005, 122, 14109 CrossRef PubMed; (b) erratum, E. Matito, M. Duran and M. Sola, J. Chem. Phys., 2006, 125, 059901 CrossRef PubMed.
- (a) R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon, Oxford, 1990 Search PubMed; (b) R. F. W. Bader, Chem. Rev., 1991, 91, 893 CrossRef CAS.
- T. A. Keith, AIMAll program Version 13.02.26, 2013, http://aim.tkgristmill.com Search PubMed.
- (a) X. Fradera, M. A. Austen and R. F. W. Bader, J. Phys. Chem. A, 1999, 103, 304 CrossRef CAS; (b) X. Fradera, J. Poater, S. Simon, M. Duran and M. Sola, Theor. Chem. Acc., 2002, 108, 214 CrossRef CAS PubMed.
- P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. v. Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317 CrossRef CAS.
- P. v. R. Schleyer, M. Manoharan, Z. Wang, X. B. Kiran, H. Jiao, R. Puchta and N. J. R. v. Eikema Hommes, Org. Lett., 2001, 3, 2465 CrossRef CAS PubMed.
- (a) P. Lazzeretti, Prog. Nucl. Magn. Reson. Spectrosc., 2000, 36, 1 CrossRef CAS; (b) R. Islas, G. Martínez-Guajardo, J. O. C. Jiménez-Halla, M. Solà and G. Merino, J. Chem. Theory Comput., 2010, 6, 1131 CrossRef CAS; (c) J. J. Torres, R. Islas, E. Osorio, J. G. Harrison, W. Tiznado and G. Merino, J. Phys. Chem. A, 2013, 117, 5529 CrossRef CAS PubMed.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165 CrossRef CAS.
- L. P. Hammett, Physical Organic Chemistry, McGraw-Hill, New York, 1970 Search PubMed.
- M. Charton, Prog. Phys. Org. Chem., 1981, 13, 119 CrossRef CAS.
- T. M. Krygowski, M. Palusiak, A. Płonka and J. E. Zachara-Horeglad, J. Phys. Org. Chem., 2007, 20, 297 CrossRef CAS.
- V. Gogonea, P. v. R. Schleyer and P. R. Schreiner, Angew. Chem., Int. Ed., 1998, 37, 1945 CrossRef CAS.
Footnotes |
| † Dedicated to Professor Tadeusz Marek Krygowski, in recognition of his outstanding contribution to the field of physical organic chemistry. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c3cp54089h |
| This journal is © the Owner Societies 2014 |