Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structural investigation of a hydrogen bond order–disorder transition in a polar one-dimensional confined ice†
Jasper
Adamson
,
Nicholas P.
Funnell
,
Amber L.
Thompson
and
Andrew L.
Goodwin
*
Department of Chemistry, University of Oxford, Inorganic Chemistry Laboratory, South Parks Road, Oxford OX1 3QR, UK. E-mail: andrew.goodwin@chem.ox.ac.uk; Fax: +44 (0)1865 274690; Tel: +44 (0)1865 272137
First published on 16th December 2013
Abstract
The hydrogen-bond arrangement within crystalline 2,3,6,7,10,11-hexahydroxytriphenylene tetrahydrate (HHTP·4H2O) undergoes an order–disorder transition at 240 K, as evidenced by the emergence and disappearance of systematic absence violations in variable-temperature single-crystal X-ray diffraction measurements. The low-temperature ordered phase is polar with ferroelectric coupling between neighbouring one-dimensional ice-like columns of hydrogen-bonded H2O molecules. At temperatures above 240 K the material adopts a paraelectric state characterised by the absence of long-range ordering between column polarisations. We discuss the mapping of this phase transition onto the problem of frustration on the canonical Ising square lattice, and suggest that HHTP·4H2O is an obvious candidate for exploring switchable ferroelectric behaviour in confined ices.
Whether the dipolar nature of the water molecule might be translated into a polar form of ice is a question that has its origin in the very earliest studies of hydrogen bonding in solid phases of water.1,2 The configurational entropy of bulk ices is such that, to date, the only successful approaches to developing polar phases have involved symmetry lowering via e.g., surface layer deposition3,4 and dimensionality reduction in confined phases;5,6 even the nature of the supposedly-polar ice XI obtained on ion doping at low temperatures remains controversial.3,7,8 For some time, the focus of confinement studies has been on water-filled carbon and inorganic nanotubes.9–14 However, the primary application of polar ices—namely, in ferroelectric devices—relies on switchable bulk dipolar alignment, which is difficult for nanotube conglomerates; consequently the design strategy has recently shifted to exploiting aligned voids within nanoporous crystalline hosts.15,16 So, for example, water confined to nanochannels in the framework material La2Cu3[NH(CH2COO)2]6 exhibits antiferroelectric ordering below the confined liquid ↔ solid transition at 350 K;17 likewise, 1D “water wires” within a copper-based coordination polymer [Cu2ICuII(CDTA)(4,4′-bpy)] have been shown to undergo a spontaneous transition between liquid and ferroelectric states at 277 K.18
Despite the observation of dielectric hysteresis in the ferroelectric phase of [Cu2ICuII(CDTA)(4,4′-bpy)], perhaps the most obvious distinction between the formation of polar states in these confined ices and that in traditional ferroelectric phases such as PbTiO3 is that polarisation always seems to emerge on cooling from a liquid parent state rather than from a paraelectric phase.21 This suggests there exists only minimal distinction between the energy scales associated with long-range dipole alignment within and between nanopores and is likely the origin of the relatively weak and temperature-specific ferroelectric hysteresis observed for these systems.18
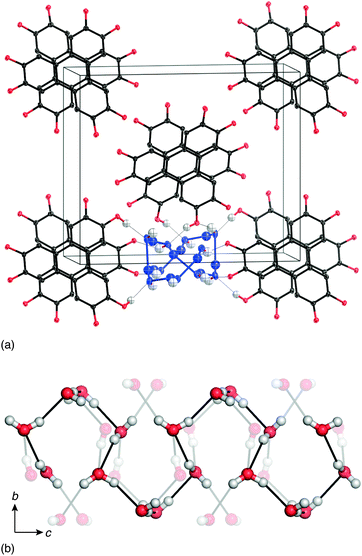
In this paper, we study the temperature-dependent evolution of 1D ice polarisation in the crystalline molecular hydrate HHTP·4H2O [Fig. 1].20 We show that 1D water-filled channels within HHTP·4H2O exhibit a well-defined polar ↔ paraelectric transition; as such the material is an excellent candidate for investigation into ice-based ferroelectric responses. HHTP-containing systems are of intense current interest in the field of molecular framework materials, where they are favoured for their thermal robustness and attractive porosity/sorption properties.22,23 Our focus is not on any covalent network assembled from HHTP, but rather on the hydrate of the molecule itself. As in all known HHTP cocrystals, the structure of this hydrate [shown in Fig. 1(b)] is dominated by the stacking of triphenylene cores into 1D columns;19,20,24 indeed this motif reflects the well-known role of triphenylene as the structural basis for a large and separate family of discotic liquid crystals.25 The surface of these columns is decorated by hydrophilic –OH groups, and consequently the voids between columns are ideally suited to water coordination. In the single previous structural study of HHTP·4H2O, it was shown that H2O molecules contained within these voids form an elaborate hydrogen-bonding network.20 Moreover, the water connectivity is one-dimensional such that the system can reasonably be considered a molecularly-confined 1D ice [Fig. 1(c)].
 | ||
| Fig. 1 (a) The HHTP molecule is planar with a hydrophobic core and hydrophilic exterior. (b) As in many solid triphenylenes, the crystal structure of HHTP·4H2O consists of a triangular array of triphenylene columns.19,20 The voids between neighbouring HHTP columns are strongly hydrophilic. It is within these channels that the water molecules are located. (c) Neighbouring water molecules within a single pore are connected via hydrogen-bonding interactions to form a 1D ice with its chain axis parallel to the crystal c axis. Some hydroxyl groups of the neighbouring HHTP molecules also participate in the hydrogen-bonding network; these are the transparent atoms and bonds shown here. In the reported structure of ref. 20, the presence of inversion centres results in O–H⋯H–O contacts between some neighbouring H2O molecules (circled). | ||
There were, however, two features of the ice-like hydrogen-bonding network proposed that seemed to us to be counterintuitive and so prompted our own structural study. First, the crystal symmetry reported in ref. 20 was a centrosymmetric orthorhombic space group Pbcn that places inversion centres within the network itself. This crystallographic subtlety has the effect of forcing direct O–H⋯H–O contacts that would be considered improbable within the established framework of ice physics [Fig. 1(c)]. And, second, the anisotropic displacement parameters associated with the water O atoms were anomalously large considering the temperature at which data were collected (100 K; root-mean-squared displacement 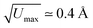 ).
).
In order to rationalise these crystallographic observations, we prepared a single-crystal sample of HHTP·4H2O and measured its X-ray diffraction pattern as a function of temperature (see ESI† for synthesis and experimental details).26–28 We collected diffraction data at 10 K intervals over the range 100–260 K, throughout both heating and cooling regimes. For completeness, we note that prolonged exposure of the crystal to the nitrogen cryostream at temperatures above 260 K resulted in gradual desolvation, which explains our focus on temperatures below this value.
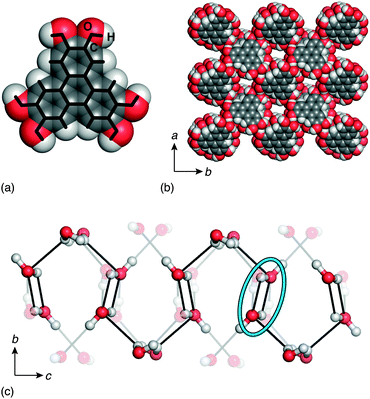
For all data sets, we were able to refine a satisfactory structural model based on the Pbcn solution of ref. 20; however, on close examination of the diffraction patterns themselves, we realised that a set of weak reflections forbidden in the Pbcn space group were unaccounted for by such a model. The intensity of these reflections was temperature dependent: they were strongest at the lowest temperatures but undetectable at 240 K. Making use of the associated reflection conditions, we could assign to the low-temperature structure the space group P21cn, which is a maximal subgroup of Pbcn obtained by removing the inversion symmetry operation. Subsequent refinement of the 100 K data set in this lower-symmetry setting gave an improved structural model in which both the hydrogen-bonding connectivity and water O atom displacement parameters made physical sense. This model is illustrated in Fig. 2(a), and full structural details are given as ESI.†
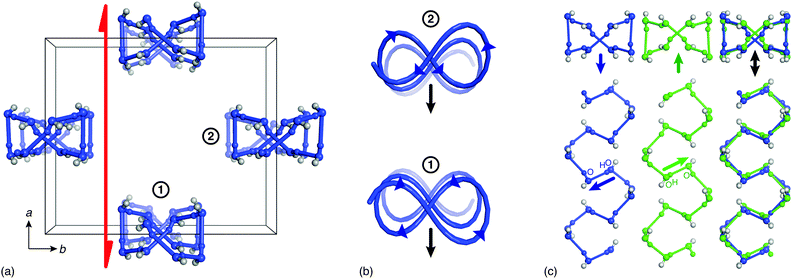
The distinction between P21cn and Pbcn structural models for low-temperature HHTP·4H2O is crucial because the former is a polar space group whereas the latter is not. Indeed the structural feature responsible for polarity within the P21cn model is precisely the ice-like hydrogen-bonding network within the water-filled channels: i.e., the ice rules break inversion symmetry [Fig. 2(b)]. While there are two polar 1D ice chains within the crystallographic unit cell, these are related to one another by the crystal symmetry in a way that reinforces the polarisation component parallel to the a crystal axis [Fig. 3]. In fact the chain geometry is of interest in its own right within the context of helical polymer motifs:29 it takes the rarely-observed form of a so-called “directed meso-helix”, an object with polarisation components both along and normal to the helix axis.30 So whereas the polarisation associated with 1D ices is usually parallel to the confinement axis,16,18 in this system the net polarisation is perpendicular to that axis (the parallel component cancelling between adjacent chains). From a practical viewpoint, the advantage is that the crystal habit is to grow as square prisms with their long axis parallel to c (i.e. the confinement axis—see ESI†); consequently the surface area is maximised in perpendicular directions—the optimal geometry for exploiting any ferroelectric response.
Turning next to the X-ray diffraction data collected at 240 K, we find that at this temperature the additional reflections forbidden in Pbcn but allowed in P21cn have zero intensity (within error). Consequently there is no crystallographic justification for lowering the symmetry beyond Pbcn in this case. As before, we obtain a numerically-satisfactory structure refinement using the model of ref. 20; however our earlier concerns regarding the physicality of this model would remain unaddressed. Instead we find that we obtain a better (and more meaningful) fit-to-data using a disordered Pbcn model containing equal proportions of the low-temperature P21cn structure and its inverse [Fig. 3(c)]. Such a model describes a paraelectric state in which the polarisations of neighbouring 1D hydrogen-bonding chains are sufficiently decoupled that long-range order disappears.
From a crystal chemical viewpoint, one might anticipate a relatively small enthalpy cost associated with interconversion of the two possible polarisation states. By comparing the HHTP molecule geometry in our P21cn structure with that observed in the Pbcn refinements (either ours for data collected at 240 K, or that reported in ref. 20), we find a root-mean-squared deviation in atomic positions of less than 0.04 Å. Consequently the interconversion mechanism involves concerted proton shuttling within the ice-like chains, much as has been observed elsewhere for ferroelectric materials based on bistable hydrogen-bonding interactions.31,32 In the present case, the inter-coupling mechanism is via hydrogen bonding between ice-like chains and the hydroxyl groups of the HHTP molecules. Because the H2O–HHTP hydrogen-bonding topology is independent of chain polarisation, the degree of ‘communication’ between chains will be small indeed.
The transition from polar to paraelectric states of HHTP·4H2O can be quantified using an order parameter derived from the intensities of those reflections unique to the P21cn space group (see ESI†). Fig. 4 shows the temperature evolution of a small relevant portion of the diffraction pattern across the transition: here the three reflections (011) (031) and (071) are forbidden in Pbcn and can be seen to decrease in intensity with heating. For each of these reflections, the corresponding order parameter ξ was calculated for each temperature according to
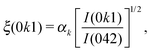 | (1) |
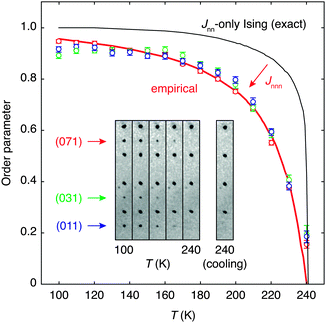 | ||
| Fig. 4 Thermal variation in the order parameter ξ, calculated from the intensities of three representative systematic absence violations according to eqn (1) (data points). The absence of a clear discontinuity at the transition temperature Tc ≃ 240 K suggests the order–disorder transition is second order in nature. Relevant sections of the single-crystal diffraction patterns are shown in the inset; these illustrate the disappearance of (0k1); k = 2n + 1 reflections on heating towards Tc. The nearest-neighbour square lattice Ising model discussed in the text predicts a sharper transition (thin line) than is observed experimentally.33 The inclusion of frustrated next-nearest-neighbour terms in the ordering Hamiltonian is known to give rise to a temperature dependency similar to the empirical curve fit shown here [bold line; eqn (5)]. | ||
To interpret the order parameter variation shown in Fig. 4 we construct a mapping of the polarisation state of HHTP·4H2O onto the square Ising model. Each 1D ice chain is capable of adopting either one of two configurations consistent with the ice rules—these are the orientations related to one another by the inversion centre present in Pbcn but absent in P21cn—and so can be assigned one of the two states e ∈ {1,−1} allowed in an Ising model. For each 1D chain there are four equidistant nearest-neighbours to which its Ising state (i.e. polarisation) will be coupled via subtle reorganisation of the connecting HHTP molecules [Fig. 5(a)]. The corresponding energy scale Jnn is (by symmetry) identical for all nearest-neighbours of all chains, giving the canonical Hamiltonian
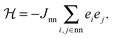 | (2) |
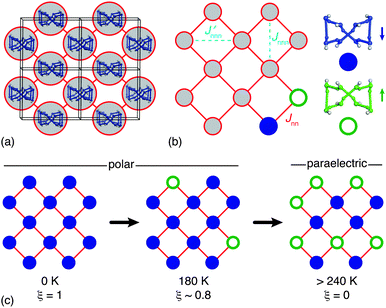 | ||
| Fig. 5 (a) Each 1D ice-like chain interacts with four neighbouring chains via HHTP hydroxyl groups. (b) The network of coupled chains has the square lattice topology. Because each chain can adopt one of two polarisation states (indicated here by filled and open circles; cf.Fig. 3), there is a direct mapping between long-range ordering of ice polarisations in HHTP·4H2O and the general problem of ordering on the Ising square lattice. Here Jnn describes the coupling strength between neighbouring 1D chains. By virtue of the orthorhombic crystal symmetry there are in fact two inequivalent next-nearest-neighbour couplings Jnnn and Jnnn′, the parity and relative magnitude of which will contribute to the discrepancy observed between experimental and theoretical ξ(T) curves as shown in Fig. 4. (c) At temperatures below Tc the system adopts a polar state in which the majority of sites share the same state (ξ > 0), but at temperatures greater than 240 K there is an equal population of both states and the system is said to be paraelectric. | ||
The topology of this coupled system is that of the square net and is two-dimensional because each 1D chain acts as a collective object. As such we can interpret the hydrogen bond order–disorder transition in HHTP·4H2O as a specific manifestation of the general and well-established problem of the square Ising model [Fig. 5(b)].33–35
In the case that nearest-neighbour interactions are the only interactions of relevance to the order–disorder process then the corresponding equilibrium behaviour of the square Ising model is known exactly.33 One anticipates a second-order phase transition between ordered (or, in the case of HHTP·4H2O, polar) and disordered (i.e., centrosymmetric) states at the critical temperature
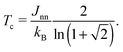 | (3) |
| ξ = [1 − sinh−4(2Jnn/kBT)]1/8, | (4) |
In practice it is likely that next-nearest-neighbour interactions cannot altogether be neglected in a physical system such as we study here. The inclusion of appropriate additional terms into the Hamiltonian of eqn (2) leads to a surprisingly-complex (and still controversial) system for which no exact solution is obtainable.35–37 Of relevance to the present situation is the observation that next-nearest-neighbour coupling constants Jnnn of opposite sign to Jnn have the effect of reducing the order parameter at lower temperatures to give a thermal variation more similar to that which we find to occur in HHTP·4H2O.35 This is the so-called ‘frustrated Ising model’, for which the phase transition is actually very weakly first-order.37 So there may be some suggestion that 1D ice polarisations couple in a ferroelectric sense for nearest neighbours in HHTP·4H2O but in an antiferroelectric sense for next-nearest neighbours. Actually the situation is even more complex in this case because the orthorhombic crystal symmetry gives rise to two distinct types of next-nearest neighbours—a problem for which we are not aware of any prior theoretical groundwork. What is known is that the relationship between Jnn and Tc given in eqn (3) holds even for the frustrated Ising case, and so we can estimate the interchain coupling strength in HHTP·4H2O to be ∼0.9 kJ mol−1. For comparison the interaction energy between two water molecules is estimated to lie between 18.8 and 30.1 kJ mol−1;38 consequently, this system displays an excellent discrimination between inter- and intra-chain energy scales. In the absence of a closed form for the temperature dependence of the order parameter for a frustrated square Ising model, we have used an empirical fit in Fig. 4 of the form
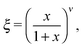 | (5) |
We attribute the accessibility of a bona fide paraelectric state in HHTP·4H2O to the very weak inter-chain coupling, which allows hydrogen bond disorder to occur without melting of the oxygen sublattice. We note specifically that the H2O oxygen atom positions remain well-defined even at temperatures above Tc ≃ 240 K; the larger-than-expected oxygen displacement parameter observed reflects only the superposition of two half-occupied oxygen sites associated with each of the two polarisation states. This observation distinguishes the behaviour of paraelectric HHTP·4H2O from that of the high-temperature phases of the related 1D ices [Cu(C6H4NO2)2] and [Cu2ICuII(CDTA)(4,4′-bpy)], within which long-range diffusive motion of the H2O occurs. Consistent with the small magnitude of Jnn is the negligible difference in HHTP geometries we observe across the order–disorder transition, which in turn explains the remarkable weakness of the additional diffraction intensities associated with symmetry breaking.
In conclusion, we find that the molecular hydrate HHTP·4H2O exhibits a hydrogen bond order–disorder transition near Tc ≃ 240 K that is associated with the development at low temperatures of long-range ferroelectric coupling between polar 1D ice chains [Fig. 5(c)]. The phase transition behaviour we observe maps qualitatively onto the problem of ordering on the Ising square lattice, with the accessibility of a paraelectric phase at temperatures above Tc suggesting that ferroelectric switching of the low-temperature polar phase should be possible. Indeed we intend to pursue this line of investigation in the immediate future. Finally, we note that our study also illustrates how molecular systems might host confined ice phases in a manner normally associated with porous covalent networks or carbon/inorganic nanotube arrays.
The authors gratefully acknowledge financial support from the E.P.S.R.C. (EP/G004528/2) and the E.R.C. (Grant Ref.: 279705).
References
- J. D. Bernal and R. H. Fowler, J. Chem. Phys., 1933, 1, 515–548 CrossRef CAS PubMed.
- S. T. Bramwell, Nature, 1999, 397, 212–213 CrossRef CAS PubMed.
- M. J. Iedama, M. J. Dresser, D. L. Doering, J. B. Rowland, W. P. Hess, A. A. Tsekouras and J. P. Cowin, J. Phys. Chem. B, 1998, 102, 9203–9214 CrossRef.
- X. Su, L. Lianos, R. Shen and G. A. Somorjai, Phys. Rev. Lett., 1998, 80, 1533–1536 CrossRef CAS.
- C. F. Luo, W. Fa, J. Zhou, J. M. Dong and X. C. Zeng, Nano Lett., 2008, 8, 2607–2612 CrossRef CAS PubMed.
- F. Mikami, K. Matsuda, H. Kataura and Y. Maniwa, ACS Nano, 2009, 3, 1279–1287 CrossRef CAS PubMed.
- S. J. Singer, J.-L. Kuo, T. K. Hirsch, C. Knight, L. Ojamäe and M. L. Klein, Phys. Rev. Lett., 2005, 94, 135701 CrossRef.
- S. J. Singer and C. Knight, in Advances in Chemical Physics, ed. S. A. Rice and A. R. Dinner, Wiley-Blackwell, Malden, U.S.A., 2012, vol. 147, pp. 1–74 Search PubMed.
- J. E. Bai, J. Wang and X. C. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 19664–19667 CrossRef CAS PubMed.
- Y. Maniwa, H. Kataura, M. Abe, S. Suzuki, Y. Achiba, H. Kira and K. Matsuda, J. Phys. Soc. Jpn., 2002, 71, 2863–2866 CAS.
- S. Ghosh, K. V. Ramanathan and A. K. Sood, Europhys. Lett., 2004, 65, 678–684 CrossRef CAS.
- Y. Maniwa, H. Kataura, M. Abe, A. Udaka, S. Suzuki, Y. Achiba, H. Kira, K. Matsuda, H. Kadowaki and Y. Okabe, Chem. Phys. Lett., 2005, 401, 534–538 CrossRef CAS PubMed.
- O. Byl, J.-C. Liu, Y. Wang, W.-L. Yim, J. K. Johnson and J. T. Yates, Jr., J. Am. Chem. Soc., 2006, 128, 12090–12097 CrossRef CAS PubMed.
- K. Koga, G. T. Gao, H. Tanaka and X. C. Zeng, Nature, 2001, 412, 802–805 CrossRef CAS PubMed.
- L. E. Cheruzel, M. S. Pometum, M. R. Cecil, M. S. Mashuta, R. J. Witterbort and R. M. Buchanan, Angew. Chem., Int. Ed., 2003, 42, 5452–5455 CrossRef CAS PubMed.
- B. Zhou, Y. Imai, A. Kobayashi, Z. Wang and H. Kobayashi, Chem. Lett., 2011, 1098–1100 CrossRef CAS.
- H. B. Cui, B. Zhou, L.-S. Long, Y. Okano, H. Kobayashi and A. Kobayashi, Angew. Chem., Int. Ed., 2008, 47, 3376–3380 CrossRef CAS PubMed.
- H.-X. Zhao, X.-J. Kong, H. Li, Y.-C. Jin, L.-S. Long, X. C. Zeng, R.-B. Huang and L.-S. Zheng, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 3481–3486 CrossRef CAS PubMed.
- T. L. Andresen, F. C. Krebs, N. Thorup and K. Bechgaard, Chem. Mater., 2000, 12, 2428–2433 CrossRef CAS.
- F. Thébault, L. Öhrström and M. Haukka, Acta Cryst., 2011, C67, o143–o145 Search PubMed.
- R. J. Nelmes, R. O. Piltz, W. F. Kuhs, Z. Tun and R. Restori, Ferroelectrics, 1990, 108, 165–170 CrossRef CAS.
- C. J. Doonan, D. J. Tranchemontagne, T. G. Glover, J. R. Hunt and O. M. Yaghi, Nat. Chem., 2010, 2, 235–238 CrossRef CAS PubMed.
- M. Hmadeh, Z. Lu, Z. Liu, F. Gándara, H. Furukawa, S. Wan, V. Augustyn, R. Chang, L. Liao, F. Zhou, E. Perre, V. Ozolins, K. Suenaga, X. Duan, B. Dunn, Y. Yamamto, O. Terasaki and O. M. Yaghi, Chem. Mater., 2012, 24, 3511–3513 CrossRef CAS.
- F. Toda, K. Tanaka, M. Takeshi, T. Nakai, I. Miyahara and K. Hirotsu, J. Phys. Org. Chem., 2000, 13, 39–45 CrossRef CAS.
- F. C. Krebs, N. C. Schiodt, W. Batsberg and K. Bechgaard, Synthesis, 1997, 1285–1290 CrossRef CAS PubMed.
- J. Cosier and A. M. Glazer, J. Appl. Crystallogr., 1986, 19, 105–107 CrossRef CAS.
- A. Altomare, G. Cascarano, C. Giacovazzo, A. Guagliardi, M. C. Burla, G. Polidori and M. Camalli, J. Appl. Crystallogr., 1994, 27, 435 Search PubMed.
- P. W. Betteridge, J. R. Carruthers, R. I. Cooper, K. Prout and D. J. Watkin, J. Appl. Crystallogr., 2003, 36, 1487 CrossRef CAS.
- L. Han and M. Hong, Inorg. Chem. Commun., 2005, 8, 406–419 CrossRef CAS PubMed.
- L. Plasseraud, H. Maid, F. Hampel and R. W. Saalfrank, Chem.–Eur. J., 2001, 7, 4007–4011 CrossRef CAS.
- Y.-Y. Yin, X.-Y. Chen, X.-C. Cao, W. Shi and P. Cheng, Chem. Commun., 2012, 48, 705–707 RSC.
- M. Szafranński, A. Katrusiak and G. J. McIntyre, Phys. Rev. Lett., 2002, 89, 215507 CrossRef.
- L. Onsager, Phys. Rev., 1944, 65, 117–149 CrossRef CAS.
- C. N. Yang, Phys. Rev., 1952, 85, 808–816 CrossRef.
- D. P. Landau, Phys. Rev. B, 1980, 21, 1285–1297 CrossRef CAS.
- A. Kalz, A. Honecker and M. Moliner, Phys. Rev. B, 2011, 84, 174407 CrossRef.
- S. Jin, A. Sen, W. Guo and A. W. Sandvik, Phys. Rev. B, 2013, 84, 144406 CrossRef.
- H. Yu and W. F. van Gunsteren, J. Chem. Phys., 2004, 121, 9549–9564 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis; experimental methods; X-ray single-crystal diffraction refinement details; order parameter calculations. CCDC 962532 and 962533. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c3cp53994f |
| This journal is © the Owner Societies 2014 |