Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Kinetic studies of the BrO + ClO cross-reaction over the range T = 246–314 K
Valerio
Ferracci
and
David M.
Rowley
*
Department of Chemistry, University College London, Christopher Ingold Laboratories, 20 Gordon Street, London WC1H 0AJ, UK. E-mail: d.m.rowley@ucl.ac.uk
First published on 4th October 2013
Abstract
The kinetics of the atmospherically important gas phase radical reaction between BrO and ClO have been studied over the temperature range T = 246–314 K by means of laser flash photolysis coupled with UV absorption spectroscopy. Charge-coupled-device (CCD) detection allowed simultaneous monitoring of both free radicals and the OClO product using ‘differential’ spectroscopy, which minimised interference from underlying UV absorbing species. In this way, the total rate coefficient for BrO + ClO → products (1) was measured, along with that for the OClO producing channel of this process BrO + ClO → OClO + Br (1c). These reaction rate coefficients are described by the Arrhenius expressions: k1/cm3 molecule−1 s−1 = (2.5 ± 2.2) × 10−12 exp[(630 ± 240)/T] and k1c/cm3 molecule−1 s−1 = (4.6 ± 3.0) × 10−12 exp[(280 ± 180)/T], where errors are 2σ, statistical only. An extensive sensitivity analysis was performed to quantify the potential additional systematic uncertainties in this work arising from uncertainties in secondary chemistry, absorption cross-sections and precursor concentrations. This analysis identified the reactions of initial and secondarily generated bromine atoms (specifically Br + O3 and Br + Cl2O) as particularly important, along with the reversible combination of ClO with OClO forming Cl2O3. Potential uncertainty in this latter process was used to define the lowest temperature of the present study. Results from this work indicate larger absolute values for k1 and k1c than those reported in previous studies, but a weaker negative temperature dependence for k1c than previously observed, resulting in a branching ratio for channel (1c) with a positive temperature dependence, in disagreement with previous studies. Reaction (1c) is the principal source of OClO in the polar stratosphere and is commonly used in atmospheric models as an indicator of stratospheric bromine chemistry. Thus these measurements might lead to a reinterpretation of modelled stratospheric OClO, which has also been suggested by previous comparisons of observations with atmospheric model studies.
Introduction
Increased atmospheric emissions of halogen-containing pollutants as a result of human activity over the twentieth century have had a dramatic impact on atmospheric ozone. This has generated significant scientific interest in understanding the reactivity of gas phase halogenated species. In particular, the self and cross-reactions of halogen monoxide free radicals, XO (where X = Cl, Br, I) which are the first-formed intermediates in the reaction of photolytically released halogen atoms with ozone, have been identified as key processes in ozone-depleting events through reaction cycles that behave catalytically. One of these reactions, the BrO + ClO cross-reaction, couples the chemistry of stratospheric bromine and chlorine1 and initiates a catalytic ozone-destroying cycle which has been estimated to be responsible for up to ∼50% of the observed ozone depletion over Antarctica during polar Springtime.2,3The BrO + ClO reaction has three known channels:
| BrO + ClO → BrCl + O2 | (1a) |
| → ClOO + Br | (1b) |
| → OClO + Br | (1c) |
The chlorine peroxy radical, ClOO, produced by channel (1b) is known to be weakly bound and, under all atmospheric conditions rapidly undergoes thermal dissociation to Cl + O2, so that channel (1b) effectively regenerates atomic halogens, Cl and Br, both of which react with ozone:
| Cl + O3 → ClO + O2 | (2) |
| Br + O3 → BrO + O2 | (3) |
In sunlight, channel (1a) also leads to ozone loss upon rapid solar photolysis of BrCl. On the other hand, solar photolysis of OClO produced in channel (1c) into O + ClO leads to a null cycle with respect to ozone as ozone is regenerated upon subsequent termolecular recombination of the O atom with O2. In terms of atmospheric measurements, at nighttime, OClO abundances are commonly used as a marker for BrO, since the BrO + ClO cross-reaction is the principal source of stratospheric OClO. In the absence of sunlight OClO concentrations depend crucially on the branching of reaction (1): as channel (1a) sequesters BrO into its nighttime reservoir form BrCl, OClO production is subsequently terminated once all BrO is converted into BrCl.4,5
Recent studies have highlighted the considerable uncertainties still affecting the product partitioning of reaction (1). Analysis of nighttime stratospheric OClO measurements by Canty and co-workers5 showed that atmospheric model predictions based on the kinetic parameters currently reported by JPL-NASA6 overestimate measured OClO abundances. To account for this observed discrepancy, Canty et al. questioned the channel partitioning currently recommended for reaction (1) and suggested a higher value for the branching ratio of channel (1a) and a corresponding lower one for that of channel (1c) at temperatures typical of the polar stratosphere. Moreover, simulations by Kawa et al.7 showed that uncertainties in the branching of the BrO + ClO cross-reaction can have a profound impact on the modelling of stratospheric ozone depletion, second only to the uncertainties in the photolysis rate of the ClO dimer, Cl2O2, thus calling for a better definition of the kinetics and therefore the product partitioning of the BrO + ClO cross-reaction at low temperatures.
The BrO + ClO cross-reaction has been the subject of several laboratory studies over a wide range of temperatures spanning from T = 220 K8,9 up to T = 408 K.10 Early studies came to conflicting conclusions on the overall rate coefficient, in part due to uncertainties on the nature of the reaction mechanism. A flash photolysis study by Basco and Dogra11 concluded that BrCl is the only product of reaction (1), whereas Clyne and Watson12 found no evidence for channel (1a) but identified channels (1b) and (c) as the product channels with equal partitioning using discharge flow with mass spectrometry. Toohey and Anderson13 were the first to fully elucidate a mechanism of the BrO + ClO cross-reaction identifying three product channels (1a)–(c) at T = 298 K using a discharge flow system coupled with mass spectrometry. These authors also found that BrCl was potentially produced in a vibrationally excited state. The study of Hills et al. represented the first attempt to characterise the temperature dependence of reaction (1) and that of its product branching. By means of discharge flow/mass spectrometry, these authors found a near zero temperature dependence of the kinetics over the range T = 241–408 K and reported the lowest values to date for the overall rate coefficient of reaction (1), k1.
Friedl and Sander (also Sander and Friedl) studied reaction (1) employing two complementary techniques over the same temperature range, T = 220–400 K. The results from a discharge flow mass spectrometry study8 and a flash photolysis UV absorption spectroscopy study9 are in excellent agreement with one another, reporting a value of k1 at T = 298 K approximately 60% greater than that previously reported by Hills et al. Moreover, Friedl and Sander observed a marked negative temperature dependence for the rate coefficients of all channels of the BrO + ClO cross-reaction, with the overall rate coefficient k1 increasing by about 70% from the highest to the lowest temperature of the range studied. The temperature dependence of the branching ratios reported by Friedl and Sander showed that channel (1a) is the minor pathway with α = k1a/k1 = 0.08 at T = 400 K and α = 0.06 at T = 220 K. Both studies of Friedl and Sander reported channel (1c) to be the dominant channel at T = 220 K. Poulet et al.14 studied the kinetics and products of the BrO + ClO cross-reaction at T = 298 K by means of discharge flow coupled with mass spectrometry. These authors reported a value of k1 in good agreement with that measured in both of the studies by Friedl–Sander. To this date, Poulet et al. are the only authors to have directly measured the BrCl yield from reaction (1), reporting a branching ratio of α = 0.12 at T = 298 K, higher than that measured in the Friedl–Sander studies.
Turnipseed et al.15 measured k1 and the branching ratios for channels (1a) and (c) over the range T = 234–406 K using discharge flow/mass spectrometry. Results from this work are in overall good agreement with both studies by Friedl and Sander, showing a negative temperature dependence of all reaction channels. However Turnipseed et al. measured a slightly stronger (negative) temperature dependence of the overall reaction rate coefficient than that reported in the studies of Friedl and Sander. Turnipseed et al. also reported a value of the branching ratio for channel (1a) at low temperatures, (α = 0.10) slightly higher than that at ambient temperature (α = 0.09), contrary to the trend observed by Friedl and Sander. Results from previous studies of reaction (1) are summarised in Table 1. Current IUPAC16 and JPL-NASA6 recommendations are based on the discharge flow/mass spectrometry and the flash photolysis studies of Friedl and Sander and those of Turnipseed et al.
| Ref. | Techniquea | T/K | p/Torr | k 1/10−11 cm3 molecule−1 s−1 | α = k1a/k1 | β = k1b/k1 | γ = k1c/k1 |
|---|---|---|---|---|---|---|---|
| a FP/UV = flashlamp photolysis/UV absorption spectroscopy; DF/MS = discharge flow/mass spectrometry; DF/RF/LMR = discharge flow/resonance fluorescence/laser magnetic resonance; LP/UV = laser photolysis/UV absorption spectroscopy. b Assumed. c At T = 304 K. | |||||||
| Basco and Dogra11 | FP/UV | 298 | 760 | 0.25 | 1b | ||
| Clyne and Watson12 | DF/MS | 298 | 0.75 | 1.34 ± 0.2 | 0 | 0.5 ± 0.18 | 0.5 ± 0.18 |
| Toohey and Anderson13 | DF/RF/LMR | 298 | 1–2 | 1.4 ± 0.2 | 0.45 | ||
| Hills et al.10 | DF/MS | 241–408 | 0.82 ± 0.1 | <0.02 | 0.45 ± 0.1 | 0.55 ± 0.1 | |
| Friedl and Sander8 | DF/MS | 220–400 | 1 | 1.29 ± 0.2 | 0.08 ± 0.03 | 0.48 ± 0.07 | |
| Sander and Friedl9 | FP/UV | 220–400 | 50–700 | 1.29 ± 0.16 | 0.59 ± 0.1 | ||
| Poulet et al.14 | DF/MS | 298 | 0.6–1 | 1.13 ± 0.15 | 0.12 ± 0.05 | 0.43 ± 0.10 | |
| Turnipseed et al.15 | DF/MS | 234–406 | 2 | 1.08 ± 0.2c | 0.09 ± 0.02c | 0.48 ± 0.07c | |
| IUPAC16 | 1.4 | 0.07 | 0.44 | 0.49 | |||
| JPL-NASA6 | 1.26 | 0.08 | 0.44 | 0.48 | |||
| This work | LP/UV | 246–314 | 760 | 1.86 ± 0.11 | 0.59 ± 0.06 | ||
Notwithstanding the reasonable agreement of previous studies on the kinetics of the BrO + ClO cross-reaction at ambient temperatures, considerable uncertainty exists for the kinetics of the individual channels and therefore the product partitioning of reaction (1) at low temperatures. The aims of this study were therefore to characterise the kinetics and branching of the BrO + ClO cross-reaction as a function of temperature using laser flash photolysis coupled with UV absorption spectroscopy. The unique properties of a charge-coupled device (CCD) detection system allowed real-time simultaneous monitoring of the two radical reagents, BrO and ClO, and of one of the products, OClO, thus enabling a direct characterisation of the total rate coefficient, k1, and of the branching for channel (1c), defined here as γ = k1c/k1.
Experimental
The kinetics of the BrO + ClO cross-reaction were studied using laser flash photolysis of Cl2–Cl2O–Br2–O3–O2–N2 gas mixtures coupled with broadband time-resolved UV absorption spectroscopy. As the principles of this technique and the apparatus used have been described in detail previously,17 only a concise account is given here.Gas handling
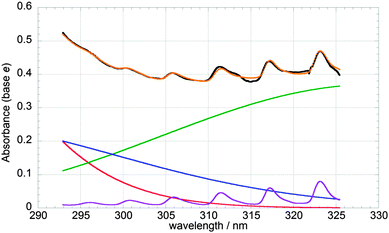
All precursor gases were delivered in flows via Teflon (PTFE) tubing to a Pyrex mixing line where they mixed with a nitrogen (BOC, >99.98% purity) carrier flow. The flow rates of nitrogen and oxygen (BOC, >99.99% purity) were set using mass flow controllers (MKS), whereas that of Cl2 (BOC, supplied as 5% by volume in N2; >99% purity) was controlled using needle valves and measured using a separately calibrated glass ball meter. Cl2O was produced in situ using the method originally described by Hinshelwood and Pritchard,18 whereby a known flow of the diluted Cl2 gas was passed through a trap containing solid dried yellow mercuric(II) oxide (HgO, Sigma-Aldrich, >99% purity). Bromine vapour was introduced into the gas mixture by passing a flow of nitrogen through a bubbler containing liquid Br2 (Acros, 99.8% purity) kept at T = 0 °C inside a Dewar flask. The bromine content in the precursor mixture was quantified spectroscopically by fitting Br2 absorption cross-sections taken from JPL-NASA to an absorbance spectrum recorded in static (i.e., in the absence of photolysis) experiments over the range λ = 450–580 nm (spectral procedures are discussed in detail below). Calculations using flow rates and the known vapour pressure of liquid bromine at T = 0 °C were in good agreement with the bromine abundances determined in the gas mixtures spectroscopically. Ozone was generated by flowing oxygen gas through a cell incorporating a mercury “pen-ray” lamp. Production of O3 using this method was calibrated separately as a function of oxygen flow through the cell via UV absorption spectroscopy.Typical concentrations of precursor gases in the pre-photolysis gas mixture were as follows: [Cl2] = 1–1.6 × 1016 molecule cm−3; [Cl2O] = 4–5 × 1015 molecule cm−3; [Br2] = 1.5–2.0 × 1016 molecule cm−3; [O3] = 2–2.5 × 1015 molecule cm−3; [O2] = 1 × 1018 molecule cm−3; [N2] = balance to 1 atm. Static (non-photolysed) spectra of the precursor gas mixture also revealed the presence of a small OClO impurity, typically corresponding to [OClO] = 5–10 × 1013 molecule cm−3, as evidenced in the absorption spectrum shown in Fig. 1, analysis of which is discussed below. As such OClO impurities typically arise from the presence of water vapour in vessels containing chlorine gas, the trap containing mercuric oxide was systematically cleaned and dried for 48 hours, then re-assembled containing fresh HgO. However, despite these procedures, the characteristic peaks resulting from the OClO spectrum were consistently observed at λ > 310 nm. As no reaction between the species in the precursor mixture is known to generate OClO, it was suspected that water vapour back-diffusing into the system was the cause of the impurity. To address this, a dry nitrogen flow was left running for 12–24 hours prior to experiments but the OClO signal was persistently observed. Following further experiments, it was observed that the peaks attributed to OClO in the precursor mixture disappeared once the ozone flow had been switched off. This suggested a correlation between ozone and the observed OClO impurity. An analogous unexpected and unexplained OClO signal was also observed in the discharge flow mass spectrometry study of the BrO + ClO cross-reaction by Friedl and Sander. These authors reported a large background signal for OClO at m/z = 67 for a gas mixture including Cl2O and ozone and attributed this to an unidentified chemical process. To this day, no reaction of gas phase ozone with either Cl2 or Cl2O yielding OClO has been reported. The presence of OClO in the precursor mixture did not however constitute a significant hindrance per se to the experiments and was in any case taken into account in the analysis of the results.
Gases were flowed continuously from the mixing line into the reaction cell, so that a fresh gas mixture was available for each photolysis event. The reaction cell consisted of the central section of a double-jacketed Spectrosil quartz vessel of 98.2 cm in length and 1.48 cm internal diameter, the inner jacket of which was connected to a recirculating thermostat unit (Huber CC 180) which allowed regulation of the cell temperature with a precision of ±0.5 K, which was calibrated separately. Flow-out of the gaseous mixture from the reaction cell during an experiment was minimal and was in any case accounted for in the analytical procedures.
Radical generation
BrO and ClO radicals were generated from reactions initiated by the photolysis of the Cl2–Cl2O–Br2–O3–O2–N2 precursor mixture. An excimer laser (Lambda Physik COMPex 201) operating at λ = 351 nm with output of typically ∼110 mJ per pulse provided the photolytic pulse. The beam exiting the laser was collimated then expanded using a pair of fused silica cylindrical lenses, then further collimated to match the cross-sectional area of the reaction cell. A dichroic reflector was used to direct the laser beam along the length of the reaction cell in a direction opposite to that of the UV analysing light.Atomic halogens were the principal products of the photolysis of the precursor gases:
| Cl2 + hν → 2Cl | (4) |
| Br2 + hν → 2Br | (5) |
The photolysis of Cl2O into Cl + ClO represented an additional minor photolysis pathway given the relatively small absorption cross-section of Cl2O at λ = 351 nm compared to those of Cl2 and Br2 (σCl2 and σBr2 are respectively ∼25 and ∼6 times greater than σCl2O at the laser wavelength).6 Under the experimental conditions used in this work, of excess Br2 over Cl2O and O3, chlorine atoms rapidly reacted to produce bromine atoms viareaction (6):
| Cl + Br2 → BrCl + Br | (6) |
Thus, the main sources of ClO and BrO radicals were the reactions of Br atoms with the Cl2O and O3 precursors respectively:
| Br + Cl2O → ClO + BrCl | (7) |
| Br + O3 → BrO + O2 | (3) |
The chlorine counterparts of reactions (7) and (3):
| Cl + Cl2O → ClO + Cl2 | (8) |
| Cl + O3 → ClO + O2 | (2) |
The photolysis of the OClO impurity, the provenance of which is discussed above, also contributed to the formation of the required radicals:
| OClO + hν → O + ClO | (9) |
As well as directly producing the ClO radical, photolysis of OClO generated O atoms whose fate, under experimental conditions, was mainly to react with the Br2 and Cl2O precursor gases to produce further BrO and ClO respectively (with ca. 6% of O atoms combining with O2 to form a small additional amount of ozone):
| O + Br2 → BrO + Br | (10) |
| O + Cl2O → ClO + ClO | (11) |
From rate calculations using k10 reported by Harwood et al. and k11 from JPL-NASA along with the precursor concentrations used in the current work, it was calculated that typically 92% of the O atoms generated by the photolysis of OClO would be expected to react through reaction (10) with the remaining 8% undergoing reaction (11) at T = 298 K.
Radical monitoring
Species in the reaction mixture were monitored by means of UV absorption spectroscopy using charge-coupled device (CCD) detection, which has been described in detail previously.20 The source of ultraviolet radiation employed was a 75 W continuous xenon arc lamp (Hamamatsu L2174); light from which was passed once through the reaction cell and then focused onto the entrance slit of a 0.25 m astigmatic Czerny–Turner spectrograph (Chromex 250IS). A 300 grooves mm−1 diffraction grating was employed in this study and the width of the spectrograph entrance slit was set to 75 μm, resulting in a spectral resolution of 1.1 nm full width half maximum (FWHM), as determined by recording and analysing emission spectra from a mercury “pen-ray” lamp. Typically a spectral range λ = 270–325 nm was monitored in the photolysis experiments carried out in the current work.Wavelength-resolved light from the spectrograph was imaged onto the top 31 rows of a CCD detector consisting of a two dimensional array of light sensitive pixels arranged in 1152 rows by 298 columns; the remaining rows of the detector were optically masked. Pixels converted incident light intensity into photocharge; each row of photocharge was then moved out of the illuminated region by means of charge transfer, thus allowing the sequential acquisition of spectra. Therefore, for each experiment, spectrally and temporally resolved transmission spectra of the reaction mixture were recorded before, during, and after photolysis. The temporal resolution of the experiment was dictated by the time elapsed between each charge transfer event (shift time), which was typically set to 5 μs in the current work.
Analysis
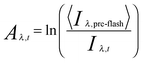 | (i) |
 | (ii) |
The ClO cross-section used to fit in eqn (ii) was obtained by degrading the higher resolution (0.8 nm FWHM) ClO differential cross-section, σClO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) diff, calibrated at the (12, 0) peak (λ = 275.2 nm) of the A2Π ← X2Π vibronic transition, measured by Boakes et al.21 to the lower resolution (1.1 nm FWHM) used in the present study. This procedure has been described in detail previously22 hence a brief summary is given here. Back-to-back experiments consisting of the photolysis of Cl2O–Cl2–N2 mixtures were performed, alternating between high (0.8 nm FWHM) and low (1.1 nm FWHM) resolution spectral settings but otherwise under identical conditions. Each experiment typically consisted of 20 co-added photolysis events. For the high resolution runs, time-resolved [ClO] was quantified using the parameterisation of σClO
diff, calibrated at the (12, 0) peak (λ = 275.2 nm) of the A2Π ← X2Π vibronic transition, measured by Boakes et al.21 to the lower resolution (1.1 nm FWHM) used in the present study. This procedure has been described in detail previously22 hence a brief summary is given here. Back-to-back experiments consisting of the photolysis of Cl2O–Cl2–N2 mixtures were performed, alternating between high (0.8 nm FWHM) and low (1.1 nm FWHM) resolution spectral settings but otherwise under identical conditions. Each experiment typically consisted of 20 co-added photolysis events. For the high resolution runs, time-resolved [ClO] was quantified using the parameterisation of σClO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) diff from Boakes et al. at this resolution. This procedure returned [ClO]t decay traces that agreed within 2% between each run and therefore indicated that the chemistry and conditions within the reaction cell were unchanged during the back-to-back experiments. Given this determination of [ClO]t and hence the average ClO concentration over the radical decay, the low resolution σClO was obtained by rearranging the Beer–Lambert law:
diff from Boakes et al. at this resolution. This procedure returned [ClO]t decay traces that agreed within 2% between each run and therefore indicated that the chemistry and conditions within the reaction cell were unchanged during the back-to-back experiments. Given this determination of [ClO]t and hence the average ClO concentration over the radical decay, the low resolution σClO was obtained by rearranging the Beer–Lambert law:
 | (iii) |
The absorption cross-sections of BrO and OClO were taken from previous work of Wilmouth et al.23 and of Wahner et al.24 respectively. The high-resolution (0.4 nm and 0.25 nm FWHM respectively) cross-sections reported in these studies were degraded to match the lower resolution employed in present study (1.1 nm FWHM) by applying Gaussian averaging kernels (specifically, a 93-point kernel for σBrO and a 29-point kernel for σOClO, both chosen as a result of the data interval). In addition, to account for the temperature dependence of vibronic absorption bands, the reference cross-sections were interpolated to each experimental temperature using the spectra recorded at T = 228 K and T = 298 K for σBrO and at T = 204 K and T = 296 K for σOClO. This procedure assumed a linear temperature dependence of the cross-sections of these halogen oxides, the validity of which has been confirmed by previous studies.21,25
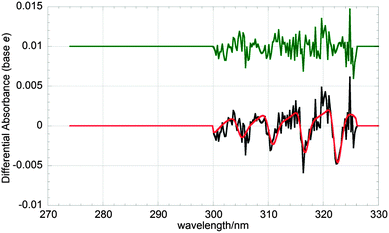
The absence of any residual spectral structure at each temperature following spectral fitting and subtraction (as shown in Fig. 3 and 4) added confidence to spectral smoothing and to the linear interpolation of the reference cross-sections over the temperature range used. The effects of potential errors in the cross-sections used were in any case tested using sensitivity analysis discussed below.
 | ||
| Fig. 4 Typical differential spectrum (black) and fit (red) averaged over t = 110–190 μs post photolysis of a precursor gas mixture. The fit consists of a linear combination of appropriately scaled ClO, BrO and OClO cross-sections, according to eqn (ii). Residuals (green) have been offset by +0.03 absorbance units for clarity. | ||
As ClO, BrO and OClO are all absorbers with spectral structure, differential fitting procedures were employed in fitting to the recorded spectra. This method, described in detail elsewhere,21 allows unequivocal monitoring of such absorbers. The procedure involves the high-pass filtering of experimental spectra and reference cross-sections to extract the structured part of the absorptions/cross-sections alone. A composite of the reference cross-sections is then fitted to the experimental spectra, minimising the sum of squares of residuals and using eqn (ii) to extract concentrations. A typical differential fit to a time-averaged spectrum containing contributions from ClO, BrO and OClO is shown in Fig. 4. This procedure was carried out for every time-resolved spectrum recorded using the CCD, to obtain temporal concentration profiles.
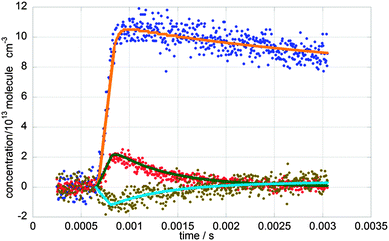
A typical concentration plot for [ClO], [BrO] and [OClO] is shown in Fig. 5, along with their respective kinetic fits (discussed below). As explained above, photolysis of the pre-existent OClO impurity present in the precursor mixture gives rise to the negative apparent OClO concentration in the immediate post-photolysis period. At longer timescales following photolysis, [OClO] (which should more correctly be termed Δ[OClO]) recovers to approximately its pre-photolysis values, resulting in the absence of significant OClO signal in the absorbance spectra recorded over these timescales, discussed above.
 | (iv) |
[BrO]t = [BrO]0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−k1′ t) exp(−k1′ t) | (v) |
Similarly, OClO build-up viachannel (1c) could be expressed as:
 | (vi) |
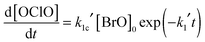 | (vii) |
Separating the variables, invoking stoichiometry and integrating results in:
 | (viii) |
Temporal concentration traces simulated using eqn (v) and (viii) were fitted to the experimental [BrO]t and [OClO]t by least-square routines optimising the values of [BrO]0, [OClO]0, k1′ and k1c′. The optimised values of the pseudo-rate coefficients k1′ and k1c′ were then divided by the average [ClO] to obtain values of k1 and k1c.
This pseudo-first order model returned excellent fits to BrO and OClO temporal traces at near-ambient temperatures (T ≥ 283 K). However this model failed to reproduce the behaviour of [OClO]t observed at lower temperatures (T < 283 K). This was attributed to complicating secondary chemistry arising at lower temperatures, principally the equilibration reaction:
| ClO + OClO + M ⇄ Cl2O3 + M | (12, −12) |
This equilibrium shifts towards the products at lower temperatures, so that whilst OClO is produced viachannel (1c) it is, at the same time, undergoing association with ClO (present in excess under experimental conditions) resulting in OClO being sequestered into Cl2O3.
Numerical integration studies showed that, given the excess of ClO, the rate of the forward reaction (12) became comparable to that of the OClO build-up from reaction (1) at low temperatures, thus imparting a diversion from the expected pseudo-first order behaviour of [OClO]t. As the [BrO] trace was only marginally affected by Cl2O3 formation, and as [ClO] remained relatively constant over the timescale of BrO decay, even at low temperatures, the pseudo-first order model could still be used to obtain reliable values of k1 even at T < 283 K.
Not only could the pseudo-first order model not account for Cl2O3 formation at low temperatures, but also, considering the rapid timescale over which reaction (1) took place, the possibility of the decay chemistry not being entirely decoupled from the formation chemistry could not be ignored. For these reasons, full numerical integration was invoked and a FACSIMILE26 model was developed, including all the known reactions of the species contained in the reaction mixture. These reactions are listed in Table 2 along with the Arrhenius expression for their kinetics where available. Simulated traces generated using FACSIMILE were fitted to the recorded temporal traces of [ClO], [BrO] and [OClO] via least-squares minimization of the residuals by optimising [Cl]0, [Br]0, [OClO]0, k1 and k1c. A typical FACSIMILE fit for traces recorded at T = 298 K is shown in Fig. 5. The FACSIMILE model successfully reproduced the observed temporal behaviour of all species including [OClO] at low temperatures and resulted in excellent fits to the recorded traces at all temperatures. Values of k1 and of k1c (at T ≥ 283 K) from the pseudo-first order model were in excellent agreement with those obtained from the FACSIMILE fits, within a maximum of 10% of one another. This agreement added confidence to the sensitivity of the experimental conditions principally to the BrO + ClO cross-reaction.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/RT) where appropriate
exp(−Ea/RT) where appropriate
| Reaction | k/cm3 molecule−1 s−1 | Ref. |
|---|---|---|
| a Units s−1. b At p = 760 Torr. c At T = 298 K. | ||
| Br + Cl2O → BrCl + ClO | 2.1 × 10−11 exp(−470/T) | JPL-NASA6 |
| Cl + Cl2O → Cl2 + ClO | 6.2 × 10−11 exp(130/T) | JPL-NASA6 |
| Br + O3 → BrO + O2 | 1.7 × 10−11 exp(−800/T) | JPL-NASA6 |
| Cl + O3 → ClO + O2 | 2.3 × 10−11 exp(−200/T) | JPL-NASA6 |
| Cl + Br2 → BrCl + Br | 2.3 × 10−10 exp(135/T) | Bedjanian et al.19 |
| BrO + ClO → BrCl + O2 | k 1a | This work |
| BrO + ClO → Br + ClOO | k 1b | This work |
| BrO + ClO → Br + OClO | k 1c | This work |
| ClOO → Cl + O2 | 2.4 × 109![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1452/T)a,b exp(−1452/T)a,b |
JPL-NASA6 |
| ClO + ClO → Cl2O2 | 3.5 × 10−14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(700/T)b exp(700/T)b |
Ferracci and Rowley27 |
| Cl2O2 → ClO + ClO | 1.0 × 1014![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−8505/T)a,b exp(−8505/T)a,b |
Ferracci and Rowley27 |
| ClO + ClO → Cl2 + O2 | 1.0 × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1590/T) exp(−1590/T) |
Ferracci and Rowley22 |
| ClO + ClO → Cl + ClOO | 3.0 × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2450/T) exp(−2450/T) |
Ferracci and Rowley22 |
| ClO + ClO → OClO + Cl | 3.5 × 10−13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1370/T) exp(−1370/T) |
Ferracci and Rowley22 |
| BrO + BrO → Br2 + O2 | 2.8 × 10−14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(860/T) exp(860/T) |
Ferracci et al.28 |
| BrO + BrO → 2Br + O2 | 2.4 × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(40/T) exp(40/T) |
Ferracci et al.28 |
| Br + Cl2 → BrCl + Cl | 1.7 × 10−15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
Dolson and Leone29 |
| Br + BrCl → Cl + Br2 | 3.3 × 10−15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
Baulch et al.30 |
| Cl + BrCl → Cl2 + Br | 1.45 × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
Clyne and Cruse31 |
| ClO + OClO → Cl2O3 | 3.1 × 10−14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(1095/T)b exp(1095/T)b |
JPL-NASA6 |
| Cl2O3 → ClO + OClO | 1.9 × 1013![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−6059/T)a,b exp(−6059/T)a,b |
JPL-NASA6 |
| Cl + OClO → ClO + ClO | 3.4 × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(160/T) exp(160/T) |
JPL-NASA6 |
| Br + OClO → BrO + ClO | 2.6 × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1300/T) exp(−1300/T) |
JPL-NASA6 |
| Cl + BrO → Br + ClO | 2 × 10−10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
Toohey–Anderson13 |
| Cl + ClO → Cl2 + O | 1.7 × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−4590/T) exp(−4590/T) |
Baulch et al.30 |
| O + ClO → Cl + O2 | 2.8 × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(85/T) exp(85/T) |
JPL-NASA6 |
| O + BrO → Br + O2 | 1.9 × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(230/T) exp(230/T) |
JPL-NASA6 |
| O + OClO → ClO + O2 | 2.4 × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−960/T) exp(−960/T) |
JPL-NASA6 |
| O + Cl2O → ClO + ClO | 2.7 × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−530/T) exp(−530/T) |
JPL-NASA6 |
| ClOO + O → ClO + O2 | 5.0 × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
Basco and Dogra32 |
| O + BrCl → BrO + Cl | 2.10 × 10−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
Clyne et al.33 |
| Br2 + O → BrO + Br | 5.1 × 10−13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(989/T) exp(989/T) |
Harwood et al.17 |
| O + O3 → O2 + O2 | 8.0 × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2060/T) exp(−2060/T) |
JPL-NASA6 |
| O + Cl2 → ClO + Cl | 7.4 × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1650/T) exp(−1650/T) |
Wine et al.34 |
| O + O2 → O3 | 8.4 × 10−16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(844/T)b exp(844/T)b |
JPL-NASA6 |
| O + OClO → ClO3 | 8.9 × 10−13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(367/T)b exp(367/T)b |
JPL-NASA6 |
Gas flow-out from the reaction cell was included in both the pseudo-first order model and the FACSIMILE model as a zero-order decay superimposed to the temporal behaviour of the species monitored. Averaging imparted to the recorded traces by the simultaneous illumination of 31 rows of the CCD detector was also taken into account by applying a 31-point sliding average to the simulated traces in both models, as has been discussed previously.20
The further possibility of the (unknown) mechanism forming OClO in the precursor mixture having an effect on the temporal profile of [OClO] and, consequently, on the extracted kinetics of channel (1c) was also investigated. Photolysis experiments were performed in the absence of Br2 but under otherwise identical conditions to those described above. The observed [OClO] temporal trace consisted of a negative step function, showing no appreciable OClO recovery following photolysis. This was consistent with FACSIMILE simulations, showing that (as expected) OClO production via one of the bimolecular channels of the ClO self-reaction would be too slow to be appreciable over the timescales used.22 It was therefore concluded that the mechanism forming OClO in the precursor mixture, although unidentified, did not significantly affect the [OClO] temporal trace.
Since the reaction mixture was designed to rapidly regenerate ClO radicals from the atomic halogens produced by some of the channels of reaction (1), the ClO decay profile exhibited sensitivity to only some of these channels. Specifically, channel (1c) would not be expected to contribute to the observed ClO decay as the Br atom produced therein would, under experimental conditions, regenerate ClO viareaction (7). Channel (1b), on the other hand, would actually be expected to result in ClO production following the rapid thermal dissociation of the product ClOO and the subsequent rapid reaction of Cl with Cl2O (reaction (8)). Channel (1a) would conversely result in ClO loss. Therefore analysis of the ClO temporal profile, also taking into account other ClO loss processes (notably ClO dimerisation), should in principle reveal sensitivity to (the difference between) k1a and k1b. In practice, however, numerical modelling using FACSIMILE indicated that the [ClO] temporal trace possessed insufficient sensitivity to channel (1a) to quantify k1a if k1b were stipulated (from the difference between k1 and k1c). Furthermore, even if some degree of independent sensitivity to k1a were present, it would be critically dependent on the secondary chemistry exhibited by the ClO radical. This would become particularly problematic at low temperatures, where the poorly characterised association of ClO + OClO, reactions (12, −12), becomes increasingly significant. It was therefore not possible to reliably determine k1a alone with the radical monitoring system employed; the values of k1a and k1b obtained from fitting the FACSIMILE model to the experimental trace were therefore only considered meaningful when combined into (k1a + k1b).
Results
The BrO + ClO cross-reaction was studied at six temperatures over the range T = 246–314 K. The data collected consisted of at least 8 experiments consisting of at least one hundred co-added photolysis events at each temperature. The values of k1 and k1c obtained from fitting the FACSIMILE model to the experimental traces are given in Table 3, along with values of the branching ratio for channel (1c), γ = k1c/k1.| T/K | k 1/10−11 cm3 molecule−1 s−1 | k 1c/10−11 cm3 molecule−1 s−1 | γ = k1c/k1 |
|---|---|---|---|
| 246 | 3.1 ± 0.10 | 1.52 ± 1.0 | 0.48 ± 0.31 |
| 257 | 2.7 ± 0.31 | 1.26 ± 0.50 | 0.46 ± 0.15 |
| 269 | 2.74 ± 0.03 | 1.26 ± 0.40 | 0.46 ± 0.14 |
| 283 | 2.58 ± 0.01 | 1.3 ± 0.30 | 0.50 ± 0.10 |
| 298 | 1.86 ± 0.11 | 1.11 ± 0.14 | 0.59 ± 0.06 |
| 314 | 1.83 ± 0.04 | 1.15 ± 0.15 | 0.63 ± 0.07 |
The Arrhenius expressions obtained for k1 and k1c from this study are reported below, along with those from the latest JPL-NASA evaluation. The errors reported are 2σ, statistical only from the Arrhenius fits.
k1/cm3 molecule−1 s−1 = (2.5 ± 2.2) × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(630 ± 240)/T] exp[(630 ± 240)/T] |
k1c/cm3 molecule−1 s−1 = (4.6 ± 3.0) × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(280 ± 180)/T] exp[(280 ± 180)/T] |
cf. JPL-NASA:
k1/cm3 molecule−1 s−1 = 3.3 × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(400/T) exp(400/T) |
k1c/cm3 molecule−1 s−1 = 9.5 × 10−13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(550/T) exp(550/T) |
Table 4 reports the Arrhenius parameters for reaction (1) and channel (1c) from previous studies, from the JPL-NASA and the IUPAC recommendations, and from the present work.
| k 1c | k 1 | |||
|---|---|---|---|---|
| A/10−13 cm3 molecule−1 s−1 | −E a/R/K | A/10−12 cm3 molecule−1 s−1 | −E a/R/K | |
| Friedl and Sander8 | 16 ± 4 | 426 ± 50 | 4.7 ± 0.5 | 320 ± 60 |
| Sander and Friedl9 | 18 | 431 | 6.1 ± 1.2 | 240 ± 60 |
| Turnipseed et al.15 | 6.7 ± 1.0 | 622 ± 94 | 2.59 ± 0.36 | 445 ± 84 |
| JPL-NASA6 | 9.5 | 550 | 3.3 | 400 |
| IUPAC16 | 16 | 430 | 4.7 | 320 |
| This work | 46 ± 30 | 280 ± 180 | 2.5 ± 2.2 | 630 ± 240 |
This work measured a stronger temperature dependence of the overall reaction rate coefficient k1, but a weaker temperature dependence of the rate coefficient of channel (1c). Comparison with previous studies is discussed below.
Discussion
Sensitivity analysis
The uncertainties in the reaction rates of both the radical formation chemistry and of the subsequent secondary chemistry propagated into potential systematic uncertainty in the final values of k1 and k1c obtained from fitting of the numerical integration model to the experimental traces. To quantify these effects, the rate coefficients of the reactions in the FACSIMILE model shown in Table 2 were sequentially perturbed upwards and downwards initially by a factor of two and the modified model was fitted to experimental temporal traces. This analysis was carried out for a sample trace at three temperatures: initially at T = 298 K, then at the two extremes of the temperature range studied, namely T = 314 K and T = 246 K.This analysis gave similar results for the sensitivity at T = 298 K and T = 314 K: the perturbation of most reaction rate coefficients had only minimal (<1%) effects on the values of k1 and k1c, with the exception of the formation reactions (3), (6), (7), (10), (11), the ClO dimerisation and the BrO self-reaction. This investigation showed that the values of k1 and k1c obtained from fitting FACSIMILE models to temporal traces were most sensitive to reactions (3) and (7): the runs in which these reactions were perturbed returned values of k1 and k1c respectively deviating by ±40% and ±10% of those obtained from the unmodified model. The sensitivity to reactions (6), (10) and (11) was more modest, with the perturbation of their rate coefficients giving rise to a deviation from the values of k1 and k1c resulting from the unperturbed model of ±2%, ±1% and ±1% respectively. Perturbation of the rate coefficients of the ClO dimerisation and of the BrO self-reaction had a negligible effect on k1c (<1%) but returned values of k1 within ±5% and ±2% respectively from those obtained from the unaltered model.
However, the perturbation of the rate coefficients of these reactions by a factor of two appeared to be an overestimate in the light of the uncertainty factors reported in the latest JPL-NASA evaluation. Therefore a second series of sensitivity runs was performed for sample traces at T = 298 K and T = 314 K, now taking into account only those reactions whose perturbation in the initial sensitivity analysis had led to a deviation in k1 and/or k1c greater than 1%. Rate coefficients for these reactions were perturbed by the actual uncertainty factors recommended by JPL-NASA. As these uncertainty factors were typically lower than the value of 2 previously used, deviations from the kinetic parameters returned from the unperturbed model were unsurprisingly somewhat less pronounced than in the previous runs. Only the perturbation of the rates of reactions (3) and (7) resulted in deviations greater than 1%: more specifically of ±10% for k1 and of ±3% for k1c. Perturbation of the rate coefficient for the ClO dimerisation produced no significant deviation in the returned value of k1c, and the returned value of k1 with this perturbation was within ±2% of that obtained from the unperturbed model. It was therefore concluded that the determinations of k1 and k1c reported in this study were affected by a maximum of ±10% by potential uncertainties in individual secondary chemical reactions at T = 298 K and T = 314 K, although of course such uncertainties may not manifest in isolation.
The results of the sensitivity analysis performed at the lowest temperature of this study, T = 246 K, were notably different from those obtained at higher temperatures. Whilst perturbation of reactions other than the radical formation chemistry and the XO (X = Cl, Br) self-reactions by a factor of two had negligible (<1%) effects on the returned values of k1 and k1c at T = 298 K and T = 314 K, the same treatment at T = 246 K led to a higher deviation (typically ∼2%) from the kinetic values obtained via the unperturbed model. This behaviour was rationalised on account of the negative temperature dependence of many of these reactions: as their rate coefficients increase at low temperatures, this secondary chemistry starts to compete more efficiently with reaction (1) and therefore has a greater effect on k1 and k1c when their rate coefficients are perturbed. However, this evidently does not apply to those reactions in the FACSIMILE model with positive temperature dependence. The observed enhanced sensitivity to secondary chemistry could also have arisen from the poorer signal-to-noise ratio observed for the temporal traces recorded at T = 246 K, which affected the capacity of the perturbed model to converge to values of k1 and k1c that do not deviate from those obtained with the unperturbed secondary chemistry. The poorer signal recorded at low temperatures was due to lower radical concentrations caused by the slower formation reactions (3) and (7) as a result of the positive temperature dependence of their rate coefficients. The concentrations of chlorine monoxide and bromine monoxide radicals in the immediate post-photolysis, [ClO]0 and [BrO]0, at T = 246 K were respectively 20% and 55% lower than those observed at T = 314 K. In addition to this, species that absorb strongly over the spectral window which were formed in this study (mainly Cl2O2 and Cl2O3) by secondary reactions are more thermally stable at T = 246 K than at ambient temperature, thus leading to a significant decrease in light transmitted through the reactive mixture at lower temperatures affecting spectroscopic measurements. In common with the results of the sensitivity analysis at T = 298 K and T = 314 K, perturbation of radical formation reactions and of the XO self-reactions by a factor of two produced the largest deviations from the values of k1 and k1c obtained with the unaltered model; however the magnitude of such deviations was larger at T = 246 K than that observed at higher temperatures. Perturbation of formation reactions (3) and (7) by a factor of two returned values of k1 and k1c which deviated from those obtained with the unperturbed model by as much as ±80% for both rate coefficients. Perturbation of reactions (6), (10) and (11) produced somewhat smaller (<10%) deviations, whilst values of k1 and k1c obtained from models with perturbed rate coefficients for the ClO dimerisation and the BrO self-reaction were within 5% of those from unperturbed models. As discussed for the sensitivity analysis to secondary chemistry at higher temperatures, an uncertainty factor of two is usually larger than current uncertainties estimated by JPL-NASA. However, most of the uncertainty factors reported in the JPL-NASA evaluation are temperature-dependent and they typically increase above and below T = 298 K. At T = 246 K they are approximately equal to two for reaction (7) and for the BrO self-reaction. Sensitivity procedures were therefore re-run for the reactions whose uncertainty factors were indeed lower than two at T = 246 K. Perturbation of reaction (3) led to deviations in k1 and k1c of ±40% and ±60% respectively, perturbation of reactions (6), (10), (11) and of the ClO dimerisation all led to smaller deviations (<5% in most cases). It is therefore concluded that the values of k1 and k1c reported here at the lowest experimental temperature adopted are significantly sensitive to potential uncertainties in reactions of bromine atoms with Cl2O (7) and ozone (3).
The sensitivity of the FACSIMILE model for the BrO + ClO cross-reaction to the ClO + OClO termolecular association, discussed above, was also negligible at the high end of the temperature range used, but became very pronounced at T = 246 K due to the enhanced thermal stability of the Cl2O3 adduct at low temperatures. Deviation of the values of k1 and k1c caused by the perturbation of the equilibrium constant of reactions (12, −12) increased from <1% at T = 298 K and T = 314 K to approximately ±90% at T = 246 K, using the JPL-NASA uncertainty factor of 1.4. It was clear that sequestration of OClO into Cl2O3 significantly affected the observed temporal behaviour of [OClO], thus interfering critically with the extraction of the rate coefficient for channel (1c). In addition to this, experimental noise on the kinetic traces at T = 246 K made it extremely hard to decouple the OClO build-up viachannel (1c) from equilibration (12, −12), to the point that the model would not readily converge to a unique value of k1c. As a consequence, the potential additional systematic errors in k1c, and consequently in its branching ratio γ, reported in Table 3 increase as the temperature is lowered, by as much as a factor of two. The effects of this sensitivity to secondary chemistry, of the lower initial radical concentrations and the poorer signal at low temperatures were therefore used to define the low temperature limit for the current study of reaction (1), where a sensitivity factor of two was considered the maximum tolerable. On the other hand, the upper limit of the temperature range used in the current study was dictated by the instrumental limitation of the thermostatting set-up.
The absorption cross-sections of ClO, BrO and OClO were evidently crucial in the determination of the temporal concentration traces and, therefore, in the extraction of kinetic information for the BrO + ClO reaction. To ascertain the effect of uncertainties in the cross-sections used on the retrieved values of k1 and k1c, each cross-section was perturbed using the recommended errors (discussed below) so that an upper and a lower limit were determined for each cross-section at each experimental temperature. The analytical procedure leading to the quantification of the absorbers, outlined above, was then repeated using one modified cross-section at a time, for all experimental data. These perturbed temporal concentration traces were then fitted with the FACSIMILE model and the returned values of k1 and k1c were compared to those obtained using unperturbed cross-sections.
As discussed previously,22 uncertainty in σClO was defined at the 2σ level from three values of the ClO cross-sections measured at T = 298 K. This gave rise to a relative error in σClO of 0.23 at T = 298 K, of 0.26 at T = 314 K and of 0.15 at T = 246 K. This temperature dependence of the relative errors reflected the uncertainties in the high-resolution differential ClO cross-sections derived by Boakes et al. and employed in the current work to obtain σClO at the resolution of the current study. The errors in the ClO cross-section were propagated through the analytical procedure and the values of k1 and k1c resulting from perturbed cross-sections were within ±12% and ±28% of those obtained using unperturbed cross-sections at T = 314 K. Similarly, at T = 246 K, values of k1 and k1c were within ±8% and ±13% of those obtained using unperturbed cross-sections.
This work employed the BrO cross-section measured by Wilmouth et al.;23 these authors reported an error of 11% for the differential cross-section of the (7,0) vibronic band of BrO at λ = 338.5 nm at T = 298 K. In this sensitivity analysis, BrO cross-sections at all experimental temperatures were perturbed by a factor of ±1.11 and then fitted to the recorded absorbance spectra to generate [BrO] traces. These traces were then fitted with a FACSIMLE model and the returned values for k1 and k1c lay within ±5% and ±3% respectively of the values obtained using the unperturbed σBrO at T = 314 K and within ±8% and ±5% at T = 246 K.
The OClO cross-sections used in the current work are those reported by Wahner et al.24 These authors identified baseline shifts as the main source of error in their measurement and recommended an uncertainty of ±4 × 10−19 cm2 molecule−1 across the absorption spectrum. However, a baseline shift would not affect the spectral fit carried out in the current work as differential fitting procedures are adopted. As described previously,22 the differential cross-section of the a(15) peak of OClO at λ = 322.78 nm was however perturbed by ±4 × 10−19 cm2 molecule−1 and the whole spectrum was scaled to match the altered differential cross-section at all experimental temperatures. Perturbed OClO cross-sections were then employed in the quantification of [OClO] via the Beer–Lambert Law and the traces thus generated were fitted with the FACSIMILE model. The returned values of k1 and k1c at T = 314 K were within ±1% and ±4% respectively of the values obtained from unaltered cross-sections; these deviations increased to ±10% and ±9% respectively at T = 246 K.
Errors in the absorption cross-sections of all three species monitored produced asymmetric deviations in the Arrhenius parameters for k1(T) and k1c(T). The returned upper and a lower limits of these parameters, expressed in Arrhenius form were therefore:
k1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) upper/cm3 molecule−1 s−1 = 2.7 × 10−12 upper/cm3 molecule−1 s−1 = 2.7 × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(636/T) exp(636/T) |
k1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lower/cm3 molecule−1 s−1 = 2.5 × 10−12 lower/cm3 molecule−1 s−1 = 2.5 × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(587/T) exp(587/T) |
k1c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) upper/cm3 molecule−1 s−1 = 9.7 × 10−12 upper/cm3 molecule−1 s−1 = 9.7 × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(130/T) exp(130/T) |
k1c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lower/cm3 molecule−1 s−1 = 2.5 × 10−12 lower/cm3 molecule−1 s−1 = 2.5 × 10−12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(390/T) exp(390/T) |
The sensitivity of the values obtained for k1 and k1c to the concentrations of precursor species was also investigated. As discussed above, the concentration of species in the precursor mixture was quantified by means of UV absorption spectroscopy. Sensitivity of the rate coefficients was studied by perturbing the values for [Br2], [Cl2], [Cl2O] and [OClO] input in the FACSIMILE model by ±10%, one at a time, at T = 298 K and at T = 246 K. At T = 298 K, the rate coefficients obtained from the model with perturbed [Br2] and [Cl2] were respectively within ±0.7% and ±0.3% of those returned from the unaltered model. However, as the [Cl2O]/[O3] ratio dictated the partitioning of the fate of Br atoms between reaction (7) and reaction (3), fluctuations in the concentrations of Cl2O and O3 had a more appreciable effect than those in Br2 and Cl2 on the returned rate coefficient, but which were in any case within ±6% of those obtained from the unperturbed model. Perturbation of the concentration of the OClO impurity present in the precursor mixture by 10% had minor effects (<1%) on the returned rate coefficients. When the same procedure was repeated at T = 246 K, an enhanced sensitivity to [Cl2O] and [O3] was observed, with perturbed models returning values of k1 and k1c within ±15% of those from unaltered models. By contrast, perturbation of precursor [OClO] had a non-negligible effect at this low temperature, resulting in deviations from the rate coefficients obtained from the unperturbed model of approximately ±25%.
The effects of the uncertainty in the flow-out of the gaseous mixture from the reaction cell were also investigated. The values of k1 and k1c returned from a FACSIMILE model in which the flow-out had been perturbed by 10% lay within <0.5% from those obtained from the unperturbed model at T = 298 K and within 1.5% at T = 246 K, indicating that uncertainty in the flow-out was a minor source of error. This behaviour was expected as gas flow-out was minimal over the fast timescale at which the BrO + ClO cross-reaction took place and was well-established by calibration of all mass flow controllers.
In conclusion, for such an inherently complex reaction system, care has to be taken to ensure that sensitivity to the target reactions is maximised, whilst sensitivity to the uncertainties in the secondary reaction kinetics, precursor concentrations and cross-sections is quantified and minimised. This study has found that uncertainty in some parameters (in particular the reactions of bromine atoms in the radical formation and secondary chemistry, ClO dimerisation, BrO self-reaction, Cl2O3 formation, as well as the absorption cross-sections of the three species monitored and precursor [Cl2O] and [O3]) do exhibit a potential effect on the inference of kinetic parameters reported here. This introduces potentially large systematic errors in the present study, if in particular the recommended kinetics for the secondary chemical reactions lie near their currently recommended error bounds. This is not likely to be unique to the present study, but has been quantified, and has been used to determine the lower limit for temperature at which reaction (1) was studied.
Comparison with previous work
Fig. 6–8 illustrate the values of k1, k1c and γ (= k1c/k1) obtained in this work in Arrhenius form, along with the results from previous studies and the current JPL-NASA recommendations.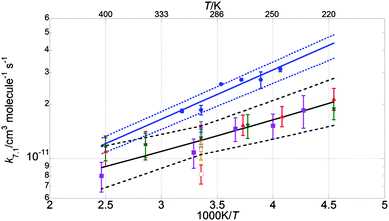 | ||
| Fig. 6 Arrhenius plot for k1. Data from this work are shown as blue circles, along with the resulting parameterisation (blue line) and the uncertainty limits (dashed blue lines) as discussed in the text. Also shown are the data from Clyne and Watson12 (pink open circles), Toohey and Anderson13 (blue diamonds), Hills et al.10 (open orange squares), Friedl and Sander8 (red triangles), Sander and Friedl9 (inverted green triangles), Poulet et al.14 (open green triangles), Turnipseed et al.15 (purple squares). The current JPL-NASA6 recommendation is shown as a black line along with its uncertainty range (dashed black lines). | ||
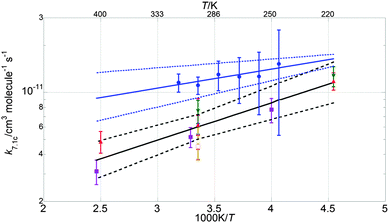 | ||
| Fig. 7 Arrhenius plot for k1c. Data from this work are shown as blue circles, along with the resulting parameterisation (blue line) and the uncertainty limits (dashed blue lines) as discussed in the text. Also shown are the data from Clyne and Watson12 (pink open circles), Toohey and Anderson13 (blue diamonds), Hills et al.10 (open orange squares), Friedl and Sander8 (red triangles), Sander and Friedl9 (inverted green triangles), Poulet et al.14 (open green triangles), Turnipseed et al.15 (purple squares). The current JPL-NASA6 recommendation is shown as a black line along with its uncertainty range (dashed black lines). | ||
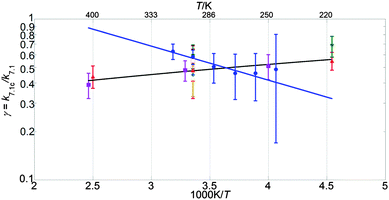 | ||
| Fig. 8 Branching ratio for k7.1c presented in Arrhenius form. Data from this work are shown as blue circles, along with the resulting parameterisation (blue line). Also shown are the data from Clyne and Watson12 (pink open circles), Toohey and Anderson13 (blue diamonds), Hills et al.10 (open orange squares), Friedl and Sander8 (red triangles), Sander and Friedl9 (inverted green triangles), Poulet et al.14 (open green triangles), Turnipseed et al.15 (purple squares) and the current JPL-NASA6 recommendation (black line). | ||
The values of k1 from the present study are approximately 70% greater than those of the current JPL-NASA recommendation over the whole temperature range studied here, and they also fall outside the JPL-NASA upper uncertainty limit at all temperatures, as shown in Fig. 6. The temperature dependence of k1 from this work is also slightly more (negatively) pronounced than that reported by previous studies as shown in Table 4. This work also measured values of the rate coefficient of channel (1c) greater than the current JPL-NASA recommendation, as shown in Fig. 7, along with a weaker temperature dependence of k1c than those from previous studies and JPL-NASA (Table 4). The branching ratio for channel (1c), γ, as a result of the temperature dependencies of k1c and k1 observed in this work, therefore became smaller as the temperature was lowered, contrary to the findings of previous studies, as illustrated in Fig. 8. However, as discussed in the previous section, uncertainties in the secondary chemistry of OClO and the reduction in signal quality at low temperatures due to the formation of stable absorbers (Cl2O2, Cl2O3), resulted in the considerable potential uncertainty in k1c and, consequently, γ at T < 283 K.
The simultaneous broadband monitoring of [ClO], [BrO] and [OClO] as a function of time, along with the employment of differential fitting techniques, constitutes a considerable advantage of the current work over, for example, the dual-wavelength study by Sander and Friedl. These authors used flash photolysis of Br2–Cl2O mixtures to generate ClO and BrO radicals, then simultaneously monitored ClO at the (12,0) vibronic peak at λ = 275.2 nm and BrO at the (7,0) vibronic peak at λ = 338.5 nm. However, multiple underlying absorbances are significant at both wavelengths. Sander and Friedl applied a correction to the absorbance recorded at λ = 275.2 nm to account for the (negative) contribution to the total absorbance arising from the Cl2O consumed in the radical formation chemistry. However, FACSIMILE simulations using the average reaction conditions described by Sander and Friedl showed that the ClO dimer, Cl2O2, could also give a non negligible contribution to the total absorbance at λ = 275.2 nm under conditions of low temperature and high pressure. At T = 220 K and p = 700 Torr, respectively the lowest temperature and the highest pressure used by Sander and Friedl, approximately 10% of the total simulated absorbance (averaged over the timescale of BrO decay, approximately Δt = 1–1.5 ms after photolysis) at λ = 275.2 nm would be expected to arise from the presence of Cl2O2. This contribution to the total absorbance fell to 3% at T = 298 K and <1% at T = 400 K, and was fully negligible at all temperatures in the low pressure regime (p = 50 Torr) as a consequence of the temperature and pressure dependence of the ClO + ClO equilibration. However, not accounting for the contributions of Cl2O2 to the total absorbance in the work of Sander and Friedl might have led to an overestimate of [ClO] at low temperatures and high pressures which could have propagated into an underestimate of k1, as k1 = k1′/[ClO]. This is consistent with the values of k1(T) from the current work diverging from those obtained by Sander and Friedl at low temperatures: whilst the two studies are in good agreement at T = 400 K, with the extrapolated k1 from this study lying within 4% of the measurement from Sander and Friedl, the extrapolated k1 at T = 220 K from this study is more than twice that measured by Sander and Friedl at the same temperature.
Similarly, underlying absorbers could potentially have interfered with the monitoring of BrO in the Sander and Friedl study at λ = 338.5 nm. These authors obtained the pseudo first-order rate coefficient for reaction (1), k1′, from the slopes of plots of the logarithm of the absorbance at λ = 338.5 nm against time. Production of BrCl directly viachannel (1a) and indirectly from Br and Cl atoms from channels (1b) and (c) undergoing reactions (6) and (7) would also have an effect on the absorbance recorded at λ = 338.5 nm, giving rise to an apparent slower decay of the absorbance. Simulations were run in FACSIMILE to assess the magnitude of this effect; neglect of underlying absorbers always resulted in an underestimate of k1′, but the extent to which this may have affected the values of k1 from Sander and Friedl could not be quantified precisely due to the (understandable) lack of details for individual experiments in their work.
Sander and Friedl determined the branching ratio of channel (1c), γ, as the ratio between the [OClO] yield measured after the [BrO] decay had proceeded to completion and the initial concentration of BrO, [BrO]0. [OClO] and [BrO]0 were obtained by Sander and Friedl in consecutive experiments conducted under identical conditions at two temperatures, T = 220 K and T = 298 K. OClO spectra were recorded 2 ms after photolysis, with a 1 ms exposure. [BrO]0 was obtained by back-extrapolating logarithmic plots of the absorbance at λ = 338.5 nm to t = 0 and then converting the initial absorbance into [BrO]0 using a value of the BrO cross-section at λ = 338.5 nm determined in the same study. As discussed above, the presence of underlying absorbers at λ = 338.5 nm may lead to an underestimate of the slope of such plots and, in turn, of the absorbance at t = 0. This would lead to an overestimate in γ. As the pressure range of the experiments on the branching ratio is not specified, it is not possible to assess whether the ClO + OClO termolecular association interfered with the [OClO] build-up at T = 220 K. However if experiments were conducted at near ambient pressure, it would result in a significant underestimate of the value reported by Sander and Friedl of γ = 0.68 at T = 220 K as some OClO genuinely produced by the BrO + ClO reaction would have been sequestered into Cl2O3.
All previous studies agree on the negative temperature dependence of the total rate coefficient, k1, and of the individual channels, with the exception of the work of Hills et al.10 Results from Hills et al. are in stark contrast to those from all other previous studies as they report a near-zero temperature dependence and a value of k1 smaller than the current JPL-NASA recommendation by approximately 35% at T = 298 K and by 60% at T = 220 K. Friedl and Sander8 attributed this disagreement to the neglect of secondary chemistry; more specifically, Hills et al. did not account for bromine atoms generated by reactions (1) and (6) which regenerated BrO viareaction (3) with the ozone present in the gas flow. Regeneration of BrO would have affected the observed kinetics of BrO, giving rise to an apparent slower decay.
All discharge flow/mass spectrometry studies of the BrO + ClO cross-reaction reported in the literature were performed under conditions of excess ClO over BrO. In these studies, Cl atoms were produced from Cl2 by microwave discharge and ClO radicals were generated either via Cl + OClO13,14 or Cl + Cl2O,15 or both.8,10 In these studies, the concentration of Cl atoms produced was either in excess over or equal to that of OClO and Cl2O, to ensure full consumption of precursor chlorine oxides and allow direct detection of OClO produced by channel (1c). However, the absence of Cl2O in the flow tube studies also prevented scavenging of bromine atoms (as occurs in the photolysis system, viareactions (3) and (7)) and hence in principle allowed the reaction:
| Br + OClO → BrO + ClO | (13) |
The presence of OClO in the precursor mixture observed in the current work was attributed to unknown chemistry involving ozone with Cl2O and/or Cl2. Friedl and Sander also reported the presence of an unexpected background OClO signal in their discharge flow study under excess ozone conditions. Similar reaction conditions of excess ozone to generate BrO viareaction (3) were also employed by Turnipseed et al. but these authors did not report any anomalous OClO signal. Thus two of the three most recent studies that have investigated the temperature dependence of the BrO + ClO cross-reaction (including the current one) might have been affected by the presence of OClO in the precursor mixture, which may, in the previous studies, have led to an overestimate of the branching ratio for channel (1c), γ. Despite the potential presence of OClO in the precursor mixture, Cl2O3 formation viareaction (12) is unlikely to have occurred in flow systems even at low temperatures (T < 250 K) due to the termolecular nature of reaction (12) and the low pressure at which these studies were performed (p = 1 Torr for Friedl and Sander and p = 2 Torr for Turnipseed et al.).
Crucially, most of the previous studies of the BrO + ClO cross-reaction8–10,12–15 were performed at low pressures (p < 2 Torr), with the exception of the work of Sander and Friedl. The discrepancy between the temperature dependencies of k1 and k1c observed in this work and those measured by Sander and Friedl discussed above may be rationalised in terms of the neglect of additional absorbers and secondary chemistry by Sander and Friedl. On the other hand, the disagreement between the present work and previous studies using discharge flow/mass spectrometry could potentially arise from the contribution of a termolecular association channel operating at high pressures, leading to the production of a stable BrClO2 adduct. The different temperature dependencies of k1 shown in the Arrhenius plot in Fig. 6 are potentially consistent with this proposed mechanism as the discrepancy between high-pressure (this study) and low-pressure (Friedl and Sander, Turnipseed et al.) values of k1 becomes more significant at low temperatures, where formation of the adduct might be expected to be more efficient. However, the existence of a termolecular component to the BrO + ClO cross-reaction can only be established by further experiments performed over a wide range of pressures as well as temperatures. Results from the current study indicate that the OClO-producing pathway of the BrO + ClO cross-reaction, channel (1c) is less efficient than previously reported at temperatures typical of the polar stratosphere. This result could potentially account for the discrepancy highlighted by Canty et al.5 between field measurements of stratospheric OClO abundances and atmospheric models.
Conclusions
The temperature dependencies of the rate coefficients of the BrO + ClO reaction (1), k1, and of the OClO producing channel, k1c, of this process have been determined by means of laser flash photolysis/UV absorption spectroscopy at six temperatures over the range T = 246–314 K, a range defined by sensitivity and instrumental considerations. Three species in the reaction mixture (ClO, BrO, OClO) were monitored simultaneously by means of their UV absorption spectra, and the use of differential fitting techniques allowed unequivocal quantification of these absorbing species in spite of the presence of several additional absorbers in the same spectral range. Both k1 and k1c exhibited negative temperature dependencies, but the absolute values of both rate coefficients were larger than previous studies at all temperatures. This discrepancy can only be partially explained in terms of potential systematic errors in the current work (notably, in the species absorption cross-sections). However, the principal reason for the discrepancy is considered to lie in secondary chemistry occurring in this and other work, arising from the complicated reacting mixture. A detailed sensitivity analysis was performed to quantify sources of potential systematic errors in the kinetic parameters reported in the present work. This has identified certain reactions, notably those involving bromine atoms, uncertainties in which may affect the present results and which therefore merit further consideration.This work finds that the BrO + ClO reaction is faster than previous studies indicate, but that the OClO producing channel is less significant, particularly at low temperatures. This may help resolve discrepancies between atmospheric models and measurements of OClO, a key indicator of stratospheric bromine chemistry.
Acknowledgements
Both authors thank Abigail Mountain and Jutta Toscano for their help in carrying out exploratory experiments and VF thanks the EPSRC for graduate funding.References
- M. B. McElroy, R. J. Salawitch, S. C. Wofsy and J. A. Logan, Nature, 1986, 321, 759 CrossRef CAS.
- P. A. Newman, M. Rex, P. O. Canziani, K. S. Carslaw, K. Drdla, S. Godin-Beekmann, D. M. Golden, C. H. Jackman, K. Kreher, U. Langematz, R. Müller, H. Nakane, Y. J. Orsolini, R. J. Salawitch, M. L. Santee, M. von Hobe and S. Yoden, Polar Ozone: Past and Present, Chapter 4 in Scientific Assessment of Ozone Depletion: 2006, Global Ozone Research and Monitoring Project – Report No. 50, World Meteorological Organization, Geneva, Switzerland, 2007, p. 572.
- K. Frieler, M. Rex, R. J. Salawitch, T. Canty, M. Streibel, R. M. Stimpfle, K. Pfeilsticker, M. Dorf, D. K. Weisenstein and S. Godin-Beekmann, Geophys. Res. Lett., 2006, 33, L10812 CrossRef.
- R. P. Wayne, G. Poulet, P. Biggs, J. P. Burrows, R. A. Cox, P. J. Crutzen, G. D. Hayman, M. E. Jenkin, G. Le Bras, G. K. Moortgat, U. Platt and R. N. Schindler, Atmos. Environ., 1995, 29, 2677 CrossRef CAS.
- T. Canty, E. D. Rivière, R. J. Salawitch, G. Berthet, J.-B. Renard, K. Pfeilsticker, M. Dorf, A. Butz, H. Bösch, R. M. Stimpfle, D. M. Wilmouth, E. C. Richard, D. W. Fahey, P. J. Popp, M. R. Schoeberl, L. R. Lait and T. P. Bui, J. Geophys. Res.: Atmos., 2005, 110, D01301 CrossRef.
- S. P. Sander, J. Abbatt, J. R. Barker, J. B. Burkholder, R. R. Friedl, D. M. Golden, R. E. Huie, C. E. Kolb, M. J. Kurylo, G. K. Moortgat, V. L. Orkin and P. H. Wine, Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies, Evaluation No. 17, 2011, JPL Publication 10-6, Jet Propulsion Laboratory, Pasadena, United States.
- S. R. Kawa, R. S. Stolarski, P. A. Newman, A. R. Douglass, M. Rex, D. J. Hofmann, M. L. Santee and K. Frieler, Atmos. Chem. Phys., 2009, 9, 8651 CrossRef CAS.
- R. R. Friedl and S. P. Sander, J. Phys. Chem., 1989, 93, 4756 CrossRef CAS.
- S. P. Sander and R. R. Friedl, J. Phys. Chem., 1989, 93, 4764 CrossRef CAS.
- A. J. Hills, R. J. Cicerone, J. G. Calvert and J. W. Birks, J. Phys. Chem., 1988, 92, 1853 CrossRef CAS.
- N. Basco and S. K. Dogra, Proc. R. Soc. London, Ser. A, 1971, 323, 417 CrossRef CAS.
- M. A. A. Clyne and R. T. Watson, J. Chem. Soc., Faraday Trans. 1, 1977, 73, 1169 RSC.
- D. W. Toohey and J. G. Anderson, J. Phys. Chem., 1988, 92, 1705 CrossRef CAS.
- G. Poulet, I. T. Lançar, G. Lavardet and G. Le Bras, J. Phys. Chem., 1990, 94, 278 CrossRef CAS.
- A. A. Turnipseed and J. W. Birks, J. Phys. Chem., 1991, 95, 4356 CrossRef CAS.
- R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi and J. Troe, Atmos. Chem. Phys., 2007, 7, 981 CrossRef CAS.
- M. H. Harwood, D. M. Rowley, R. A. Cox and R. L. Jones, J. Phys. Chem. A, 1998, 102, 1790 CrossRef CAS.
- C. N. Hinshelwood and C. R. Pritchard, J. Chem. Soc., 1923, 123, 2730 RSC.
- Y. Bedjanian, G. Laverdet and G. Le Bras, J. Phys. Chem. A, 1998, 102, 953 CrossRef CAS.
- D. M. Rowley, M. H. Harwood, R. A. Freshwater and R. L. Jones, J. Phys. Chem., 1996, 100, 3020 CrossRef CAS.
- G. Boakes, W. H. Hindi Mok and D. M. Rowley, Phys. Chem. Chem. Phys., 2005, 7, 4102 RSC.
- V. Ferracci and D. M. Rowley, Int. J. Chem. Kinet., 2012, 44, 386 CrossRef CAS.
- D. M. Wilmouth, T. F. Hanisco, N. M. Donahue and J. G. Anderson, J. Phys. Chem. A, 1999, 103, 8935 CrossRef CAS.
- A. Wahner, G. S. Tyndall and A. R. Ravishankara, J. Phys. Chem., 1987, 91, 2134 CrossRef.
- M. K. Gilles, A. A. Turnipseed, J. B. Burkholder, A. R. Ravishankara and S. Solomon, J. Phys. Chem. A, 1997, 101, 5526 CrossRef CAS.
- A. R. Curtis and W. P. Sweetenhan, FACSIMILE, AERE Harwell Publication, Oxford, 1987 Search PubMed.
- V. Ferracci and D. M. Rowley, Phys. Chem. Chem. Phys., 2010, 12, 11596 RSC.
- V. Ferracci, K. Hino and D. M. Rowley, Phys. Chem. Chem. Phys., 2011, 13, 7997 RSC.
- D. A. Dolson and S. R. Leone, J. Phys. Chem., 1987, 91, 3543 CrossRef CAS.
- D. L. Baulch, J. Duxbury, S. J. Grant and D. C. Montague, J. Phys. Chem. Ref. Data, 1981, 10, 1 CrossRef.
- M. A. A. Clyne and H. W. Cruse, J. Chem. Soc., Faraday Trans. 2, 1972, 68, 1377 RSC.
- N. Basco and S. K. Dogra, Proc. R. Soc. London, Ser. A, 1971, 323, 29 CrossRef CAS.
- M. A. A. Clyne, P. B. Monkhouse and L. W. Townsend, Int. J. Chem. Kinet., 1976, 8, 425 CrossRef CAS.
- P. H. Wine, J. M. Nicovich and A. R. Ravishankara, J. Phys. Chem., 1985, 89, 3914 CrossRef CAS.
| This journal is © the Owner Societies 2014 |