 Open Access Article
Open Access ArticleNon-covalent interactions at electrochemical interfaces: one model fits all?
Gema
Cabello
a,
Ezequiel P. M.
Leiva
b,
Claudio
Gutiérrez
a and
Angel
Cuesta
*ac
aInstituto de Química Física “Rocasolano”, CSIC, C. Serrano 119, E-28006, Madrid, Spain
bFacultad de Ciencias Químicas, Universidad Nacional de Córdoba, INFIQC, Córdoba, Argentina
cDepartment of Chemistry, School of Natural and Computing Sciences, University of Aberdeen, Aberdeen AB24 3UE, UK. E-mail: angel.cuestaciscar@abdn.ac.uk
First published on 29th May 2014
Abstract
The shift with increasing concentration of alkali-metal cations of the potentials of both the spike and the hump observed in the cyclic voltammograms of Pt(111) electrodes in sulfuric acid solutions is shown to obey the simple model recently developed by us to explain the effect of non-covalent interactions at the electrical double layer. The results suggest that the model, originally developed to describe the effect of alkali-metal cations on the cyclic voltammogram of cyanide-modified Pt(111) electrodes, is of general applicability and can explain quantitatively the effect of cations on the properties of the electrical double layer.
Introduction
Traditionally, the influence of cations on the properties of, and on the processes occurring at, the electrical double layer has received little attention. Although the adsorption of alkali-metal cations on polycrystalline Pt electrodes was already reported in the early 1970's,1,2 and although Feliu and co-workers studied in the last few decades the effect of alkali-metal cations on sulfate3,4 and phosphate5 adsorbed on Pt(111) electrodes, the report by Strmcnik et al.6 in 2009 of a remarkable cation effect on the electrocatalytic activity of Pt(111) towards the oxygen reduction reaction (ORR), the hydrogen oxidation reaction (HOR), and the methanol oxidation reaction (MOR) in alkaline solutions has provoked a surge of articles on this subject.7–15 In all these new contributions, and following Strmcnik et al.,6 the effect of the cation has been attributed to non-covalent interactions at the electrical double layer (essentially, electrostatic interactions between specifically adsorbed anions and the cations, leading to the formation of surface-anchored cation–anion, or cation–dipole pairs). However, with only two exceptions,7,9 all these studies simply reported a qualitative description of the effect, without a quantitative and systematic study that could lead to a deeper understanding of the physical and chemical phenomena behind it.Recently,9 we have shown that the effect of alkali-metal cations (M+) on the cyclic voltammogram of cyanide-modified Pt(111) electrodes in sulfuric or perchloric acid solutions can be quantitatively described by a simple model, which essentially rests on the competition between H+ and M+ for the same adsorption sites, namely, the N atom of the CN groups anchored to the surface through the C atom. We report here a systematic study of the effect of the alkali-metal cations on two voltammetric features of Pt(111) in sulfuric acid solutions associated with (bi)sulfate adsorption. Our results suggest that our previously developed model is of general applicability to non-covalent interactions at the electrical double layer.
Experimental section
The working electrode was a bead-type Pt single crystal (ca. 2 mm in diameter) prepared according to the method developed by Clavilier et al.,16 oriented and polished parallel to the (111) plane. Before each experiment, the crystal was annealed in the flame of a Bunsen burner and cooled in a H2–N2 atmosphere. Once the crystal was sufficiently cold (ca. 20 seconds after having been introduced in the flask containing the H2–N2 mixture) the H2 flux was stopped, and CO was flown into the flask, in which the electrode was left for 5 additional minutes, during which a saturated CO adlayer was formed. The CO-protected electrode was then transferred to the electrochemical cell, where the CO adlayer was oxidatively stripped from the electrode surface, a clean and well-ordered Pt(111) surface being thus exposed to the electrolyte.A two-compartment, three-electrode Pyrex-glass cell was used for the electrochemical measurements. The electrolytes were prepared using ultrapure Milli-Q water (18 MΩ cm, 3 ppb TOC), concentrated H2SO4 (Merck suprapur), concentrated HClO4 (Merck, p.a.), and M2SO4, with M = Li (Aldrich, ≥99.99%), Na (Aldrich, 99.99%), K (Merck, Suprapur, 99.999%) or Cs (Aldrich, 99.99%). Nitrogen (N50) was used to deoxygenate the solutions, hydrogen (N50) and nitrogen (N50) were used to make the H2–N2 atmosphere in which the single-crystal electrodes were cooled after annealing, and carbon monoxide (N47, aluminium alloy cylinders) was used to form the protective CO adlayer. All gases were supplied by Air Liquide. A reversible hydrogen electrode (RHE) was used as reference, and the auxiliary electrode was a Pt wire.
Results and discussion
The two voltammetric features mentioned in the introduction, namely, a spike and a hump, can be seen in Fig. 1, which shows cyclic voltammograms (CVs) of Pt(111) in 0.05, 0.1, 0.5 and 1 M sulfuric acid. The adsorption of (bi)sulfate starts just after hydrogen desorption, giving rise to a broad feature preceding the spike that appears between ca. 0.4 (1 M H2SO4) and ca. 0.5 V (0.05 M H2SO4) and signals the formation of an ordered structure with a (bi)sulfate coverage of 0.20.17 The same disorder/order phase transition, leading to the same structure, occurs on the (111) faces of Au,18,19 Rh,20 Ir,21 Pd22,23 and Cu.24 In all the cases, the observation in STM images of a secondary tunneling maximum led to suggest a hydration of this structure, an assumption that has received confirmation from radioactive labeling experiments.25 This hydrogen bond network would stabilize the ordered structure. However, whether the adlayer is composed of sulfate or bisulfate (hence the usually employed ambivalent term (bi)sulfate), and whether the coadsorbate is H3O+ or H2O, has been the subject of considerable debate.7,17,18,20,25–36 The (uncorrected for double layer charging) charge of ca. 96 μC cm−2 determined from the cyclic voltammograms, together with the 0.20 ML coverage determined from the STM images, imply that two electrons are transferred per adsorbate, i.e., they suggest that, from a purely stoichiometric point of view the adsorption process is SO42− ⇌ SO4(ad) + 2e (or SO42− + H+ ⇌ SO4 − H+(ad) + 2e if H3O+ is the coadsorbate that stabilizes the
structure with a (bi)sulfate coverage of 0.20.17 The same disorder/order phase transition, leading to the same structure, occurs on the (111) faces of Au,18,19 Rh,20 Ir,21 Pd22,23 and Cu.24 In all the cases, the observation in STM images of a secondary tunneling maximum led to suggest a hydration of this structure, an assumption that has received confirmation from radioactive labeling experiments.25 This hydrogen bond network would stabilize the ordered structure. However, whether the adlayer is composed of sulfate or bisulfate (hence the usually employed ambivalent term (bi)sulfate), and whether the coadsorbate is H3O+ or H2O, has been the subject of considerable debate.7,17,18,20,25–36 The (uncorrected for double layer charging) charge of ca. 96 μC cm−2 determined from the cyclic voltammograms, together with the 0.20 ML coverage determined from the STM images, imply that two electrons are transferred per adsorbate, i.e., they suggest that, from a purely stoichiometric point of view the adsorption process is SO42− ⇌ SO4(ad) + 2e (or SO42− + H+ ⇌ SO4 − H+(ad) + 2e if H3O+ is the coadsorbate that stabilizes the  structure).
structure).
 | ||
| Fig. 1 Cyclic voltammograms, at 50 mV s−1, of Pt(111) in 0.05 (black), 0.1 (red), 0.5 (green), and 1 M (blue) H2SO4. | ||
The  structure disappears in the potential region of the hump, about 0.75 V in 0.1 M H2SO4, what led Funtikov et al. to propose that the hump corresponds to the onset of OH adsorption.17 Adsorption of OH within the (bi)sulfate adlayer was also invoked by Marković et al.,37 and later by Saravanan et al.,38 as the origin of the hump, but this runs contrary to its experimentally observed pH dependence.3 Shingaya and Ito39 suggested that this feature corresponds to the conversion, with increasing potential, of adsorbed bisulfate to adsorbed sulfuric acid (HSO4(ad) + H+ + e ⇌ H2SO4(ad)), a suggestion that must be discarded because this process is a reduction, and, furthermore, should have a pH dependence contrary to that observed by García et al.3 The increase of the hump potential with increasing pH at pH between 2.5 and 3.5 observed by García et al.3 unambiguously shows that, in this pH region, this voltammetric feature does not involve OH adsorption. The only electroadsorption process that can be involved in both the spike and the hump is that of (bi)sulfate. However, as noted by García et al.,3 the decrease, with a slope of 60 mV, of the hump potential with increasing pH at pH > 3.5, must be due to a change of the adsorbing species, namely, to the co-adsorption of OH within the (bi)sulfate adlayer at pH > 3.5.
structure disappears in the potential region of the hump, about 0.75 V in 0.1 M H2SO4, what led Funtikov et al. to propose that the hump corresponds to the onset of OH adsorption.17 Adsorption of OH within the (bi)sulfate adlayer was also invoked by Marković et al.,37 and later by Saravanan et al.,38 as the origin of the hump, but this runs contrary to its experimentally observed pH dependence.3 Shingaya and Ito39 suggested that this feature corresponds to the conversion, with increasing potential, of adsorbed bisulfate to adsorbed sulfuric acid (HSO4(ad) + H+ + e ⇌ H2SO4(ad)), a suggestion that must be discarded because this process is a reduction, and, furthermore, should have a pH dependence contrary to that observed by García et al.3 The increase of the hump potential with increasing pH at pH between 2.5 and 3.5 observed by García et al.3 unambiguously shows that, in this pH region, this voltammetric feature does not involve OH adsorption. The only electroadsorption process that can be involved in both the spike and the hump is that of (bi)sulfate. However, as noted by García et al.,3 the decrease, with a slope of 60 mV, of the hump potential with increasing pH at pH > 3.5, must be due to a change of the adsorbing species, namely, to the co-adsorption of OH within the (bi)sulfate adlayer at pH > 3.5.
The charge density associated with the hump, about 25 μC cm−2, and ca. 12 μC cm−2 after double-layer correction, is independent of the H2SO4 concentration, and corresponds to the adsorption of 0.025 additional monolayers of sulfate, which provokes the disruption of the  structure, as has been shown by STM.17 The charge of the hump coincides with that reported by García et al.3 The fact that the potential has to be increased by ca. 0.25 V before the sulfate coverage can be increased beyond the 0.20 ML coverage reached in the spike, must be due to the stability conferred to this ordered adlayer by the hydrogen bond network.
structure, as has been shown by STM.17 The charge of the hump coincides with that reported by García et al.3 The fact that the potential has to be increased by ca. 0.25 V before the sulfate coverage can be increased beyond the 0.20 ML coverage reached in the spike, must be due to the stability conferred to this ordered adlayer by the hydrogen bond network.
We studied the effect of the alkali-metal cations on the spike and the hump. Obviously, the cation concentration cannot be varied without simultaneously altering the total anion concentration and/or the pH. The easiest way to increase the cation concentration without altering the pH and the total sulfate (SO42− + HSO4−) concentration would be to use different concentrations of alkali-metal perchlorates. We used, however, sulfates instead of perchlorates because, typically, the former contain less impurities, high purity being a must when working under ultra-clean conditions. We prepared (0.1 − x) M H2SO4 + x M M2SO4 + 2x M HClO4 solutions, whose composition is identical to 0.1 M H2SO4 + 2x M MClO4 solutions, this notation being used in the following. Since perchlorate specific adsorption is negligible, its only effect will be to increase the ionic strength of the solution, but this effect will be the same for all the alkali-metal cations.
Fig. 2 shows the CVs of Pt(111) in 0.1 M H2SO4 containing different concentrations of Li+ (Fig. 2a), Na+ (Fig. 2b), K+ (Fig. 2c) and Cs+ (Fig. 2d). Only the CVs at cation concentrations of 10−4, 10−3, 10−2 and 5 × 10−2 M are shown for the sake of clarity. Fig. 3 illustrates the effect of increasing concentrations of Li+ (black), Na+ (red), K+ (green) and Cs+ (blue) on the spike potential (squares) and on the hump potential (circles) in the CVs of Pt(111) in 0.1 M H2SO4.
 | ||
| Fig. 2 Cyclic voltammograms, at 50 mV s−1, of Pt(111) in 0.1 M H2SO4 + x M MClO4. M = Li+ (a), Na+ (b), K+ (c) or Cs+ (d). x = 10−4 (black), 10−3 (red), 10−2 (green) and 5 × 10−2 (blue). | ||
 | ||
| Fig. 3 Semilogarithmic plots of the dependence of the spike potential in the positive sweep (squares), and of the hump potential in the negative sweep (circles) in the CV at 50 mV s−1 of Pt(111) in 0.1 M H2SO4 on the concentration of alkali-metal cations (black: Li+; red: Na+; green: K+; blue: Cs+). The lines are fits of the experimental data for the spike and the hump to eqn (7) and (8), respectively. | ||
Even at the highest concentration used, the potential of the spike is but very slightly increased in all cases but Cs+, this cation additionally decreasing the intensity of the spike (Fig. 2d). The hump becomes sharper and more reversible, and its potential becomes more negative, at high concentrations of K+ and Cs+ (a similar effect was observed by García et al.3 and Garcia-Araez et al.7 in the case of Na+ at cNa+ ≥ 0.2 M). The magnitude of these effects increases in the order Li+ < Na+ < K+ < Cs+. All these results are in good agreement with previous reports.3,4,7
As shown in Fig. 3, the effect of Cs+ on the spike is similar to that found previously for a hydrogen adsorption feature on cyanide-modified Pt(111) electrodes.9 Since the spike is due to a phase transition within the sulfate adlayer, and must therefore appear at the same, critical local coverage of (H+–SO4)ad, its positive potential shift with increasing Cs+ concentration can be attributed to the substitution of H+ by Cs+. We can describe the adsorption equilibrium of (M+–SO4)ad as M+ + SO42− ⇌ M+–SO4(ad) + 2e. Assuming that both this adsorption and that of the (H+–SO4)ad pair can be described by the Langmuir isotherm, which is a good approximation at least at the lower H2SO4 concentrations, that aSO42− = cSO42−, that aH+ = cH+, and that aM+ = cM+, we can write:
 | (1) |
 | (2) |
 and
and  are the activity of adsorbed (H+–SO4)ad and (M+–SO4)ad, respectively, at the spike,
are the activity of adsorbed (H+–SO4)ad and (M+–SO4)ad, respectively, at the spike, 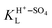 and
and 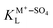 are the Langmuir constants for the adsorption of the (H+–SO4)ad and the (M+–SO4)ad pair, respectively,
are the Langmuir constants for the adsorption of the (H+–SO4)ad and the (M+–SO4)ad pair, respectively,  and
and  are their corresponding surface coverages at the spike, n is the number of electrons crossing the interface per adsorbed (H+–SO4)ad or (M+–SO4)ad pair, Δϕ is the potential drop across the electrode–electrolyte interface, F is the Faraday constant, and R and T have their usual meaning. Since Δϕ is the same in both cases, we can write:
are their corresponding surface coverages at the spike, n is the number of electrons crossing the interface per adsorbed (H+–SO4)ad or (M+–SO4)ad pair, Δϕ is the potential drop across the electrode–electrolyte interface, F is the Faraday constant, and R and T have their usual meaning. Since Δϕ is the same in both cases, we can write: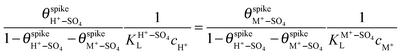 | (3) |
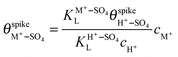 | (4) |
The spike corresponds to the formation of an ordered (H+–SO4)ad adlayer at a critical coverage, and, since it is reversible, it must obey Nernst's equation:
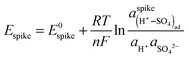 | (5) |
 are the activities of protons and sulfate in the solution, respectively, and E0spike is the standard spike potential, i.e., the spike potential at standard temperature and pressure, pH 0, and unit activity of sulfate in solution and of adsorbed (H+–SO4)ad.
are the activities of protons and sulfate in the solution, respectively, and E0spike is the standard spike potential, i.e., the spike potential at standard temperature and pressure, pH 0, and unit activity of sulfate in solution and of adsorbed (H+–SO4)ad.
In the presence of adsorbed (M+–SO4)ad pairs, and assuming Langmuir adsorption for both (H+–SO4)ad and (M+–SO4)ad, 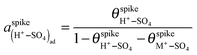 (eqn (1)). Assuming, in a first approximation, that
(eqn (1)). Assuming, in a first approximation, that  is constant, eqn (5) becomes, for a given pH and sulfate concentration in solution:
is constant, eqn (5) becomes, for a given pH and sulfate concentration in solution:
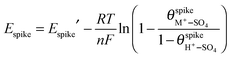 | (6) |
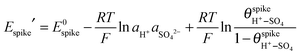 is the spike potential for a given pH and sulfate activity in solution in the absence of M+ (i.e., for zero coverage of (M+–SO4)ad). Substitution of
is the spike potential for a given pH and sulfate activity in solution in the absence of M+ (i.e., for zero coverage of (M+–SO4)ad). Substitution of  from eqn (4) into (6) yields:
from eqn (4) into (6) yields: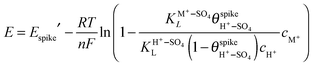 | (7) |
 and cH+ remain constant, is equivalent to the equation recently derived by us from the model developed to describe the effect of alkali-metal cations on the CV of cyanide-modified Pt(111) electrodes.9 As shown in Fig. 3, with the above assumption eqn (7) describes very well the dependence of the potential of the spike on the concentration of Cs+ for 10−4 M < cCs+ < 5 × 10−2 M, albeit with n = 0.2, a question that will be discussed below. The effect of the other cations on the spike at the concentrations used is too small to attempt a fitting. The fit yields a value of
and cH+ remain constant, is equivalent to the equation recently derived by us from the model developed to describe the effect of alkali-metal cations on the CV of cyanide-modified Pt(111) electrodes.9 As shown in Fig. 3, with the above assumption eqn (7) describes very well the dependence of the potential of the spike on the concentration of Cs+ for 10−4 M < cCs+ < 5 × 10−2 M, albeit with n = 0.2, a question that will be discussed below. The effect of the other cations on the spike at the concentrations used is too small to attempt a fitting. The fit yields a value of  of ca. 5 M−1 (which, taking into account that
of ca. 5 M−1 (which, taking into account that  and cH+ = 0.1 M, corresponds to a reasonable value of ca. 2 for
and cH+ = 0.1 M, corresponds to a reasonable value of ca. 2 for  ).
).
The height of the spike in the CV of Pt(111) electrodes decreases with decreasing the domain size of the  structure. The very small effect of Li+, Na+ and K+ on both the potential and the charge of the spike suggests that, in this potential region, and at the relatively low concentrations used here (at higher concentrations, Na+ and K+ do affect both the position and the height of the spike3,7), (Li+–SO4)ad, (Na+–SO4)ad and (K+–SO4)ad ion pairs cannot displace (H+–SO4)ad from the electrode surface (equivalently, Li+, Na+ and K+ cannot displace H+ from the (H+–SO4)ad network). This is probably due to the extra stability provided to the sulfate adlayer by the hydrogen bond network present in this structure. In contrast, the interaction of (Cs+–SO4)ad ion pairs with the Pt(111) surface seems to be strong enough to displace (H+–SO4)ad from the electrode surface, as confirmed by the fact that the positive shift of the spike potential illustrated in Fig. 3 is accompanied by a clear decrease of the spike height (Fig. 2d), indicating a decrease of the domain size of the
structure. The very small effect of Li+, Na+ and K+ on both the potential and the charge of the spike suggests that, in this potential region, and at the relatively low concentrations used here (at higher concentrations, Na+ and K+ do affect both the position and the height of the spike3,7), (Li+–SO4)ad, (Na+–SO4)ad and (K+–SO4)ad ion pairs cannot displace (H+–SO4)ad from the electrode surface (equivalently, Li+, Na+ and K+ cannot displace H+ from the (H+–SO4)ad network). This is probably due to the extra stability provided to the sulfate adlayer by the hydrogen bond network present in this structure. In contrast, the interaction of (Cs+–SO4)ad ion pairs with the Pt(111) surface seems to be strong enough to displace (H+–SO4)ad from the electrode surface, as confirmed by the fact that the positive shift of the spike potential illustrated in Fig. 3 is accompanied by a clear decrease of the spike height (Fig. 2d), indicating a decrease of the domain size of the  structure. However, the charge density in the potential region between the onset of bisulfate adsorption (just after the hydrogen adsorption region) and the double layer region remains roughly constant and independent of the Cs+ concentration, suggesting that only the domain size of this structure is affected, the total amount of adsorbed sulfate species, (H+–SO4)ad + (Cs+–SO4)ad, remaining constant.
structure. However, the charge density in the potential region between the onset of bisulfate adsorption (just after the hydrogen adsorption region) and the double layer region remains roughly constant and independent of the Cs+ concentration, suggesting that only the domain size of this structure is affected, the total amount of adsorbed sulfate species, (H+–SO4)ad + (Cs+–SO4)ad, remaining constant.
While neither K+ nor Cs+ changes the charge of (bi)sulfate adsorption below the hump, they slightly increase the charge of the hump, which is ca. 25 μC cm−2 (without double layer correction) in cation-free solutions, also with Li+ and Na+ at the concentrations used in this work, and also with K+ and Cs+ at cM+ ≤ 10−3 M. However, the charge increases to 28 μC cm−2 with K+ and Cs+ at cM+ = 10−2 M, to 30 μC cm−2 with cK+ = 5 × 10−2 M, and to 35 μC cm−2 with cCs+ = 5 × 10−2 M. Therefore, under these conditions, the total amount of adsorbed sulfate species (H+–SO4(ad) + M+–SO4(ad)) is higher than in the absence (or at low enough concentrations) of cations. The additional amount of adsorbed sulfate species increases from ca. 0.03 ML in the presence of 10−2 M K+ or Cs+ to ca. 0.04 ML in the presence of 5 × 10−2 M K+ and to ca. 0.05 ML in the presence of 5 × 10−2 M Cs+. These values agree reasonably well with the amount of K+ estimated to adsorb in this potential region (ca. 0.03 ML) by Garcia-Araez et al.7
This increase of the hump charge by the added cations renders difficult the derivation of an equation describing the behavior of the hump, because both the total adsorbate coverage and the composition of the adlayer at the hump are different in cations-free and in cations-containing solutions, for different cations, and for the same cation at different concentrations. Nonetheless, it is evident from Fig. 3 that the shift of the hump potential with increasing cation concentration can be described by an equation similar to eqn (7), but with a positive sign for the cM+ term, since the cations now cooperate, instead of competing, with the phase transition, and therefore shift negatively the potential of the hump:
 | (8) |
Although eqn (8) has not been derived using the same thermodynamic considerations as the other equations above, the negative shift of the hump potential can be intuitively understood. We have noted above that, in the absence of cations, the hump corresponds to a further increase of the bisulfate coverage by 0.025 ML, which disrupts the hydrogen-bonded  structure. The hump becomes more reversible, and its potential shifts negatively, at high enough concentrations of alkali-metal cations. In other words, in addition to helping to break the hydrogen bond network, which opposes further adsorption, the incorporation of cations increases the stability of the higher coverage and hydrogen bond-free adlayer formed in the hump.
structure. The hump becomes more reversible, and its potential shifts negatively, at high enough concentrations of alkali-metal cations. In other words, in addition to helping to break the hydrogen bond network, which opposes further adsorption, the incorporation of cations increases the stability of the higher coverage and hydrogen bond-free adlayer formed in the hump.
An intriguing result is that, in the case of Cs+, a fit of the data to eqn (7) and (8) yields n < 2 (n = 0.2 for the spike and n = 0.4 for the hump; in the case of K+, and for the hump, n = 1). In our previous work with cyanide-modified Pt(111) electrodes,9 this was attributed to the transfer through the interface of less than one electron per adsorbed pair, but this disagrees with the above analysis of the charge of the spike and the hump in the presence of Cs+. In the case of eqn (7), a more plausible explanation is that n < 2 because of the decrease of cSO42− with increasing cM+, due to the formation of MSO4− pairs in the solution, which must provoke an additional positive shift of the spike potential. The use of the Langmuir isotherm, which is obviously an oversimplification, may also contribute to the observed deviation.
Conclusions
In summary, cations can adsorb on the electrode surface forming pairs with specifically adsorbing anions. These electrostatic (or, more generally speaking, non-covalent) interactions can affect the properties of the electrode–electrolyte interface, and therefore the processes that occur in this region, including, most importantly, electrocatalytic reactions. Our model is based on a simple description of the interaction between cations and specifically adsorbed anions, and fits very well the experimental data for two completely different adsorption processes, namely, the adsorption of hydrogen on cyanide-modified Pt(111)9 and the adsorption of (bi)sulfate on Pt(111) electrodes. The model provides quantitative data regarding the interaction between the cations and chemisorbed species, allowing us to understand trends as well as deviations from anticipated trends.9In acidic media, the model must also include the competition between M+ and H+ for the interaction with surface-anchored species, or, equivalently in the case treated in this contribution, the competition between (H+–SO4)ad and (M+–SO4)ad for the same metal sites. This competition results in a threshold cation concentration below which, in acidic media, cations have no measurable effect on interfacial processes. Due to the absence of competing H+ in alkaline media, we do not expect such a threshold cation concentration to exist in this case. Rather, a continuous increase of the cation effect with increasing cation concentration is to be expected.
The recently reported effects of alkali-metal cations on several electrocatalytic reactions must be mediated by the interaction between these cations and chemisorbed species. Since these interactions seem to be adequately and quantitatively described by our model, we expect it to be useful to describe and explain those effects. In particular, taking into account the anticipated differences in the effect of cations in acidic and alkaline environments mentioned above, and the importance of pH in some relevant electrocatalytic reactions,40–42 our model could help to find optimal electrolyte compositions for electrocatalysis.
Acknowledgements
Funding from the DGI (Spanish Ministry of Education and Science) through Project CTQ2009-07017 is gratefully acknowledged. E.P.M.L. wishes to thank the Universidad Nacional de Córdoba, Argentina, for a grant within the “Programa de Movilidad Internacional de Profesores Cuarto Centenario”.Notes and references
- V. E. Kazarinov and O. A. Petry, J. Electroanal. Chem., 1970, 27, A1–A2 CrossRef.
- B. B. Damaskin, O. A. Petrii and V. E. Kazarinov, Elektrokhimiya, 1972, 8, 1373–1377 CAS.
- N. García, V. Climent, J. M. Orts, J. M. Feliu and A. Aldaz, ChemPhysChem, 2004, 5, 1221–1227 CrossRef PubMed.
- V. Climent, N. García-Araez and J. M. Feliu, Electrochem. Commun., 2006, 8, 1577–1582 CrossRef CAS PubMed.
- J. M. Feliu, M. J. Valls, A. Aldaz, M. A. Climent and J. Clavilier, J. Electroanal. Chem., 1993, 345, 475–481 CrossRef CAS.
- D. Strmcnik, K. Kodama, D. van der Vliet, J. Greeley, V. R. Stamenkovic and N. M. Marković, Nat. Chem., 2009, 1, 466–472 CrossRef CAS PubMed.
- N. Garcia-Araez, V. Climent, P. Rodriguez and J. M. Feliu, Phys. Chem. Chem. Phys., 2010, 12, 12146–12152 RSC.
- D. F. van der Vliet and M. T. M. Koper, Surf. Sci., 2010, 604, 1912–1918 CrossRef CAS PubMed.
- M. Escudero-Escribano, M. E. Zoloff Michoff, E. P. M. Leiva, N. M. Marković, C. Gutiérrez and Á. Cuesta, ChemPhysChem, 2011, 12, 2230–2234 CrossRef CAS PubMed.
- M. Nakamura, N. Sato, N. Hoshi and O. Sakata, ChemPhysChem, 2011, 12, 1430–1434 CrossRef CAS PubMed.
- D. Strmcnik, D. F. van der Vliet, K. C. Chang, V. Komanicky, K. Kodama, H. You, V. R. Stamenkovic and N. M. Marković, J. Phys. Chem. Lett., 2011, 2, 2733–2736 CrossRef CAS.
- N. Danilovic, S. Ram, D. Strmcnik, A. P. Paulikas, D. Myers, V. R. Stamenkovic and N. M. Markovic, Electrocatalysis, 2012, 3, 221–229 CrossRef CAS PubMed.
- I. Katsounaros and K. J. J. Mayrhofer, Chem. Commun., 2012, 48, 6660–6662 RSC.
- J. Suntivich, E. Perry, H. Gasteiger and Y. Shao-Horn, Electrocatalysis, 2013, 4, 49–55 CrossRef CAS.
- C. Stoffelsma, P. Rodriguez, G. Garcia, N. Garcia-Araez, D. Strmcnik, N. M. Marković and M. T. M. Koper, J. Am. Chem. Soc., 2010, 132, 16127–16133 CrossRef CAS PubMed.
- J. Clavilier, R. Faure, G. Guinet and R. Durand, J. Electroanal. Chem., 1980, 107, 205–209 CrossRef CAS.
- A. M. Funtikov, U. Stimming and R. Vogel, J. Electroanal. Chem., 1997, 428, 147–153 CrossRef CAS.
- O. M. Magnussen, J. Hageböck, J. Hotlos and R. J. Behm, Faraday Discuss., 1992, 94, 329–338 RSC.
- G. J. Edens, X. Gao and M. J. Weaver, J. Electroanal. Chem., 1994, 375, 357–366 CrossRef CAS.
- L.-J. Wan, S.-L. Yau and K. Itaya, J. Phys. Chem., 1995, 99, 9507–9513 CrossRef CAS.
- L.-J. Wan, M. Hara, J. Inukai and K. Itaya, J. Phys. Chem. B, 1999, 103, 6978–6983 CrossRef CAS.
- Y. G. Kim, J. B. Soriaga, G. Vigh and M. P. Soriaga, J. Colloid Interface Sci., 2000, 227, 505–509 CrossRef CAS PubMed.
- L.-J. Wan, T. Suzuki, K. Sashikata, J. Okada, J. Inukai and K. Itaya, J. Electroanal. Chem., 2000, 484, 189–193 CrossRef CAS.
- M. Wilms, P. Broekmann, C. Stuhlmann and K. Wandelt, Surf. Sci., 1998, 416, 121–140 CrossRef CAS.
- A. Kolics and A. Wieckowski, J. Phys. Chem. B, 2001, 105, 2588–2595 CrossRef CAS.
- K.-i. Ataka and M. Osawa, Langmuir, 1998, 14, 951–959 CrossRef CAS.
- A. Comas-Vives, J. Bandlow and T. Jacob, Phys. Chem. Chem. Phys., 2013, 15, 992–997 RSC.
- A. Cuesta, M. Kleinert and D. M. Kolb, Phys. Chem. Chem. Phys., 2000, 2, 5684–5690 RSC.
- P. W. Faguy, N. S. Marinković and R. R. Adžić, Langmuir, 1996, 12, 243–247 CrossRef CAS.
- R. Jinnouchi, T. Hatanaka, Y. Morimoto and M. Osawa, Phys. Chem. Chem. Phys., 2012, 14, 3208–3218 RSC.
- O. M. Magnussen, Chem. Rev., 2002, 102, 679–726 CrossRef CAS PubMed.
- Y. Shingaya and M. Ito, J. Electroanal. Chem., 1999, 467, 299–306 CrossRef CAS.
- F. Simeone, D. Kolb, S. Venkatachalam and T. Jacob, Angew. Chem., Int. Ed., 2007, 46, 8903–8906 CrossRef CAS PubMed.
- F. C. Simeone, D. M. Kolb, S. Venkatachalam and T. Jacob, Surf. Sci., 2008, 602, 1401–1407 CrossRef CAS PubMed.
- S. Venkatachalam and T. Jacob, Z. Phys. Chem., 2007, 221, 1393–1406 CrossRef CAS PubMed.
- K.-Y. Yeh, N. A. Restaino, M. R. Esopi, J. K. Maranas and M. J. Janik, Catal. Today, 2013, 202, 20–35 CrossRef CAS PubMed.
- N. M. Marković, B. N. Grgur, C. A. Lucas and P. N. Ross, J. Phys. Chem. B, 1999, 103, 487–495 CrossRef.
- C. Saravanan, M. T. M. Koper, N. M. Markovic, M. Head-Gordon and P. N. Ross, Phys. Chem. Chem. Phys., 2002, 4, 2660–2666 RSC.
- Y. Shingaya and M. Ito, Chem. Phys. Lett., 1996, 256, 438–444 CrossRef CAS.
- J. Joo, T. Uchida, A. Cuesta, M. T. M. Koper and M. Osawa, J. Am. Chem. Soc., 2013, 135, 9991–9994 CrossRef CAS PubMed.
- J. Joo, T. Uchida, A. Cuesta, M. T. M. Koper and M. Osawa, Electrochim. Acta, 2014, 129, 127–136 CrossRef CAS PubMed.
- S. Brimaud, J. Solla-Gullón, I. Weber, J. M. Feliu and R. J. Behm, ChemElectroChem, 2014 DOI:10.1002/celc.201400011.
| This journal is © the Owner Societies 2014 |
