Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Imaging breakdown diagrams for bromobutyne isomers with photoelectron–photoion coincidence
Andras
Bodi
* and
Patrick
Hemberger
Molecular Dynamics Group, Paul Scherrer Institute, 5232 Villigen, Switzerland. E-mail: andras.boedi@psi.ch
First published on 19th September 2013
Abstract
Internal energy selected C4H5Br+ ions were prepared by vacuum ultraviolet photoionization from the bromobutyne constitutional isomers 4-bromo-1-butyne, 1-bromo-2-butyne, and 3-bromo-1-butyne. The lowest energy dissociative photoionization channel is Br-loss. 1-Bromo-2-butyne and 3-bromo-1-butyne cations are not metastable, and based on the threshold photoionization breakdown diagrams and neutral internal energy distributions, 0 K appearance energies of E0 = 10.375 ± 0.010 and 10.284 ± 0.010 eV are obtained, respectively. A kinetic shift has been observed in the Br loss of the 4-bromo-1-butyne cation, and the experimental dissociation rates were also modeled to obtain E0 = 10.616 ± 0.030 eV. The energetics of the samples and nine C4H5 and C4H5+ structures are explored using G4 theory, which suggests that only the staggered 4-bromo-1-butyne rotamer cation loses Br to form a high-energy cyclic C4H5+ isomer, while the relative appearance energies indicate that 1-bromo-2-butyne and 3-bromo-1-butyne form the linear CH2CCCH3+ ion. The subtraction scheme for hot electron suppression in threshold photoelectron–photoion coincidence (TPEPICO) is discussed, and is used to introduce velocity map imaging (VMI-)PEPICO and data analysis. The derived onsets and the dissociation rate curve show that modeling VMI-PEPICO data taken close above or below the disappearance energy of the parent ion to obtain imaging breakdown diagrams is a feasible approach also in the presence of a kinetic shift. Imaging breakdown diagrams are advantageous when signal levels are low or short acquisition times necessary, such as in the case of reactive intermediates or in time resolved experiments, and can also be used as a fast molecular thermometer.
Introduction
Photoelectron–photoion coincidence1,2 spectroscopy can be used to prepare internal energy selected photoions and study their dissociative photoionization processes.3,4 Internal energy selection is achieved by setting the photon energy, selecting for an electron kinetic energy and thus ensuring that the excess energy deposited in the photoion is known. The measured thresholds can then be applied in the ion cycle to determine thermochemical properties, such as enthalpies of formation or proton affinities.5,6 In threshold photoelectron–photoion coincidence (TPEPICO), the photon energy is scanned and zero kinetic energy electrons serve as the start signal for photoion time-of-flight (TOF) analysis. The experimental results can then be concisely plotted in the threshold photoelectron spectrum (TPES) and the fractional parent and daughter ion abundances as a function of the photon energy in the breakdown diagram. With the advent of velocity map imaging (VMI),7,8 it became possible to focus threshold electrons onto a single, central spot of a position sensitive detector and detect them with a close to 50% collection efficiency.9 The electron kinetic energy resolution is determined by the extraction field and the spatial resolution of the detector, and can be on the order of 10 meV (1 kJ mol−1) using masked multichannel plates, and about 1 meV (0.1 kJ mol−1) with position sensitive detectors. The latter is also used in the Imaging Photoelectron–Photoion Coincidence (iPEPICO) experiment at the vacuum ultraviolet (VUV) beamline of the Swiss Light Source,10 and allowed, e.g., for the most accurate formaldehyde proton affinity measurement so far.6New generation single imaging PEPICO experiments at synchrotron light sources have recently been enhanced by double imaging setups,11,12 in which both photoelectrons and photoions are velocity map imaged in delayed coincidence. Together with the triggerless data acquisition technique,13 which enables high event frequencies at arbitrarily high ion flight times, dissociative photoionization processes can now be studied with unprecedented detail. Sequential and parallel unimolecular dissociation reactions can be modeled statistically.14 When certain nuclear or electronic degrees of freedom are disconnected in non-statistical processes, the mechanism can be established based, e.g., on the correlation between the breakdown diagram and the threshold photoelectron spectrum.15,16
The advances in the experimental hardware and data acquisition techniques have only partially been matched by improvements in the data analysis. Photoionization above the ionization energy may yield a broad photoelectron energy distribution with only a fraction of ionization events yielding threshold electrons. Kinetic energy electrons are rejected in TPEPICO, and a plausible multiplexing advantage of velocity map imaging photoelectron–photoion coincidence (VMI-PEPICO) with them: the photon energy scan is already contained in the velocity map images of slow photoelectrons. The most straightforward application of VMI images is to identify isomers in many-component mixtures based on their photoion mass-selected VMI photoelectron fingerprint.17 Several methods have also been proposed to transform VMI data and reconstruct the momentum and the kinetic energy distribution of the imaged particles,18–24 but most inversion methods propagate noise towards the center of the image, where the absolute energy resolution is best. Slow Electron Velocity Map Imaging (SEVI)25 and Slow Photoelectron Spectroscopy (SPES)26 are two techniques designed to draw on the velocity distribution information of slow electrons. VUV-VMI photoelectron spectroscopy was used to obtain the best resolved propargyl radical spectrum, as well.27 However, when, e.g., SPES is applied in photoion coincidence, the photoion mass selection only serves as a priori photoion mass discrimination. To study dissociative photoionization, the photoelectron spectrum and the coincident mass spectra have to be reconstructed simultaneously, and it is the purpose of this paper to show how and how accurately this is possible.
The iPEPICO time-of-flight mass spectrometer has two acceleration regions, one of which is at a low draw out potential. Ions dissociating on the microsecond timescale will do so in this region, and yield asymmetric peaks in the TOF distributions as well as a somewhat broadened breakdown diagram because of the excess internal energy above the threshold the parent ion needs to quantitatively dissociate before leaving the acceleration region. Absolute unimolecular decay rate constants can be obtained by peak shape modeling, and can be used to account for kinetic shifts.14 Peak shape modeling is difficult for non-volatile samples with few counts,28 or in H atom loss,29 for which the instrumental peak width is commensurate with the broadening due to the parent ion being metastable. We previously showed that, in such cases, peak shape modeling can be expanded by daughter ion TOF center of gravity (CoG) analysis to establish the dissociation rate curve. In such cases, the statistical model is fitted to the experimental breakdown curves (i.e. fractional ion abundances as a function of photon energy) and daughter ion CoG (i.e. daughter ion TOF peak center as a function of photon energy). This approach works well even with only a few hundred threshold ionization events recorded,28 and can be further generalized to include higher moments for peak deconvolution.30 The number densities can be even lower for reactive intermediates produced in flash pyrolysis,31–33 which is part of the reason dissociative photoionization studies on free radicals are few and far between.34 Photon energy scans also complicate time-dependent or pulsed, low duty cycle measurements. This can be alleviated by turning the time dimension of the photon energy scan into a spatial one and obtaining the complete breakdown diagram (BD) at a single photon energy.
We discuss the subtraction method currently used to suppress the hot electron contamination of the threshold signal in TPEPICO first.9 The lowest energy dissociative photoionization channel, Br atom loss, of three C4H5Br isomers, 4-bromo-1-butyne, 1-bromo-2-butyne, and 3-bromo-1-butyne, is then reported. These are stable and volatile samples, for which threshold and imaging breakdown diagrams (iBD) can easily be compared.
As opposed to C3H5+, which has only two covalently bound minima on the potential energy surface,35–38 numerous local minima have been identified for C4H5+ with sometimes sizeable isomerization barriers between them.39,40 Their relative energies and the dissociative photoionization mechanism of the C4H5Br isomers will be re-examined in the light of new composite method calculations. Neutral C4H5 is believed to play an important role as an intermediate in PAH formation in interstellar chemistry,41 in soot formation in fuel-rich flames.42–44 It was detected in the pyrolysis of methyl tert-butyl ether45 and proposed to be a product in the unimolecular decomposition of dimethylfuran.46 The ionic C4H5+ is a dissociative photoionization product of isoprene47 as well as a possible fragment of cyclohexadiene dications.48
Experimental approach
The photoionization experiments were carried out at the recently upgraded11 VUV beamline49 of the Swiss Light Source with the 600 lines per mm grating providing monochromatic VUV radiation with 2–3 meV resolution at 10 eV photon energy, calibrated to the Ar 11s′–14s′ autoionization lines both in the first and in the second order. The higher harmonic radiation is suppressed by the laminar grating and eliminated by a compact, differently pumped gas filter run at 10 mbar of a Kr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ar
Ar![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ne mixture with an absorption length of 10 cm.
Ne mixture with an absorption length of 10 cm.
Three C4H5Br isomers, 4-bromo-1-butyne, 1-bromo-2-butyne, and 3-bromo-1-butyne, were purchased from Sigma-Aldrich, and introduced into the iPEPICO endstation10 through a 30 cm long, 6 mm Teflon tube effusively at room temperature. The typical pressure in the experimental chamber was 1–2 × 10−6 mbar during measurement. A constant 40 or 120 V cm−1 electric field extracts photoelectrons and photoions in opposite directions in the ionization region. The electrons are velocity map imaged and serve as the start signal for the ion TOF analysis. The photoions are space focused and the TOF stop signal is provided using a Jordan TOF C-726 microchannel plate detector.
Threshold electrons are focused onto the center of the imaging detector. Kinetic energy electrons detected in a small ring region around this center spot are presumed to represent the kinetic electron background of the threshold signal well. As proposed by Sztáray and Baer,9 the threshold photoionization mass spectrum can then be obtained by subtracting the ring mass spectrum, multiplied by a factor dependent on the center/ring area ratio, from the center TOF distribution. This conceptually simple approach relies on two assumptions, namely that the hot electron contamination is mostly due to high kinetic energy electrons, with almost constant radial distribution close to the detector center, and, second, that the slow photoelectron yield does not increase too rapidly with kinetic energy. These assumptions hold most of the time for 0–10 meV electrons, but can lead to oversubtraction of the hot electron signal immediately above an intense photoelectron peak.
Results and discussion
Hot electron subtraction
The parent ion signal vanishes above the dissociative photoionization onset in the breakdown diagram of a fast dissociation.50 It has been observed for certain samples6,51 that no constant kinetic electron background subtraction factor yields exactly zero parent abundance in threshold photoionization over a wide energy range above threshold. Since the deviations were small and arose at higher photon energies than the threshold, they did not affect the derived onset or thermochemistry. However, for completeness' sake, it is worthwhile to address and assess the inherent assumptions in hot electron subtraction.
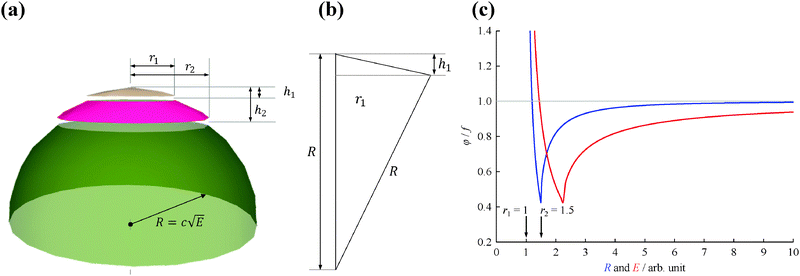
Fig. 1(a) shows the Newton sphere corresponding to E kinetic energy electrons propagating from the ionization region. Our goal is to subtract their contribution from the central r1 radius region based on the signal in the r2 outer and r1 inner diameter ring region exactly. In hot electron subtraction assuming constant collection efficiencies, the factor would be the area ratio of the two regions on the detector, i.e.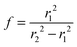 . With isotropic photoelectron angular distribution in the vertical direction, the factor, in fact, corresponds to the areas of the spherical cap and the ring that are imaged onto the respective detector areas. These, in turn, are proportional to the heights, h1 and h2 − h1, respectively, (Fig. 1(b)) and can be calculated using the radius of the Newton sphere and that of the detector area:
. With isotropic photoelectron angular distribution in the vertical direction, the factor, in fact, corresponds to the areas of the spherical cap and the ring that are imaged onto the respective detector areas. These, in turn, are proportional to the heights, h1 and h2 − h1, respectively, (Fig. 1(b)) and can be calculated using the radius of the Newton sphere and that of the detector area:
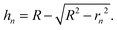 | (1) |
Consequently, the kinetic energy dependent factor for subtraction is given as:
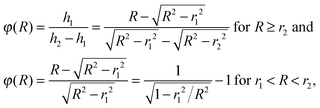 | (2) |
The radius of the Newton sphere is proportional to the momentum and to the square root of the energy, 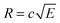 . Fig. 1(c) shows φ(R)/f and φ(E)/f with r1 = 1, r2 = 1.5 and c = 1. The exact factor first decreases quickly, as the low kinetic energy Newton sphere fills the ring area on the detector. At somewhat more than twice the maximum energy of the central area, the exact factor is only 40% of the center/ring area ratio on the detector. At higher energies, the exact factor converges relatively quickly to the detector area ratio, and reaches 90% at E = 7.
. Fig. 1(c) shows φ(R)/f and φ(E)/f with r1 = 1, r2 = 1.5 and c = 1. The exact factor first decreases quickly, as the low kinetic energy Newton sphere fills the ring area on the detector. At somewhat more than twice the maximum energy of the central area, the exact factor is only 40% of the center/ring area ratio on the detector. At higher energies, the exact factor converges relatively quickly to the detector area ratio, and reaches 90% at E = 7.
Albeit with some notable exceptions, such as water at its dissociative photoionization onset,52 or in the presence of autoionizing resonances,53 the photoelectron yield as a function of photon energy less the electron kinetic energy mirrors the photoelectron spectrum, PE(hν − Ee−), also for threshold photoionization (Ee− = 0). For a continuous electron kinetic energy distribution, the exact subtraction factor can be derived based on the known kinetic energy distribution of the electrons, normalized by the total photoelectron yield:
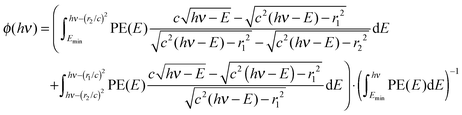 | (3) |
When based on a subtracted threshold photoelectron spectrum, PE(hν) = ec(hν) − ϕ(hν)·er(hν), where ec(hν) is the electron yield in the center and er(hν) is the electron yield in the ring, the factor depends only on the lower energy PE(E < hν), thus, the subtraction can be carried out in a self-consistent way on the TPES and the threshold ionization mass spectra simultaneously. Furthermore, the enhanced threshold photoionization cross sections (see below) can be taken into account by scaling the derived PE(E). We have tested the effect of this approach on threshold photoelectron spectra and breakdown diagrams, and found that self-consistent subtraction can be used to eliminate small oversubtraction effects in the breakdown diagram, while its effect on the TPES is marginal. Part of the reason is the threshold photoelectron peak, meaning that the hot electron contamination is by nature suppressed by the ionization mechanism, as well. Therefore, the subtraction procedure as proposed by Sztáray and Baer9 is a good approximation for the overwhelming majority of systems, and will be used to suppress the hot electron contamination herein, as well.
Threshold photoionization
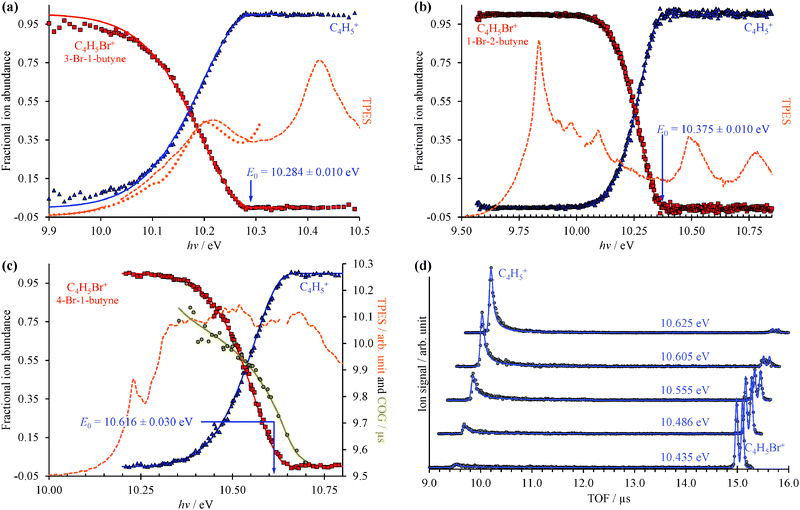
The TPES and the corresponding Br-loss breakdown diagrams for the three C4H5Br isomers are plotted from the ionization onset to the disappearance of the parent ion in Fig. 2. Based on the symmetric daughter ion TOF peaks, two isomers, 3-bromo-1-butyne and 1-bromo-2-butyne dissociate without a kinetic shift, i.e. quickly on the time scale of the experiment. In such cases, the breakdown curve of the parent ion corresponds to the cumulative distribution function of the thermal energy distribution of the neutral, bd(hν) = cdf(E0 − hν), and E0 is the only adjustable parameter to obtain the best fit to the experimental data.14 At low photon energies, 100% of the observed ion signal corresponds to the parent ion, and the low signal levels only result in somewhat increased noise at the onset of the TPES in Fig. 2(a and b). At high energies, when the total thermal energy distribution of the sample is lifted well above the dissociation threshold, the parent ion vanishes, and the fractional abundance of the daughter ion reaches 100%. The thermal energy distribution as well as the densities and numbers of states are calculated based on harmonic frequencies and rotational constants from density functional theory calculations as discussed later.The C4H5+ peak of the third isomer, 4-bromo-1-butyne, shows a marked asymmetry at low photon energies, and the parent ion dissociates slowly at threshold. The daughter ion peak center of gravity is a measure of the dissociation rate constant, and is also used in the model and plotted in Fig. 2(c), with the corresponding TOF distributions shown in Fig. 2(d). In such cases, a statistical rate curve, k(E), is calculated based on the density of states of the dissociating ion and the number of states of the transition state. In addition to varying the onset energy, the transitional frequencies of the transition state are also scaled by a factor in the RRKM approach, to reproduce the experimental breakdown diagram and the measured rates simultaneously as shown in Fig. 2(c and d).14
The CoG curve of the fragment ion peak was never used before for systems with well-resolved asymmetries in the TOF distributions, such as in 4-bromo-1-butyne. The TOF distributions in Fig. 2(d) were calculated by the breakdown curve/COG fit model of Fig. 2(c), and the agreement shows for the first time convincingly that the two approaches are indeed equivalent.
Imaging breakdown diagrams
The VMI/photoion coincidence data were taken with 900–1200 s acquisition times, which yielded noise-free images and the integration times could have been decreased further. This compares favorably with the 10 times longer total acquisition time of a threshold photoionization breakdown diagram, and gives grounds for optimism that the iBD approach may be viable even when signal levels are prohibitively low to allow for a threshold photoionization breakdown diagram scan. Angular anisotropies have not been observed, and the dimensionality of the problem is reduced by only analyzing the radial distribution of photoelectrons and coincident fragment ions. Threshold photoionization breakdown diagrams do not depend on ambient parameters such as sample pressure or photon flux, and are generally unaffected by the characteristics of the photoelectron spectrum.54 Intermediate Rydberg states can almost always channel all excess photon energy into the parent ion and yield a threshold photoelectron, filling in the Franck–Condon gaps by autoionization,55,56 with broad Franck–Condon gaps being the exception.57 The Rydberg-state mediated threshold ionization mechanism54 may also yield slow electrons, but velocity mapped photoelectron coincidence images depend on the photoelectron spectrum. The contribution of hν − E energy electrons yielding a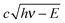 radius Newton sphere to the radial distribution at radius r can be determined as the derivative of eqn (1):
radius Newton sphere to the radial distribution at radius r can be determined as the derivative of eqn (1):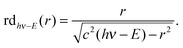 | (4) |
The reconstructed radial distribution at photon energy hν is obtained by integrating eqn (4) over the photoelectron spectrum:
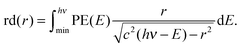 | (5) |
The constant c is determined by fitting rd(r) to argon photoelectron radial distributions with the 2P3/2 and 2P1/2 peaks. For the nominal 120 V cm−1 and 40 V cm−1 extraction fields used, 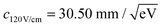 and
and 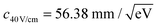 have been determined, respectively.
have been determined, respectively.
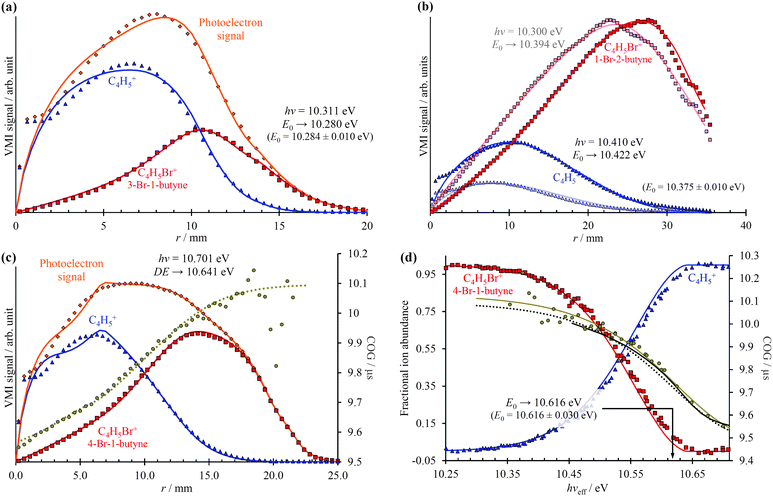
As shown in Fig. 3, photoelectrons in coincidence with a parent ion have higher kinetic energies as those in coincidence with a fragment ion. Obtaining the electron kinetic energy distribution based on the photoion mass-selected VMI images shown in Fig. 3(b) and (c), however, would discard the width and shape of the breakdown curves, which are known to correspond to the internal energy distribution of the neutral. Thus, we chose to obtain the photoelectron spectrum based on the sum of the parent and the fragment ion signal, i.e. the photoelectron yield, and then fit only the disappearance energy of the parent ion to reproduce the photoelectron images coincident with one or the other ion. The experimental radial distribution functions are integrated over 0.5 mm steps and shown as dots in Fig. 4(a)–(c).
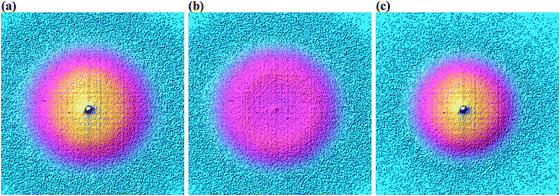 | ||
| Fig. 3 Photoelectron velocity map images for 3-bromo-1-butyne in coincidence with (a) all ions, (b) C4H5Br+ ions, and (c) C4H5+ ions at a photon energy of 10.3109 eV. | ||
In the first step of the image reconstruction, the photoelectron spectrum was approximated on a grid with 100 meV spacing and a few extra points close to zero kinetic energy to account for the threshold peak (see later). A cubic polynomial interpolation function was defined on the grid, and the grid points fitted to reproduce the experimental radial distribution function in the projection space. One such PE(E) is shown in the energy space in Fig. 2(a). It is apparent in Fig. 4(b) that the fine structure of the 1-bromo-2-butyne photoelectron spectrum is not resolved at such a low grid point density, even though it is barely visible in the radial distribution at r = 22–35 mm. On the other hand, there is virtually no noise propagation towards small radii, which is a prerequisite for an accurate breakdown diagram fit.
A surprising feature is the enhanced threshold photoelectron production apparent in all three samples, i.e. the threshold peak, which could not be reproduced faithfully by the photoelectron fits, as it corresponds to a rapid increase in the photoionization cross-sections at very low electron kinetic energies, as seen in the center peak in Fig. 3. This suggests that the autoionization mediated threshold photoionization mechanism, proposed by Guyon and Chupka,58,59 mostly contributes to threshold photoionization.
The model breakdown diagram is based on the cumulative distribution function of the neutral internal energy distribution and the disappearance energy of the parent ion, i.e. the 0 K appearance energy in fast dissociation reactions.14 The fitted photoelectron yield, PE(E), was multiplied with the breakdown diagram, projected onto the detector plane and the appearance energy was optimized to fit the experimental coincident ion mass-selected photoelectron VMI radial distributions, with the results shown as continuous lines in Fig. 4(a)–(c). Three aspects will be discussed here: (i) the effect of different extraction fields, (ii) extrapolation from within the energy range of the breakdown diagram, and (iii) modeling a kinetic shift based on daughter TOF peak center-of-gravity (CoG) data.
Contrary to our expectations, the 40 V cm−1 VMI images, obtained for 1-bromo-2-butyne and shown in Fig. 4(b), resulted in the largest error in the fitted E0, almost 50 meV or 5 kJ mol−1, when the image was obtained above the threshold (dark lines and dots), but only 20 meV or 2 kJ mol−1, when the image was obtained at hν = 10.300 eV, at 25% parent ion abundance, and the E0 fitted by extrapolation (light lines and dots). This can be compared with the 4 meV difference in between the imaging BD and threshold BD for 3-bromo-1-butyne, at an extraction field of 120 V cm−1. It is possible that the poorly reproduced enhanced threshold ionization cross sections up to 2 meV or up to r = 2.4 mm affects the derived E0 in the 40 V cm−1 case adversely. Thus, mildly higher extraction fields do not seem to decrease the accuracy of the method, and extrapolation from closely below the threshold can be just as exact as fitting an image obtained somewhat above it.
The radial distribution of the daughter ion TOF peak CoG is also plotted in Fig. 4(c) for 4-bromo-1-butyne. Consider the CoG plot in the energy space as a function of photon energy in threshold photoionization, as shown in Fig. 2(c) and 4(d). At low energies, the dissociation is so slow that the probability of a daughter ion being formed at the beginning of the extraction region is the same as that at the end. The peak shape is flat, and the CoG is in the middle of the metastable peak TOF range. At high energies, the dissociation is fast, and the CoG corresponds to the daughter ion TOF. Thus, the intermediate range corresponds to a sigmoid function, converging to the two limits with different slopes. Instead of using, e.g., a polynomial or a spline fit with a large number of unknowns, we decided to fit a Gompertz-type function60 with only four adjustable parameters to the daughter ion CoG data as a function of photon energy, i.e. parent ion internal energy:
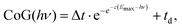 | (6) |
In addition to the photoelectron spectrum, three adjustable parameters are used to transform the VMI data for 4-bromo-1-butyne taken at a photon energy of 10.701 eV from the projection space into the energy space, as shown in Fig. 4(d). The disappearance energy of the parent ion is fitted to yield a breakdown diagram, and Gompertz function in eqn (6) yields the daughter ion center-of-gravity as a function of the effective photon energy. The same statistical approach can be applied to model the VMI-based data in Fig. 4(d) (i.e. the continuous breakdown curves and the CoG function plotted as a dotted line) as was used for the threshold photoionization breakdown diagram and center-of-gravity data in Fig. 2(c). The VMI onset energy thus derived agrees to the meV with the one based on threshold ionization, another unexpected result, which is partly a consequence of error cancellation between the center-of-gravity and breakdown curve fits to the VMI results. Consequently, kinetic shifts can be modeled just as well in the velocity map imaging based imaging breakdown diagram approach as in threshold photoionization data.
Breakdown curves are effectively molecular thermometers,61 which opens up a new use for iBD modeling. If the width of the breakdown diagram, i.e. the temperature, is an adjustable parameter, the internal energy of a system can be measured based on a single VMI image. This multiplexing advantage can be helpful in time-dependent experiments, in which it is not feasible to scan the photon energy to obtain a threshold photoionization breakdown diagram, but easily possible to obtain VMI images as a function of time, based on which a time-dependent temperature function can be obtained.
Quantum chemical calculations
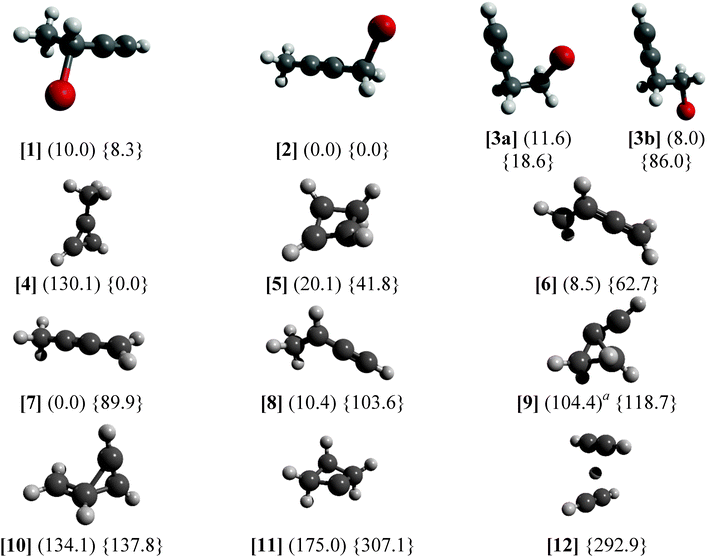
In two previous studies, it was possible to derive thermochemical values based on the dissociative photoionization onsets of constitutional isomers and a limited number of quantum chemical calculations.38,62 Such derivations require an understanding of the dissociation potential energy curve for the different isomers: if the phase space of the different isomers is shared at the dissociative photoionization threshold, the isomerization energy can be obtained as the difference in the 0 K appearance energies. This yielded isomerization energies directly for dichloroethylene isomers,62 and, by the way of a few isodesmic reactions, also for four of the five C3H5Br isomers.38 Even complex dissociation pathways are often governed by a few stationary points on the potential energy surface, as was shown for an Arduengo-type carbene, in which eight stationary points determine the dissociative photoionization mechanism over an energy range of 7 eV on the 75-dimensional potential energy surface (PES).63 The C4H5+ PES is, on the other hand, not only rich in minima and transition states, but it is also rather interconnected and anharmonic. In a previous quantum chemical study, Cunje et al. have located 14 different minima, some of which appear to be connected by internal rotation and some by bond breaking and making paths.39 They used different levels of theory for high energy minima and transition states, and reported MP4SDTQ/6-311++G(2df,p) enthalpies of formation for six of the more stable structures. When two structures were connected by β-H atom transfer, they also reported isomerization activation energies on the order of 1–1.3 eV. Douberly et al. studied the infrared spectroscopy of protonated acetylene dimers,40 which is a fifteenth, high-energy C4H5+ local minimum, and also reported MP2(fc)/6-311++G(2d,2p) energies for three lower lying isomers, which agreed with the results of Cunje et al.39In an attempt to interpret the derived dissociative photoionization onsets and to contribute to the mapping of potential energy surface of the C4H5(+) system, we have employed the G4 composite method64 of the Gaussian 09 computational chemistry suite65 to the parent species and the positively charged and neutral C4H5 structures as given by Cunje et al.39
The results in Fig. 5 show the neutral optimized structures for C4H5Br and the ionic ones for C4H5 as well as the energies for both. It is important to note that C4H5Br+ energies do not take spin–orbit effects into account, which can have a significant effect on reaction energies and affect the potential energy surface of the ion.66,67 The C4H5 PES was only sampled in the vicinity of the C4H5+ minima, and further radical isomers have been the subject of more rigorous computational studies.42,68 The C4H5+ energies correspond to singlet states, the lowest lying triplet structure is similar to [6] and lies 270 kJ mol−1 above [4]. Only the C4H5Br(+) isomers studied in this paper were calculated, whereas four further high energy minima were found to be above 280 kJ mol−1 in C4H5+ and one at 220 kJ mol−1 in C4H5. Dissociating [5] into acetylene and protonated acetylene is endothermic by 311 kJ mol−1 putting the products 353 kJ mol−1 above the most stable ion structure [4]. The C–H bond breaking in the methyl group of [4] is endothermic by 399 kJ mol−1, meaning that even the high energy structures are quite strongly bound on the global C4H5+ surface. On the other hand, the HBr-loss channel from the parent ion may open up about 50–60 kJ mol−1 (0.5–0.6 eV) above the Br-loss channel in the dissociative photoionization of [1–3] meaning that it could compete with Br-loss at higher photon energies.
The C4H5Br(+) isomers are generally close in energy with the exception of the staggered [3b] rotamer of 4-bromo-1-butyne, which is somewhat more stable than the almost eclipsed [3a] rotamer in the neutral but by almost 70 kJ mol−1 less stable than [3a] in the ion. Pure density functional theory (DFT, B3LYP/6-311++G(d,p)) calculations predict 5.5 kJ mol−1 energy difference between [3a] and [3b] on the neutral surface with a 16.5 kJ mol−1 barrier to internal rotation and only −20.0 kJ mol−1 energy difference with a barrier of 25.2 kJ mol−1 relative to [3a] on the ionic surface. The discrepancy on the ionic surface is an indication that C4H5Br+ calculations yield at least an order of magnitude less accurate relative energies than closed shell ones, i.e. with tens of kJ mol−1 uncertainty instead of a few kJ mol−1 as shown for neutral C3H5Br isomers.38
There are marked differences between the energetics of the singlet C4H5+ ion and that of the doublet C4H5 radical. The aromatic [4] is the most stable ion structure, but is not among the most stable radical isomers. Four neutral C4H5 isomers are below 20.1 kJ mol−1 of the most stable [7], whereas the next stable ion structure above [4] is [5] at 41.8 kJ mol−1. Constrained C–Br bond length scans have shown that, on the ion surface, [1] → [8] + Br, [2] → [7] + Br, and [3b] → [9] + Br can take place without a reverse barrier, whereas [3a] yields [8] + Br over a significant reverse barrier of 1.3 eV (125 kJ mol−1, the B3LYP/6-311++G(d,p) value without zero-point correction), meaning that the ionic rotamer [3a] is stable in the photon energy range studied. Thus, the relative Br-loss onset energy of 1-bromo-2-butyne [2] and 4-bromo-1-butyne [3] with respect to 3-bromo-1-butyne [1] is expected to be −3.7 kJ mol−1 (−0.038 eV) and 17.1 kJ mol−1 (0.177 eV) based on the G4 isomerization energies of these closed shell species, expected to be accurate to within a few kJ mol−1. The experimental differences, on the other hand, are 0.091 ± 0.014 eV and 0.332 ± 0.032 eV, indicating a significant discrepancy. If we assume that the dissociative photoionization of [1] also yields [7], the theoretical prediction for the relative onset energies for [2] and [3] is revised by 0.142 eV to 0.104 eV and 0.319 eV, respectively, in good agreement with the experiment. The H-transfer barrier in the radical ion is more than 1 eV,39i.e. more than the depth of the potential energy well of the ion with respect to Br-loss. Thus, the dissociative photoionization process [1] → [7] + Br requires a concerted H-transfer transition state mediated by the leaving Br-atom. However, a reliable description of the open shell parent ion PES, to confirm or refute this mechanism, poses an insurmountable computational challenge. Experimentally, on the other hand, the fact that the dissociation is fast at the threshold for both [1] and [2] indicates firmly that there is no overall H-transfer barrier, because if there were one, slow tunneling rates would be observable across it.29
Conclusions
The Br-loss threshold photoionization breakdown diagram of 4-bromo-1-butyne, 1-bromo-2-butyne, and 3-bromo-1-butyne was analyzed together with the dissociation rates of 4-bromo-1-butyne to derive dissociative photoionization thresholds to C4H5+ production. Computed isomerization energies of the neutral samples and radical cation products are discussed to shed light on the dissociative photoionization mechanism. Based on these, the eclipsed 4-bromo-1-butyne rotamer cation is stable in the energy range studied, and only the higher energy staggered rotamer cation may lose a Br atom to form a cyclic C4H5+ isomer. The appearance energy differences can be explained if the other two samples are assumed to form the same CH2CCCH3+ daughter ion. The ring-based subtraction scheme for hot electron suppression is discussed in mathematical detail, and we find that the significantly more tedious exact subtraction barely improves the threshold photoionization data. The VMI-PEPICO imaging breakdown diagrams were modeled by first fitting a low-resolution photoelectron spectrum to reproduce the observed photoelectron radial distributions, and then by optimizing the parent ion disappearance energy, which corresponds to the 0 K appearance energy of the fragments in the absence of a kinetic shift, to fit the observed photoelectron radial distributions in coincidence with parent and daughter ions. The kinetic shift in 4-bromo-1-butyne was calculated based on fitting a Gompertz function in the VMI projected space to the radial distribution of the daughter ion center of gravity in the coincident mass spectrum. The imaging breakdown diagram analysis showed that (i) the use of higher fields minimizes the effect of the threshold photoelectron peak, and can in fact lead to a more accurate onset energy, (ii) it is possible to accurately extrapolate to the threshold based on data taken at a lower photon energy than the E0, and (iii) the simultaneous modeling of kinetic shifts may actually improve the agreement between threshold and imaging breakdown diagram analysis because of error cancellation. Thus, VMI-PEPICO data taken at a single photon energy, in the vicinity of the appearance energy, can be used to determine the E0 accurately. In addition to low number density samples, such as large organics or reactive intermediates, we also propose that imaging breakdown diagrams may be useful as an internal energy measure, i.e. as fast molecular thermometers in time-resolved experiments.Acknowledgements
This work was supported by the Swiss National Centre of Competence in Research, Molecular Ultrafast Science and Technology (NCCR-MUST) and the Swiss Federal Office of Energy (BFE Contract Number 101969/152433). The experimental work reported was carried out at the VUV beamline of the Swiss Light Source, and the calculations were performed at the Merlin 4 HPC cluster at the Paul Scherrer Institute.References
- B. Brehm and E. von Puttkamer, Z. Naturforsch., A: Astrophys., Phys. Phys. Chem., 1967, 22, 8–10 CAS.
- J. H. D. Eland, Int. J. Mass Spectrom. Ion Processes, 1972, 8, 143–151 CrossRef CAS.
- T. Baer, B. Sztáray, J. P. Kercher, A. F. Lago, A. Bodi, C. Skull and D. Palathinkal, Phys. Chem. Chem. Phys., 2005, 7, 1507–1513 RSC.
- T. Nishimura, in Fundamentals of Mass Spectrometry, ed. K. Hiraoka, Springer Science + Business Media, New York, 2013, pp. 29–54 Search PubMed.
- A. Bodi, J. P. Kercher, C. Bond, P. Meteesatien, B. Sztáray and T. Baer, J. Phys. Chem. A, 2007, 110, 13425–13433 CrossRef PubMed.
- S. Borkar, B. Sztáray and A. Bodi, Phys. Chem. Chem. Phys., 2011, 13, 13009–13020 RSC.
- A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477 CrossRef CAS.
- D. W. Chandler and D. H. Parker, Adv. Photochem., 1999, 25, 59–106 CrossRef CAS.
- B. Sztáray and T. Baer, Rev. Sci. Instrum., 2003, 74, 3763–3768 CrossRef.
- A. Bodi, M. Johnson, T. Gerber, Z. Gengeliczki, B. Sztáray and T. Baer, Rev. Sci. Instrum., 2009, 80, 34101 CrossRef PubMed.
- A. Bodi, P. Hemberger, T. Gerber and B. Sztáray, Rev. Sci. Instrum., 2012, 83, 083105 CrossRef PubMed.
- G. A. Garcia, B. K. C. de Miranda, M. Tia, S. Daly and L. Nahon, Rev. Sci. Instrum., 2013, 84, 053112 CrossRef CAS PubMed.
- A. Bodi, B. Sztáray, T. Baer, M. Johnson and T. Gerber, Rev. Sci. Instrum., 2007, 78, 84102 CrossRef PubMed.
- B. Sztáray, A. Bodi and T. Baer, J. Mass Spectrom., 2010, 45, 1233–1245 CrossRef PubMed.
- J. Harvey, A. Bodi, R. P. Tuckett and B. Sztáray, Phys. Chem. Chem. Phys., 2012, 14, 3935–3948 RSC.
- J. Harvey, P. Hemberger, A. Bodi and R. P. Tuckett, J. Chem. Phys., 2013, 138, 124301 CrossRef PubMed.
- A. Bodi, P. Hemberger, D. L. Osborn and B. Sztáray, J. Phys. Chem. Lett., 2013, 2948–2952 CrossRef CAS.
- C. Bordas, F. Paulig, H. Helm and D. L. Huestis, Rev. Sci. Instrum., 1996, 67, 2257–2268 CrossRef CAS.
- M. J. J. Vrakking, Rev. Sci. Instrum., 2001, 72, 4084 CrossRef CAS.
- V. Dribinski, A. Ossadtchi, V. A. Mandelshtam and H. Reisler, Rev. Sci. Instrum., 2002, 73, 2634 CrossRef CAS.
- G. A. Garcia, L. Nahon and I. Powis, Rev. Sci. Instrum., 2004, 75, 4989–4996 CrossRef CAS.
- M. N. R. Ashfold, N. H. Nahler, A. J. Orr-Ewing, O. P. J. Vieuxmaire, R. L. Toomes, T. N. Kitsopoulos, I. A. Garcia, D. A. Chestakov, S.-M. Wu and D. H. Parker, Phys. Chem. Chem. Phys., 2006, 8, 26–53 RSC.
- G. M. Roberts, J. L. Nixon, J. Lecointre, E. Wrede and J. R. R. Verlet, Rev. Sci. Instrum., 2009, 80, 053104 CrossRef CAS PubMed.
- T. Gerber, Y. Liu, G. Knopp, P. Hemberger, A. Bodi, P. Radi and Y. Sych, Rev. Sci. Instrum., 2013, 84, 033101 CrossRef PubMed.
- D. M. Neumark, J. Phys. Chem. A, 2008, 112, 13287–13301 CrossRef CAS PubMed.
- J. C. Poully, J. P. Schermann, N. Nieuwjaer, F. Lecomte, G. Grégoire, C. Desfrançois, G. A. Garcia, L. Nahon, D. Nandi, L. Poisson and M. Hochlaf, Phys. Chem. Chem. Phys., 2010, 12, 3566–3572 RSC.
- H. Gao, Y. Xu, L. Yang, C.-S. Lam, H. Wang, J. Zhou and C. Y. Ng, J. Chem. Phys., 2011, 135, 224304 CrossRef PubMed.
- K. H. Fischer, M. Schneider, I. Fischer, B. Pfaffinger, H. Braunschweig, B. Sztáray and A. Bodi, Chem.–Eur. J., 2012, 18, 4533–4540 CrossRef CAS PubMed.
- A. Bodi, M. Daniel Brannock, B. Sztáray and T. Baer, Phys. Chem. Chem. Phys., 2012, 14, 16047–16054 RSC.
- B. West, C. Joblin, V. Blanchet, A. Bodi, B. Sztáray and P. M. Mayer, J. Phys. Chem. A, 2012, 116, 10999–11007 CrossRef CAS PubMed.
- P. Hemberger, M. Steinbauer, M. Schneider, I. Fischer, M. Johnson, A. Bodi and T. Gerber, J. Phys. Chem. A, 2010, 114, 4698–4703 CrossRef CAS PubMed.
- M. Steinbauer, P. Hemberger, I. Fischer and A. Bodi, ChemPhysChem, 2011, 12, 1795–1797 CrossRef CAS PubMed.
- F. Holzmeier, M. Lang, K. Hader, P. Hemberger and I. Fischer, J. Chem. Phys., 2013, 138, 214310 CrossRef PubMed.
- I. Fischer, T. Schüßler, H.-J. Deyerl, M. Elhanine and C. Alcaraz, Int. J. Mass Spectrom., 2007, 261, 227–233 CrossRef CAS PubMed.
- R. D. Bowen, D. H. Williams, H. Schwarz and C. Wesdemiotis, J. Am. Chem. Soc., 1979, 101, 4681–4683 CrossRef CAS.
- K. Raghavachari, R. A. Whiteside, J. A. Pople and P. V. R. Schleyer, J. Am. Chem. Soc., 1981, 103, 5649–5657 CrossRef CAS.
- J. O. Lay and M. L. Gross, J. Am. Chem. Soc., 1983, 105, 3445–3451 CrossRef CAS.
- S. Borkar, B. Sztáray and A. Bodi, Int. J. Mass Spectrom., 2012, 330–332, 100–108 CAS.
- A. Cunje, M. H. Lien and A. C. Hopkinson, J. Org. Chem., 1996, 61, 5212–5220 CrossRef CAS.
- G. E. Douberly, A. M. Ricks, B. W. Ticknor, W. C. McKee, P. v. R. Schleyer and M. A. Duncan, J. Phys. Chem. A, 2008, 112, 1897–1906 CrossRef CAS PubMed.
- C.-H. Chin, W.-K. Chen, W.-J. Huang, Y.-C. Lin and S.-H. Lee, Icarus, 2013, 222, 254–262 CrossRef CAS PubMed.
- S. E. Wheeler, W. D. Allen and H. F. Schaefer, J. Chem. Phys., 2004, 121, 8800–8813 CrossRef CAS PubMed.
- N. Hansen, S. J. Klippenstein, C. A. Taatjes, J. A. Miller, J. Wang, T. A. Cool, B. Yang, R. Yang, L. Wei, C. Huang, J. Wang, F. Qi, M. E. Law and P. R. Westmoreland, J. Phys. Chem. A, 2006, 110, 3670–3678 CrossRef CAS PubMed.
- B. Yang, Y. Li, L. Wei, C. Huang, J. Wang, Z. Tian, R. Yang, L. Sheng, Y. Zhang and F. Qi, Proc. Combust. Inst., 2007, 31, 555–563 CrossRef PubMed.
- T. Zhang, J. Wang, T. Yuan, X. Hong, L. Zhang and F. Qi, J. Phys. Chem. A, 2008, 112, 10487–10494 CrossRef CAS PubMed.
- B. Sirjean and R. Fournet, Phys. Chem. Chem. Phys., 2013, 15, 596–611 RSC.
- X. Liu, W. Zhang, Z. Wang, M. Huang, X. Yang, L. Tao, Y. Sun, Y. Xu, X. Shan, F. Liu and L. Sheng, J. Mass Spectrom., 2009, 44, 404–409 CrossRef CAS PubMed.
- T. S. Zyubina, A. M. Mebel, M. Hayashi and S. H. Lin, Phys. Chem. Chem. Phys., 2008, 10, 2321–2331 RSC.
- M. Johnson, A. Bodi, L. Schulz and T. Gerber, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 610, 597–603 CrossRef CAS PubMed.
- K. M. Weitzel, M. Malow, G. K. Jarvis, T. Baer, Y. Song and C. Y. Ng, J. Chem. Phys., 1999, 111, 8267–8270 CrossRef CAS.
- N. S. Shuman, M. Johnson, W. R. Stevens, M. E. Harding, J. F. Stanton and T. Baer, J. Phys. Chem. A, 2010, 114, 10016–10023 CrossRef CAS PubMed.
- B. Ruscic, A. F. Wagner, L. B. Harding, R. L. Asher, D. Feller, D. A. Dixon, K. A. Peterson, Y. Song, X.-M. Qian, C. Y. Ng, J. Liu, W. Chen and D. W. Schwenke, J. Phys. Chem. A, 2002, 106, 2727–2747 CrossRef CAS.
- P. M. Guyon, T. Baer and I. Nenner, J. Chem. Phys., 1983, 78, 3665–3672 CrossRef CAS.
- A. Bodi, N. S. Shuman and T. Baer, Phys. Chem. Chem. Phys., 2009, 11, 11013–11021 RSC.
- A. J. Yencha, A. J. Cormack, R. J. Donovan, A. Hopkirk and G. C. King, Chem. Phys., 1998, 238, 109–131 CrossRef CAS.
- S. Y. Truong, A. J. Yencha, A. M. Juarez, S. J. Cavanagh, P. Bolognesi and G. C. King, Chem. Phys., 2009, 355, 183–193 CrossRef CAS PubMed.
- S. Borkar, L. Ooka, A. Bodi, T. Gerber and B. Sztáray, J. Phys. Chem. A, 2010, 114, 9115–9123 CrossRef CAS PubMed.
- I. Nenner, P. M. Guyon, T. Baer and T. R. Govers, J. Chem. Phys., 1980, 72, 6587–6592 CrossRef CAS.
- W. A. Chupka, P. J. Miller and E. E. Eyler, J. Chem. Phys., 1988, 88, 3032–3036 CrossRef CAS.
- B. Gompertz, Philos. Trans. R. Soc. London, 1825, 115, 513–583 CrossRef.
- J. Harvey, R. P. Tuckett and A. Bodi, J. Phys. Chem. A, 2012, 116, 9696–9705 CrossRef CAS PubMed.
- A. Bodi, W. R. Stevens and T. Baer, J. Phys. Chem. A, 2011, 115, 726–734 CrossRef CAS PubMed.
- P. Hemberger, A. Bodi, T. Gerber, M. Würtemberger and U. Radius, Chem.–Eur. J., 2013, 19, 7090–7099 CrossRef CAS PubMed.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 84108 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. N. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- T. Baer, S. H. Walker, N. S. Shuman and A. Bodi, J. Phys. Chem. A, 2012, 116, 2833–2844 CrossRef CAS PubMed.
- M. R. Siebert, A. J. A. Aquino, W. A. de Jong, G. Granucci and W. L. Hase, Mol. Phys., 2012, 110, 2599–2609 CrossRef CAS.
- C. L. Parker and A. L. Cooksy, J. Phys. Chem. A, 1999, 103, 2160–2169 CrossRef CAS.
| This journal is © the Owner Societies 2014 |