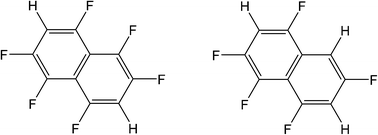
Highly fluorinated naphthalenes and bifurcated C–H⋯F–C hydrogen bonding

Abstract

The synthesis and crystal structures of 1,2,4,5,6,8-hexafluoronaphthalene and 1,2,4,6,8-pentafluoronaphthalene are reported. Intermolecular interactions are dominated by offset stacking and by C–H⋯F–C hydrogen bonds. For hexafluoronaphthalene, molecules are linked in layers with (4,4) network topology via R¹₂(6) C–H⋯(F–C)₂ supramolecular synthons that are rationalised by consideration of the calculated electrostatic potential of the molecule. Such an arrangement is prevented by the additional hydrogen atom in pentafluoronaphthalene and molecules instead form tapes via an R¹₂(8) (C–H⋯F)₂ synthon. The geometric characteristics of C–H⋯(F–C)₂ bifurcated hydrogen bonds have been analysed for crystal structures in the Cambridge Structural Database (6416 crystal structures; 9534 C–H⋯(F–C)₂ bifurcated hydrogen bonds). A geometric analysis of these hydrogen bonds has enabled the extent of asymmetry of these hydrogen bonds to be assessed and indicates a preference for symmetrically bifurcated interactions.

---

Introduction

Weak hydrogen bonds have a history of controversy in the chemical and crystallographic literature.¹ Disagreement centred on the geometric definition of hydrogen bonds and in particular on whether hydrogen bonding was restricted to cases in which the interacting atoms were situated within a specific distance of each other, notably the sum of their van der Waals radii. This debate was founded on studies of strong hydrogen bonds (O–H⋯O, N–H⋯O, O–H⋯N, etc.) for which such restricted geometric definitions were more appropriate. Since the survey, in 1982, by Taylor and Kennard of crystal structures obtained from neutron diffraction data affirmed the geometric behaviour of C–H⋯O and other hydrogen bonds with weakly polar C–H hydrogen bond donor groups,² a more extensive investigation of weaker hydrogen bonds has taken place.³ Their abundance, particularly due to C–H donor groups in organic and metal–organic compounds, often renders important the contribution of weak hydrogen bonds to self-assembly, molecular recognition, crystallisation and other phenomena involving intermolecular interactions.

Studies of the geometries of weak hydrogen bonds (D–H⋯A), particularly the archetypal C–H⋯O hydrogen bond, have demonstrated a geometric preference for hydrogen bond angles (D–H⋯A) approaching 180°,⁴ as previously established for strong hydrogen bonds. Such geometric preferences are necessarily less pronounced than for strong hydrogen bonds, and also operate over a greater range of distances including ones beyond the sum of van der Waals radii of interacting atoms.⁵

Turning to weak hydrogen bonding acceptor groups, Dunitz and Taylor examined the C–F group⁶ in a survey of crystal structures from the Cambridge Structural Database⁷ and Protein Data Bank.⁸ Their focus was on O–H⋯F–C and N–H⋯F–C hydrogen bonds and used a distance criterion of H⋯F < 2.3 Å to identify such interactions. The conclusion led the authors to title their paper “Organic fluorine hardly ever accepts hydrogen bonds.” However, far more prevalent are C–H⋯F–C interactions, but since such interactions involve both a weak hydrogen donor and a weak hydrogen bond acceptor their influence is more difficult to assess in individual crystal structures in which there may be competition with other stronger interactions in optimising crystal packing. In their study of the crystal structures of the fluorobenzenes C₆H_nF_6–n (n = 1–5), Desiraju, Nangia, Boese and coworkers demonstrated that, in the absence of competing interactions, C–H⋯F–C hydrogen bonds display similar geometric characteristics to other weak hydrogen bonds.⁹ In our analyses of crystal structures using the Cambridge Structural Database we showed that C–H⋯F–C interactions across organic, coordination and organometallic compounds exhibit geometries characteristic of weak hydrogen bonds, but are evidently weaker than C–H⋯F–M or C–H⋯F⁻ hydrogen bonds, for which greater accumulation of negative charge at the fluorine sites leads to a stronger electrostatic interaction.¹⁰

Here we report the crystal structures of 1,2,4,5,6,8-hexafluoronaphthalene and 1,2,4,6,8-pentafluoronaphthalene (Scheme 1), and examine the formation of C–H⋯F–C hydrogen bonds involving these compounds in particular, and also this class of hydrogen bonds more generally, with a focus on bifurcated interactions. Synthesis of the compounds from perfluoronaphthalene is also reported and is significant in the context of interest in C–F activation.¹¹

Scheme 1 1,2,4,5,6,8-hexafluoronaphthalene and 1,2,4,6,8-pentafluoronaphthalene.

Experimental

General

All reagents were purchased from Fluorochem Ltd., Alfa Aesar or Lancaster Synthesis Inc. and used as received. NMR spectra were collected on a Bruker AMX 500 spectrometer. GC-MS spectra were obtained on a Perkin Elmer Autosystem XL gas chromatograph interfaced to a Turbomass spectrometer.

Synthesis of 1,2,4,5,6,8-hexafluoronaphthalene and 1,2,4,6,8-pentafluoronaphthalene

The synthesis of 1,2,4,5,6,8-hexafluoronaphthalene followed a literature procedure,¹² but our experimental findings differ somewhat from those of the original source. Perfluoronaphthalene (5.00 g, 18.4 mmol), Zn powder (14.4 g, 220 mmol), ammonium chloride (5.90 g, 110 mmol) and 135 mL of 35% aqueous ammonium hydroxide were stirred continuously in a stoppered 500 mL round-bottom flask. At regular intervals, a small portion of the suspension was sampled with a Pasteur pipette and extracted with Et₂O. The solvent was removed from the organic phase leaving a white residue, which was analysed by GC-MS and NMR spectroscopy. A gradual disappearance of the perfluoronaphthalene was observed with the formation of 1,2,4,5,6,8-hexafluoronaphthalene; by the time the perfluoronaphthalene had completely reacted (6 days), the reduction of some of the product to 1,2,4,6,8-pentafluoronaphthalene was observed, as well as the formation of minute quantities of unidentified fluorinated byproducts. At that point, the reaction mixture was extracted with Et₂O (3 × 120 mL), dried over MgSO₄ and the solvent removed on a rotary evaporator. The resulting white solid was chromatographed through a 40 cm column of activated alumina, using hexane as eluent. The eluate containing only the desired product, 1,2,4,5,6,8-hexafluoronaphthalene by GC-MS was taken to dryness with a rotary evaporator (2.10 g, 48.4% yield). Colourless crystals were grown over a few days from a hexane solution at −25 °C, one of which was chosen for single crystal X-ray diffraction. ¹⁹F NMR (376.3 MHz, CDCl₃, ppm): −116.5 (m), −135.4 (m), −148.3 (m); ¹H NMR (400 MHz, CDCl₃, ppm): 7.2 (m); GC-MS m/z: 236 (M⁺), 216 (M⁺ − HF), 205 (M⁺ − CF); FT-IR (ATR, cm⁻¹): 3093 (w), 1641 (s), 1529 (w), 1387 (s), 1263 (m), 1184 (m), 1174 (m), 1120 (s), 999 (w), 943 (m), 873 (s), 853 (s).

The eluate containing 1,2,4,6,8-pentafluoronaphthalene was allowed to concentrate slowly by solvent evaporation in a small vial, resulting in colourless crystals after 2 days, one of which was chosen for single crystal X-ray diffraction. ¹⁹F NMR (376.3 MHz, CDCl₃, ppm): −108.9 (m), −110.9 (m), −121.2 (m), −137.7 (m), −148.3 (m); GC-MS m/z: 218 (M⁺), 198 (M⁺ − HF), 187 (M⁺ − CF).

X-ray crystal structures

X-ray data were collected for hexafluoronaphthalene on a Bruker KAPPA APEX 2 diffractometer at 150 K using an Oxford Cryostream n-HeliX low temperature device, and for pentafluoronaphthalene on a Bruker SMART APEX 2 diffractometer at 100 K, using an Oxford Cryostream Cobra low temperature device. The crystal structures were solved and refined against all F² values using the SHELXTL¹³ and Olex2¹⁴ suites of programs. A summary of crystal data and structure refinement is provided in Table 1. Data were corrected for absorption using empirical methods based upon symmetry-equivalent reflections combined with measurements at different azimuthal angles using the program SADABS¹⁵ for hexafluoronaphthalene and TWINABS¹⁶ for pentafluoronaphthalene. All non-hydrogen atoms were refined anisotropically. The hydrogen atoms were placed in calculated positions and refined using idealised geometries (riding model) for the moiety to which they were attached, and assigned fixed isotropic displacement parameters. Molecules of pentafluoronaphthalene are situated at crystallographic inversion centres resulting in 50 : 50 occupancy of the 1- and 5-positions by fluorine and hydrogen.

Table 1 Data collection, structure solution and refinement parameters

Name	1,2,4,5,6,8-Hexafluoronaphthalene		1,2,4,6,8-Pentafluoronaphthalene^a
a Twinned refinement. b R 1(F) = ∑(|Fo| − |Fc|)/∑|Fo|; wR2(F^2) = [∑w(Fo^2 − Fc^2)^2/∑wFo^4]^1/2; S(F^2) = [∑w(Fo^2 − Fc^2)^2/(n + r − p)]^1/2.
Molecular formula	C10H2F6		C10H3F5
Crystal colour	Colourless		Colourless
Crystal size (mm)	0.69 × 0.18 × 0.14		0.31 × 0.20 × 0.08
Crystal system	Monoclinic		Monoclinic
Space group, Z	P21/c, 4		P21/n, 2
a (Å)	7.7677(11)		8.5748(17)
b (Å)	13.5311(18)		3.6622(7)
c (Å)	7.9843(11)		12.423(3)
β (°)	106.432(6)		93.08(3)
V (Å^3)	804.92(19)		389.56(13)
Density (Mg m^−3)	1.948		1.860
Temperature (K)	150		100
μ Mo-Kα (mm^−1)	0.211		0.192
2θ range (°)	5.46 to 65.3		5.64 to 64.5
Reflections collected	19 686	All reflections^a	2550
		Component 1^a	1040
		Component 2^a	978
		Both components^a	532
Independent reflections, n (all used in refinement)	2880	All reflections,^an	1884
		Component 1^a	779
		Component 2^a	719
		Both components^a	386
Completeness to θ	97.6% to 32.65°	All reflections^a	74.03% to 32.25°
		Component 1^a	73.97% to 32.25°
		Component 2^a	74.09% to 32.25°
R int	0.0435	All reflections^a	0.0133
		Component 1^a	0.0187
		Component 2^a	0.0378
		Both components^a	0.0084
Least squares parameters, p	145		74
Restraints, r	0		0
R 1(F),^bI > 2.0σ(I)	0.0404		0.0820
wR2(F^2),^b all data	0.1294		0.2234
S(F^2),^b all data	1.043		1.102

---

Crystals of pentafluoronaphthalene were twinned. The indexing and the calculation of the relative orientation of the domains was carried out with the program CELL_NOW.¹⁶ Two domains were found and separate orientation matrices for each domain were used in the integration. For the crystal of pentafluoronaphthalene only a partial data set was collected, due to a diffractometer failure. The completeness (77.3% for sin θ/λ ≤ 0.6 Å⁻¹), although low, was adequate for the determination of the structure. Although the redundancy of the data was also low, the absorption/scaling correction appears satisfactory, and is undoubtedly helped by the low value of μ.

Hydrogen bond geometries were calculated by normalising hydrogen atom positions, post-refinement, to standard nuclear positions as determined by neutron diffraction (i.e. C–H 1.083 Å)¹⁷ as implemented in the program Mercury.¹⁸

Crystallographic database searches

Geometric data were obtained for C–H⋯(F–C)₂ hydrogen bonds, i.e. bifurcated at the donor, from the Cambridge Structural Database (CSD) [August 2012 release, version 5.33].⁷ The search included both H and D isotopes of hydrogen. Only structures that were considered by the CSD to be error-free and not disordered and for which R(F) ≤ 0.10 were included. All C–H distances were normalised to the standard neutron diffraction bond length of 1.083 Å.^17,19 Searches were restricted to interactions in which C–H⋯F ≥ 110° for both C–H⋯F angles,²⁰ and for which 2.0 ≤ F⋯F ≤ 7.0 Å for the two acceptor fluorine atoms. An upper limit on H⋯F length based upon R_HF³ ≤ 1.2 (H⋯F ≤ 2.837 Å) was applied. Charged species were not excluded. Duplicate structure determinations were inspected individually and the most reliable structure was retained. All trifurcated and higher order multifurcated interactions were removed (see Table S1† for CSD search statistics). For the analysis of the hydrogen bonds, three geometric parameters have been used, namely the H⋯F_a distance, C–H⋯F_a angle and H⋯F_a–C angle, where F_a is fluorine atom that has the shorter H⋯F distance, the other fluorine atom being designated F_b. For comparison with previous studies,¹⁰ and to permit comparison with other types of hydrogen bonds, the hydrogen bond distances have been normalised as R_HF = d(H⋯F)/(r_H + r_F), using van der Waals radii r_H 1.20 Å and r_F 1.47 Å.²¹

In order to investigate geometrical preferences we have adopted the approach of analysing a spatially normalised distance vs. angle plot using the transformed coordinate system (R_HF)³vs. (1 − cos θ), where θ = 180 − (C–H⋯F), as originally described by Lommerse et al.²² This removes inherent statistical biases of conventional distance vs. angle plots by ensuring that equal volumes of space are mapped onto equal areas of a two-dimensional plot. Some useful points of reference on these plots are: (R_HF)³ = 1.0 corresponds to d(H⋯F) = (r_H + r_F); 1 − cos θ = 0.0 corresponds to C–H⋯F = 180°; 1 − cos θ = 0.5 corresponds to C–H⋯F = 120°. The same correspondences arise for the spatially normalised distance vs. angle plot involving the H⋯F–C angle and the function 1 − cos α, where α = 180 − (H⋯F–C). Additional points of reference on this plot are: 1 − cos α = 0.75 corresponds to H⋯F–C = 104.5°; 1 − cos α = 1.0 corresponds to H⋯F–C = 90°. Histograms of C–H⋯F and H⋯F–C angles were plotted in 10° intervals and corrected for sine-dependent geometric error in the frequency of observations (cone correction) that arises in sampling such angle data from crystal structures.²³

Theoretical calculations

Electronic structure calculations for 1,2,4,5,6,8-hexafluoronaphthalene and 1,2,4,6,8-pentafluoronaphthalene were performed with the use of the SMP version of the Gaussian 09 program package²⁴ with the B3LYP functional method.²⁵ Gaussian was compiled using the Portland Compiler version 8.0-6 using the Gaussian-supplied BLAS libraries on the EMT64 architecture. In both cases, the 6-311G(d,p) basis set was used for all atoms types.²⁶ Geometry optimisations were performed in vacuo using an ultrafine integration grid and without symmetry constraints. Subsequent calculation of frequencies in the harmonic approximation confirmed the reported stationary points as minima by virtue of the fact that no imaginary frequencies were found. The 3D electrostatic potentials (ESPs) were visualised directly in Gaussview using the Gaussian checkpoint files and standard parameters, whereas the 2D ESPs were plotted using the ccp1-gui²⁷ from cube-files obtained from Gaussian checkpoint files.

Results

Syntheses

Synthesis of 1,2,4,5,6,8-hexafluoronaphthalene was accomplished by reductive defluorination of octafluoronapthalene with zinc powder in aqueous ammonia/ammonium chloride solution.¹² However, far longer reaction times than previously reported were necessary to take the reaction to completion (6 days rather than 20 hours), by which time an appreciable amount of 1,2,4,6,8-pentafluoronaphthalene formed along with other unidentified fluorinated impurities, possibly other isomers of pentafluoronaphthalene, which was not observed in the original work. The only other difference between our procedure and that previously published was our use of 35% aqueous ammonia (rather than 30%), which was expected to increase the rate of the reaction and improve the yield. We also found the reported recrystallisation from ethanol to be an ineffective method of purification of hexafluoronaphthalene. More effective was chromatography, although this required a long column of alumina. Chromatography also allowed isolation of 1,2,4,6,8-pentafluoronaphthalene as a minor product.

Crystal structures

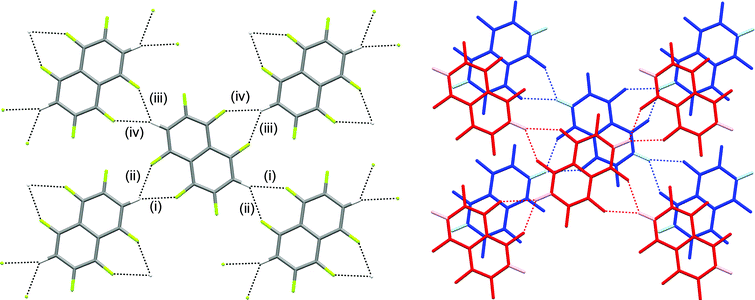
The crystal structures of hexa- and pentafluoronaphthalene proved invaluable in establishing the isomers formed in the defluorination reaction. The structure of 1,2,4,5,6,8-hexafluoronaphthalene is characterised by layers of approximately coplanar hydrogen-bonded molecules. Each molecule participates in four bifurcated C–H⋯(F–C)₂ hydrogen bonds [R¹₂(6)],²⁸ two as a hydrogen bond donor and two as an acceptor. For each molecule, these pairs of interactions are approximately collinear and the two pairs lie at approximately right angles to one another to give a two-dimensional hydrogen-bonded (4,4) network (Fig. 1). The angle between the planes of stacked pairs of hydrogen-bonded molecules is 8.18(4)° (Fig. 2).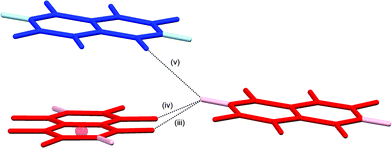

Fig. 1 Crystal structure of 1,2,4,5,6,8-hexafluoronaphthalene showing (a) one layer and (b) two layers of hydrogen-bonded molecules. C–H⋯F–C hydrogen bonds are shown as dashed lines. Hydrogen atoms are identified by lighter colours in (b). Hydrogen bond geometries C–H⋯F, C–H⋯F, H⋯F–C are: (i) 2.37 Å, 159°, 143°; (ii) 2.48 Å, 133°, 141°; (iii) 2.41 Å, 128°, 143°; (iv) 2.64 Å, 139°, 134°.

Fig. 2 Details of stacking interaction between layers in crystal structure of 1,2,4,5,6,8-hexafluoronaphthalene. Colours and labels as in Fig. 1b. Ring centroid marked with red sphere. Hydrogen bond geometries for (v) are C–H⋯F 2.94 Å, C–H⋯F 148°, H⋯F–C 118°. Interplanar angle between stacked pair of molecules is 8.18(4)°. F⋯C₆(centroid) 3.26 Å.

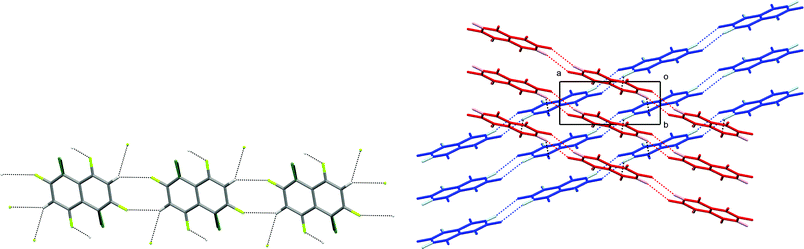
In the crystal structure of 1,2,4,6,8-pentafluoronaphthalene, molecules are situated at sites of inversion symmetry resulting in 50 : 50 site disorder between the 1- and 5-positions which contain a fluorine and hydrogen atom, respectively. The molecules are arranged in hydrogen-bonded tapes propagated by pairs of C–H⋯F hydrogen bonds in R²₂(8) motifs (Fig. 3). Parallel tapes extend along the [110] direction and [1–10] direction in alternate layers. Layers lie parallel to the (001) plane (Fig. 3b). Neighbouring tapes within each layer have an offset π-stacking arrangement between molecules whereas interaction of tapes between layers is via additional C–H⋯F hydrogen bonds, collectively involving all ring substituents except for the H/F disordered positions. Thus, the hydrogen atoms at the 3- and 7-positions form bifurcated C–H⋯(F–C)₂ hydrogen bonds, each linking three molecules.

Fig. 3 Crystal structure of 1,2,4,6,8-pentafluoronaphthalene. (a) Hydrogen-bonded tape. C–H⋯F–C hydrogen bonds are shown as dashed lines. Hydrogen and fluorine atoms at disordered sites are almost superposed and are identified by darker colours. Hydrogen bond geometries within the tape are C–H⋯F 2.51 Å, C–H⋯F 136°, H⋯F–C 151°. (b) View down the c-axis of two layers (coloured red and blue) comprising stacked parallel tapes. Hydrogen atoms are shown in lighter colours. C–H⋯F–C hydrogen bonds (dashed lines) between layers have geometries: C–H⋯F 2.56 Å, C–H⋯F 135°, H⋯F–C 127°.

Electrostatic potential calculations

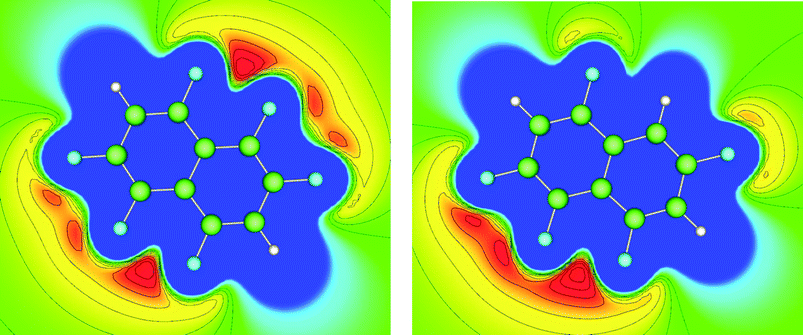
We have previously reported the anisotropic electrostatic potential around terminally bonded halogen atoms and illustrated its role in determining hydrogen bond geometries where halogens serve as hydrogen bond acceptors.^10,29 Thus, electrostatic potentials were calculated for hexa- and pentafluoronaphthalene to aid our understanding of the intermolecular interactions, particularly hydrogen bonds, in their crystal structures. Potentials in the planes of the molecules and at their van der Waals surfaces are shown in Fig. 4 and 5, respectively, and clearly indicate positive regions around hydrogen atoms and negative regions around fluorine atoms. The deepest minima lie between the fluorine atoms at the 1,8-positions (also 4,5-positions in hexafluoronaphthalene), the potential well being deeper for the pentafluoronaphthalene as there are fewer competing (electron-withdrawing) fluorine substituents. The surface of the molecules above the rings has a positive potential as is characteristic of highly fluorinated aromatic compounds.³⁰ This potential is more positive for hexafluoronaphthalene than pentafluoronaphthalene.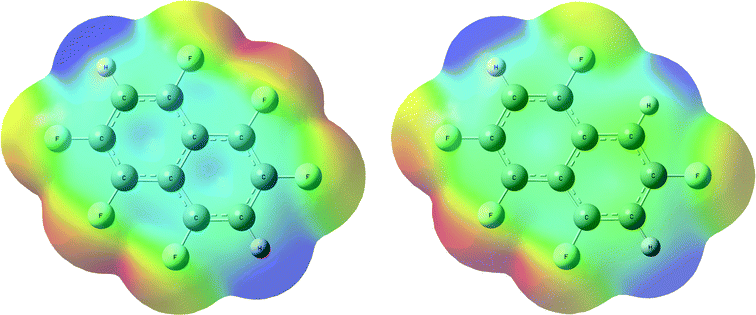

Fig. 4 Electrostatic potential calculated in the plane of the molecule for (a) 1,2,4,5,6,8-hexafluoronaphthalene and (b) 1,2,4,6,8-pentafluoronaphthalene. Colours: blue (most positive), green (neutral), red (most negative). Contours (at intervals of 10.0 kJ mol⁻¹) are shown for regions of negative potential. Potential minimum: (a) −73.8 and (b) −85.3 kJ mol⁻¹.

Fig. 5 Electrostatic potential calculated on the ρ = 0.004 a.u. isosurface (approximately the van der Waals surface) of the molecule for (a) 1,2,4,5,6,8-hexafluoronaphthalene and (b) 1,2,4,6,8-pentafluoronaphthalene. Colours: blue (most positive), green (neutral), red (most negative). A view parallel to the molecular planes of these surfaces is shown in Fig. S1.†

Survey of C–H⋯(F–C)₂ bifurcated hydrogen bond geometries

Since all hydrogen atoms involved in intermolecular interactions in the two crystal structures form C–H⋯(F–C)₂ bifurcated hydrogen bonds, we have conducted a survey of such interactions across all compounds in the CSD. Our geometric search criteria are less restrictive than those applied by Taylor and Dunitz,⁶ and more similar to those used by Hulliger and coworkers.^30a However, these previous surveys made no distinctions between simple and bifurcated interactions,³¹ whereas we have examined only C–H⋯(F–C)₂ bifurcated hydrogen bonds. Within the survey we have included interactions in which both F–C acceptor groups reside within the same molecule and ones in which the two acceptor groups belong to separate molecules, as observed in the structures of the hexa- and pentafluoronaphthalenes, respectively. The CSD search identified 6416 crystal structures containing more than 9500 bifurcated C–H⋯F hydrogen bonds. Our geometrical analysis is focussed initially on the shorter of the two C–H⋯F interactions, denoted C–H⋯F_a, since these geometries best reflect the perturbation from that of a simple hydrogen bond that results from the accommodation of a second, weaker interaction. Cone-corrected²³ C–H⋯F_a and H⋯F_a–C angle distributions (Fig. 6) show a preference for C–H⋯F angles to lie in the range 130–150°, which indicates a preference for smaller C–H⋯F angles than observed for simple C–H⋯F–C hydrogen bonds, and is consistent with reasonably symmetrical bifurcation of the C–H⋯(F–C)₂ hydrogen bonds. Fig. 6b indicates a preference for H⋯F–C angles greater than 130°, consistent with studies of simple hydrogen bonds involving fluorine acceptor groups.¹⁰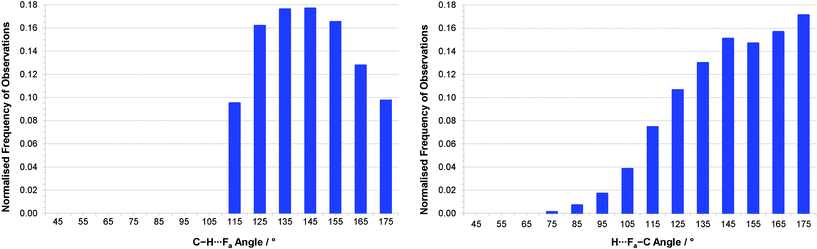

Fig. 6 (a) Distribution of (a) C–H⋯F_a angles and (b) H⋯F_a–C angles for interactions with R_HF(a)³ ≤ 1.15 (H⋯F_a ≤ 2.80 Å) after normalisation by cone correction.²³ Note that for (a), all interactions with C–H⋯F angles < 110° were excluded during the CSD search.

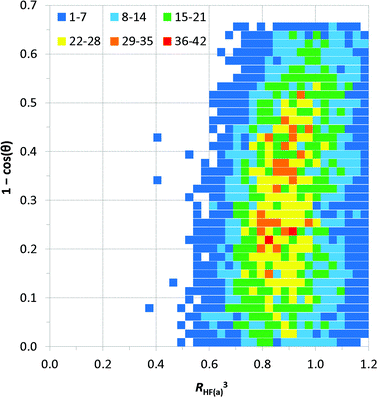
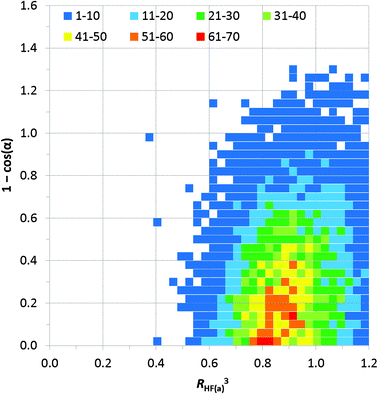
Distance vs. angle plots have been spatially normalised using the approach of Lommerse et al.²² and as in our earlier extensive study of simple hydrogen bonds involving halogens.^10b Normalised plots of H⋯F_a distance vs. C–H⋯F_a angle and H⋯F_a distance vs. H⋯F_a–C angle are shown in Fig. 7 and 8, respectively. The normal behaviour observed for simple hydrogen bonds is for a decrease in H⋯A length to correlate to an increase in D–H⋯A angle [i.e. for (R_HF(a))³ to increase with increasing 1 − cos θ in the plot of Fig. 7]. This correlation is not strong in Fig. 7, and suggests only a very slight preference of larger C–H⋯F angles for the shortest H⋯F distances, consistent with weak hydrogen bond behaviour and with the influence of bifurcation. The distribution of observations in Fig. 7 also shows bifurcated C–H⋯F interactions adopting angles across the range 110–180°, with the most frequent angle observed at approximately 138° [1 − cos θ = 0.25], reiterating the representation in Fig. 6a. Fig. 8 reinforces the conclusions from Fig. 6b, particularly at short H⋯F distances, wherein preferred H⋯F–C angles lie approximately in the range 130–180° (0.36 ≥ 1 − cos α ≥ 0).

Fig. 7 Spatially normalised plots of hydrogen bond distances (represented as R_HF(a)³) vs. angle at the hydrogen (represented as 1 − cos θ, where θ = 180 – (C–H⋯F_a)°) for C–H⋯(F–C)₂ bifurcated hydrogen bonds. The number of observations at each point on the plot is indicated by the colour-coded squares.

Fig. 8 Spatially normalised plots of hydrogen bond distances (represented as R_HF(a)³) vs. angle at the hydrogen (represented as 1 − cos α, where α = 180 – (H⋯F_a–C)°) for C–H⋯(F–C)₂ bifurcated hydrogen bonds. The number of observations at each point on the plot is indicated by the colour-coded squares.

Fig. 9 expresses the asymmetry of bifurcation in terms of distance asymmetry, i.e. the difference in length between the two H⋯F interactions, and in terms of angle asymmetry, i.e. the difference between the two C–H⋯F angles. An alternative way to express the asymmetry is shown in Fig. S2†.³²

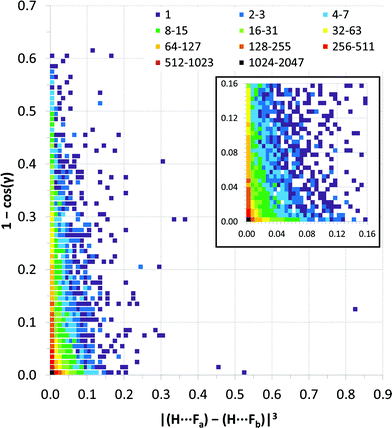Fig. 9 Distance vs. angle asymmetry of C–H⋯(F–C)₂ bifurcated hydrogen bonds. Differences between pairs of distances and differences between pairs of angles using the same scales as the normalised values in Fig. 7 and 8. [γ = |(C–H⋯F_a) − (C–H⋯F_b)|]. Inset is a magnified view (4× resolution) of the region close the origin (i.e., showing small asymmetries in bifurcation) – the same colour scale applies. The number of observations at each point on the plot is indicated by the colour-coded squares.

Discussion

Crystal structures of partially fluorinated naphthalenes

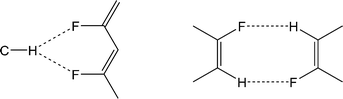
The crystal structures of 1,2,4,5,6,8-hexafluoronaphthalene and 1,2,4,6,8-pentafluoronaphthalene are dominated by C–H⋯(F–C)₂ bifurcated hydrogen bonds and offset face-face stacking, but do not involve either C–H⋯π or C–F⋯π edge-face interactions. The hexafluoronaphthalene molecules lie approximately in planes and interact via C–H⋯(F–C)₂ bifurcated hydrogen bonds (Scheme 2a) that bring together the most positive region, C–H, with the most negative region, which lies between neighbouring C–F groups at the 1,8- and 4,5-positions.³³ This potential minimum arises from the orientation and proximity of the two C–F groups which leads to an overlap and reinforcement of the most negative region around the individual fluorine atoms. It can be seen that the geometry is not suitable for such an overlap for fluorine atoms in the 1- and 2-positions (Fig. 4a), between which lies a shallower double-well potential minimum. Thus, the type of C–H⋯(F–C)₂ bifurcated hydrogen bond observed for hexafluoronaphthalene cannot arise for fluorobenzenes, and was not observed in a detailed study of their structures.⁹ The offset stacking of hexafluoronaphthalene molecules places a fluorine atom of one molecule directly above the positive ring centre of another in an electrostatically favourable arrangement (Fig. 2). The interlayer interaction is accompanied by weak trifurcation of the hydrogen bonds to include a longer interlayer C–H⋯F interaction (H⋯F 2.94 Å). Pentafluoronaphthalene contains only one strongly negative region that could accommodate the R¹₂(6) C–H⋯(F–C)₂ synthon, but location of the molecules on an inversion centre gives rise to a disorder that is inconsistent with the use of such an interaction for propagation of the packing. Instead the molecules form chains via the R²₂(8) double C–H⋯F synthon (Scheme 2b), which is observed in the crystal structures of some fluorobenzenes.⁹

Scheme 2 (a) C–H⋯(F–C)₂ supramolecular synthon [R¹₂(6)]. (b) R²₂(8) C–H⋯F supramolecular synthon.

Crystal structures of four other partially-fluorinated naphthalenes have been reported, 2-fluoronaphthalene,³⁴ 1,5- and 1,8-difluoronaphthalene³⁵ and 1,2,3,4-tetrafluoronaphthalene.³⁶ The structure of 2-fluoronaphthalene exhibits a 4-fold disorder of the fluorine over the chemically equivalent sites on the ring. The authors note that the crystal structure is isotypic but not isomorphous with the crystal structure of naphthalene, and indeed some solid solutions of the two can be formed. This suggests that C–H⋯F hydrogen bonds are unlikely to be significant in determining the crystal structure and that offset face-to-face or edge-to-face interactions are dominant instead. This resembles the conclusions made for the structure of fluorobenzene, which adopts a crystal structure isomorphous with a virtual (calculated) low energy polymorph of benzene.³⁷ 1,8-difluoronaphthalene molecules contain the pair of fluorine substituents suitable for formation of the C–H⋯(F–C)₂ synthon (Fig. 10, Scheme 2a) and indeed this region of most negative electrostatic potential lies closest to hydrogen atoms of a neighbouring molecule in the crystal structure. Pairs of approximately coplanar molecules also interact via the R²₂(8) double C–H⋯F synthon. However, the overall crystal structure relies upon (C–H⋯π) edge-to-face interactions between molecules. The structure of 1,5-difluoronaphthalene resembles that of 1,2,4,6,8-pentafluoronaphthalene in that molecules form tapes linked via the R²₂(8) double C–H⋯F synthon (Fig. 11a). Tapes are stacked such that molecules are situated in an offset face-to-face arrangement to give layers. Alternate layers contain tapes that are propagated in the [110] and [1−10] directions (Fig. 11b).

Fig. 10 Crystal structure of 1,8-difluoronaphthalene.³⁵ C–H⋯F–C hydrogen bonds are shown as dashed lines and lie in the range 2.48 ≤ H⋯F ≤ 2.85 Å (0.93 ≤ R_HF ≤ 1.07).

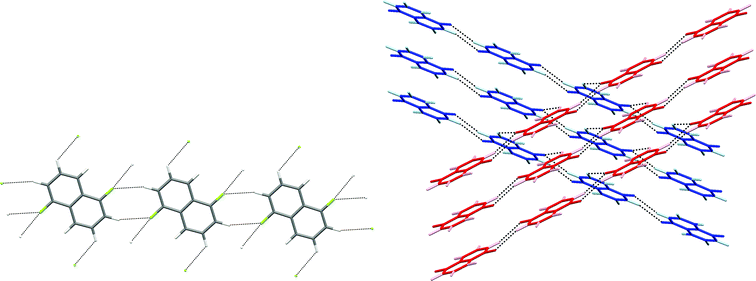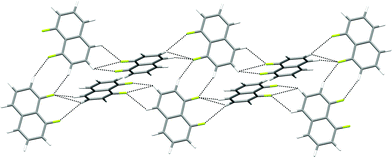
Fig. 11 Crystal structure of 1,5-difluoronaphthalene.³⁵ C–H⋯F–C hydrogen bonds are shown as dashed lines and lie in the range 2.58 ≤ H⋯F ≤ 2.65 Å (0.97 ≤ R_HF ≤ 0.99). (a) Tapes interacting via R²₂(8) double C–H⋯F synthon. (b) View of two layers (coloured red and blue) comprising stacked parallel tapes. Hydrogen atoms are identified by lighter colours.

The crystal structures of 1,2,3,4-tetrafluoronaphthalene and the analogous anthracene and phenanthracene compounds have been studied by Gavezzotti and coworkers by crystallography and PIXEL interaction energy calculations.³⁶ The calculations demonstrate that π-stacking interactions between fluorinated and non-fluorinated parts of the molecule are the predominant attractive interaction, leading to a layered structure, and suggest no significant role for C–H⋯F hydrogen bonds. However, examination of individual layers indicates that within these layers C–H groups from one molecule interact exclusively with C–F groups from neighbouring molecules (Fig. 12).

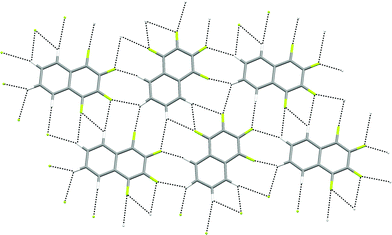Fig. 12 Crystal structure of 1,2,3,4-tetrafluoronaphthalene showing part of one layer of molecules.³⁶ C–H⋯F–C hydrogen bonds are shown as dashed lines and lie in the range 2.37 ≤ H⋯F ≤ 2.82 Å (0.89 ≤ R_HF ≤ 1.06).

Survey of bifurcated C–H⋯(F–C)₂ hydrogen bond geometries

Most published studies of hydrogen bond geometries make no distinction between simple and bifurcated interactions, although these types of hydrogen bonds show significant differences in geometries. In this study, the distribution of C–H⋯F hydrogen bond geometries in more than 9500 bifurcated C–H⋯(F–C)₂ hydrogen bonds (6416 crystal structures) has been surveyed using the CSD. The geometries are consistent with the interactions being weak hydrogen bonds. Thus, there are few H⋯F distances shorter than R_HF = 0.8 (2.14 Å), similar to that observed for simple C–H⋯F–C hydrogen bonds.^10b Simple C–H⋯F hydrogen bonds show a clear preference for C–H⋯F angles close to 180°, albeit not as great a preference as observed for stronger hydrogen bonds,^10b but such an angle preference is not expected here due to the competing demands of the two acceptor groups in the bifurcated hydrogen bonds. Indeed, the observed preference for C–H⋯F angles of 130–150° is entirely consistent with bifurcation.

To our knowledge the asymmetry of bifurcation in bifurcated hydrogen bonds has not been thoroughly examined. We have begun that process of investigation in the present study for the case of bifurcated C–H⋯(F–C)₂ hydrogen bonds. There are a number of ways in which the asymmetry might be quantified. In Fig. 9, we examine the asymmetry in hydrogen bond distance (i.e. the difference in the two H⋯F distances) and the asymmetry in hydrogen bond angle (i.e. the difference in the two C–H⋯F angles). It is clear from the scatterplot that asymmetry in distance does not require asymmetry in angle and vice versa. However, the largest cluster of points lies near the origin of the plot where asymmetry in both distance and angle is small. This suggests some preference for symmetric interactions. An alternative approach is displayed in Fig. S2† in which only the position of the hydrogen atom is considered relative to that of the two fluorine atoms. From this plot, it can be seen that when the hydrogen atom is closer to the two fluorine atoms it will tend to be located closer to bisector of the F⋯F vector, indicating asymmetry in the two H⋯F distances is reduced.

Conclusions

We have reported the synthesis and crystal structures of two partially fluorinated naphthalenes, 1,2,4,5,6,8-hexafluoronaphthalene and 1,2,4,6,8-pentafluoronaphthalene. These structures adopt C–H⋯F supramolecular synthons of types R¹₂(6) and R²₂(8) (Scheme 2), respectively, and exhibit intermolecular geometries consistent with a prominent role in crystal packing for bifurcated C–H⋯(F–C)₂ hydrogen bonds. These structures are compared with those of previously reported partially fluorinated naphthalenes, which provide further examples of these supramolecular synthons and emphasise the prevalence of bifurcated C–H⋯(F–C)₂ hydrogen bonds. The formation of bifurcated C–H⋯(F–C)₂ hydrogen bonds is consistent with attraction between the most electropositive regions and most electronegative regions on the molecules, based upon calculated electrostatic potentials. A survey of the CSD revealed 6416 crystal structures, which collectively exhibit over 9500 bifurcated C–H⋯(F–C)₂ hydrogen bonds, demonstrating the frequency of this class of interaction. A geometric analysis of these hydrogen bonds enabled the extent of asymmetry to be assessed and indicates a preference for symmetrically bifurcated interactions.

Acknowledgements

We are grateful for funding from the White Rose Consortium for network project “Molecular Engineering,” from the Cambridge Crystallographic Data Centre and the EPSRC. All DFT calculations were performed using the ‘Jupiter’ cluster of the Theoretical Chemistry Group at the University of Sheffield. We thank Drs. Peter Wood and Elna Pidcock (CCDC), and Dr. Robin Taylor (Taylor Cheminformatics Software) for helpful discussions.

References

1. (a) D. J. Sutor, Nature, 1962, 195, 68; (b) D. J. Sutor, J. Chem. Soc., 1963, 1105; (c) J. Donohue, in Structural Chemistry and Molecular Biology, ed. A. Rich and N. Davidson, Freeman, San Fransisco, USA, 1968, pp. 443–465; (d) See historical discussion in ref. 1e and 3a (pp 29–40); (e) C. H. Schwalbe, Crystallogr. Rev., 2012, 18, 191.
2. R. Taylor and O. Kennard, J. Am. Chem. Soc., 1982, 104, 5063.
3. G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond in Structural Chemistry and Biology, Oxford University Press, Oxford, UK, 1999.
4. T. Steiner and G. R. Desiraju, Chem. Commun., 1998, 891.
5. T. Steiner, Crystallogr. Rev., 1996, 6, 1.
6. J. D. Dunitz and R. Taylor, Chem. – Eur. J., 1997, 3, 89.
7. F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380.
8. (a) The RCSB PDB is located at http://www.pdb.org. See, H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242; (b) The worldwide PDB (wwPDB) is located at http://www.wwpdb.org. See, H. M. Berman, K. Henrick and H. Nakamura, Nature Struct. Biol., 2003, 10, 98.
9. V. R. Thalladi, H. Weiss, D. Blaeser, R. Boese, A. Nangia and G. R. Desiraju, J. Am. Chem. Soc., 1998, 120, 8702.
10. (a) L. Brammer, E. A. Bruton and P. Sherwood, New J. Chem., 1999, 23, 965; (b) L. Brammer, E. A. Bruton and P. Sherwood, Cryst. Growth Des., 2001, 1, 277.
11. (a) E. Clot, O. Eisenstein, N. Jasim, S. A. Macgregor, J. E. McGrady and R. N. Perutz, Acc. Chem. Res., 2011, 44, 333; (b) H. Amii and K. Uneyama, Chem. Rev., 2009, 109, 2119.
12. S. S. Laev and V. D. Shteingarts, J. Fluorine Chem., 1999, 96, 175.
13. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112.
14. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339.
15. (a) G. M. Sheldrick, SADABS, empirical absorption correction program, University of Göttingen, 1995, based upon the method of Blessing.^15b; (b) R. H. Blessing, Acta Crystallogr., Sect. A: Found. Crystallogr., 1995, 51, 33.
16. G. M. Sheldrick, CELL_NOW and TWINABS, University of Göttingen, 2000.
17. F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 1986, 42, 515.
18. (a) C. F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. van de Streek, J. Appl. Crystallogr., 2006, 39, 453; (b) C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466.
19. At the time of this study, normalisation of C−D distances was not implemented in the CSD search program CONQUEST. Thus, C−D⋯(F−C)₂ bifurcated hydrogen bonds incorrectly assigned due to failure of normalisation were removed manually.
20. (a) A CSD survey coupled with IMPT calculations of model hydrogen bonded dimers indicates very low interaction energies at hydrogen bond angles below 120°.^20b; (b) P. A. Wood, F. H. Allen and E. Pidcock, CrystEngComm, 2009, 11, 1563.
21. (a) A. Bondi, J. Chem. Phys., 1964, 68, 441; (b) More recent evaluations of van der Waals radii are available,^21c,d but have not been used here to enable consistency with previous studies.¹⁰; (c) R. S. Rowland and R. Taylor, J. Phys. Chem., 1996, 100, 7384; (d) S. Alvarez, Dalton Trans., 2013, 42, 8617.
22. J. P. M. Lommerse, A. J. Stone, R. Taylor and F. H. Allen, J. Am. Chem. Soc., 1996, 118, 3108.
23. (a) J. Kroon and J. A. Kanters, Nature, 1974, 248, 667; (b) T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48.
24. M. J. Frisch et al. , Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford, CT, 2009.
25. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
26. (a) A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639; (b) K. Raghavachari, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650; (c) M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265.
27. J. Thomas and P. Sherwood, ‘CCP1-GUI, a general-purpose visualization code for electronic structure codes’, version 0.8, Obtained from http://sourceforge.net/projects/ccp1gui. [Last accessed: 12 September 2014].
28. For a description of graph set nomenclature for describing hydrogen bonding patterns, see M. C. Etter, Acc. Chem. Res., 1990, 23, 120.
29. (a) L. Brammer, J. K. Swearingen, E. A. Bruton and P. Sherwood, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4956; (b) J. C. Mareque Rivas and L. Brammer, Inorg. Chem., 1998, 37, 4756.
30. (a) K. Reichenbächer, H. I. Süss and J. Hulliger, Chem. Soc. Rev., 2005, 34, 22; (b) G. W. Coates, A. R. Dunne, L. M. Henling, J. W. Ziller, E. B. Lobkovsky and R. H. Grubbs, J. Am. Chem. Soc., 1998, 120, 3641.
31. The term simple hydrogen bond refers to ones in which a single hydrogen bond donor interacts with a single hydrogen bond acceptor. Bifurcated here refers to hydrogen bonds that are bifurcated at the donor, i.e. a single hydrogen bond donor interacts with two separate hydrogen bond acceptors.
32. Fig. S2† provides an alternative way to depict the asymmetry of the C–H⋯(F–C)₂ hydrogen bonds by contouring a plot of the two H⋯F⋯F angles that define the geometry of the interaction. This approach ignores the position of the carbon atom in the C–H hydrogen bond donor.
33. (a) The electrostatic potential minima of −73.8 and −85.3 kJ mol⁻¹ for hexa- and pentafluoronaphthalene resembles that found for CH₂F₂ (−94.1 kJ mol⁻¹).^33b; (b) L. Brammer, E. A. Bruton and P. Sherwood, unpublished results. See E. A. Bruton, PhD thesis, University of Missouri, St. Louis, 2003.
34. (a) N. B. Chanh and Y. Haget-Bouillard, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3400; (b) A. Meresse, Y. Haget, A. Filhol and N. B. Chanh, J. Appl. Crystallogr., 1979, 12, 603.
35. A. Meresse, C. Courseille, F. Leroy and N. B. Chanh, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1975, 31, 1236.
36. (a) I. Yu. Bagryanskaya, Yu. V. Gatilov, A. M. Maksimov, W. E. Platonov and A. B. Zibarev, J. Fluorine Chem., 2005, 126, 1281; (b) F. Cozzi, S. Bacchi, G. Filippini, T. Pilati and A. Gavezzotti, Chem. – Eur. J., 2007, 13, 7177.
37. J. D. Dunitz and W. B. Schweizer, Chem. – Eur. J., 2006, 12, 6804.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1010950–1010951. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4ce01322k

---