Stereospecific generation of homochiral helices in coordination polymers built from enantiopure binaphthyl-based ligands

Abstract

The novel enantiopure dipyridyl spacer 2,2′-dimethoxy-1,1′-binaphthyl-3,3′-bis(4-pyridyl-amido) (R)-L has been designed as a robust source of axial chirality to obtain helical coordination polymers. The reaction of (R)-L and the differently substituted dithiophosphato complexes [Ni((RO)₂PS₂)₂] [R = Me (1), Et (2)] efficiently yielded coordination polymers (1·L)_∞ and (2·L)_∞, respectively, consisting of helical chains in which the nickel(II) ions of the [Ni((RO)₂PS₂)₂] units are bridged by the enantiopure L ligands. The obtained polymers differ in terms of the configuration at the metal centres, which is trans and cis for (1·L)_∞ and (2·L)_∞, respectively. The cis configuration in (2·L)_∞ generates a further element of chirality around the metal center, which occurs stereospecifically, as only one enantiomeric form is present, with homochiral helices packed with opposite screw sense in the crystal. The electronic and structural features of L, (1·L)_∞, and (2·L)_∞ have been investigated by means of DFT theoretical calculations, and the theoretical results have been compared with the experimental ones coming from single-crystal X-ray diffraction. The cis/trans isomerism displayed by the metal centers in (1·L)_∞ and (2·L)_∞ has been tentatively explained on the basis of the results of theoretical calculations performed on hypothetical pentacoordinated intermediates.

---

Introduction

The preparation of coordination polymers by the self-assembly of neutral metal complexes and donor molecules via coordination bonds or secondary bonding interactions is an emerging topic in the field of crystal engineering.¹ In this context, we have started a synthetic program based on the ability of neutral dithiophosphonato² and dithiophosphato³ Ni^II complexes to act as building blocks for the predictable assembly of inorganic coordination polymers. Due to their coordinative unsaturation, the Ni^II ions in these square planar complexes tend to complete their coordination sphere through the binding of monodentate donor molecules, such as pyridine, to yield octahedral complexes.⁴ Therefore, by using suitable N-L-N bidentate bipyridyl-based spacers, we prepared 1D coordination polymers of the [Ni(ROpdt)₂(N-L-N)]_∞ type.⁵ The primary structural motif of the polymers has been proved to depend mainly on the features of the pyridyl-based spacers such as length, rigidity, number and orientation of the donor atoms,^5,6 whereas the –OR substituents on the phosphorus atoms influence the final 3D architecture through hydrogen bonds and face-to-face or edge-to-face π–π interactions.⁵ This means that the use of suitable chiral rigid di-topic ligands featuring twisted bridging sites might induce the formation of chiral helical coordination polymers when linked to the dithiophosphonato/dithiophosphato Ni^II complexes.

The construction of infinite metal-containing helices^7,8 and the incorporation of chirality into metal–organic frameworks⁹ are areas of growing importance; on one side, there is interest in building novel supramolecular architectures able to recognize (enantio)selectively suitable inclusion guests.¹⁰ On the other, the introduction of chirality can be exploited as a tool for creating organization and function at the nanoscale.¹¹ Although either achiral or racemic ligands can be used to form chiral helical chains, the overall chirality of the product is less predictable due to the formation of racemates containing a mixture of both the enantiomeric forms.¹² On the other hand, the use of enantiopure organic ligands does not necessarily lead to helices with the same handedness.¹³

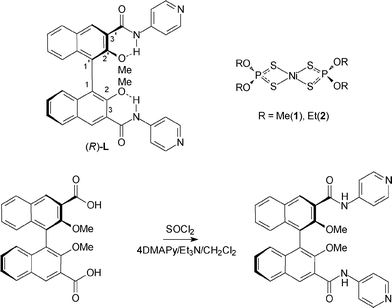
We have previously reported the incorporation of binaphthyl-based building blocks both for the rapid construction of macrocycles as chiroptical sensors and for nanoscale structuring.¹⁴ Binaphthyl-based synthons are popular in the recent literature; given their robustness, they are frequently used to impart or transfer chiral information, not only in the field of asymmetric synthesis and catalysis¹⁵ but also in materials science.¹⁶ The basic binaphthyl moiety can be conveniently functionalized in various positions, among which 4,4′ and 6,6′ positions are the most frequent ones, although access to the 3,3′ positions is also well documented (Scheme 1).¹⁷ The presence of at least two suitable metal coordination sites (for example, pyridine) is mandatory for the formation of coordination polymers. Moreover, the presence of amide functionalities can be a powerful hydrogen-bonding tool for the stabilization of the resulting assembled nanostructure, as testified by the important roles played by amide groups in the field of foldamers,¹⁸ or in the design of assembled architectures as artificial ion channel mimics.¹⁹ Here, we report on the design, synthesis and characterization of the novel helicoidal coordination polymers obtained by the reaction of the enantiopure spacer 2,2′-dimethoxy-1,1′-binaphthyl-3,3′-bis(4-pyridyl-amido) (R)-L (Scheme 1) with the differently substituted dithiophosphato complexes [Ni((RO)₂PS₂)₂] [R = Me (1), Et (2)].

Scheme 1 Top: (R)-L ligand showing the intramolecular hydrogen bonding interactions and numbering of binaphthyl moiety (left) and the dithiophosphato complexes 1 and 2 (right). Bottom: synthesis of (R)-L ligand.

Results and discussion

The binaphthyl-based building block (R)-L was designed with the aim of introducing an axially chiral spacer capable of bridging the metal connecting sites and imparting a helicoidal shape to the resultant coordination polymer. The functionalities are positioned in such a way (Scheme 1, top left) that the NH amide group is locked in an S(6)-type hydrogen-bonded system²⁰ with the neighboring phenol ether in the 2,2′ positions. This is a further element of rigidity in order to efficiently transfer the chiral information and twisting derived from the binaphthyl chiral axis to the overall coordination polymers. The (R)-L ligand was synthesized in two steps from optically pure (R)-2,2′-dimethoxy-1,1′-binaphthyl-3,3′-dicarboxylic acid under nonracemizing conditions. The precursor could be obtained in the enantiopure form after a published four-step procedure²¹ (including an enantioresolution step), starting from commercially available 2-naphthol. The dicarboxylic acid was subsequently activated as the acid chloride, and then amidation in the presence of 4-dimethylamino pyridine (excess), with triethylamine as the non-nucleophilic acid scavenger, resulted in the title compound (R)-L in moderate yields after purification by column chromatography (Scheme 1, bottom).

¹H NMR spectroscopy in CDCl₃ revealed the presence of a sharp signal for the NH proton resonances of the amide functionalities, indicating effective hydrogen bonding in noncompeting solvents, as previously reported for structurally related molecular skeletons.²²

The reactions of the dithiophosphato complexes [Ni((RO)₂PS₂)₂] [R = Me (1); Et (2)] and the difunctional L ligand with a 1 : 1 molar ratio were performed in a 1 : 1 mixture of CH₂Cl₂ and the corresponding ROH alcohols obtaining the coordination polymers [(1·L)·0.5H₂O]_∞ (from now on reported as (1·L)_∞) and (2·L)_∞, respectively, in good yields (see Experimental), all having microanalytical data corresponding to 1 : 1 adducts between the nickel complex and the L donor. Single crystals of (1·L)_∞ and (2·L)_∞ were obtained by layering an alcoholic solution of L on a CH₂Cl₂ solution of the relevant dithiophosphato complex.

Single-crystal X-ray diffraction has been performed for both compounds; crystallographic data and selected bond lengths and angles for (1·L)_∞ and (2·L)_∞ are reported in Tables 1 and 2, respectively. Compounds (1·L)_∞ and (2·L)_∞ are helically shaped polymers formed by coordination of the binaphthyl-based spacer L to the Ni^II ions of the square planar complexes 1 and 2. The [Ni((RO)₂PS₂)₂] units bridged by L and the resulting helices –L–[Ni(ROdtp)₂]–L–[Ni(ROdtp)₂]–L– are shown in Fig. 1 and 3 for (1·L)_∞ and (2·L)_∞, respectively.

Table 1 Crystal data collection and refinement for [(1·L)·(0.5H₂O)]_∞ and (2·L)_∞^a

	[(1·L)·(0.5H2O)]∞	(2·L)∞
a w = 1/[\s^2(Fo^2) + (0.0550P)^2]; P = (Fo^2 + 2Fc^2)/3. b Due to relatively poor data quality for (2·L)∞ the Flack parameter cannot be accurately refined and therefore the correct absolute structure cannot be reliably determined.
Empirical formula	C38H38N4NiO8P2S4 H2O	C42H46N4NiO8P2S4
M	936.64	983.74
Crystal system	Monoclinic	Orthorhombic
Space group	P21	P212121
a (Å)	9.6133(2)	15.332(2)
b (Å)	45.6542(12)	8.6055(10)
c (Å)	10.5801(3)	34.795(4)
α (°)	90	90
β (°)	113.202(1)	90
γ (°)	90	90
Volume (Å^3)	4267.92(19)	4590.8(10)
Z	2	4
D calc (Mg m^−3)	1.458	1.423
μ (mm^−1)	0.781	0.729
θ min–max (°)	2.9–27.1	3.0–25.0
T (K)	120	120
Refl. collected/unique	44 414/18 504	26 414/7285
Refl. obs. (I > 2σI)	13 551	4710
R/RINT	0.0587/0.066	0.1495/0.158
wR2	0.1325	0.3147
Min/max res. D. (e A^−3)	−0.36, 0.75	−0.73, 1.16
GoF	1.019	1.162
Flack par	0.048(12)	0.27(6)^b

---

Table 2 Selected bond lengths (Å) and angles (°) for (1·L)_∞ and (2·L)_∞

(1·L)∞
Ni1–S1	2.5385(15)	Ni2–S5	2.5196(16)
Ni1–S2	2.5001(15)	Ni2–S6	2.4738(17)
Ni1–S3	2.5490(15)	Ni2–S7	2.4647(16)
Ni1–S4	2.4900(15)	Ni2–S8	2.5232(16)
Ni1–N1	2.093(4)	Ni2–N2	2.074(5)
Ni1–N3	2.085(4)	Ni2–N4	2.084(4)
S1–P1	1.983(2)	S5–P3	1.985(2)
S2–P1	1.9675(19)	S6–P3	1.974(2)
S3–P2	1.983(2)	S7–P4	1.986(2)
S4–P2	1.9731(19)	S8–P4	1.987(2)
N1–Ni1–N3	179.05(16)	N2–Ni2–N4	179.63(17)
S1–Ni1–S2	81.70(5)	S5–Ni2–S6	82.03(5)
S1–Ni1–S3	178.74(5)	S5–Ni2–S7	96.23(53)
S1–Ni1–S4	97.48(5)	S5–Ni2–S8	178.42(6)
S2–Ni1–S3	99.42(5)	S6–Ni2–S7	178.25(6)
S2–Ni1–S4	179.00(5)	S6–Ni2–S8	99.43(5)
S3–Ni1–S4	81.40(5)	S7–Ni2–S8	82.32(5)
S1–Ni1–N1	89.70(12)	S5–Ni2–N2	91.19(13)
S1–Ni1–N3	89.48(12)	S5–Ni2–N4	88.71(12)
S2–Ni1–N1	90.78(12)	S6–Ni2–N2	90.38(13)
S2–Ni1–N3	88.65(12)	S6–Ni2–N4	89.26(12)
S3–Ni1–N1	90.88(12)	S7–Ni2–N2	89.50(13)
S3–Ni1–N3	89.96(12)	S7–Ni2–N4	90.86(12)
S4–Ni1–N1	89.79(12)	S8–Ni2–N2	89.40(13)
S4–Ni1–N3	90.77(12)	S8–Ni2–N4	90.71(12)
S1–P1–S2	113.06(9)	S5–P3–S6	111.75(10)
S3–P2–S4	112.32(9)	S7–P4–S8	111.49(9)
O1–P1–O2	96.8(2)	O5–P3–O6	94.5(3)
O3–P2–O4	97.4(2)	O7–P4–O8	95.5(2)

---

(2·L)∞
Ni1–S1	2.513(6)	Ni1–N21	2.094(14)
Ni1–S2	2.499(5)	S1–P1	2.007(9)
Ni1–S3	2.514(5)	S2–P1	1.949(7)
Ni1–S4	2.538(6)	S3–P2	2.010(7)
Ni1–N1	2.092(15)	S4–P2	1.989(9)
N1–Ni–N21	91.6(5)	S3–Ni–S4	80.86(19)
S1–Ni–S2	79.66(19)	S3–Ni–N1	90.6(4)
S1–Ni–S3	98.4(2)	S3–Ni–N21	94.5(4)
S1–Ni–S4	93.28(16)	S4–Ni–N1	171.4(5)
S1–Ni–N1	87.4(4)	S4–Ni–N21	89.7(4)
S1–Ni–N21	167.0(4)	S1–P1–S2	108.5(3)
S2–Ni–S3	174.43(17)	S3–P2–S4	110.0(3)
S2–Ni–S4	93.99(19)	O61–P1–O71	92.8(8)
S2–Ni–N1	94.6(4)	O41–P2–O51	99.9(7)
S2–Ni–N21	87.6(4)

---

Fig. 1 (a) Helical chain structure of (1·L)_∞ with a selected atom numbering scheme; (b) view of one spiral along the 010 direction. H atoms have been omitted for clarity; symmetry codes: ′, −1 − x, 0.5 + y, −z; ′′, −1 − x, −0.5 + y, −z.

The structure of compound (1·L)_∞ consists of a homochiral right-handed helical chain in which the nickel(II) ions of the [Ni((MeO)₂PS₂)₂] units are bridged by the enantiopure L ligands (Fig. 1). The polymer crystallizes in the monoclinic P2₁ chiral space group, with two [Ni((MeO)₂PS₂)₂] units, two L ligands, and one water molecule in the asymmetric unit. The coordination environment around both the two symmetry-independent nickel ions results in a distorted octahedron with four sulphur atoms from two bidentate (MeO)₂PS₂ units on the equatorial plane and two nitrogen atoms from the bridging ligands in a trans fashion occupying the axial positions, with N–Ni–N angles of 179.05(16)° and 179.63(17)° (Table 2).

It is interesting to note that the coordination environments around Ni1 and Ni2 differ in terms of the orientation of the methoxy substituents at the P atoms, all pointing at the pyridine rings bonded to the same coordination core, with the exception of MeO(1) and MeO(4) which are engaged in strong H bonds with the amide groups of the adjacent helices (see the following). The binaphthyl moieties feature torsion angles of 71.1(7)° (C78–C77–C97–C98) and 114.5(6)° (C38–C37–C57–C58) along the pivotal 1,1′-bond joining the two naphthyl units, similar to those found in analogous 2,2′-dimethoxy-1,1′-binaphthyl molecules, normally ranging from 70° to 113°.‡ However, the dihedral angle between the ring planes is quite consistent at 71.84° and 71.17° for the C37–C57 and C77–C97 binaphthyl moieties, respectively. The two spacers differ in terms of the orientation of the 2,2′-methoxy substituents, which are convergent in the case of MeO(O39)/MeO(O59) and divergent in the case of MeO(O79)/MeO(O99) (Fig. 1b).

The spirals run parallel along the b direction involving a crystallographic 2-fold screw axis (Fig. 1), with a helical pitch of 45.65 Å, coincident with the b-axis length, and intertwine with each other in both the a and the c directions in a densely interlocked architecture stabilized by an intricate net of H bonds, mainly involving the amido groups, the water molecules and both the binaphthyl- and P-methoxy substituents [MeO (O79), MeO(O1), and MeO(O4), respectively; see Table 3]. The packing of adjacent spirals leads to a compact tridimensional network similar to the arrangement of partially embedded parallel springs running along b and shifted in the ac plane and intertwined in order to reciprocally occupy the empty space of one spiral with the spires of the adjacent ones (Fig. 2).

Table 3 Intermolecular hydrogen bonds for (1·L)_∞ and (2·L)_∞

D–H⋯A	D–H (Å)	H⋯A (Å)	D⋯A (Å)	D–H⋯A (°)
(1·L)∞
O1W–H1W⋯O6^a	0.86(4)	2.21(4)	2.960(6)	146(4)
N27–H27⋯O1^b	0.90(5)	2.15(4)	3.003(6)	156(4)
N87–H87⋯O4^c	0.87(5)	2.16(5)	3.022(6)	172(4)
C4–H4B⋯O79^b	0.98	2.41	3.373(7)	167
C23–H23⋯O1^b	0.95	2.54	3.316(7)	140
C26–H26⋯O88^d	0.95	2.32	3.149(6)	146
C35–H35⋯O8^e	0.95	2.39	3.260(7)	152
C46–H46⋯O68^f	0.95	2.29	3.048(7)	136
C55–H55⋯O2^b	0.95	2.43	3.255(6)	146
C66–H66⋯O48^d	0.95	2.38	3.123(7)	134
C86–H86⋯O28^g	0.95	2.38	3.218(7)	147

---

(2·L)∞
Symmetry codes:a −1 − x, 0.5 + y, −1 − z.b 1 + x, y, z.c −1 + x, y, z.d 1 + x, y, 1 + z.e x, y, −1 + z.f −2 − x, −0.5 + y, −1 + z.g −1 + x, y, −1 + z.h x, 1 + y, z.i −0.5 + x, 0.5 – y, 2 − z.j −0.5 + x, 1.5 − y, 2 − z.k x, −1 + y, z.l 2 − x, 1.5 + y, 1.5 − z.
N7–H7⋯S1^h	0.88	2.53	3.396(15)	169
N27–H62⋯O21^i	0.88	2.16	2.976(19)	154
N27–H62⋯O39^j	0.88	2.49	2.913(19)	111
C3–H3⋯O39^k	0.95	2.39	3.18(2)	141
C5–H5⋯S1^h	0.95	2.85	3.645(18)	141
C33–H33⋯O71^l	0.95	2.54	3.45(3)	162

---

Fig. 2 Packing views of intertwining helices along the 010 (a) and 100 (b) directions. H atoms have been omitted and the spirals have been pointed out by using different colors for clarity.

Fig. 3 View of one spiral of (2·L)_∞ along the 100 (a) and 010 directions (b) with a selected atom numbering scheme. H atoms have been omitted for clarity; symmetry codes: ′, −0.5 + x, 1.5 − y, 2 − z; ′′, 0.5 + x, 1.5 − y, 2 − z.

The structure of compound (2·L)_∞ consists of one-dimensional left-handed helical chains in which the nickel(II) atoms of the [Ni(EtOpdt)₂] units are bridged by the enantiopure L ligands (Fig. 3). The polymer crystallizes in the orthorhombic P2₁2₁2₁ chiral space group, with one [Ni((EtO)₂PS₂)₂] unit and one L ligand in the asymmetric unit. The coordination environment around the nickel ion results in a distorted octahedron with four sulphur atoms from two bidentate (EtO)₂PS₂ units and two nitrogen atoms from the pyridine rings of two bridging L ligands disposed in a cis configuration with a N–Ni–N angle of 91.6(5)° (Table 2). The binaphthyl moiety features a torsion angle of 97(2)° (C16–C17–C37–C38) and a dihedral angle of 76.55° between the two ring systems. The spirals run parallel along the a direction involving a crystallographic 2-fold screw axis (Fig. 3), with a helical pitch of 15.33 Å, coincident with the a-axis length. Homochiral helices pack with opposite screw sense in the crystal (top and bottom helices in Fig. 4a).

Fig. 4 (a) View of the helices (2·L)_∞ running along the −100 (top) and 100 (bottom) directions; (b) packing view along the a axis showing alternating planes formed by intertwining spirals running along the −100 (yellow) and 100 (blue) directions. H atoms have been omitted for clarity.

Spirals with the same orientation intertwine with each other and pack in a quite compact arrangement formed by stacking planes formed by helices running either along 100 or −100 (blue and yellow in Fig. 4b, respectively). It is interesting to point out that, different from what was previously observed for (1·L)_∞, the crystal packing of (2·L)_∞ does not involve the P atom substituents given that spirals intertwine through H bonds involving the amido groups, the MeO substituents and the pyridine rings of the binaphthyl ligands and the S1 atom coordinated to the metal ion. The planes formed by differently oriented helices pack on each other leaving small empty spaces of about 120 ų, comprising 2.6% of the cell volume.

DFT calculations

An insight into the electronic features of (1·L)_∞ and (2·L)_∞ can be provided by theoretical calculations carried out at the DFT level. As model compounds, the monomer units 1·2L and 2·2L, featuring the central nickel(II) ion in trans and cis coordination geometries, respectively, have been considered. The isolated complex 1 shows metric parameters very similar to those found in the few examples deposited in the Cambridge Structural Database.²³ In particular, the Ni–S and P–S bond distances (2.266 and 2.007 Å, respectively) are only slightly longer than those that have been experimentally structurally characterised.²⁴

A natural bond analysis (NBA) carried out on 1 at the optimised geometry has shown the Ni centre to be positively charged (Q_Ni = +0.212). Wiberg bond indices²⁵ reflect as expected the average P–S bond orders larger than unity (WBI_PS = 1.173) and remarkably strong Ni–S bonds (WBI_NiS = 0.642). Notably, the electronic structure of 1 in its ground state shows a low-lying calculated virtual molecular orbital (MO), namely, Kohn–Sham LUMO+3, almost exclusively composed of the 3d_z² atomic orbital (AO) of the metal ion. This KS-MO is therefore available to receive electron density from Lewis σ-donors, such as pyridine, to coordinatively saturate the nickel(II) centre and yield an octahedral trans-disposed complex. Accordingly, the L ligand is calculated to show two filled MOs (HOMO-2 and HOMO-3), constituting the in-phase and out-of-phase combinations of the pyridine σ-type lone pairs localised on the N donor atoms (NBO charge, −0.503 e).

In order to investigate the isomerism of the complexes derived from the reaction of bis(dithiophosphate) nickel(II) complexes with pyridine (Py) donors, the structures of both cis and trans isomers of 1·2Py were optimised. The two isomers were almost isoenergetic, with their total electronic energies differing by only 1 kcal mol⁻¹ in the gas phase (Fig. 5). The optimised metric parameters§ clearly show a remarkable trans effect exerted by the pyridine ligand. The hypothetical pentacoordinated species 1·Py was optimised with both square pyramidal and trigonal bipyramidal coordination arrangements at the metal centre, the former structure being more stable by about 11 kcal mol⁻¹. It is conceivable that a pseudorotation²⁶ or turnstile rotation mechanism in the intermediate pentacoordinate complex²⁷ might be involved in the formation of the final cis or trans isomers. This mechanism could explain the isomerism experimentally found in the case of (1·L)_∞ and (2·L)_∞. The metric parameters optimised for 1·2L and 2·2L are very close to those calculated for 1·2Py (cis and trans isomers, respectively) at the same level of theory and can be finely compared with those determined in the crystal structure of (1·L)_∞ and (2·L)_∞ (Table 4).

Fig. 5 Sums of the total electronic energies calculated for the systems 1 + 2Py, 1·Py (trigonal bipyramid coordination) + Py, 1·Py (square-pyramid coordination) + Py, and 1·2Py (cis and trans isomers) relative to the most stable complex. Ball and stick drawings of the metal complexes at their optimised geometries are also depicted.

Table 4 Selected bond distances (d, Å) and Wiberg bond indices (WBI) calculated for 1·2L and 2·2L at the DFT level

	1·2L		2·2L
	d	WBI	d	WBI
Ni–S	2.569	0.333	2.540	0.339
	2.528	0.354	2.534	0.348
	2.530	0.333	2.540	0.339
	2.518	0.362	2.534	0.348
Ni–N	2.116	0.244	2.111	0.256
	2.116	0.247	2.111	0.256

---

In particular, the Ni–N bonds show Wiberg indices typical of polarised covalent bonds (average values, 0.245 and 0.256 for 1·2L and 2·2L, respectively). Notably, NBA shows a remarkably more positive charge on nickel (+0.712 and +0.709 e for 1·2L and 2·2L, respectively) as compared to that calculated for the same atom in 1. This suggests a more polarised nature of the bonds between the dithiophosphato ligands and the metal centre in the octahedral complexes with respect to 1. This is reflected in a remarkable lengthening in Ni–S bond lengths, verified experimentally by X-ray diffraction measurements. The weakening in the Ni–S bonds is also pointed out by the relevant bond indices (average value, 0.346).

Conclusions

The new binaphthyl-based 2,2′-dimethoxy-1,1′-binaphthyl-3,3′-bis(4-pyridyl-amido) (R)-L building block has been deliberately designed with the aim of creating an axially chiral spacer capable of bridging the metal connecting sites and imparting a helical shape to the resultant coordination polymer. DFT calculations performed on the free ligand have shown the donor ability of the pyridine σ-type lone pairs localised on the N donor atoms towards the metal centres. The subsequent reaction of the neutral dithiophosphato complexes [Ni((RO)₂PS₂)₂] [R = Me (1), Et (2)] as coordinatively unsaturated metal building blocks and the enantiopure (R)-L as a spacer has allowed the assembly of the two novel helicoidal coordination polymers (1·L)_∞ and (2·L)_∞.

Although the starting Ni(II) complexes 1 and 2 feature similar square planar geometries, the obtained polymers differ in terms of the configuration of the pyridine ligands bound to the metal, which is trans and cis for (1·L)_∞ and (2·L)_∞, respectively, thus generating in (2·L)_∞ a further element of chirality at the octahedral coordinated metal ion. The generation occurs stereospecifically, as only one enantiomeric form is present in the corresponding helices. This difference is also reflected in the resulting polymers that feature different helical pitches (45.65 and 15.33 Å for (1·L)_∞ and (2·L)_∞, respectively) and different screw sense. Notwithstanding the inner differences between the polymers, their helical nature confirms that the primary structure of the polymers is directly controlled by the choice of spacers. Therefore, chiral rigid di-topic ligands featuring twisted bridging sites such as (R)-L can be used to prepare chiral helical coordination polymers when linked to the dithiophosphato Ni^II complexes.

DFT calculations performed on the cis and trans isomers of 1·2Py and on the hypothetical pentacoordinated species 1·Py (in both square planar and trigonal bipyramidal geometries) taken as model compounds showed that the two isomers are almost isoenergetic. Different intermolecular interactions ensuing from the nature of the P-substituents in the dithiophosphato complexes can be evoked to explain the structural diversities in the topology and in the final 3D-architecture of the polymer.

Further work is in progress in our laboratory with the aim of studying the effects of the building blocks on the resulting structures in order to reach an extensive control of the ensuing nanoscale products.

Experimental

Materials and methods

All commercially available compounds were used as received. Bis[O-alkyl-dithiophosphato]Ni complexes {[Ni((RO)₂PS₂)₂], R = Me (1), Et (2)}²⁸ and (R)-2,2′-dimethoxy-1,1′-binaphthyl-3,3′-dicarboxylic acid²¹ were synthesised according to previously reported procedures. THF and CH₂Cl₂ were dried on CaH₂ and distilled before use. ¹H and ¹³C NMR spectra were recorded at 25 °C in CDCl₃ on 200 or 300 MHz NMR spectrometers using the residual solvent signal as the internal standard. Mass spectra were recorded using an electrospray ionization spectrometer. Analytical thin-layer chromatography was performed on silica gel, chromophore-loaded, commercially available plates. Flash chromatography was carried out using silica gel (pore size, 60 Å, 230–400 mesh). Optical rotations were measured on a polarimeter with a sodium lamp (λ = 589 nm) and are reported as follows: [α]_D (c = g (100 mL)⁻¹, solvent). Elemental analyses were performed with an EA1108 CHNS-O Fisons instrument. FT-infrared spectra were recorded on a Thermo Nicolet 5700 spectrometer at room temperature using a flow of dry air. Middle IR spectra (resolution, 4 cm⁻¹) were recorded using KBr pellets with a KBr beam splitter and KBr windows.

X-ray diffraction

X-ray structure determinations and crystallographic data for compounds (1·L)_∞ and (2·L)_∞ were collected at 120(2) K by means of combined phi and omega scans on a Bruker-Nonius Kappa CCD area detector situated at the window of a rotating anode (graphite Mo-K_α radiation for (1·L)_∞ and 10 cm confocal mirrors for (2·L)_∞, λ = 0.71073 Å). The structures were solved by direct methods, SHELXS-97, and refined on F² using SHELXL-97.²⁹ Anisotropic displacement parameters were assigned to all non-hydrogen atoms. Hydrogen atoms were included in the refinement, but thermal parameters and geometry were constrained to ride on the atom to which they are bonded. The data were corrected for absorption effects using SADABS V2.10.³⁰ A possible disordered water molecule was found in (1·L)_∞: on modeling the Q-peak as an oxygen atom, the site is found to be approximately 1/4 occupied. It is not possible to be certain whether this is indeed a water molecule or just an artifact. For compound (2·L)_∞ the R factor is slightly higher than usual due to the crystal only diffracting weakly as indicated by the data collection resolution despite using a rotating anode X-ray generator. However, the gross connectivity of the structure can be unambiguously determined and it is reliable enough to permit geometric comparisons. An ISOR restraint was used for the non-positive definite C25 thermal modeling, and DELU and SIMU restraints were also employed globally. The carbon and hydrogen atom U_eq(max)/U_eq(min) ratio is larger than expected due to the slight rotation of the methyl group C63 creating a larger ellipsoid, which could not be modeled as disordered. Both structures have been deposited with the Cambridge Crystallographic Data Centre (deposition numbers CCDC 1002587 and CCDC 1002588 for (1·L)_∞ and (2·L)_∞, respectively).

DFT calculations

Quantum mechanical DFT calculations were performed on 1, L, pyridine (Py), 1·2Py (cis and trans isomers), the two possible conformers of the hypothetical intermediate 1·Py, 1·2L and 2·2L. Calculations were carried out by adopting the mPW1PW³¹ hybrid functional. Schäfer, Horn and Ahlrichs pVDZ basis sets were used for all atomic species.³² In all cases, geometry optimisations were followed by frequency calculations aimed to verify the nature of the energy minima. For all the optimised molecules, a full NBO³³ analysis was carried out. The program Molden 5.0 (ref. 34) was used to investigate the charge distributions and molecular orbital shapes.

Syntheses

(R)-L. A solution of (R)-2,2′-dimethoxy-1,1′-binaphthyl-3,3'-dicarboxylic acid (280 mg, 0.69 mmol) in SOCl₂ (10 mL) was heated to reflux for 4 h. The solvent was removed in vacuo and the residue dissolved in dry CH₂Cl₂ (10 mL). A solution of 4-dimethylaminopyridine (195 mg, 2.07 mmol, 3 eq.) and Et₃N (175 mg, 1.75 mmol, 2.5 eq.) in dry CH₂Cl₂ (20 mL) was then added, and the mixture was heated under reflux overnight. After cooling to room temperature, the organic phase was washed with brine and dried (Na₂SO₄) and the residue was purified by column chromatography (SiO₂; AcOEt and then AcOEt/MeOH, 8/2) to yield (R)-L (110 mg, 29%) as a white solid. [α]²⁵_D = −26.4 (c = 0.022, MeOH); ¹H NMR (200 MHz, CDCl₃): δ 10.19 (s, 2H, NHCO), 9.03 (s, 2H, binaphthyl-H4), 8.60 (d, 4H, J = 5.7, β-pyridine), 8.14 (d, 2H, J = 8.1, binaphthyl), 8.03 (d, 4H, J = 8.7, aromatic), 7.70 (d, 4H, J = 5.7, β-pyridine), 7.58 (t, 2H, J = 6.6, binaphthyl), 7.42 (t, 2H, J = 6.6, binaphthyl), 7.19 (d, 2H, J = 8.7, binaphthyl), 3.46 (s, 6H, OCH₃). ESI-MS, m/z (%) = 1131.1 [2M + Na]⁺ (70%), 577.4 [M + Na]⁺ (100%). Elemental analysis found (calc. for C₃₄H₂₆N₄O₄; formula mass = 554.2 amu); C, 73.3 (73.6); H, 4.7 (4.7); N, 9.8 (10.1).

[Ni((MeO)₂PS₂)·L)·0.5H₂O]_∞, (1·L)_∞. A solution of [Ni((MeO)₂PS₂)₂] (10.5 mg, 0.05 mmol) and L (11.0 mg, 0.05 mmol) was prepared in 0.5 mL of CH₂Cl₂ and placed into a straight sample tube. Onto this solution 2 mL of pure EtOH was layered carefully. The sample tube was sealed with parafilm and left to stand at room temperature for 8 weeks. (1·L)_∞ (4.1 mg, 0.004 mmol, 22% yield) was obtained as green crystals suitable for X-ray analysis. M.p.: 208–210 °C (d). Elemental analysis found (calc. for C₃₈H₃₈N₄O₈P₂S₄Ni·0.5(H₂O); formula mass = 936.63 amu): C, 48.41 (48.73); H, 4.10 (4.20); N, 5.91 (5.98); S, 14.05 (13.69). FT-IR (KBr, 4000–40 0 cm⁻¹): 2939 vw, 2836 vw, 1686 s, 1588 s, 1509 s, 1456 w, 1420 m, 1350 vw, 1330 m, 1298 m, 1210 s, 1016 s, 919 w, 788 ms, 675 m, 539 mw cm⁻¹.

[Ni((EtO)₂PS₂)·L]_∞, (2·L)_∞. A solution of [Ni((EtO)₂PS₂)₂] (8.6 mg, 0.02 mmol) and L (11.1 mg, 0.02 mmol) was prepared in 0.5 mL of CH₂Cl₂ and placed into a straight sample tube. Onto this solution 2 mL of pure EtOH was layered carefully. The sample tube was sealed with parafilm and left to stand at room temperature for 8 weeks. (2·L)_∞ (6.5 mg, 0.007 mmol, 33% yield) was obtained as green crystals suitable for X-ray analysis. M.p.: 204–206 °C (d). Elemental analysis found (calc. for C₄₂H₄₆N₄O₈P₂S₄Ni; formula mass = 983.7 amu): C, 51.15 (51.28); H, 4.77 (4.71); N, 5.77 (5.70); S, 13.75 (13.04). FT-IR (KBr, 4000–400 cm⁻¹): 1678 s, 1590 s, 1510 s, 1458 vw, 1422 m, 1388 vw, 1332 s, 1297 m, 1199 m, 1157 w, 1018 s, 943 s, 835 w, 756 m, 660 m, 623 vw, 543 m cm⁻¹.

Acknowledgements

Financial support from the University of Pavia and MIUR (PRIN 2004 to MCA and DP, and PRIN2009 A5Y3N9 to DP) is gratefully acknowledged. The authors would like to thank EPSRC for funding the UK National Crystallography Service. Dr. Riccardo Montis (Università degli Studi di Cagliari, Italy) is kindly acknowledged for the useful discussion.

Notes and references

1. M. Du, C.-P. Li, C.-S. Liu and S.-M. Fang, Coord. Chem. Rev., 2013, 257(7–8), 1282–1305; O. K. Farha and J. T. Hupp, Acc. Chem. Res., 2010, 43(8), 1166–1175; C. J. Sumby, Aust. J. Chem., 2013, 66(4), 397–400; J. Reedijk, Chem. Soc. Rev., 2013, 42(4), 1776–1783; L. Brammer, Chem. Soc. Rev., 2004, 33, 476–489; S. Kitagawa and R. Matsuda, Coord. Chem. Rev., 2007, 251(21–24), 2490–2509.
2. M. Arca, A. Cornia, F. A. Devillanova, A. C. Fabretti, F. Isaia, V. Lippolis and G. Verani, Inorg. Chim. Acta, 1997, 262, 81–84; W. E. van Zyl and J. D. Woollins, Coord. Chem. Rev., 2013, 257(3–4), 718–731.
3. I. Haiduc, Handbook of Chalcogen Chemistry, ed. F. A. Devillanova, Royal Society of Chemistry, 2006, pp. 593–643.
4. M. C. Aragoni, M. Arca, F. Demartin, F. A. Devillanova, C. Graiff, F. Isaia, V. Lippolis, A. Tiripicchio and G. Verani, J. Chem. Soc., Dalton Trans., 2001, 2671–2677; L. Bolundut, I. Haiduc, E. Ilyes, G. Kociok-Köhn, K. C. Molloy and S. Gómez-Ruiz, Inorg. Chim. Acta, 2010, 363(15), 4319–4323.
5. M. C. Aragoni, M. Arca, N. R. Champness, A. V. Chernikov, F. A. Devillanova, F. Isaia, V. Lippolis, N. S. Oxtoby, G. Verani, S. Z. Vatsadze and C. Wilson, Eur. J. Inorg. Chem., 2004, 10, 2008–2012; M. C. Aragoni, M. Arca, N. R. Champness, M. De Pasquale, F. A. Devillanova, F. Isaia, V. Lippolis, N. S. Oxtoby, G. Verani and C. Wilson, CrystEngComm, 2005, 7(60), 363–369; M. C. Aragoni, M. Arca, M. Crespo, F. A. Devillanova, M. B. Hursthouse, S. L. Huth, F. Isaia, V. Lippolis and G. Verani, CrystEngComm, 2007, 9(10), 873–878.
6. L. Monnereau, M. Nieger, T. Muller and S. Bräse, Adv. Funct. Mater., 2014, 24, 1054–1058.
7. H.-F. Chow, K.-N. Lau, Z. Ke, Y. Liang and C.-M. Lo, Chem. Commun., 2010, 46(20), 3437–3453; E. C. Constable, N. Hostettler, C. E. Housecroft, N. S. Murray, J. Schönle, U. Soydaner, R. M. Walliser and J. A. Zampese, Dalton Trans., 2013, 42(14), 4970–4977; C. Piguet, M. Borkovec, J. Hamacek and K. Zeckert, Coord. Chem. Rev., 2005, 249(5–6), 705–726.
8. T.-T. Luo, H.-C. Wu, Y.-C. Jao, S.-M. Huang, T.-W. Tseng, Y. Wen, G.-H. Lee, S.-M. Peng and K.-L. Lu, Angew. Chem., Int. Ed., 2009, 48(50), 9461–9464; Y. Cui, S.-J. Lee and W. Lin, J. Am. Chem. Soc., 2003, 125, 6014–6015; D. Bradshaw, J. B. Claridge, E. J. Cussen, T. J. Prior and M. J. Rosseinsky, Acc. Chem. Res., 2005, 38(4), 273–282; B. Joarder, A. K. Chaudhari and S. K. Ghosh, Inorg. Chem., 2012, 51(8), 4644–4649.
9. J. Della Rocca, D. Liu and W. Lin, Acc. Chem. Res., 2011, 957–968; L. Ma, J. M. Falkowski, C. Abney and W. Lin, Nat. Chem., 2010, 2, 838–846.
10. W. Xuan, M. Zhang, Y. Liu, Z. Chen and Y. Cui, J. Am. Chem. Soc., 2012, 134(16), 6904–6907; A. D. Cutland-Van Noord, J. W. Kampf and V. L. Pecoraro, Angew. Chem., Int. Ed., 2002, 41, 4667–4670.
11. Chem. Soc. Rev., 2009, 38(3), whole issue; H. Wang, Chirality, 2010, 22(9), 827–837; J. K. Okuma, R. Itoyama, A. Sou, N. Nagahora and K. Shioj, Chem. Commun., 2012, 48(90), 11145–11147; M. Caricato, A. K. Sharma, C. Coluccini and D. Pasini, Nanoscale, 2014, 6, 7165–7174.
12. R. E. Morris and X. Bu, Nat. Chem., 2010, 2(5), 353–361; J. Zhang, S. Chen, T. Wu, P. Feng and X. Bu, J. Am. Chem. Soc., 2008, 130(39), 12882–12883; E. Yashima, K. Maeda, H. Lida, Y. Furusho and K. Nagai, Chem. Rev., 2009, 109(11), 6102–6211; K. K. Bisht and E. Suresh, Inorg. Chem., 2012, 51(18), 9577–9579.
13. M. Albrecht, Chem. Rev., 2001, 101(11), 3457–3497; Y. Liu, W. Xuan and Y. Cui, Adv. Mater., 2010, 22(37), 4112–4135; D. Pijper and B. L. Feringa, Soft Matter, 2008, 4(7), 1349–1372; H. Cao, X. Zhu and M. Liu, Angew. Chem., Int. Ed., 2013, 52(15), 4122–4126.
14. A. Bencini, C. Coluccini, A. Garau, C. Giorgi, V. Lippolis, L. Messori, D. Pasini and S. Puccioni, Chem. Commun., 2012, 48, 10428–10430; A. Moletti, C. Coluccini, D. Pasini and A. Taglietti, Dalton Trans., 2007, 1588–1592; C. Coluccini, A. Mazzanti and D. Pasini, Org. Biomol. Chem., 2010, 8, 1807–1815; C. Coluccini, D. Dondi, M. Caricato, A. Taglietti, M. Boiocchi and D. Pasini, Org. Biomol. Chem., 2010, 8, 1640–1649; M. Caricato, C. Coluccini, D. Dondi, D. A. Vander Griend and D. Pasini, Org. Biomol. Chem., 2010, 8, 3272–3280; M. Caricato, A. Olmo, C. Gargiulli, G. Gattuso and D. Pasini, Tetrahedron, 2012, 68, 7861–7866.
15. M. Yoon, R. Srirambalaji and K. Kim, Chem. Rev., 2012, 112(2), 1196–1231; T. J. Ward, Anal. Chem., 2006, 78(12), 3947–3956; P. S. Bhadury, Y. Yao and Y. He, Curr. Org. Chem., 2012, 16(15), 1730–1753; D. Kampen, C. M. Reisinger and B. List, Top. Curr. Chem., 2010, 291, 395–456; H. Pellissier, Adv. Synth. Catal., 2012, 354(2–3), 237–294.
16. L. Pu, Acc. Chem. Res., 2012, 45(2), 150–163; Q. Li, H. Guo, Y. Wu, X. Zhang, Y. Liu and J. Zhao, J. Fluoresc., 2011, 21(6), 2077–2084; J. Jiao, X. Liu, X. Mao, J. Li, Y. Cheng and C. Zhu, New J. Chem., 2013, 37(2), 317–322.
17. C. Coluccini, A. Castelluccio and D. Pasini, J. Org. Chem., 2008, 73, 4237–4240; J. M. Brunel, Chem. Rev., 2005, 105, 857–898.
18. I. Huc, Eur. J. Org. Chem., 2004, 17–29; Y. Baudry, G. Bollot, V. Gorteau, S. Litvinchuk, J. Mareda, M. Nishihara, D. Pasini, F. Perret, D. Ronan, N. Sakai, M. R. Shah, A. Som, N. Sorde, P. Talukdar, D.-H. Tran and S. Matile, Adv. Funct. Mater., 2006, 16, 169–179.
19. M. Wenzel, J. R. Hiscock and P. A. Gale, Chem. Soc. Rev., 2012, 41, 480–520.
20. M. C. Etter, Acc. Chem. Res., 1990, 23, 120–126.
21. D. J. Cram, R. Helgeson, S. C. Peacock, L. J. Kaplan, L. A. Domeier, P. Moreau, K. Koga, J. M. Mayer, Y. Chao, M. G. Siegel, D. H. Hoffman and G. D. Y. Sogah, J. Org. Chem., 1978, 43, 1930–1946; M. Asakawa, H. M. Janssen, E. W. Meijer, D. Pasini and J. F. Stoddart, Eur. J. Org. Chem., 1998, 983–986; C. Xin, S. Da, D. Dong, J. Liu and R. Wei, Tetrahedron: Asymmetry, 2002, 13, 1937–1940.
22. S. Colombo, C. Coluccini, M. Caricato, C. Gargiulli, G. Gattuso and D. Pasini, Tetrahedron, 2010, 66, 4206–4211; M. Caricato, N. J. Leza, C. Gargiulli, G. Gattuso, D. Dondi and D. Pasini, Beilstein J. Org. Chem., 2012, 8, 967–976.
23. F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388.
24. Ni–S1 2.218, Ni–S2 2.225, P–S1 1.984, P–S2 1.979, CDS refcode DMTPON, V. Kastalsky and J. F. McConnell, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem, 1969, 25, 909–915.
25. K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096.
26. R. S. Berry, J. Chem. Phys., 1960, 32, 933–938.
27. M. E. Cass, K. K. Hii and H. S. Rzepa, J. Chem. Educ., 2006, 83, 336.
28. M. C. Aragoni, M. Arca, M. Crespo, F. A. Devillanova, M. B. Hursthouse, S. L. Huth, F. Isaia, V. Lippolis and G. Verani, Dalton Trans., 2009, 2510–2520.
29. G. M. Sheldrick, SHELX suite of programs for crystal structure solution and refinement, Univ. of Göttingen, Germany, 1997.
30. G. M. Sheldrick, SADABS V2.10, 2003.
31. C. Adamo and V. Barone, J. Chem. Phys., 1998, 108, 664–675.
32. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
33. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
34. G. Schaftenaar and J. H. Noordik, J. Comput.-Aided Mol. Des., 2000, 14, 123–134.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 1002587 and 1002588. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4ce01101e

‡ The range has been calculated from the dihedral torsion angles found in molecules containing analogous 2,2′-dimethoxy-1,1′-binaphthyl fragments (47 structures, 74 fragments, average value = 87.8°) from a search in the Cambridge Structural Database System version 5.35, 2014.

§ Selected optimised distances for the cis isomer of 1·2Py: Ni–N, 2.131 Å; Ni–S (trans to N) 2.539; Ni–S (trans to S) 2.516 Å. Selected optimised distances for the trans isomer of 1·2Py: Ni–N, 2.129 Å; Ni–S, 2.526 Å.

---