X-ray irradiation induced reduction and nanoclustering of lead in borosilicate glass

Abstract

We have studied the formation of nanoparticles in lead sulfide (PbS)-doped borosilicate glass subjected to a two-step nucleation and growth heat treatment using in situ small-angle X-ray scattering (SAXS). The microstructure produced was subsequently characterized using X-ray powder diffraction (XRD) and transmission electron microscopy (TEM). While PbS nanocrystals of ca. 2 nm diameter are formed throughout the sample during the heat treatment, larger monodisperse Pb nanocrystals (diameter ca. 50 nm) are formed due to exposure to the X-ray beam, yielding space-selective nanoparticle growth. Time-resolved SAXS spectra are in the early stages consistent with diffusion-limited growth of the Pb particles. We attribute the X-ray-induced formation of nanocrystalline Pb to X-ray photoreduction of the Pb²⁺ atoms.

---

Introduction

X-ray diffraction is generally regarded by the materials science community as a non-destructive characterization technique that is able to probe the microstructure of solids in situ. However, in spite of being generally viewed as benign compared to electron microscopy or laser irradiation, intense synchrotron X-ray beams can lead to radiation damage^1–3 or even to structure formation.^4–6 Despite a significant body of knowledge about radiation damage in soft condensed matter⁷ and aqueous^8,9 and biological systems,^10–14 little has been reported about the structure-modifying interactions of monochromatic photons in the 5 < E < 40 keV range in hard condensed matter such as crystalline or vitreous materials. In such samples, radiation damage has usually been considered to be negligible since the energy levels are too low for direct atomic displacement.¹⁵ Sample heating due to absorbed X-rays is not thought to play an appreciable role either, unless one is working on samples close to the absolute zero temperature or using white beam techniques.¹⁶ Nevertheless, the possibility of X-ray-induced electron transfer and corresponding oxidation-reduction processes cannot be neglected.

Controlled precipitation of metallic and semiconductor nanoparticles in glass is of interest to photochromic glass and glass ceramics technology¹⁷ as well as in the areas of photonics, optoelectronics and catalysis.^18–23 Semiconductor nanocrystals or quantum dots (QDs) of Pb-based IV–VI semiconductors (e.g. PbS, PbSe, PbTe) are particularly interesting as they show some of the strongest quantum confinement effects owing to their relatively large exciton Bohr radii.²⁴ This attribute makes Pb-based IV–VI quantum dots particularly attractive materials for applications in nonlinear photonics and solar cells. One of the simplest preparation routes for producing quantum dots embedded in an inert and durable matrix still remains solid-phase precipitation of QDs in glassy hosts via nucleation and growth.²⁵ Synthesis of QDs by nucleation and growth in glass is particularly attractive as it is an inexpensive and relatively easy way to form quantum dots with excellent size control.²⁶

Owing to the high electron density contrast between PbS particles and oxide glass, such characterization is ideally suited to time-resolved Small and Wide Angle X-ray Scattering (SAXS/WAXS).^27,28 Here we report the results of an in situ small-angle X-ray scattering study of the thermally induced nucleation and growth of PbS quantum dots in borosilicate host glass and the serendipitous finding that larger Pb crystals form under the influence of the X-ray beam. This result suggests that deep X-ray lithography, which has been used to create functional materials by direct patterning of sol–gel, hybrid organic–inorganic and mesoporous films,²⁹ could also be applied to borosilicate glass at elevated temperatures.

Experimental

Glass synthesis

Borosilicate glass of composition (mol%) 58.7% SiO₂-21.4% K₂O-7.1% B₂O₃-3.0% CaO-8.8% BaO, nominally doped with 2 wt% PbS, was prepared from constituent oxides (and carbonates for K and Ca) and PbS by melting in a silica crucible for 4 hours at 1400 °C in air. The melt was homogenized by mechanical stirring and cast on graphite. The resulting glass was annealed at 500 °C for 30 minutes before cooling down to ambient temperature by shutting off the furnace. The loss of S from the melt via sublimation and of Pb via high-temperature reduction followed by density separation results in glass that contained approximately 0.8 mol% Pb and 0.06 mol% S, as determined by electron probe micro-analysis (EPMA). The local environment of lead atoms was verified by fluorescence EXAFS and transmission EXAFS using the BM26A beamline at the ESRF³⁰ at 80 K in an Oxford Instruments cryostat. The Pb L_III-edge (13.035 keV) EXAFS spectra obtained from the glass samples before heat treatment show that most lead atoms have oxygen nearest neighbours and could be fitted without introducing Pb–Pb or Pb–S interactions, indicating that neither metallic Pb particles nor PbS (galena) is formed during initial sample preparation.

Small-angle X-ray scattering (SAXS)

Samples of dimensions 3 mm × 5 mm × 50 μm were prepared for SAXS measurements which were carried out on beamline BM26B³¹ at the European Synchrotron Radiation Facility in Grenoble and on beamline 7.3.3 at the Advanced Light Source (Berkeley).³²

All samples underwent a 2-step heat treatment consisting of a particle nucleation anneal at 575 °C followed by an isothermal particle growth anneal at a higher temperature. Two experimental protocols were followed for the lower temperature anneal used to nucleate PbS quantum dots.

One series of samples was annealed in a tube furnace in air at 575 °C for 6 hours (ex situ nucleation); the samples reached 575 °C from ambient within 20 minutes with negligible temperature overshoot. These pre-nucleated samples were then measured in situ in the X-ray beam whilst undergoing an isothermal anneal at 630 °C, 640 °C or 650 °C in a thermal gradient-free furnace for up to 5 hours.

The second set of samples was annealed in a furnace at 575 °C for 2 to 3 hours in the X-ray beam (in situ nucleation) immediately followed by an isothermal in situ particle growth anneal identical to that described above.

SAXS data were collected continuously at a photon energy of 12 keV at a rate of one frame (data set) per minute using a Dectris Pilatus 1M area detector.³³ The X-ray flux was 5 × 10¹¹ photons s⁻¹ on a 300 μm diameter spot. The scattering vector is given by q = 4π sin θλ⁻¹.

The area directly irradiated during the SAXS experiments is significantly smaller than the total sample size, thus irradiated and non-irradiated parts with identical thermal history could subsequently be characterized by X-ray powder diffraction and electron microscopy. These areas are hereafter referred to as “irradiated” and “non-irradiated”. By virtue of in situ measurements, all SAXS data correspond to “irradiated” areas. SAXS patterns were corrected for incident X-ray intensity, sample transmission and background scattering using the FIT2D software package.³⁴ The software package SASfit³⁵ was used to model these SAXS patterns.

X-ray powder diffraction (XRD)

XRD data were collected from samples previously heat treated and measured in the SAXS experiments using a spot size of 0.5 mm² aligned on areas darkened (irradiated during the SAXS measurement) and immediately adjacent (non-irradiated) using the Swiss-Norwegian BM01A beamline at the ESRF, Grenoble. Samples were mounted between 25 μm thick Kapton support sheets and were rotated back and forth through 10° in the X-ray beam in order to minimise the measurement of incorrect peak intensities which can arise if the crystallites are not randomly oriented in the sample. Data were collected using a Dectris Pilatus 2M area detector³⁶ at an incident energy of 17.8 keV.

TEM

Scanning transmission electron microscopy (STEM) data were collected on an aberration-corrected TEAM 0.5 instrument at the National Center for Electron Microscopy at Lawrence Berkeley National Laboratory. Samples were prepared by the focused ion beam lift-out technique³⁷ from both X-ray-irradiated and non-irradiated regions of the sample. The resulting samples were thinned to approximately 100 nm in order to reduce the effects of damage from the Ga⁺ ion beam. STEM data were collected in high-angle annular dark-field (HAADF) mode at 300 kV with a convergence angle of 19 mrad and a collection angle of 68–340 mrad. Using custom software written in Matlab®, a total number of 950 particles were automatically detected from a series of STEM images of the X-ray-irradiated region. The images were smoothed by a Gaussian filter before particle detection. Particle detection was performed on gradient images to treat regions with different background levels and hence different thicknesses simultaneously. Rough particle locations were determined by thresholding the gradient image. Particle centers and radii were then obtained by a circular Hough transform as implemented in Matlab® with highest possible sensitivity to detect small features of less than 10 pixels and to account for agglomerated particles.

Results

SAXS

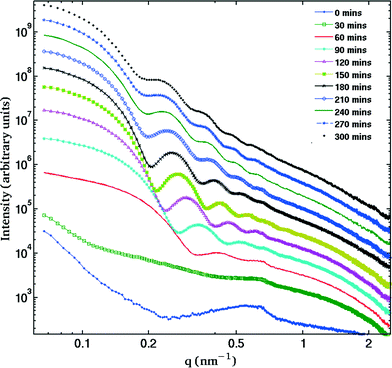
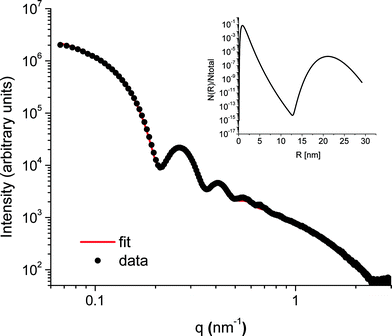
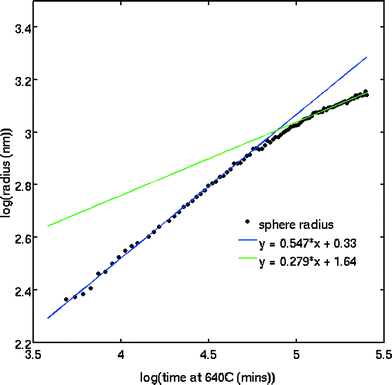
The SAXS patterns obtained after X-ray irradiation at 575 °C for 2.5 hours in situ show no measureable difference from those obtained after ex situ annealing at 575 °C for 6 hours. These SAXS patterns are consistent with the presence of particles of ca. 2 nm diameter. When the temperature is raised to 630 °C or higher, rapid particle growth commences with particles of the order of 14 nm diameter formed after 30 minutes. Fig. 1 illustrates the evolution over a 5 hour isothermal anneal at 640 °C, where zero minutes corresponds to the pattern obtained at the end of the 575 °C pre-anneal. Surprisingly, a simple sphere model for the particles, whether monodisperse or of a simple polydisperse form such as log-normal, is unable to reproduce a higher q (> ≈ 0.6 nm⁻¹) scattering intensity as annealing progresses. These data imply the persistent presence of a significant population of small (radius ≈1–2 nm) particles in the samples but are too background sensitive to permit detailed analysis of this particle size distribution. Using data containing a clear structure, a model consisting of a bimodal log-normal distribution of spherical particles was found as illustrated in Fig. 2. These fit parameters were then extended iteratively to shorter and longer times. Polydispersity increases at long annealing times, which may be interpreted by growth of the smaller particles (also suggested by TEM) or Ostwald ripening of the larger particles (or both). The temporal evolution of the radius of the larger particles is shown in Fig. 3. The mean particle radius R initially grows with time t as R(t) ∼ t^1/2 but slows down at longer times R(t) ∼ t^1/3. This is consistent with a crossover from diffusion-limited growth at short times to Ostwald ripening at long times.³⁸

Fig. 1 Evolution of the SAXS patterns over in situ 5 hour annealing at 640 °C. Curves are shown for 30 minutes intervals and are displaced vertically for clarity. The presence of several fringes is characteristic of a very monodisperse distribution.

Fig. 2 Representative SAXS data from the sample annealed for 2 h 40 minutes at 640 °C. The data are fitted by a bimodal distribution of solid spheres. The inset shows the particle size distribution obtained with this fit.

Fig. 3 Fitted particle radius (Pb particles) as a function of time illustrating the initial R ~ √t behaviour, indicating a diffusion-limited growth process, and the crossover to (tentatively) Ostwald ripening.

Pb L_III-edge EXAFS

The formation of PbS nanocrystals upon heat treatment is manifested in the appearance of Pb–S nearest neighbors and Pb–Pb next-nearest neighbors in the EXAFS spectra. No significant differences are observed between samples nucleated in situ and ex situ. The X-ray beam size is larger than that employed for SAXS measurements so it is not possible to select solely an irradiated area; both irradiated and non-irradiated areas of the sample were measured simultaneously.

Powder diffraction

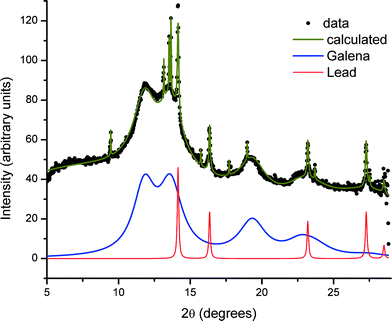
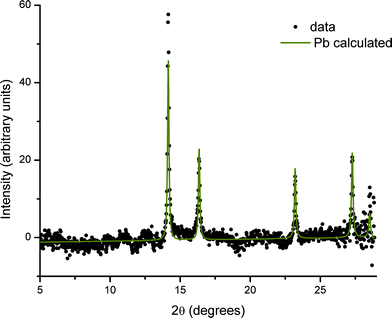
The XRD pattern obtained from the glass sample after irradiation during SAXS measurements, and specifically from the directly irradiated area, is shown in Fig. 4. The pattern shows both very broad diffraction peaks corresponding to small crystallites of PbS and much sharper peaks arising from considerably larger particles of crystalline material. Close inspection reveals that there must be at least two of these crystalline phases in addition to PbS, since these data include peaks with a width limited by the instrumental resolution, together with peaks that are slightly broadened. The broadened reflections correspond to metallic lead. Analysis of the Scherrer broadening of these peaks gives diameters for the particles of PbS 2(1) nm and Pb 57.7(8.3) nm for one sample and PbS 2(1) nm and Pb 36.6(1.6) nm for a second sample. We therefore conclude that the evolving scattering pattern in the SAXS data during high-temperature annealing corresponds to the growth of nanoparticles of metallic Pb.

Fig. 4 Powder diffraction data (BM01, ESRF) of an annealed glass sample exposed to X-rays whilst at elevated temperatures after background subtraction. Below the data the solid blue line is the contribution from PbS and the red line with narrower peaks highlights a metallic lead phase. Other peaks are associated with unidentified crystallites.

In contrast, regions of the samples not exposed to X-rays during SAXS measurements (non-irradiated regions) show no evidence of the presence of elemental Pb nanoparticles. This is illustrated in Fig. 5 where the difference in scattering obtained between irradiated and non-irradiated positions of the same sample shows that the components are identical except for the presence of Pb.

Fig. 5 Difference between XRD patterns taken in an irradiated and non-irradiated area of the same sample. The solid line (Pb calculated) is a fit to the crystal structure of lead with a lattice parameter of 4.9506 Å (fixed) and Lorentzian peak broadening.

Analysis of XRD patterns taken from the irradiated areas after the in situ SAXS anneal yields the relative ratios of 3.84(0.26)% Pb/96.16(0.26)% PbS from one sample and 6.63(0.28)% Pb/93.37(0.28)% PbS from a second sample. This ratio is remarkably different, and approximately reversed, from a ratio of Pb : PbS of ~93% : 7% obtained from chemical analysis of the original glass, which EPMA gave as 0.838(0.057) mol% Pb and 0.059(0.012) mol% S. Since the XRD analysis is only sensitive to crystalline material, this observation indicates that most of the lead remains dispersed through the matrix, coordinated to oxygen, in agreement with the Pb L_III-edge EXAFS results.

The identity of the phase or phases producing the remaining narrow diffraction peaks is not clear at this stage. These peaks change dramatically in intensity and even presence over the sample surface. This suggests large crystals with a preferred orientation, such as might be formed at the surface. SEM images (which we included in the ESI†) show such crystals. Although of academic interest, these surface crystals are very unlikely to be of relevance to the bulk effects we describe.

Optical microscopy

The changes in morphology inferred from the SAXS and XRD data are also evident in the macroscopic sample appearance. After annealing, the samples are optically darkened in the region illuminated by the X-ray beam, the remainder of the sample merely gaining an inhomogeneous yellowish-brown tint.

TEM

The TEM images of the irradiated region of a sample annealed for 5 hours at 640 °C clearly show two well-defined populations of spherical particles agreeing with the SAXS and XRD results discussed above (see Fig. 6). The larger particles have a diameter of 54 ± 6 nm; the smaller particles are more polydisperse with an average diameter of 18 ± 5 nm and a size range of 10 to 30 nm diameter (see Fig. 7). There is no evidence from the HAADF STEM images that the larger Pb particles are a core–shell mixture of Pb and PbS.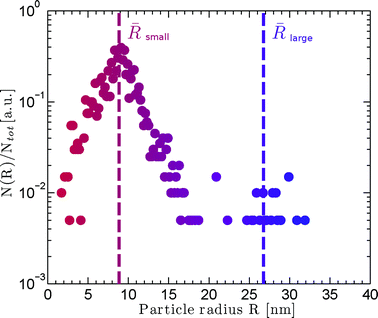

Fig. 6 STEM image of the region of a sample irradiated in situ at 640 °C for 5 hours in the SAXS experiment revealing a large number of small PbS particles and a small number of larger Pb particles. The sample is thinned to two different thicknesses.

Fig. 7 Particle size histogram computed from the circular Hough transform of (total number) particles from the STEM image. There are a large number of small particles and a few much larger particles.

A region of the same sample, imaged just outside the irradiated area, is illustrated in Fig. 8. In this area the PbS particles are smaller and close to the 2–3 nm range observed by SAXS and XRD. The large particles are entirely absent in this area, again agreeing with the XRD data.

Fig. 8 STEM image of the region of a sample adjacent to an area irradiated in situ at 640 °C for 5 hours in the SAXS experiment. There are no large Pb particles.

Discussion

Photoreduction of Pb

Visible and ultraviolet light are known to cause photoinduced modifications in certain glasses including silver-containing glass and chalcogenide glass.¹⁵ The conventional wisdom is that the incident photons excite electrons leading to anisotropic charge distributions and bond breakage. Both photoinduced precipitation of silver metal out of a silver chalcogenide glass³⁹ and diffusion of silver ions into the irradiated region of silver chalcogenide glass⁴⁰ have been observed in this way. X-ray photons have higher energy, but even the most intense X-ray beam produces several orders of magnitude fewer photons than, for instance, the 500 W mercury lamp used in the cited literature. Nevertheless, X-ray irradiation also alters nanoparticle formation in glass. In situ X-ray irradiation of a soda-lime glass has been shown to assist the formation of gold nanoparticles, increasing the number of particles by an order of magnitude and delaying Ostwald ripening.⁵ These authors hypothesise that defects serving as nucleation sites are created by X-ray irradiation despite the elevated temperature of in situ annealing. It has also been reported that irradiation by 10 keV X-rays from a synchrotron source not only increases the number of crystallisation nucleation sites in the region directly exposed to the beam, but also far beyond, an effect ascribed to photoelectrons created by scattered radiation.⁴

In addition there is a growing body of evidence that X-ray irradiation reduces metallic cations in glass. Nanosized gold particles have been produced by reduction of Au⁺ under Rh Kα irradiation at 600 °C,⁴¹ where we note that simultaneous irradiation and heating were necessary. Reibstein et al. observed the reduction of Ag⁺ to Ag⁰ under Cu Kα radiation in ionic sulfophosphate glass,⁴² Eichelbaum et al. described the synchrotron X-ray radiation-induced reduction of Au⁺ to Au⁰ and of Ag⁺ to Ag⁰ in soda lime silicate glass,⁴³ Ferreira et al.⁴⁴ and Zhang and Sheng⁴⁵ observed the synchrotron X-ray photoreduction of Fe³⁺ in low iron content soda-lime silicate glass, whilst Vahedi et al.⁴⁶ described the synchrotron X-ray reduction of Sm³⁺ to Sm²⁺ in fluorophosphate and fluoroaluminate glass. Finally Corrias⁴⁷ has evidence of the reduction of Cd²⁺ during X-ray Cu Kα irradiation of a glass system containing CdSe dots surrounded by CdS arms (“octopods”) at room temperature. Ferreira et al.⁴⁴ noted that a fairly constant amount of iron was photoreduced by the synchrotron beam, whatever the total iron content in the sample. These authors also found that photoreduction could be prevented by increasing the temperature.

In this study, we report that simultaneous X-ray irradiation and high temperature promote the formation of metallic nanoparticulate Pb. Such particles cannot be formed in glass by thermal annealing without irradiation and X-ray-promoted growth of Pb nanoparticles has not previously been reported to the best of our knowledge.

Pb exists in considerable excess over S in the as-prepared glass. However, Pb L_III-edge EXAFS results indicate that Pb in the as-prepared glass is in an oxide-like environment. Annealing at a temperature of 640 °C allows breakage of Pb–O bonds and thermal diffusion of the resulting Pb²⁺ through the glass to combine with S to form clusters of PbS, irrespective of irradiation. Our sample preparation protocol appears to produce a great many nucleation sites leading to a large number of small galena particles and a rapid exhaustion of sulfur. The thermally driven formation of PbS particles is no surprise. In contrast, the formation of pure Pb crystallites in the irradiated volume is unexpected. Lead can exist as either Pb⁴⁺, when incorporated as a network former in the glass network, or Pb²⁺ when this is not the case. Evidently, even if Pb atoms are capable of thermally driven diffusion through the network, crystallite formation is not possible unless the charges are somehow compensated for. We observe a fairly monodisperse population of relatively large particles of Pb in X-ray-irradiated regions, suggesting a small number of nucleation sites for their growth.

The question then arises as to whether X-ray radiation provides photoelectrons for the reduction of Pb²⁺ to form Pb⁰ atoms. It is known that X-ray irradiation may induce various defects such as nonbridging oxygen hole centers (NBOHC), boron oxygen hole centers (BOHC), boron electron centers and even alkali electron centers (where alkali cations trap electrons) in borosilicate glass.^41,48,49 These electronic defects are unstable; they may be annealed out by raising the temperature to a few hundred degrees, or they decay over months or years at room temperature. Several authors suggest that NBOHC or BOHC provides electrons that can combine with neighboring cations to reduce the latter;^41,44,46 increasing the temperature allows these defects to relax and inhibits the photoreduction process. In our system we suggest that lead cations trap electrons under X-ray irradiation

Pb²⁺ + 2e⁻ → Pb⁰

where D⁺ is a defect. The D⁺ defects may subsequently relax via local bonding reconstructions at these elevated temperatures. For example, if D⁺ represents defects associated with excess oxygen such as NBOHC then the latter may be annealed by evolution of excess oxygen from the glass. Once formed, the Pb⁰ atoms, despite their larger radius, are expected to be significantly more mobile than Pb²⁺ ions, as the former do not bond to other atoms. These Pb⁰ atoms diffuse through the glass structure and combine with other Pb⁰ atoms to form nanoclusters of Pb metal that subsequently grow with time. It may be noted here that only a small fraction of nanocrystalline Pb compared to PbS is formed; the limiting factor is not the amount of Pb in excess of S in the glass. The limiting factor is most probably the defect concentration required for the generation of photoelectrons responsible for the reduction of Pb²⁺ ions.

X-ray heating

Creation of particles of lead up to 50 nm in diameter obviously implies diffusion within the glass and relaxation of the network. Whilst a temperature of 640 °C might be considered to be thermodynamically sufficient, the observation that these particles are only formed in the irradiated area of the sample leads us to consider whether beam heating effects may play a role. Beam heating is an important consideration for samples irradiated by X-ray free electron laser (XFEL) sources,^50,51 but although individual photons in these beams may carry energies similar to synchrotron X-rays, fluxes are so high in XFEL sources that the energy deposited in samples is of the order of 10¹⁶–10¹⁷ W cm⁻². In this study we have a flux of ~5 × 10¹¹ photons s⁻¹ at an energy of 12 keV on a 300 μm diameter spot. This translates to a power of 1.36 W cm⁻², which is very small compared to any type of laser irradiation. Beam heating effects are sometimes observed at these fluxes in low-temperature X-ray diffraction studies where heat capacity and thermal conductivity become very low,⁵² but they are usually negligible in inorganic samples at room temperature. Typically thermal diffusion results in efficient thermal spreading of the deposited energy and almost uniform internal temperatures (see ref. 16 for example) but structural changes attributed to X-ray beam heating by similar fluxes have been reported.^53,54

Macroscopic heating is surely negligible (as commented above), but the question of differential heating of the heavily absorbing clusters of lead (and perhaps consequently their nanoscale environment) on a very local, and transient, level remains. We have therefore modeled the transient heating expected for lead particles dispersed in the glassy matrix due to radiation absorption. We consider one particle with a spherical shape, radius R₀ and temperature T(t). The problem is formulated in spherical coordinates such that the temperature equation reads:

in which λ (J m⁻¹ K⁻¹ s⁻¹) is the heat conduction coefficient, ρ (kg m⁻³) is the density, C_p (J kg⁻¹ K⁻¹) the heat capacity at constant pressure, i (J s⁻¹) the photon energy absorbed by the nanoparticle (estimated from the incident photon flux and the absorption coefficient of lead⁵⁵) and m_p is the mass of the nanoparticle. Every particle is surrounded by a volume of the matrix material with radius R₁ that is half of the average distance between the dispersed particles. At this distance heat flow is assumed to be zero. We do not consider any boundary effects around the particle, nor do we consider the macroscopic heat sink. The initial and boundary conditions are thus given by:

T(r, t = 0) = 0; T(0, t) = T_p; ∇_r(T(r = R₁, t)) = 0

The absorption in the matrix material is assumed to be zero. This transient temperature problem is solved numerically using MATHEMATICA, applying the numerical method of lines.⁵⁶ For a lead particle with radius R₀ = 1 nm, i = 8.526 × 10⁻¹⁸ J s⁻¹ and from the material parameters given in Table 1 we obtain the transient temperature profile illustrated in Fig. 9.

Table 1 Material parameters

	Particles	Matrix
ρ (kg m^−3)	11 340	2200
C p (J kg^−1 K^−1)	128.62	750–830
λ (W m^−1 K^−1)	35.3	1.08–1.2

---

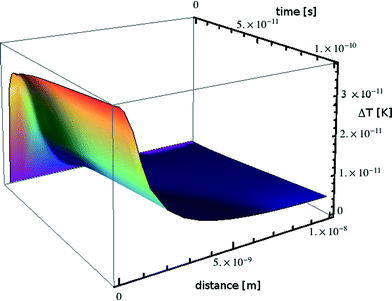Fig. 9 Transient heating calculated for a nanoparticle of lead embedded in a borosilicate glass matrix.

Over a time scale of 10⁻¹⁰ s the particle warms by some 4 × 10⁻¹¹ K. If the simulation is allowed to continue for 10 s the particle warms by 0.5 K with a negligible temperature gradient between particles; this situation would be counteracted in reality by a decrease in external heating power, leading us to the conclusion that beam heating effects are nonexistent in accordance with the very low power absorbed.

Nevertheless, although the time-averaged energy absorbed is very small, it is important to remember that the photon energy arrives in quanta. Using the linear absorption coefficient of lead we calculate that one photon is absorbed by a 1 nm spherical nanoparticle every 3 3/4 minutes on average in our experimental configuration; averaging over a second is very misleading. If the energy of one 12 keV photon absorbed by a 1 nm radius nanoparticle of lead was converted adiabatically to heat this would correspond to increasing the temperature of the nanoparticle by 3.15 × 10⁵ K! This simplistic classical view is wrong; photon energy is absorbed and then re-radiated by the absorbing atom via several processes over a distance related to the energy absorption cross section.⁵⁵ What energy will ultimately be dissipated as heat (and where) depends on the details of electron–phonon coupling and is beyond the scope of this paper, however, a lower bound on the effect can be found by using the bulk energy absorption coefficient of lead.⁵⁵ This value leads to 0.014% of the photon energy being retained (and ultimately converted to heat) within a linear distance of 1 nm. This is equivalent to a temperature increase of 44 K, and since these processes occur on attosecond and femtosecond timescales this would be an adiabatic effect. Numbers are arguably higher if the real geometry is considered. Glass is a much weaker photon absorber, and the linear energy absorption coefficient is a factor of 40 or lower, so energy deposition is concentrated in the lead-rich regions. Thus in our system, where the Pb diffusion coefficient depends strongly on temperature, heating cannot be excluded over distances of a few nanometers and timescales of 10⁻¹⁰ s to 10⁻⁹ s. This may also explain the increased size and definition of PbS particles in the irradiated portion compared to the un-irradiated portion of the sample measured by TEM.

Kinetics of growth of Pb nanocrystals

The kinetics of crystallization of the Pb nanoparticles can be analyzed using the Avrami equation⁵⁷ where the volume fraction of the crystallized phase α(t) is given by

α(t) = 1 − exp[−Ktⁿ]

The constant K depends on details of the crystallites' growth rate and shape, and n, the “Avrami exponent”, has a theoretical value between 1 and 4 determined by the dimensionality of growth and whether growth is interface or diffusion limited. TEM images show that we have grown spherical particles to a good approximation. The crystalline volume fraction is therefore proportional to the cube of the particle radius R, and R can be determined directly from the SAXS data. For 3-dimensional growth, the Avrami exponent, n, may be described by

n = k + 3m

where the number of particles N ∼ t^k and the size of the crystallite ∼t^m. For nucleation followed by growth (zero nucleation rate), k = 0; for interface limited growth, m = 1; diffusion limited growth, m = 1/2.⁵⁸

The variation in the size of Pb nanoparticles, as determined by SAXS, follows the Avrami function to a good approximation and yields an Avrami exponent of 1.8 (±0.5), consistent with a fixed number of particles (zero nucleation rate) and diffusion-limited growth. This result is also qualitatively consistent with the observation that at the early stages we have a rather monodisperse distribution of particle sizes over a long annealing time.

Fig. 3 shows that there is no unlimited growth of the particles. After the initial growth, which the SAXS data show render a rather monodisperse Pb particle population, the growth rate slows down. This is accompanied by a broadening of the particle size distribution: the SAXS patterns show a slow drift of the form factor fringes to lower q values, i.e. particle growth, but accompanied by the scattering fringes becoming less pronounced, i.e. an apparent increase in polydispersity. This behaviour is consistent with an Ostwald ripening process in which the larger particles grow at the expense of smaller particles (see Fig. 3). Since we did not observe an increase in scattering intensity we can rule out further additions of Pb from the matrix. This does not necessarily indicate that the matrix is depleted in Pb²⁺, rather, it indicates that the matrix is depleted in Pb⁰. We suggest that the concentration of Pb⁰ is determined by the number of Pb²⁺ interactions with X-ray photoelectrons and the lifetime of these Pb⁰ atoms. The number, the lifetime and the diffusion rate determine if these atoms are available for further increasing the size of Pb particles, and it is not surprising that equilibrium between the Pb in the matrix and the Pb in particles is established.

Conclusions

In this present work we report that X-ray irradiation at elevated temperatures promotes the formation of metallic nanoparticulate Pb. Such particles cannot be formed in the glass by thermal annealing without irradiation and X-ray-promoted growth of Pb nanoparticles has not previously been reported to the best of our knowledge. The finding that irradiation by X-rays can lead to the formation of a monodisperse population of relatively large nanoparticles of Pb is a rather unexpected result. Our in situ SAXS measurements show that the growth of these particles is diffusion limited. We have demonstrated that there is no macroscopic heating of our samples by the beam, but note that the time-averaged photon power may be misleading when considering local transient effects arising from photon absorption. The small percentage of lead involved in this process suggests that either transient radiation induced defects or trace elements are involved in the process.

X-ray irradiation did not preclude the growth of nanoparticles of PbS in the irradiated area. A high-temperature annealing period in combination with irradiation has thus produced samples containing two distinct populations of nanoparticles. It is interesting to speculate that this phenomenon could be adapted to create functional materials.

Acknowledgements

The Netherlands Organisation for Scientific Research (NWO) and the Swiss-Norwegian beamlines are gratefully acknowledged for allowing access to their facilities at the ESRF. We thank Irina Snigireva, ESRF, for the scanning electron microscopy measurements. Eric Schaible is thanked for help with the experiments at the Advanced Light Source. Beamline 7.3.3 of the Advanced Light Source is supported by the Director of the Office of Science, Office of Basic Energy Sciences of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. Transmission electron microscopy experiments were performed at NCEM, which is supported by the Office of Science, Office of Basic Energy Sciences of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. Other colleagues at the ESRF, particularly Michael Wullf and Mark Newton, are thanked for their helpful discussion.

Notes and references

1. R. J. Davies, M. Burghammer and C. Riekel, Macromolecules, 2008, 41, 7251–7253.
2. H. D. Barth, E. A. Zimmermann, E. Schaible, S. Y. Tang, T. Alliston and R. O. Ritchie, Biomaterials, 2011, 32, 8892–8904.
3. J. M. Holton, J. Synchrotron Radiat., 2009, 16, 133–142.
4. V. Martis, S. Nikitenko, S. Sen, G. Sankar, W. van Beek, Y. Filinchuk, I. Snigireva and W. Bras, Cryst. Growth Des., 2011, 11, 2858–2865.
5. D. Tatchev, A. Hoell, M. Eichelbaum and K. Rademann, Phys. Rev. Lett., 2011, 106, 085702.
6. P. Innocenzi, L. Malfatti, T. Kidchob, S. Costacurta, P. Falcaro, B. Marmiroli, F. Cacho-Nerin and H. Amenitsch, J. Synchrotron Radiat., 2011, 18, 280–286.
7. A. Pinna, B. Lasio, M. Piccinini, B. Marmiroli, H. Amenitsch, P. Falcaro, Y. Tokudome, L. Malfatti and P. Innocenzi, ACS Appl. Mater. Interfaces, 2013, 5, 3168–3175.
8. J. G. Mesu, A. M. Beale, F. M. F. de Groot and B. M. Weckhuysen, J. Phys. Chem. B, 2006, 110, 17671–17677.
9. R. A. Mayanovic, A. J. Anderson, H. A. N. Dharmagunawardhane, S. Pascarelli and G. Aquilanti, J. Synchrotron Radiat., 2012, 19, 797–805.
10. V. I. Feldman, A. A. Zezin, S. S. Abramchuk and E. A. Zezina, J. Phys. Chem. C, 2013, 117, 7286–7293.
11. A. Merlino, M. R. Fuchs, A. Pica, A. Balsamo, F. S. N. Dworkowski, G. Pompidor, L. Mazzarella and A. Vergara, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2013, 69, 137–140.
12. G. N. George, I. J. Pickering, M. J. Pushie, K. Nienaber, M. J. Hackett, I. Ascone, B. Hedman, K. O. Hodgson, J. B. Aitken, A. Levina, C. Glover and P. A. Lay, J. Synchrotron Radiat., 2012, 19, 875–886.
13. E. F. Garman and R. L. Owen, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2006, 62, 32–47.
14. E. F. Garman, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2010, 66, 339–351.
15. H. Jain, J. Optoelectron. Adv. Mater., 2003, 5, 5–22.
16. A. Mhaisekar, M. J. Kazmierczak and R. Banerjee, J. Synchrotron Radiat., 2005, 12, 318–328.
17. S. D. Stookey, G. H. Beall and J. E. Pierson, J. Appl. Phys., 1978, 49, 5114–5123.
18. B. Capoen, A. Chahadih, H. El Hamzaoui, O. Cristini and M. Bouazaoui, Nanoscale Res. Lett., 2013, 8, 266.
19. G. Mattei, P. Mazzoldi and H. Bernas, Materials Science with Ion Beams, 2010, vol. 116, pp. 287–316.
20. J. Li, X. Y. Hu, Y. Gu and Q. H. Gong, Opt. Lett., 2010, 35, 4051–4053.
21. Y. Tang and W. L. Cheng, Langmuir, 2013, 29, 3125–3132.
22. G. Li and R. C. Jin, Acc. Chem. Res., 2013, 46, 1749–1758.
23. S. V. Kershaw, A. S. Susha and A. L. Rogach, Chem. Soc. Rev., 2013, 42, 3033–3087.
24. F. W. Wise, Acc. Chem. Res., 2000, 33, 773–780.
25. G. Kellermann and A. F. Craievich, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 054106.
26. J. A. Jimenez, M. Sendova and H. Liu, J. Lumin., 2011, 131, 535–538.
27. W. Bras, G. N. Greaves, M. Oversluizen, S. M. Clark and G. Eeckhaut, J. Non-Cryst. Solids, 2005, 351, 2178–2193.
28. W. Bras, S. M. Clark, G. N. Greaves, M. Kunz, W. van Beek and V. Radmilovic, Cryst. Growth Des., 2009, 9, 1297.
29. L. Malfatti, D. Marongiu, S. Costacurta, P. Falcaro, H. Amenitsch, B. Marmiroli, G. Grenci, M. F. Casula and P. Innocenzi, Chem. Mater., 2010, 22, 2132–2137.
30. S. Nikitenko, A. M. Beale, A. M. J. van der Eerden, S. D. M. Jacques, O. Leynaud, M. G. O'Brien, D. Detollenaere, R. Kaptein, B. M. Weckhuysen and W. Bras, J. Synchrotron Radiat., 2008, 15, 632–640.
31. W. Bras, I. P. Dolbnya, D. Detollenaere, R. van Tol, M. Malfois, G. N. Greaves, A. J. Ryan and E. Heeley, J. Appl. Crystallogr., 2003, 36, 791–794.
32. P. Alexander Hexemer, W. Bras, J. Glossinger, E. Schaible, E. Gann, R. Kirian, A. MacDowell, M. Church, B. Rude and H. Padmore, J. Phys.: Conf. Ser., 2010, 247, 012007.
33. C. Broennimann, E. F. Eikenberry, B. Henrich, R. Horisberger, G. Huelsen, E. Pohl, B. Schmitt, C. Schulze-Briese, M. Suzuki, T. Tomizaki, H. Toyokawa and A. Wagner, J. Synchrotron Radiat., 2006, 13, 120–130.
34. A. P. Hammersley, S. O. Svensson, M. Hanfland, A. N. Fitch and D. Hausermann, High Pressure Res., 1996, 14, 235–248.
35. J. Kohlbrecher, SASfit, Paul Scherrer Institute, Laboratory for Neutron Scattering, CH-5232 Villigen PSI, Switzerland.
36. C. Broennimann, Dectris Ltd., https://www.dectris.com.
37. M. H. F. Overwijk, F. C. van den Heuvel and C. W. T. Bulle-Lieuwma, J. Vac. Sci. Technol. B, 1993, 11, 2021.
38. A. Cumming, P. Wiltzius and F. S. Bates, Phys. Rev. Lett., 1990, 65, 863–866.
39. S. Maruno and T. Kawaguchi, J. Appl. Phys., 1975, 46, 5312–5314.
40. N. Yoshida and K. Tanaka, J. Appl. Phys., 1995, 78, 1745–1750.
41. J. W. Sheng, K. Kadono and T. Yazawa, J. Non-Cryst. Solids, 2003, 324, 295–299.
42. S. Reibstein, D. Möncke, J. Herbst, D. Schumacher, A. Höll and L. Wondraczek, presented in part at the 12th International Conference on the Structure of Non-crystalline Materials (NCM12), Riva del Garda, Italy, 2013.
43. M. Eichelbaum, K. Rademann, A. Hoell, D. M. Tatchev, W. Weigel, R. Stosser and G. Pacchioni, Nanotechnology, 2008, 19, 135701.
44. P. G. Ferreira, D. de Ligny, O. Lazzari, A. Jean, O. C. Gonzalez and D. R. Neuville, Chem. Geol., 2013, 346, 106–112.
45. J. Zhang and J. Sheng, Opt. Mater., 2013, 35, 1138–1140.
46. S. Vahedi, G. Okada, B. Morrell, E. Muzar, C. Koughia, A. Edgar, C. Varoy, G. Belev, T. Wysokinski, D. Chapman and S. Kasap, J. Appl. Phys., 2012, 112, 073108.
47. A. Corrias, personal communication.
48. I. A. Shkrob, B. M. Tadjikov and A. D. Trifunac, J. Non-Cryst. Solids, 2000, 262, 6–34.
49. I. A. Shkrob and V. F. Tarasov, J. Chem. Phys., 2000, 113, 10723–10732.
50. D. S. Whittaker, E. Wagenaars and G. J. Tallents, Phys. Plasmas, 2011, 18, 103116.
51. D. S. Whittaker, E. Wagenaars and G. J. Tallents, Phys. Plasmas, 2011, 18, 013105.
52. Fitch, International Tables for Crystallography.
53. T. Xie, L. L. Bai, J. Y. Liu, G. Q. Zhao, X. H. Sun and J. Zhong, Carbon, 2013, 56, 385–388.
54. C. X. Zhao, Y. F. Li, Y. C. Chen, J. Q. Wu, B. Wang, F. T. Yi, S. Z. Deng, N. S. Xu and J. Chen, Nanotechnology, 2013, 24, 275703.
55. J. H. Hubbell and S. M. Seltzer, NIST: X-Ray Mass Attenuation Coefficients, http://www.nist.gov/pml/data/xraycoef/.
56. W. E. Schiesser, The numerical method of lines : integration of partial differential equations, Academic Press, London, 1991.
57. I. Gutzow and J. Schmelzer, The Vitreous State: Thermodynamics,Structure, Rheology and Crystallization, Springer, Berlin, 1995.
58. V. M. Fokin, E. D. Zanotto, N. S. Yuritsyn and J. W. P. Schmelzer, J. Non-Cryst. Solids, 2006, 352, 2681–2714.

---

Footnote

† Electronic supplementary information (ESI) available: SEM image of the annealed sample and EXAFS characterization. See DOI: 10.1039/c4ce00937a

---