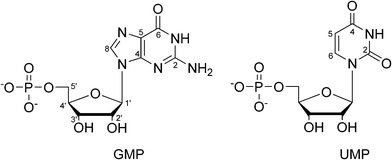
Dynamics of water molecules and sodium ions in solid hydrates of nucleotides

Abstract

Nuclear magnetic resonance experiments, together with molecular dynamics simulations and NMR calculations, are used to investigate mobility of water molecules and sodium ions in solid hydrates of two nucleotides. The structure of guanosine monophosphate system (GMP) is relatively rigid, with a well-ordered solvation shell of the nucleotide, while the water molecules in the uridine monophosphate system (UMP) are shown to be remarkably mobile, even at −80 °C. The disorder of water molecules is observed in the ¹³C, ³¹P, and ²³Na solid-state NMR experiments as multiple signals for equivalent sites of the nucleotide corresponding to different local arrangements of the solvation shell. Deuterium NMR spectra of the samples recrystallized from D₂O also confirm differences in water mobility between the two systems. The experiments were complemented with NMR calculations on an ensemble of structures obtained from DFT molecular dynamics (MD) simulations. The MD simulations confirmed higher water mobility in the UMP system and the calculated chemical shifts and quadrupolar couplings were consistent with the experimental data. The disordered solvation shell in UMP is likely to be a good model for solvated nucleotides in general, with fast reorientation of water molecules and fluctuations in the hydrogen-bond network.

---

Introduction

A thorough description of the structure of the solvent shells surrounding nucleic acid (NA) systems is important for understanding most molecular recognition processes, ranging from sequence-specific DNA recognition^1–4 to drug–nucleic acid interactions^5–7 and DNA conduction. The stability and conformational flexibility of nucleic acids are due largely to interactions with the aqueous surroundings,^8,9 while localized structural water molecules effectively extend specific nucleic acid structures around the groove regions of multistranded nucleic acids.^8,10 The development of an adequate description of the hydration and electrostatic properties of the highly charged nucleic acids is thus essential for future modelling of nucleic acid structures.⁸

Because RNA and DNA are polyanions, their structure and biological function depends strongly on their association with metal ions. However, the dynamic non-covalent nature of these interactions has continually presented challenges to the development of accurate and quantitative descriptions.¹¹ Metal ions are involved in almost every aspect of nucleic acid chemistry, ranging from neutralization of the anionic nucleic acids¹² through specific stabilization of three-dimensional structures of NA molecules up to their effect as cofactors in RNA-mediated catalysis.¹³

Several spectroscopic methods have been employed in recent years to study the structures of hydrated ions and their aqueous environment.¹⁴ Although hydration patterns are difficult to study directly, techniques such as dielectric¹⁵ and terahertz¹⁶ spectroscopy, fluorescence labelling,¹⁷ optical spectroscopies,^18,19 and nuclear magnetic resonance²⁰ have revealed important information about the interaction of biomolecules with water in solutions, such as the number of water molecules in the first solvation shell, the affinity of water molecules for different groups, and the strength of the intermolecular hydrogen-bond interactions. However, the solvation shell dynamics are difficult to assess by these techniques.

The three-dimensional structure determinations of biological macromolecules, such as proteins and nucleic acids, by X-ray crystallography have significantly improved our understanding of biological processes. However, since it is very hard to identify hydrogen atoms accurately using X-ray diffraction, a detailed discussion of protonation and hydration sites can only be speculated upon so far.²¹ Direct detection of light alkali metal ions by diffraction techniques is also challenging, especially for sodium cations, because their X-ray scattering contributions are virtually identical to those of water, and Na⁺⋯O distances are only slightly shorter than strong hydrogen bonds between well-ordered water molecules.²² This often renders it impossible to identify Na⁺ ions, even with state-of-the-art diffraction techniques.

Here, we present a multinuclear NMR investigation of two hydrates of sodium salts of nucleotides (depicted in Fig. 1), namely disodium guanosine-5′-phosphate heptahydrate (GMP) and disodium uridine-5′-phosphate heptahydrate (UMP). These two systems represent typical examples of solid forms of nucleotides, which generally crystallise in the form of hydrates. Because of the high water content in the crystal lattice, they also represent a simple model of solvated nucleotides. Three crystal structures of GMP, all derived for data obtained at ambient temperature, have been deposited in Cambridge crystallographic structural database (CSD): GUOPNA01, GUOPNA10,²³ and GUOPNA11.²⁴ GUOPNA11 is re-analysis of GUOPNA01, where no hydrogen atoms were positioned. There are two non-equivalent molecules of GMP in the asymmetric unit (Z′ = 2). These have almost identical conformation, but differ in the arrangement of the surrounding solvent shell. The position of all water oxygen sites and sodium ions was determined by the X-ray analyses, and no disorder in the oxygen sites was observed. However, only 20 and 23 out of 28 water hydrogen atoms were located from a difference Fourier map in the GUOPNA10 and GUOPNA11 structures, respectively. The structures of GUOPNA10 and GUOPNA11 differ in hydrogen positions, most importantly the ribose O2′–H orientation, leading to a slightly different hydrogen-bonding network in the two crystal structures (see Fig. S1 in ESI†). Because of the structural uncertainty, we redetermined the GMP structure at 120 K by X-ray diffraction. The ²³Na MQMAS spectrum of GMP has been reported, and shows four spectral regions, consistent with the four distinct Na⁺ sites observed by X-ray analysis. Quadrupolar coupling constants and asymmetry parameters were extracted from the MQMAS spectra and assigned to individual Na⁺ sites on the basis of a simple correlation between C_Q and the number and type of surrounding ligands.²⁵ Similar tentative assignments of sodium signals have been done also for other sodium salts of nucleotides.^26,27

Fig. 1 Structure of the studied nucleotides with atom numbering.

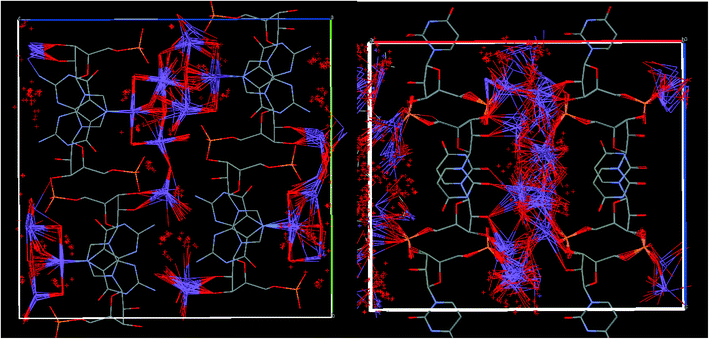
In contrast, a high degree of disorder of sodium ions and water molecules was observed in the crystal structure of UMP (CSD code SURIPH10, Fig. 2).²⁸ The nucleotide molecules form layers, and the disordered water molecules and sodium ions are located in channels between the UMP molecules, which are equivalent (Z′ = 1) according the X-ray analysis. This disordered aqueous layer might reasonably serve as a model of the solvation shell of nucleotides in solution.

Fig. 2 Left: crystal structure of UMP (SURIPH10 structure²⁸) – water molecules and sodium ions are disordered in the channel formed by the nucleotide molecules; right: crystal structure of GMP determined in this work.

By applying multiple NMR techniques, together with molecular dynamics (MD) and DFT calculations of NMR parameters, we investigate the nature of the disorder in the UMP crystal structure. Density functional theory molecular dynamics (DFT-MD) provides insight into the structure and dynamics of the nucleotide solvation shells. It has been demonstrated that DFT-MD simulations are superior to classical force-field simulations when modeling hydration shells of polar molecules; DFT-MD provided more structured solvation shells, and NMR calculations based on the DFT-MD simulations were in very good agreement with experiment.^20,29,30 The combination of NMR experiments with theoretical calculations makes it possible to connect experimental observations with structural and dynamic characteristics of the studied systems.

Methods

The samples of GMP and UMP were obtained from Sigma-Aldrich and recrystallized from H₂O and D₂O mixtures with methanol, ethanol or acetone. The content of crystal water molecules was determined by elemental analysis (ESI†) and it differed only slightly, in the range 6.5–7 water molecules per nucleotide, depending on the crystallisation conditions. ¹³C CP MAS spectra of the UMP samples recrystallized from different solvent mixtures were virtually identical.

Crystal data for GMP were collected at 120 K on an Agilent Gemini S-Ultra diffractometer (ω-scan, 0.5° per frame) yielding 9320 independent reflections (R_merg = 0.1005). The structure was solved by direct method and refined by full-matrix least squares on F² for all data using SHELXTL³¹ and OLEX2 (ref. 32) software. The crystal data and experimental details are summarized in the ESI.† All non-hydrogen atoms were refined with anisotropic displacement parameters. H-atoms were placed into the calculated (OLEX2) positions and refined in riding mode. Final wR₂(F²) = 0.2118 for all data (609 refined parameters), conventional R₁(F) = 0.0794 for 6470 reflections with I ≥ 2σ, GOF = 1.029. Crystallographic data for the structure have been deposited with the Cambridge Crystallographic Data Centre as supplementary publication CCDC-987999.

High-resolution ²H, ¹³C, and ³¹P solid-state NMR spectra were obtained using a Varian/Chemagnetics InfinityPlus spectrometer operating at 76.7 MHz for ²H, 125.7 MHz for ¹³C, 202.3 MHz for ³¹P, and 499.7 MHz for ¹H and/or a Bruker Avance III spectrometer operating at the same frequencies. Samples were packed into 4 or 5 mm magic angle spinning rotors and measurements taken using a MAS rate of 10 kHz using cross polarisation (¹³C, ³¹P) or direct excitation (²H). No correction was made to the set temperatures to correct for the frictional heating of the sample under sample spinning. Variable temperature experiments were done at low temperatures first, to minimise the dehydration of the samples. ¹H and ²H T₁ (spin–lattice) relaxation times were determined directly in ¹H/²H spectra using a series of saturation recovery experiments with 10 kHz MAS (saturation used: 1000 π/2 pulses separated by 1 ms delay). While showing some interesting trends, the relaxation data could not be interpreted with great confidence; the results and discussion can be found in the ESI.†²³Na MQMAS spectra were acquired using a Varian VNMRS 400 spectrometer operating at 105.78 MHz for ²³Na. A two-pulse plus z-filter version of the experiment was used, with a 0.2 s recycle delay, 10 kHz spin rate and 256 increments in the indirectly detected dimension. The typical CP conditions used were: recycle delay 4 s, contact time 2 ms, acquisition time 40 ms. Carbon-13 spectra were referenced with respect to external neat tetramethylsilane by setting the high-frequency signal from a replacement sample of adamantane to 38.5 ppm. Phosphorus spectra were referenced with brushite (δ = 1 ppm), deuterium spectra with D₂O (δ = 4.8 ppm), and sodium spectra with solid NaCl (δ = 0 ppm). Spinning sideband analysis using iterative fitting of the full ²H and ³¹P spectra was performed in Gsim³³ and pNMRsim³⁴ programs.

The NMR tensors of the infinite crystals were calculated by the CASTEP program,³⁵ version 6.0, which is a DFT-based code. Electron-correlation effects were modeled using the generalized gradient approximation of Perdew, Burke, and Ernzerhof.³⁶ For the atomic position optimization, we employed ‘on-the-fly’ pseudopotentials, a planewave cutoff energy of 600 eV, with integrals taken over the Brillouin zone using a Monkhorst–Pack³⁷ grid with a minimum k-point sampling of 0.05 Å⁻¹. The NMR calculations were performed using the GIPAW approach^38,39 at a larger cutoff of 900 eV.

To better understand the mobility of the solvation shells in both structures, molecular dynamics (MD) was performed at high temperature, followed by optimizations of geometry snapshots from the MD runs. Our X-ray diffraction structure of GMP was used as the starting structure for the MD simulation of this system. The SURIPH10 structure from CSD was used for UMP, after manually adding sodium ions and water molecules into the positions with the highest residual electron density, and consistent with sodium ions being five- or six-coordinated to water or nucleotide oxygens. The starting UMP structure (depicted in Fig. S2, fractional coordinates in ESI†) was then optimised. This partially random generation of the initial structure does not necessarily lead to the global energy minimum, but the potential energy equilibrated quickly at the beginning of the MD simulation, which indicates that the structure was suitable for the simulation. Born–Oppenheimer molecular dynamics (BOMD) simulations were run in CASTEP using an NVT ensemble maintained at a constant temperature of 1000 K using a Langevin thermostat, a 0.5 fs integration time step, ultrasoft pseudopotentials,⁴⁰ a planewave cutoff energy of 300 eV, and with integrals taken over the Brillouin zone using a Monkhorst–Pack³⁷ grid of a minimum k-point sampling of 0.1 Å⁻¹. The MD parameters were tested with respect to the convergence of atomic forces; an increase of the cutoff energy or k-point sampling led to changes in the calculated forces lower than 0.1 eV Å⁻¹. The lattice parameters and the positions of the nucleotide molecules were fixed to the experimental values, and so no dispersion corrections were required to maintain cell volumes during the MD simulations. No symmetry constraints were applied during the runs. Simulation runs of 5 ps were performed for both compounds. 23 geometries were selected at 0.6, 0.8, 1.0…5.0 ps of each run for geometry optimisation. The five lowest energy optimised UMP structures (differing by less than 1 eV per unit cell from the lowest energy) were used for NMR calculations (see Fig. S3 in the ESI†).

Results

X-ray

The lattice parameters and positions of heavy atoms of the redetermined crystal structures of GMP and UMP disodium salts heptahydrates were in good agreement with the previous crystal structures. No disorder was observed in the GMP structure measured at 120 K, and all hydrogen atoms could be located. The ribose O2′–H orientation was identical to that of GUOPNA10 structure. However, the positions of water molecules and sodium ions in the UMP structure could not be determined because of the disorder.

NMR

Two signals corresponding to the two non-equivalent molecules of GMP are present in the ³¹P NMR spectra in the temperature range −40 to 40 °C together with a third signal, which corresponds to a dehydrated form (Fig. 3). The signal assignment is based on CASTEP calculations (see below). The phosphate group P1 and P2 are acceptors of 9 and 10 hydrogen bonds, respectively. When the sample was left at 40 °C, the intensity of the two GMP signals steadily decreased while the intensity of the signal of the dehydrated form increased (Fig. S4†). The chemical shifts of the GMP signals are noticeably temperature dependent. The temperature shift is reversible and so is not associated with the dehydration. The ³¹P chemical shift anisotropy estimated from spinning side band patterns is ca. 60 ± 10 ppm and the asymmetry, η, is close to 0.1. The small value of the anisotropy is not surprising given the close-to-tetrahedral geometry of the phosphate groups. The estimated error of the anisotropy is relatively high due to the limited number of spinning sidebands associated with this small CSA, although quantification is still possible in this limit⁴¹ (see Fig. S5† for an illustration).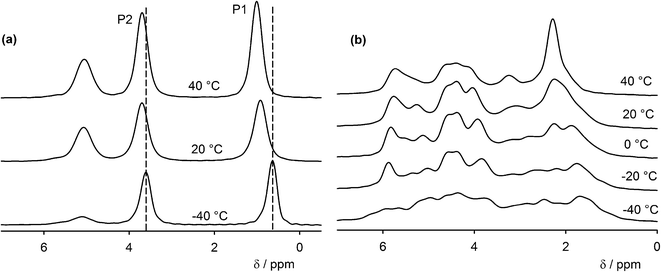

Fig. 3 (a) Variable temperature ³¹P CP-MAS NMR spectra of GMP. The signal at 5 ppm belongs to the dehydrated form. (b) Variable temperature ³¹P CP-MAS NMR spectra of UMP. The dashed lines are guides for the eye to follow the temperature changes. Centre-bands only are shown; complete spectra are in the ESI† (Fig. S6).

On the other hand, much more complicated ³¹P NMR spectra were observed for UMP. X-ray crystallography determined Z′ to be 1, which should lead to a single phosphorus signal in the spectra, but at −40 °C we observed a broad distribution of phosphorus signals between 1 and 6.5 ppm. With increasing temperature, the spectrum becomes narrower, but at least seven phosphorus sites can still be distinguished at 40 °C. The spectral narrowing is reversible, but the sample dehydrates irreversibly at temperatures above 40 °C. The observation of more than one phosphorus signal may be explained by the disorder of the water molecules and sodium ions in the channels between the UMP molecules; different positions and orientations of the water and sodium will influence the phosphorus chemical shift of the phosphate group and individual signals for each geometry will be observed if the rate of exchange between different local geometries is slow. The relative intensities of the spinning side bands were similar to those of the GMP crystals, i.e. the chemical shift anisotropy is similar for all phosphorus sites in both samples.

¹³C cross-polarization (CP) magic-angle spinning (MAS) NMR is an efficient method for crystal structure characterization, including determining Z′ by means of comparing the number of observed resonances with the number of nonequivalent carbon atoms present in the molecule.^42,43 Similarly to the ³¹P spectra, two sets of signals corresponding to the two non-equivalent GMP molecules accompanied by one set of signals of the dehydrated form were observed in the ¹³C NMR spectra of GMP in a broad temperature range (−80–40 °C), and a distribution of signals was observed in carbon spectra of UMP (Fig. 4 and S7†). The UMP signals start to merge into one set of signals at 40 °C, but dehydration occurs at higher temperatures. It is likely that the spectrum at 40 °C is close to the fast exchange limit. However, the narrow range of NMR frequencies spanned by a given site (of the order of 200 Hz) means that the exchange rates are low in absolute terms, and the barriers involved must, therefore, be relatively high. It is, therefore, unsurprising that the fast-exchange limit is not reached for all the ³¹P resonances at 40 °C, Fig. 3(b), since these span a significantly larger range of frequencies (about 1200 Hz). It is clear from the ³¹P spectrum, however, that multiple sites and effective barriers are involved, with the fast exchange regime for different sites being reached at different temperatures.

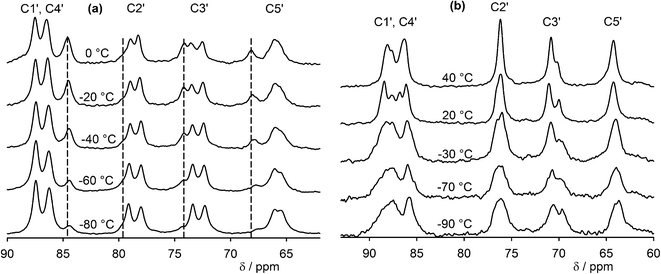Fig. 4 Variable temperature ¹³C CP-MAS spectra (ribose region) of (a) GMP (dashed lines indicate the dehydrated form) and (b) UMP. See Fig. 1 for atom numbering. The aromatic regions of the spectra are shown in the ESI (Fig. S7).

The sodium MQMAS spectrum of GMP at −70 °C (Fig. 5) is similar to the spectrum reported previously.²⁵ At room temperature the signals broaden and start to merge indicating that the sodium ions may be able to exchange their positions in the crystal structure, although there is also likely be broadening associated with relatively slow dynamics on the order of the MAS frequency (10 kHz).^44,45 Again, the ²³Na MQMAS spectrum of UMP exhibits more signals than the two expected from the crystal structure, and broadening of the signals is apparent at room temperature. It is noticeable, however, that the room temperature spectrum shows evidence of two broad features, although the highly disordered nature of the Na environments observed by XRD means these cannot be linked in an obvious way to the crystal structure.

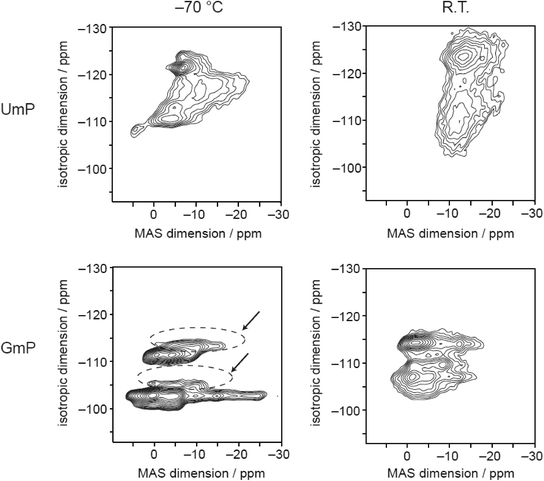Fig. 5 ²³Na MQMAS spectra of UMP and GMP; the signals of the dehydrated form of GMP are indicated by dashed circles and arrows.

Some care is required when interpreting the deuterium spectra of the nucleotides crystallised from D₂O since these also contain signals from exchangeable protons i.e. 2 ribose–OH groups and 3 (GMP) or 1 (UMP) amine/amide hydrogens. Moreover many, if not all, of these sites will be undergoing chemical exchange via the hydrogen bonding network. The dominant signal in the ²H MAS spectrum of UMP–D₂O is remarkably narrow (only a few spinning side bands are observed), and decreasing the temperature to −80 °C does not lead to significant changes. This is most likely to be a single signal arising from the water + ribose OH hydrogens; there is evidence, see Fig. S8,† of a weak shoulder around 10 ppm which can be tentatively assigned to the uridine NH. It is likely that the exchange between the 14 water and 2 ribose hydrogens is sufficiently fast (compared to the quadrupolar interactions) for a single averaged set of quadrupolar parameters (dominated by those of the water) to be observed. The experimental parameters obtained by spectral fitting (Fig. 6) are C_Q = 35 ± 1 kHz, η = 0.52 ± 0.10 at 22 °C, and C_Q = 38 ± 1 kHz and η = 0.25 ± 0.10 at −80 °C. Typical values of the ²H quadrupolar coupling constant in various “rigid” solids varies from 160 to 340 kHz with 0 ≤ η ≤ 0.15 and the spectra thus indicate that the water molecules in UMP–D₂O are highly mobile over the whole temperature range and the rate of water reorientation is on the order of hundreds of kHz or higher.⁴⁶ The degree of dynamic disorder at −80 °C is surprising; only a modest broadening associated with some slowing of dynamics is observed. Presumably the water molecules are effectively in a metastable state, with multiple low energy barriers, and are unable to settle into a well-defined energetic minimum. The GMP–D₂O sample proved difficult to obtain and sensitive to dehydration; the partial results obtained are presented in Fig. S9† and associated discussion in the ESI.†

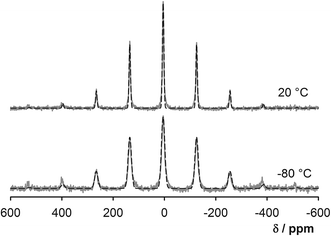Fig. 6 Experimental ²H MAS spectra (MAS rate 10 kHz) of UMP at 20 °C and −80 °C (grey solid lines) and simulated spectra (black dashed lines).

Molecular dynamics

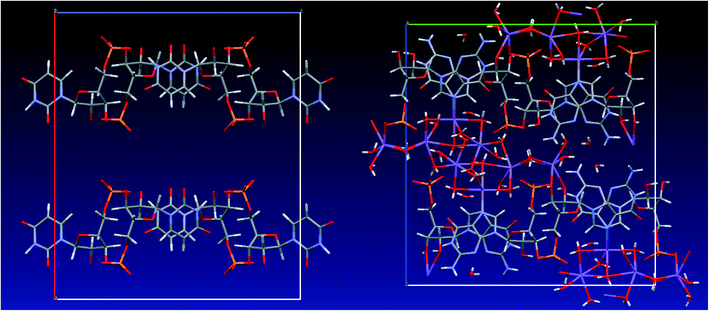
We estimated above the frequency of some of the exchange processes in the UMP crystal to be in the order of several hundreds of Hz from the carbon and phosphorus variable temperature NMR spectra (in addition to very fast dynamics observed via T₁ relaxation, see ESI†). This time scale is beyond the reach of classical or DFT molecular dynamics, with typical simulation lengths in nanosecond or picosecond time scale, respectively. Therefore, we performed an “unphysical” DFT molecular dynamics simulations at high temperature (1000 K) and with fixed positions of the nucleotide atoms. Geometry snapshots from these MD simulations were optimised and then the structures and energies were compared. Hence, the unphysical MD served as a tool for generating local energy minima structures rather than for providing exchange rates of the slow dynamics. We have applied a similar strategy recently for prediction of vibrational frequencies of liquid water and fused silica.⁴⁷ Other methods, such as Monte Carlo simulations, might be used for this purpose, but the resulting structure ensemble is expected to display similar structural characteristics.

In the case of GMP, all the generated structures had a similar arrangement of the sodium ions and water molecules, including the overall hydrogen-bonding network (see Fig. 7), which means that the solvation shell lies in a deep potential energy well and no other local energy minima were accessed by the MD simulation. On the other hand, the generated UMP structures differ significantly, with sodium ions and water molecules occupying different positions in the channels formed by the nucleotide molecule.

Fig. 7 Overlay of 23 snapshots from MD simulation after geometry optimisation of GMP (left) and UMP (right). Colour coding: carbon – grey, nitrogen – blue, oxygen – red, phosphorus – yellow, sodium – magenta.

In the course of the MD simulations of UMP, we observed continuous reorientation of water molecules leading to different structures of the hydrogen-bond network in the geometry snapshots. Occasionally, individual water molecules moved between coordination spheres of the surrounding sodium ions, i.e. the shortest Na⋯O distance connected a given water molecule with different sodium atoms in the course of the simulation. However, the simulations were not sufficiently long for individual water molecules to explore the whole space in the nucleotides' channels; the average RMSD of the water oxygen and sodium atom positions from the starting structure was 2.11 and 1.96 Å, respectively (compared to the much smaller RMSDs of 0.88 and 0.91 Å, respectively, observed for the GMP system).

The limited length of the MD simulations may lead to insufficient sampling of the configurational space and other low energy minima might be missing in the ensemble, and the unphysical nature of the simulations limit the scope for quantitative analysis. We can, however, clearly see differences in the dynamic behaviour of the two systems, which reflect the results of the diffraction experiments, i.e. the solvation shell in the GMP crystal is regularly ordered, whereas sodium atoms and water molecules in the UMP crystal can be found in different arrangements, leading to the inability of the diffraction experiments to describe the UMP solvation shell.

NMR calculations

NMR parameters were calculated for the initial geometry-optimized GMP structure. The difference between the calculated chemical shifts of the two non-equivalent phosphorus atoms is 4.7 ppm and the calculated chemical shift anisotropy is 65 ppm for both phosphorus sites, which is in reasonable agreement with the experimental values (3.0 ppm chemical shift difference at −40 °C, CSA ca. 60 ppm). The good agreement of the experimental CSA with the CSA calculated for geometry optimized (static) structure indicates little dynamics of the phosphate groups, providing some justification for fixing the phosphate groups in the MD simulations. The calculated sodium quadrupolar coupling constants also agree well with the experimental values, but the assignment differs from that published previously on the basis of a simple correlation between C_Q and ion-binding geometry.²⁵ The largest calculated quadrupolar coupling constant is found for one of the sodium atoms coordinated to six water molecules, while the largest experimental coupling was tentatively assigned to the sodium atom coordinated to four water molecules and two nitrogen atoms (see Table 1). The experimental ²³Na chemical shifts cover too narrow a range (about 4 ppm) for the calculated Na shieldings to provide useful additional information.

Table 1 Experimental and calculated ²³Na quadrupolar coupling constants in GMP

Sodium site	Na coordination^a	C Q,calc/MHz	C Q,exp/MHz^b
a W – water molecule; OH – ribose hydroxyl group; N – guanine nitrogen atom N7. b The experimental values are from ref. 25 (uncertainties not given), but our assignment based on CASTEP calculations interchanges the quadrupolar couplings of Na3 and Na4.
Na1	4W,2OH	1.44	1.30
Na2	6W	1.67	1.85
Na3	6W	2.27	2.30
Na4	4W,2N	1.75	1.85

---

We also calculated NMR parameters for the five lowest energy optimised geometry snapshots from the MD simulations of UMP. The limited length of the MD simulation and the number of NMR calculations is partly compensated by the size of the unit cell (eight nucleotide molecules, 16 sodium ions, and 56 water molecules). No symmetry constraints were applied during the simulations, therefore the structure of the solvation shell of the eight nucleotide molecules differed, and so the nucleotide ³¹P NMR parameters were averaged for 40 local solvation arrangements. Importantly, the NMR data (span of chemical shifts and averaged quadrupolar couplings) calculated for the individual optimised snapshot geometries are qualitatively consistent with the results averaged for the five structures. For example, the calculated phosphorus chemical shifts are distributed over similar ranges in the five snapshots (see Table S1 in ESI†), i.e. increasing the number of structures for NMR calculation is unlikely to change the qualitative picture significantly. We do not see any clear correlation between the calculated phosphorus chemical shifts and the hydration pattern (number of hydrogen bonds or number of sodium ions in close vicinity) of the phosphate group.

The calculated phosphorus chemical shift anisotropy is found in the range of 55–66 ppm and is almost unaffected by the dynamics, i.e. the shielding tensor of one phosphorus site averaged over the five optimised structures is very close to the individual CSA tensors. Carbon chemical shifts of individual sites were distributed over 2.8–9.0 ppm with the narrowest distribution for carbon C4, which had also the narrowest line in experimental spectra, and the broadest distribution for carbon atoms C5 and C6, which have also the broadest experimental signal (see Fig. S7 in ESI†). The convergence of the carbon chemical shift spans with the number of geometry snapshots is illustrated in Fig. S10.†

The calculated deuterium quadrupolar couplings of the water hydrogens in the five optimised UMP structures can be found in a broad range 130–290 kHz, which is much more than the experimental value of 35–38 kHz. As we have previously demonstrated, fast vibrational/librational motion in “rigid” solids leads to reduction of chemical shift anisotropy and quadrupolar couplings by only a few per cent and cannot thus explain this difference between calculated and experimental deuterium quadrupolar couplings.⁴⁸ When electric field gradient tensors of the hydrogen atoms in individual water molecules are averaged (i.e. assuming fast C₂ jumps of water), the quadrupolar couplings of the 56 nonequivalent water molecules are reduced to ca. 100–150 kHz. On the other hand, when the electric field gradient tensors of all water hydrogen atoms in each of the five individual optimised structures are averaged, the resulting range of deuterium quadrupolar coupling constants is 25–31 kHz (η = 0.07–0.47), which agrees much better with the experimental value. This agreement confirms the high mobility of the water molecules. When EFG tensors of the ribose OH hydrogens are averaged together with all water protons (assuming that site exchange is fast compared to the quadrupolar couplings), the calculated quadrupolar couplings are reduced by further ca. 10 kHz.

The experimental sodium spectra of UMP are too complex to compare with the calculations directly, and there was no evidence in the calculation results of two average Na environments that appear to be observed in the room temperature MQMAS spectrum. It is likely that the CASTEP calculations are not sufficiently robust for ²³Na shifts to try to explain rather subtle features of the experiment, because the shift range is quite narrow. From the inspection of the MQMAS spectra it can be expected that the experimental sodium quadrupolar couplings will be of the same order as in the case of GMP, i.e. a few MHz. When calculated EFG tensors of the individual sodium sites are averaged for the five UMP structures, the resulting 16 sodium quadrupolar couplings are in the range 0.9–2.4 MHz, which is in a qualitative agreement with the experiment. On the other hand, when the EFG tensors of all sodium sites are averaged, the calculated quadrupolar coupling is close to 0.4 MHz, which would lead to much narrower sodium spectra. This is in agreement with the distribution of chemical shifts observed experimentally.

Conclusions

Significant differences in the NMR spectra of UMP and GMP systems were observed. The ¹³C and ³¹P spectra of GMP are consistent with the crystal packing found by X-ray diffraction (Z′ = 2). On the other hand, the splitting of carbon, phosphorus, and sodium spectra of UMP into multiple sets of signals is not consistent with one nucleotide molecule in the asymmetric cell (Z′ = 1) found by X-ray diffraction experiments. Furthermore, the overall width of the deuterium MAS spectrum of UMP is significantly narrower than that of GMP, which can be explained by high water mobility in this system. The narrow deuterium MAS spectrum was observed even at −80 °C.

The presented NMR experiments prove major differences in the dynamics of the solvation shell in the two studied systems. Water molecules and sodium ions are relatively rigid in the GMP structure, while they are very mobile in the UMP system, even at temperatures far below 0 °C. The disordered channels in the UMP crystals could be described as a rubbery state, with increasing thermal energy turning previously static disorder into dynamic disorder. The variable temperature NMR spectra of the UMP system exhibit continuous changes of the spectral parameters (chemical shifts, relaxation times, and quadrupolar coupling constants), which confirms the existence of multiple local arrangements of the UMP solvation with a slow interconversion between them. The energy barriers involved in the interconversions have probably a broad distribution; different energy barriers are overcome at different temperatures leading to continuous changes of the spectra.

The differences in the dynamic behaviour of the two systems are further confirmed by the MD simulations and NMR calculations. The structure of the GMP solvation layer was stable, even at the unphysical MD simulation at 1000 K. On the other hand, the MD simulation of the UMP system led to continuous changes in the hydrogen-bond network and the structure of the solvation shell. The spans of carbon and phosphorus chemical shifts calculated for the ensemble of structures exctracted from the UMP simulation were in qualitative agreement with the experiments. The short time of the simulation did not allow the water molecules to explore the whole configurational space, but when the calculated deuterium electric field gradient tensors of all water hydrogen atoms were averaged, the resulting deuterium quadrupolar coupling agreed well with the experimental value.

The method of generation of the ensemble of structures of disordered solvation shell by molecular dynamics simulation at high temperature within a fixed host structure, is a straightforward way of finding different local minima on the potential energy hypersurface (similar to simulated annealing). However, the MD method cannot be used for a quantitative interpretation of the dynamics of the system, because the simulations were performed at unphysical conditions.

The disordered solvation shell in UMP is probably close to the situation in solution with fast reorientation of water molecules and fluctuations in the hydrogen-bond network. The combination of X-ray diffraction and NMR experiments with MD simulations and calculations of NMR parameters can thus provide detailed information on the solvation shell dynamics on a molecular level.

Acknowledgements

The research leading to these results has received funding from the People Programme (Marie Curie Actions) of the European Union's Seventh Framework Programme (FP7/2007–2013) under REA grant agreement no. 299242. The work has been also supported by the Czech Science Foundation (grant no. 13-24880S). ²³Na MQMAS experiments were provided by David C. Apperley through the EPSRC UK National Solid-state NMR Service at Durham, and the X-ray diffraction experiments were done by Dmitry S. Yufit.

References

1. Z. Otwinowski, R. W. Schevitz, R. G. Zhang, C. L. Lawson, A. Joachimiak, R. Q. Marmorstein, B. F. Luisi and P. B. Sigler, Nature, 1988, 335, 321–329.
2. F. Spyrakis, P. Cozzini, C. Bertoli, A. Marabotti, G. E. Kellogg and A. Mozzarelli, BMC Struct. Biol., 2007, 7.
3. A. Furmanchuk, O. Isayev, O. V. Shishkin, L. Gorb and J. Leszczynski, Phys. Chem. Chem. Phys., 2010, 12, 3363–3375.
4. C. R. Robinson and S. G. Sligar, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 2186–2191.
5. B. Jayaram and T. Jain, Annu. Rev. Biophys. Biomol. Struct., 2004, 33, 343–361.
6. N. G. Walter, Mol. Cell, 2007, 28, 923–929.
7. P. Auffinger and Y. Hashem, Curr. Opin. Struct. Biol., 2007, 17, 325–333.
8. E. Westhof, Annu. Rev. Biophys. Biophys. Chem., 1988, 17, 125–144.
9. W. Saenger, Annu. Rev. Biophys. Biophys. Chem., 1987, 16, 93–114.
10. H. R. Drew and R. E. Dickerson, J. Mol. Biol., 1981, 151, 535–556.
11. Nucleic Acid-Metal Ion Interactions, ed. N. V. Hud, Royal Society of Chemistry, Cambridge, 2009.
12. J. J. Howard, G. C. Lynch and B. M. Pettitt, J. Phys. Chem. B, 2011, 115, 547–556.
13. J. Müller, Metallomics, 2010, 2, 318–327.
14. Y. Marcus, Chem. Rev., 2009, 109, 1346–1370.
15. A. Oleinikova, P. Sasisanker and H. Weingartner, J. Phys. Chem. B, 2004, 108, 8467–8474.
16. S. Ebbinghaus, S. J. Kim, M. Heyden, X. Yu, U. Heugen, M. Gruebele, D. M. Leitner and M. Havenith, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20749–20752.
17. D. Summerer, S. Chen, N. Wu, A. Deiters, J. W. Chin and P. G. Schultz, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 9785–9789.
18. K. H. Hopmann, K. Ruud, M. Pecul, A. Kudelski, M. Dračínský and P. Bouř, J. Phys. Chem. B, 2011, 115, 4128–4137.
19. J. Kapitán, M. Dračínský, J. Kaminský, L. Benda and P. Bouř, J. Phys. Chem. B, 2010, 114, 3574–3582.
20. M. Dračínský, J. Kaminský and P. Bouř, J. Phys. Chem. B, 2009, 113, 14698–14707.
21. M. P. Blakeley, P. Langan, N. Niimura and A. Podjarny, Curr. Opin. Struct. Biol., 2008, 18, 593–600.
22. V. Tereshko, C. J. Wilds, G. Minasov, T. P. Prakash, M. A. Maier, A. Howard, Z. Wawrzak, M. Manoharan and M. Egli, Nucleic Acids Res., 2001, 29, 1208–1215.
23. C. L. Barnes and S. W. Hawkinson, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1982, 38, 812–817.
24. S. K. Katti, T. P. Seshadri and M. A. Viswamitra, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1981, 37, 1825–1831.
25. G. Wu and A. Wong, Solid-state nuclear magnetic resonance studies of alkali metal ions in nucleic acids and related systems, in NMR Spectroscopy of Biological Solids, ed. A. Ramamoorthy, CRC Press, Boca Raton, 2006.
26. G. Wu and J. F. Zhu, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 61, 1–70.
27. F. A. Perras and D. L. Bryce, J. Phys. Chem. C, 2012, 116, 19472–19482.
28. T. P. Seshadri, M. A. Viswamitra and G. Kartha, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 925–927.
29. M. Dračínský, H. M. Möller and T. E. Exner, J. Chem. Theory Comput., 2013, 9, 3806–3815.
30. T. Liang and T. R. Walsh, Phys. Chem. Chem. Phys., 2006, 8, 4410–4419.
31. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
32. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
33. V. Zorin, Gsim – a visualisation and processing program for solid-state NMR, http://gsim.sourceforge.net, 2014.
34. P. Hodgkinson, pNMRsim: a general simulation program for large problems in solid-state NMR, http://www.dur.ac.uk/paul.hodgkinson/pNMRsim, 2014.
35. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570.
36. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
37. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
38. C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 6324, 245101.
39. J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401.
40. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
41. P. Hodgkinson and L. Emsley, J. Chem. Phys., 1997, 107, 4808–4816.
42. R. K. Harris, Analyst, 2006, 131, 351–373.
43. D. C. Apperley, R. K. Harris and P. Hodgkinson, Solid-State NMR: Basic Principles & Practice, Momentum Press, New York, 2012.
44. S. Antonijevic, S. E. Ashbrook, S. Biedasek, R. I. Walton, S. Wimperis and H. X. Yang, J. Am. Chem. Soc., 2006, 128, 8054–8062.
45. S. E. Ashbrook, Phys. Chem. Chem. Phys., 2009, 11, 6892–6905.
46. B. O'Hare, M. W. Grutzeck, S. H. Kim, D. B. Asay and A. J. Benesi, J. Magn. Reson., 2008, 195, 85–102.
47. M. Dračínský, L. Benda and P. Bouř, Chem. Phys. Lett., 2011, 512, 54–59.
48. M. Dračínský and P. Hodgkinson, CrystEngComm, 2013, 15, 8705–8712.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 987999. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4ce00727a

---