Directionality of π-holes in nitro compounds

Abstract

A statistical survey of the Cambridge Structural Database reveals that the interaction between the π-holes of nitro groups and electron-rich atoms is somewhat directional. High-level ab initio computations indicate energies up to −6.6 kcal mol⁻¹.

---

Intermolecular interactions determine how molecules interact with one another, and are thus fundamental to inquiries in areas like supramolecular chemistry and molecular biology.¹ It is well-appreciated that even weak interactions (e.g., hydrogen bonding involving C–H) can bear functional relevance, especially when several such forces work in concert.² This begs the question what weak interactions can be identified as possibly functionally relevant.

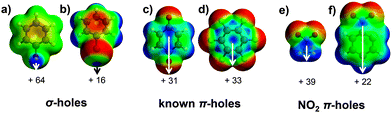
Hydrogen (H) and halogen (Hlg) bonds are by far the best established intermolecular forces.³ The regions of electropositive potential on R–H and R–Hlg (Fig. 1a and b, phenol and bromobenzene, respectively) can be described as unpopulated σ* antibonding orbitals along the R–H/Hlg vector.^7b,c These ‘σ-holes’ have also been identified on atoms that belong to the oxygen, nitrogen and carbon families, and their binding to electron-rich entities is referred to as chalcogen-,⁴ pnicogen-,⁵ and tetrel-bonding,⁶ respectively.

Fig. 1 Some σ-and π-holes with their electropositive potential in kcal mol⁻¹ (MP2/6-311+G**).

In analogy to the σ-hole, a π-hole can be seen as an electropositive potential located on an unpopulated π*-orbital. The best-known π-hole interactions involve carbonyl compounds (e.g., p-quinone, as shown in Fig. 1c): Bürgi and Dunitz⁷ uncovered the trajectory along which a nucleophile attacks the π-hole of a carbonyls' C-atom, and π-hole interactions involving amides are known to persist in protein structures.⁸ Aromatic rings bearing electron withdrawing substituents, such as hexafluorobenzene (Fig. 1d), can also function as π-holes.⁹ Interactions involving such π acidic aromatic rings are generally referred to as anion- or lone pair-π interactions.¹⁰

A recent theoretical study revealed that a π-hole can also be found on a nitro group.¹¹ Association of this π-hole with electron-rich entities (ElR, e.g., H₂O and Cl⁻) was estimated to vary in strength between −0.5 and −27.9 kcal mol⁻¹. Fig. 1e and f illustrate the π-holes in nitromethane and nitrobenzene, respectively. One might thus wonder if the ‘NO₂^π⋯ElR’ interaction bears any functional relevance. The first step towards answering this question is to establish whether this intermolecular force is actually directional. Analysis of the data compiled within the Cambridge Structural Database (CSD)¹² has proven to be an exquisite tool for revealing the directional nature of traditional and non-canonical intermolecular forces. We thus set out to evaluate the CSD using a methodology that is particularly apt for ascertaining the directional character of weak intermolecular forces.⁹

Aliphatic and aromatic C–NO₂ compounds that are abundant within the CSD were considered: there are 900 crystallographic information files (CIFs) containing nitromethane, and 14 227 CIFs containing an aromatic nitro compound where the NO₂ moiety is flanked by two ortho-H's (this allows the NO₂ and C₆H₂ moieties to be relatively coplanar). Fig. 2a illustrates the query used to obtain initial datasets from the CSD.

Fig. 2 Illustrations of the method used to analyse directionality of intermolecular interactions between an electron-rich atom (ElR., N, P, As, O, S, Se, Te, F, Cl, Br, I or At) and a nitro group (in this illustration nitromethane).

An entry was considered a hit when the intermolecular distance (D) between the C–N centroid (blue) and any electron-rich atom (red, ElR = N, P, As, O, S, Se, Te, F, Cl, Br, I or At) was ≤5 Å. The initial dataset was thus confined within a sphere with a radius of 5 Å, centred on the C–N centroid. The spatial separation (d) between ElR and the CNO₂ plane was also retrieved from the CSD. The xy coordinates relative to this plane were determined as described elsewhere.¹³ By virtue of Pythagoras's theorem, the parallel displacement parameter r could be derived from D and d. The CN^centroid–N–ElR angle (α) was measured as well.

For this study, only the data characterized by y = ±2 Å were considered, which are therefore located within the 4 Å wide spherical segment, as illustrated in Fig. 2b–d. The data can thus be characterized by the parallel displacement (r) within this spherical segment, either towards the NO₂ group (α < 90°) or towards the other atoms attached to C (α > 90°). To analyse directionality, we applied a method described in detail elsewhere.^9,13,14 This method entails computing the parameter P(r),‡ which signifies the distribution of the data along r that is corrected for the volume occupied by the host and for a random scattering of data. When P ≠ 1, non-accidental clustering of data is established and P > 1 is indicative of an attractive interaction.

The P versus r plots for CH₃NO₂ (black circles) and C₆H₂NO₂ (open circles) are shown on the left hand side of Fig. 3. For both ‘hosts’, P > 1 around r = 0, indicating some directionality of the π-hole. The P-values of 2–3 are similar to those observed for C–H⋯π^phenyl hydrogen bonding.¹⁵ In the case of CH₃NO₂, the observed clustering is spread out over the region ranging from r = −1 to +1 Å. It is likely that CH⋯ElR hydrogen bonding also contributes to the observed distribution. The clustering observed for aromatic NO₂ is spread out over the region from r = 0 to +1 Å, and hydrogen bonding cannot contribute in this case. It was further assessed how exactly the data are distributed within the data characterized by −1 > r < 1 Å. Thus, the relative hit fraction was plotted as a function of the van der Waals corrected CN^centroid⋯ElR distance, as shown on the right hand side of Fig. 3. For both central groups, roughly 20% van der Waals overlap is present. These two plots together indeed show that a nitro moiety can be a directional π-hole donor.

Fig. 3 Analysis of the directional nature of CNO₂ π-holes. Left: directionality plots of P vs. r for CH₃NO₂⋯ElR (●, N_tot = 6 680) and C₆H₂NO₂⋯ElR (○, N_tot = 33 523) of the data characterized by D ≤ 5 Å and y ± 2 Å; right: N_relativevs. v/d Waals corrected CN_centroid–ELR distance (assuming (^vdWC + ^vdWN)/2 = 1.625 Å) for CH₃NO₂⋯ElR (●, N_tot = 1 231) and C₆H₂NO₂⋯ElR (○, N_tot = 4 727) of the data characterized by D ≤ 5 Å and r ± 1 Å.

We have theoretically analysed (see the ESI† for details) several representative complexes between electron-rich moieties and nitrobenzene (Fig. 4a; a similar study with nitromethane is reported elsewhere).¹¹ The interaction energies and some geometric features of the complexes are summarized in Table 1. The interaction energies are similar for nearly all complexes ranging from −2.3 to −6.6 kcal mol⁻¹ and the most favourable one corresponds to chloride complex 7. The π-hole in nitrobenzene is located along the C–N bond and close to the nitrogen atom (see Fig. 1f and 4b). We have included both ElR⋯N and ElR⋯C distances (denoted as D_N and D_C, respectively) in Table 1. All complexes exhibit similar D_N and D_C distances and in all cases the electron-rich atom is located over the C–N bond, in agreement with results of the MEP analysis. The interaction energy is modest in complex 6 due to the low basicity of the sp-hybridized nitrogen atom of the HCN molecule.

Fig. 4 (a) Complexes 1–7 studied in this work. (b) A pictorial representation of the complementarity of the MEP surfaces of nitrobenzene and trimethylamine.

Table 1 BSSE corrected interaction energies (E, kcal mol⁻¹) and equilibrium distances from the electron-rich atom to the N (D_N) and C (D_C) atoms of the C–NO₂ moiety (in Å) of complexes 1–7 at the RI-MP2/def2-TZVPD//PB86-D3/def2-TZVPD level of theory

Complex	E	D N	D C
1	−6.2	2.770	2.932
2	−4.3	3.636	3.547
3	−4.4	2.825	2.931
4	−4.7	3.416	3.448
5	−4.7	2.956	3.001
6	−2.3	3.181	3.191
7	−6.6	3.204	3.047

---

The optimized geometries of some complexes are shown in Fig. 5, including the “atoms-in-molecules”¹⁶ (AIM) distribution of critical points computed for complexes 1 (lone pair donor ElR) and 5 (anionic ElR). The optimized geometries and critical point distribution for the rest of the complexes are included in the ESI.† It can be clearly observed in Fig. 5 and Fig. S1 (ESI†) that the position of the ElR atom of the interacting molecule coincides with the location of the π-hole in all complexes, indicating that the interaction is basically electrostatic in nature. The AIM analysis of 1 is complicated since it shows five bond critical points symmetrically distributed. One bond critical point (ρ = 1.54 × 10² a.u.) connects both nitrogen atoms characterizing and confirming the π-hole interaction. In addition, two bond critical points (ρ = 0.62 × 10² a.u.), which connect two hydrogen atoms of trimethylamine to two carbon atoms of the ring, reveal the presence of two C–H/π interactions. Moreover, two additional bond critical points (ρ = 0.70 × 10² a.u.) connecting two hydrogen atoms to the oxygen atoms of the nitro group, reveal the presence of two C–H⋯O interactions. The charge density computed at the bond critical point that connects both nitrogen atoms is considerably greater than the ones measured at the other bond critical points (1.54 × 10²vs. ∼0.66 × 10²). Therefore, the complexation is dominated by the π-hole interaction with some contribution of the other two interactions. In complex 7, the distribution shows a single bond critical point that connects Cl⁻ to the carbon atom, instead of the nitrogen atom, confirming the interaction.

Fig. 5 (a–c) Optimized π-hole complexes 1, 3 and 7 studied in this work. (d and e) Distribution of critical points in complexes 1 and 7 (bond and ring critical points are represented by red and yellow spheres, respectively). Bond paths connecting bond critical points are represented.

In conclusion, we have demonstrated that the nitro groups in nitromethane and nitrobenzene are able to interact favourably with electron-rich molecules by means of the π-hole that is located above and below the C–N bond. The interaction is characterized by the presence of a bond critical point that connects the ElR atom to the C–N bond. More importantly, the statistical survey of the CSD study reveals that the interaction between the π-holes of nitro-groups and electron-rich atoms is directional. Nitro groups are widespread amongst small organic molecules and to date the protein data bank (PDB) contains 380 ligands that bear an –NO₂ moiety. It is thus reasonable to anticipate an experimental study unveiling the functional relevance of this novel π-hole interaction.

AB and AF thank MINECO of Spain (projects CTQ2011-27512/BQU and CSD2010-00065, FEDER funds) for financial support.

Notes and references

1. (a) H. J. Schneider, Angew. Chem., Int. Ed., 2009, 48, 3924–3977; (b) H. J. Schneider and A. Yatsimirski, Principles and methods in supramolecular chemistry, Wiley, Chichester, 2000.
2. (a) T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76; (b) M. Brandl, M. S. Weiss, A. Jabs, J. Suhnel and R. Hilgenfeld, J. Mol. Biol., 2001, 307, 357–377.
3. (a) Hydrogen Bonding: New Insights, ed. S. Grabowski, Springer, Heidelberg, 2006; (b) M. Erdélyi, Chem. Soc. Rev., 2012, 41, 3547; (c) E. Parisini, P. Metrangolo, T. Pilati, G. Resnati and G. Terraneo, Chem. Soc. Rev., 2010, 39, 3772.
4. (a) M. Iwaoka, S. Takemoto and S. Tomoda, J. Am. Chem. Soc., 2002, 124, 10613–10620; (b) D. B. Werz, R. Gleiter and F. Rominger, J. Am. Chem. Soc., 2002, 124, 10638–10639; (c) P. Sanz, O. Mó and M. Yáñez, Phys. Chem. Chem. Phys., 2003, 5, 2942–2947.
5. (a) S. Zahn, R. Frank, E. Hey-Hawkins and B. Kirchner, Chem. – Eur. J., 2011, 17, 6034–6038; (b) S. Scheiner, J. Chem. Phys., 2011, 134, 094315; (c) J. E. Del Bene, I. Alkorta, G. Sánchez-Sanz and J. Elguero, J. Phys. Chem. A, 2012, 116, 9205–9213; (d) P. Kilian, A. M. Z. Slawin and J. D. Woollins, Chem. – Eur. J., 2003, 9, 215–222.
6. (a) A. Bauzá, T. J. Mooibroek and A. Frontera, Angew. Chem., Int. Ed., 2013, 52, 12317–12321; (b) S. J. Grabowski, Phys. Chem. Chem. Phys., 2014, 16, 1824–1834; (c) A. Bauzá, T. J. Mooibroek and A. Frontera, Chem. – Eur. J., 2014, 20, 10245–10248; (d) A. Bauzá, T. J. Mooibroek and A. Frontera, Chem. Commun., 2014, 50, 12626–12629.
7. (a) H. B. Burgi, Inorg. Chem., 1973, 12, 2321–2325; (b) H. B. Burgi, J. D. Dunitz and E. Shefter, J. Am. Chem. Soc., 1973, 95, 5065–5067; (c) H. B. Burgi, J. D. Dunitz, J. M. Lehn and G. Wipff, Tetrahedron, 1974, 30, 1563–1572.
8. (a) P. H. Maccallum, R. Poet and E. J. Milnerwhite, J. Mol. Biol., 1995, 248, 374–384; (b) G. J. Bartlett, A. Choudhary, R. T. Raines and D. N. Woolfson, Nat. Chem. Biol., 2010, 6, 615–620; (c) M. Harder, B. Kuhn and F. Diederich, ChemMedChem, 2013, 8, 397–404.
9. (a) T. J. Mooibroek and P. Gamez, CrystEngComm, 2012, 14, 3902–3906; (b) T. J. Mooibroek and P. Gamez, CrystEngComm, 2012, 14, 1027–1030.
10. A. Frontera, P. Gamez, M. Mascal, T. J. Mooibroek and J. Reedijk, Angew. Chem., Int. Ed., 2011, 50, 9564–9583.
11. A. Bauza, R. Ramis and A. Frontera, J. Phys. Chem. A, 2014, 118, 2827–2834.
12. F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388.
13. K. E. Ranaghan, J. E. Hung, G. J. Bartlett, T. J. Mooibroek, J. N. Harvey, D. N. Woolfson, W. A. van der Donk and A. Mulholland, Chem. Sci., 2014, 5, 2191–2199.
14. (a) T. J. Mooibroek and P. Gamez, CrystEngComm, 2013, 15, 1802–1805; (b) T. J. Mooibroek and P. Gamez, CrystEngComm, 2013, 15, 4565–4570.
15. T. J. Mooibroek and P. Gamez, CrystEngComm, 2012, 14, 8462–8467.
16. (a) R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, USA, 1994; (b) R. F. W. Bader, Chem. Rev., 1991, 91, 893–928; (c) R. F. W. Bader, Atoms in Molecules, Encyclopaedia of Computational Chemistry, 1998, vol. 1, pp. 64–86.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cc09132a

‡
N_r = the number of hits in between two r-values; N_total = the total number of hits; V^free_r = the volume in between two r-values minus the volume of the host in between these two r-values (hence, the free volume), as found within a 4 Å wide symmetrical spherical segment of a sphere with a 5 Å radius; V^free_total is the volume of a 4 Å wide symmetrical spherical segment of a sphere with a 5 Å radius minus the volume of the host in that body. Models of the central groups were constructed using averages of interatomic distances and angles and assuming generally accepted van der Waals radii. All volumes were computed using Autodesk® Inventor® Professional.

---