The influence of the enantiomeric ratio of an organic ligand on the structure and chirality of metal–organic frameworks

Abstract

We have prepared three distinct polyamino acid-based metal–organic frameworks (MOFs) with different chiralities and porosities using the same chemistry, by simply modifying the enantiomeric ratio of the chiral organic ligand used.

---

Metal–organic frameworks (MOFs) are crystalline porous solids constructed by linking metal ions/clusters to organic ligands through coordination bonds.¹ Currently, MOFs are among the most attractive porous materials due to their diverse compositions and structures, which are characterised by ordered arrays of pores that can be used for gas storage,² separation,³ catalysis,⁴ drug capture and delivery,⁵ imaging⁶ and sensing.⁷ The strategic design of the organic ligands to be used (known as the linker design approach)⁸ has proven critical for tuning the structure of MOFs and thus, for achieving the desired functionality for a target application. This is because the characteristics of the ligands can influence the structural topology,⁹ internal pores (surface and volume), and other properties of the resulting MOFs. Several variables have already been identified and have since been incorporated into the ligand-designing process,⁹ including the geometry and length,¹⁰ the post-synthetic addition of certain functional groups,¹¹ and the use of functional ligands with pre-determined properties such as fluorescence¹² and chirality.¹³ For example, researchers have shown that the pore size (from 14 to 98 Å) of a series of Mg(II)-based MOFs isostructural to MOF-74 (or CPO-27) can be tuned by increasing the length of the organic ligand (starting with dihydroxy-terephthalate and going up to eleven phenyl rings), without modifying its functional groups.¹⁴ Alternatively, some authors have reported enhancement of the catalytic activity of MOFs by post-synthetic incorporation of Lewis acid metal centres on the pore surfaces.¹⁵ Lastly, researchers have demonstrated that the luminescence properties of Zn(II)-based MOFs can be tailored according to the organisation of the fluorescent stilbene dicarboxylic acid ligand around the Zn(II), leading to stronger or weaker ligand–ligand chromophore interactions.¹⁶

Herein we report that the enantiopurity of a chiral ligand used in MOF synthesis can be exploited to influence the structure and chirality of the resulting MOFs. Chiral ligands are commonly used to synthesise homochiral porous MOFs.¹⁷ They can also be synthesised from achiral building blocks in which their arrangement within the structure is chiral.¹⁸ These approaches have recently attracted great interest because of the potential for chiral MOFs in enantioselective separation¹⁹ and asymmetric catalysis.²⁰ Prior to our study, isostructural homochiral or racemic MOFs have been prepared by combining Cu(II) or Zn(II) with 4,4′-bipyridine and D- or DL-camphoric acid, respectively.²¹ Also, researchers have reported that Zn(II)–Co(II)-based MOFs and amorphous solids are obtained by using racemic and enantiopure metalloligands, respectively,²² and that the framework interpenetration in Cu(II)-based MOFs can be controlled by using R- or racemic-2,2′-diethoxy-1,1′-binaphthyl-4,4′6,6′-tetrabenzoate ligands and solvent molecules of different sizes.²³ However, to the best of our knowledge, there are no previous reports showing the influence of the enantiomeric ratio (er) of chiral organic ligands in the formation of MOFs.

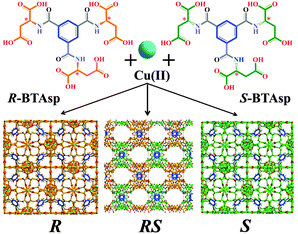
Our strategy relies on the design of two enantiomorphs that act as enantiomerically pure ligands with opposite chirality, when used alone, or as a racemic mixture of ligands, when an equimolar ratio is used. They can also be mixed in different ratios to prepare solutions of different er values (hereafter, S : R). Both ligands, (1S,3S,5S)-benzene tricarbonyl tri-(aspartic acid) (S-BTAsp) and (1R,3R,5R)-benzene tricarbonyl tri-(aspartic acid) (R-BTAsp) (Fig. 1), combine the rigidity of the phenyl ring (blue) with the coordination ability, chirality and flexibility of the aspartate carboxylic groups (S, orange; R, green; Fig. 1). For detailed information on the synthesis and characterisation of enantiomerically pure S- and R-BTAsp, see Section S1 and Fig. S1 and S2 (ESI†). We demonstrate that the reaction of Cu(II) with either enantiomerically pure ligand (S- or R-BTAsp), or with the racemic mixture RS-BTAsp, under identical reaction conditions yields three 3D polyamino acid-based MOFs: two isostructural and homochiral, non-porous (but with large void volumes) MOFs with opposite optical activity (hereafter, S and R); and a third, achiral, MOF (hereafter, RS), which contains 1D pores accessible for gas uptake (Fig. 1). We also show that the formation and purity of the MOFs are directly affected by the er of the S-/R-BTAsp mixture used.

Fig. 1 Schematic illustration of the enantiopure ligands R- and S-BTAsp. Under identical conditions, the reaction of Cu(II) with R-BTAsp alone, or mixtures of S- and R-BTAsp, or S-BTAsp alone affords the three distinct MOFs R, RS and S (bottom), respectively, which differ by chirality and/or porosity.

Reaction of Cu(NO₃)₂·6H₂O with S-BTAsp in a slightly acidic (pH 6) aqueous solution at room temperature for 24 hours afforded octahedral crystals (yield: 67%; Section S1 and Fig. S3 and S9, ESI†). Single-crystal XRD revealed a 3D network of formula [Cu₃(S-BTAsp)(H₂O)₃]·12.75H₂O, S, which crystallises in the chiral F23 space group (Table S1, ESI†). The basic unit of S is a Cu₂ paddlewheel unit, in which each Cu(II) is coordinated to four carboxylate O atoms, from four adjacent aspartate functions, and to one H₂O molecule. Each carboxylate group of the aspartate residue bridges two Cu(II) centres within the Cu₂ paddlewheel unit; consequently, a single S-BTAsp ligand binds to twelve Cu(II) centres (Fig. 2a). Within S, the aspartate residues of a single S-BTAsp have the same conformation, as confirmed by measurement of the side chain dihedral angle: −66.65° (Fig. S4 and S5, and Table S2, ESI†). The specific folding of the aspartate groups of S-BTAsp, and the coordination around the Cu(II)-paddlewheel unit, together create a 3D structure that incorporates two types of void volumes: (i) a 3D channel system, formed of cavities (internal diameter: 7.0 Å, considering van der Waals radii (vdW); Fig. 2b and Fig. S6, ESI†) connected by small pores (dimensions: 7.0 Å × 3.5 Å, considering vdW radii) and (ii) larger, isolated cages, in which the shortest separation between their centroid and their vdW surface is 6.8 Å, indicating that a sphere with a volume of 1340 ų can fit inside them (Fig. 2c and Fig. S7, ESI†). The large cages are not accessible, as the largest window aperture is found to be between HOH⋯OCNH and CH⋯HCH, at a distance of 3.4 Å and 0.5 Å, respectively, including vdW radii of the atoms (Fig. S8, ESI†). The 3D channel system and the large cages combine for a total void space of 52% per unit cell (Fig. 2d).²⁴

Fig. 2 (a–d) Crystal structure of S. (a) Binding mode of the ligand S-BTAsp. (b) Single cavity forming the 3D channel system, in which the purple ball illustrates the internal diameter (7.0 Å). (c) Single large cage delimited by 8 S-BTAsp ligands and 18 Cu(II) paddlewheels. The yellow ball represents the internal void volume (1340 ų) within the cage. (d) Packing of S along the c-axis, showing the organisation of the large cages (yellow balls) and cavities (purple balls) forming the channel system. (e–h) Crystal structure of RS. (e) Coordination of BTAsp ligand to nine Cu(II) centres. (f) Left- or right-handed helices made by connecting the Cu(II) ions to either S-BTAsp or R-BTAsp, respectively, along the b-axis. (g) Stick representation of one pore channel (dimensions: of 9.1 Å × 4.3 Å), and (h) Connolly surface representation of RS viewed in 3D. Atom colour code: Cu: sky blue; C: grey; O: red; N: blue; and H: yellow.

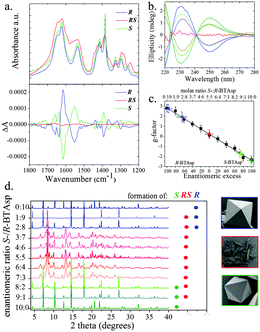
We prepared R using the same conditions as for S, except that instead of S-BTAsp, we used R-BTAsp (yield: 70%; obtained as a pure phase, as confirmed using elemental analysis and SEM; Fig. S3, ESI†). Interestingly, the PXRD patterns demonstrated that both S and R are isostructural (Fig. S9, ESI†). In addition, the infrared (IR) spectra of S and R are nearly identical, also confirming that they are isostructural (Fig. 3a). The opposite chirality between S and R was confirmed by solid-state Vibrational Circular Dichroism (VCD): their chirality is defined by the coordination network between the Cu(II) ions and the carboxylate groups, which have specific absorptions in the infrared region (Fig. 3a). For the VCD spectra, a mirror-image relationship is observed between the enantiomeric pairs of S and R (Fig. 3a). The most relevant inverted VCD signals are observed at 1623 cm⁻¹ and 1417 cm⁻¹, which primarily correspond to asymmetric and symmetric stretching bands, respectively, of the carboxylate groups; and at 1537 cm⁻¹, which is attributed to the bending of the N–H bond. Both frameworks were also studied using ECD by disassembling them under acidic conditions (pH 2.0; Fig. 3b). For S and R, identical ECD signals of their corresponding enantiomeric S- or R-BTAsp ligands, respectively, were observed (Fig. S10, ESI†).

Fig. 3 (a) IR (top) and VCD (bottom) spectra of S, R and RS. (b) ECD spectra collected after the disassembly of the MOF crystals synthesised using er of 10 : 0, 9 : 1 and 8 : 2 (and vice versa) of S-BTAsp/R-BTAsp and er 5 : 5. (c) Plot of g-values against enantiomeric excess of S-BTAsp/R-BTAsp. The triangles represent the g-values calculated from the MOFs synthesised using er of 0 : 10 (blue), 1 : 9 (sky blue), 2 : 8 (purple), 5 : 5 (red), 8 : 2 (dark yellow), 9 : 1 (light green) and 10 : 0 (green). (d) PXRD patterns and FESEM images of the MOFs resulting when various ratios of S-BTASp/R-BTAsp were used in the reaction with Cu(II).

To explore the influence of the enantiopurity of R- and S-BTAsp ligands on MOF synthesis, we first prepared a racemic mixture using equimolar amounts (er = 5 : 5) of the two ligands (Fig. S2, ESI†), and then reacted it with Cu(II), using the same experimental conditions as for the isolation of S and R. In contrast to the formation of the octahedral crystals of S or R after 24 h, intergrown needle-like crystals began to form after 15 to 17 days (yield: 35%; purity confirmed by PXRD, elemental analysis and SEM; Fig. S3 and S9, ESI†). Single-crystal XRD revealed the formation of a new 3D MOF, of formula [Cu₃(RS-BTAsp)(H₂O)₄]·7.5H₂O, RS, which crystallises in the centrosymmetric Pcnm orthorhombic space group (Table S1, ESI†). Within RS, there are three distinct Cu(II) ions: Cu#1, which has square pyramidal geometry; and Cu#2 and Cu#3, both of which have square planar geometry (Fig. S11, ESI†). Each aspartate group of the BTAsp within RS is bound to three Cu(II) ions, giving a total connectivity per ligand of nine Cu(II) ions (Fig. 2e). A striking difference observed between S or R and RS, is that the side-chain dihedral angles of the three aspartate groups within a single BTAsp ligand in RS vary (73.47°, −60.42° and −71.74°; Fig. S4 and S5, and Table S2, ESI†). In RS, the coordination of the BTAsp ligand around the three distinct Cu(II) leads to the formation of columnar left- and right-handed helices (Fig. 2f), in which the benzene rings of the BTAsp are stacked along the b-axis, introducing weak π–π stacking interactions (distance: 4.0 Å; Fig. 2f and Fig. S11–S13, ESI†). This organisation generates 1D channels (dimensions: 9.1 Å × 4.3 Å, considering vdW radii) running along the b-axis (Fig. 2g and h). The channels are filled with four H₂O molecules coordinated to Cu#3 (Fig. 2g and h, and Fig. S12 and S13, ESI†) and 7.5 guest H₂O molecules. The total accessible void volume of RS is 32% per unit cell,²⁴ and the calculated pore volume in RS is 0.181 cm³ g⁻¹.

To further evaluate the importance of the enantiopurity of the BTAsp ligand in the resulting MOF, we systematically prepared different mixtures of S- and R-BTAsp (from 9 : 1 to 1 : 9, including the enantiopure 10 : 0 and 0 : 10), and then reacted each mixture with Cu(II) under the conditions used for the isolation of S, R and RS. We observed that the use of a slight excess of either S- or R-BTAsp (7 : 3 and 6 : 4, or vice versa) always led to the formation of the achiral RS phase, just as when synthesised using the equimolar mixture (5 : 5). For all reactions, the formation and purity of RS was confirmed using Field Emission SEM (FESEM), PXRD (Fig. 3d) and ECD after disassembly of the product at pH 2 (at which point we could not detect any signal by ECD; Fig. S14, ESI†). Contrariwise, when a large excess of either S- or R-BTAsp (9 : 1 and 8 : 2, or vice versa) was used, we mainly observed the formation of octahedral crystals indicative of the homochiral S or R, respectively, as confirmed by both PXRD (Fig. 3d) and ECD (Fig. 3b). However, the presence of low-intensity Bragg reflections (2θ: 8.3° and 13.2°), together with the different ECD intensity maxima,²⁵ revealed that a small amount of RS had also formed together with S or R.

To quantify the amounts of S, R and RS formed in the aforementioned reactions, we disassembled the product crystals at pH 2, and then determined the corresponding enantiomeric excess (ee) of the free S- or R-BTAsp. We used an analytical method based on the calculation of the anisotropy factor: the g-factor, a concentration-independent parameter derived from the absorbance and ellipticity of the chiral ligand (Section S9, ESI†).²⁶ In a first step, this method was validated by confirming the linearity of the g-factor calculated in pure samples of S- or R-BTAsp in the working concentration range (0.04 mg mL⁻¹ to 0.06 mg mL⁻¹; Fig. S15, ESI†). The analytical calibration curve (R² = 0.994) was measured by calculating the g-factor of different mixtures of S- and R-BTAsp (from 9 : 1 to 1 : 9, including the enantiopure 10 : 0 and 0 : 10), and then plotting them against the enantiomeric excess (ee). As shown in Fig. 3c, the straight line nearly intercepts the “x” axis at 0% ee—the value expected for the racemic mixture. To test this method, a series of control experiments was performed, in which the ee of pure samples of S, R and RS was measured. The g-values of the enantiopure S and R, and of the racemic RS, were −2.4 ± 0.4, 2.8 ± 0.4 and 0.2 ± 0.4, respectively, corresponding to the expected 99.3 ± 8.7 ee (S-BTAsp), 97.5 ± 7.9 ee (R-BTAsp) and 0.7 ± 8.8 ee (R-BTAsp), respectively (Fig. 3c). Finally, the g-values of the MOF crystals resulting from the reactions run with a large excess of either isomer (9 : 1 and 8 : 2, and vice versa) were measured. These values were found to be: −1.7 ± 0.4 [9 : 1; 71.4 ± 7.2 ee (S-BTAsp)], −1.8 ± 0.4 [8 : 2; 75.5 ± 6.4 ee (S-BTAsp)], 1.9 ± 0.5 [2 : 8; 65.2 ± 11.0 ee (R-BTAsp)] and 2.0 ± 0.5 [1 : 9; 67.6 ± 10.8 ee (R-BTAsp)]. Importantly, these ee values, together with the previously described PXRD data, demonstrate that both ligands indeed participate in the construction of the MOFs in these reactions. Here, if one assumes that a combination of S and RS is simultaneously formed when 9 : 1 and 8 : 2 ratios are used (or R and RS for the 1 : 9 and 2 : 8 ratios), then the percentage of S relative to RS (or R relative to RS for the 1 : 9 and 2 : 8 ratios) is simply given by the corresponding ee value (∼65 to 75%).

Thermogravimetric analysis (TGA) of isostructural S and R indicated a continuous weight loss of 25.1% and 26.3%, respectively, from 30 °C to 200 °C, which we attributed to the loss of all H₂O molecules (calcd 27.7%; Fig. S16, ESI†). Above 200 °C, both frameworks decompose in multiple steps. The TGA profile of RS shows a weight loss of 11.2% from 30 °C to 200 °C, which we ascribed to the removal of the 7.5 guest H₂O molecules (calcd 14.6%; Fig. S16, ESI†). Also, RS begins to decompose stepwise at 200 °C. To further evaluate the thermal stability of S and RS, TGA data were complemented with in situ Variable Temperature PXRD (VT-PXRD) experiments performed in a closed capillary tube. VT-PXRD revealed that S (and therefore, R) slowly collapses and becomes an amorphous solid above 100 °C (Fig. S17, ESI†). This finding is consistent with the TGA data and with the PXRD pattern of the activated S after lyophilisation at −50 °C and 0.07 mbar (Fig. S18, ESI†), showing that the collapse of S (and therefore, of R) occurs gradually, upon the loss of H₂O molecules. Contrariwise, the VT-PXRD patterns of RS show that it loses much of its crystallinity at a far higher temperature (200 °C) than does S.

As expected, type II isotherms (77 K and 1 bar) of S and of R revealed that they are non-porous to N₂. This is due to their low stability upon removal of the guest H₂O molecules, as confirmed by TGA and PXRD (Fig. S18, ESI†). In contrast, RS (once activated by solvent exchange with chloroform for 72 hours (Fig. S19, ESI†) and subsequent outgassing at 40 °C overnight)²⁷ is porous to N₂ (92.7 cm³ g⁻¹ at 0.96 bar; BET surface area: 263 m² g⁻¹ at p/p⁰ = 0.05–0.3) at 77 K, for which it showed a reversible typical type-I isotherm (Fig. S20a, ESI†). The pore volume for RS, derived from the N₂ adsorption branch using the Dubinin–Radushkevich equation,²⁸ was found to be 0.142 cm³ g⁻¹, which is somewhat smaller than the value (0.181 cm³ g⁻¹) estimated from the static crystal structure. The type-I N₂ isotherm of RS prompted us to investigate its CO₂ sorption and to assess the strength of the interactions between RS and CO₂. RS is porous to CO₂ (79.8 cm³ g⁻¹ at 195 K and 0.85 bar) at 195 K, showing a type-I isotherm (Fig. S20b, ESI†). At 273 K and 0.85 bar, RS adsorbed 38.3 cm³ g⁻¹ of CO₂, whereas at 295 K and 0.85 pressure, it adsorbed 25.5 cm³ g⁻¹ of CO₂. Isosteric heats of adsorption (Q_st) of RS for CO₂ were calculated from the virial-type expression,²⁹ using the adsorption branches of the isotherms measured at 273 K and 295 K (Fig. S21, ESI†). At zero coverage, Q_st was calculated to be 27.5 kJ mol⁻¹, but it gradually decreased to 18.5 kJ mol⁻¹ at high loadings.

In conclusion, we have demonstrated that the ratio of two opposite enantiomeric ligands can influence the final structure of the resulting MOFs. We showed that by simply modifying the ratio of S-BTAsp/R-BTAsp in a MOF reaction, the structure of the resulting MOF could be tuned between the three structures R, RS and S, which exhibit different porosity and chirality properties. The systematic identification of new parameters that determine MOF structures is important, as it will enable a greater understanding of structure–function relationships and therefore, enable better engineering of MOFs for targeted applications.

This work was supported by the MINECO-Spain under the project PN MAT2012-30994 and EU FP7 ERC-Co 615954. I.B. thanks SENESCYT-Ecuador for a PhD fellowship, I.I. thanks MINECO for a Ramón y Cajal grant and K.C.S. thanks the EU for a Marie Curie Fellowship (300390 NanoBioMOFs FP7-PEOPLE-2011-IEF). The authors express their gratitude to the Diamond Light Source for access to beamline I19.

Notes and references

1. S. Kitagawa and R. Matsuda, Coord. Chem. Rev., 2007, 251, 2490–2509.
2. (a) R. E. Morris and P. S. Wheatley, Angew. Chem., Int. Ed., 2008, 47, 4966–4981; (b) B. Li, H.-M. Wen, H. Wang, H. Wu, M. Tyagi, T. Yildirim, W. Zhou and B. Chen, J. Am. Chem. Soc., 2014, 136, 6207–6210.
3. P. Nugent, Y. Belmabkhout, S. D. Burd, A. J. Cairns, R. Luebke, K. Forrest, T. Pham, S. Ma, B. Space, L. Wojtas, M. Eddaoudi and M. J. Zaworotko, Nature, 2013, 495, 80–84.
4. W.-Y. Gao, Y. Chen, Y. Niu, K. Williams, L. Cash, P. J. Perez, L. Wojtas, J. Cai, Y.-S. Chen and S. Ma, Angew. Chem., Int. Ed., 2014, 53, 2615–2619.
5. P. Horcajada, R. Gref, T. Baati, P. K. Allan, G. Maurin, P. Couvreur, G. Férey, R. E. Morris and C. Serre, Chem. Rev., 2011, 112, 1232–1268.
6. A. Carné-Sánchez, C. S. Bonnet, I. Imaz, J. Lorenzo, É. Tóth and D. Maspoch, J. Am. Chem. Soc., 2013, 135, 17711–17714.
7. H. Xu, F. Liu, Y. Cui, B. Chen and G. Qian, Chem. Commun., 2011, 47, 3153–3155.
8. (a) F. A. Almeida Paz, J. Klinowski, S. M. F. Vilela, J. P. C. Tome, J. A. S. Cavaleiro and J. Rocha, Chem. Soc. Rev., 2012, 41, 1088–1110; (b) W. Lu, Z. Wei, Z.-Y. Gu, T.-F. Liu, J. Park, J. Park, J. Tian, M. Zhang, Q. Zhang, T. Gentle Iii, M. Bosch and H.-C. Zhou, Chem. Soc. Rev., 2014, 43, 5561–5593.
9. M. Zhang, M. Bosch, T. Gentle III and H.-C. Zhou, CrystEngComm, 2014, 16, 4069–4083.
10. M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 295, 469–472.
11. S. J. Garibay, Z. Wang, K. K. Tanabe and S. M. Cohen, Inorg. Chem., 2009, 48, 7341–7349.
12. K. C. Stylianou, R. Heck, S. Y. Chong, J. Bacsa, J. T. A. Jones, Y. Z. Khimyak, D. Bradshaw and M. J. Rosseinsky, J. Am. Chem. Soc., 2010, 132, 4119–4130.
13. C. J. Kepert, T. J. Prior and M. J. Rosseinsky, J. Am. Chem. Soc., 2000, 122, 5158–5168.
14. H. Deng, S. Grunder, K. E. Cordova, C. Valente, H. Furukawa, M. Hmadeh, F. Gándara, A. C. Whalley, Z. Liu, S. Asahina, H. Kazumori, M. O'Keeffe, O. Terasaki, J. F. Stoddart and O. M. Yaghi, Science, 2012, 336, 1018–1023.
15. M. J. Ingleson, J. P. Barrio, J. Bacsa, C. Dickinson, H. Park and M. J. Rosseinsky, Chem. Commun., 2008, 1287–1289.
16. C. A. Bauer, T. V. Timofeeva, T. B. Settersten, B. D. Patterson, V. H. Liu, B. A. Simmons and M. D. Allendorf, J. Am. Chem. Soc., 2007, 129, 7136–7144.
17. (a) Y. Liu, W. Xuan and Y. Cui, Adv. Mater., 2010, 22, 4112–4135; (b) N. L. Strutt, H. Zhang and J. F. Stoddart, Chem. Commun., 2014, 50, 7455–7458.
18. R. E. Morris and X. Bu, Nat. Chem., 2010, 2, 353–361.
19. M. C. Das, Q. Guo, Y. He, J. Kim, C.-G. Zhao, K. Hong, S. Xiang, Z. Zhang, K. M. Thomas, R. Krishna and B. Chen, J. Am. Chem. Soc., 2012, 134, 8703–8710.
20. C.-D. Wu, A. Hu, L. Zhang and W. Lin, J. Am. Chem. Soc., 2005, 127, 8940–8941.
21. J. Zhang, Y.-G. Yao and X. Bu, Chem. Mater., 2007, 19, 5083–5089.
22. S. J. Garibay, J. R. Stork, Z. Wang, S. M. Cohen and S. G. Telfer, Chem. Commun., 2007, 4881–4883.
23. L. Ma and W. Lin, Angew. Chem., Int. Ed., 2009, 48, 3637–3640.
24. A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7–13.
25. A. E. Holmes, S. Zahn and J. W. Canary, Chirality, 2002, 14, 471–477.
26. (a) P. Horváth, A. Gergely and B. Noszál, Talanta, 1997, 44, 1479–1485; (b) M. T. Reetz, K. M. Kühling, H. Hinrichs and A. Deege, Chirality, 2000, 12, 479–482.
27. J. An, O. K. Farha, J. T. Hupp, E. Pohl, J. I. Yeh and N. L. Rosi, Nat. Commun., 2012, 3, 604.
28. F. R. Rouquerol, J. Rouquerol and K. S. W. Sing, Adsorption by Powders and Porous Solids: Principles, Methodology and Applications, Academic Press, 1998.
29. S. A. Al-Muhtaseb and J. A. Ritter, Ind. Eng. Chem. Res., 1998, 37, 684–696.

---

Footnote

† Electronic supplementary information (ESI) available: Synthetic details and crystallographic information. CCDC 1005432 (R), 1005433 (S) and 1005434 (RS). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4cc06190j

---