“Perfecting” pure shift HSQC: full homodecoupling for accurate and precise determination of heteronuclear couplings

Abstract

Fully homodecoupled HSQC spectra can be obtained through the use of a new pulse sequence element, “perfectBIRD”. By way of illustration, we show that perfectBIRD decoupling allows one-bond residual dipolar couplings (RDCs), which provide important NMR restraints for structure elucidation, to be measured with outstanding precision, even in methylene groups.

---

The ever-growing drive in modern chemistry to create increasingly complex systems creates a need for improved analytical tools for their study. While it is usually considered desirable to increase the amount of information provided by a given analytical technique, there are times when information overload means that it is far more useful instead to decrease it. High-resolution solution state NMR spectroscopy, in which narrow chemical shift ranges conspire with extensive scalar coupling to give highly overlapped spectra, is a case in point. Here “pure shift” techniques can be used to suppress the effects of homonuclear couplings,¹ collapsing multiplets to singlets, simplifying spectra and facilitating the extraction of information previously obscured.

Among the different approaches used to achieve broadband homonuclear decoupling of NMR spectra in the real-time direct dimension,^1c,d,2 in indirect dimensions,³ or in a pseudo-direct, interferogram, dimension,⁴ the bilinear rotation decoupling (BIRD) scheme^3b is particularly suitable for many heteronuclear correlation experiments involving dilute heteronuclei (e.g. natural abundance ¹³C). In such cases isotope filtration incurs no extra sensitivity penalty; indeed the signal-to-noise ratio increases in some applications when multiplet structures collapse.^1b,d,5

The BIRD element allows control over the effects of vicinal and long-range homonuclear couplings and both one-bond and long-range heteronuclear couplings. However it relies on the one-bond coupling to a dilute heteronucleus to distinguish between homonuclear coupling partners, and hence cannot be used to decouple geminal interactions. The latter not only cause remaining signal multiplicity due to homonuclear interactions to be present, but can also lead to significant spectral distortion. This makes BIRD pure shift methods less attractive for the study of systems containing diastereotopic methylene protons, frequently encountered in organic compounds.

To circumvent this limitation, we have incorporated BIRD decoupling into a modified perfect echo pulse sequence,⁶ to form what we refer to as a “perfectBIRD” pulse sequence element. This new sequence element provides full homonuclear broadband decoupling even in the case of diastereotopic methylene protons, at the expense of a doubling of the natural (but not instrumental) linewidth.

Here we illustrate the use of perfectBIRD decoupling in experiments to determine one-bond RDCs. RDCs have proven to be very useful for the structure determination of organic and organometallic compounds.⁷ However, RDC analysis in organic compounds is usually prone to be underdetermined, due to the small number of couplings observable. Thus it is of prime importance to obtain all possible information, including the two one-bond RDCs for diastereotopic methylene protons.

For simple AX spin systems the (original) perfect echo pulse sequence (Fig. 1a) refocuses fully both chemical shift and coupling evolution, at time 4τ, for all τ.^6,8 Dropping the last pulse of the perfect echo (shown in grey) yields a sequence element which refocuses homonuclear coupling evolution in AX systems at time 4τ, while introducing a net chemical shift evolution over a period 2τ. Differential chemical shift evolution however prohibits the repetitive application of perfect echoes with small τ, recently used in other methods,⁹ to achieve decoupling even in complex spin systems. As BIRD pulse elements are able to refocus the effects of weak coupling between protons that are bound to a ¹³C nucleus directly through one bond (¹H^d) and those that are remotely attached (¹H^r),^3b,5b replacement of the first 180° pulse in the original perfect echo sequence by a BIRD^d,X element (inversion for ¹H^d and ¹³C) leaves only geminal couplings and strong coupling contributions not refocused at the central 90° pulse in the perfect echo, enabling its use to refocus weak couplings for two geminal coupling partners ¹H^d even if embedded in a complex spin system. To make sure that both ¹J_CH evolution and chemical shift evolution of ¹H^d are refocused at time (III), proton inversion pulses are used at the midpoints of periods t′₂/2 + τ_a and t′₂/2 + τ_b. A combination of a broadband proton inversion and a BIRD^d element (inversion for ¹H^d only) is then used to replace the second 180° pulse of the perfect echo, preserving chemical shift evolution and heteronuclear couplings for ¹H^d while refocusing couplings between the prefocused diastereotopic protons, ¹H^d and ¹H^r, as well as heteronuclear long-range couplings, at the end of the pulse sequence element.

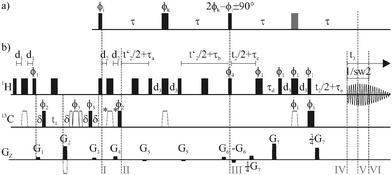Fig. 1 (a) Perfect echo pulse sequence as proposed by Takegoshi, Ogura and Hikichi.⁶ The pulse shown in grey can be dropped to introduce a net chemical shift evolution during 2τ. (b) A generalized pulse sequence for perfectBIRD homodecoupled HSQC experiments. Hard 90°-pulses are shown as narrow filled bars and 180°-pulses as wide filled bars, broadband inversion and refocusing pulses used on ¹³C are shown as open symbols. All experiments shown in the main text use t′₂ = t₂ to achieve decoupling for diastereotopic protons. In contrast, setting t′₂ = 0 for all t₂ allows the acquisition of clean absorptive doublets even for protons with non-negligible geminal coupling during d₂ (see the ESI†). The delays d₁ and d₃ are adjusted to match (4 ¹J_CH)⁻¹ and (2 ¹J_CH)⁻¹, respectively. In CLIP (CLean In-Phase) experiments d₂ = d₁ and the pulses marked with an asterisk are used, while in CLAP (CLean Anti-Phase) experiments these pulses are omitted and d₂ = δ.¹⁰δ equals the length of the gradients plus a recovery delay, τ_a = (4 sw2)⁻¹ + τ_c + τ_e + p₁ − 2 d₂ − p₃ − p₁₄, τ_b = (4 sw2)⁻¹ + τ_c + τ_e + p₁, τ_c = (4 sw2)⁻¹, τ_d = τ_c + τ_e, τ_e = δ + 350 μs, where p₁ and p₃ are the lengths of the hard 90° pulse on proton and carbon respectively and p₁₄ is the length of the broadband inversion pulse on ¹³C. G₂ and G₄ are set according to the ratio of gyromagnetic ratios and G₂ is inverted in alternating experiments to achieve the frequency sign encoding along t₁ according to the echo/antiecho procedure. The pulse phases used are: Φ₁ = 1, Φ₂ = 0 2, Φ₃ = 0 0 0 0 2 2 2 2, Φ₄ = 1 1 3 3, Φ_rec = 0 2 0 2 2 0 2 0.

A generalized pulse scheme for CLean In-/Anti-Phase¹⁰ (CLIP/CLAP) HSQC experiments, widely employed in the measurement of one-bond scalar and total couplings, that uses the perfectBIRD homonuclear decoupling element is given in Fig. 1b. The perfect echo period spans times (I) to (V), with its central mixing pulse positioned at (III). In contrast to the CLIP/CLAP HSQC experiments without homodecoupling, the direct acquisition period normally found after (II) is replaced by the perfectBIRD element described above.

Construction of a free induction decay with negligible homonuclear coupling modulation is achieved using the interferogram-based approach, recently employed in F₂-heterocoupled CLIP/CLAP HSQC spectra with BIRD decoupling in the proton dimension.^5g,h Data are collected between times (IV) and (VI), for time 1/sw2 equal to the time increment in t₂ and centred on the point of full coupling refocusing. Keeping 1/sw2 ≪ 1/(2 J_HH), where J_HH is of the order of typical proton–proton couplings, restricts data collection to times over which proton–proton coupling evolution can be neglected. A full 3D time domain signal s(t₁, t₂, t₃) is collected, from which a 2D signal s(t₁, t₂*) is constructed such that t₂* = t₂ + t₃. This leads to a signal sampled uniformly in t₂* for the total time (1/sw2) TD_F2, where TD_F2 is the number of points sampled in t₂. This data treatment requires 1/sw2 to be an integer multiple of the dwell time used for F₃. Construction of the 2D time signal from the 3D dataset is performed conveniently using a Bruker AU program available at http://nmr.chemistry.manchester.ac.uk/. Afterwards s(t₁, t₂*) can be subjected to double Fourier transformation as usual.

To illustrate the potential of perfectBIRD decoupled HSQC experiments, we determined one-bond ¹H–¹³C-RDCs for (+)-isopinocampheol (IPC, structure shown in Fig. 2) along the pure shift dimension (F₂*) of the experiments. This compound is frequently used for method development in RDC analysis due to its rigidity, the chemically differing entities present in the molecule and its good signal dispersion.

Fig. 2 F ₂-heterocoupled CLIP HSQC spectra without homonuclear decoupling (black), and with BIRD (blue) and with perfectBIRD (red) homonuclear decoupling during acquisition, collected for (+)-IPC in isotropic CD₂Cl₂ solution at 600 MHz proton frequency. Experiment durations were 10.5 min, 7.1 h and 9.4 h, respectively. The structure of the analyte is shown in the figure, with the numbering used. The corresponding proton spectrum is displayed at the top. For selected protons, traces along the proton dimension are shown. The decoupled spectra are shifted in the carbon dimension for easier comparison.

For the measurement of scalar one-bond heteronuclear coupling constants (¹J_CH), we collected ¹³C–¹H F₂-heterocoupled CLIP/CLAP HSQC spectra without ¹H–¹H homodecoupling,¹⁰ and with BIRD^5h and perfectBIRD decoupling in the proton dimension, for a sample containing (+)-IPC in isotropic solution. As shown in Fig. 2, good homonuclear decoupling is achieved for protons that are bound to primary and tertiary carbons with both BIRD and perfectBIRD decoupling. In contrast, geminal couplings in methylene groups, and signal distortions stemming from geminal coupling evolution during the pulse sequences, are only suppressed when the perfectBIRD decoupling element is used. A very clean baseline is obtained in homodecoupled CLAP spectra, as cross-peaks arising from long-range ¹H–¹³C-couplings are also suppressed by the decoupling scheme applied (see Fig. S1, ESI†). For many applications, these very favourable spectral properties more than compensate for the additional experiment time needed to collect the pure shift NMR spectra. It should be noted that there is also a modest (at least for small, rapidly-tumbling molecules) reduction in the signal intensity, and additional line broadening, due to transverse relaxation during the decoupling element. In our current implementation we chose to include the gradient pulses labelled 6 in Fig. 1, sacrificing a further factor of two in signal, in order to minimise spectral artefacts.

While one-bond coupling constant extraction is usually a minor problem in isotropic solution, the larger proton–proton couplings, resulting in increased line widths, and the wider range of one-bond coupling constants frequently complicate coupling constant extraction for weakly aligned samples. As shown in Fig. 3, homonuclear decoupling can lead to significant simplification of the spectra observed for weakly aligned samples, facilitating spectral interpretation and coupling constant extraction. The example shown demonstrates clearly the advantage of introducing the additional decoupling of diastereotopic methylene protons, although the reduction in signal intensity between BIRD and perfectBIRD decoupled experiments is more pronounced here, as transverse relaxation is faster in the aligned sample.

Fig. 3 F ₂-heterocoupled CLAP HSQC spectra of (+)-IPC in the PBDG/CD₂Cl₂ lyotropic liquid crystalline phase (Δν_Q = 107.6 Hz), collected without homonuclear decoupling (pos. black, neg. cyan), and with BIRD (pos. blue, neg. magenta) and with perfectBIRD (pos. red, neg. green) decoupling in the proton dimension at 600 MHz proton frequency. Experiment durations were 10.5 min, 2.8 h and 3.2 h, respectively. Traces taken along the proton dimension are shown in the insets. In the proton dimension, no chemical shift referencing has been applied.

A particular challenge in this system is the decoupling of protons 7a and 7s: at roughly −38.4 Hz, the geminal total coupling between these two protons is much larger than couplings typically observed in isotropic solution – a problem frequently encountered in RDC measurements. The solution is to increase the decoupling range by shortening the data chunk duration 1/sw2, once again allowing clean singlets to be obtained, but at a reduced signal to noise ratio.

During this study an alternative approach to suppress geminal couplings, using a constant-time variant of the BIRD decoupled experiment, was proposed.^5g The constant-time approach necessarily limits the range of couplings accessible, while the perfectBIRD method can accommodate a wide range of ²T_HH, making perfectBIRD particularly attractive for measurements on aligned samples.

Fig. 3 also illustrates a limitation of the perfectBIRD decoupling element when applied to anisotropic samples: decoupling only works properly for groups with a maximum of two geminal coupling partners. This is a direct consequence of the fact that the perfect echo only leads to full refocusing of coupling evolution for a single coupling, or if τ is short compared to all 1/T_HH. As both conditions are violated for methyl groups in anisotropic samples, the triplets observed using BIRD decoupling are only partially collapsed using perfectBIRD decoupling (see inset 10). In isotropic solution this problem does not arise.

In small organic molecules, strong coupling effects are quite common, though not present in the case studied. Neither the perfect echo nor the BIRD element will fully refocus the effects of strong coupling,^3b,11 and complete decoupling of strongly coupled protons remains an unsolved challenge in pure shift NMR (as in many other methods). The precise measurement of RDCs from strongly coupled spins is an issue best addressed using specialized approaches;¹² as illustrated in the ESI†, strong coupling can be identified in homodecoupled spectra through characteristic changes in signal shapes.

The spectra shown for (+)-IPC, and additional experiments on chloroform, representing a simple AX test system, were used to test the influence of perfectBIRD homonuclear decoupling on the accuracy and precision of coupling constant measurements (see ESI†). Considering accuracy first, under the experimental conditions used, systematic errors in homodecoupled measurements of coupling constants were less than 0.05 Hz, greater than those for measurements by some conventional methods but negligible in the context of RDC measurements that typically have uncertainties of several tenths of a Hz. In contrast, the precision of ¹T_CH measurements was significantly improved by homodecoupling in the practical example of (+)-IPC, because of the simplification of line shapes and the avoidance of signal overlap caused by homonuclear couplings.

The confidence intervals shown in Tables 1 and 2 have two contributions: a very conservative estimate of the possible effects of the systematic errors noted (±0.1 Hz, double the observed uncertainty range) and the results of confidence interval estimation performed according to the procedure of Kummerlöwe et al.¹³ In many cases these confidence intervals show a significant improvement with BIRD and perfectBIRD, particularly for methylene signals in the latter case. Couplings extracted from the CLAP HSQC spectra are given in Table S5 (ESI†). From the values obtained we conclude that homonuclear decoupling can indeed improve the precision of coupling constant measurements in the high-resolution proton dimension, which is particularly beneficial for RDC-based structure analysis in the case of diastereotopic methylene protons.

Table 1 Scalar couplings extracted from the CLIP HSQC spectra of (+)-IPC in isotropic CD₂Cl₂ solution shown in Fig. 2

	No decoupling	BIRD decoupling	PerfectBIRD decoupling
	^1 J CH / Hz	^1 J CH / Hz	^1 J CH / Hz
FID-res:	0.76 Hz	1.02 Hz	1.02 Hz
1	140.57 ± 0.32	140.56 ± 0.11	140.59 ± 0.11
2	126.67 ± 0.17	126.65 ± 0.11	126.59 ± 0.12
3	141.67 ± 0.11	141.69 ± 0.11	141.71 ± 0.12
4s	126.35 ± 0.18	126.35 ± 0.24	126.34 ± 0.13
4a	127.04 ± 0.12	127.02 ± 0.19	127.07 ± 0.13
5	140.79 ± 0.32	140.72 ± 0.14	140.64 ± 0.23
7s	134.87 ± 0.35	134.81 ± 0.13	134.79 ± 0.17
7a	136.98 ± 0.15	136.94 ± 0.20	136.94 ± 0.12
8	124.56 ± 0.16	124.51 ± 0.12	124.51 ± 0.12
9	123.61 ± 0.11	123.66 ± 0.11	123.70 ± 0.12
10	124.75 ± 0.13	124.69 ± 0.11	124.64 ± 0.15

---

Table 2 Total couplings extracted from the CLIP HSQC spectra of (+)-IPC in anisotropic CD₂Cl₂/PBDG solution (Δν_Q = 107.6 Hz) shown in Fig. S2 (ESI)

	No decoupling	BIRD decoupling	PerfectBIRD decoupling
	^1 T CH / Hz	^1 T CH / Hz	^1 T CH / Hz
FID-res:	0.76 Hz	3.05 Hz	3.05 Hz
1	160.67 ± 3.42	160.92 ± 0.84	160.19 ± 0.54
2	117.27 ± 1.60	117.00 ± 0.19	116.53 ± 0.47
3	158.31 ± 0.51	158.38 ± 0.33	158.51 ± 0.44
4s	144.03 ± 0.12	143.85 ± 0.37	143.83 ± 0.19
4a	122.54 ± 0.16	122.59 ± 0.44	122.56 ± 0.12
5	138.10 ± 0.97	137.40 ± 0.82	137.12 ± 1.00
7s	133.78 ± 1.77	134.03 ± 2.86	133.79 ± 0.32
7a	106.89 ± 1.04	106.98 ± 0.86	106.81 ± 0.77
8	131.70 ± 0.48	131.82 ± 0.59	131.66 ± 0.29
9	118.57 ± 0.19	118.71 ± 0.56	118.96 ± 0.47
10	121.28 ± 0.21	121.09 ± 0.60	120.87 ± 0.77

---

In this communication, we have introduced a homonuclear decoupling element, based on the BIRD and perfect echo techniques, which is able to collapse splittings due to geminal couplings between diastereotopic methylene protons. Pure shift F₂-heterocoupled HSQC spectra of exceptional quality can be obtained, allowing highly precise measurements of one-bond couplings in the high-resolution proton dimension, even in weakly aligned media. We expect that the extended measurement times needed for these experiments will prove to be well justified, by the higher precision of the coupling constants extracted and the improved ease of analysis, when complex structures are to be solved. Modifications of the technique that also achieve heteronuclear decoupling in the high-resolution dimension are under development, and could be used to collect HSQC spectra with full homo- and heteronuclear decouplings in both dimensions as well as very high resolution in the proton dimension.

Financial support of this work by the Merck Society for Arts and Science Foundation, the ERC (grant no. 257041), the Engineering and Physical Sciences Research Council (grant nos. EP/I007989/1 and EP/L018500/1) and by TÁMOP-4.2.2/A-11/1/KONV-2012-0025, OTKA K 105459, TÁMOP-4.2.4.A/2-11-1-2012-0001, Richter Gedeon Talentum Alapítvány is gratefully acknowledged.

Notes and references

1. (a) M. Nilsson and G. A. Morris, Chem. Commun., 2007, 933–935; (b) P. Sakhaii, B. Haase and W. Bermel, J. Magn. Reson., 2009, 199, 192–198; (c) N. H. Meyer and K. Zangger, Angew. Chem., Int. Ed., 2013, 52, 7143–7146; (d) L. Paudel, R. W. Adams, P. Király, J. A. Aguilar, M. Foroozandeh, M. J. Cliff, M. Nilsson, P. Sándor, J. P. Waltho and G. A. Morris, Angew. Chem., Int. Ed., 2013, 52, 11616–11619.
2. A. Lupulescu, G. L. Olsen and L. Frydman, J. Magn. Reson., 2012, 218, 141–146.
3. (a) A. Bax, A. F. Mehlkopf and J. Smidt, J. Magn. Reson., 1979, 35, 167–169; (b) J. R. Garbow, D. P. Weitekamp and A. Pines, Chem. Phys. Lett., 1982, 93, 504–509.
4. (a) K. Zangger and H. Sterk, J. Magn. Reson., 1997, 124, 486–489; (b) A. J. Pell, R. A. E. Edden and J. Keeler, Magn. Reson. Chem., 2007, 45, 296–316.
5. (a) A. Bax, J. Magn. Reson., 1983, 53, 517–520; (b) D. Uhrín, T. Liptaj and K. E. Kövér, J. Magn. Reson., Ser. A, 1993, 101, 41–46; (c) T. N. Pham, T. Liptaj, K. Bromek and D. Uhrín, J. Magn. Reson., 2002, 157, 200–209; (d) K. Fehér, S. Berger and K. E. Kövér, J. Magn. Reson., 2003, 163, 340–346; (e) K. E. Kövér and G. Batta, J. Magn. Reson., 2004, 170, 184–190; (f) C. M. Thiele and W. Bermel, J. Magn. Reson., 2012, 216, 134–143; (g) T. Reinsperger and B. Luy, J. Magn. Reson., 2014, 239, 110–120; (h) I. Timári, L. Kaltschnee, A. Kolmer, R. W. Adams, M. Nilsson, C. M. Thiele, G. A. Morris and K. E. Kövér, J. Magn. Reson., 2014, 239, 130–138.
6. K. Takegoshi, K. Ogura and K. Hikichi, J. Magn. Reson., 1989, 84, 611–615.
7. (a) C. M. Thiele, Concepts Magn. Reson., Part A, 2007, 30A, 65–80; (b) C. M. Thiele, Eur. J. Org. Chem., 2008, 5673–5685; (c) G. Kummerlöwe and B. Luy, TrAC, Trends Anal. Chem., 2009, 28, 483–493; (d) R. R. Gil, Angew. Chem., Int. Ed., 2011, 50, 7222–7224; (e) B. Böttcher and C. M. Thiele, eMagRes, John Wiley & Sons, Ltd, 2012, vol. 1, pp. 169–180.
8. P. C. M. van Zijl, C. T. W. Moonen and M. von Kienlin, J. Magn. Reson., 1990, 89, 28–40.
9. (a) J. A. Aguilar, M. Nilsson, G. Bodenhausen and G. A. Morris, Chem. Commun., 2012, 48, 811–813; (b) R. W. Adams, C. M. Holroyd, J. A. Aguilar, M. Nilsson and G. A. Morris, Chem. Commun., 2013, 49, 358–360; (c) B. Baishya, C. L. Khetrapal and K. K. Dey, J. Magn. Reson., 2013, 234, 67–74; (d) T. F. Segawa and G. Bodenhausen, J. Magn. Reson., 2013, 237, 139–146; (e) J. A. Aguilar, R. W. Adams, M. Nilsson and G. A. Morris, J. Magn. Reson., 2014, 238, 16–19.
10. A. Enthart, J. C. Freudenberger, J. Furrer, H. Kessler and B. Luy, J. Magn. Reson., 2008, 192, 314–322.
11. R. V. Mulkern, J. L. Bowers, S. Peled, R. A. Kraft and D. S. Williamson, Magn. Reson. Med., 1996, 36, 775–780.
12. (a) B. Yu, H. van Ingen, S. Vivekanandan, C. Rademacher, S. E. Norris and D. I. Freedberg, J. Magn. Reson., 2012, 215, 10–22; (b) B. Yu, H. van Ingen and D. I. Freedberg, J. Magn. Reson., 2013, 228, 159–165.
13. G. Kummerlöwe, S. Schmitt and B. Luy, Open Spectrosc. J., 2010, 4, 16–27.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details of the spectra shown, spectra with absorptive doublet features for geminal protons, experimental analysis of ¹J_CH accuracy and precision, figures with characteristic spectral features for strongly coupled systems, further spectra used for RDC extraction, pulse programs, structural models for IPC and RDC analysis results. See DOI: 10.1039/c4cc04217d

---