Amine-based solvents for exfoliating graphite to graphene outperform the dispersing capacity of N-methyl-pyrrolidone and surfactants

Abstract

Four organic amine-based solvents were discovered which enable direct exfoliation of graphite to produce high-quality and oxygen-free graphene nanosheets. These solvents outperform previously used solvents and additives such as N-methyl-pyrrolidone and surfactants in terms of their dispersing capacity. The resulting dispersions allow the facile fabrication of zeolitic imidazolate framework (ZIF)–graphene nanocomposites with remarkable CO₂ storage capability.

---

High-yield exfoliation and dispersion of graphene into the liquid phase is critical for both fundamental studies and practical applications.¹ Although the aggressive oxidation of graphite allows its exfoliation in polar solvents to yield graphene oxide (GO),² the structure and electrical properties of reduced GO (rGO) are never fully restored resulting in significant disadvantages for many applications. In order to overcome this issue, direct exfoliation of pristine graphite to obtain graphene would be the production method of choice. To date, coating graphene with a number of surfactants³ or polymers⁴ has been successful for its stabilization. However, we note that surfactants or polymers are third-phase dispersing agents and need to be removed after processing for most of the envisaged applications. It would thus be simpler and more attractive to work only with two-phase dispersion, i.e., solvent and graphene. This would have two distinct advantages: it can be easily scaled up and the obtained graphene is free from oxidation. The previously best known and most successful solvent for graphene exfoliation is N-methylpyrrolidone (NMP).^5a,b Despite extensive efforts in this field,^5,6 the exfoliation and dispersion of pristine graphene can only be achieved in a limited number of systems and suffer from drawbacks, such as relatively low concentration, and poor exfoliation quality and dispersion stability. In such scenarios it is important to develop novel solvents for graphene exfoliation, especially those with superior dispersing capability but with comparatively lower toxicity, to exploit the full potential of graphene chemistry.

Herein, we demonstrate a number of new solvents for graphite exfoliation yielding pristine few-layer graphene (FLG). We show that graphene can be exfoliated and dispersed at higher concentrations in four dispersing agents, namely 3,3′-iminobis(N,N-dimethylpropylamine) (DMPA), N-[3-(dimethylamino)propyl]methacrylamide (DMAPMA), 2-(tert-butylamino)ethyl methacrylate (BAEMA) and 2-(dimethylamino)ethyl methacrylate (MAEMA) than in any previously used solvents⁵ or surfactants.^3b,d,4a Molecular dynamics simulation rationalizes the existence of strong solvent–graphene interactions resulting in small free energy costs by dispersion. Finally, we show that these dispersions have promising applications in making conductive films and for the facile fabrication of zeolitic imidazolate framework-8 (ZIF-8)–graphene nanocomposites with high CO₂ storage capacity.

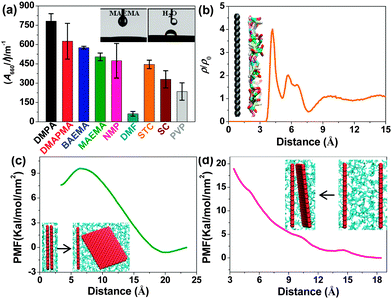
Materials and methods associated with the suggested process are described in detail in the ESI.† After being subjected to just 1 h of tip ultrasonication followed by centrifugation, stable graphene dispersions in nine amine-based solvents (Table S1, ESI†) were readily obtained. The Tyndall effect of the dispersion confirmed its colloidal nature (Fig. S1a, ESI†). As control, graphene dispersions were also prepared using other known good solvents such as NMP and dimethylformamide (DMF), the surfactants sodium cholate (SC) and sodium taurodeoxycholate (STC), and the polymer polyvinylpyrrolidone (PVP) at the optimal dispersant concentration in each case. Fig. 1a and Table S1 (ESI†) show the absorbance per unit-cell-length at 660 nm (A₆₆₀/l) of the resulting dispersions. Note that the four amine-containing acrylates DMPA, DMAPMA, BAEMA and MAEMA are substantially more effective in exfoliating graphene than the other tested solvents. In particular, the dispersing capacity of DMPA is more than 1.5 times higher than that of NMP. This is the first example of a solvent with a dispersing capacity surpassing the upper values observed in previously known solvents and in three-phase dispersions. Approximately 98% of graphene remained stably dispersed without sedimentation over long periods (Fig. S1b, ESI†). Importantly, DMAPMA, BAEMA and MAEMA compare more favourably than the most common graphene dispersing solvent, NMP, from the viewpoint of cost and hazard associated with the solvent (see ESI†). The dispersing capacity of 2-[[(butylamino)carbonyl]oxy]ethyl acrylate, 2-(diethylamino)ethyl metharylate, bis[2-(N,N-dimethylamino)ethyl] ether and 3-(diethylamino)propyl amine for graphene is much higher than DMF albeit lower than for NMP, SC, STC and PVP. Undoubtedly, this expands the library of available exfoliating solvents with new members, which should be very useful for further processing and applications of graphene. In all cases, the UV-Vis absorbance spectra appear flat and featureless. The absorption coefficient α (660 nm) was measured for a series of diluted samples, displaying a value of about 3417 mL mg⁻¹ m⁻¹ in agreement with earlier studies (Fig. S1c, ESI†).^5a,b The concentration remaining after centrifugation (C_G) can thus be estimated based on the Beer–Lambert law (A = aC_Gl; a is the absorption coefficient, and l is the cell length). Interestingly, the dispersion retained its high stability regardless of imposed harsh conditions, such as freezing in liquid N₂ (−196 °C) or heating (150 °C) for 2 h, or addition of 20 vol% of third-phase poor solvents such as ethanol, acetone, hexane, tetrahydrofuran, acetonitrile and benzene. For maximisation of the amount of dispersed graphene, the processing procedure was optimized (see Fig. S2a and b, ESI†). Starting with pre-exfoliated graphite in isopropanol obtained through 12 h of bath ultrasonication greatly promoted the exfoliation level attaining a graphene concentration of up to ≈1.4 mg mL⁻¹ in a yield of 14%. The concentration was further enhanced to 3.5 mg mL⁻¹ in a yield of ≈41% upon redispersing the sediments by means of 15 min of mild ultrasonication (Fig. S2c, ESI†). Furthermore, a dramatic increase in concentration to up to ≈15 mg mL⁻¹ was achieved simply by dispersing filtered few-layer graphene powder (Fig. S2d, ESI†). These high-concentration graphene dispersions will significantly facilitate practical applications such as composite formation.

Fig. 1 (a) A₆₆₀/l UV/VIS data for varying dispersions that were prepared in an analogous manner each at its optimal dispersant concentration (STC: 3, SC: 0.1, PVP: 10 mg mL⁻¹) (in all cases: initial graphite concentration C_G,I = 10 mg mL⁻¹). Inset: the photographs show the contact angle of MAEMA and water drops on graphite captured instantly. (b) Interfacial density profile of MAEMA on the graphene surface. Inset: interfacial snapshot. (c) Simulated PMF for the exfoliation process. (d) Simulated PMF for the aggregation process.

Contact angle measurements showed very good wettability of the graphitic surfaces in MAEMA (the inset of Fig. 1a). This observation may suggest large solvent–graphene interactions resulting in a small enthalpy of mixing, which is consistent with the results of molecular dynamics (MD) simulation (for details, see ESI†). Fig. 1b shows an obviously isolated solvent layer near the graphene surface, demonstrating that the strong affinity of the solvent molecules for graphene promotes the formation of an interfacial dense layer. Orientation analysis (Fig. S4, ESI†) reveals that MAEMA molecules exhibit a parallel packing performance near the carbon surface, which provides an improved surface interaction. Further steered MD simulation was carried out to evaluate the thermodynamic free energy (potential of mean force, PMF) for the exfoliation and aggregation between two single graphene sheets in the solvent. A small increase in PMF (Fig. 1c) during the exfoliation corresponds to a small energy cost of dispersion, whereas, as the two graphene sheets approach each other (Fig. 1d), an enhanced free energy barrier (≈7.8 kT nm⁻²) occurs suggesting that this solvent is able to provide effective resistance against the aggregation of graphene sheets. A further decomposition of the PMF (Fig. S5, ESI†) clearly reveals the solvent-induced effect. This PMF simulation shows on the molecular level that the proposed amine-based solvents can efficiently disperse and stabilize graphene.

To gain insight into the exfoliation level and quality of the dispersed flakes, a number of characterization methods were applied (vide infra). X-ray diffraction (XRD) patterns of the resulting samples indicate high crystallinity of the hexagonal structure. A significant weakening in the intensity of the (004) and the (006) reflections occurred (Fig. S5a, ESI†), which concurs with the characteristics observed for randomly stacked few-layer graphene.^4b No characteristic peak typical for graphene oxide at 10° was found, thus indicating the high quality of graphene without any oxidation. X-ray photoelectron spectroscopy (XPS) analysis revealed the dominant C 1s peak at 284.5 eV corresponding to sp² graphitic carbon (Fig. S5b, ESI†). The main C=C peak corresponds to ∼85.8% of the spectrum and the quantity of O in the graphene samples was estimated to be as low as 1.53 at%. The exfoliation process did not chemically functionalize the graphite flakes to a major extent. Typical scanning electron microscopy (SEM) images (Fig. S6a and b, ESI†) along with EDX elemental maps (Fig. S6c–f, ESI†) and transmission electron microscopy (TEM) (Fig. 2a and b) images show large quantities of graphene-like flakes stabilized by the amine-based solvent. Stacked thin sheets with a possibly folded morphology are shown in Fig. 2b. Thick multi-layer sheets were rarely observed. The exfoliated flakes appeared to be of high quality and free of holes or other damage. A small portion of few-layer graphene showed Moiré patterns due to rotational stacking faults, which likely resulted from the back folding of top graphene layers during exfoliation. Fig. 2c shows a high-resolution TEM (HRTEM) image of a flake with well-defined edges. The fast Fourier transform (FFT, inset) of the image shows intense {10-10} spots, whereas the {2-1-10} spots are too weak which is additionally indicative of monolayer graphene.^5a Fig. S7a (ESI†) and Fig. 2d–f show bilayer, trilayer, four- and five-layer graphene sheets, respectively. A filtered HRTEM image (Fig. 2g) of a thin flake clearly illustrates the hexagonal nature of the graphitic structure. Intensity analysis (Fig. 2h) along the dashed line in Fig. 2g reveals a hexagonal width of 0.24 nm close to the expected value of 0.25 nm.^3a The Raman spectrum of thin films prepared by filtering MAEMA dispersions shows an intense G band (≈1564 cm⁻¹), a second-order two phonon mode 2D (also called G′) band (≈2687 cm⁻¹) and a disorder-related D peak (≈1344 cm⁻¹) (Fig. S7c, ESI†). The 2D line can be described as a single symmetrical Lorentzian peak in agreement with the Raman spectrum of randomly stacked flakes comprising fewer than 5 layers. The average peak intensity of the D band relative to the G band (I_D/I_G) for 25 different regions is ≈0.17, which further demonstrates the high quality if it is compared to high-quality rGO showing an I_D/I_G ≥ 0.5.⁷ The in-plane crystallite size of graphene was determined to be approximately 129.6 ± 8.6 nm based on the integrated area ratio of the D band and G band (A_D/A_G) using the equation 560(A_D/A_G)⁻¹/E⁴, where E is the laser energy (1.96 eV).^4b The distance between defects, L_D, and the defect density in the basal plane of graphene, n_D, was calculated to be ≈49.0 ± 1.9 nm and ≈1.9 × 10¹⁰ ± 1.2 × 10⁹ cm⁻², respectively, using the approximations of L_D² (nm²) = 4300(I_D/I_G)⁻¹/E⁴ and n_D (cm⁻²) = 10¹⁴/πL_D².^4b Raman mapping of I_D/I_G (Fig. S7d, ESI†) over 25 regions (Fig. S7b, ESI†) displays low defect densities of graphene with an overall large domain size. Given that the area occupied by a carbon atom in graphite is (3^3/2/4)d², where d is the carbon–carbon bond length (0.1421 nm), the unperturbed domain size is correlated with about 91 200 carbon atoms, which is nine times larger than those (≤9900 carbon atoms) observed for chemically derived graphene.⁷ These results strongly suggest the high quality of graphene nanosheets produced using the approach proposed in this work.

Fig. 2 TEM images of (a) large numbers of few-layer graphene flakes and (b) stacked thin sheets with possibly folded edges. Graphene nanoribbons were occasionally observed as shown in (a) marked in the dashed rectangle. HRTEM images of (c) monolayer, (d) trilayer, (e) four- and (f) five-layer graphene sheets. Inset in (c): FFT pattern displaying a six-fold symmetry typical of the hexagonal crystal structure. (g) A filtered HRTEM image of FLG. (h) Intensity analysis along the dashed line in (g).

Solvent-stabilized graphene dispersions can be used in a range of applications including the formation of conductive films. The film prepared from dispersions in MAEMA without annealing exhibited a mean conductivity of 1.9 ± 0.4 ×10⁴ S m⁻¹. This value compares well with films formed by filtration of NMP-based graphene dispersions.^5b High-concentration graphene dispersions also allow the design of new graphene-based nanocomposites using solution chemistry. We demonstrate the facile fabrication of ZIF-8 nanocrystals (NCs) at ambient T and low ZIF precursor concentration (0.17 mg mL⁻¹) in MAEMA. The reaction temperature (∼22 °C) is far below 80 °C employed in previous amide systems.^8a The rapid formation of ZIF-8 likely originated from the strong deprotonating nature of the solvent MAEMA. Furthermore, ZIF-8 NCs with a mean size of 37.8 nm were found to readily decorate the surface of the graphene sheets (Fig. 3a, Fig. S8 and S9, ESI†). To our knowledge, this is the first example of incorporation of a metal–organic framework structure with pristine graphene. Most previous studies employed graphene oxide, the properties of which are substantially different due to the high defect concentration from those of pristine graphene.^8b The composites displayed enhanced CO₂ uptake (64.4 mL (STP) g⁻¹ at 1 (p/p₀)) compared to pristine FLG (21.0 mL (STP) g⁻¹) (Fig. 3b), showing a great potential in CO₂ hydrogenation catalysis. Further work in this area is underway.

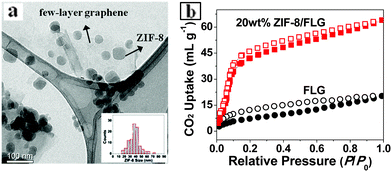Fig. 3 (a) TEM image of ZIF-8/FLG. Inset: size-distribution histogram of ZIF-8 NCs. (b) CO₂ adsorption–desorption isotherms (at 195 K) for FLG and 20 wt% ZIF-8/FLG.

In conclusion, we have demonstrated nine novel solvents in which high-yield stable graphene dispersions were obtained directly from graphite without resorting to rigorous oxidation and reduction chemistry. This breakthrough will pave the way towards the scaling up of graphene production, thus making it very useful for further processing and applications.

This work was supported by the Cluster of Excellence RESOLV (EXC 1069) funded by the Deutsche Forschungsgemeinschaft (DFG).

Notes and references

1. (a) J. Malig, N. Jux and D. M. Guldi, Acc. Chem. Res., 2013, 46, 53; (b) J. N. Coleman, Acc. Chem. Res., 2013, 46, 14; (c) A. Ciesielskia and P. Samorì, Chem. Soc. Rev., 2014, 43, 381; (d) W. Du, X. Jiang and L. Zhu, J. Mater. Chem. A, 2013, 1, 10592.
2. W. S. Hummers and R. E. Offeman, J. Am. Chem. Soc., 1958, 80, 1339.
3. (a) M. Lotya, Y. Hernandez, P. J. King, R. J. Smith, V. Nicolosi, L. S. Karlsson, F. M. Blighe, S. De, Z. Wang, I. T. McGovern, G. S. Duesberg and J. N. Coleman, J. Am. Chem. Soc., 2009, 131, 3611; (b) M. Lotya, P. J King, U. Khan, S. De and J. N. Coleman, ACS Nano, 2010, 4, 3155; (c) J. W. T. Seo, A. A. Green, A. L. Antaris and M. C. Hersam, J. Phys. Chem. Lett., 2011, 2, 1004; (d) Z. Sun, J. Masa, Z. Liu, W. Schuhmann and M. Muhler, Chem. – Eur. J., 2012, 18, 6972.
4. (a) A. S. Wajid, S. Das, F. Irin, H. S. T. Ahmed, J. L. Shelburne, D. Parviz, R. J. Fullerton, A. F. Jankowski, R. C. Hedden and M. J. Green, Carbon, 2012, 50, 526; (b) Z. Sun, S. Pöller, X. Huang, D. Guschin, C. Taetz, P. Ebbinghaus, J. Masa, A. Erbe, A. Kilzer, W. Schuhmann and M. Muhler, Carbon, 2013, 64, 288; (c) Z. Sun, J. Vivekananthan, D. A. Guschin, X. Huang, V. Kuznetsov, P. Ebbinghaus, A. Sarfraz, M. Muhler and W. Schuhmann, Chem. – Eur. J., 2014, 20, 5752.
5. (a) Y. Hernandez, V. Nicolosi, M. Lotya, F. M. Blighe, Z. Sun, S. De, I. T. McGovern, B. Holland, M. Byrne, Y. K. Gun'ko, J. J. Boland, P. Niraj, G. Duesberg, S. Krishnamurthy, R. Goodhue, J. Hutchison, V. Scardaci, A. C. Ferrari and J. N. Coleman, Nat. Nanotechnol., 2008, 3, 563; (b) U. Khan, A. O'Neill, M. Lotya, S. De and J. N. Coleman, Small, 2010, 6, 864; (c) A. O'Neill, U. Khan, P. N. Nirmalraj, J. Boland and J. N. Coleman, J. Phys. Chem. C, 2011, 115, 5422.
6. A. J. Oyer, J. M. Y. Carrillo, C. C. Hire, H. C. Schniepp, A. D. Asandei, A. V. Dobrynin and D. H. Adamson, J. Am. Chem. Soc., 2012, 134, 5018.
7. S. Eigler, M. Enzelberger-Heim, S. Grimm, P. Hofmann, W. Kroener, A. Geworski, C. Dotzer, M. Rockert, J. Xiao, C. Papp, O. Lytken, H. P. Steinruck, P. Müller and A. Hirsch, Adv. Mater., 2013, 25, 3583.
8. (a) A. Phan, C. J. Doonan, F. J. Uribe-Romo, C. B. Knobler, M. O'Keeffe and O. M. Yachi, Acc. Chem. Res., 2010, 43, 58; (b) R. Kumar, K. Jayaramulu, T. K. Maji and C. N. R. Rao, Chem. Commun., 2013, 49, 4947.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental and simulation details, SEM, XRD, XPS and TGA. See DOI: 10.1039/c4cc03923h

---