Polygermanes: bandgap engineering via tensile strain and side-chain substitution

Abstract

Successful synthesis of the phenylisopropyl hexagermane (Chem. Commun. 2013, 49, 8380) offers an exciting opportunity to synthesize a new class of low-dimensional germanium compounds with novel optical and electronic properties. Using the phenylisopropyl hexagermane as a model template, we have performed an ab initio study of electronic properties of polygermanes. Our density functional theory calculations show that the polygermane is a quasi-one-dimensional semiconductor with a direct bandgap, and its valence and conduction bands are mainly contributed by the skeletal Ge atoms. We have also explored effects of tensile and compressive strains and various side-chain substituents on the bandgap. The bandgap of polygermanes can be reduced upon attaching larger-sized substituents to the side chains. More importantly, applying a tensile/compressive strain can modify the bandgap of polygermanes over a wide range. For poly(diphenlygermane), the tensile strain can result in significant bandgap reduction due to the increasingly delocalized charge density in the conduction band. Moreover, a strong compressive strain can induce a direct-to-indirect semiconductor transition owing to the change made in the band-edge states. A similar strain effect is seen in polystannanes as well.

---

Polymers and catenated compounds of the heavier group 14 elements have attracted growing interest due to their intriguing optical and electronic properties stemming from their inherent σ-delocalization. Their potential applications include use in photoconductors, optical materials, and nonlinear optics.^1–12 Although synthesis and properties of silicon- and tin-containing polymers and oligomers have been intensively studied, the related germanium congeners have received less attention due in part to the challenge in obtaining germanium oligomers with suitably high yields. Nevertheless, the promise of new optical and electronic properties of organogermanium compounds, which may be enhanced relative to silicon-based analogues owing to the smaller band gap and higher electron and hole mobility in germanium, has prompted persistent efforts in their preparation and characterization.^13–18 Recently, a linear phenylisopropyl hexagermane, Prⁱ₃Ge(GePh₂)₄GePrⁱ₃, has been successfully synthesized.¹⁹ This Ge₆ compound is the longest linear molecular oligogermane characterized to date, which can be viewed as a validation of the conjecture that discrete linear oligogermanes with sufficiently long Ge chains might exhibit similar properties to their polymeric analogues. For instance, like polygermanes,⁶ the phenylisopropyl hexagermane exhibits fluorescence in the near UV region. Considering that the linear Ge₆ compound can serve as an effective oligomer model for long polygermane systems, it is interesting and timely to investigate the structural and electronic properties of polygermanes, especially poly(diphenylgermane) (GePh₂)_n. To this end, we have explored bandgap engineering in polygermanes by changing the substituents in the side chains or by applying mechanical strains, using first-principles density functional theory (DFT) calculations. Strain engineering is known as an effective approach to achieve continuously tunable bandgaps as those successfully done in quasi-one-dimensional boron nitride (BN) nanoribbons and quasi-two-dimensional transition-metal dichalcogenides.^20–25 Moreover, the importance of strain engineering in germanium has also been demonstrated since tensile strain can not only increase the light emission efficiency but also tune the emission wavelength.^26,27 Here, we show that polygermanes are quasi-one-dimensional semiconductors. Importantly, the bandgap of polygermanes can be tuned over a wide range by applying either tensile or compressive strains. Like other low-dimensional semiconducting materials, such as graphene or BN nanoribbons, relatively large strains may be applied onto the more flexible polygermanes to achieve wider tunability of the bandgap. If confirmed experimentally, the strain engineering of the semiconducting polygermanes may be exploited for applications in nanoelectronic or optoelectronic devices.

Structure optimization was carried out using a three-dimensional periodic tetragonal supercell, which contains four Ge atoms along the z axis to fully simulate the structural segments in linear Prⁱ₃Ge(GePh₂)₄GePrⁱ₃. DFT calculations are performed within the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA).²⁸ More computational details are given in the ESI.† In addition, calculation results based on the more accurate hybrid HSE06 functional are also given in the ESI,† which confirm the trend of the bandgap change predicted by the PBE calculations.

First, the atomic positions and z-lattice vector are relaxed to obtain the optimized geometry of (GePh₂)_n. Although the Ge–Ge single bond distance in discrete oligogermanes is typically within the range of 2.43–2.49 Ų⁹ (e.g., the recently reported value of 2.4710(3) Å for the hexagermane¹⁹), it is acceptable that the calculated average Ge–Ge bond distance in a unit cell of (GePh₂)_n is 2.549 Å, in view of overestimation of the bond lengths by PBE calculations.³⁰ The calculated average Ge–Ge–Ge bond angle of (GePh₂)_n is 115.16°, very close to the average value of 115.74(1)° measured in Prⁱ₃Ge(GePh₂)₄GePrⁱ₃.¹⁹

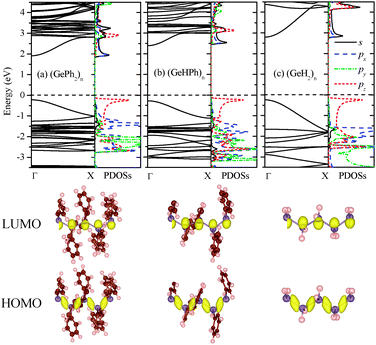
Next, the band structure of (GePh₂)_n was computed. As shown in Fig. 1(a), it is clear that poly(diphenylgermane) is a semiconductor with a direct bandgap of 2.13 eV at the Γ point. By substituting the phenyl group(s) in (GePh₂)_n with H atom(s), poly(hydrophenylgermane) (GeHPh)_n or poly(dihydrogermane) (GeH₂)_n is obtained. Their band structures are shown in Fig. 1(b) and (c), respectively. Both exhibit a direct band gap, of 2.72 and 3.03 eV, respectively. Thus, the bandgap can be reduced by several tenths of eV when larger substituents are attached. The band-edge states are mainly contributed by the skeletal Ge atomic orbital (AO). As shown by computed charge density distribution and partial density of states (PDOSs) of Ge atoms (Fig. 1), the lowest unoccupied molecular orbital (LUMO) is mainly contributed by the skeletal Ge 4s and 4p_x AOs while the highest occupied molecular orbital (HOMO) is composed mainly of Ge 4p_z (along the skeletal axis). So the bandgap reduction is relatively small even when the side-chain groups are changed dramatically from H to phenyl, which is similar to that of polysilanes whose band-edge states are mainly contributed by the skeletal Si AOs.³¹ For (SiXY)_n, the bandgap is 4.53, 3.73, and 3.61 eV for XY = H₂, HPh, and Ph₂, respectively.

Fig. 1 Computed band structures and PDOSs of Ge atoms in the unit cell of (a) (GePh₂)_n, (b) (GeHPh)_n, and (c) (GeH₂)_n. The s, p_x, p_y, and p_z PDOSs are denoted by solid, dashed, dash dot, and short dashed lines, respectively. The purple, brown, and pink balls represent Ge, C, and H atoms, respectively. The Fermi level is marked by a horizontal dashed line. The lower panels illustrate the charge density distribution of HOMO and LUMO bands, respectively. The isosurface value is 0.008 e Å⁻³.

As noted above, the average Ge–Ge bond lengths of (GeHPh)_n and (GeH₂)_n are 2.469 and 2.451 Å, respectively, both shorter than that of (GePh₂)_n. When larger functional groups are substituted in the side chains, the average Ge–Ge bond lengths are expected to be longer, which is likely responsible for the slight reduction of the bandgap. Thus, we speculate that applying mechanical strains to the skeletal Ge chains may be an effective way to tune the bandgap of polygermanes. Compared to bulk materials, low-dimensional materials often allow a larger dynamic range for elastic strain.²² For example, a maximum elastic strain even over 20% was predicted for the boron nitride nanoribbon systems.³²

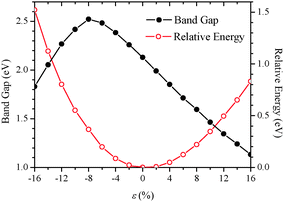
Fig. 2 displays computed relative energies and bandgaps of (GePh₂)_n with respect to the uniaxial strain along the z-direction. The strain ε is defined as ε = (c − c₀)/c₀%, where c and c₀ are the z-lattice parameters with and without the deformation. Clearly, the change in relative energies exhibits a monotonically increased tendency for both compressive and tensile strains, indicating that the wide strain range considered is elastic, that is, no structural transition or breakage occurs in the strain range considered. In this strain range, a monotonic decrease of bandgaps with strains is observed. For example, 16% tensile strain reduces the bandgap of (GePh₂)_n to 1.131 eV, about a half of the bandgap of unstrained (GePh₂)_n. Hence, the bandgap of poly(diphenylgermane) can be broadly tuned by applying uniaxial elastic strains. Under compression, the bandgap is enlarged initially until ε = −8%, then decreases with a further increase of the compressive strain. To understand the origin of this strain dependence of the bandgap, computed band structures and charge densities at different strains are shown in Fig. 3 and 4.

Fig. 2 Computed bandgap and relative energy of (GePh₂)_nvs. strain ε. Strain is applied to the optimized structure (ε = 0) through uniaxial deformation in the z-direction, for which negative ε represents compressive strain and positive tensile strain.

Fig. 3 Computed (a) band structure of (GePh₂)_n under different uniaxial tensile strains. PDOSs of Ge atoms at the strains of 4% and 16% are displayed for comparison; (b) charge densities of HOMO and LUMO states at ε = 16%.

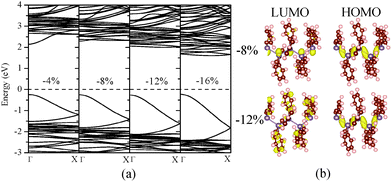Fig. 4 Computed (a) band structure of (GePh₂)_n under different uniaxial compressive strains; (b) charge densities corresponding to the HOMO and LUMO states at ε = −8 or ε = −12%.

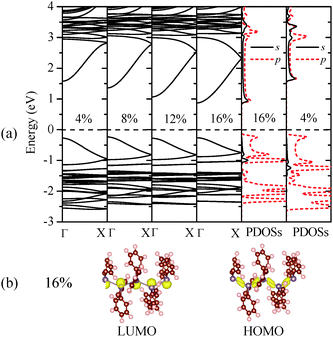
Fig. 3(a) shows that the direct-bandgap character of (GePh₂)_n is still retained under different uniaxial tensile strains. As the tensile strain increases, the HOMO band exhibits little changes, while the LUMO band is relocated closer to the Fermi level, leading to reduced bandgaps. The computed PDOSs offer more insight into the mechanism of bandgap reduction induced by the tensile strains. By comparing the PDOSs shown in Fig. 3(a) it was found that the conduction band bottom states span over a broader energy range (∼1.5 eV) at ε = 16% than that (∼1.2 eV) at ε = 4%, consistent with their band structures. Thus, at higher tensile strains, the LUMO states are more delocalized due to the extended Ge–Ge bond lengths. For the HOMO, however, no alteration is seen in the corresponding charge densities at different tensile strains. As shown in Fig. 3(b), even when the tensile strain reaches 16%, the charge density distribution in the band-edge states retains the same skeletal-Ge characteristics. We thus conclude that the increase of the average Ge–Ge bond length in polygermanes leads to increasingly delocalized conduction band bottom states and thus reduced bandgaps.

A similar mechanism is applicable for relatively weak compressive strains (up to ε = −8%), at which the compressed (GePh₂)_n still exhibits a direct bandgap with the band-edge states of Ge AOs given in Fig. 4. The enlarged bandgap from 2.129 to 2.522 eV under the compressive strain from 0 to −8% can be related to the decreased average Ge–Ge bond length from 2.549 to 2.479 Å and therefore the upward shift of the lowest conduction band. For the compressive strain beyond −8%, the bandgap is reduced and changed to an indirect gap. By analysis of charge densities of HOMO and LUMO states, it can be seen from Fig. 4(b) that although the HOMO state still stems from the skeletal Ge 4p_z orbitals, the LUMO state is mainly contributed by the side-chain substituents for the compressive strain beyond −8%. Thus, the bandgap reduction under higher compressive strains is due to the variation in band-edge states. In passing, we note that polystannanes possess qualitatively similar electronic properties with either side-chain substituents or under mechanical strains. The results of strain engineering of the bandgap are given in the ESI.†

In conclusion, we have performed DFT calculations to study effects of side-chain substitution and mechanical strains on the electronic properties of polygermanes. Polygermanes exhibit a direct bandgap character and their band-edge states are attributed mainly to skeletal Ge, which can lead to relatively small band-gap reduction when the side-chain groups are changed from H to phenyl. On the other hand, the bandgap of polygermanes can be tuned over a much broader range by applying mechanical strains. It is found that under the tensile strains, the bandgap of (GePh₂)_n decreases with the increase of strain since the conduction band bottom states become more delocalized. Compressive strains up to −8% can enlarge the bandgap. Further increase of the compressive strain results in the direct-to-indirect bandgap transition with a gradually reduced bandgap due to the variation of band-edge states.

We are grateful to Dr Shuang Chen and Dr Ning Lu for valuable discussions. WF acknowledges the Natural Science Foundation of China under No. 11074107, the State Scholarship Fund provided by the China Scholarship Council through No. 201308320156, and the computing support by the High Performance Computing Center of Nanjing University. XCZ was supported by ARL (Grant No. W911NF1020099) and the UNL Holland Computing Center.

Notes and references

1. R. D. Miller and J. Michl, Chem. Rev., 1989, 89, 1359–1410.
2. R. G. Jones and S. J. Holder, Polym. Int., 2006, 55, 711–718.
3. T. Hayashi, Y. Uchimaru, N. P. Reddy and M. Tanaka, Chem. Lett., 1992, 647–650.
4. J.-C. Baumert, G. C. Bjorklund, D. H. Jundt, M. C. Jurich, H. Looser, R. D. Miller, J. Rabolt, R. Sooriyakumaran, J. D. Swalen and R. J. Twieg, Appl. Phys. Lett., 1988, 53, 1147–1149.
5. T. Kodaira, A. Watanabe, O. Ito, M. Matsuda, S. Tokura, M. Kira, S. Nagano and K. Mochida, Adv. Mater., 1995, 7, 917–919.
6. Y. Huo and D. H. Berry, Chem. Mater., 2005, 17, 157–163.
7. J.-P. Majoral and A.-M. Caminade, Chem. Rev., 1999, 99, 845–880.
8. M. L. Amadoruge and C. S. Weinert, Chem. Rev., 2008, 108, 4253–4294.
9. Y. Y. Durmaz, M. Kukut, N. Monszner and Y. Yagci, Macromolecules, 2009, 42, 2899–2902.
10. M. Okano, N. Matsumoto, M. Arakawa, T. Tsuruta and H. Hamano, Chem. Commun., 1998, 1799–1800.
11. F. Choffat, P. Smith and W. Caseri, Adv. Mater., 2008, 20, 2225–2229.
12. M. Trummer, F. Choffat, P. Smith and W. Caseri, Macromol. Rapid Commun., 2012, 33, 448–460.
13. T. Azemi, Y. Yokoyama and K. Mochida, J. Organomet. Chem., 2005, 690, 1588–1593.
14. M. L. Amadoruge, J. A. Golen, A. L. Rheingold and C. S. Weinert, Organometallics, 2008, 27, 1979–1984.
15. M. L. Amadoruge, A. G. DiPasquale, A. L. Rheingold and C. S. Weinert, J. Organomet. Chem., 2008, 693, 1771–1778.
16. C. S. Weinert, Dalton Trans., 2009, 1691–1699.
17. E. K. Schrick, T. J. Forget, K. D. Roewe, A. C. Schrick, C. E. Moore, J. A. Golen, A. L. Rheingold, N. F. Materer and C. S. Weinert, Organometallics, 2013, 32, 2245–2256.
18. Y. Matsuura, J. Appl. Phys., 2014, 115, 043701.
19. K. D. Roewe, A. L. Rheingold and C. S. Weinert, Chem. Commun., 2013, 49, 8380–8382.
20. F. Guinea, M. I. Katsnelson and A. Geim, Nat. Phys., 2010, 6, 30–33.
21. Z. H. Ni, T. Yu, Y. H. Lu, Y. Y. Wang and Y. P. Feng, ACS Nano, 2008, 11, 2301–2305.
22. T. Zhu and J. Li, Prog. Mater. Sci., 2010, 55, 710–757.
23. J. Qi, X. Qian, L. Qi, J. Feng, D. Shi and J. Li, Nano Lett., 2012, 12, 1224–1228.
24. P. Johari and V. B. Shenoy, ACS Nano, 2012, 6, 5449–5456.
25. N. Lu, H. Guo, L. Li, J. Dai, L. Wang, W.-N. Mei, X. Wu and X. C. Zeng, Nanoscale, 2014, 6, 2879–2886.
26. J. R. Sánchez-Pérez, C. Boztug, F. Chen, F. F. Sudradjat, D. M. Paskiewicz, R. B. Jacobson, M. G. Lagally and R. Paiella, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 18893–18898.
27. M. J. Süess, R. Geiger, R. A. Minamisawa, G. Schiefler, J. Frigerio, D. Chrastina, G. Isella, R. Spolenak, J. Faist and H. Sigg, Nat. Photonics, 2013, 7, 466–472.
28. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
29. M. Dräger, L. Ross and D. Simon, Rev. Silicon, Germanium, Tin Lead Compd., 1983, 7, 299.
30. K. Y. Kim, D. Cho, B. Cheong, D. Kim, H. Horii and S. Han, J. Appl. Phys., 2013, 113, 134302.
31. K. Takeda, H. Teramae and N. Matsumoto, J. Am. Chem. Soc., 1986, 108, 8186–8190.
32. M. Topsakal and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 024107.

---

Footnote

† Electronic supplementary information (ESI) available: Computational details; comparison using the LDA and GGA exchange–correlation functionals; results of the hybrid HSE06 functional calculations; GGA results of electronic properties of polystannanes and effects of mechanical strains. See DOI: 10.1039/c4cc03907f

---