A new metal–organic framework with ultra-high surface area

Abstract

A new mesoporous MOF, Zn₄O(bpdc)(btctb)_4/3 (DUT-32), containing linear ditopic (bpdc²⁻; 4,4′-biphenylenedicarboxylic acid) and tritopic (btctb³⁻; 4,4′,4′′-[benzene-1,3,5-triyltris(carbonylimino)]tris-benzoate) linkers, was synthesised. The highly porous solid has a total pore volume of 3.16 cm³ g⁻¹ and a specific BET surface area of 6411 m² g⁻¹, adding this compound to the top ten porous materials with the highest BET surface area.

---

During the last two decades metal–organic frameworks (MOFs) have continuously set new records in terms of specific surface area and pore volume, pushing the high pressure storage capacity for energetic molecules such as hydrogen and methane further and further.¹

In order to avoid the disadvantageous formation of interpenetrated structures we propose the use of two different types of elongated linkers, one with a polar functionality, and another with a purely aromatic core structure. In the following we will show that this concept leads to a highly porous non-interpenetrated MOF structure but requires a distinct activation procedure due to the stronger interaction forces between solvating molecules and the polar functional groups of one linker.

As the polar tritopic linker 4,4′,4′′-[benzene-1,3,5-triyltris(carbonylimino)]trisbenzoic acid (H₃btctb), which has been very successfully applied in the synthesis of porous MOFs,² was used. 4,4′-Biphenylenedicarboxylic acid (H₂bpdc) was chosen as the more hydrophobic linker because of the ideal di- and tritopic linker length ratio (L_D/L_T) of 0.63. According to Matzger et al., for the formation of copolymerization MOFs, the geometric factor describing the length ratio of the linkers as well as the connectivity to the cluster plays a key role in the formation of the given structure.³ For known MOFs the L_D/L_T ratios lie within a region from 0.44 to 0.66 (Table S1, ESI†).

The solvothermal reaction of H₃btctb and H₂bpdc with zinc nitrate yields coffin-shaped transparent crystals of Zn₄O(bpdc)(btctb)_4/3 (DUT-32, DUT – Dresden University of Technology), while an excess of H₃btctb or H₂bpdc in the reaction mixture leads to the formation of byproducts: Zn₄O(btctb)₂ (DUT-59), Zn₄O(btctb)₂(DMF)(H₂O)_1.5 (ref. 2a) or Zn₄O(bpdc)₃ (IRMOF-10).⁴ DUT-59 is isoreticular to MOF-177⁵ (for more details see ESI†).

Interestingly, DUT-32 has a framework isorecticular to UMCM-2⁶ with a rare umt topology crystallizing in the P6₃/m space group.‡ The phase purity of bulk samples of DUT-32 was confirmed by powder X-ray diffraction measurements (see ESI†). The overall composition of the solvated material was determined by thermal (Fig. S7, ESI†) and elemental analysis, as well as ¹H-NMR (Fig. S8, ESI†), and can be described as Zn₄O(bpdc)(btctb)_4/3(DEF)_39.7(H₂O)_11.3.

The structure of DUT-32 consists of two symmetry-independent Zn₄O⁶⁺ octahedral secondary building units. Both of them are surrounded by four btctb³⁻ and two bpdc²⁻ linkers. The ditopic bpdc²⁻ ligands at the first Zn₄O⁶⁺ cluster are arranged in a trans orientation, while the cis orientation of linkers relative to each other is found at the second cluster (Fig. 1 and Fig. S5, ESI†). With these types of connectivity, a 3D framework is constructed with three different but huge mesopores (30 × 40 Å, 28 × 32 Å and 20 × 26 Å, considering van der Waals radii of the atoms), and one smaller micropore (14 × 18 Å) (Fig. S1 and S2, ESI†). The crystallographic density of the desolvated DUT-32 is extremely low, only 0.27 g cm⁻³, and is close to the density of MOF-210 (0.25 g cm⁻³).⁷

Fig. 1 (a) Two crystallographically independent diastereomeric SBUs in DUT-32; (b) simplified representation of DUT-32. Cluster – green, tritopic linker – blue, ditopic linker – orange.

However, not only the crystallographic porosity, but also real gas accessible volume of the compound generated after removal of solvent molecules are crucial for the manufacture of porous materials for numerous areas of application. Activation of DEF-containing DUT-32 samples by conventional heating under vacuum results in a non-porous materials. Similar results were observed for the solvent-exchange activation method using dichloromethane, chloroform or alcohols like methanol or ethanol.

For supercritical drying, the amide solvent incorporated into the pores was exchanged first with absolute ethanol, which shows high miscibility with liquid CO₂ and is commonly used for MOF activation. The resulting material exhibits an unexpected type IV nitrogen physisorption isotherm and relatively low BET surface area (838 m² g⁻¹) and micropore volume (0.36 cm³ g⁻¹) (Fig. S9, ESI†) indicating a network distortion. However, a very high total pore volume of 2.91 cm³ g⁻¹ was calculated. PXRD measurements performed for the sample after drying indicate a complete loss of crystallinity.

Interestingly, a resolvation of this amorphous material with DEF and heating at 373 K for one day restores the crystallinity partly (Fig. S6a, ESI†). We suggest that due to its ability to form hydrogen bonds, ethanol binds quite strongly to the amide moieties of the network. Therefore, a complete exchange of the ethanol by CO₂ within the pores does not occur, leading to a structural rearrangement with a loss of crystallographically defined porosity during removal of residual ethanol. A complete structural collapse of the network probably does not occur because of the extremely high total pore volume which is close to the theoretical value of 3.21 cm³ g⁻¹, the completely intact morphology of the dried crystals and the recovery of the network by resolvation.

For the supercritical drying process the choice of the solvent is mainly based on its miscibility with liquid CO₂.^8,9 Therefore, the influence of solvents with minor polarity on the porosity was investigated. Applying the same drying protocol but using anhydrous acetone instead of ethanol on the same material (sample mass 100 mg) with a resting time in CO₂ of one day (replacing the liquid CO₂ 3 times a day) resulted in a material with completely different textural properties. PXRD measurements show that the crystallinity of the sample remains intact (Fig. S6, ESI†). This is also reflected in the N₂ physisorption isotherm which shows a typical shape for a MOF material with small mesopores and reaches saturation at 935 cm³ g⁻¹, indicating a total pore volume of 1.44 cm³ g⁻¹ (Fig. S9b, ESI†).

However, this value remains too low in comparison to the geometrically calculated pore volume of 3.21 cm³ g⁻¹, indicating insufficient activation. Interestingly, upon decreasing the amount of the sample for SCD drying from 100 mg to 30 mg and keeping the resting time in liquid CO₂ and replacement cycles the same (one day, three times a day, respectively), a sample with a significantly enhanced porosity was obtained. The adsorbed N₂ volume reaches a value of 1470 cm³ g⁻¹ representing a total pore volume of 2.27 cm³ g⁻¹ (Fig. S9b, ESI,† circles). Similar results can be observed by using amyl acetate instead of acetone indicating that for larger amounts of the sample the solvent exchange process with liquid CO₂ takes more time. These results show that the MOF/liquid_CO₂ ratio as well as resting time in liquid CO₂ (or corresponding CO₂ exchange frequency) have a crucial impact on the textural properties of DUT-32.

It could be shown that by systematically extending the resting time in liquid CO₂ (and exchange frequency), the porosity of DUT-32 can be significantly improved, finally reaching the theoretical limit (Fig. 2). The nitrogen uptake at 77 K increases steadily from 935 cm³ g⁻¹ (one day in liquid CO₂) up to a maximum of 2040 cm³ g⁻¹ (seven days in liquid CO₂). The maximum value corresponds to a specific pore volume of 3.16 cm³ g⁻¹, which is remarkable. A further increase of exchange time to ten days showed only a slight porosity improvement with an adsorbed volume of nitrogen of 2080 cm³ g⁻¹.

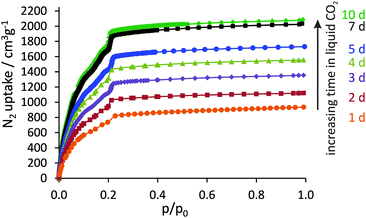Fig. 2 N₂ physisorption isotherms at 77 K of DUT-32 after supercritical drying from amyl acetate as solvent with different resting times in liquid CO₂ during the drying process.

Applying consistency criteria suggested by Rouquerol and Llewellyn¹⁰ to the N₂ physisorption isotherm for a sample with a resting time of seven days in liquid CO₂ (further denoted as DUT-32_7d) results in an apparent BET surface area as high as 6411 m² g⁻¹ (see ESI†). This value is close to the geometrical surface area of DUT-32 calculated using the Poreblazer V1.2 program¹¹ (5981 m² g⁻¹). Additionally, the nitrogen adsorption isotherm was simulated using multipurpose simulation code MUSIC.¹² The simulated isotherm fits well with the experimental one (Fig. S13, ESI†). By applying the BET theory to the simulated isotherm in the same relative pressure region as for the experimental one (p/p₀ 0.09–0.13), the surface area of 6255 m² g⁻¹ was calculated.

DUT-32 also has excellent gas storage properties. For H₂ the excess maximum capacity is achieved at 53 bar and reaches 85 mg g⁻¹ (7.8 wt%; 22.9 mg cm⁻³) (Fig. 3) which is only surpassed by MOF-210 (86 mg g⁻¹)⁷ and NU-100 (99.5 mg g⁻¹).¹³ Considering the enormous pore volume, the total capacity at 80 bar corresponds to 166 mg g⁻¹ (14.21 wt%; 44.9 mg cm⁻³) which is among the highest gravimetric values reported for porous materials.

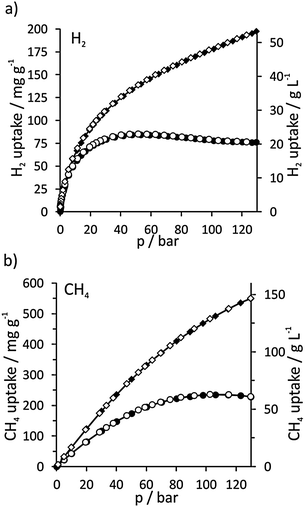Fig. 3 H₂ (a, 77 K) and CH₄ (b, 298 K) physisorption isotherms of DUT-32_7d; excess (●), total (◆); filled and empty symbols correspond to the adsorption and desorption, respectively.

Recently Yildirim et al.^1c claimed that a hypothetical MOF with optimal methane storage properties should have a pore volume of 3.2 cm³ g⁻¹, a density of 0.27 g cm⁻³ and a surface area of 7500 m² g⁻¹ to be able to adsorb 0.5 g methane per gram of MOF (195 cc (STP) cc⁻¹) at 65 bar. Interestingly, DUT-32 has the porosity characteristics which are very close to those of the desired hypothetical MOF: pore volume of 3.16 cm³ g⁻¹ and density of 0.27 g cm⁻³. DUT-32's maximum excess methane capacity at 298 K is reached with 0.24 g g⁻¹ at 105 bar (corresponding to 65 mg ml⁻¹). Due to the large pore volume, DUT-32 achieves a total desired CH₄ storage capacity of 0.55 g g⁻¹ (149 g L⁻¹, 210 cm³ (STP) cm⁻³) at 130 bar.

Summarizing, we have presented a new metal–organic framework (DUT-32) with a rare umt topology that can be easily scaled up due to the simple linker synthesis using cheap starting materials. Careful adjustment of the activation conditions revealed an ultrahigh porosity with a nitrogen uptake of 2080 cm³ g⁻¹ (STP) corresponding to a total pore volume of 3.16 cm³ g⁻¹ and an apparent BET area of 6411 m² g⁻¹, adding this compound to the top ten materials with the highest BET surface area.

The authors are grateful for the financial support from the DFG (SPP 1362), and the HZB. Special thanks goes to Dr G. Auffermann for carrying out the elemental analyses, and Dr I. Baburin for simulations.

Notes and references

1. (a) H. Frost, T. Düren and R. Q. Snurr, J. Phys. Chem. B, 2006, 110, 9565; (b) H. Frost and R. Q. Snurr, J. Phys. Chem. C, 2007, 111, 18794; (c) Y. Peng, V. Krungleviciute, I. Eryazici, J. T. Hupp, O. K. Farha and T. Yildirim, J. Am. Chem. Soc., 2013, 135, 11887; (d) J. A. Mason, M. Veenstra and J. R. Long, Chem. Sci., 2014, 5, 32.
2. (a) X. Song, Y. Zou, X. Liu, M. Oh and M. S. Lah, New J. Chem., 2010, 34, 2396; (b) R. Ma, C. Chen, B. Sun, X. Zhao and N. Zhang, Inorg. Chem. Commun., 2011, 14, 1532; (c) S. Banerjee, N. N. Adarsh and P. Dastidar, Soft Matter, 2012, 8, 7623; (d) Y. Zhang, Q. Wang, Y.-J. Xiao, J. Han and X.-L. Zhao, Polyhedron, 2012, 33, 127; (e) L. Rajput, D. Kim and M. S. Lah, CrystEngComm, 2013, 15, 259; (f) Y.-Q. Chen, S.-J. Liu, Y.-W. Li, G.-R. Li, K.-H. He, Z. Chang and X.-H. Bu, CrystEngComm, 2013, 15, 1613.
3. K. Koh, A. G. Wong-Foy and A. J. Matzger, J. Am. Chem. Soc., 2010, 132, 15005.
4. M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 295, 469.
5. H. K. Chae, D. Y. Siberio-Perez, J. Kim, Y. Go, M. Eddaoudi, A. J. Matzger, M. O'Keeffe and O. M. Yaghi, Nature, 2004, 427, 523–527.
6. K. Koh, A. G. Wong-Foy and A. J. Matzger, J. Am. Chem. Soc., 2009, 131, 4184.
7. H. Furukawa, N. Ko, Y. B. Go, N. Aratani, S. B. Choi, E. Choi, A. O. Yazaydin, R. Q. Snurr, M. O'Keeffe, J. Kim and O. M. Yaghi, Science, 2010, 329, 424.
8. J. E. Mondloch, O. Karagiaridi, O. K. Farha and J. T. Hupp, CrystEngComm, 2013, 15, 9258–9264.
9. A. W. Francis, J. Phys. Chem., 1954, 58, 1099.
10. J. Rouquerol, P. Llewellyn and F. Rouquerol, Stud. Surf. Sci. Catal., 2007, 160, 49.
11. L. Sarkisov and A. Harrison, Mol. Simul., 2011, 37(14), 1248; A. Gupta, S. Chempath, M. J. Sanborn, L. A. Clark and R. Q. Snurr, Mol. Simul., 2003, 29, 29.
12. A. Gupta, S. Chempath, M. J. Sanborn, L. A. Clark and R. Q. Snurr, Mol. Simul., 2003, 29, 29.
13. O. K. Farha, A. Özgür Yazaydın, I. Eryazici, C. D. Malliakas, B. G. Hauser, M. G. Kanatzidis, S. T. Nguyen, R. Q. Snurr and J. T. Hupp, Nat. Chem., 2010, 2, 944.

---

Footnotes

† Electronic supplementary information (ESI) available: Synthetic details, single crystal X-ray structure analysis details, PXRD patterns, thermogravimetric analysis and NMR data. CCDC 968887 and 968888. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4cc00113c

‡ Crystallographic data: C_252.5H_491.3N₆₈O_43.7Zn₄, M = 5441.09 g mol⁻¹, hexagonal, P6₃/m (Nr. 176), a = 50.710(7) Å, c = 62.920(13) Å, V = 140 122(40) ų, Z = 18, ρ_calc. = 1.161 g cm⁻³, λ = 0.88561 Å, T = 293 K, 2θ_max = 28.2°, reflections collected/unique 118 656/60 048, R_int = 0.0497, R₁ = 0.0688, wR₂ = 0.1815, S = 1.010, largest diff. peak 0.229 e Å⁻³ and hole −0.196 e Å⁻³. CCDC 968887.

---