Does the metal protect the ancillary ligands? C–H strengthening and deactivation in amines and phosphines upon metal-binding

Abstract

DFT and CCSD(T) calculations show that the weakest C–H bonds of N- and P-donor ligands are strengthened and deactivated upon metal-binding. The increase in C–H BDE and ΔG^‡ for H abstraction ranges from ca. 1 to 15 kcal mol⁻¹.

---

Chelating amines, phosphines and other N- and P-donor ligands are widely used as ancillary ligands in homogenous catalysts based on late transition metals.¹ These ligands stabilize the metal centre and provide the chemical environment required for transforming reactants into products. In addition, the stability of these ligands, which is based on the low reactivity of their aliphatic backbones, plays a key role in catalyst robustness.^2–9 Nonetheless, under the harsh conditions required for some catalysts, e.g. an air atmosphere, strong oxidants and/or high temperatures, these ligands can undergo degradative transformations^10–15 leading to catalyst deactivation. In particular, the C–H bonds adjacent to the N and P lone pairs (LP) may undergo homolytic cleavage.^16–19 In this work, DFT(M06) and CCSD(T) calculations show that these C–H bonds are strengthened and deactivated upon metal-binding. This conclusion is in consonance with the experiments recently reported by Bietti et al. showing the C–H deactivation of amines by acids²⁰ and metal salts.²¹

The relative stability of several chelating ligands (L = en, dmpe, dppea, DuPHOS, mcp, dien, tacn, bpym) bound to late transition metals (M = Fe, Ru, Co, Ir, Pd, Pt) in complexes 1–8 (Fig. 1) was explored by means of DFT(M06) calculations. The strength of the C–H bonds in the α position with respect to N and P in the free ligand, L(C–H), was determined relative to the metal-bound ligand, ML(C–H), by computing the radical stabilization energy (RSE; eqn (1)), which is defined as the ΔH_0K of the isodesmic reaction given in eqn (2).

RSE = BDE(L(C–H)) − BDE(ML(C–H)) = ΔH_0K (1)

L(C–H) + ML(C˙) → L(C˙) + ML(C–H) ΔH_0K (2)

RSE is a relative quantity, which has been traditionally used to explore substituent effects on the stability of the methyl radical, by using CH₄/CH₃˙ as a reference.²² In this study, L(C–H)/L(C˙) is used as a reference to assess the influence of metal coordination on the stability of the C radical in the ligand. In this framework, the RSE equals the difference between the C–H bond dissociation energies (BDE) in ML(C–H) and L(C–H) (eqn (1)). Remarkably, all RSE computed for the chelating ligands in complexes 1–8 have negative values (Table 1), i.e. these C–H bonds are strengthened when the ligand coordinates to the metal.

Table 1 Calculated thermodynamics and kinetics parameters (eqn (1), (3) and (6))

Complex	M/L	Position	RSE	ΔΔG^‡	k L/kML
a CCSD(T) values. All other values are at the DFT(M06) level.
1	Pd/en	CH2(NH2)	−9.4	−6.9	1.2 × 10^5
1	Pd/en	CH2(NH2)	−9.9	−4.4	1.8 × 10^3
2	Pt/dmpe	CH2PMe2	−4.5	−6.3	4.5 × 10^4
3	Ru/dppea	CH2(NH2)	−6.4	−8.5	1.6 × 10^6
3	Ru/dppea	CH2(PPh2)	−1.7	−2.7	9.8 × 10^1
4	Pt/DuPHOS	CH(PR2)	−3.3	−3.4	3.2 × 10^2
5	Fe/mcp	CH(NR2)	−7.1	−4.8	3.4 × 10^3
5	Fe/mcp	CH2(NR2)	−0.5	−1.4	1.0 × 10^1
6	Co/dien	CH2(NH)	−9.8	−9.4	7.5 × 10^6
6	Co/dien	CH2(NH2)	−9.4	−10.7	7.1 × 10^7
7	Ir/tacn	CH2(NHR)	−15.0	−14.2	2.5 × 10^10
8	Pt/bpym	β-CH(NR)	−8.1	−12.1	7.5 × 10^8
8	Pt/bpym	δ-CH(NR)	−2.8	−1.4	1.1 × 10^1
9	Mg/TEA	CH2(NR2)	−5.1	−6.4	5.3 × 10^4

---

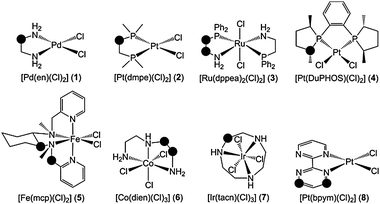Fig. 1 Complexes 1–8. RSE (eqn (1)) and ΔΔG^‡ (eqn (3)) were calculated for the positions marked with the circles.

For the en ligand in complex 1 (Fig. 1), RSE has a value of −9.4 kcal mol⁻¹ (Table 1), i.e. the C–H BDE of this amine ligand is 9.4 kcal mol⁻¹ higher when it chelates the PdCl₂ moiety. RSE was also computed for a phosphorus analogue of the en ligand, dmpe, bound to Pt (2). In this species, the RSE calculated for the methylene position was −4.5 kcal mol⁻¹. The comparison of these two RSE values suggests that, upon coordination of the ligand to the metal, C–H bonds attached to N are more strengthened than those attached to P. This is clearly the case for the dppea ligand in complex 3. The CH₂(NH₂) unit of this N,P-donor ligand yields RSE = −6.4 kcal mol⁻¹, whereas the CH₂(PPh₂) unit yields RSE = −1.7 kcal mol⁻¹. In 4, the tertiary C–H of the DuPHOS ligand has a fairly negative RSE of −3.3 kcal mol⁻¹. Complexes 5–8 have a wide range of RSE between the minimum and maximum values found in this study, which are −15.0 kcal mol⁻¹ for the secondary C–H bonds of the tacn ligand in 7 and −0.5 kcal mol⁻¹ for the benzyl C–H bonds of the mcp ligand in 5. Rather negative values of RSE were also observed for the tertiary C–H bonds of the mcp ligand in 5, −7.1 kcal mol⁻¹, and the secondary C–H bonds of the dien ligand in 6, −9.8 kcal mol⁻¹ and −9.4 kcal mol⁻¹. Aryl sp² C–H bonds can also be strengthened in N-donor ligands based on aromatic N-heterocycles. This is the case of the bpym ligand bound to Pt in complex 8. Interestingly, the C–H BDE increases by 8.1 kcal mol⁻¹ in the β position but only by 2.8 kcal mol⁻¹ in the δ position, thus showing the relevance of the relative position of the C–H bond.

The strengthening of the C–H bonds in complexes 1–8 can also have a significant impact on their kinetic reactivity. This issue was explored by defining and computing ΔΔG^‡ (eqn (3)), which measures the influence of the metal on the energy barrier for H abstraction from the ligand by the methoxy radical (eqn (4) and (5)). ΔΔG^‡ was then used to calculate the ratio between the rate constants for the free and metal-bound ligand at 298 K, k_L/k_ML (eqn (6)).

ΔΔG^‡ = ΔG_L^‡ − ΔG_ML^‡ (3)

L(C–H) + CH₃O˙ → L(C˙) + CH₃OH ΔG_L^‡ (4)

ML(C–H) + CH₃O˙ → ML(C˙) + CH₃OH ΔG_ML^‡ (5)

k_L/k_ML = exp(−ΔΔG^‡/RT) (6)

Remarkably, as for the RSE, ΔΔG^‡ has negative values for all complexes 1–8 (Table 1); i.e. ΔG_L^‡ < ΔG_ML^‡, showing that these C–H bonds, in addition to being strengthened, are also deactivated when the ligand coordinates to the metal. C–H strengthening and deactivation have been already correlated experimentally.²³ This relationship is intuitive and may seem obvious but, in other chemical systems, the strongest chemical bonds are preferentially cleaved^24,25 when no radicals are involved. In the phosphines, the alternative oxidation of P by the methoxy radical was not explored.^26,27

The C–H bonds of the en ligand in complex 1 (Fig. 1), which are strengthened by 9.4 kcal mol⁻¹, are significantly deactivated as shown by the negative value of ΔΔG^‡, −6.9 kcal mol⁻¹ (Table 1); i.e. radical H abstraction is five orders of magnitude faster in the free en ligand than in 1, k_L/k_ML = 1.2 × 10⁵. In the phosphine ligands, which showed softer C–H strengthening when compared to the amines, this deactivation effect is somewhat reduced. The rate constants for H abstraction from dmpe and DuPHOS decrease by four and two orders of magnitude when these ligands are bound to Pt in complexes 2 and 4, respectively. Moreover, in complex 3, the higher strengthening of the C–H bonds attached to N (RSE = −6.4 kcal mol⁻¹), when compared to those attached to P (RSE = −1.7 kcal mol⁻¹), involves a stronger deactivation of the former positions, as shown by the values of ΔΔG^‡, −8.5 kcal mol⁻¹ (k_L/k_ML = 1.6 × 10⁶) and −2.7 kcal mol⁻¹ (k_L/k_ML = 9.8 × 10¹), respectively. In complexes 5, 6 and 7, C–H deactivation upon coordination to the metal can also be rather significant, with k_L/k_ML ranging from one to ten orders of magnitude. In complex 8, the position of the abstracted H relative to the metal has a strong influence on the extent of C–H deactivation. For the β position, which showed the highest C–H strengthening (RSE = −8.1 kcal mol⁻¹), ΔΔG^‡ equals −12.1 kcal mol⁻¹ (k_L/k_ML = 7.5 × 10⁸), whereas for the δ position, which showed the lowest C–H strengthening (RSE = −2.8 kcal mol⁻¹), ΔΔG^‡ equals −1.4 kcal mol⁻¹ (k_L/k_ML = 1.1 × 10¹). The wide range of values found for RSE and ΔΔG^‡ suggests that both quantities are very sensitive to the chemical environment of the C–H bond, including the nature of the donor atom, the metal and the coordination geometry. In line with this, the plot of ΔΔG^‡ (y) vs. RSE (x) shows a moderate correlation (Fig. S1, ESI†), with the linear regression yielding y = 0.92x − 0.86 kcal mol⁻¹ (r² = 0.80). This r² value seems satisfactory considering the diverse nature of complexes 1–8. Furthermore, for non-equivalent positions within the same complex (3, 5, 8), the apparent trend is that the stronger the C–H bond, the less reactive it is.

To gain further insight into the origin of the C–H strengthening, the electronic structures of the species used to compute the RSE (eqn (1)) were explored in detail for the [Ir(tacn)(Cl)₃] complex (7), which showed the largest effect (Table 1). The spin density (ρ) of the free tacn radical (ρ₁ in Fig. 2) shows that the unpaired electron is delocalized over C and N; the local spin densities on these atoms are ρ_C = 0.79 and ρ_N = 0.16, respectively. This species is thus stabilized by a 3e/2c interaction between the donor (N LP) and acceptor (C radical),²⁸ which is reinforced by the parallel alignment of the orbitals. The local spin densities in the metal-bound system (ρ₂), [Ir(tacn˙)(Cl)₃], ρ_C = 0.95 and ρ_N = −0.03, show that this interaction is suppressed when the N LP coordinates to the metal centre. The higher stabilization of the C radical in the free tacn ligand than in the metal-bound contributes to the negative value of the RSE found for this system, −15.0 kcal mol⁻¹ (Table 1). The origin of the C–H deactivation effect was also explored by analysing the spin densities of the H abstraction transition states (ρ₃ and ρ₄) used to compute ΔΔG^‡ (eqn (3)) for complex 7. In the metal-free system, the spin density is delocalized over the O atom of the radical abstractor and the C and N atoms of the ligand, whereas, in the metal-bound system, is only significant for C and O. These data show that the incipient C radical of the H abstraction transition state is stabilized by the N LP only in the metal-free system, thus contributing to the negative value of ΔΔG^‡ found for this system, −14.2 kcal mol⁻¹ (Table 1).

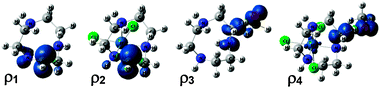Fig. 2 Spin densities of free tacn˙ (ρ₁), [Ir(tacn˙)Cl₃] (ρ₂) and the H abstraction transition states for free tacn (ρ₃) and [Ir(tacn)Cl₃] (ρ₄).

The hyperconjugation of the N LP with the parallel antibonding σ*(C–H) orbital was explored by means of NBO analysis (version 5.9). The NLMO (Natural Localized Molecular Orbital) of the σ*(C–H) orbital, where this interaction is most apparent, shows that the contribution of the N LP is lower when the tacn ligand coordinates to Ir (see Fig. S2 in the ESI†), yielding a lower stabilization energy for the N LP → σ*(C–H) interaction; 10.1 kcal mol⁻¹ (free tacn), 4.4 kcal mol⁻¹ ([Ir(tacn)(Cl)₃]). In line with these data, the C–H bond distance shortens from 1.113 Å in free tacn to 1.100 Å in [Ir(tacn)(Cl)₃]. The reduced hyperconjugation of the N LP with the σ*(C–H) orbital in the metal-bound system thus also contributes to the strengthening and deactivation of the C–H bonds α to N.²⁸ The lower Lewis basicity of the P LP compared to N provides a rational basis for the softer effects found for the C–H bonds α to P, when compared to those α to N (Table 1).

Highly accurate CCSD(T) calculations were also performed for system 1. The RSE value computed at this level of theory, −9.9 kcal mol⁻¹, is in excellent agreement with that computed at the DFT(M06) level, −9.4 kcal mol⁻¹ (Table 1). The CCSD(T) value of ΔΔG^‡ is also negative, −4.4 kcal mol⁻¹, and does not deviate much from the DFT(M06) result, −6.9 kcal mol⁻¹. Furthermore, very similar results were obtained for complexes 2, 7 and 8 when other functionals were used (Table S1, ESI†).

This may not be a universally applicable proof of the C–H strengthening and deactivation effects observed in this study. Nonetheless, support comes from a recent experimental study, in which Bietti and co-workers reported similar results for organic bases undergoing H abstraction reactions with the cumyloxyl radical (PhC(CH₃)₂O˙).²¹E.g., the rate constant for H abstraction from the secondary C–H bonds of triethylamine (TEA) was at least two orders of magnitude higher with free TEA (k) than in the presence of [Mg(ClO₄)₂] (k_Mg). The authors suggest that the coordination of Mg to the N LP of TEA is the origin of this effect. This hypothesis was explored by following the approach used for complexes 1–8 (eqn (1)–(6)). The structures of the Mg–TEA complex (9) and the associated transition state for H abstraction by PhC(CH₃)₂O˙ are given in Fig. S3 (ESI†). The RSE and ΔΔG^‡ values found for this system (Table 1) are negative, −5.1 kcal mol⁻¹ and −6.4 kcal mol⁻¹, respectively. These data show that the secondary C–H bonds of TEA are strengthened and deactivated upon coordination of its lone pair to Mg. The value of ΔΔG^‡ yields a theoretical k/k_Mg = 5.3 × 10⁴, in consonance with the kinetics experiments that yielded k/k_Mg > 200.²¹

In summary, we have shown that N- and P-donor ancillary ligands become more robust upon coordination to a metal centre. This effect arises from the coordination of the N and P LPs and may also reduce the acidity of the C–H bond. Given the large changes found, this effect cannot be ignored in assessing and optimizing catalyst robustness.

A.N. and D.B. acknowledge O. Eisenstein and R.H. Crabtree for fruitful discussions, the Research Council of Norway for funding (Grant 179568/V30) and the Norwegian Supercomputing Program for computational resources (Grant nn4654k).

Notes and references

1. R. H. Crabtree, The Organometallic Chemistry of the Transition Metals, John Wiley & Sons, New Jersey, 2005.
2. P. W. N. M. van Leeuwen, Appl. Catal., A, 2001, 212, 61–81.
3. X. Solans-Monfort, C. Copéret and O. Eisenstein, J. Am. Chem. Soc., 2010, 132, 7750–7757.
4. J. Rabeah, M. Bauer, W. Baumann, A. E. C. McConnell, W. F. Gabrielli, P. B. Webb, D. Selent and A. Brueckner, ACS Catal., 2013, 3, 95–102.
5. M. M. Abu-Omar, P. J. Hansen and J. H. Espenson, J. Am. Chem. Soc., 1996, 118, 4966–4974.
6. T. E. Barder and S. L. Buchwald, J. Am. Chem. Soc., 2007, 129, 5096–5101.
7. P. E. Garrou, Chem. Rev., 1985, 85, 171–185.
8. M. B. Dinger and J. C. Mol, Organometallics, 2003, 22, 1089–1095.
9. L. V. Mattos, G. Jacobs, B. H. Davis and F. B. Noronha, Chem. Rev., 2012, 112, 4094–4123.
10. U. Hintermair, S. M. Hashmi, M. Elimelech and R. H. Crabtree, J. Am. Chem. Soc., 2012, 134, 9785–9795.
11. A. Savini, P. Belanzoni, G. Bellachioma, C. Zuccaccia, D. Zuccaccia and A. Macchioni, Green Chem., 2011, 13, 3360–3374.
12. M. Lenze, E. T. Martin, N. P. Rath and E. B. Bauer, ChemPlusChem, 2013, 78, 101–116.
13. M. J. Bartos, S. W. Gordon-Wylie, B. G. Fox, L. James Wright, S. T. Weintraub, K. E. Kauffmann, E. Münck, K. L. Kostka, E. S. Uffelman, C. E. F. Rickard, K. R. Noon and T. J. Collins, Coord. Chem. Rev., 1998, 174, 361–390.
14. T. J. Collins, Acc. Chem. Res., 1994, 27, 279–285.
15. L. S. Park-Gehrke, J. Freudenthal, W. Kaminsky, A. G. Dipasquale and J. M. Mayer, Dalton Trans., 2009, 1972–1983.
16. M. L. Coote, C. Y. Lin and H. Zipse, Carbon-Centered Free Radicals: Structure, Dynamics and Reactivity, Wiley, New Jersey, 2010.
17. A. S. Menon, D. J. Henry, T. Bally and L. Radom, Org. Biomol. Chem., 2011, 9, 3636–3657.
18. F. G. Bordwell, X. Zhang and M. S. Alnajjar, J. Am. Chem. Soc., 1992, 114, 7623–7629.
19. J. M. Mayer, Acc. Chem. Res., 1998, 31, 441–450.
20. M. Salamone, I. Giammarioli and M. Bietti, Chem. Sci., 2013, 4, 3255–3262.
21. M. Salamone, L. Mangiacapra, G. A. DiLabio and M. Bietti, J. Am. Chem. Soc., 2013, 135, 415–423.
22. M. L. Coote, C. Y. Lin, A. L. J. Beckwith and A. A. Zavitsas, Phys. Chem. Chem. Phys., 2010, 12, 9597–9610.
23. J. R. Bryant and J. M. Mayer, J. Am. Chem. Soc., 2003, 125, 10351–10361.
24. D. D. Wick and W. D. Jones, Organometallics, 1999, 18, 495–505.
25. E. Clot, C. Mégret, O. Eisenstein and R. N. Perutz, J. Am. Chem. Soc., 2006, 128, 8350–8357.
26. M. Bietti, A. Calcagni and M. Salamone, J. Org. Chem., 2010, 75, 4514–4520.
27. B. Ding and W. G. Bentrude, J. Am. Chem. Soc., 2003, 125, 3248–3259.
28. D. J. Henry, C. J. Parkinson, P. M. Mayer and L. Radom, J. Phys. Chem. A, 2001, 105, 6750–6756.

---

Footnote

† Electronic supplementary information (ESI) available: Optimized energies and geometries, computational details and references. See DOI: 10.1039/c3cc47686c

---