A molecular dynamics study on pH response of protein adsorbed on peptide-modified polyvinyl alcohol hydrogel†
Tian-Yang
Sun
ab,
Li-Jun
Liang
a,
Qi
Wang
*a,
Aatto
Laaksonen
b and
Tao
Wu
*a
aSoft Matter Research Center and Department of Chemistry, Zhejiang University, Hangzhou, 310027, P. R. China. E-mail: qiwang@zju.edu.cn; tao_wu@zju.edu.cn
bDepartment of Materials and Environmental Chemistry, Arrhenius Laboratory, Stockholm University, Stockholm, SE-10691, Sweden
First published on 28th November 2013
Abstract
The interactions between proteins and functional biomaterials under different physical and environmental conditions need to be understood when designing biomedical devices. Herein, we present a molecular dynamics simulation study of the fragment antigen-binding (Fab) of trastuzumab (a monoclonal antibody) and its complex with a peptide-modified polyvinyl alcohol (PVA) hydrogel at different pH values. Consistent with experiments, PVA when modified by charged ligands does shrink as a direct response to a drop in the pH. The protein maintains a stable conformation when adsorbed on the hydrogel matrix with a varied pH, showing no signs of denaturation in all simulated systems, suggesting that peptide-grafted PVA is a good biocompatible material. Under neutral conditions, the hydrogel alone stabilizes the interactions between the protein and the peptide ligands. Strikingly under acidic conditions the protein–ligand interactions are disrupted by a collective protonation of ligands. A sharp decrease in the interaction energies, accompanied by the sudden increase of the protein–ligand distance, indicates a rapid pH response in the protein–hydrogel complex. This will be important in protein delivery and purification. The effect of pH on the interactions and the dynamics of the protein and the sudden pH response of the hydrogel at the atomic level present a new functional perspective in developing new hydrogels with desirable properties.
Introduction
Hydrogels are three-dimensional cross-linked hydrophilic polymeric networks that swell in water without dissolving. Because of their inherent mechanical strength and high water content, together with their biocompatibility, hydrogels are widely used in a great variety of biomedical and pharmaceutical applications,1,2 such as molecular imaging,3 biosensors,4 tissue engineering,5 filtration/separation processes6 and therapeutic drug delivery.7 Some hydrogels are sensitive to environmental changes, with swelling/shrinking caused by changes in pH, temperature, ionic strength, etc. A wide variety of these stimuli-responsive hydrogels (smart hydrogels) have been developed for delivery and separation with hydrogel-based biomaterials as carriers.8–15 In particular, pH-sensitive hydrogels have attracted much attention recently in (protein) drug delivery.16 However, a major limitation of using hydrogels in protein delivery is the protein denaturation due to pH changes or adsorption. Thus, gaining more knowledge of smart hydrogels and their use as support and vehicles for large biomolecules is important. It is crucial to be able to describe and predict their interactions with biomacromolecules and to understand the influence of different conditions on their stability in order to further exploit their potential.17Polyvinyl alcohol (PVA) based biomaterials, being non-fouling, non-toxic and biocompatible, have been used in biomedical and pharmaceutical applications, including many of the Food and Drug Administration (FDA)-approved biomedical devices.18–20 However, the relatively low swelling and the weak response capacity of the pure PVA hydrogel are currently limiting its application as smart biomaterials.21,22 Fortunately it can be easily improved by modifying the hydroxyl groups and designing a variety of different cross-linked topologies. Different modifications of the secondary hydroxyl groups have been reported in the literature.23,24 In particular, modifications with designed ligands can yield highly functional hydrogels targeting specific sites. For instance, they could be used for affinity-based separation and targeted delivery.25 The optimal performance of this type of biomaterial requires stable interactions and inherent robustness.
Computational methods, such as all-atom molecular dynamics (MD) simulations, offer good possibilities to model, simulate and investigate these potential new biomaterials on the molecular level as well as predict suitable properties by modifications.26–28 Previous simulation work, carried out in our group, has been successful in protein adsorption and encapsulation on a surface of hard materials.29,30 Raffaini et al. studied the protein adsorption on glassy PVA, which provided a general view of protein–hydrophilic surface interaction.31 While modeling of protein interactions with soft materials offers new challenges. MD simulation studies on protein/hydrogel systems are still scarce in the literature. In particular, studies on the behavior of smart hydrogels under different physical conditions and environments are still virtually non-existing although they have been rather extensively studied by various experimental techniques.32–34 Related MD studies in the past mainly focused on the structure and dynamics of water and cross-linked networks in hydrogels. Chiessi et al.35,36 developed a high-degree hydration model for PVA to study the polymer and water dynamics by MD simulation. They found that the polymer–water interactions largely govern both the polymer conformation and water diffusion. Having access to a reliable PVA model gives us a good starting point to study in detail the dynamics and interactions inside the polymer matrix. In view of the particular importance of protein–polymer and protein–ligand interactions in drug delivery and protein purification, both initial screening and detailed studies of these interactions are necessary, which is also the goal of the current work.
In this study, we have chosen a peptide-grafted PVA as an environment-sensitive matrix to build up the model of a cross-linked hydrogel, interacting with a monoclonal antibody drug, trastuzumab (commercial name: Herceptin). It is used in the treatment of breast cancer and other types of HER2 (human epidermal growth factor receptor 2) positive cancer forms. In our previous study, a charged affinity peptide Glu-Asp-Pro-Trp (EDPW) was designed, specific to this widely used anti-cancer drug.37 It is selected here as a modifier for the three-dimensional (3D) cross-linked PVA hydrogel in this study. First, simulations are carried out with both the free ligands (without hydrogel) and the immobilized ligands to the targeted protein to study the influence of immobilization on protein–ligand affinity, as well as the protein stability. An important part of this study is, however, to investigate the details of the influence of the acidic environment on the hydrogel–protein system and the protein stability by MD simulations carried out at neutral pH (pH ∼ 7.0) and low pH (pH ∼ 3.0).
Materials and methods
The cross-linked PVA model was built using a topology similar to that reported by Chiessi et al.36 The model consists of a 3D network structure, as illustrated in Fig. 1A. The starting scaffold of the polymeric network has been built by six PVA chains (Mw = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), oriented in the simulation box in parallel with respect to the Cartesian axes. All the PVA chains in the model have the same degree of polymerization (DP = 42). The chains are covalently cross-linked with an ester bond through the head unit of one chain to the middle of another. Each chain was thereafter modified by attaching four EDPW ligands with the C-terminal carboxylic ester bond (two ligands on each side of the PVA junction) yielding a hydrogel matrix (Mw = 23
000), oriented in the simulation box in parallel with respect to the Cartesian axes. All the PVA chains in the model have the same degree of polymerization (DP = 42). The chains are covalently cross-linked with an ester bond through the head unit of one chain to the middle of another. Each chain was thereafter modified by attaching four EDPW ligands with the C-terminal carboxylic ester bond (two ligands on each side of the PVA junction) yielding a hydrogel matrix (Mw = 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700).
700).
Then, the polymer network was initially placed in a vacuum for a 130 ps simulation to let it relax and shrink to an appropriate size used in PVA preparation as in vacuum drying.38 Then a 2 ns relaxation was performed to equilibrate the PVA in solution. The radius of gyration of the PVA carbon atoms is shown in Fig. 1B to represent the size of the matrix during simulation. In our previous study,37 we compared three tetrapeptide affinity ligands, designed for trastuzumab. It was found in MD simulations that EDPW had the strongest binding affinity, as well as the best conformational stability. The structure data file of the trastuzumab Fab (fragment antigen-binding) fragment was obtained from Protein Data Bank (PDB) ID code: 1N8Z.39 In order to further reduce the simulation time of the protein–ligand binding process, we did start the study by taking the Fab-EDPW binding structure from our previous study37 and substituted it with one of the twenty-four immobilized ligands forming a protein–hydrogel complex as shown in Fig. 1C. The ligand binding to the Fab binding site was defined as a specific binding ligand (SBL), and the other ligands were defined as non-specific-binding ligands (NBL).
We prepared two systems to simulate different pHs. Protonation states were assigned using the software package PROPKA 3.1 for the charged residues.40 For all simulated systems, the N-termini and basic residues (Lys and Arg) were protonated and C-termini were deprotonated. The acidic residues (Asp and Glu) were deprotonated at neutral pH around 7.0. There are 24 of them on the protein surface and 2 in each ligand (see Table S1 in ESI†) with a pKa higher than 3.0. According to the relationship between pH and pKa, more than 90% of the 8 acidic residues with a pKa higher than 4.0 will be protonated at pH 4, and more than 50% of the other 16 residues and ligands will be protonated at pH 3–4. In order to observe an obvious phenomenon, all of these 24 acidic residues and ligands were protonated to simulate their states under acidic conditions at a pH as low as 3.0. All His residues were kept neutral since they were buried inside the protein. The summary of the simulation systems is given in Table 1; a water box with a 10 Å distance from the surface of the system to the box wall was placed around the protein–hydrogel/ligand complex.
| N Cl− | N Na+ | Overall charge | Number of atoms | Simulation time/ns | ||
|---|---|---|---|---|---|---|
| Protein | Ligands | |||||
| N is the number of ions added to neutralize the system. | ||||||
| pH 7.0 | 3 | 0 | +5 | −2 | ∼47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
8 |
| pH 7.0, hydrogel | 0 | 19 | +5 | −24 | ∼145![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
12 |
| pH 3.0, hydrogel | 53 | 0 | +29 | +24 | ∼145![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
12 |
All the MD simulation systems were built and run with NAMD 2.741 using CHARMM27 parameters42 and a TIP3P43 water model. Cubic periodic boundary conditions were used, and the long-range electrostatic interactions were calculated by the particle mesh Ewald44 approach with the cutoff distance of 12 Å for the separation of the direct and reciprocal space. A cut-off switching function, starting at a distance of 12 Å and reaching zero at 14 Å, was used for non-bonded van der Waals interactions. Simulations were carried out in an NPT ensemble with a Langevin dynamics thermostat (298 K) and a Langevin piston Nosé–Hoover barostat (101.325 kPa).45,46 The time step was set to 2 fs for integration of Newton's equations. Visual molecular dynamics (VMD)47 was used to prepare input files and analyze the MD trajectories as well as for visualization. The time-dependent interaction energy, Eint(t), for all the systems in MD simulations is defined similarly to our previous work:48
| Eint(t) = EP+L(t) − EP(t) − EL(t) | (1) |
In eqn (1), Eint(t) stands for the interaction between the model protein and the ligand at time t during the MD simulation, and EP+L(t), EP(t) and EL(t) respectively refer to the total potential energy of the protein–ligand complex, the potential energy of protein and that of the ligand at time t during simulations. The electrostatic and van der Waals interaction energies were calculated in the same way. Eint(t) is the quantitative indicator of the instantaneous interaction between the two molecules corresponding to each simulation moment, which is different from the interaction energy in the general sense.27
Results and discussion
Conformational changes of hydrogel
To reproduce the whole conformational changes of stimuli-hydrogel observed in experiments is difficult in molecular simulations because of the long response time. Significant responses of the PVA conformation and protein adsorption to pH changes were observed during 12 ns simulations, which can be considered as an initial stage reflection. Prolonged simulations up to 35 ns confirmed the same response tendency as the first 12 ns without any other response mode observed (see Fig. S1 in ESI†). The root mean square deviations (RMSD) of the hydrogel backbones (PVA carbon atoms) in protein–hydrogel complex are shown in Fig. 2A, reflecting at pH 7.0 an increase to about 0.9 nm after 6 ns, and then a levelling off, while at pH 3.0 it increases again after 7 ns and stabilizes around 1.5 nm after 10 ns. Calculation of the radius of gyration (Rg) can give insight into the general properties and behaviour of the used polymer model, such as the degree of compactness and the time to reach structural and conformational equilibrium. The value of Rg of the PVA matrix during the simulation (Fig. 2B) shows that the matrix expands to an Rg value of 2.84 ± 0.05 nm during the last 3 ns in the neutral state. At low pH it begins to shrink around 7 ns, corresponding to the same time point as the RMSD-jump in Fig. 2A. The average value of Rg during the last 3 ns is 2.48 ± 0.02 nm. This significant reduction of the Rg represents a shrinking of hydrogel at lower pH. The solvent accessible surface area (SASA) was measured using a small probe molecule with a radius of 1.4 Å. As shown in Fig. 2C, a similar pattern in the curve is also found as in Fig. 2B, showing that the SASA decreases about 2 nm2 at low pH. The decrease of SASA of the PVA matrix also leads to a compact conformation as a response to a low pH, which could be explained by the change of hydrophilicity of hydrogel-matrix. The protonation of Glu and Asp in immobilized ligands leads to a lower hydrophilicity with fewer adsorbed water molecules, which is consistent with a pH-triggered shrinking of many other pH-sensitive hydrogels.49 The significant conformational changes are the key properties of a smart hydrogel in the development of many biomedical devices. However, the protein stability and interactions between hydrogels and biomolecules play a central role in the use of this type of biomaterial, which was analyzed in the following sections. | ||
| Fig. 2 (A) Root mean square deviation (RMSD); (B) radius of gyration (Rg) of PVA chains (carbon atoms) and (C) solvent accessible surface areas (SASA) of the PVA matrix at different pH. | ||
Conformational changes of protein
The RMSD of the backbone atoms of the SBL and protein (C, Cα, N, O) are displayed as functions of time in Fig. 3 of all simulated systems: protein with a free ligand (first row, denoted as “free”), protein with hydrogel at pH 7.0 (second row, denoted as “pH 7.0”) and protein with hydrogel at pH 3.0 (third row, denoted as “pH 3.0”). The obtained RMSD values of the protein are relatively stable around 2 Å for each complex from the very beginning, and the SBL remained fairly constant with a minimal deviation within the binding pocket. It indicates that the molecular systems behave well thereafter. A small jump in the RMSD value around 5 ns in the “free” SBL curve (first row in Fig. 3) suggests a more flexible conformation of the SBL without immobilization effects of PVA. It is also confirmed by the interaction energy curves of the SBL to the protein (Fig. S2 in ESI†) before immobilization when compared to the already immobilized system. These results indicate that the SBL can be restricted to the binding pocket of the protein, forming a more stable conformation and stronger interaction by immobilization onto the PVA hydrogel. This makes this type of PVA hydrogel a good scaffold or carrier of bioactive ligands.The RMSD and the root mean square fluctuations (RMSF) are used to further analyze the degree of conformational changes in different simulated systems and to quantify the protein stability. We compare the configurations for three protein structures under different conditions during the ligand binding as well as the conformational changes of the PVA matrix at different pH values. The deviations of the protein and PVA chains in the last frame are calculated by a structural alignment on the protein backbone atoms (presented as Fig. S3 in ESI†). The protein and SBL are almost identical as revealed by a RMSD of 2.082 Å after immobilization at pH 7.0 and 2.125 Å at pH 3.0, respectively, while significant differences are found in the PVA matrix. The RMSD obtained for carbon atoms of PVA between the two configurations is 11.232 Å. Generally, the PVA has a larger RMSD value with a compressed conformation when the pH decreases, while the protein is relatively stable at all studied conditions with small differences in its conformation.
The RMSF values of each alpha carbon, calculated from the last 1 ns trajectory data of protein in different systems are shown in Fig. 4. The RMSF values of most of the residues are within the limit of 2 Å sharing the same pattern. It is interesting that the residues near the hydrogel (residues 1–110) and the other part of the protein behave differently to the environmental change. Residues near the hydrogel are more sensitive to the environment than the other part of the protein. At the neutral environment, residues near the hydrogel are more stabilized by the hydrogel showing a lower RMSF than that in the “free” ligand system. The RMSD value of this part is also smaller than the other parts, revealing a restricted mobility of the protein as shown in Fig. 5. By contrast, the fluctuation of residues away from the hydrogel becomes stronger especially for the light chains (LC). In the acidic system, the RMSF value of the residues near the hydrogel, especially near the heavy chain (HC), is significantly higher. Interestingly, the fluctuation of residues away from the hydrogel is lower than that in the other two systems and especially for the LC. In spite of this, the RMSD results show the same trend, namely, that the motion of the closer part is restrained by the hydrogel. Moreover, the RMSDs of the protein at pH 3.0 are higher than those at pH 7.0, indicating a pronounced pH response of the protein. These results imply that the presence of hydrogel may enhance the stability and lower the flexibility of protein under neutral conditions, while the effect of stabilization is weakened or even lost at low pH. The response of protein to the pH changes occurs mainly at the site of the non-hydrogel-binding part. Detailed conformational changes of the protein at the low pH are discussed below.
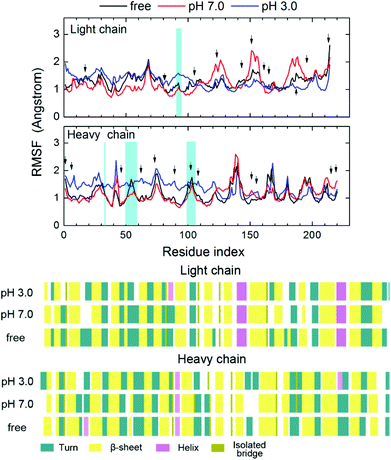 | ||
| Fig. 4 (A) The root mean square fluctuations (RMSF) of the Cα atoms of the protein. (B) Secondary structure of protein in the last frame. | ||
Fig. 4 also shows the RMSFs of all the protonated residues at pH 3.0 (Asp and Glu) which are marked out with a black arrow in the acidic system. Most residues around them present a somewhat higher RMSF value at pH 3.0 than at the neutral state, but with the same trend of fluctuation, except for the binding site (blue shadow in Fig. 4A). It indicates that the conformational change of the protein is caused by the protein–ligand interaction rather than the change of a protonation state. Fig. 4B shows the final secondary structure of the protein in the different simulated systems when evaluated by the VMD sequence viewer. After the immobilization under different conditions, the protein β-sheet and alpha-helix were slightly influenced, whereas the beta-turn did partially disappear under the neutral condition, indicating that the presence of PVA and the change of pH would lead to a minor conformational change without disrupting the overall folding pattern of the protein. This result is in agreement with the experiments50 in which the PVA modified surface could minimize protein denaturation because of its hydrophilicity. It is also consistent with computational studies31 about protein adsorption on glassy PVA that the hydrophilic surface could stabilize the protein with a minor denaturation compared with hydrophobic surface adsorption.
Consequently, it reveals that the immobilization and the pH change have very little influence on the secondary structure and the stability of the protein. In addition, the protein near the PVA is much more stable and responds less to the pH change, indicating a fully stable protein conformation when embedded into the hydrogel.
Protein hydrogel interactions
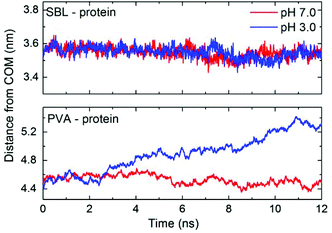
As shown in Fig. 6, the interaction energy between the protein and the hydrogel matrix has been divided into three parts: PVA, SBL and NBL. The interaction energies between the protein and the PVA part of the hydrogel follow roughly the same pattern and same values at different pH values. The curve first decreases slowly, and then fluctuates around 50 kcal mol−1 in the last part. The absolute value of interaction energy between the immobilized SBL and the protein is 305.2 ± 10.9 kcal mol−1 during the last 1 ns, while it is 272.6 ± 14.0 kcal mol−1 in the “free” ligand system (Fig. S2 of the ESI†). It shows that the interaction of the protein with the immobilized ligand is more stable and stronger than that with the “free” ligand. This phenomenon is in consistent with some previous studies on smaller systems.51 Moreover, the interaction between the ligands and the protein was distinctly reduced and almost disappeared for both the SBL and the NBL under the acidic condition. It is found that the electrostatic interactions are the main contributors to the binding of both the protein and EDPW (data not shown). Protonation of EDPW at pH 3.0 disrupts this binding, and leads to a shrinkage of the PVA. This pushes the matrix and the protein away from each other as shown in Fig. 7. The distance between the centre of mass (COM) of SBL and that of the protein at pH 3.0 decreases slightly as happens also at the neutral pH rather than increasing, due to the weakened interactions. A sudden change at around 7 ns, which is consistent with the time point shown in Fig. 2, explains the unexpected results. Due to the rearrangement of hydrogel conformation, no separation process of protein–ligand was observed during the simulation time. Therefore, the significant conformational changes in both protein and hydrogel, and the disruption of the interaction between the protein and the hydrogel indicate a response tendency of the protein–hydrogel system at different pHs. However, multi-scaled modelling and long-time simulations should be used to fully understand the whole dynamics of the response of smart hydrogel and adsorbed protein to microenvironment changes. | ||
| Fig. 6 Interaction energies between protein and PVA chains (first row), specific binding ligand (SBL, second row), non-specific binding ligands (NBL, third row) at different pH. | ||
Conclusions
A pH-responsive PVA-based hydrogel was built for the purpose of absorbing a protein and releasing it. MD simulations were performed to study the conformational changes of the hydrogel and the protein and the protein–hydrogel interactions as a response to the environmental stimuli. Herein, the simulations are short compared to the time scale of conformational changes of hydrogel and protein in response to an environment which may take minutes or hours. However, we are encouraged by the fact that some conformational changes in adsorbed systems have been observed. It is found that the PVA matrix shrinks to a more compact conformation as a response to an acidic condition. The presence of the PVA can stabilize the protein conformation and also results in a more stable interaction between the protein and the ligand. However, low pH sharply reduces both the specific and the non-specific binding of the protein–ligand interactions, but without causing any large unwanted conformational changes in the protein. Moreover, the stabilization effect and the lowering of the flexibility of the protein near the hydrogel part found in this work generalized the protein–hydrogel interactions. It can be expected that the penetration of protein into a larger hydrogel matrix in practical use will also lead to a total stabilization of the protein. Finally significant changes of the PVA matrix, greater response of the protein and the disruption of the protein–ligand interactions at low pH suggest an initial response of the pH-sensitive hydrogel taking place on the atomic level.Acknowledgements
This work was supported by the National Natural Science Foundation of China (no. 21273200, 21074115, and J1210042) and Zhejiang Innovation Program for Graduates.Notes and references
- A. S. Hoffman, Adv. Drug Delivery Rev., 2002, 54, 3–12 CrossRef CAS.
- N. A. Peppas, J. Z. Hilt, A. Khademhosseini and R. Langer, Adv. Mater., 2006, 18, 1345–1360 CrossRef CAS.
- U. Hasegawa, S. M. Nomura, S. C. Kaul, T. Hirano and K. Akiyoshi, Biochem. Biophys. Res. Commun., 2005, 331, 917–921 CrossRef CAS PubMed.
- S. A. Asher, V. L. Alexeev, A. V. Goponenko, A. C. Sharma, I. K. Lednev, C. S. Wilcox and D. N. Finegold, J. Am. Chem. Soc., 2003, 125, 3322–3329 CrossRef CAS PubMed.
- A. Khademhosseini and R. Langer, Biomaterials, 2007, 28, 5087–5092 CrossRef CAS PubMed.
- J. J. Kim and K. Park, Bioseparation, 1998, 7, 177–184 CrossRef CAS.
- J. M. Chan, L. Zhang, K. P. Yuet, G. Liao, J. W. Rhee, R. Langer and O. C. Farokhzad, Biomaterials, 2009, 30, 1627–1634 CrossRef CAS PubMed.
- Y. Qiu and K. Park, Adv. Drug Delivery Rev., 2001, 53, 321–339 CrossRef CAS.
- I. Tomatsu, K. Peng and A. Kros, Adv. Drug Delivery Rev., 2011, 63, 1257–1266 CrossRef CAS PubMed.
- R. T. Olsson, M. A. Azizi Samir, G. Salazar-Alvarez, L. Belova, V. Strom, L. A. Berglund, O. Ikkala, J. Nogues and U. W. Gedde, Nat. Nanotechnol., 2010, 5, 584–588 CrossRef CAS PubMed.
- S. Nakamaru, S. Maeda, Y. Hara and S. Hashimoto, J. Phys. Chem. B, 2009, 113, 4609–4613 CrossRef CAS PubMed.
- I. Gorelikov, L. M. Field and E. Kumacheva, J. Am. Chem. Soc., 2004, 126, 15938–15939 CrossRef CAS PubMed.
- N. Shi and V. M. Ugaz, Phys. Rev. Lett., 2010, 105, 108101 CrossRef.
- H. Susanto and M. Ulbricht, Langmuir, 2007, 23, 7818–7830 CrossRef CAS PubMed.
- T. Vermonden, R. Censi and W. E. Hennink, Chem. Rev., 2012, 112, 2853–2888 CrossRef CAS PubMed.
- N. A. Peppas, P. Bures, W. Leobandung and H. Ichikawa, Eur. J. Pharm. Biopharm., 2000, 50, 27–46 CrossRef CAS.
- E. A. Vogler, Biomaterials, 2012, 33, 1201–1237 CrossRef CAS PubMed.
- S. K. Sahoo, J. Panyam, S. Prabha and V. Labhasetwar, J. Controlled Release, 2002, 82, 105–114 CrossRef CAS.
- K. Burczak, T. Fujisato, M. Hatada and Y. Ikada, Biomaterials, 1994, 15, 231–238 CrossRef CAS.
- C. Hassan and N. Peppas, Advances in Polymer Science, Springer, Berlin, Heidelberg, 2000, vol. 153, pp. 37–65 Search PubMed.
- A. Tedeschi, F. Auriemma, R. Ricciardi, G. Mangiapia, M. Trifuoggi, L. Franco, C. De Rosa, R. K. Heenan, L. Paduano and G. D'Errico, J. Phys. Chem. B, 2006, 110, 23031–23040 CrossRef CAS PubMed.
- S. Hua, H. Ma, X. Li, H. Yang and A. Wang, Int. J. Biol. Macromol., 2010, 46, 517–523 CrossRef CAS PubMed.
- R. H. Schmedlen, K. S. Masters and J. L. West, Biomaterials, 2002, 23, 4325–4332 CrossRef CAS.
- A. Lejardi, A. Etxeberria, E. Meaurio and J. R. Sarasua, Polymer, 2012, 53, 50–59 CrossRef CAS PubMed.
- H. Vu-Quang, M. K. Yoo, H. J. Jeong, H. J. Lee, M. Muthiah, J. H. Rhee, J. H. Lee, C. S. Cho, Y. Y. Jeong and I. K. Park, Acta Biomater., 2011, 7, 3935–3945 CrossRef CAS PubMed.
- S. Wang and E. E. Dormidontova, Biomacromolecules, 2010, 11, 1785–1795 CrossRef CAS PubMed.
- Y. Kang, Y. C. Liu, Q. Wang, J. W. Shen, T. Wu and W. J. Guan, Biomaterials, 2009, 30, 2807–2815 CrossRef CAS PubMed.
- L. Petridis, R. Schulz and J. C. Smith, J. Am. Chem. Soc., 2011, 133, 20277–20287 CrossRef CAS PubMed.
- X. Chen, T. Wu, Q. Wang and J. W. Shen, Biomaterials, 2008, 29, 2423–2432 CrossRef CAS PubMed.
- J. W. Shen, T. Wu, Q. Wang and Y. Kang, Biomaterials, 2008, 29, 3847–3855 CrossRef CAS PubMed.
- G. Raffaini and F. Ganazzoli, Phys. Chem. Chem. Phys., 2006, 8, 2765–2772 RSC.
- L. R. Carr, J. E. Krause, J. R. Ella-Menye and S. Jiang, Biomaterials, 2011, 32, 8456–8461 CrossRef CAS PubMed.
- X. He, J. Ma and E. Jabbari, Langmuir, 2008, 24, 12508–12516 CrossRef CAS PubMed.
- R. Jayakumar, A. Nair, N. S. Rejinold, S. Maya and S. V. Nair, Carbohydr. Polym., 2012, 87, 2352–2356 CrossRef CAS PubMed.
- E. Chiessi, F. Cavalieri and G. Paradossi, J. Phys. Chem. B, 2005, 109, 8091–8096 CrossRef CAS PubMed.
- E. Chiessi, F. Cavalieri and G. Paradossi, J. Phys. Chem. B, 2007, 111, 2820–2827 CrossRef CAS PubMed.
- T. Y. Sun, Q. Wang, J. Zhang, T. Wu and F. Zhang, Int. J. Mol. Sci., 2013, 14, 16836–16850 CrossRef CAS PubMed.
- M. M. Pereira, J. R. Jones, R. L. Orefice and L. L. Hench, J. Mater. Sci. Mater. Med., 2005, 16, 1045–1050 CrossRef CAS PubMed.
- H. S. Cho, K. Mason, K. X. Ramyar, A. M. Stanley, S. B. Gabelli, D. W. Denney and D. J. Leahy, Nature, 2003, 421, 756–760 CrossRef CAS PubMed.
- M. H. M. Olsson, C. R. Sondergaard, M. Rostkowski and J. H. Jensen, J. Chem. Theor. Comput., 2011, 7, 525–537 CrossRef CAS.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- S. E. Feller, Y. Zhang, R. W. Pastor and B. R. Brooks, J. Chem. Phys., 1995, 103, 4613–4621 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- J. W. Shen, T. Wu, Q. Wang and H. H. Pan, Biomaterials, 2008, 29, 513–532 CrossRef CAS PubMed.
- W. H. Chiang, V. T. Ho, W. C. Huang, Y. F. Huang, C. S. Chern and H. C. Chiu, Langmuir, 2012, 28, 15056–15064 CrossRef CAS PubMed.
- L. B. Carneiro, J. Ferreira, M. J. L. Santos, J. P. Monteiro and E. M. Girotto, Appl. Surf. Sci., 2011, 257, 10514–10519 CrossRef CAS PubMed.
- A. Jain and H. S. Ashbaugh, Biomacromolecules, 2011, 12, 2729–2734 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Summary of residues, interaction energies and superposition of protein-hydrogel snapshots. See DOI: 10.1039/c3bm60213c |
| This journal is © The Royal Society of Chemistry 2014 |