The “Phase-of-the-Moon” paradox in uncertainty estimation
Analytical Methods Committee, AMCTB No 61
First published on 24th March 2014
Abstract
In chemical measurement, many extraneous influences affect the magnitude of an analytical signal and thereby contribute to the uncertainty of the result. Some of these influences are predictable: others can be quite unexpected, the weather for example. Atomic spectrometry can be affected by gusts of wind that cause pressure changes in the fume extraction system. That makes the flame or plasma move relative to the instrument optics. There are tales of a spectrography laboratory where precision was degraded on the mornings when cleaners had applied a wax polish to the floor. The solvent of the polish contained enough UV-absorbing compounds to attenuate the light transmission in air-path spectrometers. But the phase of the Moon is predictable and any conceivable effect it could have on measurement uncertainty can be derived from physics.
Strictly, however, it is the position of the Moon in the sky (not the phase) that can affect the weight of an object, just as it affects the tides through the varying direction of its gravitational force. This in turn affects the determination of mass, and therefore of concentration. Physicists can calculate this effect: they tell us that the weight of a 1 g mass can vary to a maximum extent of about 0.2 µg, or 0.00002% relative. (Note: a beam balance would not be prone to this effect.) This discrepancy is many orders of magnitude too small to impinge on analytical uncertainties—analysts can safely ignore the inconstant Moon. But this trivial example points to a general problem that poses a real dilemma for analytical scientists.
Unpredictable influences
For the Moon the maximum contribution to uncertainty can be calculated from the laws of physics. But how can we deal with the host of influences on the analytical signal for which it is quite impossible to predict effects from first principles? The Guide to the Expression of Uncertainty in Measurement (GUM)1 and its Eurachem/CITAC interpretation for analysts2 tell us how. We test for any effect of an influence empirically, that is, by conducting an experiment. If we find an effect we correct it. But whether or not we see a bias, we are supposed to add to the uncertainty budget a contribution equal to the uncertainty in the experimental outcome.This is how the Eurachem/CITAC Guide puts it. In Section 3.1.3: “Bias should be shown to be negligible or corrected for but in either case the uncertainty associated with the determination of the bias remains an essential component of overall uncertainty”. In Section 7.7.10: “The effects of any remaining factors should be estimated separately, either by experimental variation or by prediction from established theory. The uncertainty associated with such factors should be estimated, recorded and combined with other contributions in the normal way”.
A thought experiment
How would that apply to the effect of the Moon if we had no access to a physicist? We can proceed by means of a thought experiment. A hypothetical naïve analyst might test for any effect by replicating analytical results with the moon on the horizon (xi, i = 1,n) and at its zenith (or nadir) (yj, j = 1,m), and testing for significant difference between the means. The analyst would almost always find no significant effect—the analytical precision would be far too coarse. But the difference between the means (![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) − ȳ) would have a standard deviation of
− ȳ) would have a standard deviation of 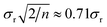 for repeatability standard deviation σr and a reasonable m = n = 4. This standard deviation is the naïve analyst's estimate of uncertainty associated with testing for the bias arising from variation in the position of the Moon. (The uncertainty should in fact be bigger than that, as our naïve analyst has omitted run-to-run variation – but we will see that this has no effect on our present discussion.)
for repeatability standard deviation σr and a reasonable m = n = 4. This standard deviation is the naïve analyst's estimate of uncertainty associated with testing for the bias arising from variation in the position of the Moon. (The uncertainty should in fact be bigger than that, as our naïve analyst has omitted run-to-run variation – but we will see that this has no effect on our present discussion.)
Although the test itself was non-significant, the default position is that, according to GUM principles, this contribution should be added to the uncertainty budget. Suppose the analytical method in question gave results with a preliminary estimate of uncertainty u. The revised uncertainty would be 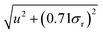 . As we could roughly expect σr ≈ u/2, the revised uncertainty would amount to 1.06u. The naïve analyst would have added 6% relative to the estimated uncertainty to account for an effect known to be effectively absent. Had the uncertainty been correctly estimated, the additional uncertainty would be larger still.
. As we could roughly expect σr ≈ u/2, the revised uncertainty would amount to 1.06u. The naïve analyst would have added 6% relative to the estimated uncertainty to account for an effect known to be effectively absent. Had the uncertainty been correctly estimated, the additional uncertainty would be larger still.
A change of 6% percent in an uncertainty estimate is hardly noticeable, but the number of conceivable influences on the analytical signal is legion. Think of all of the potential interferences from concomitant substances in the test solution, or trivial changes in the laboratory environment. Were we to adopt the same principle for all such influences, every time we tested a new null influence (that is, potentially but not actually interfering) by the method outlined above, the combined uncertainty would increase by virtue of a new contribution of 0.71σr. If we considered only ten null influences using this principle, the combined uncertainty would rise to at least 1.5u, a 50% increase in uncertainty. This seems even more inappropriate when we consider that such tests are largely intended to confirm the expected absence of many effects. This comprises the paradox: we should be reducing our uncertainty, not increasing it.
Back to reality
Of course, this does not happen in real life because analysts are sensible people and have limited time at their disposal. But it highlights a latent snag in a mechanical implementation of GUM principles: for any potential influence we must implicitly choose between two options:(i) to check whether a putative influence is significant and include the appropriate contribution to the uncertainty budget; or
(ii) to assume from the outset that there is exactly zero influence and, as a corollary, no uncertainty contribution.
This is not always a straightforward decision. The key question is where and how we draw the line.
Option (i) can usually be encompassed efficiently by replicating the whole analytical procedure, with a large number of major influences randomised each time. That happens automatically to a large extent in interlaboratory experiments.3 (Systematic influences such as method bias, not covered by such randomisation, will be mostly obvious and can be addressed efficiently by inter alia the use of reference materials.) Further possible random effects, such as matrix interference can be addressed by a ruggedness test, which is especially efficient for handling a large suite of null effects. The combined uncertainty can then be obtained by the reconciliation approach.2,4 That is broadly speaking the usual way of estimating uncertainty in analytical chemistry and takes care of nearly all of the problems.
But the fact remains that there will always be a host of conceivable influences, very likely of negligible effect, that it would not be feasible to study by interlaboratory study, certified reference material, or ruggedness test. That is where option (ii) comes into play. However conscientiously they may implement the principles of GUM, analysts simply have no alternative but to use professional judgement in deciding to treat many conceivable but implausible influences as non-existent or, at least, completely negligible.
Conclusions
Judgement is essential in choosing which influences to consider in method validation and uncertainty evaluation. This exercise of judgement should be acknowledged as a crucial aspect of the analyst's professional skills. And the GUM and the Eurachem/CITAC Guide support this view. This is what the Eurachem Guide says. In Section 7.14.1: “The evaluation of uncertainty is neither a routine task nor a purely mathematical one; it depends on detailed knowledge of the nature of the measurand and of the measurement method and procedure used”. In Section 7.14.4: “There are numerous instances in analytical chemistry when … judgement is required”.In chemical metrology, expert judgement is the essential complement to guides and statistics.
M. Thompson and S. L. R. Ellison
This Technical Brief was written on behalf of the Validation Subcommittee and approved by the Analytical Methods Committee on 21/02/14.
References
- JCGM100:2008, Guide to the expression of uncertainty in measurement (GUM), Bureau International des Poids et Mesures, Sèvres, France, http://www.bipm.org/en/publications/guides/gum.html.
- Quantifying uncertainty in analytical measurement, ed. Williams A., Ellison S.L.R. and Roesslein M., Eurachem/CITAC Guide, 2000, 2nd edn, http://www.eurachem.com/ Search PubMed.
- AMC Technical Briefs No 53: Dark uncertainty, www.rsc.org/amc.
- S. L. R. Ellison and V. J. Barwick, Estimating measurement uncertainty: Reconciliation using a cause and effect approach, Accredit. Qual. Assur., 1998, 3, 101–105 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2014 |


