Electroanalysis of pindolol on a GCE modified with reduced graphene oxide

Abstract

In this work, the application of an innovative, environmentally friendly reduced graphene oxide–glassy carbon (RGO–GC) electrode is described. Using the RGO–GC electrode, basic electrochemical properties (such as the number of protons and electrons involved in an oxidation process, heterogeneous rate constant, diffusion coefficient and electron transfer coefficient) of pindolol (PND) were studied. It was observed that the indole moiety is a part of the pindolol molecule where oxidation takes place. Additionally, a square-wave stripping voltammetric method for the quantitative determination of PND was developed. The influence of various factors such as pH, buffer concentration and SWSV (square wave stripping voltammetry) parameters were studied. The best results in terms of signal shape and intensity were recorded in a BR buffer at pH 5.0. This electroanalytical procedure was used to determine pindolol on the RGO–GC electrode in a concentration range of 1 × 10⁻⁷ to 1 × 10⁻⁵ mol L⁻¹. The precision, repeatability and accuracy of the method were checked. The detection and quantification limits were found to be 2.6 × 10⁻⁸ and 8.6 × 10⁻⁸ mol L⁻¹, respectively. The method has been satisfactorily applied to the determination of pindolol in urine samples and pharmaceutical formulations.

---

Introduction

Drug analysis is an important field of analytical chemistry that is undergoing stable, rapid growth and is performed in different phases of pharmaceutical development such as formulation and stability studies, pharmacological testing and quality control. In hospitals, drug analysis plays a meaningful role in cases of drug intoxication, drug therapy, bioavailability and pharmacokinetic studies or anti-drug control.^1,2 In such cases, validated and dependable analytical methods for drug analysis are required.

Pindolol (RS)-1-(1H-indol-4-yloxy)-3-(isopropylamino)propan-2-ol (Fig. 1) belongs to a heterogeneous group of drugs commonly prescribed in the treatment of angina pectoris, hypertension and cardiac arrhythmias, which are also used as doping agents in sport.³ Thus, pindolol is a nonselective beta blocker with partial beta-adrenergic receptor 5HT1A antagonist activity. In high doses, it causes pulse rate and bronchodilation increase, also exhibiting membrane stabilizing and antiarrhythmic effects.⁴ Pindolol is also an effective agent to cure hypertension in pregnancy, a disease that complicates up to 5% of all pregnancies.^5–8 In such cases, pindolol does not cause any changes in the uterus or blood flow and has no effect on cardiac functions and haemodynamics of the fetus.⁶ What more, initial open label clinical studies have showed that the coadministration of pindolol with SSRIs (selective serotonin reuptake inhibitors) accelerated and/or enhanced antidepressant effects of SSRIs,^9,10 which resulted in the symptomatic relief of depression within days rather than weeks.¹¹

Fig. 1 Chemical structure of pindolol.

Pindolol has been determined using colorimetric,¹² spectrophotometric,^13–16 spectrometric^17,18 and chromatographic^16,19–24 methods. To the best of our knowledge, there are no published results of any voltammetric studies. Voltammetric techniques are meaningful methods for the trace analysis of many organic and inorganic substances. Among these techniques, square-wave voltammetry^25,26 is nowadays one of the most advanced pulse voltammetric techniques used in various types of research but mainly in analytical,^27–31 mechanistic^32–34 and kinetic studies of electrode processes.^35–37 In the last decade, growing interest in the application of graphene and its derivatives to various types of studies^38,39 has been observed because of its promising properties.⁴⁰ Various applications have been demonstrated for graphene, such as sensors,⁴¹ polymer composites,⁴² transparent electrodes⁴³ and hydrogen storage.⁴⁴ Glassy carbon electrodes modified with reduced graphene oxide have been satisfactorily applied in many kinds of studies.^45,46 In this paper, we report the application of a reduced graphene oxide modified glassy carbon electrode for the elaboration of basic electrochemical properties of pindolol and its quantitative determination in real samples.

Experimental

Instrumentation

Voltammetric measurements were carried out using an μAutolab Type III (Eco Chemie) controlled with GPES software (General Purpose Electrochemical System, version 4.9, EcoChemie). A single compartment glass cell was mounted in the M164 electrode stand (MTM-ANKO, Cracow, Poland). Experiments were performed in a three-electrode system consisting of Ag/AgCl (3 mol L⁻¹ KCl) as a reference electrode, Pt wire as a counter electrode, and RGO–GC as a working electrode. Measurements of pH were made using a pH-meter (Elmetron, Poland) with a combined glass electrode. Spectrophotometric and microscopic measurements were made using a Cary 100 Bio UV-Vis spectrophotometer (Agilent) and Dimension Icon Atomic Force Microscope (Bruker), respectively.

Solutions

All reagents were of analytical grade and demineralised double distilled water was used in all experiments. Pindolol was purchased from Sigma Aldrich (St. Louis, MO) and used for preparing 10 mL of a 1.00 × 10⁻³ mol L⁻¹ stock standard solution by dissolving 2.48 mg of PND in methanol (due to that, the supporting electrolyte always contained 10% of methanol). Working solutions of lower concentrations were freshly prepared by the appropriate dilution of the stock standard solution. Britton–Robinson (BR) buffer solutions of different pH values were prepared by the addition of sodium hydroxide solution to a phosphoric, boric and acetic acid mixture. The final pH was checked using a pH-meter. Reduced graphene oxide was obtained from graphene oxide and checked as described in the literature.⁴⁷ Visken (Novartis Pharma) tablets were purchased from a local pharmacy. All electrochemical measurements were carried out at the ambient temperature of the laboratory.

RGO–GC electrode preparation

As mentioned in the previous section, RGO was prepared according to method described in the literature.⁴⁷ Briefly, 50 mg of ascorbic acid was added to 50 mL (0.1 mg × mL⁻¹) of an aqueous dispersion of graphene oxide at room temperature under vigorous stirring. The efficiency of reduction was checked by UV-Vis absorption spectroscopy (Fig. 2). A strong absorption peak of the GO solution at 233 nm corresponds to the π → π* transition.⁴⁸ Graphene oxide has a very weak absorption in the UV-Vis range because of the destruction of the conjugated π system. After reduction, the π → π* transition band shifts from 233 to 270 nm, and the absorbance in the whole visible range strongly increases. These results confirm the restoration of the conjugated structure of graphene.⁴⁹

Fig. 2 UV-Vis absorption spectra of the GO and RGO solutions.

0.5 mg of the reduced graphene oxide was added to 0.5 mL dimethylfuran. A stable homogenous suspension was obtained with use of an ultrasonic bath in which the solution was kept for 40 min. The glassy carbon electrode surface between experiments was cleaned by polishing with a 0.05 μm alumina slurry, rinsed with methanol and water, and dried in air. The RGO–GC was prepared by dropping 4.0 μL of the RGO/DMF by a micropipette. After 1 hour, DMF was evaporated, and the electrode was ready to use. A new RGO surface was prepared daily. To remove any possible residues adsorbed on the electrode surface (before and between measurements), the working electrode was cleaned electrochemically with cyclic voltammetry scanning from −2.0 to 2.0 V (in the supporting electrolyte without PND).

Analysis of commercial pharmaceutical samples

To prepare solutions of the commercial pindolol samples, a representative amount (8) of Visken tablets were crushed to a powder using a mortar. Then, an appropriate mass of the powder was transferred to a 10 mL volumetric flask and filled up to volume with methanol (C_PND = 1.00 × 10⁻³ mol L⁻¹). Non-dissolved solids were removed after centrifugation. In all experiments, voltammograms were recorded under the same conditions as for pure pindolol. The Visken solution was analyzed using the standard addition method. To obtain the final concentrations of PND in the range of the calibration curve, the Visken solution was suitably diluted with the supporting electrolyte. Recoveries were calculated after five replicate experiments.

Analysis of urine samples

Morning mid-stream drug-free urine samples were collected from healthy volunteers. Spiked urine solutions were prepared as follows: 5.0 × 10⁻⁸ mol (sample 1), 2.5 × 10⁻⁷ mol (sample 2) and 5.0 × 10⁻⁷ mol (sample 3) of PND were placed in a 5 mL volumetric flask and filled up to volume with urine. Urine samples were analyzed using the standard addition method. In each experiment, 500 μL (sample 1), 100 μL (sample 2) or 50 μL (sample 3) of the spiked urine solution was placed in the voltammetric cell, and a voltammogram was recorded for the sample. Each addition of standard contained 5 nmol of PND. Recoveries were calculated after five replicate experiments.

Validation of the method

A calibration curve (described with the linear regression equation y = bx + a) was constructed plotting PND peak current (I_p, A) against its concentration (C, mol L⁻¹) in the range from 1.0 × 10⁻⁷ to 1.0 × 10⁻⁵ mol L⁻¹. To evaluate the sensitivity of the SWSV analysis, the limit of detection (LOD) and limit of quantification (LOQ) were calculated; they were 3 s m⁻¹ and 10 s m⁻¹, respectively, as calculated from the calibration curves, where m is the slope of the calibration curve, and s is the standard deviation of the peak currents (five runs).⁵⁰ In order to check the correctness of the method, the precision and recovery of the method were also calculated for different concentrations in the linear range. The reproducibility of the peak current and potential was calculated on the basis of five measurements on different days.⁵⁶ The repeatability of the procedure was estimated with five measurements at the same PND concentration. In order to check the selectivity of the proposed method, some introductory studies were executed regarding possible interference compounds present in the typical samples on which the method would be used. In the whole validation process, recovery was calculated with the formula: recovery = 100% + [(found − added)/added] × 100%, confidence interval: t(S/n^1/2), p = 95%, n = 5 and coefficient of variation: CV = (SD × ave⁻¹) × 100%, where ave represents the average from measured values, and SD represents the standard deviation between those values.

Results and discussion

Optimization of electrode modification

Various modifying solutions (based on graphene oxide, reduced graphene oxide and carbon nanotubes) were tested in preliminary studies. Only modifications based on the reduced graphene oxide suspension caused a significant increase of pindolol peak current in comparison to a bare glassy carbon electrode. Next, several RGO suspensions were examined in order to obtain well-shaped PND signals. Among the tested solvents [dimethylfuran (DMF), chloroform (CRF), Nafion, diethyl ether (DEE), methanol, acetone, acetonitrile and dichloromethane (DCM)], only RGO suspensions in DMF, CRF, DEE, DCM and Nafion were mechanically stable on the electrode surface. Those suspensions were tested in detail. PND signals recorded on a GC electrode modified with RGO/CRF, RGO/Nafion and RGO/DCM had much worse morphology than those recorded on a RGO/DMF and RGO/DEE-modified electrode. As, independent from the ratio RGO : solvent (m [mg] : v [mL]), the PND signals were 1.5 times higher on the RGO/DMF-modified GC electrode, dimethylfurane was chosen as the optimal solvent for reduced graphene oxide. This was in good agreement with previous studies, which have proven that DMF is an appropriate solvent for preparing an RGO suspension.^51,52 Next, the ratio between the quantities of RGO and DMF was examined (in the range 0.1–1.0 mg RGO/0.5 mL DMF). The highest PND signals were registered when the modifying solution contained 0.5 mg of RGO and 0.5 mL of DMF. Then, different dropping volumes (0.5–12 μL) of this solution were dropped onto a glassy carbon electrode surface. Because of the PND peak height and shape, a volume of 4 μL was chosen for further studies.

Estimation of electrode real surface areas

Electroactive areas of the electrodes used were obtained by cyclic voltammetry using 5.00 × 10⁻³ mol L⁻¹ K₃Fe(CN)₆ and K₄Fe(CN)₆ as a model redox system at different scan rates. For reversible processes, the anodic peak current I_p depends on the electroactive area of the electrode (A) as described in the equation:⁵³I_p = 2.69 × 10⁵n^3/2AC*D^1/2ν^1/2, where n is the number of electrons involved in the redox reaction, C* is the concentration of ferrocyanide, ν represents the scan rate and D is the diffusion coefficient of the ferricyanide ion (for Fe(CN)₆³⁻ and for Fe(CN)₆⁴⁻ (ref. 54 and 55)). On the basis of K₃Fe(CN)₆ reduction and K₄Fe(CN)₆ oxidation from the slopes of I_pvs. ν^1/2, the dependence of the real surface areas of bare GC and RGO–GC was calculated. The electroactive surface of the RGO–GC working electrode was 0.0118 cm² and 0.0122 cm² for Fe(CN)₆³⁻ and Fe(CN)₆⁴⁻, respectively. The bare GC active surface was equal to 0.0090 cm² (for both Fe(CN)₆³⁻ and Fe(CN)₆⁴⁻). Therefore, the modified electrode had an increased surface area of 134%, which was confirmed by AFM microscopy. The AFM images (tapping mode) of the unmodified and modified GC are shown in Fig. 3. Measured surface roughness for the GC and RGO–GC were 0.839 and 10.4 nm, respectively.

Fig. 3 AFM images of the unmodified (left image) and RGO-modified (right image) glassy carbon electrode.

Optimization of supporting electrolyte and SWSV parameters

Since the composition of the supporting electrolyte is one of the variables that commonly and strongly influences the peak shape and height, it is necessary to check the effect of pH on the system investigated. In order to find the optimal medium for pindolol oxidation, various supporting electrolytes (Britton–Robinson, citrate, acetate, phosphate, citrate–phosphate buffers) were examined. As mentioned in the Solutions section, the supporting electrolyte always contained 90% of the examined buffer solution and 10% methanol, methanol addition is commonly used in the determination of drugs soluble in alcohol.^56,57 The best results in regard to peak height and shape were observed in BR, where signals were almost two times higher in comparison to the other supporting electrolytes tested. Hence, to achieve a high selectivity and sensitivity, the BR buffer was chosen for our detailed studies. As can be seen in Fig. 4A and B, the highest pindolol signals were recorded in BR at pH 5.0. As surfactants are commonly used in voltammetric determinations due to fact that their proper concentration have good influence on the signals of electroactive substances,^58,59 the effect of the content of various surfactants (SDS, CTAB, Triton X-100) in the supporting electrolyte on the PND signal was tested. Only the presence of sodium dodecyle sulfate (SDS) caused a significant increase of the recorded pindolol peaks. Because of that in further studies, the supporting electrolyte contained SDS at an optimum concentration level of 1.00 × 10⁻³ mol L⁻¹ (Fig. 4D – curve c).

Fig. 4 C _PND = 5.0 × 10⁻⁶ mol L⁻¹, E_SW = 25 mV, ΔE = 5 mV, f = 25 Hz. (A) SW voltammograms recorded at different pHs of BR buffer; (B) plot of the PND peak current vs. various pHs of BR buffer; (C) plot of the PND peak potential vs. various pHs of BR buffer; (D) influence of SDS on PND signal (a) without SDS, (b) C_SDS = 1.0 × 10⁻⁴ mol L⁻¹, (c) C_SDS = 1.0 × 10⁻³ mol L⁻¹.

Square wave voltammetry (SWV) was chosen as a more sensitive technique in comparison with differential pulse voltammetry (DPV). Therefore, in the next step, SWSV parameters were optimized. First, the influence of the pulse amplitude (E_SW) on the PND signals was examined. In accordance to SWV theory,²⁵ the PND peak currents exhibit a linear dependence with the E_SW for amplitude values from 10 to 50 mV. For analytical applications, an amplitude of 50 mV was chosen. The effective rate of potential variation in square wave voltammetry is the product between scan increment (ΔE) and frequency (f). ΔE may increase the recorded signal and technique sensitivity; however, for large step potential values, the widening and deterioration of the signal are observed, thus diminishing the resolution of the technique. In this study, the optimal scan increment was found to be 7 mV. During the optimization of frequency (from 8 to 250 Hz), it was found that with an amplitude of 50 mV and a step potential 7 mV, only a frequency of 50 Hz ensured a well-shaped PND signal and low background current. Then, the influence of accumulation potential E_acc and accumulation time t_acc was examined. The optimum values chosen for analytical purposes were an accumulation potential of 0.5 V and an accumulation time t_acc of 10 s.

Electrochemical properties of pindolol

First, cyclic and square wave voltammetry was applied to explain the electrochemical behaviour and properties of pindolol. SW voltammograms were obtained using the RGO–GC (Fig. 5) showed features similar to those obtained by CV (Fig. 5 inset). As can be seen on the CV voltammogram of the PND, one anodic peak is visible at a potential of about 1 V. The lack of a cathodic peak on the reverse scan indicates that the charge transfer during pindolol oxidation is electrochemically irreversible. It is confirmed by the SWV experiment illustrated in Fig. 5, where the net current (resultant), forward current (related to the oxidation process) and backward current (related to the reduction process) are shown. The courses of the forward and backward components clearly indicate an irreversible oxidation process.

Fig. 5 SW voltammograms for a 5 × 10⁻⁶ mol L⁻¹ PND solution in a BR buffer (pH = 5.0), f = 25 Hz, ΔE = 5 mV, E_SW = 25 mV; inset: CV voltammogram of a 5 × 10⁻⁵ mol L⁻¹ PND solution in a BR buffer (pH = 5.0) at a scan rate of 100 mV s⁻¹.

Next, the number of electrons involved in pindolol oxidation was estimated. The difference between peak potential and half-height peak potential is described as |E_p − E_p/2| = 47.7/(αn),^60,61 and is equal to 49 mV for pindolol. Considering α = 0.5 (α will be discussed later in detail),⁶² the number of electrons is n = 1.95–2. The number of electrons was also calculated using the equation: ΔE_p/Δlog f = (2.3RT)/(αnF). The dependence E_pvs. log f is described with the equation E_p = 0.545 log f + 0.932. The number of electrons calculated from the slope is 2.18–2. Next, it was found that the PND peak potential is linearly dependent with pH (E_p = −0.0596 pH + 1.38, Fig. 4C). As the oxidation of pindolol can be described by pindolol → pindolol[ox] + xH⁺ + ne⁻ (where pindolol[ox] is the oxidized form of pindolol), the Nernst equation for this process can be written as E = E⁰ + RT/nF ln[(a_pindolol[ox])(a_H+)^x/(a_pindolol)]. Because the slope of E_pvs. pH dependence is equal to −2.3xRT/nF, considering the number of electrons n = 2, the calculated number of protons is 1.99–2.

Subsequently, the cyclic voltammograms of pindolol were recorded at different scan rates in the range 10–1000 mV. The pindolol oxidation peak shifted towards more positive potentials with increasing scan rate, pointing behavior characteristic for an irreversible electrochemical reaction.⁶² In a BR buffer at pH 5.0, the dependence of the peak current vs. square root of scan rate yielded a straight line, which can be expressed with the equation, I_p = 6.3 × 10⁻⁶ν^1/2 + 1.1 × 10⁻⁸ (R² = 0.995), indicating that electrooxidation is a diffusion-controlled process. This was confirmed by examining the log I_pvs. log ν dependence (log I_p = 0.49 log ν − 5.19, R² = 0.991). The slope of this dependence is expected to be 1 and 0.5 for adsorption-controlled and diffusion-controlled reactions, respectively.⁶² The obtained value of 0.49 confirms that pindolol oxidation is a diffusion-controlled process.

Next, chronoamperometric measurements were used for the diffusion coefficient investigation. Fig. 6 shows the registered chronoamperograms for different concentrations of PND (10–50 μM) in a BR buffer at pH 5.0. The current corresponding to the electrochemical reaction of an electroactive species with a diffusion coefficient is described by Cottrell's equation,^53,60I = nFAC*(D/πt)^1/2, where n is number of electrons, C* the bulk concentration (mol cm⁻³), A is the electrode area (cm²) and F is Faraday's constant. For each concentration dependence, I vs. t^−1/2 was constructed. The slopes of the resulting straight lines were then plotted against pindolol concentration (Fig. 6A). From the resulting slope the Cottrell equation, the diffusion coefficient was found to be 1.18 × 10⁻⁶ cm² s⁻¹. To estimate the heterogeneous electron transfer rate constant (k⁰) and electron transfer coefficient (α), equation I_p = 0.277FAC*k⁰ exp[−αf(E_p − E⁰)] was employed.^53,60 First, the E⁰ value was determined on the basis of the relationship between peak current and scan rate (I_p = 0.0648ν + 1.0022). E⁰ can be estimated by extrapolating the straight line to ν = 0.⁶³⁻⁶⁵E⁰ was found to be 1.00 V (Fig. 6B). Then, the dependence of ln I_p on (E_p − E⁰) was constructed (ln I_p = 21.908(E_p − E⁰) − 13.177). As the intercept is equal to ln(0.277FAC*) + ln k⁰, and the slope equal to −αf (where f = F/RT), k⁰ and α were found to be 3.69 × 10⁻³ cm s⁻¹ and 0.56, respectively. As can be seen, the calculated α value is very close to those considered in preliminary mechanistic studies.

Fig. 6 Chronoamperograms obtained at the RGO–GC in the presence of 10 μL, 20 μL, 30 μL, 40 μL 50 μL of PND; in a BR buffer, at pH 5.0, the electrode potential 0.95 V vs. Ag/AgCl; (A) plots of the slopes of the straight lines against pindolol concentration; (B) influence of scan rate on PND peak potential.

Analytical application and analysis of real samples

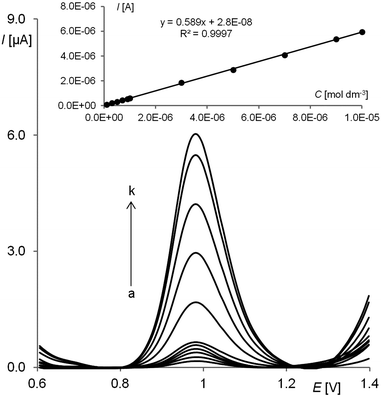
Fig. 7 shows the SW voltammograms recorded for pindolol at concentrations in the range of 1.0 × 10⁻⁷–1.0 × 10⁻⁵ mol L⁻¹ in a BR buffer at pH 5.0 after the optimization of experimental SWSV parameters. The inset illustrates the linear analytical curve obtained. An average of five consecutive measurements was used for the construction of the calibration curve. Basic statistical parameters were calculated as described in the Validation of the method section and are listed in Table 1. Table 2 presents the precision and recovery of the method calculated for different concentrations in the linear range.

Fig. 7 SW voltammetric response of the RGO–GC for different pindolol concentrations [(a) 0.1, (b) 0.3, (c) 0.5, (d) 0.7, (e) 0.9, (f) 1.0, (g) 3.0, (h) 5.0 (i) 7.0, (j) 9.0 and (k) 10.0 μmol L⁻¹] in a BR buffer at pH 5.0. The other experimental conditions were amplitude E_sw = 50 mV, step potential ΔE = 7 mV, frequency f = 50 Hz, t_acc = 10 s and E_acc = 0.5 V.

Table 1 Quantitative determination of pindolol in a BR buffer at pH = 5.0 by SWSV. Basic statistical data of the regression line

Linear concentration range (mol L^−1)	1.0 × 10^−7–1.0 × 10^−5
Slope of calibration graph (A L mol^−1)	0.589
Intercept (A)	2.80 × 10^−8
Correlation coefficient	0.9997
Number of measurements	5
LOD (mol L^−1)	2.6 × 10^−8
LOQ (mol L^−1)	8.6 × 10^−8
Reproducibility of peak current (RSD%)	1.5
Reproducibility of peak potential (RSD%)	1.4
Repeatability of peak current (RSD%)	0.8
Repeatability of peak potential (RSD%)	0.2

---

Table 2 Recovery and precision of pindolol peak currents at various PND concentrations

Concentration given [μmol L^−1]	Concentration found [μmol L^−1]	Confidence interval [×10^−6]	Precision CV [%]	Recovery [%]
0.1000	0.1035	0.0045	4.9	103.5
0.300	0.309	0.013	5.0	103.1
0.500	0.511	0.032	7.2	102.2
0.700	0.710	0.025	4.1	101.4
0.900	0.876	0.031	4.0	97.4
1.000	0.994	0.003	0.4	99.4
3.00	3.11	0.191	7.0	103.7
5.00	4.88	0.017	0.4	97.7
7.00	6.89	0.185	3.1	98.5
9.00	9.07	0.082	1.0	100.8
10.0	10.0	0.039	0.4	100.3

---

Next, a commercial pharmaceutical formulation (Visken) was analysed to estimate the validity of the developed method. Recovery studies were performed by addition of known amounts of the PND standard solution to the analysed sample (as described in the Analysis of commercial pharmaceutical samples section) (Fig. 8A). The Visken tablets matrix did not cause appearance of any additional signals in the examined potential window so it can be concluded that the proposed methodology does not suffer from any significant errors of matrix interference. The calculated recovery is in good agreement with the labelled content (Table 3). Next, to check the practical applicability of the developed method spiked human urine samples were analysed with the standard addition method (as described in Analysis of urine samples section) (Fig. 8B). As it is well known, human urine as a complex matrix is often difficult to analyze because of the presence of uric acids, salts and nitrogenous products of metabolism. In these studies urine samples were used without dilution and pre-separation or pre-concentration steps. It is clearly shown in Fig. 8B that the PND signal is practically free from matrix interferences. According to that the proposed procedure can be successfully and easily used in the evaluation of recovery curves. The data associated with the obtained recovery curves in the urine samples are listed in Table 3.

Fig. 8 Shows SW voltammograms of PND determination in Visken (A) and urine (B; sample 1) using the standard addition method (s-sample; a–c – standard additions). The other experimental conditions were amplitude E_sw = 50 mV, step potential ΔE = 7 mV, frequency f = 50 Hz, t_acc = 10 s and E_acc = 0.5 V.

Table 3 Results of pindolol determination in Visken tablets and urine samples by SWSV

Visken
Declared amount [mg]	Found [mg]	Confidence interval	Precision CV [%]	Recovery [%]
5.00	4.96	0.11	2.0	99.1

---

Urine samples
Sample	Added [μmol L^−1]	Found [μmol L^−1]	Confidence interval [×10^−6]	Precision CV [%]	Recovery [%]
1	10.00	10.25	0.42	3.6	102.5
2	50.00	51.09	2.15	4.8	102.2
3	100.00	98.92	3.94	4.4	98.9

---

Interferences

In order to assess the possible analytical applications of the procedure described above, the effect of interfering species such as drugs (amlodipine, penicylamine, meclastin, drotaverine, propylthiouracil, tizanidine, acetylsalicylic acid, ambazone, atorvastatin, ramipril, cetylpiridine, ibuprofen, captopril, cetirizine, dextromethorphan, ascorbic acid, diosmin, diclofenac and metamizole) or substances commonly found in pharmaceuticals and/or biological fluids (glucose, fructose, saccharose, L-lysine, L-proline, glycine, L-threonine, tryptophan, valine, phenylalanine, Ca²⁺, Mg²⁺, Fe²⁺, Al³⁺, SO₄²⁻ and F⁻). Interferents were added to a 1 × 10⁻⁶ mol L⁻¹ pindolol solution at concentration ratios of 1 : 0.1, 1 : 0.5, 1 : 1, 1 : 5, 1 : 10, 1 : 50, and 1 : 100. The responses were compared with the results obtained for the pure pindolol standard solution. The quantitative determination of pindolol is impossible in the presence of atorvastatin, diclofenac and acetylsalicylic acid. Other studied substances do not interfere (signal change < 5%) in the quantitative determination of PND. Exemplary voltammograms are shown in Fig. 9.

Fig. 9 SW voltammograms of PND determination in the presence of ibuprofen (IBP), (a) 1 × 10⁻⁶ mol L⁻¹ PND, 5 × 10⁻⁷ mol L⁻¹ IBP, (b) 1 × 10⁻⁶ mol L⁻¹ PND and 5 × 10⁻⁶ mol L⁻¹ IBP. The other experimental conditions were amplitude E_sw = 50 mV, step potential ΔE = 7 mV, and frequency f = 50 Hz, t_acc = 10 s and E_acc = 0.5 V.

Mechanism of pindolol electrooxidation

The number of protons and electrons involved in the electrooxidation of pindolol is identical and equal to two (described in detail in the Electrochemical properties of pindolol section). Such amounts and the presence of an indole moiety in the PND structure suggests a possibility of its oxidation.^66–69 The appearance of the peak in the potential range characteristic for this type of mechanisms also confirms this thesis. What more, compounds with structures similar to pindolol (fluvastatin, melatonin and indoramin) were also examined on the RGO–GC as model compounds during this research.

As for the studied compounds, comparable electrochemical properties (number of electrons and protons, peak potential and irreversible oxidation) were observed, and it was stated that the indole moiety is a part of the pindolol molecule where oxidation takes place.^66–69 The possible pathway of pindolol oxidation is presented in Fig. 10. In the suggested mechanism, oxidation occurs first on the nitrogen atom in the indole ring of the molecule, leading finally to the hydroxylation of the benzene ring.^69–71

Fig. 10 Suggested oxidation pathway of pindolol.

Conclusions

The electrochemical behaviour of pindolol was established and studied for the first time. The number of protons and electrons involved in pindolol oxidation, heterogeneous rate constant, diffusion coefficient and electron transfer coefficient were determined. A new, cheap, simple and precise square wave stripping voltammetric method was optimized for the quantitative determination of pindolol in bulk form, pharmaceutical formulation and urine samples. It was shown that in the analysis of real samples, direct analysis was possible, and no time-consuming preparation steps were necessary. What more, complex matrixes such as tablets or urine components do not interfere in pindolol determination on the RGO–GC electrode under optimized conditions. High selectivity, sensitivity, together with the fast and easy electrode preparation and high repeatability, are the main advantages of the studied electrode. What more, the developed method is also environmentally friendly and offers lower detection limit (2.6 × 10⁻⁸ mol L⁻¹), in comparison to i.e. (5 μg mL⁻¹),¹⁵ (15 ng mL⁻¹),¹⁹ longer linear ranges (1.0 × 10⁻⁷–1.0 × 10⁻⁵ mol L⁻¹), in comparison to i.e. (0.04–1.2 μg mL⁻¹),³ (5–120 μg mL⁻¹)¹³ (1.14–17.07 μg mL⁻¹),^17,18 (5–150 ng mL⁻¹),²³ (2.5–30 ng mL⁻¹)²⁴ and guarantee simpler sample preparation than all previously known spectroscopic and chromatographic methods^12–24 for quantitative PND determination.

Acknowledgements

Financial support of the Grant 506/1123 from the Ministry of Science and Higher Education is gratefully acknowledged. The authors would like to thank Dr Andrzej Leniart for AFM images and Dr Monika Skowron-Jaskólska for spectrophotometric measurements.

Notes and references

1. B. Nigovic, M. Marusic and S. Juric, J. Electroanal. Chem., 2011, 663, 72–78.
2. S. Nussbaumer, P. Bonnabry, J. L. Veuthey and S. Fleury-Souverain, Talanta, 2011, 85, 2265–2289.
3. T. P. Ruiz, C. Martinez-Lozano, V. Tomas and J. Carpena, Talanta, 1998, 45, 969–976.
4. J. Ballesteros and L. F. Callado, J. Affective Disord., 2004, 79, 137–147.
5. M. F. Hebert, D. B. Carr, G. D. Anderson, D. Blough, G. E. Green, D. A. Brateng, E. Kantor, T. J. Benedetti and T. R. Easterling, J. Clin. Pharmacol., 2005, 45, 25–33.
6. S. A. Qasqas, C. McPherson, W. H. Frishman and U. Elkayam, Curr. Cardiol. Rev., 2004, 12, 240–261.
7. S. Montan, I. Ingemarsson, K. Marsal and N. O. Sjoberg, Br. Med. J., 1992, 304, 946–949.
8. J. Rasanen and P. Jouppila, Eur. J. Obstet. Gynecol. Reprod. Biol., 1995, 62, 195–201.
9. F. Artigas, V. Perez and E. Alvarez, Arch. Gen. Psychiatry, 1994, 51, 248–251.
10. P. Blier and R. Bergeron, J. Clin. Psychopharmacol., 1995, 15, 217–222.
11. P. Blier and C. de Montigny, Trends Pharmacol. Sci., 1994, 15, 220–226.
12. M. S. Mahrous, A. S. Issa and N. S. Ahmed, Talanta, 1992, 39, 69–72.
13. R. A. S. Lapa, J. L. F. C. Lima, B. F. Reis, J. L. M. Santos and E. A. G. Zagatto, Anal. Chim. Acta, 1998, 366, 209–215.
14. I. Panderi and M. Parissipoulou, Int. J. Pharm., 1993, 99, 327–331.
15. D. Pecanac, D. Radulovic, L. Zivanovic and S. Agatonovickustrin, J. Pharm. Biomed. Anal., 1991, 9, 861–864.
16. A. Jończyk and Z. Nowakowska, Acta Pol. Pharm., 1996, 53, 171–175.
17. S. Khalil and N. Borham, J. Pharm. Biomed. Anal., 2000, 22, 235–240.
18. S. Khalil and M. M. El-Rabiehi, J. Pharm. Biomed. Anal., 2000, 22, 7–12.
19. M. Teltingdiaz, M. T. Kelly, C. Hua and M. R. Smyth, J. Pharm. Biomed. Anal., 1991, 9, 889–893.
20. B. J. Shields, J. J. Lima, P. F. Binkley, C. V. Leier and J. J. Mackichan, J. Chromatogr., 1986, 378, 163–171.
21. B. Diquet, J. J. Nguyenhuu and H. Boutron, J. Chromatogr., 1984, 311, 430–433.
22. M. Bangah, G. Jackman and A. Bobik, J. Chromatogr., 1980, 183, 255–259.
23. H. T. Smith, J. Chromatogr., Biomed. Appl., 1987, 415, 93–103.
24. M. Guerret, J. Chromatogr., 1980, 221, 387–392.
25. V. Mirceski, S. Komorsky-Lovric and M. Lovric, Square-wave voltammetry: theory and applications, Springer, Heidelberg, 2007.
26. M. Lovric, Square-wave voltammetry in: Electroanalytical methods: guide to experiments and applications, Springer-Verlag, Berlin, 2002.
27. S. Smarzewska, S. Skrzypek and W. Ciesielski, Electroanalysis, 2012, 24, 1966–1972.
28. K. Vytřas, I. Svancara and R. Metelka, J. Serb. Chem. Soc., 2009, 74, 1021–1033.
29. S. Smarzewska, R. Metelka, D. Guziejewski, M. Skowron, S. Skrzypek, M. Brycht and W. Ciesielski, Anal. Methods, 2014, 6, 1884–1889.
30. A. Nosal-Wiercinska, M. Grochowski, S. Skrzypek and D. Guziejewski, Desalin. Water Treat., 2013, 51, 1700–1704.
31. A. C. Chen and B. Shah, Anal. Methods, 2013, 5, 2158–2173.
32. M. Lovric, D. Jadresko and S. Komorsky-Lovric, Electrochim. Acta, 2013, 90, 226–231.
33. D. Jadresko, J. Electroanal. Chem., 2013, 693, 56–59.
34. S. Skrzypek, V. Mirceski, S. Smarzewska, D. Guziejewski and W. Ciesielski, Collect. Czech. Chem. Commun., 2011, 76, 1699–1715.
35. V. Mirceski, E. Laborda, D. Guziejewski and R. G. Compton, Anal. Chem., 2013, 85, 5586–5594.
36. V. Mirceski, D. Guziejewski and K. Lisichkov, Electrochim. Acta, 2013, 114, 667–673.
37. D. Krulic and N. Fatouros, J. Electroanal. Chem., 2011, 652, 26–31.
38. L. Wang, X. H. Zang, Q. Y. Chang, C. Wang and Z. Wang, Anal. Methods, 2014, 6, 253–260.
39. X. Wang, S. H. Zhong, Y. He and G. W. Song, Anal. Methods, 2012, 4, 360–362.
40. S. Stankovich, D. A. Dikin, G. H. B. Dommett, K. M. Kohlhaas, E. J. Zimney, E. A. Stach, R. D. Piner, S. T. Nguyen and R. S. Ruoff, Nature, 2006, 442, 282–286.
41. J. T. Robinson, F. K. Perkins, E. S. Snow, Z. Q. Wei and P. E. Sheehan, Nano Lett., 2008, 8, 3137–3140.
42. S. H. Domingues, R. V. Salvatierra, M. M. Oliveirab and A. J. G. Zarbin, Chem. Commun., 2011, 47, 2592–2594.
43. J. P. Zhao, S. F. Pei, W. C. Ren, L. B. Gao and H. M. Cheng, ACS Nano, 2010, 4, 5245–5252.
44. G. K. Dimitrakakis, E. Tylianakis and G. E. Froudakis, Nano Lett., 2008, 8, 3166–3170.
45. Y. H. Tang, R. Huang, C. B. Liu, S. L. Yang, Z. Z. Lu and S. L. Luo, Anal. Methods, 2013, 5, 5508–5514.
46. X. Xi and L. Ming, Anal. Methods, 2012, 4, 3013–3018.
47. J. L. Zhang, H. J. Yang, G. X. Shen, P. Cheng, J. Y. Zhang and S. W. Guo, Chem. Commun., 2010, 46, 1112–1114.
48. Y. Zhou, Q. L. Bao, L. A. L. Tang, Y. L. Zhong and K. P. Loh, Chem. Mater., 2009, 21, 2950–2956.
49. D. Li, M. B. Muller, S. Gilje, R. B. Kaner and G. G. Wallace, Nanotechnology, 2008, 3, 101–105.
50. S. A. Ozkan, Electroanalytical methods in pharmaceutical analysis and their validation, HNB Publishing, New York, 2012.
51. I. K. Moon, J. Lee, R. S. Ruoff and H. Lee, Nat. Commun., 2010, 1, 73.
52. D. Zhao, H. Liu, F. Wang, Q. Feng and M. Li, Anal. Sci., 2013, 29, 625–630.
53. A. J. Bard and L. R. Faulkner, Electrochemical Methods, Wiley, New York, 2001.
54. S. F. Wang and Q. Xu, Bioelectrochemistry, 2007, 70, 296–300.
55. R. M. Dornellas, R. A. A. Franchini, A. R. da Silva, R. C. Matos and R. Q. Aucelio, J. Electroanal. Chem., 2013, 708, 46–53.
56. B. Dogan, S. A. Ozkan and B. Uslu, Anal. Lett., 2005, 38, 641–656.
57. A. Golcu, B. Dogan and S. A. Ozkan, Anal. Lett., 2005, 38, 1913–1931.
58. R. Shrivastav, S. Piara Satsangee and R. Jain, ECS Trans., 2012, 50, 23–36.
59. M. B. Gholivand, G. Malekzadeh and M. Torkashvand, J. Electroanal. Chem., 2013, 704, 50–56.
60. C. M. A. Brett and A. M. O. Brett, Electroanalysis, Oxford University Press, Oxford, 1998.
61. R. G. Compton, Understanding Voltammetry, 2 edn., Imperial College Press, London, 2011.
62. D. K. Gosser, Cyclic Voltammetry, VCH, New York, 1994.
63. L. Rojas, L. Molero, R. A. Tapia, R. del Rio, M. A. del Valle, M. Antilen and F. Armijo, Electrochim. Acta, 2011, 56, 8711–8717.
64. S. Majdi, A. Jabbari, H. Heli, H. Yadegari, A. Moosavi-Movahedi and S. Haghgoo, J. Solid State Electrochem., 2009, 13, 407–416.
65. F. Armijo, I. Torres, R. Tapia, L. Molero, M. Antilen, R. del Rio, M. A. del Valle and G. Ramirez, Electroanalysis, 2010, 22, 2269–2276.
66. D. Kul, M. Gumustas, B. Uslu and S. A. Ozkan, Talanta, 2010, 82, 286–295.
67. S. Yilmaz, B. Uslu and S. A. Ozkan, Talanta, 2001, 54, 351–360.
68. S. Suzen, B. T. Demircigil, E. Buyukbingol and S. A. Ozkan, New J. Chem., 2003, 27, 1007–1011.
69. N. Karadas, B. Bozal-Palabiyik, B. Uslu and S. A. Ozkan, Sens. Actuators, B, 2013, 186, 486–494.
70. K. Humphries and G. Dryhurst, J. Pharm. Sci., 1987, 76, 839–847.
71. K. Sagar, J. M. F. Alvarez, C. Hua, M. R. Smyth and R. Munden, J. Pharm. Biomed. Anal., 1992, 10, 17–21.

---