Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A hydrodynamically optimized nano-electrospray ionization source and vacuum interface†
M.
Pauly‡
*a,
M.
Sroka
b,
J.
Reiss
b,
G.
Rinke
a,
A.
Albarghash
a,
R.
Vogelgesang
a,
H.
Hahne
c,
B.
Kuster
c,
J.
Sesterhenn
b,
K.
Kern
ad and
S.
Rauschenbach
*a
aMax-Planck-Institute for Solid State Research, Heisenbergstr. 1, D-70567 Stuttgart, Germany. E-mail: matthias.pauly@ics-cnrs.unistra.fr; s.rauschenbach@fkf.mpg.de
bTechnical University Berlin, Ernst Reuter Platz 555, D-01300 Berlin, Germany
cChair of Proteomics and Bioanalytics, Technische Universität München, Emil-Erlenmeyer-Forum 5, D-85354 Freising-Weihenstephan, Germany
dInstitut de Physique de la Matière Condensée, Ecole Polytechnique Fédérale de Lausanne, CH-1015 Lausanne, Switzerland
First published on 30th January 2014
Abstract
The coupling of atmospheric pressure ionization (API) sources like electrospray ionization (ESI) to vacuum based applications like mass spectrometry (MS) or ion beam deposition (IBD) is done by differential pumping, starting with a capillary or pinhole inlet. Because of its low ion transfer efficiency the inlet represents a major bottleneck for these applications. Here we present a nano-ESI vacuum interface optimized to exploit the hydrodynamic drag of the background gas for collimation and the reduction of space charge repulsion. Up to a space charge limit of 40 nA we observe 100% current transmission through a capillary with an inlet and show by MS and IBD experiments that the transmitted ion beams are well defined and free of additional contamination compared to a conventional interface. Based on computational fluid dynamics modelling and ion transport simulations, we show how the specific shape enhances the collimation of the ion cloud. Mass selected ion currents in the nanoampere range available further downstream in high vacuum open many perspectives for the efficient use of electrospray ion beam deposition (ES-IBD) as a surface coating method.
Introduction
Electrospray ionization (ESI)1,2 generates intact molecular ions, which are used for mass spectrometry,3,4 ion mobility spectrometry (IMS)5 or for ion beam deposition methods like soft landing.6,7 The coupling of an API source to the mass spectrometer's first vacuum chamber is usually made via a pinhole, or more frequently through a transfer capillary. Its opening diameter defines the gas load on the first stage of the differentially pumped vacuum system and is thus strongly limited by the available pumping speed. Typically capillaries with an inner diameter of 0.5–0.7 mm and a length of 5–20 cm or pinholes of less than 0.5 mm diameter are used for the initial transfer of ions into vacuum. With moderately sized pumps a pressure gradient of 2–3 orders of magnitude is generated.Upstream of the transfer capillary, the ESI source can be operated with high ionization efficiency. At low flow rates and low concentrations all molecules in a solution can be ionized.8,9 Downstream, sophisticated in vacuo ion optics can reach a transmittance of 50–100%.10 During the transfer from atmospheric pressure to vacuum however a major fraction of the ion current is lost. In principle these losses are higher for high flow rates and high concentration of the molecules in the solution. For the ion transfer alone, the present literature suggests a transmittance of up to 20% for low flow interfaces (micro- or nanospray, ca. 500 nL min−1),8,11–15 an individual example shows close to 50%.15 Transmission ratios reported for conventional interfaces operated at high flow rates are usually much lower than for nanospray.8,11–13 More often, the transmittance is known to be low, but is not quantified explicitly.
Several loss mechanisms such as space charge expansion, diffusion, transport in the electric field, or turbulence are suggested, however, only in a few cases were they identified and quantified. For short capillary vacuum interfaces, for instance, it has been shown that a large fraction of the ion current is lost at the rim of the entrance hole and a smaller fraction within the capillary itself, while the loss due to space charge and diffusion becomes more important for long capillaries.13,15
Improving the ion transmission by changing the geometry16 has been approached for instance by using multiple sprayers,17,18 multiple capillaries,19,20 specially shaped electrodes,21 and flared capillary inlets.22–24 Contouring of the field at the capillary inlet and throughout the entire conductance pathways into vacuum has improved transmission efficiency and overcame some of the space charge limitations.25–29 More recent developments aim at directly influencing the gas flow by adding gas streams29–33 or by using hydrodynamic devices.34–37 Even the complete avoidance of the vacuum transfer by placing the ESI-emitter within vacuum has been demonstrated.9 All these methods do increase the ion transmission into vacuum, some significantly. Unfortunately, most studies present relative ion intensities for certain compounds rather than electrical currents, which complicates the comparison between different sources and does not allow for absolute quantification of the transmission.34,35,38 Moreover, the calculation of the motion of the background gas in a complex geometry and further its effect on the ion motion are computationally demanding and thus complicate the modelling and predicting of the performance of an ion source.
Therefore, the knowledge about the ion transport in API sources remains mostly empirical and there is no fundamental understanding of the principles that could be employed to systematically optimize this key component. Nevertheless, a few studies report absolute current measurements,12–15,39,40 from which transmissions in the range of 1–20% for capillary interfaces are calculated. Most importantly, Lin et al. showed that the losses at the inlet account for 50–99% for various capillaries.39 In contrast, Page et al. reported that 90% of the losses occur within the capillary itself for a short capillary to the emitter distance, whereas 50% of the losses occur at the inlet when the distance between the emitter and the capillary is increased.15
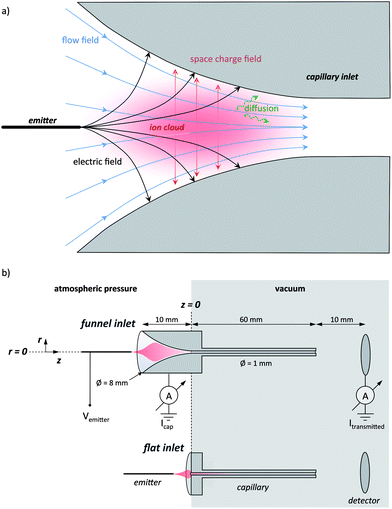
To understand the origin of the ion losses and rationally improve the performance, we initially consider the motion of an ion in an ESI interface close to atmospheric pressure, which is governed by static electric fields, space charge fields, hydrodynamic drag and diffusion, depicted in Fig. 1a. Electric forces originate from the high voltages applied between the emitter and the capillary and depend mostly on the magnitude of the voltage and the geometry of the electrodes in the interface. Additionally, the ion cloud generated by the electrospray plume expands due to the Coulomb repulsion of its own space charge. Space charge forces scale with the charge density and are further influenced by the specific geometry of the surrounding electrodes. Hydrodynamic forces are caused by the interaction of the particle with the surrounding fluid, which is usually air or N2 containing some vaporized solvent. The hydrodynamic force field strongly depends on the interface geometry defining the fluid flow. Furthermore, the acceleration of the ions by electric forces causes ion–gas-collisions that can be described macroscopically by a drag force compensating the electrical force. The resulting drift motion depends on the ion mobility and on the local properties of the gas. Finally, diffusion is dependent on the properties of the gas and the ion itself as well as on the concentration gradients present.
Among all these acting forces, only the hydrodynamic drag force can be collimating i.e. it can have a vector component that is pointing towards the axis of the capillary. Electrostatic and space charge forces typically point outwards. This initial consideration shows that an optimization of an atmospheric pressure interface has to be pursued either by reducing the dispersing effects of the electric forces and diffusion or by acting on the fluid flow to use it for actively collimating the ion cloud. It becomes further apparent that the reasons for ion losses are the high electric fields required for electrospray ionization and the electric field of the space charge, while the radial velocity component of the fluid flow must become zero at the wall and thus cannot be responsible for ion losses.
To improve the performance of nano-ESI capillary vacuum interfaces we conducted a study, systematically comparing a specifically designed, funnel shaped capillary with a conventional, flat capillary geometry of an otherwise identical configuration (Fig. 1b). We reason that the hydrodynamic flow in the funnel will collimate the ion cloud while at the same time reduce the space charge expansion due to an axial acceleration of the ions at the place of their generation and thus significantly improve the performance. In this study we quantify the ion losses in both types of nano-electrospray (ES) interfaces experimentally by absolute current measurements and interpret the findings with the help of ion transport simulations based on computational fluid dynamic calculations.
Experimental and computational methods
Atmospheric pressure interface
A stainless steel tube of 6 cm length with an inner diameter of 1.0 mm is the transfer capillary between the ambient environment and the vacuum chamber (see ESI† for further details). It is soldered into a stainless steel cylinder of 8 mm diameter and 1 cm length. Two different capillary types are studied: a conventional shape, in which the stainless steel cylinder at the capillary entrance is flat, and a funnel shape, which is crafted into the cylinder by electro-erosion (see Fig. 1b). The funnel has an entrance opening of 8 mm in diameter, which smoothly reduces to the capillary diameter along a 10 mm length, while the curvature angle is approaching 0°.The capillary is mounted, electrically connected to a copper cylinder, which contains a 50 W cartridge heater, a Pt100 thermometer and a high voltage (SHV) wire connection (Fig. S1 in the ESI†). This assembly is held by a PTFE socket, electrically insulated from the vacuum chamber. Voltages of up to 5 kV are applied to the whole assembly which is heated to 200 °C during measurements.
Electrosprays are generated using glass emitters made from pulling capillaries of 75 μm inner diameter and 365 μm outer diameter to create a defined apex of reduced diameter. For the measurement of the spatial acceptance, commercial emitters (uncoated silica PicoTips, 150 μm outer diameter and 10 μm inner diameter, New Objective) are used since they are stable for a very long time. The emitters are cut to 5 cm length and then connected to the spray solution feed through a finger-tight peek union containing a liquid junction electrode to apply the electrospray voltage. This assembly is mounted on a movable stage allowing the precise positioning of the emitter in three dimensions. We define the zero positions as the capillary axis for the radial direction r and the capillary entrance for the azimuthal direction z (see Fig. 1b).
Transmission measurements
For the transmission measurements the described API interface assembly is mounted to a vacuum chamber pumped by a roots pump (Leybold Ruvac WSU 151, 153 m3 h−1) backed with a rotary pump (Leybold Trivac D16B, 16 m3 h−1). During operation, the pressure, measured at a distant wall in the chamber, is 4 mbar.Solutions of 10−2 to 10−5 M Rhodamine B (RhoB) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 H2O/MeOH solvent mixture are used for the transmission quantification (further experimental details are given in SII†). A syringe pump (Harvard Apparatus Pump 11) is used to set the flow of 0.5–1 μL min−1. High voltages (Vemitter = 1–5 kV) are applied to the liquid junction electrode to generate the electrospray.
1 H2O/MeOH solvent mixture are used for the transmission quantification (further experimental details are given in SII†). A syringe pump (Harvard Apparatus Pump 11) is used to set the flow of 0.5–1 μL min−1. High voltages (Vemitter = 1–5 kV) are applied to the liquid junction electrode to generate the electrospray.
The ion currents are measured with Keithley 616 electrometers or with equivalently sensitive, self-build current–voltage converters that can be floated on high voltages. Connected to the capillary and to a metal plate placed 1 cm downstream of the capillary exit in vacuum, these instruments are set to a sensitivity of 10 pA. Both the capillary and the detector plate are grounded. The current measured in vacuum is referred to as the transmitted current Itransmitted in the following. The current measured on the capillary is referred to as the loss current or capillary current Icapillary. These electrical currents are caused by analyte ions, but can also be due to charged droplets, clusters, solvent ions or other contaminants. The total emitted current is calculated as the sum of the transmitted and capillary currents i.e. Iemitted = Icapillary + Itransmitted. In addition, undetected leakage currents Ileak are possible on the ambient pressure and on the low pressure sides of the capillary. However, on the vacuum side, the detector is placed close to the capillary exit, which excludes ions leaving for the pump or chamber wall. The observation of unity transmittance in some cases confirms this. The absence of any leakage current on the ambient pressure side was verified in a separate experiment: using only an emitter and a collector plate of otherwise the same geometry as the interface, the same current was measured at both terminals (see Fig. S4†). Moreover, by placing the emitter at a position where the transmitted current becomes zero, the relationship Iemitted = Icapillary is verified several times during each measurement, which excludes any leakage current on the atmospheric pressure side.
As a benchmark for the performance of the capillary interface alone, we define the transmittance as the ratio of the transmitted current and the emitted current. The overall performance of an ion source moreover depends on the ionization yield as well and is expressed in the sampling efficiency, which is defined as the ratio of the flux of molecular ions entering the vacuum through an aperture or capillary and the flux of molecules entering the source dissolved in a liquid.41
Mass spectrometry and electrospray ion beam deposition
By reducing the capillary diameter to 0.75 mm while keeping the same funnel shape the interface is matched to the pressure requirement of 1 mbar in the first pumping stage of our ES-IBD apparatus,42–44 which contains a linear time-of-flight (TOF) mass spectrometer. This mass spectrometer is used for the verification of the purity of the ion beam. It is mounted in the 4th differentially pumped chamber at a pressure of 10−7 mbar and has a resolution of m/Δm = 1000 and a dynamic range of three decades. Mass spectra are recorded using a 10−4 M RhoB solution in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 H2O
1 H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MeOH solvent, and a 0.01 mg mL−1 (≈8 × 10−7 mol L−1) Cytochrome C (CytC) solution in a 3
MeOH solvent, and a 0.01 mg mL−1 (≈8 × 10−7 mol L−1) Cytochrome C (CytC) solution in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : 1 H2O
: 1 H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MeOH to which 2% formic acid has been added.
MeOH to which 2% formic acid has been added.
To probe the ion beam for contamination that cannot be detected by mass spectrometry, like neutral molecules and clusters or very large charged clusters, we perform scanning tunnel microscopy (STM) imaging of atomically clean Cu(111) samples after deposition of the CytC ion beam by ES-IBD from the funnel interface. The depositions take place in the sixth vacuum chamber at 10−10 mbar and the samples were then transferred in situ to the STM for characterization.42–44 The current is continuously measured on the sample, which gives access to the total charge deposited expressed in pAh (1 pAh corresponds to the charge deposited from a 1 pA ion beam for 1 h, i.e. 3.6 × 10−9 C).
Computational fluid dynamics and ion trajectory simulations
The motion of the ions in the interface is simulated using SIMION 8 (ref. 45) with the SDS package46 to include the influence of a neutral background gas in motion. The simulation calculates the trajectory of an ion fully defined by mass, charge, position and velocity in the electric field generated by metallic electrodes defined by their geometry and applied voltage.The gas flow is described by the two dimensional compressible Navier–Stokes equations of the ideal gas (Section S-III in the ESI†). Standard conditions for air are used. The friction is described by the usual Sutherland law. The simulation builds on characteristic rewriting of the Navier–Stokes equations,47 which works in pressure, velocity and entropy, from which all thermodynamically relevant quantities can be derived. The simulation is run in time until a steady state of the flow is reached.
Due to the symmetry of the geometry, the flow simulations are done in two dimensions. In reducing the dimensionality, we do not expect qualitative changes in the characteristics of the gas flow, albeit locally quantitative deviations will occur. Assuming identical conditions in the capillary, the velocities in the inlet section of the two dimensional geometry will be higher, because for a given diameter the same mass flux is distributed over a smaller cross-section. Following the same argument, the gradients for pressure and velocity will be steeper in a 2d simulation as compared to a full 3d model. The most significant difference caused by the 2d simulation is a suppression of turbulences, which however would only occur within the transfer tube in a gas flowing at a constant velocity and not in the interface where the gas is accelerated.
The ions for the example trajectory calculations are defined as RhoB singly positive charged ions (m/z = 443) and trajectories are calculated by applying a static voltage of 2.5 kV to the emitter electrode and 0 V to the capillary (Section S-IV in the ESI†). The space charge of the ion beam is not considered in the simulations and only later calculated along specific ion paths to be compared to the other influences on the ion beam. Therefore the effect of the external electric field from the voltage applied on the emitter and of the electric field of the space charge is expressed in velocities. For their calculation the mobility is expressed as K = K0(P0/P)(T/T0) with P the local pressure from the computational fluid dynamic calculations and the local temperature T = 300 K considered as constant (P0 = 1000 mbar and T0 = 273 K). The value of the reduced mobility (K0 = 9.2 × 10−5 m2 V−1 s−1) is the value estimated using the SDS package of SIMION from the molecular mass of RhoB.
Results and discussion
Ion transmission characteristics
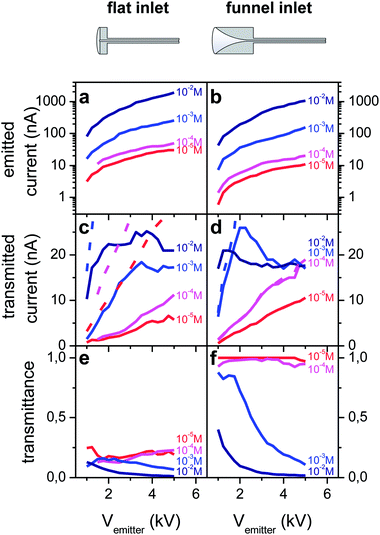
Spray voltage, solution concentration and flow rate are the main parameters that determine the ion current generated by an ES emitter. We use the strong dependencies on spray voltage and concentration to vary the emitted current over many orders in magnitude,13,48,49 while the flow rate is held constant at 0.5 μL min−1 to avoid unstable sprays caused by too low flow rates and the generation of large droplets caused by too high flow rates. Currents ranging from several picoampere (pA) up to a few μA are generated from RhoB solutions with concentrations between 10−5 M and 10−2 M and spray voltages of 1–5 kV (Fig. 2a and b).The electric field at the emitter apex is a key parameter in determining the electrospray current. To comparatively investigate the transmission characteristics of conventional and funnel interfaces, emitter positions are selected such that the distance between the emitter apex and the capillary wall is approximately the same in both cases, which results in a similar electric field distribution and magnitude in the vicinity of the apex. Because the funnel extends into the half space of z < 0 mm, opening up from 1 mm to 8 mm diameter (see Fig. 1) the emitter at position z = −6.5 mm is located within the funnel at a distance of 2 mm to the capillary wall. Thus for the flat capillary the equivalent position is z = −2 mm.
For these geometric parameters we find emission current characteristics Iemitted(Vemitter) that are identical for both interface types over the studied concentration range (Fig. 2a and b). If, as in Fig. 2, different emitters are used for the characterization of the two different capillaries, the characteristics differ in current by a factor of less than one order of magnitude, but show otherwise identical behaviour. Our emitter fabrication method has only limited reproducibility. Thus each emitter has a unique geometry, with a slightly different tip diameter, which can cause a shift in the emission current for the same flow rate and concentration. If the same emitter is used with both interfaces, we find the identical characteristics for both interfaces (see for instance Fig. S3B(a) and (b)†).
The transmitted current measured on the metal plate detector in vacuum increases with the emitted current until a maximum value of approximately 20 nA is reached and then stays constant on further increasing the spray voltage (Fig. 2c and d). This current limit exists for both flat and funnel-shaped interface types. It further depends on the individual emitter, the transfer capillary diameter, the emitter position, and the solution concentration (see ESI section S-IX†).
Although the net current transmitted into vacuum reaches the same top values for both capillary types, the transmittance, defined as the ratio between the current transferred through the capillary and the total emission current, is significantly different. The flat capillary's transmittance never exceeds 20% (Fig. 2e), whereas up to 100% of the emitted current can be measured in vacuum if the capillary with a funnel shaped inlet is used (Fig. 2f). In the measurement shown in Fig. 2, the unity transmittance is observed for the 10−5 M and 10−4 M solutions over the entire range of 1–5 kV applied to the emitter, i.e. for emission currents up to 20 nA. In general, with the 1 mm capillary, up to 40 nA can be observed at 100% transmission using an optimal emitter (Fig. S2 in the ESI†). Above this threshold, only the loss current measured on the capillary increases further with the electrospray voltage or the solution concentration, which translates to a decreasing transmittance. It should also be noted that the transmittance of the flat capillary is higher than values reported in the literature as well,11–14 because the capillary used here has a diameter of 1 mm, larger than those used for other studies (typically 0.4–0.6 mm).
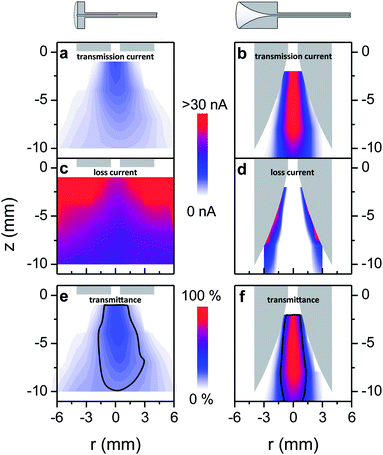
To compare both capillary types and better understand the influence of the geometry, a transmission and loss current map were measured and a transmittance map was calculated (Fig. 3). This was done at a working point of Vemitter = 2.5 kV. The maximal values for the transmission current for both capillaries are found when the tip is aligned with the capillary axis (r = 0 mm) and is brought as close as possible to the 1 mm diameter capillary entrance at z = 0 mm (Fig. 3a and b). Away from this position in the radial and axial direction the transmitted current decreases. The funnel interface reaches a peak transmission of 30 nA, while for the flat capillary only 6.5 nA is detected. The corresponding relative transmittance reaches 100% for the funnel capillary and up to 23% for the flat interface.
The map of the loss current (Fig. 3c and d) approximately resembles an inverse image of the transmission current map, because the emission current is the sum of transmitted and loss currents. As the emission depends on the electric field at the emitter apex, the emitted current increases when the distance between the emitter and the capillary is reduced. This occurs in the axial direction for both interfaces and in the radial direction for the funnel interface (see ESI Fig. S3†). For both interface types we see that electrosprays generated at such a small distance to the capillary wall provide higher emitted current but also cause significant losses. Both the absolute current transmitted as well as the relative transmittance are lower in regions close to the capillary wall.
The transmittance map (Fig. 3e and f) also offers a way to define and measure the volume for which the ions are effectively sampled into the transfer capillary. For instance the volumes of at least half of the maximal transmittance are approximately of the same size for both geometries. Hence, positioning of the emitter requires the same precision for both interfaces. However, the absolute intensities transmitted within these volumes differ greatly (Fig. 3a and b).
When interpreting the measured current- and relative-transmittance maps, one must keep in mind that the emitter position and the position where the ions are generated are not identical, but rather a plume of macroscopic size is generated downstream the emitter apex, in which gas phase ions are created out of charged droplets.50 The shape of the ES-plume, as well as the distribution of droplets and ions in it, is determined by space charge and external electric fields as well as the hydrodynamic drag.
We see for both interface geometries that positioning the emitter close to the wall is one major cause of ion losses, which is certainly due to electric fields, whereas it cannot be decided whether space charge or external fields are the main cause for that. When the emitter is positioned away from the wall, the confined geometry of the funnel leads to a significant improvement of the transmission for emitter positions within the funnel, while the transmission of a current generated in the free space in front of the interface is the same for both interfaces.
Summarized, the current measurements show that under conditions of a fixed set of parameters, e.g. spray voltage, solution concentration, flow rate and emitter performance, the funnel interface transmits higher currents than the flat capillary interface when the emitter is positioned at an optimal position within the funnel. Up to 100% of the ions generated by an electrospray can be transferred to the vacuum with the funnel capillary, whereas the transmittance for the flat capillary is limited to 25%. Independent of the geometry of the inlet section, however, beyond a transmission current limit, increasing the electrospray emission current does not increase the transmitted current further and thus the relative transmission decreases.
While for the vacuum transmittance of capillary interface values around 20% are reported,11–14 for modified aperture interfaces of larger than usual diameter very high sampling efficiencies of up to 80% can be achieved, which implies an inlet transmittance of at least this value.41 The direct comparison of our experiment with the work of Schneider et al.41 is very insightful as both experiments require larger than the typical pumping speed for the first vacuum chamber to compensate for the increased gas load from the large diameter capillary or large aperture, respectively. Both experiments use approximately the same solution flow rate of 500 nL min−1 and molecules in the same mass range. The solution concentration, however, differs by orders of magnitude. Schneider et al. worked with a solution of 1.6 × 10−9 M, which would generate a current of 1.3 pA of the singly charged analyte ions at a given flow rate and 100% ionization efficiency. They estimated that the detected 6.8 × 105 counts per second relate to a sampling efficiency of 80% and hence a vacuum transmission above that. For the funnel capillary source we achieved 100% vacuum transmission with solutions of 10−4 M and below, with 10−3 M we still reach 90%. Assuming that the current relates to analyte ions only, which is shown by mass spectrometry measurements (see section ‘Chemical characterization’), we can relate the maximal current of 40 nA detected in vacuum to a sampling efficiency of 50%, as we estimate 80 nA of analyte ion current from the 10−4 M solution. For 10−5 M solutions the maximum transmitted current is 10 nA, which suggests a sampling efficiency of around 100% (see ESI section S-VIII†). These numbers represent an ion source of high intensity and efficiency, provided that the transmitted current consists exclusively of analyte ions. This indeed crucial point will be addressed in detail in the following section. Nevertheless the measurements show that unity transmission of ion currents up to 40 nA to vacuum is possible.
Chemical characterization
We have shown in the previous section that the modified capillary allows transmitting up to 100% of the ions produced at atmospheric pressure up to a threshold current. However, the measurement of a net current does not yield information on the nature of the charged species that constitute this current. The enhanced transmittance does represent an improvement only if the performance of the funnel source with respect to the chemical composition and contamination of the ion beam is comparable to conventional sources. In particular, by measuring electric current one cannot distinguish between ionized, desolvated analyte molecules and charged contaminants like ionized solvent molecules, ionized clusters or even charged solvent droplets containing analyte molecules. Their presence, however, can have a negative effect on the performance of a mass spectrometer or an ES-IBD experiment.These concerns were addressed by characterizing the ion beam using mass spectrometry, current transmission of a rf-only quadrupole and ion beam deposition experiments with RhoB and CytC as reference compounds. The combination of these techniques allows us to exclude all relevant types of contaminants, including neutral and charged clusters, droplets, fragments, neutrals and ions other than the analyte.
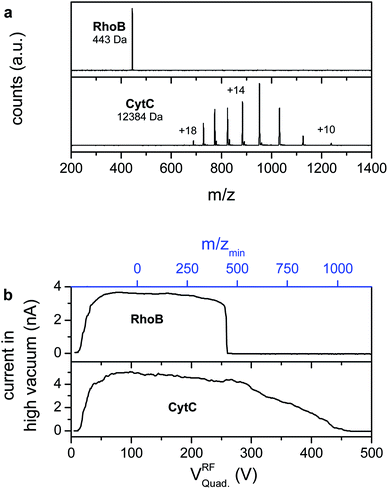
Fig. 4a shows mass spectra of ion beams generated by a nano-ESI source with a funnel capillary interface, acquired with the linear TOF mass spectrometer of our ES-IBD experiment.42–44,51–53 The integration of the funnel capillary did not alter the mass spectra qualitatively as compared to the commercial pneumatically assisted source (Agilent Techn.) used before. However the detected intensity at the TOF detector (ETP 14882) increased to an extent that the dynode voltage had to be significantly reduced from 2.9 kV to 2.4 kV in order to detect an unsaturated signal. According to the detector specifications, this decrease compensates for an increase in intensity of 2–3 orders of magnitude, which fits with the increase in the absolute current detected in the TOF chamber.
Solutions of 10−4 M RhoB in water/methanol, as used for the characterization of the transmission, as well as a solution of 0.01 mg mL−1 CytC in water/methanol with 2% formic acid are electrosprayed in positive mode. The RhoB mass spectrum shows one single peak, which can be assigned to the singly charged molecular cation (m/z = 443 Th), whereas the CytC mass spectrum shows the characteristic pattern of several charge states due to multiple protonation (m = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384 Da, +10 < z < +18).52,54 In both experiments no other peaks can be detected, which demonstrates the absence of ionized contaminants.
384 Da, +10 < z < +18).52,54 In both experiments no other peaks can be detected, which demonstrates the absence of ionized contaminants.
However, high mass clusters and other chemical noise that would not yield individual peaks in a mass spectrum can be a significant fraction of the net current. Thus, in addition to the TOF-mass spectrometry, the ion current has been measured on an electrode plate in the fourth pumping stage (10−7 mbar) while sweeping the rf-voltage of a quadrupole ion guide operated in rf-only mode (Fig. 4b). In this mode the ion guides have a sharp lower m/z-cutoff, while high mass ions are indiscriminately transmitted. The obtained data are equivalent to a mass spectrum integrated over m/z, in which heavily charged clusters and other high m/z-chemical noise would appear as a current at high rf-voltages, whereas all peaks have vanished from the mass spectra. Moreover, this measurement detects the absolute ion current in the high vacuum stage of the instrument through an electrometer and is thus, in particular, not affected by saturation effects, which allows the determination of the fraction of the current that is transmitted into high vacuum.
Above a certain rf-voltage required to establish ion transmission through the quadrupole (approximately 20 V), an ion current of up to 5 nA is detected for both compounds. The current is constant for low rf-voltages. For the RhoB beam, sweeping the quadrupole rf-voltage further engenders a sudden drop of the current to zero at 260 V, corresponding to the suppressed transmission of the RhoB ion, which is confirmed by TOF-MS (upper panel in Fig. 4b). For the CytC beam the decrease is not abrupt due to the distribution of the current into several charge states of different mass-to-charge ratios (lower panel in Fig. 4b). Thus one would expect steps that correspond to the transmission of each charge state, those, however, are smeared out due to the limited resolving power of the quadrupole in rf-only mode. Above Vrf = 450 V the current recorded for CytC is equal to zero as well, coinciding with the disappearance of the lowest charge state peaks from the mass spectrum. In both cases the tolerance is a few picoamps. Thus, based on these and the mass spectrometry measurements, any significant amount of charged contaminants, in particular charged clusters and droplets, can be excluded.
The detected current of 5 nA in high vacuum for both ion beams further shows that a large fraction of the ions, passing through the capillary into the first vacuum chamber, is further transmitted into the high vacuum of the fourth pumping stage. For the 0.75 mm capillary used in these experiments, a current limit cut-off around 20 nA was measured (see ESI Fig. S9†), from which we estimate a transmittance for the whole apparatus from leaving the capillary to high vacuum of ∼25%. This is in agreement with previous measurements on our ES-IBD apparatus using other ion sources. It further confirms that the funnel source emits a well-defined, pure ion beam, while for instance leakage currents, gas discharges or other artefacts misinterpreted as molecular ion current can be dismissed. Thus the data from TOF-MS and quadrupole sweeps measured in high vacuum are representative for the ion beam entering the vacuum system through the capillary.
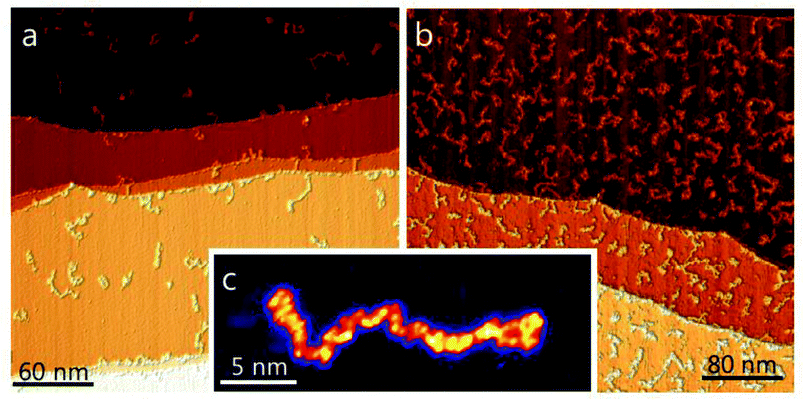
Finally, the CytC ion beam has been deposited on atomically flat and clean surfaces of a Cu(111) single crystal in the ultra-high vacuum (p = 2 × 10−10 mbar) of the 6th pumping stage at low and high coverage and imaged in situ by STM (Fig. 5, see ESI† S-V for experimental details). This measurement is the most sensitive to neutral contamination, which would be detected as adsorbates on the surface when present in small quantity. If a large amount of charged or neutral contaminants would be deposited, the surface quickly became contaminated to a point where STM imaging is entirely impossible as a strongly contaminated surface would not allow for a stable tunnel junction.51,53
Due to the possibility of chemical interaction with the surface,55,56 it is not possible to infer the chemical state of a molecule after ion beam deposition directly from an STM image alone. It is apparent, however, that only string-shaped structures, characteristic of soft-landed unfolded proteins, are observed on an otherwise clean surface.52 The observed morphology, molecular- as well as surface-structures are identical to previous experiments with the same molecules deposited under the same conditions using either a commercial, pneumatically assisted, orthogonal electrospray source52 or a conventional cylindrical ion transfer capillary with an in-line nano-ES.
In addition, the observed molecular coverage fits to the amount of deposited charge, which indicates that nothing but CytC molecules were transporting the charge to the surface. The ion beam deposition experiment allows for a determination of the mass-to-charge ratio fully independent of the mass spectrometer. The deposited charge is found by integrating the ion current over the deposition time (15 pAh and 50 pAh for the low- and high-coverage respectively) and the number of molecules is measured by extrapolating the molecular coverage observed with STM to the whole sample (see Fig. 5a and b).40,53 For the presented experiments we find values between 12 and 21 charges per molecule, which reasonably fits with the corresponding mass spectrum. Since this method includes all charge carriers that arrive at the surface this result allows us to exclude the presence of ions other than those seen in the mass spectra.
Moreover, a large number of samples and STM images of similar quality using many different molecules and surfaces were produced since the incorporation of the funnel ion source into the ES-IBD apparatus.
The data obtained from current measurements, mass spectrometry, quadrupole sweeps, and finally STM after IBD in ultrahigh vacuum (UHV) characterize the ion source in many, distinctly different aspects. Their combination provides enough evidence to the matter of whether the transmitted ion current consists of charged droplets or desolvated ions. This is crucial, since capillaries of larger diameter, here 1 mm (or 0.75 mm for the ES-IBD instrument), could be problematic regarding droplet desolvation. The indicators for a well-defined molecular ion beam without droplets, clusters, or contaminants are: ion currents stable over a long time, clean TOF mass spectra, a sharp step in the ion current to zero for the Q2 sweeps, and atomically clean surfaces after ion beam deposition. In addition we see a clear indication of desolvation in the temperature characteristic of the transmitted current at 125 °C. Around this temperature the transmitted current increases from 7 nA to 30 nA, marking the transition of a droplet containing beam to one of gas phase ions (ESI S-VII, Fig. S8†). One might even speculate that the funnel geometry provides a more efficient heating due to the close proximity of the heated capillary wall to the emitter, and hence desolvation works well despite the fact that larger diameter capillaries are used. Finally, we did not detect any sign of an ill-defined ion beam, or droplet-containing ion beams, such as increased pressure in the UHV stages, high currents that do not react to voltages applied to electrostatic lenses, or strongly fluctuating, unstable ion currents.
Modelling of the vacuum transfer
To understand the origin of both the enhanced transmittance through the capillary associated with the modified inlet shape and the observed current limit, in the following we consider the motion of individual ions through both capillary geometries. Several representative trajectories of individual ions are simulated (Fig. S5 and S6 in the ESI†). The influence of the space charge is not included in the simulations, but later estimated based on these trajectories. Rather than modelling the whole system including electrospray, droplet evolution, ion motion and space charge for a large number of charged particles, with our approach we are able to extract data for each of the influencing factors and compare their effect on the ion transport.Like in the current measurement experiments, the capillaries considered in the simulations have a diameter of 1 mm. The emitter is placed at an axial position of z = −10 mm and z = −5 mm for the funnel shaped and flat capillary respectively. A potential of 2.5 kV is defined for the emitter and 0 V for the capillary. The ions are modelled as RhoB singly charged ions with a mass of 443 u. Their starting position is located in the plane 2.5 mm downstream of the emitter, a position where gas phase ions are likely to be generated in an electrospray plume.50,57,58
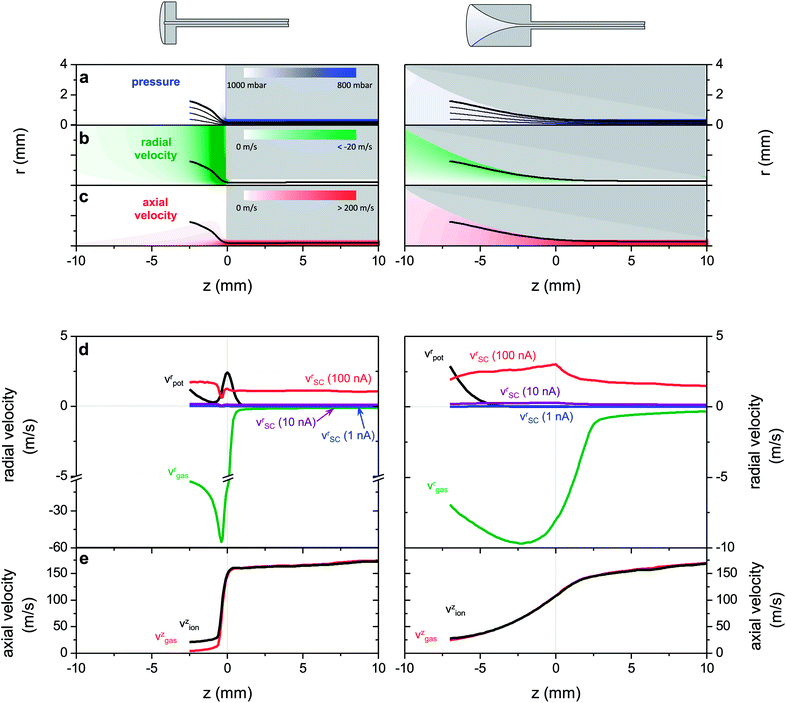
The first step in modelling is the fluid dynamics calculations for both geometries (ESI S-III†). Fig. 6a and c display the results in the form of pressure, radial and axial velocity. In both cases the gas flows within the 1 mm tube with an approximately constant velocity of 200 m s−1 at a pressure of 800 mbar, while the pressure reduction and the velocity increase occur in the funnel- or free-space region, respectively. Once the gas enters the cylindrical part of the capillary the flow becomes choked and turbulences can occur. This is not observed in the simulation results because the two dimensional geometry will not allow for the reproduction of the turbulent flow. In the interface region we do not expect turbulences to occur at all because the gas flow is accelerated, which suppresses turbulences even at Reynolds numbers larger than 4000.59
The flow in the inlet section is characterized by a smooth pressure gradient, evenly distributed across the whole funnel, while the pressure drop is stronger but very much localized at the orifice for the flat interface. The large region of pressure gradient corresponds to a large region of moving gas in the funnel inlet with radial velocities of up to 12 m s−1 pointing towards the axis. For the flat inlet, high velocities are only found close to the orifice, yet the velocities are even higher, reaching up to 70 m s−1 radial velocity. The distribution of the gas motion intuitively shows how the funnel shape supports the sampling of the generated ions. Ions generated within the large region inside the funnel or close to the capillary entry, respectively, are collimated by the force exerted by the radial gas velocity component, while a high axial velocity drags the ions towards the capillary inlet.
In the following step, trajectory simulations are performed to compare the effect of the hydrodynamic drag to that of the electric fields from electrodes and space charge. The ions move in the electric field generated by the voltage applied to the emitter and are influenced by the moving background gas. Some trajectories are superimposed in Fig. 6a. It appears that they are closely following the stream lines of the gas flow, hence that the hydrodynamic drag is dominating the ion motion. The potential difference between the emitter and capillary is necessary to generate an electrospray, however the ion trajectory appears not to be strongly affected by the presence of this electrostatic force. As a consequence, without taking space charge forces into account all ions from a starting disc of more than 5 mm diameter are effectively transmitted for both geometries. This would translate in the experimental result as both capillaries displaying 100% transmittance, which is clearly not the case for the flat capillary. Losses are thus due to the space charge expansion of the electrospray plume or of the ion beam.
The motion of ions is fully described by the superposition of the electric force, the drag force and the space charge forces. Ion losses due to diffusion can be ignored, because the diffusion length for the residence time of ions in the capillary is in the order of micrometres (ESI S-IVB†), which is negligible compared to the capillary dimensions and the radial displacement due to space charge forces. In the regime of high pressure background gas, the mean free path length of the ion motion becomes extremely low in the order of 30 nm (Section S-IVA in the ESI†). Thus on the macroscopic scale an external force like the electric force on the ion F = Eq does not lead to an accelerated motion, but rather to a drift of constant velocity vd = KE characterized by a mobility constant K, which depends on the properties of the gas, but is independent of the motion of the ion. This motion can be added to the motion of the gas with the velocity vgas leading to
| v = vgas + K(Eext + Esc) = vgas + vext + vsc | (1) |
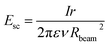 | (2) |
We choose to consider the data for the outermost trajectories, plotted as a bold line in Fig. 6a, as they represent the borderline case in which all interactions are most pronounced and thus losses would occur first. In Fig. 6d the radial components of the gas velocity (green), the drift velocity due to the external electric field (black) and the drift velocity induced by space charge (for 1 nA, 10 nA and 100 nA; blue, violet and red) are displayed as a function of the axial coordinate for the ion path plotted as a bold line in Fig. 6a. The axial velocity of the gas and of the ion is shown in Fig. 6e, which is the same for all three currents, since no axial force component of the space charge was considered.
For both geometry types only the radial gas velocity has a negative sign, meaning that it has a collimating effect on the ion cloud and it is the only collimating force in the inlet. Also this velocity component is higher than all the other velocities. For the flat capillary its magnitude is much higher compared to that of the funnel shape, but the region of this high gas velocity is limited to the close vicinity of the capillary entrance, whereas it extends over a large region for the funnel capillary. The radial drift velocity caused by the external electric field is always positive, thus decollimating. Yet, it is only significantly closer to the emitter for both capillary types and in addition it causes a strong decollimating effect at the very entrance of the flat capillary, which is avoided in the funnel inlet due to the fact that the emitter is positioned within the funnel.
The drift velocity induced by the space charge is plotted for different currents from 1 nA to 100 nA in Fig. 6d. It is approximately constant along the ion path, and found to scale mainly with the total ion current. Even though beam radius Rbeam, radial particle position r and particle velocity v change over orders of magnitude along the trajectory, they cancel each other's effects on the space charge force (see eqn (2)). Moreover we find that the radial velocity component due to space charge is almost negligible for currents of 1–10 nA and only reaches values comparable to the gas velocity above 10 nA (for instance, vsc = 1 m s−1 for I = 50 nA).
In the axial direction the ions in the funnel are transported into the capillary exclusively by the hydrodynamic drag, which is represented by the matching curves for the axial velocities in Fig. 6e. The gap between those two curves for the flat interface shows that only the electric field moves the ions towards to the orifice because the axial gas velocity here is almost negligible.
The quantitative comparison shows that the hydrodynamic force in the funnel region is strong enough to collimate the ion cloud even for currents as high as 100 nA, while the decollimating external electric force is very weak in this region. For the flat capillary, however, high gas velocities are only present within a small region that cannot cover the entire electrospray plume and at the same time the strong electric fields at the rim of the capillary add to decollimation. This is reflected in the fact that 100% of the ion current can be transmitted with the funnel shape, whereas only 25% of the ion current is transmitted through the flat shape even for currents below the observed space charge limit.
In the sampling region of the funnel or in front of the flat inlet, the gas velocities exceed the velocities of the space charge expansion for 100 nA by an order of magnitude or more. Thus the inlet cannot be responsible for the observed current limit. Within the 1 mm tube however, the space charge gives rise to the only significant radial velocity component. An ion at 200 m s−1 passes the 60 mm long capillary in 0.3 ms. For an ion at the edge of a beam of 100 nA this leads to a velocity of 2 m s−1 and the trajectory deviates by 0.6 mm in the radial direction, which is larger than the capillary radius. Thus a significant number of ions may be lost on the interior walls of the capillary at such a current value. As this effect is independent of the geometry of the inlet section, it can explain the observed current limit for both interface types. Moreover it is in agreement with our observations for smaller diameter capillaries, which show a reduced current limit for otherwise identical behavior.
Summary and conclusions
The high molecular coverage shown in Fig. 5b is obtained after a deposition time of a few minutes with a current of 1–2 nA under ultrahigh vacuum, whereas the same experiment took several hours with our previous ion source, which usually allowed for 10–100 pA of deposition current in UHV. This documents that the funnel interface is a substantial advancement over conventional and nano-ESI APIs, which is achieved by two major improvements: first, a higher transmission ratio of up to 100%, and second, an increased net current for otherwise identical conditions like spray voltage and concentration. Currents as high as 40, 20 and 3 nA have been obtained for the 1, 0.75 and 0.50 mm diameter capillaries respectively. The improvement in terms of absolute ionic current in vacuum is comparable to what has been previously obtained with multi-capillary inlets.19,20 The latter requires a more extensive modification of the atmospheric interface as compared to the ease of implementation of the funnel-shaped capillary presented here, it however also performs better with high flow rates, due to a larger active volume and better desolvation in the small diameter capillaries.Based on computational fluid dynamics calculations and ion trajectory simulations, the evaluation of the different forces acting on the ions shows that the hydrodynamic flow dominates the ion motion at the capillary inlet, while electrostatic forces are of lesser importance. The funnel design generates a large volume of high radial velocity, which allows for efficient sampling and thus for the 100% transmittance observed. For high currents (>20 nA), the space charge force becomes relevant first in the transfer tube, which is expressed in the absolute current limit.
The tests with our electrospray mass spectrometer and ion beam deposition experiment42–44 illustrate that the improved performance of the funnel interface has the potential to enhance sensitivity or selectivity as well as sample utilization and throughput61,62 in mass spectrometry or ion beam deposition applications. Initial tests with a commercial mass spectrometer (i.e. an LTQ Orbitrap) and with small diameter capillaries however showed only small improvements. It seems that the high gas load passing through the large diameter capillaries of 1 mm and 0.75 mm is crucial to generate a collimating flow field of sufficient gas velocity (Fig. S7 and S9 in the ESI†).
While the modifications made seem small and fairly simple as compared to conventional nanospray interfaces, the novelty of the funnel source is not only the rather simple adjustment of the inlet geometry of a conventional in-line ion source geometry. Key to the enhanced performance of our funnel source is the fact that the nanospray emitter is placed inside of a funnel that constitutes the inlet of a capillary instead of in front of the flat cut capillary orifice. This union of the funnel and the emitter represents a conceptual difference of great importance for the design of atmospheric pressure ion sources: the background gas is not only an imposition that has to be removed before the ions can be analysed in vacuum. On the contrary, the gas flow is the most efficient way to control ion transport at high pressures.
Thus the ion motion in moving gases represents a highly interesting field for future theoretical and experimental work, where our modelling approach could contribute to a better understanding of ion transport or to the development of better ion sources, gas phase reactors and high pressure ion optics.6,8,10,63 For instance, with an enhancement of electrospray ion currents in vacuum into the range of microamps, preparative mass spectrometry could gain technological relevance as a surface coating technique.
The fact that we can relate the observed current limit to the capillary and not to the inlet section suggests that shapes could be found that have even better characteristics than the one presented. While the funnel shape could be further improved empirically, the model sketched in this paper can be used for a rational optimization. We show how the ion motion in the interface can be described by simple analytical relations. Together with a fast, precise and reliable CFD calculation of the gas flow this model forms a basis for further optimizations of ion sources. However, since we have seen that already very low gas velocities can strongly influence the behaviour of the ions, high precision is required and thus CFD will always be the challenging part of such studies despite the simplicity of the geometries.
Acknowledgements
The authors thank Dr Hartmut Schlichting for the discussion and the support with the current measurements, as well as Dr Ludger Harnau and Dr Peter B. O'Connor for fruitful discussions.References
- J. B. Fenn, M. Mann, C. K. Meng, S. F. Wong and C. M. Whitehouse, Science, 1989, 246, 64–71 CAS.
- T. R. Covey, B. A. Thomson and B. B. Schneider, Mass Spectrom. Rev., 2009, 28, 870–897 CrossRef CAS PubMed.
- B. Domon and R. Aebersold, Science, 2006, 312, 212–217 CrossRef CAS PubMed.
- R. D. Smith, J. A. Loo, R. R. O. Loo, M. Busman and H. R. Udseth, Mass Spectrom. Rev., 1991, 10, 359–452 CrossRef CAS.
- D. E. Clemmer and M. F. Jarrold, J. Mass Spectrom., 1997, 32, 577–592 CrossRef CAS.
- G. E. Johnson, Q. Hu and J. Laskin, Annu. Rev. Anal. Chem., 2011, 4, 83–104 CrossRef CAS PubMed.
- J. Cyriac, T. Pradeep, H. Kang, R. Souda and R. G. Cooks, Chem. Rev., 2012, 112, 5356–5411 CrossRef CAS PubMed.
- I. Manisali, D. D. Y. Chen and B. B. Schneider, TrAC, Trends Anal. Chem., 2006, 25, 243–256 CrossRef CAS PubMed.
- I. Marginean, J. S. Page, A. V. Tolmachev, K. Tang and R. D. Smith, Anal. Chem., 2010, 82, 9344–9349 CrossRef CAS PubMed.
- R. T. Kelly, A. V. Tolmachev, J. S. Page, K. Tang and R. D. Smith, Mass Spectrom. Rev., 2010, 29, 294–312 Search PubMed.
- D. R. Zook and A. P. Bruins, Int. J. Mass Spectrom. Ion Processes, 1997, 162, 129–147 CrossRef CAS.
- A. El-Faramawy, K. W. M. Siu and B. A. Thomson, J. Am. Soc. Mass Spectrom., 2005, 16, 1702–1707 CrossRef CAS PubMed.
- I. Marginean, R. T. Kelly, D. C. Prior, B. L. LaMarche, K. Tang and R. D. Smith, Anal. Chem., 2008, 80, 6573–6579 CrossRef CAS PubMed.
- J. S. Page, I. Marginean, E. S. Baker, R. T. Kelly, K. Tang and R. D. Smith, J. Am. Soc. Mass Spectrom., 2009, 20, 2265–2272 CrossRef CAS PubMed.
- J. S. Page, R. T. Kelly, K. Tang and R. D. Smith, J. Am. Soc. Mass Spectrom., 2007, 18, 1582–1590 CrossRef CAS PubMed.
- G. T. T. Gibson, S. M. Mugo and R. D. Oleschuk, Mass Spectrom. Rev., 2009, 28, 918–936 CrossRef CAS PubMed.
- P. Mao, H.-T. Wang, P. Yang and D. Wang, Anal. Chem., 2011, 83, 6082–6089 CrossRef CAS PubMed.
- R. T. Kelly, J. S. Page, K. Tang and R. D. Smith, Anal. Chem., 2007, 79, 4192–4198 CrossRef CAS PubMed.
- T. Kim, H. R. Udseth and R. D. Smith, Anal. Chem., 2000, 72, 5014–5019 CrossRef CAS.
- T. Kim, K. Tang, H. R. Udseth and R. D. Smith, Anal. Chem., 2001, 73, 4162–4170 CrossRef CAS.
- L. Zhou, L. Zhai, B. Yue, E. Lee and M. Lee, Anal. Bioanal. Chem., 2006, 385, 1087–1091 CrossRef CAS PubMed.
- S. Wu, K. Zhang, N. K. Kaiser, J. E. Bruce, D. C. Prior and G. A. Anderson, J. Am. Soc. Mass Spectrom., 2006, 17, 772–779 CrossRef CAS PubMed.
- D. Prior, J. Price and J. Bruce, US Pat., 6455846, 2002.
- G. L. Glish and R. M. Danell, US Pat., 6703611, 2004.
- E. W. Sheehan and R. C. Willoughby, US Pat., 6914243, 2005.
- R. C. Willoughby, E. W. Sheehan and D. Fries, presented in part at the Proceedings of the 2nd ASMS Conference on Mass Spectrometry and Allied Topics, Nashville, Tennessee, May 23–27, 2004 Search PubMed.
- R. Saf, M. Goriup, T. Steindl, T. E. Hamedinger, D. Sandholzer and G. Hayn, Nat. Mater., 2004, 3, 323–329 CrossRef CAS PubMed.
- R. C. Willoughby and E. W. Sheehan, US Pat., 6943347, 2005.
- C. Jolliffe, G. Javahery, L. Cousins and S. Savtchenko, US Pat., 7659505, 2010.
- R. Ramanathan, N. Raghavan, S. N. Comezoglu and W. G. Humphreys, Int. J. Mass Spectrom., 2011, 301, 127–135 CrossRef CAS PubMed.
- Z. Takáts, J. M. Wiseman, B. Gologan and R. G. Cooks, Anal. Chem., 2004, 76, 4050–4058 CrossRef PubMed.
- R. Wang, P. Allmendinger, L. Zhu, A. Gröhn, K. Wegner, V. Frankevich and R. Zenobi, J. Am. Soc. Mass Spectrom., 2011, 22, 1234–1241 CrossRef CAS PubMed.
- Y. Zhu and K. D. Nugent, US Pat., 8227750, 2012.
- L. Zhou, B. Yue, D. V. Dearden, E. D. Lee, A. L. Rockwood and M. L. Lee, Anal. Chem., 2003, 75, 5978–5983 CrossRef CAS PubMed.
- A. M. Hawkridge, L. Zhou, M. L. Lee and D. C. Muddiman, Anal. Chem., 2004, 76, 4118–4122 CrossRef CAS PubMed.
- R. B. Dixon, D. C. Muddiman, A. M. Hawkridge and A. G. Fedorov, J. Am. Soc. Mass Spectrom., 2007, 18, 1909–1913 CrossRef CAS PubMed.
- G. Robichaud, R. B. Dixon, A. S. Potturi, D. Cassidy, J. R. Edwards, A. Sohn, T. A. Dow and D. C. Muddiman, Int. J. Mass Spectrom., 2011, 300, 99–107 CrossRef CAS PubMed.
- R. B. Dixon and D. C. Muddiman, Rapid Commun. Mass Spectrom., 2007, 21, 3207–3212 CrossRef CAS PubMed.
- B. Lin and J. Sunner, J. Am. Soc. Mass Spectrom., 1994, 5, 873–885 CrossRef CAS.
- M. Volný and F. Tureček, J. Mass Spectrom., 2006, 41, 124–126 CrossRef PubMed.
- B. B. Schneider, H. Javaheri and T. R. Covey, Rapid Commun. Mass Spectrom., 2006, 20, 1538–1544 CrossRef CAS PubMed.
- N. Thontasen, G. Levita, N. Malinowski, Z. Deng, S. Rauschenbach and K. Kern, J. Phys. Chem. C, 2010, 114, 17768–17772 CAS.
- S. Rauschenbach, R. Vogelgesang, N. Malinowski, J. W. Gerlach, M. Benyoucef, G. Costantini, Z. Deng, N. Thontasen and K. Kern, ACS Nano, 2009, 3, 2901–2910 CrossRef CAS PubMed.
- S. Rauschenbach, F. L. Stadler, E. Lunedei, N. Malinowski, S. Koltsov, G. Costantini and K. Kern, Small, 2006, 2, 540–547 CrossRef CAS PubMed.
- D. A. Dahl, Int. J. Mass Spectrom., 2000, 200, 3–25 CrossRef CAS.
- A. D. Appelhans and D. A. Dahl, Int. J. Mass Spectrom., 2005, 244, 1–14 CrossRef CAS PubMed.
- J. Sesterhenn, Comput. Fluids, 2000, 30, 37–67 CrossRef.
- M. S. Alexander, M. D. Paine and J. P. W. Stark, Anal. Chem., 2006, 78, 2658–2664 CrossRef CAS PubMed.
- J. F. De La Mora and I. G. Loscertales, J. Fluid Mech., 1994, 260, 155–184 CrossRef.
- A. Wortmann, A. Kistler-Momotova, R. Zenobi, M. C. Heine, O. Wilhelm and S. E. Pratsinis, J. Am. Soc. Mass Spectrom., 2007, 18, 385–393 CrossRef CAS PubMed.
- S. Kahle, Z. Deng, N. Malinowski, C. Tonnoir, A. Forment-Aliaga, N. Thontasen, G. Rinke, D. Le, V. Turkowski, T. S. Rahman, S. Rauschenbach, M. Ternes and K. Kern, Nano Lett., 2011, 12, 518–521 CrossRef PubMed.
- Z. Deng, N. Thontasen, N. Malinowski, G. Rinke, L. Harnau, S. Rauschenbach and K. Kern, Nano Lett., 2012, 12, 2452–2458 CrossRef CAS PubMed.
- S. Rauschenbach, G. Rinke, N. Malinowski, R. T. Weitz, R. Dinnebier, N. Thontasen, Z. Deng, T. Lutz, P. M. de Almeida Rollo, G. Costantini, L. Harnau and K. Kern, Adv. Mater., 2012, 24, 2761–2767 CrossRef CAS PubMed.
- D. S. Wagner and R. J. Anderegg, Anal. Chem., 1994, 66, 706–711 CrossRef CAS.
- V. Grill, J. Shen, C. Evans and R. G. Cooks, Rev. Sci. Instrum., 2001, 72, 3149–3179 CrossRef CAS PubMed.
- M. Volný, W. T. Elam, B. D. Ratner and F. Tureček, Anal. Chem., 2005, 77, 4846–4853 CrossRef PubMed.
- R. Wang and R. Zenobi, J. Am. Soc. Mass Spectrom., 2010, 21, 378–385 CrossRef CAS PubMed.
- M. Girod, X. Dagany, V. Boutou, M. Broyer, R. Antoine, P. Dugourd, A. Mordehai, C. Love, M. Werlich, J. Fjeldsted and G. Stafford, Phys. Chem. Chem. Phys., 2012, 14, 9389–9396 RSC.
- H. Schlichting and K. Gersten, Boundary-Layer Theory, Springer, Berlin, Heidelberg, 2000 Search PubMed.
- P. S. Babu, A. Goswami and V. S. Pandit, Phys. Plasmas, 2011, 18, 103117 CrossRef PubMed.
- M. Bantscheff, M. Schirle, G. Sweetman, J. Rick and B. Kuster, Anal. Bioanal. Chem., 2007, 389, 1017–1031 CrossRef CAS PubMed.
- P. Mallick and B. Kuster, Nat. Biotechnol., 2010, 28, 695–709 CrossRef CAS PubMed.
- Z. Takáts, J. M. Wiseman, B. Gologan and R. G. Cooks, Science, 2004, 306, 471–473 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3an01836a |
| ‡ Present address: Institut Charles Sadron, CNRS-University of Strasbourg, 23 rue du Loess, F-67034 Strasbourg, France. |
| This journal is © The Royal Society of Chemistry 2014 |