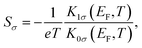Non-magnetic doping induced a high spin-filter efficiency and large spin Seebeck effect in zigzag graphene nanoribbons

Abstract

Based on nonequilibrium Green's functions (NGF) and density-functional theory (DFT), we investigate the magnetotransport properties and magnetothermoelectric effects in zigzag graphene nanoribbons (ZGNRs) with non-magnetic doping on the double ribbon edges. One of the carbon atoms without hydrogen saturation in each ribbon edge is replaced by one boron (B) or one nitrogen (N) atom. Compared with boron–boron (BB) and nitrogen–nitrogen (NN) double-edge doping, the boron–nitrogen (BN) double-edge doping induces a perfect spin-filter effect with 100% negative spin polarization at the Fermi level. Moreover, we find that the thermoelectric effect can be enhanced by the double-edge doping. Interestingly, the spin Seebeck effect in NN- and BN-doped ZGNRs becomes comparable with the charge Seebeck effect and even larger than it. These results originate from the spin-dependent transmission node near the Fermi level induced by the non-magnetic doping. These findings strongly suggest that the double-edge-doped ZGNRs are promising materials for spintronics and thermo-spintronics.

---

Introduction

Graphene was first discovered experimentally in 2004.¹ It has a typical two-dimensional honeycomb structure made up entirely of carbon atoms (1s²2s²2p²). Owing to its superior physical properties and potential applications in electronics and spintronics, graphene has attracted considerable attention.^2,3 Recently, some experimental studies have shown that graphene nanoribbons (GNRs) can be produced by patterning the graphene sheet into ribbons or by chemical methods.^4,5 Jiao et al. proposed an approach to producing GNRs with smooth edges and a narrow width by unzipping multi-walled carbon nanotubes.⁶ According to the edge characteristics, the GNRs are divided into armchair graphene nanoribbons (AGNRs) and zigzag graphene nanoribbons (ZGNRs). Many theoretical and experimental studies have shown that AGNRs are semiconducting with the energy gap scaling as the inverse of their width,^7,8 and ZGNRs are magnetic semiconductors with spin-polarized edge states.^9,10 The energy gap of ZGNRs is attributed to an unusual antiferromagnetic coupling between opposite-edge carbon atoms and its size is also inversely proportional to its width.

In 2006 Son et al. provided a pioneering idea of inducing a half-metallic behavior in zigzag GNRs by an external electric field.⁹ In addition, chemical dopants can also change the electronic and magnetic properties of ZGNRs. For instance, Dutta et al. performed a first-principles calculation to explore the electronic properties of ZGNRs modified with chemical dopants, boron (1s²2s²2p¹) and nitrogen (1s²2s²2p³). When two middle zigzag carbon chains are replaced by boron–nitrogen (BN) chains, the modified ZGNR exhibits both semiconducting and intrinsic half-metallic behaviors under the influence of an external electric field.¹¹ Lin et al. showed that a topological line defect could also yield a half-metallic behavior when it is close to one edge.¹² A single-spin negative differential resistance in beryllium (Be)-edge-doped ZGNRs has also been reported,¹³ indicating that one single-spin current has a negative differential resistance whereas the opposite single-spin current shows a monotonic behavior as the external bias increases. In ref. 14, the authors investigated the spin-polarized transport properties of hybrid graphene nanoribbons, and showed a remarkable width-dependent magnetic behavior. Zheng et al. investigated the effects of nitrogen (N) and boron (B) impurities on the electron transmission function of ZGNRs by first principles calculations.¹⁵ Their results showed that bound states and quasibound states can be introduced by a B/N impurity, resulting in many interesting transport properties. Biel et al. presented a first-principles calculation of the quantum transport in chemically doped graphene nanoribbons by B and N impurities.¹⁶ A resonant backscattering was yielded, and they further found an unusual acceptor–donor transition in ZGNRs.

Thermoelectric effects convert heat energy into electric energy or vice versa. Some experiments have demonstrated the capability of measuring the Seebeck coefficient at atomic and molecular junctions.^17,18 More recently, using the imaging capability of the scanning tunneling microscope (STM), Evangeli et al. provided an approach to measuring continuously and simultaneously the thermopower and conductance of C₆₀ molecular junctions.¹⁹ The surface reconstruction can occur at the interface of C₆₀ absorbed on the Cu(111) substrate at room temperature. Then Hsu et al. investigated the effects of such reconstruction on the thermopower of C₆₀ molecular junctions.²⁰ Widawsky et al. investigated the length-dependent conductance and thermopower of Au–C bonded single-molecule junctions. A nonlinear relationship between the thermopower and the molecular length was shown, while the conductance decreases exponentially as the molecular length increases.²¹ Encouragingly, Uchida et al. measured a spin voltage from a temperature gradient in a metallic magnet (Ni₈₁Fe₁₉) with the help of a latest developed spin-detection technique.²² This phenomenon is called the spin Seebeck effect and provides a method to produce a pure spin current by using the temperature field. Until now this pioneering experiment has inspired many theoretical and experimental studies on the spin thermoelectric effect in various systems.^23–27 The new branch of spintronics can be named as “thermo-spintronics” or “spin-caloritronics”, and focuses on studies of the manipulation of the spin degree of freedom by temperature fields. Recently, the spin-dependent thermoelectric effect in spin valves, consisting of ZGNRs with different configurations, has been investigated by first-principles calculations combined with non-equilibrium Green's functions.²⁸ Moreover, a mean-field Hubbard model has also been employed to investigate thermally driven spin-polarized transport properties of a locally gated ZGNR. The thermal magnetoresistance can reach 10⁵% at small gate voltages.²⁹

In this paper, we investigate simultaneously the spin-filter effect and thermoelectric performance of ZGNRs with chemical dopants. The proposed molecular devices are shown in Fig. 1, which are divided into three regions: left electrode, scattering region, and right electrode. One of the carbon atoms without hydrogen saturation in each ribbon edge is replaced by one B or N atom. It is found that the BN double-edge-doped ZGNR shows a half-metallic behavior with 100% negative spin polarization at the Fermi level. Moreover, we also find that the spin Seebeck effect can become comparable with the charge Seebeck effect in these non-magnetic doped ZGNRs and even larger than it. The findings here can be interpreted as the results of the spin-dependent transmission node near the Fermi level.

Fig. 1 Schematic of two-probe systems for four non-magnetic-doped ZGNRs. (a), (b), (c) and (d) are without doping (CC–ZGNR), with boron and boron doping (BB–ZGNR), nitrogen and nitrogen doping (NN–ZGNR), and boron and nitrogen doping (BN–ZGNR) at the two edges of the ZGNRs, respectively. The gray balls are carbon atoms, and the bright balls are hydrogen atoms. The blue and brown balls represent nitrogen and boron atoms, respectively.

Theoretical methods

All ab initio calculations including the structure relaxation, transmission function, band structure, and density of states (DOS) in this work are implemented by using the ATK (Atomistix ToolKit) package, which is based on the density-functional theory (DFT) combined with the nonequilibrium Green's function (NGF) method.^30,31 The electron wave function is expanded in a basis set of double zeta orbitals plus one polarization orbital (DZP). To separate ZGNRs in neighbor supercells and ensure the suppression of the coupling between them, a vacuum region of width 15 Å is adopted. All structures in Fig. 1 are optimized until the inter-atomic forces are less than 0.05 eV Å⁻¹. The energy cutoff is chosen to be 150 Ry and the size of the mesh grid in k space for the electrode parts is 1 × 1 × 100. In the ATK package the spin-dependent transmission function τ_σ(ε) of electrons with a spin index σ and energy ε is

τ_σ(ε) = Tr[Γ^L_σ(ε)G^r_σ(ε)Γ^R_σ(ε)G^a_σ(ε)], (1)

where Γ^L(R)_σ(ε) is the line-width function of electrons with a spin index σ and energy ε describing the coupling between the scattering region and the left (right) electrode. The retarded Green's function is obtained by G^r_σ(ε) = [εI − H + i(Γ^L_σ + Γ^R_σ)/2]⁻¹, where I is the unit matrix and H is the Hamiltonian of the scattering region. The advanced Green's function G^a_σ(ε) is obtained from the relationship G^a_σ = [G^r_σ]^†. The spin polarization at the Fermi level E_F is determined bywhere E_F is the Fermi level of the electrodes in the absence of the external voltage. In the linear response region the spin-dependent Seebeck coefficient can be obtained by^32,3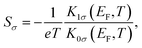3where K_νσ(E_F,T) = −∫dε{∂f(ε,E_F,T)/∂ε}(ε − E_F)^ντ_σ(ε)(ν = 0,1). T and e are the electrode's temperature and electron charge, respectively. Furthermore, f(ε,E_F,T) = [1 + e^{(ε−E_F)/k_BT}]⁻¹ is the Fermi–Dirac distribution function in the electrodes and k_B is the Boltzmann constant. If τ_σ(ε) has a smooth change near the Fermi level, S_σ in the low-temperature region reduces to³⁴

The above equation clearly shows that S_σ is not only related to the magnitude of τ_σ(ε) but also related to the slope of τ_σ(ε) at the Fermi level. Therefore, the study of S_σ can provide more information than current–voltage investigations. But if τ_σ(ε) has a huge change near the Fermi level, eqn (4) is no longer applicable even in the low-temperature region. For instance, a symmetrical transmission node at the Fermi energy yields an obvious enhancement of single-molecule thermoelectric effects on the two sides of the node.³⁵

Results and discussions

In this work, we only consider the ferromagnetic state, which plays a very important role in the spin-polarized transport properties near the Fermi level of the ZGNRs.^36,37 Moreover, the ZGNRs can be derived from an antiferromagnetic ground state to a ferromagnetic state by a magnetic field. Now we start with the study of the spin-filter effect for the four two-probe systems based on ZGNRs shown in Fig. 1. In the left column of Fig. 2, we show the transmission function τ_σ as a function of the electron energy. For a perfect ZGNR without any doping, each spin channel at the Fermi level is completely open. In this case the transmission function τ_σ is 1 and the spin polarization ζ is zero (see Fig. 2(a) and Table 1). It is interesting to note that the spin-up and spin-down transmission functions exhibit different sensitivities to the double-edge doping. In the BB–ZGNR the spin-up transmission function at the Fermi level is suppressed, while the spin-down one almost remains unchanged (see Fig. 2(b) and Table 1). In contrast, the spin-up transmission function at the Fermi level in the NN–ZGNR does not change, while the spin-down one is suppressed as shown in Fig. 2(c). Therefore, the spin polarization can be modulated from negative to positive when two B atoms are replaced by two N atoms. If one of the two B atoms is replaced by one N atom, we find that a spin-up transmission node is exactly located at the Fermi level. The spin-down transmission function τ_↓ is also slightly suppressed (see Fig. 2 (d)). The corresponding spin polarizations for the BB–, NN–, and BN–ZGNRs are shown in Table 1. In particular, it should be noted that the value of ζ for the BN–ZGNR approaches −100%, indicating the coexistence of a metallic state for spin-down electrons and an insulating state for spin-up electrons at the Fermi level. These transmission nodes near the Fermi level are attributed to the appearance of some quantum states close to the Fermi level induced by the double-edge doping. In the DOS spectrum (see the middle column in Fig. 2) and band structure (see the right column in Fig. 2), we see clearly that these quantum states indeed appear near the Fermi level. Our results are similar to those reported in ref. 38. The locations of these quantum states are marked by blue arrows, as shown in Fig. 2. For the BB–ZGNR, one spin-up quantum state near the Fermi level appears, and a spin-down quantum state for the NN–ZGNR appears near the Fermi level. But for the BN–ZGNR, the spin-up and spin-down quantum states appear concurrently at different locations near the Fermi level, resulting in two transmission nodes with different spin components.

Fig. 2 Transmission functions (left column), density of states (middle column) and band structure (right column) for the four ZGNRs. The band structure is obtained by taking the center region as the periodic structure. From top to bottom, the structure is CC–ZGNR, BB–ZGNR, NN–ZGNR, and BN–ZGNR, respectively. The black solid lines denote spin-up components and the read dashed lines for the spin-down ones. The blue arrows show the locations of the single-spin quantum states induced by the double-edge doping.

Table 1 Transmission function and spin polarization at the Fermi level E_F

Molecule	τ ↑	τ ↓	ζ
CC–ZGRN	1	1	0%
BB–ZGRN	0.1638	0.9993	−71.8%
NN–ZGRN	0.9839	0.5318	29.8%
BN–ZGRN	0.0009	0.7122	−99.7%

---

To further understand the spin anisotropy at the Fermi level, we show the corresponding spin-dependent local density of state (LDOS) in Fig. 3. For the pure ribbon (CC–ZGNR), the spin-up and spin-down electronic states are uniformly distributed along the z direction in the scattering region. Moreover, quantum size effects make the electrons pile up on the two edges of the CC–ZGNR. When one of the carbon atoms without hydrogen saturation in each ribbon edge is replaced by one B atom (see Fig. 1(b)), the spin-up electronic states along the z direction become nonuniform in the scattering region and the corresponding LDOS close to left and right electrodes is obviously suppressed. However, the spin-down LDOS at the Fermi level is almost unchanged. Consequently, τ_↑ at the Fermi level is suppressed, while τ_↓ is retained. In the NN–ZGNR the situation is inverse. For example, the spin-down LDOS is obviously suppressed in the NN scattering region and the region close to electrodes, while the spin-up LDOS is retained. This fact results in 29.8% spin polarization. A more intriguing phenomenon in the BN–ZGNR is that the spin-up electronic state at the Fermi level is completely localized in the scattering region and the corresponding LDOS is mainly concentrated in the center region of one edge. The spin-down LDOS at the Fermi level is slightly suppressed in the BN scattering region and the region close to electrodes. These facts induce a transmission node for spin-up electrons at the Fermi level (τ_↑(E_F) ≃ 0), and there is a finite value for the spin-down transmission function (τ_↓(E_F) = 0.7). Accordingly, the spin polarization at the Fermi level approaches −100%. An ideal spin-filter effect is achieved in the BN–ZGNR.

Fig. 3 Spin-dependent LDOS of four two-probe systems at the Fermi level.

The study of the Seebeck effect can provide an effective avenue to explore the electronic structures of the devices. The sign of the Seebeck coefficient is related to its type. For example, a negative Seebeck coefficient suggests an n-type device, while a positive Seebeck coefficient corresponds to a p-type device. In the left panel of Fig. 4 we plot S_σ as a function of the temperature for the CC–, BB–, NN–, and BN–ZGNRs, respectively. The spin Seebeck coefficient S_S(=(S_↑ − S_↓)/2) and charge Seebeck coefficient S_C(=(S_↑ + S_↓)/2) versus the temperature are plotted in the right panel of Fig. 4. In the CC–ZGNR, τ_σ, without any change near the Fermi level, induces a relatively small Seebeck effect in the low-temperature region. But when T is larger than 200 K, S_σ is slightly enhanced. This result originates from the contributions of side electronic states as the temperature increases, and one should note a two-peak structure near the Fermi level in the transmission spectrum of the CC–ZGNR (see Fig. 2(a)). For the BB–ZGNR and NN–ZGNR, we find that the sign of S_σ is negative, which indicates that these devices are n-type. The results can be explained by eqn (4). The slope of τ_σ of the BB–ZGNR and NN–ZGNR at the Fermi level is positive, which results in a negative value of S_σ due to S_σ ∝ − τ^′_σ(ε)/τ_σ(ε)|_ε=EF. For the BB–ZGNR, we have τ^′_↑(E_F) > τ^′_↓(E_F) and τ_↑(E_F) < τ_↓(E_F), while the relationships for the NN–ZGNR are τ^′_↑(E_F) < τ^′_↓(E_F) and τ_↑(E_F) > τ_↓(E_F). Therefore, |S_↑| is larger than |S_↓| in the BB–ZGNR, while |S_↓| is larger than |S_↑| for the NN–ZGNR. We also note that τ_↓ at the Fermi level for the NN–ZGNR has a larger value than τ_↑ at the Fermi level for the BB–ZGNR. This fact results in a larger value of S_↑ for the BB–ZGNR than S_↓ for the NN–ZGNR. More interestingly, S_↑ for the BN–ZGNR shows an obvious nonmonotonic behavior as the temperature increases. In the low-temperature region S_↑ has a positive maximum at about 25 K. The sign of S_↑ changes from negative to positive as the temperature increases, which indicates that the type of devices can be manipulated by the temperature. This result is ascribed to an asymmetrical transmission node for spin-up electrons at the Fermi level. For T ≤ 100 K the transmission function τ_↑ below the Fermi level plays a more important role than τ_↑ above the Fermi level. This fact results in a positive value of S_↑. As the temperature increases, τ_↓ above the Fermi level will contribute more and more to S_↑. Therefore, S_↑ becomes negative for T ≥ 100 K. In addition, it is interesting that S_C and S_S become comparable in the high-temperature region for the NN–ZGNR and in the low-temeprature region for the BN–ZGNR. S_S is even larger than S_C for the BN–ZGNR (see the inset of Fig. 4(h)).

Fig. 4 Spin-dependent Seebeck coefficient S_σ as a function of temperature for (a) CC–ZGNR, (c) BB–ZGNR, (e) NN–ZGNR, and (g) BN–ZGNR. The corresponding spin Seebeck coefficient S_S and charge Seebeck coefficient S_C as functions of temperature for (b) CC–ZGNR, (d) BB–ZGNR, (f) NN–ZGNR, and (h) BN–ZGNR. The inset in (h) magnifies the region 0 ≤ T ≤ 50 K.

Conclusions

In summary, we have studied the effects of non-magnetic doping in the ribbon edges on magneto-transport properties and magneto-thermoelectric effects of ZGNRs. ZGNR-based devices with a high spin-filter efficiency and large spin thermoelectric effect have been proposed. The spin-dependent transmission function near the Fermi level can be effectively modulated by double-edge doping; as a result, the spin-filter efficiency and spin thermoelectric effect are enhanced. When one carbon atom without hydrogen saturation in each edge is replaced simultaneously by one boron and one nitrogen atom, an ideal half-metallic behavior is found. The reason is that a spin-up localized state emerges at the Fermi level and the spin-up channel is completely closed. More interestingly, the spin Seebeck effect S_S is comparable to and even larger than the charge Seebeck effect S_C for the BN–ZGNR. In general, these findings strongly suggest that simple chemical dopants can induce a perfect spin-filter effect and large spin Seebeck effect in ZGNRs.

Acknowledgements

The authors thank the support of the National Natural Science Foundation of China (NSFC) under Grants No. 11247028, 61306122, 61274101 and 91121021. The work was also sponsored by Qing Lan Project.

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666.
2. A. K. Geim, Rev. Mod. Phys., 2011, 83, 851.
3. K. S. Novoselov, Rev. Mod. Phys., 2011, 83, 837.
4. L. Tapaseto, G. Dobrik, P. Lambin and L. P. Biró, Nat. Nanotechnol., 2008, 3, 397.
5. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183.
6. L. Y. Jiao, L. Zhang, X. R. Wang, G. Diankov and H. J. Dai, Nature, 2009, 458, 877.
7. V. Barone, O. Hod and G. E. Scuseria, Nano Lett., 2006, 6, 2748.
8. M. Y. Han, B. Özyilmaz, Y. B. Zhang and P. Kim, Phys. Rev. Lett., 2007, 98, 206805.
9. Y. W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803.
10. J. Jung, T. Pereg-Barnea and A. H. MacDonald, Phys. Rev. Lett., 2009, 102, 227205.
11. S. Dutta, A. K. Manna and S. K. Pati, Phys. Rev. Lett., 2009, 102, 096601.
12. X. Q. Lin and J. Ni, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075461.
13. T. T. Wu, X. F. Wang, M. X. Zhai, H. Liu, L. P. Zhou and Y. J. Jiang, Appl. Phys. Lett., 2012, 100, 052112.
14. A. R. Botello-Méndez, E. Cruz-Silva, F. López-Urias, B. G. Sumpter, V. Meunier, M. Terrones and H. Terrones, ACS Nano, 2009, 3, 3606.
15. X. H. Zheng, I. Rungger, Z. Zeng and S. Sanvito, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 235426.
16. B. Biel, X. Blase, F. Triozon and S. Roche, Phys. Rev. Lett., 2009, 102, 096803.
17. P. Reddy, S. Y. Jang, R. A. Segalman and A. Majumdar, Science, 2007, 315, 1568.
18. K. Baheti, J. A. Malen, P. Doak, P. Reddy, S. Y. Jang, T. D. Tilley, A. Majumdar and R. A. Segalman, Nano Lett., 2008, 8, 715.
19. C. Evangeli, K. Gillemot, E. leary, M. T. González, G. Rubio-Bollinger, C. J. Lambert and N. Agraït, Nano Lett., 2013, 13, 2141.
20. B. C. Hsu, C. Y. Lin, Y. S. Hseieh and Y. C. Chen, Appl. Phys. Lett., 2012, 101, 243103.
21. J. R. Widawsky, W. Chen, H. Vázquez, T. Kim, R. Breslow, M. S. Hybertsen and L. Venkataraman, Nano Lett., 2013, 13, 2141.
22. K. Uchida, S. Takahashi, K. Harii, J. Ieda, W. Koshibae, K. Ando, S. Maekawa and E. Saitoh, Nature, 2008, 455, 778.
23. S. Bosu, Y. Sakuraba, K. Uchida, K. Saito, T. Ota, E. Saitoh and K. Takanashi, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 83, 224401.
24. C. M. Jaworski, J. Yang, S. Mack, D. D. Awschalom, J. P. Heremans and R. C. Myers, Nat. Mater., 2010, 9, 898.
25. K. Uchida, H. Adachi, T. An, T. Ota, M. Toda, B. Hillebrands, S. Maekawa and E. Saitoh, Nat. Mater., 2011, 10, 737.
26. H. Adachi, J. Ohe, S. Takahashi and S. Maekawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 094410.
27. Y. Dubi and M. Di Ventra, Rev. Mod. Phys., 2011, 83, 131.
28. M. G. Zeng, W. Huang and G. C. Liang, Nanoscale, 2013, 5, 200.
29. Z. Y. Zhao, X. C. Zhai and G. J. Jin, Appl. Phys. Lett., 2012, 101, 083117.
30. J. Taylor, H. Guo and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 63, 245407.
31. Atomistix ToolKit: Manual, Version 2008. 10.
32. Y. Dubi and M. Di Ventra, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 081302(R).
33. Y. S. Liu, X. F. Yang, F. Chi, M. S. Si and Y. Guo, Appl. Phys. Lett., 2012, 101, 213109.
34. Y. S. Liu, Y. R. Chen and Y. C. Chen, ACS Nano, 2009, 3, 3497.
35. J. P. Bergfield and C. A. Stafford, Nano Lett., 2009, 9, 3072.
36. T. B. Martins, R. H. Miwa, A. J. R. da Silva and A. Fazzio, Phys. Rev. Lett., 2007, 98, 196803.
37. C. Q. Qu, C. Y. Wang, L. Qiao, S. S. Yu and H. B. Li, Chem. Phys. Lett., 2013, 578, 97.
38. E. Cruz-Silva, Z. M. Barneett, B. G. Sumpter and V. Meunier, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 155445.

---