The synthesis of rhodium substituted ε-iron oxide exhibiting super high frequency natural resonance

Abstract

In this study, we demonstrate a synthesis of rhodium substituted ε-iron oxide, ε-Rh_xFe_2−xO₃ (0 ≤ x ≤ 0.19), nanoparticles in silica. The synthesis features a sol–gel method to coat the metal hydroxide sol containing Fe³⁺ and Rh³⁺ ions with a silica sol via hydrolysis of alkoxysilane to form a composite gel. The obtained samples are barrel-shaped nanoparticles with average long- and short-axial lengths of approximately 30 nm and 20 nm, respectively. The crystallographic structure study using X-ray diffraction shows that ε-Rh_xFe_2−xO₃ has an orthorhombic crystal structure in the Pna2₁ space group. Among the four non-equivalent substitution sites (A–D sites), Rh³⁺ ions mainly substitute into the C sites. The formation mechanism of ε-Rh_xFe_2−xO₃ nanoparticles is considered to be that the large surface area of the nanoparticles increases the contribution from the surface energy to Gibbs free energy, resulting in a different phase, ε-phase, becoming the most stable phase compared to that of bulk or single crystal. The measured electromagnetic wave absorption characteristics due to natural resonance (zero-field ferromagnetic resonance) using terahertz time domain spectroscopy reveal that the natural resonance frequency shifts from 182 GHz (ε-Fe₂O₃) to 222 GHz (ε-Rh_0.19Fe_1.81O₃) upon rhodium substitution. This is the highest natural resonance frequency of a magnetic material, and is attributed to the large magnetic anisotropy due to rhodium substitution. The estimated coercive field for ε-Rh_0.19Fe_1.81O₃ is as large as 28 kOe.

---

Introduction

As electronic devices and telecommunication technologies advance, the demand for electromagnetic wave absorbing materials to prevent electromagnetic interference is on the rise. Hence, the search for appropriate materials is an important materials science issue.^1–3 Electromagnetic wave absorbing materials include magnetic materials and composite materials composed of electrically conductive and dielectric materials. Magnetic materials absorb electromagnetic waves by magnetic loss, and include spinel ferrite such as Ni_xZn_1−xFe₂O₄ (1 kHz to 10 GHz),^4–6 soft magnetic metal such as Fe powder (1 kHz to 10 GHz),^7,8 and hexagonal ferrite such as BaFe₁₂O₁₉ (1 GHz to 80 GHz).^9–11 Composite materials between electrically conductive and dielectric materials absorb electromagnetic waves through dielectric loss, and include composite materials between carbon materials and urethane foam (1 MHz to 10 GHz).^12,13 However, the prevalent use of wireless communications and radar systems in recent years, which use high frequency electromagnetic waves called millimeter waves (30–300 GHz),^14–17 requires the development of materials that absorb millimeter waves exceeding 100 GHz.

Our research group has recently demonstrated electromagnetic wave absorption of ε-iron oxide (ε-Fe₂O₃), which exhibits a large coercive field (H_c) of 20 kOe,^18–28 due to magnetic loss at 182 GHz.²⁹ Furthermore, we found that substituting ε-iron oxide with non-magnetic ions, such as Al³⁺ and Ga³⁺, can control the absorption frequency from 182 GHz to 35 GHz,^29–31 and in 2012, we achieved absorption frequencies above 182 GHz up to 209 GHz with rhodium-substituted ε-iron oxide (ε-Rh_xFe_2−xO₃).³²

Herein we successfully develop a synthesis method of ε-Rh_xFe_2−xO₃ suitable for large-scale synthesis, and achieve an electromagnetic wave absorption frequency of 222 GHz, which exceeds the previously reported frequency and corresponds to the highest frequency for windows of air in millimeter waves (220 GHz).

Results and discussion

Previously, we synthesized ε-Rh_xFe_2−xO₃ nanoparticles in a SiO₂ matrix using mesoporous silica as a template.³² In addition to being labor intensive, this method produces small quantities of ε-Rh_xFe_2−xO₃. In contrast, the present method employs a sol–gel method^33,34 to synthesize ε-Rh_xFe_2−xO₃ by coating a metal hydroxide sol with a silica sol via hydrolysis of alkoxysilane to form a composite gel (Fig. 1a). This sol–gel synthesis has four steps: (i) generation of the metal hydroxide, (ii) formation of the silica matrix, (iii) sintering, and (iv) removal of the silica matrix (see the Experimental section). Nine samples (samples 1 to 9) with varying concentrations of Fe and Rh were synthesized.

Fig. 1 (a) Schematic diagram of ε-Rh_xFe_2−xO₃ nanoparticle synthesis using the sol–gel method. (i) Aqueous ammonia is added to an aqueous solution containing both rhodium nitrate and ferric nitrate, yielding the sol of rhodium and iron hydroxide, (Rh_xFe_2−x)(OH)₆ (shown in brown). (ii) TEOS (Si(OC₂H₅)₄) is added to the reaction solution to yield a complex gel, (Rh_xFe_2−x)(OH)₆/SiO₂, coated with a sol of silica (shown in light blue) via hydrolysis. (iii) Sintering the obtained gel in air yields Rh_xFe_2−xO₃ in silica. Sintering at 1080 °C, which is higher than the glass transition temperature, causes nanoparticle aggregation and accelerates crystallization. (iv) SiO₂ coated material is added to a NaOH solution to react and remove the SiO₂ matrix as a Na₂SiO₃ solution. (b) TEM images of the final products after removing the silica matrix (samples 1, 3, 5, 7, and 9).

Fig. 1b shows the transmission electron microscope (TEM) images of the obtained samples. The TEM images indicate that the samples are composed of barrel-shaped nanoparticles. The average long- and short-axial lengths of each sample are: (33 ± 15) × (24 ± 11) nm (1), (35 ± 16) × (25 ± 11) nm (2), (36 ± 17) × (26 ± 12) nm (3), (35 ± 16) × (27 ± 12) nm (4), (36 ± 18) × (27 ± 14) nm (5), (29 ± 17) × (21 ± 13) nm (6), (27 ± 18) × (19 ± 12) nm (7), (23 ± 14) × (16 ± 9) nm (8), and (22 ± 13) × (16 ± 9) nm (9), respectively. The average aspect ratio (i.e., [long axis length]/[short axis length]) of each sample is approximately 1.4 (Fig. S2 and Table S2†).

The crystallographic structures of the obtained samples were studied using powder X-ray diffraction (XRD). As shown in Fig. 2a, the XRD patterns of the obtained samples indicated that the ε-phase was formed in all the samples. Besides the ε-phase, each sample contains the α-phase or γ-phase. Fig. 2b shows the phase ratios of the samples. The compositions for the ε-phase are ε-Fe₂O₃ (1), ε-Rh_0.03Fe_1.97O₃ (2), ε-Rh_0.05Fe_1.95O₃ (3), ε-Rh_0.08Fe_1.92O₃ (4), ε-Rh_0.10Fe_1.90O₃ (5), ε-Rh_0.14Fe_1.86O₃ (6), ε-Rh_0.15Fe_1.85O₃ (7), ε-Rh_0.18Fe_1.82O₃ (8), and ε-Rh_0.19Fe_1.81O₃ (9) (Table 1).³⁵ The lattice constants of the ε-phase are roughly the same regardless of the increases in the concentration of rhodium substitution, i.e., a-axis: 5.0917 ± 0.0003 Å (1) → 5.1110 ± 0.0009 Å (9), b-axis: 8.7857 ± 0.0005 Å (1) → 8.7980 ± 0.0015 Å (9), and c-axis: 9.4783 ± 0.0008 Å (1) → 9.4722 ± 0.0031 Å (9) (Table 1), because the ionic radius of Rh³⁺ (0.67 Å) is approximately the same as that of Fe³⁺ (0.65 Å).³⁶ Among the four non-equivalent substitution sites (A–D sites), Rh³⁺ ions mainly substitute into the C sites (Fig. 3). Additionally, as the amount of Rh substitution increases, the A- and B-sites also begin to be substituted. The details of the crystal structure analysis are described in the ESI.†

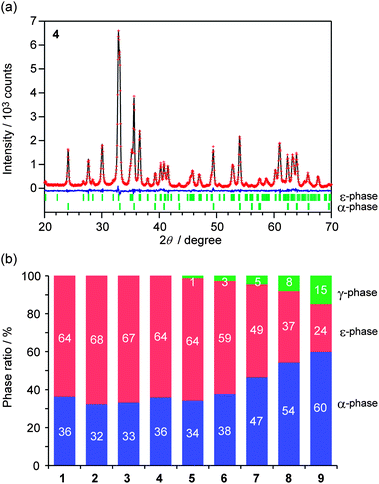Fig. 2 (a) Powder X-ray diffraction pattern and Rietveld analysis result of sample 4. Red dots, black line, and blue line represent the observed values, calculated values, and the residual error, respectively. Bars denote Bragg peak positions of the ε- and α-phases. (b) Phase ratios of the samples obtained from the Rietveld analyses. Red, blue, and green represent ε-, α-, and γ-phases, respectively.

Table 1 Crystallographic parameters of ε-Rh_xFe_2−xO₃. Composition x(ε), weight fraction W(ε), lattice constant (a, b, c), lattice volume (V), and Rh occupancy at A–D sites

		1	2	3	4	5	6	7	8	9
x(ε)		0	0.03	0.05	0.08	0.10	0.14	0.15	0.18	0.19
W(ε)/wt%		64	68	67	64	64	59	49	37	24
a/Å		5.0917 (3)	5.0945 (3)	5.0966 (3)	5.0999 (3)	5.1020 (3)	5.1055 (3)	5.1067 (4)	5.1095 (5)	5.1110 (9)
b/Å		8.7857 (5)	8.7867 (5)	8.7881 (5)	8.7900 (5)	8.7906 (5)	8.7941 (6)	8.7932 (7)	8.7951 (9)	8.798 (2)
c/Å		9.4783 (8)	9.4773 (7)	9.4761 (8)	9.4745 (7)	9.4735 (8)	9.4734 (9)	9.4699 (11)	9.471 (2)	9.472 (3)
V/Å^3		424.00 (5)	424.24 (5)	424.43 (5)	424.72 (5)	424.88 (5)	425.34 (6)	425.24 (7)	425.59 (10)	425.9 (2)
Rh occupancy/%	A	0	0	0	0	0	0 (1)	0 (1)	2 (2)	3 (3)
	B	0	0 (0)	0 (0)	0 (0)	0 (0)	2 (1)	2 (1)	2 (3)	5 (4)
	C	0	6 (0)	11 (0)	17 (0)	21 (0)	26 (1)	29 (1)	32 (2)	31 (3)
	D	0	0	0	0	0	0	0	0	0

---

Fig. 3 (a) Crystallographic structure of ε-Rh_xFe_2−xO₃. (b) Rh occupancies versus substitution ratios of x(ε) at the A–D sites. Dotted lines are a guide to the eye.

Next we discuss the formation mechanism of ε-Rh_xFe_2−xO₃ nanoparticles in the present synthesis. In general, the bulk or single-crystal Fe₂O₃ transforms from γ-Fe₂O₃ to α-Fe₂O₃ when the temperature is elevated.³⁷ However, the large surface area of the nanoparticles increases the contribution from the surface energy to the Gibbs free energy (G),³⁸ which is responsible for a different phase, ε-phase, becoming the most stable phase compared to that of bulk or single crystals.^39–41Fig. 4 depicts the particle size (d) dependence of the free energy per molar volume (G/V_m) for the γ-phase, ε-phase, and α-phase.^42,43 The G/V_mversus d curve of the ε-phase intercepts the G/V_mversus d curves of the γ-phase and α-phase, indicating that particle sizes in between these intercept points make the ε-phase as the most stable phase. In our method, synthesizing Rh_xFe_2−xO₃ as nanoparticles yields particle sizes that make the ε-phase most stable.

Fig. 4 Schematic curves of Gibbs free energy per unit volume for each phase of Fe₂O₃ (solid lines) and Rh_xFe_2−xO₃ (dotted lines), (G_i/V_m,i), versus particle size (d) where i = γ, ε, and α.^42,43 Green, red, and blue lines represent the γ-, ε-, and α-phases, respectively. If rhodium substitution elevates the chemical potential of Rh_xFe_2−xO₃, and the increase of the chemical potential of the ε-phase is greater than those of the other two phases, the particle size range where the ε-phase is most stable becomes narrower. This explains why the α-phase and γ-phase co-exist.

The reason for the difficulty to obtain a single ε-phase in the Rh-substituted system can be explained by the fact that the chemical potential of Rh_xFe_2−xO₃ increases due to rhodium substitution. If the chemical potential of the ε-phase increases largely compared to the other two phases, the G/V_mversus d curve of the ε-phase becomes relatively higher, narrowing the particle size range where the ε-phase is most stable. A narrower range explains the co-existence of the α- and γ-phases.

The following possibility can be cited as the reason that the particles have a barrel-shaped morphology. In (Rh_xFe_2−x)(OH)₆/SiO₂, which is a precursor, a small amount of Fe³⁺ and Rh³⁺ ions is included in silica. Their presence reduces the glass transition temperature compared to pure silica.⁴⁴ Thus, aggregation of nanoparticles progresses in the silica matrix, which increases the crystallization degree and forms the barrel-shaped nanoparticles.

A terahertz time domain spectroscopy (THz-TDS) system was set up to measure electromagnetic wave absorption properties in the millimeter wave region (Fig. 5). Fig. 6 shows the measured millimeter wave absorption spectra of ε-Rh_xFe_2−xO₃. As we previously reported,²⁹ sample 1, which is ε-Fe₂O₃, shows an absorption peak centered at 182 GHz. Rhodium substitution increases the resonance absorption frequency: 187 GHz (2), 192 GHz (3), 197 GHz (4), 202 GHz (5), 207 GHz (6), 213 GHz (7), 217 GHz (8), and 222 GHz (9). Sample 9 breaks our previously reported record of 209 GHz for ε-Rh_0.14Fe_1.86O₃,³² and currently has the highest electromagnetic wave resonance frequency for a magnetic material.

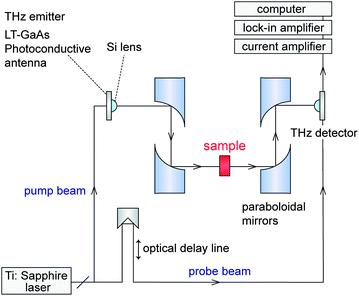Fig. 5 Schematic diagram of the THz-TDS measurement system.

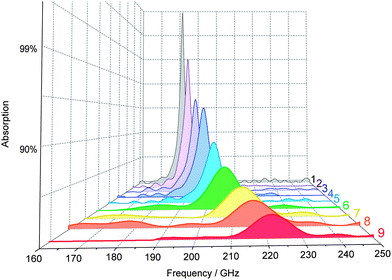Fig. 6 Millimeter wave absorption spectra measured at room temperature.

The mechanism of electromagnetic wave absorption in magnetic materials is mainly caused by magnetic loss due to magnetic domain wall motion or natural resonance (zero-field ferromagnetic resonance).⁴⁵ The observed high-frequency millimeter wave absorption in the present material is attributed to the natural resonance phenomenon. The mechanism is described below. When an electromagnetic wave is irradiated into a magnetic material, the magnetic component of the electromagnetic wave tilts the magnetization from the anisotropy field (H_a). Once the magnetization is tilted, it precesses around H_a due to the gyromagnetic effect. A resonance occurs at the frequency matching this precession and causes electromagnetic wave absorption. The resonance frequency f_r can be expressed as: f_r = νH_a/2π, where ν is the gyromagnetic constant. Because a uniaxial magnetic anisotropic sample exhibits a proportional relationship between H_a and the coercive field (H_c), we investigated the H_c values of the samples.

Fig. 7 shows the magnetization versus external magnetic field curve at room temperature (300 K). Although samples 1 to 4 show an increase in H_c as the amount of rhodium substitution increases, i.e., 21.7 kOe (1), 22.5 kOe (2), 22.9 kOe (3), and 23.9 kOe (4), samples 5 to 9 exhibit a distortion in the hysteresis loop with a negative effect on H_c, i.e., 23.9 kOe (5), 22.6 kOe (6), 15.5 kOe (7), 4.2 kOe (8), and 0.9 kOe (9) (Fig. 8a, black open squares). To estimate the true H_c value of the ε-phase, we applied a correction that considered the contributions of the α-phase and the γ-phase. The estimated H_c values for ε-Rh_xFe_2−xO₃ were 21.9 kOe (ε-Fe₂O₃), 22.5 kOe (ε-Rh_0.03Fe_1.97O₃), 22.9 kOe (ε-Rh_0.05Fe_1.95O₃), 24.0 kOe (ε-Rh_0.08Fe_1.92O₃), 25.2 kOe (ε-Rh_0.10Fe_1.90O₃), 26.3 kOe (ε-Rh_0.14Fe_1.86O₃), 26.7 kOe (ε-Rh_0.15Fe_1.85O₃), 27.7 kOe (ε-Rh_0.18Fe_1.82O₃), and 28.1 kOe (ε-Rh_0.19Fe_1.81O₃) (Fig. 8a, red solid circles). The last two H_c values exceed our previously reported value, and are the highest values among metal oxides to date. ESI contains detailed magnetic characteristics with respect to their temperature dependences.†

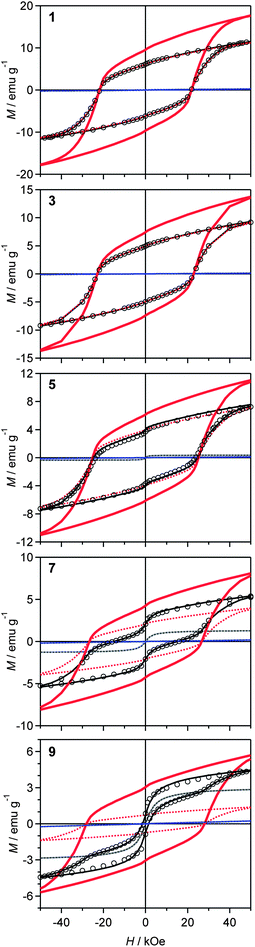Fig. 7 Magnetization versus external magnetic field curves at 300 K. Open circles are the observed values. Dotted lines represent contributions from each phase (red, blue, and gray dotted lines represent the ε-, α-, and γ-phases, respectively). Black solid lines are their sum. Red solid lines denote the estimated value for a single-phase ε-Rh_xFe_2−xO₃.

Fig. 8 (a) H_cversus x(ε) plots. Solid red circles and black open squares represent the estimated H_c values and observed H_c values, respectively. Red dotted lines are a guide to the eye. (b) f_rversus H_c plots.

The correlation between H_c and f_r demonstrates a monotonic increase in f_r with H_c (Fig. 8b). This means that rhodium substitution increases H_c, which indicates an increase in the magnetic anisotropy, H_a, and achieves a high f_r of 222 GHz.

Conclusions

Herein the highest natural resonance frequency to date of 222 GHz is reported for a high frequency electromagnetic wave absorption material, ε-Rh_xFe_2−xO₃. This material was synthesized via the sol–gel method, which uses a liquid-phase reaction where water is the only solvent. This method is simple and is possible for industrial scale synthesis. Additionally, the lack of organic solvents and surfactants makes this method economical and environmentally friendly.

220 GHz is the highest-frequency window of air. Around this frequency, electromagnetic wave absorption by air is small. Consequently, this frequency band is expected as a carrier frequency for wireless communications.^46–49 The materials developed herein should be useful as millimeter wave absorbing materials for unnecessary electromagnetic waves, which cause electromagnetic interference.

Experimental section

Synthesis

Samples 1–9 were prepared by the sol–gel method. First, 10.2 ml of aqueous ammonia (13 mol dm⁻³) was added while stirring 240 ml of an aqueous solution with the following Fe(NO₃)₃ and Rh(NO₃)₃ concentrations: (Fe(NO₃)₃, Rh(NO₃)₃) = (62.5 × 10⁻³, 0 mol dm⁻³) (1), (61.3 × 10⁻³, 1.25 × 10⁻³ mol dm⁻³) (2), (60.0 × 10⁻³, 2.50 × 10⁻³ mol dm⁻³) (3), (58.8 × 10⁻³, 3.75 × 10⁻³ mol dm⁻³) (4), (57.5 × 10⁻³, 5.00 × 10⁻³ mol dm⁻³) (5), (56.3 × 10⁻³, 6.25 × 10⁻³ mol dm⁻³) (6), (54.7 × 10⁻³, 7.81 × 10⁻³ mol dm⁻³) (7), (53.1 × 10⁻³, 9.38 × 10⁻³ mol dm⁻³) (8), and (51.6 × 10⁻³, 10.9 × 10⁻³ mol dm⁻³) (9). Successively, 22.6 ml of tetraethoxysilane (TEOS) was added to this solution, and stirred for 20 hours. Then, the obtained gel was separated by centrifugation, washed with distilled water, and dried. The obtained dry powder was sintered in air for four hours at 1080 °C. An aqueous solution of sodium hydroxide was added to the sintered powder, and stirred for one day at 60 °C. The solution was centrifuged and washed to obtain the final products. We adopted the sintering temperature of 1080 °C, since it had a high ε-phase ratio among the various sintering temperatures in the range of 1020–1300 °C.

Characterization

Elemental analysis of the prepared samples was performed using an inductively coupled plasma mass spectroscopy (ICP-MS) system, Agilent Technologies 7700. The TEM images were collected with a JEOL JEM-2000EX transmission electron microscope, where the accelerating voltage was 200 kV. The XRD patterns were measured at 294 K using a Rigaku Ultima IV and a Rigaku RINT2100 with Cu Kα radiation (λ = 1.5418 Å), and Rietveld analyses were performed using the RIETAN-FP program.⁵⁰

Millimeter wave absorption measurement

Electromagnetic wave absorption properties in the millimeter wave region were measured by a THz-TDS system, where a pump–probe measurement system was used. Ultra short pulse with a time duration of 20 fs and a center photon energy of 1.55 eV generated from a mode-locked Ti:sapphire femtosecond pulse laser at a repetition rate of 76 MHz was divided into a pump and probe beam. The pump pulse was irradiated into a dipole type low-temperature-grown GaAs photoconductive antenna, which generated a THz pulse. The THz pulse was condensed with a Si lens and a set of paraboloidal mirrors and was irradiated into the sample. The electric field of the transmitted THz pulse wave formed in the time domain was obtained by changing the delay time between the pump and the probe pulses. Powder-form samples were filled in paper cells (6.5 mm × 6.5 mm × 4.8 mm for samples 1–8 and 6.5 mm × 6.5 mm × 8 mm for sample 9) with filling ratios of 29–31 vol%. In the present millimeter wave absorption study, the sample thickness of at least 3 mm was necessary to avoid interference from the edges of the cell. The obtained spectra were calibrated as spectra of 30 vol% of the ε-phase, 4.8 mm thickness.

Magnetic property measurement

The magnetic properties were measured using a superconducting quantum interference device (SQUID) magnetometer, Quantum Design, MPMS 7. Field cooled magnetization (FCM) curves were measured in the temperature range of 4–550 K, where the cooling rate was −1 K min⁻¹. Magnetic hysteresis loops were measured at 300 K.

Acknowledgements

The present research was supported partly by the Core Research for Evolutional Science and Technology (CREST) program of the Japan Science and Technology Agency (JST); a Grant-in-Aid for Young Scientists (S) from the Japan Society for the Promotion of Science (JSPS); DOWA Technofund; the Asahi Glass Foundation; a Grant for the Global COE Program “Chemistry Innovation through Cooperation of Science and Engineering”; Advanced Photon Science Alliance (APSA) from the Ministry of Education, Culture, Sports, Science and Technology of Japan (MEXT); JSPS KAKENHI Grant Number 24850004; Office for Gender Equality, the University of Tokyo; the Cryogenic Research Center, the University of Tokyo; the Center for Nano Lithography & Analysis, the University of Tokyo, supported by MEXT. M. Y. is grateful to Advanced Leading Graduate Course for Photon Science (ALPS) and JSPS Research Fellowships for Young Scientists. We are grateful to Ms Y. Kitano for her technical support and Mr Y. Kakegawa and Mr H. Tsunakawa for collecting the TEM images.

References and notes

1. K. J. Vinoy and R. M. Jha, in Radar Absorbing Materials, Kluwer, Boston, 1996.
2. S. Celozzi, R. Araneo and G. Lovat, in Electromagnetic Shielding, Wiley-Interscience: IEEE Press, New Jersey, 2008.
3. C. M. Watts, X. Liu and W. J. Padilla, Adv. Mater., 2012, 24, OP98.
4. Y. Naito and K. Suetake, IEEE Trans. Magn., 1971, 19, 65.
5. R. K. Selvan, V. Krishnan, C. O. Augustin, H. Bertagnolli, C. S. Kim and A. Gedanken, Chem. Mater., 2008, 20, 429.
6. F. Wang, J. Liu, J. Kong, Z. Zhang, X. Wang, M. Itoh and K. Machida, J. Mater. Chem., 2011, 21, 4314.
7. M. Matsumoto and Y. Miyata, IEEE Trans. Magn., 1997, 33, 4459.
8. Z. Yu, Z. Yao, N. Zhang, Z. Wang, C. Li, X. Han, X. Wub and Z. Jiang, J. Mater. Chem. A, 2013, 1, 4571.
9. S. Sugimoto, S. Kondo, K. Okayama, H. Nakamura, D. Book, T. Kagotani, M. Homma, H. Ota, M. Kimura and R. Sato, IEEE Trans. Magn., 1999, 35, 3154.
10. Y. Chen, T. Sakai, T. Chen, S. D. Yoon, A. L. Geiler, C. Vittoria and V. G. Harris, Appl. Phys. Lett., 2006, 88, 062516.
11. K. A. Korolev, J. S. McCloy and M. N. Afsar, J. Appl. Phys., 2012, 111, 07E113.
12. Y. Yang, M. C. Gupta, K. L. Dudley and R. W. Lawrence, Adv. Mater., 2005, 17, 1999.
13. Z. Liu, G. Bai, Y. Huang, Y. Ma, F. Du, F. Li, T. Guo and Y. Chen, Carbon, 2007, 45, 821.
14. M. J. W. Rodwell, in High Speed Integrated Circuit Technology, towards 100 GHz Logic, World Scientific, Singapore, 2001.
15. K. C. Huang and Z. Wang, in Millimeter Wave Communication Systems, Wiley-IEEE Press, New Jersey, 2011.
16. J. Capmany and M. Novak, Nat. Photonics, 2007, 1, 319.
17. D. Dawson, L. Samoska, A. K. Fung, K. Lee, R. Lai, R. Grundbacher, P.-H. Liu and R. Raja, IEEE Microw. Wireless Compon. Lett., 2005, 15, 874.
18. J. Jin, S. Ohkoshi and K. Hashimoto, Adv. Mater., 2004, 16, 48.
19. E. Tronc, C. Chanéac and J. P. Jolivet, J. Solid State Chem., 1998, 139, 93.
20. M. Popovici, M. Gich, D. Niznansky, A. Roig, C. Savii, L. Casas, E. Molins, K. Zaveta, C. Enache and J. Sort, Chem. Mater., 2004, 16, 5542.
21. J. Jin, K. Hashimoto and S. Ohkoshi, J. Mater. Chem., 2005, 15, 1067.
22. K. Kelm and W. Mader, Z. Anorg. Allg. Chem., 2005, 631, 2383.
23. E. Tronc, C. Chaneac, J. P. Jolivet and J. M. Greneche, J. Appl. Phys., 2005, 98, 053901.
24. M. Kumoo, J. Rehspringer, A. Hutlova, C. D'Orleans, S. Vilminot, C. Estoumes and D. Niznansky, Chem. Mater., 2005, 17, 1106.
25. T. Nakamura, Y. Yamada and K. Yano, J. Mater. Chem., 2006, 16, 2417.
26. M. Hermanek and R. Zboril, Chem. Mater., 2008, 20, 5284.
27. Y. Kusano, T. Fujii, J. Takada, M. Fukuhara, A. Doi, Y. Ikeda and M. Takano, Chem. Mater., 2008, 20, 151.
28. J. Tucek, R. Zboril, A. Namai and S. Ohkoshi, Chem. Mater., 2010, 22, 6483.
29. A. Namai, S. Sakurai, M. Nakajima, T. Suemoto, K. Matsumoto, M. Goto, S. Sasaki and S. Ohkoshi, J. Am. Chem. Soc., 2009, 131, 1170.
30. S. Ohkoshi, S. Kuroki, S. Sakurai, K. Matsumoto, K. Sato and S. Sasaki, Angew. Chem., Int. Ed., 2007, 46, 8392.
31. S. Sakurai, S. Kuroki, H. Tokoro, K. Hashimoto and S. Ohkoshi, Adv. Funct. Mater., 2007, 17, 2278.
32. A. Namai, M. Yoshikiyo, K. Yamada, S. Sakurai, T. Goto, T. Yoshida, T. Miyazaki, M. Nakajima, T. Suemoto, H. Tokoro and S. Ohkoshi, Nat. Commun., 2012, 3, 1035.
33. L. L. Hench and J. K. West, Chem. Rev., 1990, 90, 33.
34. B. L. Cushing, V. L. Kolesnichenko and C. J. O'Connor, Chem. Rev., 2004, 104, 3893.
35. The values of x for each phase of Rh_xFe_2−xO₃ [x(ε), x(α), and x(γ)] were obtained as follows. Sintering precursors at 1180 °C (x = 0), 1160 °C (0.12), 1140 °C (0.30), and 1140 °C (0.36) gave single-phase nanoparticles of α-Rh_xFe_2−xO₃. Rietveld analysis on the obtained α-Rh_xFe_2−xO₃ nanoparticles revealed a linear increase in the lattice constants (a and c) and lattice volume (V) as x(α) increased. This linear relationship was used to obtain x(α) in α-Rh_xFe_2−xO₃ for samples 1–9. For samples 1–4, which were composed of the ε- and α-phases, the x(ε) values in the ε-Rh_xFe_2−xO₃ phase were obtained by considering the compositions of the α-phase, the weight ratio between the phases obtained from the Rietveld analysis, and the quantity of Rh in the entire sample obtained from the ICP-MS measurement. This revealed a linear relationship between the lattice constants (a, b, and c) and lattice volume (V) and x(ε) for the ε-Rh_xFe_2−xO₃ phase. This linear relationship was used to obtain x(ε) in ε-Rh_xFe_2−xO₃ of samples 5–9. For samples 5–9, which were composed of the ε, α, and γ-phases, the x(γ) values in the γ-Rh_xFe_2−xO₃ phase were obtained by considering the compositions of the ε- and α-phases, the weight ratio between the phases obtained from the Rietveld analysis, and the quantity of Rh in the entire sample. The details are described in the ESI†.
36. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751.
37. K. J. Standley, in Oxide Magnetic Materials, Clarendon Press, Oxford, 1972.
38. H. Zhang and J. F. Banfield, J. Mater. Chem., 1998, 8, 2073.
39. J. M. McHale, A. Auroux, A. J. Perrotta and A. Navrotsky, Science, 1997, 277, 788.
40. H. L. Wen, Y. Y. Chen, F. S. Yen and C. H. Huang, Nanostruct. Mater., 1999, 11, 89.
41. S. Ohkoshi, Y. Tsunobuchi, T. Matsuda, K. Hashimoto, A. Namai, F. Hakoe and H. Tokoro, Nat. Chem., 2010, 2, 539.
42. S. Sakurai, A. Namai, K. Hashimoto and S. Ohkoshi, J. Am. Chem. Soc., 2009, 131, 18299.
43. S. Ohkoshi, S. Sakurai, J. Jin and K. Hashimoto, J. Appl. Phys., 2005, 97, 10K312.
44. S. N. Houde-Walter, J. M. Inman, A. J. Dent and G. N. Greaves, J. Phys. Chem., 1993, 97, 9330.
45. S. Chikazumi, in Physics of Ferromagnetism, Oxford University Press, New York, 1997.
46. J. W. Archer, R. Lai, R. Grundbacher, M. Barsky, R. Tsai and P. Reid, IEEE Microw. Wireless Compon. Lett., 2001, 11, 4.
47. M. Urteaga, D. Scott, S. Krishnan, Y. Wei, M. Dahlstrom, Z. Griffith, N. Parthasarathy and M. J. W. Rodwell, IEEE J. Solid-State Circuits, 2003, 38, 1451.
48. D. Dawson, L. Samoska, A. K. Fung, K. Lee, R. Lai, R. Grundbacher, P.-H. Liu and R. Raja, IEEE Microw. Wireless Compon. Lett., 2005, 15, 874.
49. I. Minin, in Microwave and Millimeter Wave Technologies: from Photonic Bandgap Devices to Antenna and Applications, Intech Press, New York, 2010.
50. F. Izumi and K. Momma, Solid State Phenom., 2007, 130, 15.

---

Footnote

† Electronic supplementary information (ESI) available: The detailed information of synthesis, investigation of the sintering temperature, TEM study, crystal structure analysis, and magnetic properties. See DOI: 10.1039/c3tc30805g

---