Lithium and oxygen adsorption at the β-MnO₂ (110) surface

Abstract

The adsorption and co-adsorption of lithium and oxygen at the surface of rutile-like manganese dioxide (β-MnO₂), which are important in the context of Li–air batteries, are investigated using density functional theory. In the absence of lithium, the most stable surface of β-MnO₂, the (110), adsorbs oxygen in the form of peroxo groups bridging between two manganese cations. Conversely, in the absence of excess oxygen, lithium atoms adsorb on the (110) surface at two different sites, which are both tri-coordinated to surface oxygen anions, and the adsorption always involves the transfer of one electron from the adatom to one of the five-coordinated manganese cations at the surface, creating (formally) Li⁺ and Mn³⁺ species. The co-adsorption of lithium and oxygen leads to the formation of a surface oxide, involving the dissociation of the O₂ molecule, where the O adatoms saturate the coordination of surface Mn cations and also bind to the Li adatoms. This process is energetically more favourable than the formation of gas-phase lithium peroxide (Li₂O₂) monomers, but less favourable than the formation of Li₂O₂ bulk. These results suggest that the presence of β-MnO₂ in the cathode of a non-aqueous Li–O₂ battery lowers the energy for the initial reduction of oxygen during cell discharge.

---

1 Introduction

Manganese dioxide (MnO₂) has been widely investigated as a cathode material in lithium-ion batteries, due to their Li intercalation capacity (forming Li_xMnO₂ phases), low toxicity, and relative low cost compared to oxides of other metals like Co or Ni.^1–4 Several MnO₂ polymorphs have been investigated in the context of Li-ion cells, including α-MnO₂ (hollandite), β-MnO₂ (pyrolusite), γ-MnO₂ (nsutite) and R-MnO₂ (ramsdellite).¹ Contrasting with other polymorphs, the rutile-structured phase (β-MnO₂) does not seem to be able to intercalate Li in the bulk, while mesoporous samples of the same polymorph do exhibit high Li uptake.⁵ A recent computer simulation study by Tompsett et al.⁶ has shown that there is an energy barrier (>0.6 eV) for diffusion of Li from the surface to the bulk of β-MnO₂, which they demonstrate to be due to the much higher electrostatic potential (and therefore higher insertion energy) within the bulk. It thus seems plausible that most of the Li incorporated in β-MnO₂ lies at the surface (that is, in the walls of the pores), which would explain why mesoporous samples are able to accommodate much more Li than highly crystalline samples.

The Li–air system is a novel battery technology which promises higher specific energy than Li-ion batteries. In this battery the cathode reaction is not the formation of an intercalation compound but the reduction of oxygen gas in the presence of Li⁺ ions forming lithium peroxide Li₂O₂ (or LiOH in the aqueous version).^7–11 Manganese oxides may also play an important role here: it has been shown that nanostructured MnO₂ in different polymorphic states are able to catalyse the formation and decomposition of Li₂O₂ in the cathode, thus decreasing the overpotentials required for the operation of the Li–air cell.¹² In this case it is the surface rather than the bulk of the manganese oxide which controls its function in the cathode, and therefore the lack of Li intercalation in bulk β-MnO₂ should not limit its utilization. Understanding the behaviour of the cathode catalysts is the key for improving the function of Li–air batteries.¹³

In order to gain insight into the molecular processes occurring at the Li–air battery cathode reaction in the presence of β-MnO₂, we have investigated the simultaneous adsorption of lithium and oxygen at the most stable surface of this oxide, the (110), using computer simulations. We first consider the pure β-MnO₂ surfaces and their redox behaviour as a function of oxygen chemical potential, then the Li adsorption in the absence of excess oxygen and the transfer of electrons between the Li adatoms and the surface, and finally oxygen adsorption at the lithiated surface. In the subsequent sections, MnO₂ refers to the β polymorph, unless otherwise stated.

2 Methodology

2.1 Density functional theory calculations

Periodic DFT calculations were performed with the VASP program,^14,15 using the generalized gradient approximation (GGA) in the form of the Perdew–Burke–Ernzerhof exchange-correlation functional modified for solids (PBEsol).¹⁶ In order to correct for the poor description of d orbitals in GGA functionals, we use the GGA + U approach. Cockayne and Li have shown that a Hubbard-corrected PBEsol + U(+J) functional with U = 2.8 eV and J = 1.2 eV (following the approach of Liechtenstein et al.,¹⁷ where the two parameters enter independently in the corrected functional) produces electronic properties in good agreement with experiment.¹⁸ In contrast to the uncorrected PBEsol functional, the PBEsol + U functional produces a gap at the Fermi level, thus reproducing the experimentally observed semiconducting character of MnO₂ (see Fig. 1). The reasons why the description of MnO₂ requires the use of the two-parameter Liechtenstein's approach have been discussed in detail in a recent paper.¹⁹

Fig. 1 Electronic density of states (DOS) for antiferromagnetic MnO₂ bulk, (a) without “+U” Coulomb correction term (red) and (b) with the “+U” correction (black).

The projected augmented wave method^20,21 was used to describe the interaction between the valence electrons and the core, and the core states (up to 3p in Mn, and 1s in O) were kept frozen at the atomic reference states. The number of plane waves was determined by a kinetic energy cutoff of 500 eV, and a 6 × 6 × 9 mesh of k-points was employed for the bulk unit cell calculations. These parameters were checked with respect to convergence of the bulk total energy. For surface calculations, the number of k-points was adapted to achieve a similar sampling density in the reciprocal space.

A collinear antiferromagnetic ordering (Fig. 2) is imposed in all our calculations, as in previous work of Kresse et al.²² This is the lowest-energy magnetic configuration within the rutile unit cell, but not the magnetic groundstate of this oxide: there is a complex non-collinear screw-type magnetic structure below 92 K.²³ The low value of the transition temperature to paramagnetism is indicative of very weak coupling, which means that the calculated total energies will be practically unaffected by the chosen spin arrangement.

Fig. 2 Rutile unit cell of MnO₂ showing the magnetic arrangement used in the calculations. Red spheres represent O anions, and purple spheres with arrows represent spin polarised Mn cations.

2.2 Stability and redox thermodynamics of surfaces

We consider the stabilities of five low-index surface orientations ((110), (010), (001), (111) and (011)) by performing periodic calculations of slabs with stoichiometric composition, thicknesses between 11 and 14 Å (depending on the orientation), and vacuum gaps of ∼14 Å (Fig. 3). The two surfaces of each slab are symmetrically equivalent, and this equivalence is kept during all of the calculations to prevent the formation of an electric dipole that can be associated with asymmetric slabs. The cell parameters of the slab are kept constant during the calculations, based on the relaxed cell parameters of the bulk. For MnO₂, the calculated unit cell parameters are a = 4.366 Å and c = 2.961 Å, which gives an acceptable agreement with experimental values a_exp = 4.399 Å and c_exp = 2.872 Å (deviations of −0.8% and +3.1% for a and c, respectively, and of 1.6% in the cell volume).²⁴ In our surface simulations, all atoms in the slabs are fully relaxed, and the surface energies (γ) are obtained using the standard expression:where E_slab is the energy of the slab, E_bulk is the energy of an equivalent amount of bulk, and 2A is the combined area of both surfaces within the slab unit cell. The equilibrium morphology of a MnO₂ particle (ignoring higher Miller indices) is constructed using Wulff's method,²⁵ where the distance to a given surface from the centre of the particle is proportional to the surface energy.

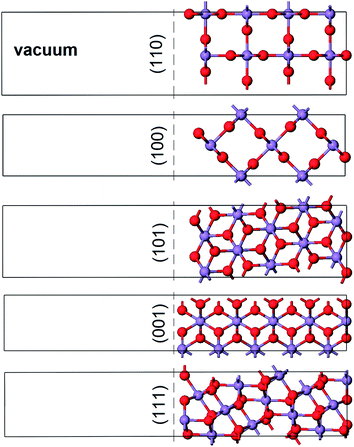Fig. 3 Unit cells containing the slabs used for modelling the low-index surfaces of rutile MnO₂.

We examine the most stable surface further by removing or adding oxygen atoms to form non-stoichiometric compositions. Note that we always preserve the symmetrical equivalence of the two surfaces of the slab when removing or adding atoms. The discussion of the stabilities of non-stoichiometric surface terminations is based on the ab initio thermodynamics formalism first introduced by Scheffler et al.²⁶

The surface free energy is calculated as:

whereis the excess number of O ions at each surface of the slab (N_O and N_Mn are the numbers of O anions and Mn cations in the slab model, respectively). It is possible to express the chemical potential of oxygen, assuming equilibrium with the gas phase, as:

The first term within the bracket is the DFT energy of the oxygen molecule. The second term is the difference in the Gibbs free energy per O₂ molecule between 0 K and T, at p₀ = 1 bar; this contribution can be extracted from thermodynamic tables²⁷ in order to avoid the explicit simulation of the gas phase, as done in previous studies.^28,29 The last term represents the change in free energy of the oxygen gas when the pressure changes from p₀ to p at constant temperature T, assuming ideal gas behaviour. We follow the usual convention of expressing the oxygen chemical potential with reference to half the energy of the O₂ molecule, that is:

so that the chemical potential is independent of calculated quantities. In the evaluation of the slab energies we then must subtract half of the energy of the O₂ molecule for each oxygen atom in the slab, for consistency. With this method, it is possible to plot the surface free energies given by eqn (2) for different surface compositions as a function of chemical potential, and discuss the redox behaviour of the surface. More details about the method can be found elsewhere.^28,29

3 Results and discussion

3.1 Surface stability and morphology for pure MnO₂

The surface energies for each of the five low Miller index crystallographic planes are given in Table 1. As with isostructural transition metal oxides such as TiO₂ and VO₂, the most stable surface is the (110).^30,31 These surface energies were used to calculate the planes exposed to the equilibrium morphology of an MnO₂ particle (Fig. 4). The particle volume is largely bounded by the (110) and (101) planes. Calculations performed using classical pair-wise interatomic potentials have produced a similar though more rounded morphology due to a higher (110) surface energy.³² Experimentally, the morphology of MnO₂ particles is strongly dependent on synthesis conditions, but the observed tendency to form particles with large aspect ratio is consistent with our results.³³

Table 1 Surface energy for low miller index MnO₂ surfaces

Surface plane	γ (J m^−2)
(110)	1.151
(100)	1.431
(101)	2.031
(001)	2.203
(111)	3.610

---

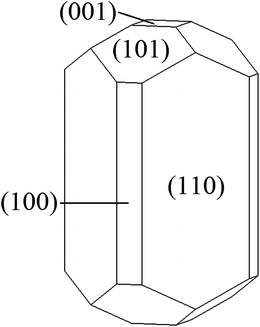Fig. 4 Wulff's construction of the equilibrium morphology for a MnO₂ particle.

As in TiO₂(110) and VO₂(110), the main relaxations in MnO₂ (110) occur normal to the surface, with the 5-fold coordinated manganese atoms relaxing inward and the 6-fold coordinated manganese atoms and the in-plane oxygen atoms relaxing outward (Fig. 5).

Fig. 5 Lateral view of the MnO₂ (110) relaxed surface.

3.2 Redox properties of the pure MnO₂ (110) surface

In order to discuss the redox properties of the (110) surface of MnO₂, we calculate the surface free energies of different stoichiometries. We only consider variations in the oxygen content (the number of manganese atoms is fixed). Five values of Γ are possible if we stick to bulk-like oxygen positions: Γ = 0 (stoichiometric surface), Γ = 1 & 2 (partially and totally oxidized surfaces), and Γ = −1 & −2 (partially and totally reduced surfaces). Here, total reduction means the removal of the full top layer of bridging oxygen ions, while total oxidation means the addition of a full layer of oxygen ions forming manganyl-like terminations on top of the previously unsaturated Mn sites. “Mono-peroxo” and “bridging-peroxo” modes of O₂ adsorption (shown in Fig. 6), where the molecule remains undissociated, are also considered, and these situations will be compared to the Γ = 2 manganyl bulk-like termination.

Fig. 6 Fully oxidised (Γ = 2) surface terminations.

To correct for the poor PBEsol description of redox enthalpies we use an adjusted value for the O₂ energy, similar to the correction proposed by Wang et al.³⁴ The value is determined such that when the PBEsol calculated energies for a number of metal oxide bulk are used to determine enthalpies of formation, the values are corrected to agree with the experimental enthalpies (Fig. 7). The correction, in the case of MnO₂, should also improve the poorer description of molecules by the PBEsol functional compared to standard PBE, as the former is designed to model extended systems.

Fig. 7 Effect of the correction (0.87 eV) required for the PBEsol O₂ energy to match the experimental values of oxide formation energies.

Now, we discuss the thermodynamics of reduction/oxidation on the surface as a function of temperature and partial pressure of oxygen. Fig. 8 shows the variation of the surface free energies for different surface terminations as a function of chemical potential. In the bottom graph we included a vertical line that marks the boundary between the regions of stability of MnO₂ and Mn₂O₃ in their bulk forms. This is estimated from the change in enthalpy of the reaction:

2Mn₂O₃ + O₂ → 4MnO₂, (6)

ΔH = −1.68 eV, which we obtain from the experimental formation energies of the two oxides. At the chemical potential μ_O = ΔH, the free energy of the above reaction changes sign (again, we neglect small contributions from the variation of enthalpies with temperature and from the difference in entropy between the two oxides). The area to the left of the vertical line in the chemical potential plot thus corresponds to the conditions under which bulk Mn₂O₃ is thermodynamically stable with respect to bulk MnO₂. Under ambient conditions, for example, MnO₂ is in the stable bulk phase.

Fig. 8 Top: relative surface free energies for different surface terminations of the MnO₂ surface as a function of oxygen chemical potential. The labels (a), (b) and (c) for the Γ = 2 lines refer to different configurations of adsorbed oxygen; bridging peroxo, mono-peroxo and manganyl, respectively. Bottom: chemical potential of oxygen in the gas phase as a function of temperature and oxygen partial pressure.

Fig. 8 shows that the two reduced terminations considered (Γ = −2 & −1) are not stable at moderate T and p conditions. Complete reduction of the MnO₂ surface cannot be expected, except for extremely reducing conditions where bulk Mn₂O₃ is more stable than bulk MnO₂ (i.e. left of the vertical line in Fig. 8). Under mildly reducing conditions (approximately −1.7 eV < μ_O < −0.6 eV) the Γ = 0 stoichiometry is always the most stable. Under oxidising conditions (lower temperatures and/or high oxygen partial pressures), although Γ = 1 oxidation is unfavourable, the specific bridging-peroxo Γ = 2 mode of oxidation is stable. The stoichiometric composition, moreover, becomes unstable with respect to the bridging-peroxo mode of Γ = 2 oxidation at approximately ambient temperature and pressure. The general trend towards a stoichiometric surface, or a surface with adsorbed oxygen, is consistent with the presence of some Mn⁵⁺ ions at the surface of MnO₂ films. XPS of MnO₂ microstructures gives a Mn to O ratio of 1 : 2.12, which is evidence for a moderate oxidation of the oxide surfaces.³⁵ Other recent theoretical investigations present similar trends in oxidation/reduction, although with less stabilisation of surface oxidation.³⁶ This result may be due to not considering the adsorption of bridging-type oxygen, where the adsorbate maintains its molecular character.

Vacancy formation energies were calculated from the energies of the Γ = −1 and Γ = −2 slabs. Bridging O vacancies have a formation energy of 1.87 eV, while it costs 4.25 eV to remove both bridging oxygen atoms, that is, reduction becomes more difficult with the removal of each bridging O (4.25/2 eV > 1.87 eV).

Adsorption energies were calculated for the four oxidised configurations (one with Γ = +1, and three with Γ = +2), with respect to oxygen in an isolated O₂ molecule. Adsorption of an oxygen atom on a 5-fold coordinated Mn site yields an adsorption energy of 0.53 eV. Γ = +2 surfaces were calculated with manganyl, mono-peroxo and bridging-peroxo configurations, which yield adsorption energies of +1.16 eV, −0.02 eV, and −1.15 eV respectively. These figures show that adsorption of oxygen can be both endo- and exothermic, depending on whether or not oxygen maintains its molecular character on the surface. The formation of manganyl species from adsorbed oxygen is a local minimum in the adsorption energy landscape, but is the least favourable configuration and is indeed thermodynamically unfavourable with respect to desorption. The bridging peroxo unit is probably the most favoured because it is shared between two Mn surface cations and requires the least charge transfer per Mn cation of all possible oxidised species. Minimal charge transfer from Mn to O occurs as the Mn cations have already a formal oxidation state of +4 in MnO₂.

3.3 Charge transfer from lithium adatoms to surface Mn cations

Understanding the surface behaviour of Li-doped MnO₂ is important in the context of MnO₂-based Li–air batteries. We now consider the mode of the transfer of an electron from a Li adatom to a surface Mn cation. The first step is to determine onto which surface site Li preferentially adsorbs.

Different possible adsorption sites on the surface were systematically tested and the results are reported in Table 2. We find that Li adatoms are more stable in sites of high oxygen coordination. The site with lowest adsorption energy (−1.80 eV) is that where Li is triply coordinated, bonded to two bridging and one in-plane oxygen atoms (bbi). Another adsorption site, with almost the same adsorption energy, has Li coordinated to one bridging and two in-plane oxygen atoms (bii). Sites with Li bonded to only two bridging oxygen (bb), or to one bridging oxygen (b) do not correspond to local minima of the potential energy landscape and can only be stabilised by symmetry constraints. When the initial symmetry is broken the Li adatoms move away from these sites.

Table 2 Energies and bond lengths for the three different stable modes of adsorption. The labels “nn” and “nnn” refer to nearest-neighbour and next-nearest-neighbour charge transfer, as explained in the text

Li adsorption site	Adsorption energy (eV)	d(Li–Oi) (Å)	d(Li–Ob) (Å)
bbi	−1.80	2.00	1.94, 1.97
bii(nnn)	−1.76	2.03 × 2	1.80
bii(nn)	−1.62	2.10 × 2	1.79

---

We now examine the electron transfer from Li adatoms, in the bbi and bii sites, to the surface cations. A Bader analysis shows that in all cases the adsorbed Li adopts a positive charge (∼+0.9|e|), which indicates that an electron has been donated to the surface. Clearly, this electron should go to the manganese cations, because the oxygen anions formally have a complete electron shell. In order to identify which Mn cations were reduced, we look at the integration of the spin density over the Mn Bader volumes, which generally gives a better indication of cation reduction than the charge density.^37,38 For the reduced Mn cation we find a clear increase in the spin moment of 0.99 μ_B within the Bader volume.

For the bbi site, there are three symmetrically distinct possibilities for where the electron localises on the surface cations: one 5-fold Mn and two 6-fold Mn cations. Each of these is tested in turn, initially localising the electron on each site and then relaxing the electronic and geometric structure. The initial localisation was forced by using a computational “trick”: we temporarily substitute Mn by Fe in the site where we want to force localisation. Because Fe is more stable in the 3+ oxidation state than in the 4+, the geometry relaxation leads to a structural distortion favourable to the presence of a 3+ cation in that lattice site. When we put Mn back in that position, it tends to reduce preferably over those in other lattice positions. Following this procedure, we find that the Mn(6-fold) cations are not stable for localisation of the extra electron, that is, the transferred electron always goes to the Mn(5-fold) cation at the surface, regardless of the initial localisation.

For a bii lithium adatom, again there are three distinct possibilities for the localisation of the transferred electron. The localisation on the Mn(6-fold) cation is again found to be unstable. Electron localisation on the two different Mn(5-fold) cations (relative to the Li position) leads to different adsorption energies: the electron localises on the Mn(5-fold) cation that is the next-nearest neighbour (nnn) to the Li adatom, where it is 0.14 eV more stable than in the nearest neighbour (nn) position. This behaviour, which arises from the higher elastic energy in accommodating the distortions produced by both the adatom and the reduced cation in very close positions, is the opposite of what is expected in terms of pure electrostatics: if the Coulomb effect was dominant, the nn Mn cation would be reduced, in order to decrease the Mn–Li repulsion. The non-Coulombic charge localisation effect has been found in other cases of charge transfer between adatoms and oxide surfaces.³⁸ The three discussed adsorption sites are shown in Fig. 9, and their energies are summarised in Table 2.

Fig. 9 Top view of the MnO₂ (110) surface with lithium adsorbed at bbi, bbi(nnn) and bii(nn) sites. Mn (purple), O (red) & Li (green). A larger sphere represents a reduced cation.

3.4 Oxygen adsorption at the Li/MnO₂ (110) surface

Finally, we consider the adsorption of oxygen (two O atoms per surface cell, Γ = 2) on the Li/MnO₂ (110) surface. In order to investigate the stability of Li–O–O–Li species, which are known to be important in the Li–air battery, we also consider two Li atoms per surface cell, assuming that they both occupy the most stable bbi sites. It should be noted that since there are only two bbi sites at each surface in our simulation cell, this structure corresponds to full coverage of the bbi sites at the surface, that is, a monolayer of Li adatoms. Therefore, based on the results discussed above, all the Mn(5-fold) surface cations can be expected to be reduced before oxygen adsorption, which has been confirmed using Bader analysis.

We investigate a number of oxygen adsorption configurations, in some cases keeping the molecular bond between the two oxygen atoms, and in others assuming dissociative adsorption. We found four different stable configurations, which are shown in Fig. 10. Some of the configurations initially considered were found to be unstable (in the sense of not being a minimum in the adsorption energy landscape). For example, although a configuration with one oxygen atom directly on top of each Li is a stationary point, it is in fact unstable and relaxes (if the symmetry of the initial configuration is broken) to a peroxo configuration bridging between two Li atoms, as in Fig. 10c. The oxygen adsorption energy in this Li-peroxo configuration is −1.81 eV/O₂.

Fig. 10 Stable adsorption configurations for two oxygen atoms at the Li/MnO₂ (110) surface.

The Li-peroxo is not the only stable peroxo adsorption configuration: a peroxo group bridging directly between the two previously unsaturated Mn cations, as in Fig. 10b (E_ads = −2.00 eV/O₂), and a peroxo group perpendicular to the surface and binding to Li on one end and to Mn on the other end, as in Fig. 10d (E_ads = −1.27 eV/O₂), are also stable. However, the most stable configuration found was the dissociative adsorption where there is an oxygen atom on the “bulk-like” positions on top of each of the Mn cations, but with additional bonds formed with the Li adatoms, as in Fig. 10a (E_ads = −2.25 eV/O₂).

These results show that, due to the presence of cation sites amenable to oxidation, oxygen adsorption on the Li/MnO₂ (110) surface is much more favourable than on the pure MnO₂ (110) surface. In Fig. 11 we show that the range of chemical potentials at which oxygen adsorption (at a coverage of two O atoms per cell) is stable with respect to the non-oxidised surface, extends beyond −1 eV, which is ∼0.5 eV below the threshold in the Li-free surface, meaning that the Li/MnO₂ (110) surface will remain oxidised up to temperatures of ∼1000 K at ambient oxygen pressure.

Fig. 11 Surface free energies of the oxidised Li/MnO₂ (110) surfaces with respect to the non-oxidised termination.

3.5 Effect of MnO₂ in the cathode reaction in a Li–air battery

The above results can help us understand better the cathode reaction in a Li–air battery, in the presence of MnO₂. During the battery discharge process, molecular oxygen is reduced in the cathode, in the presence of Li cations and electrons, forming lithium peroxide (Li₂O₂) particles:

O₂ + 2Li⁺ + 2e⁻ → Li₂O₂. (7)

If we compare the energy of formation of bulk Li₂O₂ (a hexagonal crystal,³⁹ shown in Fig. 12a) with the energy of formation of the surface lithium oxide at MnO₂ (110) (Fig. 10d), the former is lower by 1.25 eV/Li. This agrees with the experimental observation that Li₂O₂ is the main product of the cathode reaction in Li–air batteries (both in the presence and in the absence of MnO₂).¹² However, in the initial stage of growth of Li₂O₂ in the cathode, the small Li₂O₂ clusters have a high energy per formula unit relative to the bulk. For example, we have calculated that the Li₂O₂ monomer (Fig. 12b, initial geometry from ref. 40) is 3.55 eV per formula unit (or 1.78 eV/Li) higher in energy than the Li₂O₂ bulk, and therefore also higher in energy than the surface lithium oxide. This implies that the initial reduction of oxygen in the cathode occurs more favourably via the dissociative adsorption of the oxygen molecule at the lithiated MnO₂ surface, forming the structures described above (Fig. 10d), than via the formation of small unsupported Li₂O₂ clusters. If it is possible for the Li₂O₂ particles to grow in contact with these LiO/MnO₂ surfaces, then the barrier for the formation of the lithium peroxide particles at the cathodes would be reduced.

Fig. 12 Structure of Li₂O₂ (a) in the bulk form (hexagonal P6₃/mmc space group) and (b) as a monomer, showing the relaxed O–O distances.

4 Conclusions

The main conclusions of our study of the redox behaviour of the pure and lithiated (110) surface of rutile-structured MnO₂ are as follows:

(a) The stoichiometric MnO₂ (110) surface is very stable under reducing conditions, and can be expected to resist significant reduction under most temperatures and oxygen partial pressures of interest. The adsorption of oxygen, on the other hand, is relatively favourable at low to ambient temperatures and high partial pressures of oxygen. This adsorption mainly occurs in the form of peroxo species bridging between two surface Mn cations.

(b) The preferred site for the Li adatom is one where the adatom is tri-coordinated to one in-plane and two bridging oxygen atoms. Charge transferred from the Li always localises on the coordinatively unsaturated (5-fold) Mn surface cations, irrespective of the Li adsorption site.

(c) Oxygen adsorption is stabilised by the presence of Li at the surface. The most stable adsorption mode is dissociative, where oxygen atoms saturate the coordination of Mn surface cations, and at the same time bind to the Li adatoms.

(d) The formation of the surface lithium oxide is energetically more favourable than the formation of gas-phase lithium peroxide (Li₂O₂) monomers, but less favourable than the formation of Li₂O₂ bulk, which suggest that the presence of β-MnO₂ in the cathode of a Li air battery lowers the energy for the initial reduction of oxygen. An experimental verification of this conclusion from electrochemical studies would be welcome.

Acknowledgements

Via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work made use of the facilities of HECToR, the UK's national high-performance computing service, which is provided by UoE HPCx Ltd at the University of Edinburgh, Cray Inc. and NAG Ltd, and funded by the Office of Science and Technology through EPSRC's High End Computing Programme. The work was also funded by the South African Research Chair Initiative of the Department of Science and Technology and the National Research Foundation in South Africa.

References

1. M. M. Thackeray, Prog. Solid State Chem., 1997, 25, 1–71.
2. Y. Xia, K. Tatsumi, T. Fujieda, P. P. Prosini and T. Sakai, J. Electrochem. Soc., 2000, 147, 2050–2056.
3. A. R. Armstrong and P. G. Bruce, Nature, 1996, 381, 499–500.
4. F. Cheng, J. Zhao, W. Song, C. Li, H. Ma, J. Chen and P. Shen, Inorg. Chem., 2006, 45, 2038–2044.
5. F. Jiao and P. G. Bruce, Adv. Mater., 2007, 19, 657–660.
6. D. A. Tompsett, S. C. Parker, P. G. Bruce and M. S. Islam, Chem. Mater., 2013, 25, 536–541.
7. M. Armand and J. M. Tarascon, Nature, 2008, 451, 652–657.
8. P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J.-M. Tarascon, Nat. Mater., 2011, 11, 19–29.
9. K. Abraham and Z. Jiang, J. Electrochem. Soc., 1996, 143, 1–5.
10. R. Black, B. Adams and L. Nazar, Adv. Energy Mater., 2012, 2, 801–815.
11. J. Christensen, P. Albertus, R. S. Sanchez-Carrera, T. Lohmann, B. Kozinsky, R. Liedtke, J. Ahmed and A. Kojic, J. Electrochem. Soc., 2011, 159, R1–R30.
12. A. Débart, A. J. Paterson, J. Bao and P. G. Bruce, Angew. Chem., 2008, 120, 4597–4600.
13. Y. Shao, S. Park, J. Xiao, J.-G. Zhang, Y. Wang and J. Liu, ACS Catal., 2012, 2, 844–857.
14. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
15. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50.
16. J. P. Perdew, A. Ruzsinszky, G. b. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
17. A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467–R5470.
18. E. Cockayne and L. Li, Chem. Phys. Lett., 2012, 544, 53–58.
19. D. A. Tompsett, D. S. Middlemiss and M. S. Islam, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 205126.
20. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
21. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
22. C. Franchini, R. Podloucky, J. Paier, M. Marsman and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 195128.
23. A. Yoshimori, J. Phys. Soc. Jpn., 1959, 14, 807–821.
24. K. D. Rogers, Powder Diffr., 1993, 8, 240–244.
25. G. Wulff, Z. Kristallogr. Miner., 1901, 34, 449–530.
26. X. G. Wang, W. Weiss, M. Shaikhutdinov, M. Ritter, F. Petersen, R. Wagner, R. Schlogl and M. Scheffler, Phys. Rev. Lett., 1998, 81, 1038–1041.
27. M. W. J. Chase, NIST-JANAF Thermochemical Tables, American Institute of Physics, New York, 1998.
28. R. Grau-Crespo, C. R. A. Catlow and N. H. De Leeuw, J. Catal., 2007, 248, 77–88.
29. K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 035406.
30. A. Kiejna, T. Pabisiak and S. Gao, J. Phys.: Condens. Matter, 2006, 18, 4207.
31. T. A. Mellan and R. Grau-Crespo, J. Chem. Phys., 2012, 137, 154706.
32. R. R. Maphanga, S. C. Parker and P. E. Ngoepe, Surf. Sci., 2009, 603, 3184–3190.
33. L. Zhang, Z.-H. Liu, X. Tang, J. Wang and K. Ooi, Mater. Res. Bull., 2007, 42, 1432–1439.
34. L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107.
35. B. Tang, G. Wang, L. Zhuo and J. Ge, Nanotechnology, 2006, 17, 947.
36. G. A. Oxford and A. M. Chaka, J. Phys. Chem. C, 2011, 115, 16992–17008.
37. M. M. Branda, N. J. Castellani, R. Grau-Crespo, N. H. de Leeuw, N. C. Hernandez, J. F. Sanz, K. M. Neyman and F. Illas, J. Chem. Phys., 2009, 131, 094702.
38. N. C. Hernandez, R. Grau-Crespo, N. H. de Leeuw and J. F. Sanz, Phys. Chem. Chem. Phys., 2009, 11, 5246–5252.
39. L. G. Cota and P. de la Mora, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 133–136.
40. K. C. Lau, R. S. Assary, P. Redfern, J. Greeley and L. A. Curtiss, J. Phys. Chem. C, 2012, 116, 23890–23896.

---