Conjugated donor–acceptor (D–A) copolymers in inverted organic solar cells – a combined experimental and modelling study†
Venla
Manninen
*a,
Mika
Niskanen
a,
Terttu I.
Hukka
a,
Felix
Pasker
b,
Simon
Claus
b,
Sigurd
Höger
b,
Jinseok
Baek
c,
Tomokazu
Umeyama
c,
Hiroshi
Imahori
c and
Helge
Lemmetyinen
a
aDepartment of Chemistry and Bioengineering, Tampere University of Technology, P. O. Box 541, FI-33101, Tampere, Finland. E-mail: venla.manninen@tut.fi; Fax: +358 3 3115 2108
bKekulé-Institut für Organische Chemie und Biochemie, Rheinische Friedrich-Wilhelms-Universität Bonn, Gerhard-Domagk-Str. 1, 53121 Bonn, Germany
cDepartment of Molecular Engineering, Institute for Integrated Cell-Materials Sciences (WPI-iCeMS), Graduate School of Engineering, Kyoto University, Nishikyo-ku, Kyoto 615-8510, Japan
First published on 29th April 2013
Abstract
Quantum chemical methods are useful for materials design to improve the performance of organic bulk heterojunction (BHJ) solar cells. However, more integrated studies of quantum chemical modelling and experimental results need to be performed to further improve both the materials design and understanding of the related photo-induced processes and photocurrent generation. In this work we investigated the internal relationship between the molecular structures of four donor–acceptor (D–A) copolymers (P1–P4) and their photovoltaic performances. The effects of the molecular structures on the generation of photo-induced charge carriers, exciton diffusion, dissociation and carrier transmission were compared by combining density functional theory (DFT) calculations of intrinsic geometric, electronic and optical properties with the results of electrochemical, spectroscopic, thermal, AFM and solar cell measurements of the polymers. The quantum chemical methods, which provided a tool to assess the electronic properties and conjugation length in the polymers, highly support the experimental results and therefore the usefulness of quantum chemistry for solar cell materials design.
Introduction
Copolymers with electron rich and electron deficient moieties alternating along the polymer backbone have performed well as electron donors in polymer solar cells. By adding different substituents to the polymer backbone, the redox and structural properties of the polymer can be controlled, which offers a method for preparing tailored low band gap (LBG) polymers for photovoltaic applications. Benzodithiophene derivatives as the electron rich unit have demonstrated excellent photovoltaic properties as tunable electron donors,1–7 whereas benzotriazole with various substituents has been used as an electron acceptor8–11 in LBG donor–acceptor (D–A) polymers. Intramolecular charge transfer (ICT) properties of tailored LBG copolymers based on alternating benzodithiophene and benzotriazole derivatives have demonstrated excellent photovoltaic properties in D–A polymers, which have been studied experimentally in the conventional indium tin oxide (ITO)|poly(3,4-ethylenedioxythiophene)–poly(styrenesulfonate) (PEDOT:PSS)|polymer:[6,6]-phenyl-C60-butyric acid methyl ester (PC60/70BM)|Ca|Al organic bulk-heterojunction (BHJ) solar cells.12,13The photocurrent generation in organic BHJ solar cells takes place in both polymer and fullerene phases and is initiated by photoexcitation and formation of excitons. During their lifetime, prior to decay back to the ground state, the excitons need to diffuse to the donor–acceptor interface for dissociation. The Coulombic binding potential of excitons has to be overcome through differences in the chemical potentials of the hole transporting material (HTM) and the electron transporting material (ETM). The separated charged polarons, the electron and the hole, migrate through the HTM and ETM phases and are collected at the electrodes. Photocurrent generation is a stepwise process, where all the principal stages need to be optimized to produce photocurrent efficiently. Therefore, the essential qualifications have been established for the design and intrinsic material properties of HTM polymers. A planar structure of the polymer backbone is desired to decrease the band gap energy (Eg) around 1.77 eV,14 to shift the polymer absorption to the red towards the maximum intensity range of the solar irradiation, and to minimize the reorganization energy upon excitation. Also, suitable energy levels are necessary for efficient charge transfer, charge separation at the HTM/ETM interface and charge collection at the electrodes.
In addition to experimental methods, properties of conjugated polymers as donor materials can be studied computationally. Information can be obtained about polymer chain geometries, orbitals, HOMO and LUMO energies, electron affinities, ionization potentials, effective conjugation lengths, and various excited state properties.15–27 While many of these properties are accessible through experiments, combining the methods gives more details on the performance of the chosen polymers as donor materials. In a real bulk system, intermolecular interactions affect the polymer chain geometry and its properties. However, modeling of the polymer bulk and donor–acceptor interfaces is difficult, because the areas of interest are likely to contain thousands of atoms. Moreover, the periodic boundary conditions cannot be effectively used, as the materials are often amorphous or semicrystalline, consisting of only small crystalline domains. The systems are often too big for density functional theory (DFT) and correlated method calculations, whereas semiempirical methods are often not accurate enough for such complex systems. As a result, most commonly only isolated polymer chains are studied computationally and the models are either short oligomeric chains15–17 or infinite polymers that are built using periodic boundary conditions.28–33 When oligomeric models are used the polymer properties can be obtained by presenting the results as a function of inverse constitutional repeating units (1/n) and extrapolating.15,34–36
In this work, the relationship between the molecular structures of four different donor–acceptor (D–A) copolymers (P1–P4) and their photovoltaic performances is investigated. To this aim, a new polymer (P4, Fig. 1) with alternating benzodithiophene and benzotriazole moieties was synthesized, characterized and used as a donor material in inverted37 ITO|zinc oxide (ZnO)|polymer:PC60BM/PC70BM|tris-(8-hydroxyquinoline)aluminum (Alq3)|Au (Fig. 2) organic solar cells. P4 was compared with three previously studied38 D–A donor polymers containing 2-aryl-2H-benzotriazoles and bis(thiopheno)dialkylfluorenes (P1–P3, Fig. 1). The well-known donor material, poly(3-hexylthiophene) (P3HT, Fig. 2), was used as a reference polymer.
 | ||
| Fig. 1 Chemical structures of the polymers P1–P4. | ||
 | ||
| Fig. 2 Chemical structures of PC60BM, PC70BM, Alq3 and reference polymer P3HT. | ||
The intrinsic material properties of the D–A polymers were studied with DFT using oligomeric and periodic isolated chain models. The geometries, HOMO and LUMO levels, molecular orbitals and lowest energy excitations of the polymers were computed and the results were combined with the experimental data to get a better understanding of the relationship between the photovoltaic performance and molecular structures. In addition, active layer structures of the solar cells were analyzed using AFM. Eventually, the stabilities of the prepared cells were compared six months after the cell preparation. This is possible due to the long lifetime of inverted structure organic solar cells with an air-stable Au anode.
Photovoltaic performance
The polymers were tested as donor materials in inverted ITO|ZnO|polymer:PCBM|Alq3|Au solar cells using the well-known P3HT:PC60BM as a reference cell. Energy levels of the materials of the constructed solar cells are important for the cell performance. The energy level diagram for the cell materials is shown in Fig. 3, where both the experimental (CV of P4, see ESI†) and computational values of the HOMO and LUMO energy levels are presented. Because the LUMO energy levels of the donor polymers are higher than those of the acceptor fullerene derivatives, each polymer is expected to be able to donate electrons to the acceptor molecules in the cell structure. Alq3 as a buffer layer prevents efficiently the unwanted flux of electrons to the direction of the metal (Au) anode. In addition, the HOMO levels of the polymers do not differ remarkably from each other. Thus, the open circuit voltage (VOC), which is proportional to the energy difference between the HOMO of the donor and the LUMO of the acceptor, should not vary remarkably between different donor–acceptor combinations.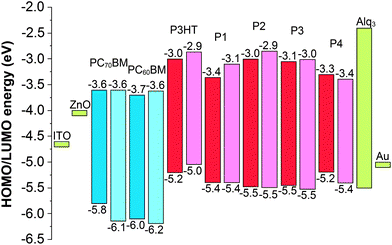 | ||
| Fig. 3 Energy level diagram of the donor molecules (red), acceptor molecules (blue), buffer layer materials (green) and electrodes (green) used in the organic solar cells.39 The experimental values are shown in dark blue/red and the modeled values in light blue/red. | ||
Photovoltaic parameters of the prepared solar cells using P1, P2 and P4 as donor materials, measured the following day after the cell preparation, are presented in Table 1 and the corresponding I–V curves are shown in Fig. 4. The cell efficiency using P3 as a donor material was negligible and therefore it is not included in the solar cell results, but P3 was kept in the calculations to allow comparison.
| Active layer components (film thickness, nm) | Mass ratio polymer:PCBM | J sc (mA cm−2) | V oc (V) | FF (%) | η best (%) | η avg (%) |
|---|---|---|---|---|---|---|
| P3HT:PC60BM (100) | 1.26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−3.09 | 0.52 | 68.96 | 3.04 | 2.47 |
| P1:PC60BM (65) | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.99 3.99 |
−1.53 | 0.48 | 42.35 | 0.83 | 0.58 |
| P1:PC70BM (55) | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.63 4.63 |
−0.73 | 0.34 | 40.31 | 0.27 | 0.25 |
| P2:PC60BM (130) | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.14 4.14 |
−0.65 | 0.43 | 28.86 | 0.21 | 0.12 |
| P4:PC60BM (40) | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.69 2.69 |
−1.17 | 0.45 | 41.18 | 0.57 | 0.43 |
| P4:PC70BM (30) | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.09 3.09 |
−1.13 | 0.41 | 58.71 | 0.74 | 0.66 |
 | ||
| Fig. 4 I–V curves of the P1/P2/P4:PC60BM/PC70BM cells measured the following day after the cell preparation. | ||
P1–P3 have been tested earlier in conventional ITO|PEDOT:PSS|polymer:PC60BM|Ca|Al solar cells,38 in which case the reported η values were higher than here in the case of inverted solar cells. The reasons for this could be that the certified measuring system could not be applied when measuring the inverted solar cells studied here. Also, different cell efficiencies for the same polymer, P3HT, have been reported depending on the cell structure. The average η for the P3HT:PCBM BHJ solar cells reported during the years 2002–2010 is around 3%.40 In the conventional P3HT:PC60BM cell structure the values of η are from 3% to 4%,41,42 whereas in the inverted cell structure the reported η values are slightly lower, i.e. 2% to 3%.39b,d,e,43,44 In this article, the polymers are used in the inverted cell structure and therefore the efficiencies of different polymers as donor materials can be compared and discussed.
The efficiencies of the solar cells differ remarkably depending on the donor–acceptor combinations, which cannot be explained in terms of the energy levels of the compounds. For example, based on the energy difference between the HOMO of the donor and the LUMO of the acceptor (Fig. 3), a higher VOC could be expected for the P1:PC60BM cell than that for the P3HT:PC60BM cell. However, the former has a lower VOC, 0.48 V, than the latter, 0.52 V. Similarly, the same VOC values could be expected for the P3HT:PC60BM and P4:PC60BM cells, because of the same measured HOMO energies (−5.2 eV) of the donor polymers. Nevertheless, VOC values are different, 0.52 V and 0.45 V for P3HT and P4, respectively. In the cases of P1 and P4 the donor polymers give very different efficiencies depending on the acceptors, PC60BM or PC70BM, even though the acceptors have almost the same HOMO and LUMO energies. For understanding these discrepancies a closer quantum mechanical insight into the polymers' molecular geometry, electronic structure and donor–acceptor interaction is necessary.
Modelling of the polymer geometry and electronic structure related properties
In the computational models of P1–P4 the solubility enhancing long alkyl side chains, –OC10H21, –OCH2CH(C2H5)C4H9, –C6H13 and –C8H17 were replaced by short side chains, i.e. –OCH3 and –CH3, respectively. This reduced the computational time and allowed modeling of oligomeric chains up to n = 7–8 and thus investigation of the convergence of the HOMO–LUMO gaps. The periodic models were built based on the optimized oligomer structures. The constitutional repeating unit (CRU) of P1 is bent due to the dithiophene 2-phenyl benzotriazole moiety so the periodic P1 model was built from two P1 CRUs which create a zigzagging, almost planar polymer backbone. The methyl substituents of the two 3-methylthiophene rings in the CRU enlarge the backbone dihedral angles in P2 and P3, which prohibits planarity. As a result, it is expected that the π-conjugation weakens or is broken at some points in the backbones of the P2 and P3 polymers. For these polymers the periodic models were constructed of three CRUs, which create a helical backbone. We note, however, that there are ways to build alternative periodic models for P2 and P3. The periodic model of P4 consists of a linear and almost planar single CRU. The fully optimized periodic models are presented in Fig. 5.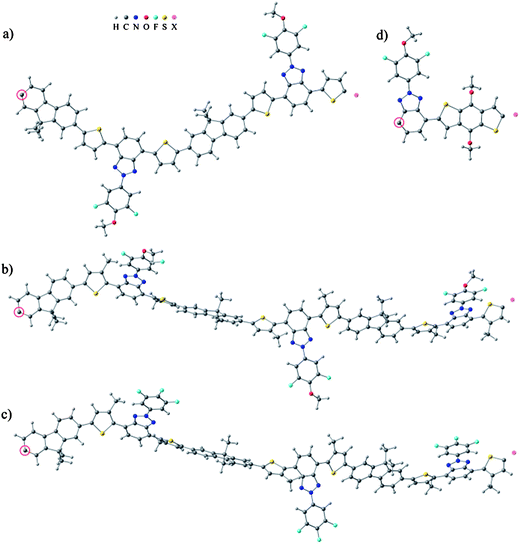 | ||
| Fig. 5 Periodic models of (a) P1, (b) P2, (c) P3 and (d) P4. The repeating structure is copied and translated from the circled carbon atom to the position marked as a pink dummy-atom. | ||
The geometries of the oligomeric and periodic models with full side chains were also fully optimized to compare the backbone dihedral angles to those of the models with short side chains. The backbone dihedral angles of P1 and P4 did not change. However, those of P2 and P3 increased due to the steric effects caused by the hexyl substituents of the two 3-hexylthiophenes.
Energy level gaps, orbitals and TD-DFT calculations
The HOMO–LUMO gaps of the short side chain oligomeric models and the gaps between the highest occupied crystal orbital and the lowest unoccupied crystal orbital (the HOCO–LUCO gap) of the short side chain periodic models were examined. The HOMO–LUMO gap energies of oligomers approach the HOCO–LUCO gap energies of the periodic models as the oligomer length is increased (see ESI, Table S3†), so the HOCO–LUCO gaps are taken as final computational results for the P1–P4 polymers. The HOCO–LUCO gaps were direct band gaps. The computational energies were shifted by subtracting 0.62 eV from the values so that the computational HOCO and experimental HOMO levels of P1 are equal. The shifted HOCO and LUCO energies based on the periodic calculations are presented and compared to the experimental HOMO and LUMO energies in Fig. 3. The HOCO–LUCO gaps are systematically only a bit larger (0.12 eV to 0.26 eV) than the experimental values obtained by cyclic voltammetry, and the agreement between the energy levels is qualitatively good.The HOMO–LUMO gaps of the short oligomers and the HOCO–LUCO gaps of the periodic models with the full side chains were examined as well. Incorporating the full side chains does not change the gaps of P1 and P4 in the longest oligomers and periodic models, but the gap increases slightly in the case of P2 (0.08 eV) and P3 (0.06 eV) due to increased steric stress caused by the 3-hexylthiophene moieties that hinder the π-conjugation.
Next, the frontier molecular orbitals of P1–P4 were analysed. The D–A polymers consist of electron rich and electron deficient moieties to achieve a narrower HOMO–LUMO gap. The CRUs of P1, P2 and P3 are composed of three different building blocks, of which fluorene and thiophene derivatives are the electron rich moieties and 2-phenyl benzotriazole derivatives are the electron deficient moieties. In P4 the electron rich moiety is the benzodithiophene derivative and the electron deficient moiety is the 2-phenyl benzotriazole derivative. Periodic models are used to calculate and visualize the orbitals. This way the CRUs along the polymer backbone have the same orbital energy levels and the molecular orbitals are distributed equally in the CRUs along the infinite, non-terminating polymer chain. The orbitals are presented in Fig. 6 and the contributions to the orbitals from different backbone fragments are presented in Table 2. In P1, P2 and P3 the HOCO is evenly distributed, i.e. delocalized, along the polymer backbone whereas the LUCO is much more localized on the 2-phenyl benzotriazole moieties, particularly in P2 and P3. In the case of P2 and P3, localization most probably results from a weaker π-conjugation along the polymer backbone, as suggested above. In P4 both HOCO and LUCO are evenly delocalized along the polymer backbone, although the LUCO spreads further into the 2-phenyl benzotriazole derivative. The differences in localizations of the LUCOs are expected to affect the exciton diffusions in P1–P4, because the LUCO is partly occupied in excitation and participates in exciton diffusion.
 | ||
| Fig. 6 The HOCO (left) and LUCO (right) of the P1–P4 polymers and P3HT. | ||
| HOCO | LUCO | |||||
|---|---|---|---|---|---|---|
| Electron rich | Electron deficient | Electron rich | Electron deficient | |||
| Fluorene | Thiophene | Benzotriazole | Fluorene | Thiophene | Benzotriazole | |
| P1 | 31.0 | 46.3 | 22.7 | 15.2 | 29.0 | 55.8 |
| P2 | 34.2 | 48.1 | 17.7 | 11.5 | 23.6 | 64.9 |
| P3 | 35.1 | 47.9 | 17.0 | 9.4 | 21.0 | 69.6 |
| Benzodithiophene | Benzodithiophene | |||||
| P4 | 73.8 | 26.2 | 40.4 | 59.6 | ||
The effect of the length of the oligomer on the first excitation energy and its composition was studied by time-dependent density functional theory (TD-DFT). The calculated excitation energies are given in Table 3. As the length of the oligomer is increased, the first excitation energy gets smaller. However, with the longest calculated oligomers the TD-DFT results underestimate the excitation energy. This is rather common for B3LYP and usually, if TD-DFT results matching the experimental values are desired, PBE0 or novel functionals are used together with a solvation model. Additionally, the used basis set is rather small. Comparative calculations using the 6-311+G* basis set are presented in the ESI.† The orbital contributions of the first excitation were examined to justify the use of the HOCO–LUCO gap as the lowest excitation energy of the polymer. For all oligomers the main component of the first excitation was found to be from the HOMO to the LUMO. The HOMO to LUMO contribution remains dominant (>70% in P4, n = 8) in the total excitation as the length of the oligomer increases, but other contributions, such as HOMO-1 to LUMO + 1 appear as well, as they get closer to the energy of HOMO–LUMO transition. These orbitals are typical for the low energy excitations of conjugated systems, which contain π and π* orbitals.
| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | E ecg | E optg | |
|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 2.44 | 2.16 | 2.07 | 2.03 | 2.02 | 1.99 | — | — | 2.03 | 2.08 |
| P2 | 2.63 | 2.42 | 2.37 | 2.34 | 2.33 | 2.31 | — | — | 2.47 | 2.34 |
| P3 | 2.55 | 2.35 | 2.30 | 2.27 | 2.26 | 2.26 | — | — | 2.40 | 2.30 |
| P4 | 2.66 | 2.20 | 2.01 | 1.91 | 1.86 | 1.83 | 1.81 | 1.80 | 1.89 | 1.91 |
Maximum conducive chain length
The maximum conducive chain length (NMCC)35 was calculated using the DFT results to compare the conjugation degree of the polymers. For this method the HOMO–LUMO gaps were plotted as a function of 1/N (N is the number of double bonds along the shortest path of the polymer backbone). The infinite polymer HOMO–LUMO band gap was extrapolated for each polymer from the oligomer results. Polynomial fits were used for the extrapolation. The third degree polynomial fits described the plots of the HOMO–LUMO gaps of the oligomers well and leveled as they approached x = 0. The polynomial fits and extrapolated gaps are given in the ESI.† The 1/NMCC value was obtained from the intersection of the line y(x) = b drawn from the extrapolated HOMO–LUMO gap of an infinite polymer and a line drawn through the steepest descending part of the HOMO–LUMO plot (see ESI, Fig. S11†). The extrapolated HOMO–LUMO gaps were used for all polymers, because the oligomeric series did not approach the periodic values exactly for P2 and P3, though the differences were small (≤0.05 eV). A likely explanation for the differences is the flexibility of the P2 and P3 oligomeric models compared to the periodic models. The NMCC can be obtained accurately for polymers with short CRUs. However, as the number of double bonds increases in the CRU, less data points are available for the fitting procedure. This can cause problems if the non-saturated region, where the HOMO–LUMO gap values drop fast, has only one or two data points. The method seems to work reliably for P1 and P4, but for P2 and P3 it is likely that the excitation energy saturates too fast (see ESI). Thus the NMCC values for P2 and P3 should be considered as upper limits rather than exact values. The obtained NMCC values are 62 for P1, ≤ 47 for P2, ≤ 37 for P3 and 59 for P4. We can see that P1 and P4 have higher NMCC values than P2 and P3. Also, the conjugation can be expected to be more expanded in P1 and P4 because the HOMO–LUMO gap of their oligomers approaches the infinite polymer limit more slowly. Typically the NMCC values are much lower, in the range of 18–22 in conjugated polymer chains.35 Possible reasons for the high NMCC values obtained are the donor–acceptor architecture as well as the large CRU sizes of the studied polymers.Polymer–PCBM interactions
Single P1 and P4 monomers with full side chains were studied together with the molecular PC60BM and PC70BM acceptors in combined models to see how their interaction affects the energy levels. The energy levels of the combined models were compared to the energy levels of the isolated monomers and PCBMs. The PCBMs were arranged in three completely different positions: (i) close to the side chains away from the main backbone, (ii) close to the electron rich moiety of the monomer and (iii) close to the electron deficient moiety of the monomer (Fig. 7), and the models were fully optimized.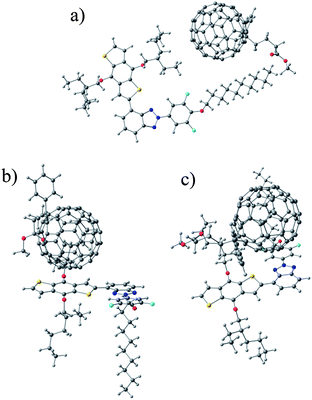 | ||
| Fig. 7 Models where PCBM is close to (a) the side chains of P4, (b) the electron rich moiety of P4 and (c) the electron deficient moiety of P4. | ||
The obtained molecular orbital energies are presented in Fig. 8. Bringing either PC60BM or PC70BM close to the polymer monomer changes the HOMO and LUMO values of the PCBMs and monomers slightly, i.e. −0.13 eV to +0.09 eV, compared to the isolated PCBMs and monomers. The P1 monomer behaves similarly with both PC60BM and PC70BM. The P4 monomer, however, behaves differently depending on the PCBMs (see Fig. 8). The largest changes in energies are observed in the model consisting of the P4 monomer and PC70BM. Both the HOMO and LUMO energies of PC70BM increase and those of P4 decrease, which leads to a larger P4 monomer HOMO–PC70BM LUMO gap when PC70BM is close to either the electron rich or the electron deficient moiety of the P4 monomer. While the molecular model cannot describe the real interfaces of an active material, it can be seen that interaction of the donor and acceptor changes the energy levels of both molecules and affects the electronic properties.
 | ||
| Fig. 8 Molecular orbital energies of the isolated monomers, PCBMs and combined models. | ||
Relationship between the photovoltaic performance and molecular structures of the donor polymers
The first prerequisite to produce photocurrent is the absorption of light to generate excitons. The overall cell absorption (Fig. 12) initiates from the absorption of the intrinsic donor and acceptor materials, which are presented in Fig. 9. The absorption maximum of P4, at 612 nm, is remarkably red-shifted compared to those of P2 and P3, at 443 nm and 448 nm respectively, and that of P1, at 537 nm. As shown in Fig. 5, the backbones of P2 and P3 are helical due to the steric hindrance of the hexyl chains attached to the thiophene rings, which weakens the π-conjugation in the polymer backbone. The structure of P1 is zigzagging, but planar, due to missing hexyl chains. Therefore π-conjugation is stronger and absorption of P1 is red-shifted compared to P2 and P3. A more planar structure of P4 compared to those of P1–P3 was achieved by exclusion of the thiophene moieties from the polymer backbone. In the nearly planar backbone of P4 the conjugation is the strongest and absorption of photons becomes possible at longer wavelengths (>600 nm) compared to P1–P3. | ||
| Fig. 9 Normalized absorption (solid lines) and emission (dashed lines, λex = 485 nm) of the donor polymers P1 (red), P2 (orange), P3 (yellow) and P4 (blue) and absorption of the acceptors PC60BM (dash-dotted line) and PC70BM (dotted line) in CHCl3. | ||
The absorption of PC60BM covers effectively the wavelengths up to 400 nm in CHCl3 solution, whereas PC70BM absorbs at a wider wavelength range up to 700 nm. The absorptions of P1–P3 overlap widely with the absorptions of both PC60BM and PC70BM. Absorption of P4 takes place at longer wavelengths and it does not overlap with the absorptions of PC60BM and PC70BM as widely as the three other polymers. Therefore, photons over a wider wavelength range up to 700 nm will be collected by the solar cell with P4 compared to the other cells with P1–P3 as the donor material.
In addition to a wider range of absorption a planar and rigid backbone is desired to prevent energy losses caused by reorganization upon excitation. The molecular frontier orbitals (Fig. 6) show that the LUMO orbitals promote planar structure. Therefore, the energy losses, i.e. Stokes shifts (Table 4), of P2 and P3 are remarkably larger than those of P1 and P4.
After excitation the excitons need to diffuse to the donor–acceptor interface along the polymer phase. Therefore excited state properties of the polymers have a principal effect on the exciton diffusion. The lifetime of the excited state defines the diffusion duration. The exciton diffusion effectivity i.e. the speed of the exciton, together with the lifetime, defines the diffusion length. The lifetime of P4, 2.14 ns, is longer than those of P1–P3, 1.64 ns, 1.10 ns and 1.00 ns, respectively (see ESI, TCSPC†). The exciton diffusion effectivity in the excited state of the polymers can be compared based on the molecular frontier orbitals shown in Fig. 6. The LUMOs of P2 and P3 are strongly located in the benzotriazole moieties of the polymer backbones and the orbitals are not continuous. Therefore, the exciton diffusion length in the excited states of P2 and P3 might be decreased if the excitons are trapped in the LUMO orbital spatial gaps. The LUMO orbitals of P1 and P4 have continuous electron density throughout the polymer backbones. Also, the calculated NMCC values of P1 and P4, 62 and 59 respectively, are larger than those of P2 and P3, 47 and 37 respectively. NMCC values correlate with the conjugation length in the polymer backbones. Thus, excitons can be expected to diffuse further in P1 and P4 than in P2 and P3.
Next, after exciton diffusion to the donor–acceptor interface, the Coulombic binding energy of excitons has to be overcome to separate the charges. Due to the red-shifted absorption the optical band gap of P4, 1.91 eV, calculated from the onset wavelength of the absorption spectrum, is smaller than those of P1–P3, 2.08 eV, 2.34 eV and 2.30 eV, respectively. The difference in the band gap energies measured by using the transport technique (CV) and optical excitation, Eecg – Eoptg, can be directly correlated with the exciton binding energy (EB)45 and the conjugation length in a polymer.46 The bigger the difference in the band gap energy, the higher the exciton binding energy and the shorter the conjugation length. The values of Eecg − Eoptg (Table 4) in the cases of P1 and P4 are close to zero, within the error of experiments, and smaller than those of P2 and P3. Thus, less energy is needed to separate the excitons created in P1 and P4 than in P2 and P3.
The emission spectra of the combined polymer:PCBM films, the intensity of which is corrected according to the absorbance of the films, are presented in Fig. 10. The emission of P1 from 675 nm to 775 nm is more efficiently quenched with PC60BM than with PC70BM. This predicts better electron transfer from P1 to PC60BM than to PC70BM, which can be also seen as an increase in the PC60BM acceptor emission from 550 nm to 650 nm. The emission of P4 from 600 nm to 700 nm is more efficiently quenched with PC70BM than with PC60BM, which supports better electron transfer from P4 to PC70BM than to PC60BM. The fluorescence decay curves of the combined films are shown in the ESI (Fig. S12).†
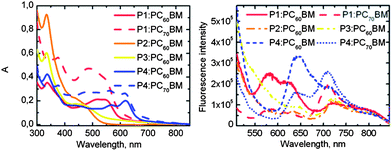 | ||
| Fig. 10 Absorption and emission (corrected according to absorbance) spectra of the polymer:PCBM photoactive layers. | ||
Eventually, the separated charge carriers are transported to the electrodes along the ETM and HTM paths in the BHJ layer. The carrier transport in the ETM and HTM together with the morphology of the phase-separated network governs the transport. The HOMOs of P1–P4 are relevant for the hole transport in the materials. Our models do not include thermal motion that would change the energy of CRUs with respect to each other, so the obtained HOMO electron densities are rather evenly distributed (Table 2). However, longer conjugation along the backbones leads to better hole transport in P1 and P4 than in P2 and P3, as in the latter, backbone twists are more likely and may create hole traps.
The differences in the molecular structures of the polymers lead to differences in phase separation and morphology in the interpenetrating network of the BHJ structures. A rough insight into the active layer morphology was achieved by the AFM images of the cells (Fig. 11). Usually, small roughness (RMS = root mean square) values and small grain features are correlated with enhanced crystallinity, which offers better energy conversion efficiency.47 Based on the DSC measurements of P1–P4 (see ESI† and ref. 38), there are no remarkable differences in the crystallinity, but P4 is thermodynamically more stable than P1–P3. Therefore, RMS values are valuable for estimating the morphology of the BHJ structure formed by the polymers. The RMS value of P1:PC70BM, 1.92 nm, is significantly larger than that of the P1:PC60BM film, 0.45 nm. Large aggregates with large grain features can be seen in the P1:PC70BM film. Aggregation may lead to current losses due to excessively long conduction paths compared to the exciton diffusion length in the P1:PC70BM film. Therefore, the excitons created in the P1:PC70BM cell recombine before reaching the donor–acceptor interface more probably than in the P1:PC60BM cell, and the P1:PC60BM cell (η = 0.80%) worked better than the P1:PC70BM cell (η = 0.35%). In the case of P2 the active layer morphology formed by P2:PC60BM seems fairly uniform. Thus, it seems that P2 is capable of forming a good quality BHJ layer with PC60BM. However, as discussed before, due to the gaps in the LUMO and small NMCC values, both exciton and charge transfer are inefficient in P2 and the performance of the cell remains low (η = 0.12%). Active layer morphologies of the P4:PC60BM and P4:PC70BM cells appear very similar, and also the RMS values, 0.92 and 0.94 respectively, are practically the same. Thus, the film formation properties do not seem to cause the difference between the performances of the P4:PC60BM (η = 0.33%) and P4:PC70BM (η = 1.03%) cells. Because PC60BM absorbs efficiently only up to 400 nm, the absorption and the exciton formation of the P4:PC60BM solar cell device will mainly take place in the P4 donor phase, whereas in the P4:PC70BM device both the donor and the acceptor participate in the exciton creation. Even though the combined film of P4:PC70BM is thinner (30 nm) than the P4:PC60BM film (40 nm), the superiority of P4:PC70BM is caused by the higher absorption of the cell.
 | ||
| Fig. 11 AFM images of the P1:PC60BM/PC70BM and P4:PC60BM/PC70BM cells. | ||
Lastly, the EPCEs of the cells show (see Fig. 12) how efficiently absorption of photons leads to current production. The absorption of the cells with P1 is remarkably higher than that of the cells with P4, which originates from the differences of the active layer thicknesses in the optimized cells (Table 1). However, the P4:PC70BM cell produced the highest η, although this cell has a remarkably lower absorption up to 600 nm than the cells with P1. This further validates better exciton diffusion and charge transport in P4 compared to P1. The absorbance of the P1:PC70BM cell is higher from 400 nm to 500 nm than that of the P1:PC60BM cell, but the EPCE of P1:PC70BM is lower in the same wavelength range. This is consistent with the assumption that the exciton transfer is better due to the smoother morphology of the P1:PC60BM cell.
 | ||
| Fig. 12 Absorption and EPCE spectra of the P1:PC60BM/PC70BM and P4:PC60BM/PC70BM cells. | ||
The superiority of P3HT as a donor material compared to the copolymers tested here can be explained by structural differences, which influence both the exciton diffusion and hole transfer between adjacent polymer chains. The bulky side chains in P1–P4 decrease the π–π stacking between adjacent polymer chains and reduce the intermolecular interaction.5,48 The photogenerated excitons are transported in the polymer phase of the BHJ blend only one-dimensionally along the backbones of the polymers,49 and hopping between the chains is limited. Also, after exciton dissociation, holes are transferred only one-dimensionally along the polymer chains. Intermolecular exciton diffusion and hole transfer in the regioregular P3HT is possible due to H-aggregation in thin films.42,50 The polymer self-organizes into two-dimensional π-stacked lamellar structures, which allow two-dimensional charge transport.51
Stability measurements
The efficiencies of the solar cells were measured again ∼ six months after the cells were prepared to compare the stabilities of the cells of different donor–acceptor combinations with time. The photovoltaic parameters of the cells and the changes in the η and VOC values compared to those measured on the following day after the cells were prepared are presented in Table 5 (for I–V curves, see ESI†). The largest increase in the efficiency, 37.7%, was measured for the P4:PC70BM cell after the storage of 6 months. The largest decrease in the efficiency, 42.9%, was measured for the P2:PC60BM cell. The VOC values increased remarkably, 0.13 V, 0.13 V and 0.18 V, for the P1:PC60BM, P2:PC60BM and P4:PC70BM cells, respectively, during the storage.| Active layer | J sc (mA cm−2) | V OC (V) | FF (%) | η best (%) | η avg (%) | Δη (%) | ΔVOC (V) |
|---|---|---|---|---|---|---|---|
| P3HT:PC60BM | −2.46 | 0.55 | 59 | 2.16 | 2.06 | −29 | +0.03 |
| P1:PC60BM | −1.31 | 0.56 | 40 | 0.80 | 0.70 | −3.6 | +0.08 |
| P1:PC70BM | −0.69 | 0.47 | 40 | 0.35 | 0.28 | +30 | +0.13 |
| P2:PC60BM | −0.31 | 0.56 | 25 | 0.12 | 0.09 | −43 | +0.13 |
| P4:PC60BM | −0.63 | 0.43 | 45 | 0.33 | 0.30 | −42 | −0.02 |
| P4:PC70BM | −1.01 | 0.59 | 62 | 1.03 | 0.93 | +38 | +0.18 |
The serial resistances (Rs) and shunt resistances (Rsh) of the cells were calculated (see ESI, Table S2†) as explained in the literature.52 Based on the changes in η values, the morphology of the cells is expected to change during the storage. Therefore, the resistances were calculated from both the I–V curves measured the following day after the cell preparation and the I–V curves of the aged cells. Rs is closely related to the intrinsic resistance and thickness of the semiconductor layer and it should be as small as possible. Rsh can be correlated with the charge recombination and leakage current in the cell and it should be as large as possible.
Clearly the P4:PC70BM cell underwent the largest increase in Rsh, from 2759 Ω cm2 to 7062 Ω cm2, during the storage. This means that the amount of recombinations was decreased due to the improved morphology of the P4:PC70BM layer. Therefore a better fill factor was produced by the cell. In addition, the increase in the cell efficiency during the storage can be specifically assigned to the highly improved VOC (+0.18 V). The changes in the active layer morphology cause changes also in the HOMO and LUMO levels of the donor and acceptor. The changes in the energy levels are dependent on the position of the donor polymers in relation to the acceptor molecules at the donor–acceptor interface, as shown before (Fig. 8). The largest changes in the HOMO and LUMO energies were observed in the computational model consisting of the P4 monomer and PC70BM, which leads to a larger P4 monomer HOMO–PC70BM LUMO gap, i.e. higher VOC, when PC70BM is close to either the electron rich or the electron deficient moiety of the P4 monomer. This suggests that during the 6 month storage the molecules in the active layer move in relation to each other to form a more ideal BHJ structure, which changes the energy levels of the donor polymer and acceptor molecules and improves the cell voltage remarkably.
Materials and methods used for studying the polymer structures and photovoltaic performance
The Gaussian 09 program package53 was used to model isolated chains of the polymers presented in Fig. 1 or the corresponding oligomers. The B3LYP hybrid density functionals54–57 combined with the 6-31G* basis set were used in the calculations. A periodic boundary condition (translation vector, Tv, in the input) was applied in one dimension in the case of polymer models. A default option was used for the number of k-points, which resulted in 9, 6, 6, and 27 k-points due to the sizes of the P1, P2, P3, and P4 periodic models, respectively. As a test, optimization with only 11 k-points for the P4 model was done and the results were identical to the 27 k-point case. This means that the default k-point values are adequate for our models. The structures were optimized and frequency calculations were performed on the shortest oligomers (n = 1–2) to ensure that the optimized structures were at minima. Additionally, the first excitation in the UV-Vis spectra of the oligomeric chains (n ≤ 6–8) was calculated using TD-DFT. Chemcraft58 was used for visualization of the structures and molecular orbitals.The solvents and Alq3 (99.995%) were purchased from Sigma-Aldrich and used without further purification. The solar cell samples were prepared on ITO coated glass substrates (1.2 cm × 3.5 cm) purchased from Solems. Zinc–acetate (Zn(OCOCH3)2·2H2O) for ZnO layer preparation was purchased from Sigma-Aldrich. The reference polymer, P3HT, was purchased from Rieke Metals, and acceptors PC60BM (99.0%) and [6,6]-phenyl-C70-butyric acid methyl ester (99.0%, PC70BM) from Nano-C. The P1–P3 polymers were synthesized at the Kekulé-Institut für Organische Chemie und Biochemie der Rheinischen Friedrich-Wilhelms-Universität Bonn following the Suzuki-polycondensation procedure38 and P4 as described below.
The synthetic scheme of P4 is presented in Scheme 1. 4,7-Dibromo-2-(4-decyloxy-3,5-difluorophenyl)-2H-benzotriazole 1 (102 mg, 0.188 mmol), 2,6-bis(trimethyltin)-4,8-bis(2-ethylhexyloxy)benzo[1,2-b:3,4-b']dithiophene 2 (145 mg, 0.188 mmol) and Pd(PPh3)4 (12 mg, 10.4 μmol) were stirred for 68 h at 105 °C in a mixture of toluene (abs., 6 mL) and DMF (abs., 1.5 mL) under argon. The polymer was end capped by the addition of 2-(tributylstannyl)-thiophene (16 mg, 42.9 μmol) and additional stirring for 2 h. Then, 2-bromothiophene (100 mg, 0.613 mmol) was added and the mixture was stirred for another 4 h. After cooling to room temperature and filtration through celite, the polymer was precipitated by addition of the organic phase to MeOH. The polymer was extracted using a Soxhlet-apparatus with acetone for 3 h, n-hexane for 4 h and MTBE for 4 h. The polymer was redissolved in THF and precipitated from MeOH. The precipitate was collected by filtration and dried in vacuo at 70 °C to yield a blue solid (139 mg, 89%). 1H NMR (500 MHz, 373 K, 1,2-dichlorobenzene-d4, δ, ppm, see ESI†): 9.19–7.39 (m, 1H), 5.13–3.23 (m, 2H), 2.31–0.88 (m, 14H). 19F NMR (471 MHz, 373 K, 1,2-dichlorobenzene-d4, δ, ppm, see ESI†): −125 (br, 2F). GPC (THF, polystyrene): Mn = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 g mol−1, PDI = 4.6.
200 g mol−1, PDI = 4.6.
 | ||
| Scheme 1 Synthesis of P4. | ||
The steady state absorption and fluorescence were measured employing a UV-3600 Shimadzu UV-VIS-NIR spectrophotometer and a Jobin Yvon-SPEX fluorolog. The fluorescence lifetimes were determined in CHCl3 (99.0–99.4%) solution using a time correlated single photon counting (TCSPC) system equipped with a Picoharp 300 controller and a PDL 800-B driver for excitation and a microchannel plate photomultiplier (Hamamatsu R3809U-50) for detection in a 90° configuration. The excitation wavelength was 405 nm and the pulse frequency was 2.5 MHz. The experimental set-up of the measuring instrumentation was similar for all polymers.
External photon-to-current efficiency (EPCE) measurements of the solar cells were monitored using a voltage/current measuring instrument (E5272A, Agilent Technologies). The excitation light source was a Xe-arc lamp coupled with a monochromator for selecting the excitation wavelength. The excitation power density alternated between 0.12 mW cm−2 and 0.68 mW cm−2 depending on the wavelength of 400 to 800 nm where the background current from ITO is negligible.59 Stepwise (light-on/off) currents produced by the excitations as a function of time were measured with 0 V. The EPCE spectra were calculated by averaging the measured currents.
To determine the active layer thickness of each polymer:PCBM blend, a narrow strip of the film was removed with a cotton stick dipped in CHCl3 and the step was measured with a Veeco Wyko NT-1100 profilometer. The profilometry data were recorded from 230 × 300 μm2 and analyzed in phase shift interferometry (PSI) mode. The vertical resolution of this method is close to 1 Å according to the instrument manual and the horizontal resolution of the objective (20× magnification) is 0.75 μm.
Solar cells were constructed on commercial ITO covered glass substrates. The ITO layer was taped and lacquered for aqua regia etching to achieve a patterned ITO. The etched plates were cleaned by sonicating in acetone, chloroform, SDS solution (20 mg sodium dodecyl sulphate in 500 mL Milli-Q H2O), Milli-Q H2O and 2-propanol 30 min in each, in this order, and dried in a vacuum at 150 °C for one hour. After a 10 min N2 plasma cleaning procedure (Harrick Plasma Cleaner PDG-236), a 20 nm ZnO layer was deposited by 1 min spin-coating in a WS-400B-6NPP/LITE spin-coater from Laurell Technologies from 50 g L−1 zinc-acetate in 96% 2-methoxyethanol and 4% ethanolamine solution following the literature process.37
The photoactive layer compounds P1, P2, P3, P4 or P3HT and PC60BM or PC70BM were dissolved in 1,2-dichlorobenzene and stirred (250 rpm) overnight at 50 °C. The temperature was raised to 70 °C for 30 min prior to spin-coating of the BHJ photoactive layer from the polymer:PCBM blend for 5 minutes (600 rpm) in the spin-coater under N2 flow. The spin-coated films were annealed in a vacuum at 110 °C for 10 min. The buffer layer and the Au anode were evaporated in the vacuum evaporator under ∼3 × 10−6 mbar pressure. The evaporation rate and film thickness were controlled by evaporator crystals to deposit ∼5 nm thick buffer and ∼50 nm thick Au anode layers on top of the photoactive layer. The cells were stored in an ambient atmosphere in the dark before measurements and analysis.
The photovoltaic parameters were obtained and calculated from current–voltage (I–V) curves, which were measured in the dark and under simulated AM 1.5 sunlight illumination (50 mW cm−2) using an Agilent E5272A source/monitoring unit. A voltage of −0.20 V to 0.60 V was applied in 10 mV steps. The measurements were carried out in an ambient atmosphere at room temperature without encapsulation of the devices. The illumination was produced by a filtered Xe-lamp (Oriel Corporation & Lasertek) in the Zuzchem LZC-SSL solar simulator. The illumination power density was measured by using a Coherent Fieldmax II LM10 power meter. Because a certified measuring system could not be employed, the absolute efficiency values are not directly comparable with the other published results. However, the reported efficiencies and the relative efficiency changes are comparable within the presented devices.
The photoactive layer morphologies of the different donor-acceptor combinations in the solar cell samples were inspected with AFM at the Department of Molecular Engineering in Kyoto University. The measurements were carried out with an Asylum Technology MFP-3D-SA instrument in the AC mode.
Conclusions
We studied the internal relationship between the molecular structures of four donor–acceptor (D–A) copolymers (P1–P4) and their photovoltaic performances. Molecular geometries and the properties related to the electron structures of P1–P4 were studied by DFT using B3LYP. The copolymers were used as donor materials in inverted organic ITO|ZnO|donor:acceptor|Alq3|Au solar cells. The DFT information on electron structure related properties was combined with the results of photovoltaic, electrochemical, spectroscopic, and thermoanalytical measurements.The cell with P4 as a donor material performed better and was more stable than the cells with P1–P3. The optimizations of the CRUs resulted in a more planar structure for P4 than for P1–P3. Also, the computed frontier molecular orbitals show that the LUMOs of P2 and P3 are not continuous as the electron densities are concentrated on the benzotriazole moieties of the copolymers. Therefore, the better exciton transfer properties of P4 are due to a more planar molecular structure with a continuous LUMO electron density. Moreover, P4 has better charge transfer properties as HTM, which is consistent with the bigger NMCC values computed for P4 and P1 than for P2 and P3.
Further calculations show that interaction between the donor and acceptor molecules affects their electronic structures, which changes the energy levels of both molecules. During the six month storage the molecules in the active layer move with respect to each other, which changes the energy levels. The biggest calculated energy level changes of the donor HOMO and the acceptor LUMO of the P4:PC70BM cell correlate with the increased VOC of the cell. AFM studies on the active layers of the solar cells yielded insight into the morphology which allowed us to better analyze the differences between the solar cell performances of different donor:acceptor combinations.
These studies show that computational methods are a valuable tool for defining the molecular structure related properties of D–A copolymers and for predicting their performances as donor materials. The DFT calculations provided data, which supplement the experimental results. Therefore, even more research and clarification of the available computational methods are important for chemists in the evolving field of organic materials and photovoltaics.
Acknowledgements
Computing resources provided by the CSC – IT Center for Science Ltd, administrated by the Finnish Ministry of Education, and the National Doctoral Programme in Nanoscience (NGS-NANO) are gratefully acknowledged.References
- J. Hou, M.-H. Park, S. Zhang, Y. Yao, L.-M. Chen, J.-H. Li and Y. Yang, Macromolecules, 2008, 41, 6012–6018 CrossRef CAS.
- J. Hou, H.-Y. Chen, S. Zhang, R. I. Chen, Y. Yang, Y. Wu and G. Li, J. Am. Chem. Soc., 2009, 131, 15586–15587 CrossRef CAS.
- Y. Zhang, S. K. Hau, H.-L. Yip, Y. Sun, O. Acton and A. K.-Y. Jen, Chem. Mater., 2010, 22(9), 2696–2698 CrossRef CAS.
- S. C. Price, A. C. Stuart and W. You, Macromolecules, 2010, 43, 4609–4612 CrossRef CAS.
- Q. Shi, H. Fan, Y. Liu, J. Chen, L. Ma, W. Hu, Z. Shuai, Y. Li and X. Zhan, Macromolecules, 2011, 44, 4230–4240 CrossRef CAS.
- L. Dou, J. Gao, E. Richards, J. You, C.-C. Chen, K. C. Cha, Y. He, G. Li and Y. Yang, J. Am. Chem. Soc., 2012, 134, 10071–10079 CrossRef CAS.
- B. Aïch, J. Lu, S. Beaupré, M. Leclerc and Y. Tao, Org. Electron., 2012, 13, 1736–1741 CrossRef.
- H. Wettack, F. Pasker and S. Höger, Macromolecules, 2008, 41, 9513–9515 CrossRef.
- L. Zhang, C. He, J. Chen, P. Yuan, L. Huang, C. Zhang, W. Cai, Z. Liu and Y. Cao, Macromolecules, 2010, 43, 9771–9778 CrossRef CAS.
- B. Peng, A. Najari, B. Liu, P. Berrouard, D. Gendron, Y. He, K. Zhou, M. Leclerc and Y. Zou, Macromol. Chem. Phys., 2010, 211, 2026–2033 CrossRef CAS.
- J. Min, Z.-G. Zhang, S. Zhang, M. Zhang, J. Zhang and Y. Li, Macromolecules, 2011, 44, 7632–7638 CrossRef CAS.
- S. C. Price, A. C. Stuart, L. Yang, H. Zhou and W. You, J. Am. Chem. Soc., 2011, 133, 4625–4631 CrossRef CAS.
- Z. Zhang, B. Peng, B. Liu, C. Pan, Y. Li, Y. He, K. Zhou and Y. Zou, Polym. Chem., 2010, 1, 1441–1447 RSC.
- J. Roncali, Macromol. Rapid Commun., 2007, 28, 1761–1775 CrossRef CAS.
- G. R. Hutchison, Y.-J. Zhao, B. Delley, A. J. Freeman, M. A. Ratner and T. J. Marks, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 035204 CrossRef.
- S. Xiao, A. C. Stuart, S. Liu, H. Zhou and W. You, Adv. Funct. Mater., 2010, 20, 635–643 CrossRef CAS.
- Z. El Malki, S. M. Bouzzine, L. Bejjit, M. Haddad, M. Hamidi and M. Bouachrine, J. Appl. Polym. Sci., 2011, 122, 3351–3360 CrossRef CAS.
- S. Habuchi, H. Fujita, T. Michinobu and M. Vacha, J. Phys. Chem. B, 2011, 115, 14404–14415 CrossRef CAS.
- Y. Wang, Q. Peng, Q. Hou, K. Zhao, Y. Liang and B. Li, Theor. Chem. Acc., 2011, 129, 257–270 CrossRef CAS.
- V. Lukeš, P. Rapta, K. R. Idzik, R. Beckert and L. Dunsch, J. Phys. Chem. B, 2011, 115, 3344–3353 CrossRef.
- Q. Li, C. Zhong, J. Huang, Z. Huang, Z. Pei, J. Liu, J. Qin and Z. Li, J. Phys. Chem. B, 2011, 115, 8679–8685 CrossRef CAS.
- C. Risko, M. D. McGehee and J.-L. Brédas, Chem. Sci., 2011, 2, 1200–1218 RSC.
- P. M. Beaujuge, S. V. Vasilyeva, D. Y. Liu, S. Ellinger, T. D. McCarley and J. R. Reynolds, Chem. Mater., 2012, 24, 255–268 CrossRef CAS.
- H. Toufik, S. M. Bouzzine, F. Lamchouri, M. Nawdali, M. Hamidi and M. Bouachrine, J. Mater. Environ. Sci., 2012, 3, 286–293 CAS.
- G. L. Gibson, T. M. McCormick and D. S. Seferos, J. Am. Chem. Soc., 2012, 134, 539–547 CrossRef CAS.
- Z. Lin, J. Bjorgaard, A. G. Yavuz, A. Iyer and M. E. Köse, RSC Adv., 2012, 2, 642–651 RSC.
- A. Abbotto, M. Seri, M. S. Dangate, F. De Angelis, N. Manfredi, E. Mosconi, M. Bolognesi, R. Ruffo, M. M. Salamone and M. Muccini, J. Polym. Sci., Part A: Polym. Chem., 2012, 50, 2829–2840 CrossRef CAS.
- L. Ling and J. B. Lagowski, J. Mol. Struct.: THEOCHEM, 2010, 944, 146–155 CrossRef CAS.
- B. G. Janesko, J. Chem. Phys., 2011, 134, 184105 CrossRef.
- J. M. Granadino-Roldán, A. Garzón, G. García, M. Moral, A. Navarro, M. P. Fernández-Liencres, T. Peña-Ruiz and M. Fernández-Gómez, J. Phys. Chem. C, 2011, 115, 2865–2873 Search PubMed.
- Y. Li and I. Dabo, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 155127 CrossRef.
- A. Ferretti, G. Mallia, L. Martin-Samos, G. Bussi, A. Ruini, B. Montanari and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235105 CrossRef.
- L. Deng, W. Shen, X. Xie, L. Jiang, B. Liu and M. Li, Struct. Chem., 2012, 23, 97–106 CrossRef CAS.
- S. S. Zade and M. Bendikov, Org. Lett., 2006, 8, 5243–5246 CrossRef CAS.
- J. Gierschner, J. Cornil and H.-J. Egelhaaf, Adv. Mater., 2007, 19, 173–191 CrossRef CAS.
- S. S. Zade, N. Zamoshchik and M. Bendikov, Acc. Chem. Res., 2011, 44, 14–24 CrossRef CAS.
- M. S. White, D. C. Olson, S. E. Shaheen, N. Kopidakis and D. S. Ginley, Appl. Phys. Lett., 2006, 89, 143517 CrossRef.
- F. M. Pasker, M. F. G. Klein, M. Sanyal, E. Barrena, U. Lemmer, A. Colsmann and S. Höger, J. Polym. Sci., Part A: Polym. Chem., 2011, 49, 5001–5011 CrossRef CAS.
- (a) HOMO and LUMO levels of P1, P2 and P3, see: ref. 38; (b) HOMO and LUMO levels of P3HT and PC60BM, see: A. K. K. Kyaw, X. W. Sun, C. Y. Jiang, G. Q. Lo and D. W. Zhao, Appl. Phys. Lett., 2008, 93, 221107 CrossRef; (c) HOMO and LUMO levels of PC70BM, see: E. L. Ratcliff, J. Meyer, K. X. Steirer, N. R. Armstrong, D. Olson and A. Kahn, Org. Electron., 2012, 13, 744–749 CrossRef CAS; (d) Conduction band of ZnO, see: ref. 37; (e) HOMO and LUMO levels of Alq3, see: A. Tolkki, K. Kaunisto, J. P. Heiskanen, W. A. E. Omar, K. Huttunen, S. Lehtimäki, O. E. O. Hormi and H. Lemmetyinen, Thin Solid Films, 2012, 520, 4475–4481 CrossRef CAS.
- M. T. Dang, L. Hirsch and G. Wantz, Adv. Mater., 2011, 23, 3597–3602 CrossRef CAS.
- F. Zhang, Z. Zhuo, J. Zhang, X. Wang, X. Xu, Z. Wang, Y. Xin, J. Wang, J. Wang, W. Tang, Z. Xu and Y. Wang, Sol. Energy Mater. Sol. Cells, 2012, 97, 71–77 CrossRef CAS.
- G. Hukic-Markosian, T. Basel, S. Singh, Z. Valy Vardeny, S. Li and D. Laird, Appl. Phys. Lett., 2012, 100, 213903 CrossRef.
- V. Manninen, W. Omar, J. Heiskanen, H. Lemmetyinen and O. Hormi, J. Mater. Chem., 2012, 22(43), 22971–22982 RSC.
- S. Dey, P. Vivo, A. Efimov and H. Lemmetyinen, J. Mater. Chem., 2011, 21, 15587–15592 RSC.
- I. G. Hill, A. Kahn, Z. G. Soos and R. A. Pascal, Jr, Chem. Phys. Lett., 2000, 327, 181–188 CrossRef CAS.
- M. Knupfer, Appl. Phys. A: Mater. Sci. Process., 2003, 77, 623–626 CrossRef CAS.
- P. Boland, S. S. Sunkavalli, S. Chennuri, K. Foe, T. Abdel-Fattah and G. Namkoong, Thin Solid Films, 2010, 518, 1728–1731 CrossRef CAS.
- Y. Huang, X. Guo, F. Liu, L. Huo, Y. Chen, T. Russel, C. Han, Y. Li and J. Hou, Adv. Mater., 2012, 24, 3383–3389 CrossRef CAS.
- L. Yang, H. Zhou and W. You, J. Phys. Chem. C, 2010, 114, 16793–16800 CAS.
- Y. Yamagata and F. C. Spano, J. Chem. Phys., 2012, 136, 184901 CrossRef.
- J. Clark, C. Silva, R. Friend and F. Spano, Phys. Rev. Lett., 2007, 98, 206406 CrossRef.
- M.-S. Kim, B.-G. Kim and J. Kim, ACS Appl. Mater. Interfaces, 2009, 1(6), 1264–1269 CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1998, 98, 5648–5652 CrossRef.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- G. A. Zhurko, Chemcraft Version 1.60, http://www.chemcraftprog.com.
- S. Yang, L. Fan and S. Yang, J. Phys. Chem. B, 2004, 108, 4394–4404 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: 1H and 19F NMR spectra, CV, TCSPC, DSC, Rs, Rsh, NMCC and HOMO–LUMO gaps. See DOI: 10.1039/c3ta10686a |
| This journal is © The Royal Society of Chemistry 2013 |
