Directed self-assembly

Eric M. Furst

---

1. Introduction

Self-assembly is one of the most unique attributes of soft matter. The “flexibility” of soft materials, a defining characteristic singled out by Pierre-Gilles de Gennes in his 1991 Nobel lecture,¹ reflects the constant rearrangement of soft matter's constituent molecules, macromolecules, proteins, and colloids under the influence of their thermal energy. The ability of these entities to explore many configurations leads to spontaneous self-organization into arrangements that are favored by their sheer statistical probability, the interactions between constituents, or both of these “entropic” and “enthalpic” driving forces. In short, many soft materials naturally equilibrate into structures that minimize the free energy of the system. The seemingly preternatural process of self-assembly is akin to constantly shaking a box of tiny building blocks, like Lego bricks, and having them arrange themselves.

Examples of self-assembly abound in nature and industry. It is a key organizing principle in biology, giving rise to intrinsic functional compartments of lipid bilayer membranes, for instance. Similarly complex functions are achieved by the self-assembly of amphiphilic surfactant molecules; the solubilizing power of soaps and detergents derives from the spontaneous formation of micelles.² The flow properties of modern body-washes, shampoos, and a multitude of other consumer products are determined by the formation of more complex surfactant assemblies, such as entangled solutions of worm-like micelles.^3–5 Diblock copolymers form analogous associative colloids and vesicles.^6,7 By entropic interactions alone, hard spheres, rod-shaped colloids, and other particle geometries form crystals with symmetries that depend on their shape.^8–10 Gem opals are naturally forming colloidal crystals¹¹ and a lovely aesthetic reminder of how self-assembled structures alter the transport of light and, potentially, other forms of energy.

Given its fundamental importance and technological utility, scientists and engineers have studied study self-assembly in soft materials for many years. The principles of classical and statistical thermodynamics provides a framework to understand self-organization, and a means to calculate the equilibrium structures that arise given the concentration and interactions between molecules or particles.¹² The recent surge in the synthesis of potential molecular and particulate building blocks is one of the reasons self-assembly has become an attractive means for fabricating functional nanomaterials. Over the past decade, the synthesis of uniform colloids and nanoparticles with unique shapes and chemical functions has grown tremendously, providing an impressive library from which to build new functional soft materials.^13–18

Today's focus on self-assembly couldn't come at more opportune time. Advances in technology that address the global need for new nanomaterials and devices in areas as diverse as medicine, energy production, energy storage, separations, and catalysis will benefit tremendously from manufacturing processes that harness the simple elegance, cost-effectiveness, and scalability of self-assembly. Inexpensive, functional nanomaterials and devices fabricated from the “bottom-up,” wherein an amalgam of building blocks in a dispersed, homogeneous phase is cast, printed, or deposited, then spontaneously arranges into coherent nanoscale structures will lead to a host of new ways to manipulate the transport of matter and energy. The use of self-assembly in consumer products is prescient. After all, these structured materials perform sophisticated functions—flowing on demand, carrying away unwanted substances, and depositing others that are desirable—at very low cost.

What does it mean to direct self-assembly? The act of directing implies a form of control over the self-assembly process, while retaining the principal elements (and benefits) of spontaneous self-organization. The use of this term, like “self-assembly” itself, is often imprecise.¹⁹ Some imagine the possibility that nanostructures could be “directed” to self-assemble at specific sites in the body to deliver medicines or repair tissues.²⁰ It is often used to mean designing (programming) self-assembly by altering the chemistry, patchiness, or geometric shape of building blocks^21,22 or templating a self-assembly process through the system boundary, such as a patterned substrate.^23,24 In other cases, the term “directed” describes self-assembly in the presence of an externally applied field that introduces or modifies the interactions between constituents, leading to structures and phases that would not otherwise form in its absence. Electric and magnetic fields^25–32 are frequently used, but recent work has studied assembly in structured solvents³³ and at curved fluid interfaces.³⁴ Finally, it can refer to a process that uses an external means, typically flows or fields, to “nudge” the system into a desired (and presumably equilibrium) state.

In the next section, I discuss the kinetics and thermodynamics of self-assembly in colloidal suspensions, which illustrate why some form of direction or control is often necessary.

2. One view of directed self-assembly

Equilibrium thermodynamics identifies self-assembled structures of interest, providing a road-map for self-assembly processes. A wide number of particle and macromolecular building blocks have known phase diagrams, including ellipsoids,^35–38 Janus and patchy particles,^39–49 dimers,^50–53 polyhedra,⁵⁴ and dipolar particles,^55,56 and various particle shapes in magnetic and electric fields.^57,58 Whether or not these equilibrium phases are accessible is another matter, especially on timescales relevant to processing or manufacturing. Despite thermodynamic driving forces, the kinetics of self-assembly will influence, and even trap or limit, the formation of the desired structures and phases.

2.1. Kinetic barriers to self-assembly

A benign kinetic limitation to self-assembly may manifest as polycrystallinity or domain sizes in colloidal crystals or block copolymer phases as a result of nucleation kinetics.⁵⁹ In extreme cases, kinetic bottlenecks trap the system far from the desired equilibrium phase. Those who develop simulations to calculate phase equilibria know this phenomenon well and have developed methods to circumvent local minima when searching for the global free energy minimum that identifies the equilibrium phase.⁶⁰

In colloidal and nanoparticle assembly, attempts to reach close-packed structures of the equilibrium phase diagram are hindered by glassy arrest. Even hard spheres, for which face-centered cubic (FCC) crystals are the sole equilibrium phase above a volume fraction ϕ = 0.545, spontaneously form crystals only within a narrow range of concentrations; disordered glasses are observed at ϕ = 0.58 and above, although glassy suspensions do often form crystals eventually.^61–63 With increasing attractive interactions, the hard sphere “repulsive glass” first fluidizes, then arrests again as an “attractive glass,”⁶⁴ which roughly connects to a gel line at lower volume fractions.⁶⁵

Anisotropic particles may present a greater challenge for self-assembly, as recent work to form close-packed structures from symmetric dicolloids illustrates. Dimer colloids, or dicolloids, like those shown in Fig. 1, readily crystallize when confined in thin films,^66,67 but attempts to crystallize these particles in the bulk leads to disordered, random packings. The equilibrium phase diagram, calculated by Monte Carlo simulation,^50–53 is shown in Fig. 2 as the phase volume fraction versus the dicolloid aspect ratio. Even this simple change in shape relative to spheres leads to new structures, such as plastic crystals, a different close-packed structure (centered monoclinic), and aperiodic phases. The expected non-ergodicity transitions, overlaid on this phase diagram, also depend on the particle aspect ratio.

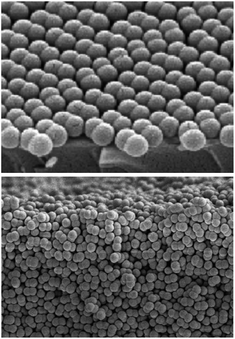Fig. 1 Dicolloid particles of polystyrene latex with lobe diameter 267 ± 5 nm and aspect ratio α = 1.58. When concentrated in the bulk, these particles form random packings. Adapted with permission from D. Forster et al.⁷¹ Copyright 2011 American Chemical Society.

Fig. 2 The thermodynamic phases of dicolloid particles (symbols) and non-ergodicity transitions (solid lines). The equilibrium phases are fluid (F), plastic crystal (PC), and close-packed crystal (CP1). An aperiodic structure exists in a narrow region close to α = 2. Three non-ergodicity transitions are identified for symmetric dicolloids: plastic glass (orange line), center-of-mass (red), and double glass (blue). The lines are shifted in volume fraction such that the non-ergodicity transition coincides with the experimental colloidal glass transition ϕ = 0.58 for α = 1.

At first, it may seem that the crystallization of high aspect ratio particles is less susceptible to kinetic arrest. The glass volume fraction is a nonmonotonic function of aspect ratio, and a “maximally fluidic” state is achieved at α ∼ 1.4. However, the solid-fluid phase coexistence and single phase solid also lie at higher volume fractions relative to spheres. Moreover, unlike spheres, as they concentrate, the cage escape trajectories for dicolloid and other anisotropic particles involve a combination of rotation and center-of-mass translation,^68,69 making crystal nucleation, which requires the mutual alignment of particles, more difficult.

2.2. Circumventing bottlenecks to self-assembly

Together, the calculated equilibrium phases and kinetic barriers of dicolloids provide the necessary maps for designing a self-assembly process.⁷⁰ In this context, directing self-assembly consists of identifying a strategy to circumvent kinetic arrest and achieve the equilibrium phase.

For dicolloids, one such path is to first bias the particle orientation of a dilute suspension, then concentrate it.⁷¹ This route retains the essential features and benefits of self-assembly: self-organization with minimal interference. The method is illustrated in Fig. 3. Dicolloid particles are aligned by an AC electric field into a dilute, nematic-like fluid. Concentrating them in this state by convection to a drying front results in close-packed crystals. Field gradients in dielectrophoretic assembly^26,27,72,73 can also been used to concentrate particles in aligned states.³¹

Fig. 3 Dicolloid assembly by a directing electric field based on Forster et al.⁷¹ The equilibrium phases of dumbbells with aspect ratio α = 1.58 in this study include an isotropic fluid (F) and close-packed (CP) structure. Aligning fields with strength ε induce a transition from isotropic (I) to nematic (N). Suspensions arrest into a gel-like phase at sufficiently high field strengths.

Much remains to be understood for this form of directed self-assembly. Electric fields quickly align anisotropic particles, but also induce interactions due to polarization.^30,74 These interactions are evident by the particle chaining in Fig. 3. At sufficiently high electric field strengths, the induced interactions lead to a gel-like phase of percolated particle chains. Macroscopically, the suspension forms a solid. This rheological transition is the basis of electrorheological fluids and related magnetorheological fluids.^75–77 Similar to glassy states, strong localization of particles within the microstructure arrests further progress towards the equilibrium phase. The same forces that lead to successful self-assembly can leave them arrested in a glass or gel far from the desired equilibrium state. Thus, many intriguing and important questions remain for field-directed assembly: How do the boundaries of the non-equilibrium states change during the process? Does an optimum directing path to self-assembly exist? How does the process depend on particle shape or interactions? The method is also open to more sophisticated forms of control of the external fields that incorporate in situ measurements of the structure.⁷⁸

Directed assembly as illustrated above can be characterized by an attempt to avoid the non-equilibrium gel and glassy states, or at least minimize their influence. In contrast, other routes to self-assembly start from these arrested states, and the equilibrium phase is reached by measured, periodic forcing. For example, colloidal glasses of spherical particles anneal into close-packed crystals when subjected to an oscillatory shear.^79,80 Shear annealing is represented in Fig. 4. Provided that the colloidal glass is subjected to oscillatory shear with a sufficiently high amplitude, the suspension will eventually form the face-centered cubic phase.

Fig. 4 A representation of directed assembly enabled through the measured, periodic forcing of the system. The schematic shows the hypothetical path followed by a process in which colloidal glasses are annealed through oscillatory shear.

Analogous to shear annealing a colloidal glass, we recently demonstrated a route to phase separation in magnetically responsive colloidal suspensions starting from the strongly interacting, gel-like state by toggling or modulating the field periodically (Fig. 5).⁸¹ One of the advantages of toggled fields may be its insensitivity to the suspension temperature. Rather than fine tuning the strength of the interactions among particles, this simple annealing scheme can be used to create a broad envelope for assembly of ordered particle structures.

Fig. 5 (A) Colloidal phase separation starting from a gel-like state using a toggled field. A suspension of 0.65% superparamagnetic colloidal particles by volume subject to a 1500 A m⁻¹ field toggled at 0.66 Hz. Dark areas in the images indicate colloid-rich regions. The view is perpendicular to the applied field. (B) A schematic representation of a different path to self-assembly using a directing field from Swan et al.⁸¹ A gel-like state is first formed at high field strength, then annealed by toggling the field. Used with permission, copyright 2012 National Academy of Sciences of the United States of America.

3. Overview of the themed issue

The above discussion illustrates one view of what it means to direct self-assembly: to guide a system beyond its kinetic bottlenecks towards the equilibrium state. However, the field continues to evolve rapidly. The present themed issue touches on many of the directions, challenges, and opportunities of directed self-assembly.

First, we are fortunate to have several excellent reviews as part of the themed issue, each of which provides an overview of the deep history and recent advances in macromolecular and colloidal self-assembly. Du Yeol Ryu and Thomas P. Russell (DOI: 10.1039/c3sm51083b) provide an extensive overview of block copolymer assembly and the myriad ways that are emerging to direct the overall organization of their rich structures. Second, Brugarolas, Tu and Lee (DOI: 10.1039/c3sm50888a) have generously contributed a comprehensive review on colloidal assembly at fluid interfaces. A nice example of peptide assembly mediated by fluid interfaces is the contribution by Ferreira, Reis and Azevedo (DOI: 10.1039/c3sm51189h). Kruglova et al. (DOI: 10.1039/c3sm50845e) review the methods for directing colloidal assembly, particularly for photonic applications. Readers will appreciate the wide range of methods they summarize, from interface templating to the use of directing fields.

A number of studies presented in the themed issue focus on self-assembly of colloids in external electric and magnetic fields. Byrom and Biswal (DOI: 10.1039/c3sm50306b) use a unique combination of diamagnetic and paramagnetic particles to form open, kinetically trapped two-dimensional lattices with unique rectilinear shapes. Ruditskiy, Ren and Kretzschmar (DOI: 10.1039/c3sm50839k) study the structures formed by metallo-dielectric Janus particles in orthogonal electric and magnetic fields. The iron oxide patches induce magnetic dipoles that bias the quadrupolar interactions from the combined electric field response of the metal and polymer latex. The ferromagnetism of the iron oxide “locks in” the otherwise transient structure. Uniaxial and multiaxial fields are also used by Solis and Martin (DOI: 10.1039/c3sm50820j) to control the structure of a platelet suspension and its thermal conductivity. Nöjd and colleagues (DOI: 10.1039/c3sm51226f) study the equilibrium phase diagram of soft microgel particles in electric fields, including the transitions from the isotropic fluid to a string phase to a body centered tetragonal (BCT) crystal phase at low particle concentrations and a reversible solid–solid crystal transition at higher concentrations. Finally, Zaidouny et al. (DOI: 10.1039/c3sm50945a) use an altogether different field to direct the assembly of colloids into triangular, rhombic and square phases: light.

Several contributions focus on the design of particle building blocks for self-assembly, and in particular, demonstrate how particles can be engineered to couple to external fields. Monodisperse, super-paramagnetic, prisms of arbitrary cross-section and large magnetic susceptibility are the subject of the contribution by Tavacoli and co-workers (DOI: 10.1039/c3sm51589c). Using a print-like process, superparamagnetic nanoparticles are formed into larger particles with shapes that range from stars to discs. In a similar vein, Shields et al. (DOI: 10.1039/c3sm51119g) fabricate metallo-dielectric colloids with defined geometry and patchiness and study their assembly in electric and magnetic fields. In an analogous way, liquid crystal solvents can also act as directing fields for particle assembly. Cavallaro and colleagues (DOI: 10.1039/c3sm51167g) use the topological defects induced by a washer-shaped particle and its anchoring to a liquid crystal medium to direct the assembly of ring-sphere composite assemblies.

McGinley and colleagues (DOI: 10.1039/c3sm50950h) envision hierarchical structures built from particles. Their approach leads to the formation of colloidal clusters that are formed from host colloidal crystals containing a second particle species. Following the initial assembly, all particle bonds are selectively dissociated except those associated with the impurity species. The necessary selective bonding is enabled through transient bridges of DNA. A second example of the rich possibilities of DNA-mediated colloidal and nanoparticle interactions comes from Rudiuk and co-workers (DOI: 10.1039/c3sm50710f) who assemble silver nanoparticles into well-defined “star” aggregates. Crassous et al. take a different approach to hierarchical nanoparticle assembly using mixtures of oppositely charged gold nanoparticles and spherical polyelectryle brush polymers. These investigators create individual three-dimensional structures, such as single-walled nanotubes, based simply on the mixing ratio between particles and polymer.

As Schneider and co-workers show (DOI: 10.1039/c3sm50959a) the expanding library of particle shapes provides new opportunities to tailor transport processes in materials. In this case, anisotropic spheroids exhibit new modes of phonon resonance that could be used to control sound propagation in particle assemblies. Plasmonic nanoparticle assemblies are studied by Grzelczak, Sánchez-Iglesias and Liz-Marzán (DOI: 10.1039/c3sm51015h). Potentially useful as building blocks for materials with novel properties in catalysis, light emission, and charge transport,^82,83 these investigators report the formation of spherical binary clusters consisting of nanoparticle building blocks with different sizes.

The contribution of Avendaño, Liddell Watson and Escobedo (DOI: 10.1039/c3sm50833a) is an excellent example of the role thermodynamic calculations have for systematically identifying potential structures of interest in self-assembly over a large parameter space. These authors report the phase diagrams for confined hemispherical caps under different degrees of confinement. Even this subtle change in shape from spheres leads to important differences in the phase diagram of confined suspensions. The predictive capabilities of thermodynamic calculations are also used by Edwards, Beltran-Villegas and Bevan (DOI: 10.1039/c3sm50809a) to identify the electric field strength necessary to assemble small systems of particles in a “dielectrophoretic bottle.” This investigation then analyzes the phase space trajectories along local and global order parameters to develop a unique insight into the kinetic bottlenecks to colloidal self-assembly. A third contribution, by Schoen and co-workers (DOI: 10.1039/c3sm50830g) touches similar themes but draws from the broad field of protein and peptide self-assembly. The authors use clathrin proteins as a model to study the thermodynamic and kinetic pathways of self-assembly. One of the highlights of this contribution is its insight into the roles that both specific and non-specific interactions play in guiding the kinetics of the self-assembly process.

Finally, Truzzolillo and colleagues (DOI: 10.1039/c3sm50731a) map out the non-equilibrium states of soft nanoparticles with attractive interactions. Their work is representative of studies that are needed to understand kinetic bottlenecks for directed self-assembly for this especially large class of soft colloids.

4. Looking forward

As seen from the contributions to this themed issue, “directed self-assembly” encompasses a wide and vibrant range of work, with broad themes that include identifying the “road maps” to self assembly through their equilibrium and non-equilibrium states, the design and function of novel building blocks, and the use of applied fields for inducing or directing self-assembly.

In this article, I only briefly touched on a few of the many questions and opportunities that lie ahead. As the library of protein, peptide, particle, and macromolecular building blocks continues to grow, identifying potential self-assembled structures of interest is paramount. As with past work, in silico assembly is essential for identifying these structures and guiding experiments. Furthermore, many studies have focused on the self-assembly of “single component” systems. Given the large parameter space of multi-component mixtures of building blocks, a computational toolbox is needed to identify potential structures of interest, and possibly the kinetics of self-assembly.

In the narrower context in which “directing self-assembly” means circumventing kinetic bottlenecks, there is plenty to be understood about the boundaries of the non-equilibrium states throughout a directing process. Except for the starting state, the gel and glass limits represented in Fig. 4 and 5 are almost entirely hypothetical. For instance, one could wonder under what circumstances during the oscillatory shear processing of a strong gel at low volume fraction the equilibrium fluid-crystal coexistence could be achieved? This points to the growing need to study the properties of driven non-equilibrium states, both experimentally and theoretically.^84–87

Finally, there is a grand challenge for self-assembly: de novo design. Given a desired micro or nano-structure, can the building blocks and directing process be identified to achieve it? Recent theory points to the potential for designing interaction potentials to achieve complex structures,^88–92 but the “inverse problem” for directed self-assembly will doubtlessly require a concerted effort of theory, simulation, and experiment.

Acknowledgements

E. M. F. thanks J. Swan, J. Vermant, P. Spicer and D. Vlassopoulos for stimulating discussions and acknowledges the financial support of NASA (grant nos NNX07AD02G, NNX10AE44G and NNX10AE44G) for microgravity studies of field-directed colloidal self-assembly, NSF for work involving the directed self-assembly of dicolloids (CBET-0930549) and the microrheology of colloidal glasses and gels (CBET-1235955), and the Department of Energy, Basic Energy Sciences (DE-FG02-09ER46626) to study directed self-assembly of nanoparticles in electric fields.

References

1. P.-G. de Gennes, Angew. Chem., Int. Ed. Engl., 1992, 31, 842–845.
2. K. J. Mysels, S. Frankel and K. Shindoa, Soap Films, Pergamon Press, New York, 1959.
3. M. E. Cates and S. J. Candau, J. Phys.: Condens. Matter, 1990, 2, 6869–6892.
4. M. E. Helgeson, T. K. Hodgdon, E. W. Kaler, N. J. Wagner, M. Vethamuthu and K. P. Ananthapadmanabhan, Langmuir, 2010, 26, 8049–8060.
5. N. Dan and S. A. Safran, Adv. Colloid Interface Sci., 2006, 123–126, 323–331.
6. L. Zhang and A. Eisenberg, Science, 1995, 268, 1728–1731.
7. B. M. Discher, Y. Y. Won, D. S. Ege, J. C. Lee, F. S. Bates, D. E. Discher and D. A. Hammer, Science, 1999, 284, 1143–1146.
8. P. N. Pusey and W. van Megen, Nature, 1986, 320, 340–342.
9. M. Adams, Z. Dogic, S. L. Keller and S. Fraden, Nature, 1998, 393, 349–352.
10. L. Rossi, S. Sacanna, W. T. M. Irvine, P. M. Chaikin, D. J. Pine and A. P. Philipse, Soft Matter, 2011, 7, 4139.
11. J. V. Sanders, Nature, 1964, 204, 1151–1153.
12. J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, New York, 3rd edn, 2011.
13. S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557–562.
14. M. Grzelczak, J. Vermant, E. M. Furst and L. M. Liz-Marzan, ACS Nano, 2010, 4, 3591–3605.
15. A. B. Pawar and I. Kretzschmar, Macromol. Rapid Commun., 2010, 31, 150–168.
16. S. Sacanna and D. J. Pine, Curr. Opin. Colloid Interface Sci., 2011, 16, 96–105.
17. M. J. Solomon, Curr. Opin. Colloid Interface Sci., 2011, 16, 158–167.
18. S. Sacanna, D. J. Pine and G.-R. Yi, Soft Matter, 2013, 9, 8096–8106.
19. B. A. Grzybowski, C. E. Wilmer, J. Kim, K. P. Browne and K. J. M. Bishop, Soft Matter, 2009, 5, 1110.
20. S. I. Stupp, Nano Lett., 2010, 10, 4783–4786.
21. M.-P. Valignat, O. Theodoly, J. C. Crocker, W. B. Russel and P. M. Chaikin, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 4225–4229.
22. S. Gangwal, A. Pawar, I. Kretzschmar and O. D. Velev, Soft Matter, 2010, 6, 1413–1418.
23. A. van Blaaderen, R. Ruel and P. Wiltzius, Nature, 1997, 385, 321–324.
24. A. van Blaaderen, J. P. Hoogenboom, D. L. J. Vossen, A. Yethiraj, K. Visscher and M. Dogterom, Faraday Discuss., 2003, 123, 107–119.
25. K. D. Hermanson, S. O. Lumsdon, J. P. Williams, E. W. Kaler and O. D. Velev, Science, 2001, 294, 1082–1086.
26. S. O. Lumsdon, J. P. Williams, E. W. Kaler and O. D. Velev, J. Appl. Phys., 2003, 82, 949.
27. S. Lumsdon, E. Kaler and O. Velev, Langmuir, 2004, 20, 2108–2116.
28. J. P. B. Singh, F. Nettesheim, N. J. Wagner and E. M. Furst, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 050401.
29. A. F. Demirors, P. M. Johnson, C. M. Van Kats, A. van Blaaderen and A. Imhof, Langmuir, 2010, 26, 14466–14471.
30. P. J. Beltramo and E. M. Furst, Electrophoresis, 2013, 34, 1000–1007.
31. M. M. Panczyk, J.-G. Park, N. J. Wagner and E. M. Furst, Langmuir, 2013, 29, 75–81.
32. A. A. Shah, H. Kang, K. L. Kohlstedt, K. H. Ahn, S. C. Glotzer, C. W. Monroe and M. J. Solomon, Small, 2012, 8, 1551–1562.
33. J. Loudet, P. Barois and P. Poulin, Nature, 2000, 407, 611–613.
34. M. J. Cavallaro, L. Botto, E. P. Lewandowski, M. Wang and K. J. Stebe, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 20923–20928.
35. D. Frenkel and B. M. Mulder, Mol. Phys., 2002, 100, 201–217.
36. M. Radu, P. Pfleiderer and T. Schilling, J. Chem. Phys., 2009, 131, 164513.
37. A. Donev, F. H. Stillinger, P. M. Chaikin and S. Torquato, Phys. Rev. Lett., 2004, 92, 255506.
38. P. Pfleiderer and T. Schilling, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 020402.
39. T. Vissers, Z. Preisler, F. Smallenburg, M. Dijkstra and F. Sciortino, J. Chem. Phys., 2013, 138, 164505.
40. F. Romano and F. Sciortino, Nat. Commun., 2012, 3, 975.
41. J. M. Tavares, L. Rovigatti and F. Sciortino, J. Chem. Phys., 2012, 137, 044901.
42. J. M. Tavares, P. Teixeira, M. T. Da Gama and F. Sciortino, J. Chem. Phys., 2010, 132, 234502.
43. F. Sciortino, A. Giacometti and G. Pastore, Phys. Rev. Lett., 2009, 103, 237801.
44. M. C. Hagy and R. Hernandez, J. Chem. Phys., 2012, 137, 044505.
45. C. De Michele, T. Bellini and F. Sciortino, Macromolecules, 2011, 45, 1090–1106.
46. F. Romano, E. Sanz, P. Tartaglia and F. Sciortino, J. Phys.: Condens. Matter, 2012, 24, 064113.
47. F. Romano, E. Sanz and F. Sciortino, J. Chem. Phys., 2010, 132, 184501.
48. F. Romano, E. Sanz and F. Sciortino, J. Chem. Phys., 2011, 134, 174502.
49. F. Romano and F. Sciortino, Nat. Mater., 2011, 10, 171–173.
50. C. Vega, E. P. A. Paras and P. A. Monson, J. Chem. Phys., 1992, 96, 9060–9072.
51. C. Vega, E. P. A. Paras and P. A. Monson, J. Chem. Phys., 1992, 97, 8543–8548.
52. M. Marechal and M. Dijkstra, Soft Matter, 2011, 7, 1397–1408.
53. M. Marechal and M. Dijkstra, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 061405.
54. U. Agarwal and F. A. Escobedo, Nat. Mater., 2011, 10, 230–235.
55. W. R. Toor and T. C. Halsey, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 8617–8623.
56. A. Goyal, C. K. Hall and O. D. Velev, J. Chem. Phys., 2010, 133, 064511.
57. A. Hynninen and M. Dijkstra, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 051402.
58. A.-P. Hynninen and M. Dijkstra, Phys. Rev. Lett., 2005, 94, 138303.
59. K. Schätzel and B. J. Ackerson, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 3766–3777.
60. D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic Press, New York, 2nd edn, 2002.
61. W. van Megen and S. Underwood, Phys. Rev. Lett., 1993, 70, 2766–2769.
62. P. N. Pusey, E. Zaccarelli, C. Valeriani, E. Sanz, W. C. K. Poon and M. E. Cates, Philos. Trans. R. Soc. London, Ser. A, 2009, 367, 4993–5011.
63. J. Zhu, M. Li, R. Rogers, W. Meyer, R. H. Ottewill, S.-S. S. Crew, W. B. Russel and P. M. Chaikin, Nature, 1997, 387, 883–885.
64. K. N. Pham, A. M. Puertas, J. Bergenholtz, S. U. Egelhaaf, A. Moussaïd, P. N. Pusey, A. B. Schofield, M. E. Cates, M. Fuchs and W. C. K. Poon, Science, 2002, 296, 104–106.
65. V. Trappe and P. Sandkuhler, Curr. Opin. Colloid Interface Sci., 2004, 8, 494–500.
66. I. D. Hosein, B. S. John, S. H. Lee, F. A. Escobedo and C. M. Liddell, J. Mater. Chem., 2009, 19, 344–349.
67. J.-G. Park, J. D. Forster and E. R. Dufresne, J. Am. Chem. Soc., 2010, 132, 5960–5961.
68. R. Zhang and K. S. Schweizer, J. Chem. Phys., 2010, 133, 104902.
69. R. Zhang and K. S. Schweizer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 060502.
70. D. J. Beltran-Villegas and M. A. Bevan, Soft Matter, 2011, 7, 3280–3285.
71. D. Forster, J.-G. Park, M. Mittal, H. Noh, C. F. Schreck, C. S. O'Hern, H. Cao, E. M. Furst and E. R. Dufresne, ACS Nano, 2011, 8, 6695–6700.
72. S. Gangwal, O. J. Cayre and O. D. Velev, Langmuir, 2008, 24, 13312–13320.
73. J. M. McMullan and N. J. Wagner, Soft Matter, 2010, 6, 5443–5450.
74. M. Mittal, P. P. Lele, E. W. Kaler and E. M. Furst, J. Chem. Phys., 2008, 129, 064513.
75. A. Gast and C. Zukoski, Adv. Colloid Interface Sci., 1989, 30, 153.
76. T. C. Halsey and W. Toor, Phys. Rev. Lett., 1990, 65, 2820–2823.
77. M. Parthasarathy and D. J. Klingenberg, Mater. Sci. Eng., R, 1996, 17, 57–103.
78. J. J. Juárez and M. A. Bevan, Adv. Funct. Mater., 2012, 22, 3833–3839.
79. B. J. Ackerson, J. Rheol., 1990, 34, 553–590.
80. J. M. McMullan and N. J. Wagner, J. Rheol., 2009, 53, 575–588.
81. J. W. Swan, P. A. Vasquez, P. A. Whitson, E. M. Fincke, K. Wakata, S. H. Magnus, F. D. Winne, M. R. Barratt, J. H. Agui, R. D. Green, N. R. Hall, D. Y. Bohman, C. T. Bunnell, A. P. Gast and E. M. Furst, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16023–16028.
82. A. Guerrero-Martínez, M. Grzelczak and L. M. Liz-Marzan, ACS Nano, 2012, 6, 3655–3662.
83. M. Grzelczak and L. M. Liz-Marzan, Langmuir, 2013, 29, 4652–4663.
84. G. Petekidis, A. Moussaid and P. N. Pusey, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2002, 66, 051402.
85. K. N. Pham, G. Petekidis, D. Vlassopoulos, S. U. Egelhaaf, W. C. K. Poon and P. N. Pusey, J. Rheol., 2008, 52, 649–676.
86. I. Gazuz, A. M. Puertas, T. Voigtmann and M. Fuchs, Phys. Rev. Lett., 2009, 102, 248302.
87. N. Koumakis, M. Laurati, S. U. Egelhaaf, J. F. Brady and G. Petekidis, Phys. Rev. Lett., 2012, 108, 098303.
88. M. C. Rechtsman, F. H. Stillinger and S. Torquato, Phys. Rev. Lett., 2005, 95, 228301.
89. M. Rechtsman, F. Stillinger and S. Torquato, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 011406.
90. M. C. Rechtsman, F. H. Stillinger and S. Torquato, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 021404.
91. M. C. Rechtsman, F. H. Stillinger and S. Torquato, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 031403.
92. H. Cohn and A. Kumar, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 9570–9575.

---