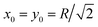Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Particle invasion, survival, and non-ergodicity in 2D diffusion processes with space-dependent diffusivity
Andrey G.
Cherstvy
a,
Aleksei V.
Chechkin
abc and
Ralf
Metzler
*ad
aInstitute for Physics & Astronomy, University of Potsdam, 14476 Potsdam-Golm, Germany. E-mail: rmetzler@uni-potsdam.de
bInstitute for Theoretical Physics, Kharkov Institute of Physics and Technology, Kharkov 61108, Ukraine
cMax-Planck Institute for the Physics of Complex Systems, Nöthnitzer Straße 38, 01187 Dresden, Germany
dDepartment of Physics, Tampere University of Technology, 33101 Tampere, Finland
First published on 2nd January 2014
Abstract
We study the thermal Markovian diffusion of tracer particles in a 2D medium with spatially varying diffusivity D(r), mimicking recently measured, heterogeneous maps of the apparent diffusion coefficient in biological cells. For this heterogeneous diffusion process (HDP) we analyse the mean squared displacement (MSD) of the tracer particles, the time averaged MSD, the spatial probability density function, and the first passage time dynamics from the cell boundary to the nucleus. Moreover we examine the non-ergodic properties of this process which are important for the correct physical interpretation of time averages of observables obtained from single particle tracking experiments. From extensive computer simulations of the 2D stochastic Langevin equation we present an in-depth study of this HDP. In particular, we find that the MSDs along the radial and azimuthal directions in a circular domain obey anomalous and Brownian scaling, respectively. We demonstrate that the time averaged MSD stays linear as a function of the lag time and the system thus reveals a weak ergodicity breaking. Our results will enable one to rationalise the diffusive motion of larger tracer particles such as viruses or submicron beads in biological cells.
I. Introduction
For a typical bacterial cell such as E. coli, various proteins, large cellular complexes, nucleic acids, lipids, etc. occupy some 30–40% of the cell volume.1–4 The exact implications of this macromolecular crowding on the characteristics of diffusing particles of various sizes are still under debate.5,6 Another source impeding the free diffusion of larger particles in eukaryotic cells stems from a network of cytoskeletal filaments and internal membranes like the endoplasmic reticulum or the nuclear membrane. Such forms of crowding impair the particle diffusivity inside a cell and may alter the law of diffusion altogether, from Brownian motion to a subdiffusive law. In the latter case, the mean squared displacement (MSD) scales as7| 〈x2(t)〉 ≃ tβ, | (1) |
Measuring the apparent local diffusivity of small proteins in bacterial26 and eukaryotic27 cells reveals a nontrivial dependence on the position in the cell. One reason for this spatial variation of the diffusivity may be the cell's geometrical shape.26 Thus, certain cell types possess a ‘fried egg-shape’ (Fig. 1) with a significant variation of the cell thickness from the periphery towards the nucleus. A higher apparent abundance of proteins in the cytosol near the nucleus, interpreted as a higher cytoplasm diffusivity, may simply originate due to the 2D imaging of the fully 3D particle trajectories. Away from the thicker perinuclear region, the cell periphery offers only a thin, nearly 2D domain for the particle diffusion.
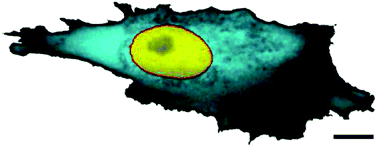 | ||
| Fig. 1 The variation of local diffusivity in the cytoplasm of a mammalian cell. The FRAP intensity of the cyan colour refers to the local effective porosity of the cytoplasm, scaling with the volume fraction available for protein diffusion. Scale bar is 10 μm. The image is taken from ref. 27; courtesy to Jörg Langowski. | ||
Another source for the variations of the local diffusivity is the heterogeneity of the density of the macromolecular crowding in the cytoplasm and nucleoplasm, as well as of the dense cytoskeletal meshwork near the cell periphery, and the accumulation of large cellular organelles in a perinuclear region. How exactly this affects the porosity of the cytoplasm and the diffusivity of tracers of different sizes is not well established.28,29 Specifically, substantial deviations from the Stokes–Einstein law for protein tracers of varying molecular weights (MW) diffusing in the E. coli cytoplasm were observed and the diffusivity shown to follow the scaling law D ∼ MW−0.7.30 Small tracer proteins apparently experience a higher porosity near the nucleus of mammalian cells,27 while the diffusion of larger proteins becomes progressively restricted.30 Thus, from a biological perspective, a 2D stochastic model with spatially varying diffusivity may mimic the effects on the diffusion of tracer particles in the heterogeneous environment of the crowded cellular cytoplasm and will serve as an empirical description of secondary processes such as intracellular, diffusion-controlled reactions. We here study the physical properties of such a heterogeneous diffusion process (HDP).
Important clues come from viral particles, a major class of naturally occurring diffusers in the bacterial cytoplasm. After internalisation by receptor-driven endocytosis,31 viruses often recruit highly processive cellular motor proteins32,33 which ensure fast and efficient viral transport between the cell periphery and the nucleus, where the viral replication and assembly often occur.34,35 The intra-cellular dynamics of viruses and their multi-step infection pathways, as monitored by single-particle tracking, exhibit some features of anomalous diffusion.15 For instance, the scaling exponent β of the viral motion is shown to depend on the region of the cytoplasm in which the diffusion takes place.
Three different modes of transport for adeno-associated viruses36,37 were identified in living substrate-adhered HeLa cells.15,38,39 The first is Brownian motion with β = 1 albeit with a much smaller diffusion coefficient than in dilute aqueous solution. The second mode is that of subdiffusion with β = 0.5, …, 0.9 and with a broad apparent distribution of diffusivities. The third mode is that of motor-driven transport of viruses via quasi-1D persistent walks along microtubular filaments, mediated by molecular motors driven by energy from ATP conversion. Upon infection, the ballistic, driven motion with β = 2 yields an effective drift of virions towards the nucleus. These diffusion-based and active modes of viral transport can interchange. Although the fraction of actively transported virions is relatively small,15 this ‘active pathway’ is often vital for a successful viral infection. Small viruses can reach the nucleus solely by thermal diffusion, while larger virions have no chance but rely on the active transport mechanism. Indeed, an accumulation of viruses near the nucleus was shown to be inhibited by microtubuli-depolymerising drugs (e.g., nocodazole) that suppress motor-assisted virus transport.40
Several recent models of intermittent transport41,42 were implemented to describe the kinetics of viral infection, and search optimisation models with 2D versus 3D intermittent dynamics were developed.43,44 A number of diffusion,45 diffusion–reaction–advection,40 and kinetic transport46 models were suggested to rationalise the features of intracellular virus trafficking. In particular, the kinetics of spreading of a viral population starting at the cell membrane and the accompanying nucleus invasion times were computed46 and compared to typical time scales of viral infection recorded experimentally.47,48 In a series of theoretical and computer simulation studies Holcman and colleagues49–53 modelled the process of viral trafficking as a sequence of alternating Brownian 2D diffusive excursions and ballistic motor-powered propulsions along radially ordered microtubular filaments. The dynamical characteristics of viral invasion were computed in such a 2D planar pie-like model. The probability density function (PDF) and the mean time of nucleus invasion by viruses were evaluated.51 More advanced theoretical models can also include a rate of viral degradation in the cytoplasm,46 the kinetics of viral binding to microtubuli, and some bi-directionality of virus transport by the motors.
Here we consider the passive, thermally driven diffusion of tracer particles of sizes comparable to a virus capsid in a model cell. To construct our model we include the following information. From the viral trajectories reported in ref. 15 and 38 we conclude that those particles exhibiting normal diffusion with β = 1 preferentially take azimuthal pathways at about constant separation from the cell nucleus. Such propagation likely takes place in a region of the cell cytoplasm with a roughly constant diffusivity. In contrast, that part of the viral population that diffuses anomalously mainly travels in the radial direction. We propose below that heterogeneities of the medium during the journey of a particle from the cell membrane to the nucleus give rise to anomalous (in particular, sub-diffusive) features for this second population of particles.
Recently, extending previous studies54 we examined the effects of position-dependent diffusivities on the ensemble and time averaged characteristics for 1D HDPs.55,56 We tested several functional forms for D(x) (power-law, logarithmic, and exponential) to rationalise their implications on diffusive and ergodic properties of the process. For power-law forms of D(x) we predicted from stochastic simulations and analytical calculations the regimes of sub- and super-diffusive behaviour. The conditions for weak ergodicity breaking were also analysed in detail, an important feature when the information from single particle tracking studies is evaluated in terms of time averages.6 The diffusion turns out to be weakly non-ergodic in 1D solely due to the heterogeneities of the medium, and, despite a non-Brownian scaling of the MSD, the time averaged MSD was shown to follow a strictly linear growth with lag time. These features are similar to those for continuous time random walk processes.57
For the 2D HPDs examined below we also find non-ergodic behaviour. In addition, we compute a number of biologically relevant quantities such as the survival probability S(t) of particles in a circular domain for both diffusion from the inside of the cell to the outside and vice versa, the first-passage time dynamics for reaching the domain boundary, the PDF for the spreading of diffusing particles starting at the cell centre, at the cell boundary, and for initially uniformly distributed walkers.
This paper is organised as follows. In Section II we introduce the basic notations and the main quantities to be analysed. We outline the numerical scheme used in computations as well as the implemented theoretical concepts. In Section III we report the main simulation results and support them by asymptotic analytic calculations. We analyse the effects of the system heterogeneity and polar cell geometry on diffusive, kinetic, and ergodic properties of the HDP. In Section IV the conclusions are drawn and possible applications of the results are discussed.
II. MODEL
Our model cell is a circular domain with a reflecting outer boundary, mimicking the situation that internalised viruses do not leave the cell again. We analyse the following form of the diffusivity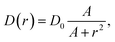 | (2) |
The dependence (2) is in qualitative agreement with the experimentally measured trends for the diffusivity of small fluorescently labelled proteins in the cytoplasm of mammalian NLFK and HeLa cells.27 It also reflects the above observation that azimuthal diffusion is fully Brownian, i.e., in our language, the diffusivity remains constant. The simulation method described below is readily applicable to other D(r) forms.
We note here that from the currently available experimental data on the heterogeneous nature of the diffusivity in biological cells (see, e.g., ref. 27) it is not possible to determine the exact functional form of D(r). It is equally impossible to exactly quantify how strongly the diffusivity changes from the cell nucleus to the cell periphery for a tracer particle of a given size. Apart from the effect of the size and chemical details of the tracer particle, strong effects originate from the cell type and stage with the associated distribution of cytoskeletal elements, as well as from the variation of the cell thickness. Once more detailed information becomes available with the framework developed herein, it will be possible to infer the exact anomalous diffusion and ergodic properties of the tracer motion.
We characterise the HDP in terms of the ensemble-averaged MSD of particles defined via the PDF P(r, φ, t),
| 〈r2(t)〉 = ∫∫r2P(r, φ, t)rdrdφ. | (3) |
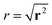 of length T, the time averaged MSD is defined as the sliding average with the lag time Δ,
of length T, the time averaged MSD is defined as the sliding average with the lag time Δ,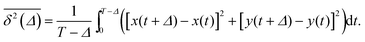 | (4) |
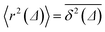 holds, the behaviour of the two quantities remains different even for T → ∞ in weakly non-ergodic systems. In particular, individual realisations of time averaged quantities become irreproducible.6,57,58
holds, the behaviour of the two quantities remains different even for T → ∞ in weakly non-ergodic systems. In particular, individual realisations of time averaged quantities become irreproducible.6,57,58
The ergodicity breaking parameter EB characterises the deviation of the system from the ergodic behaviour. It contains the second moment of the time averaged MSD and is defined as follows59,60
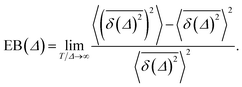 | (5) |
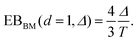 | (6) |
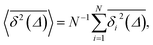 | (7) |
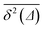 values around the mean
values around the mean 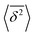 , the condition Δ/T ≪ 1 should be satisfied.
, the condition Δ/T ≪ 1 should be satisfied.
We also define the survival probability S(t) of particles in the circular domain with outer and inner absorbing boundaries, and the particles are released at the opposite boundary. The probability of particles in this scenario is not conserved and S(t) tends to zero as time progresses. The PDF of the first passage is then defined as −dS(t)/dt and the mean first passage time as 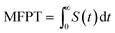 . We evaluate the statistics of the first arrival times directly from the generated trajectories, r(t).
. We evaluate the statistics of the first arrival times directly from the generated trajectories, r(t).
At every time step in the computer simulations we use the Klimontovich–Hänggi61 post-point scheme to evaluate the two coupled Langevin equations with independent noise sources,
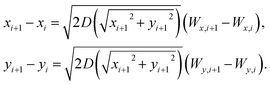 | (8) |
We note that we could also use the Stratonovich scheme to simulate the process. For the MSD, similar to the 1D case,55 the difference between the two representations occurs only in the prefactor and is of order unity. The Hänggi–Klimontovich post-point interpretation implemented below is a natural combination of the physical continuity equation and the constitutive law.61 It is also more practical for the computation of the survival and first passage statistics of tracer particles on a finite circular domain, as discussed in detail elsewhere.62
III. Results
A. MSD and time averaged MSD
The computed ensemble and time averaged MSD as well as the mean time averaged MSD are shown in Fig. 2 for the case of free diffusion of a particle with diffusivity (2). For the 1D case, the MSD for a diffusivity of the form D(x) = D0|x|−2 reveals the subdiffusive scaling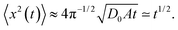 | (9) |
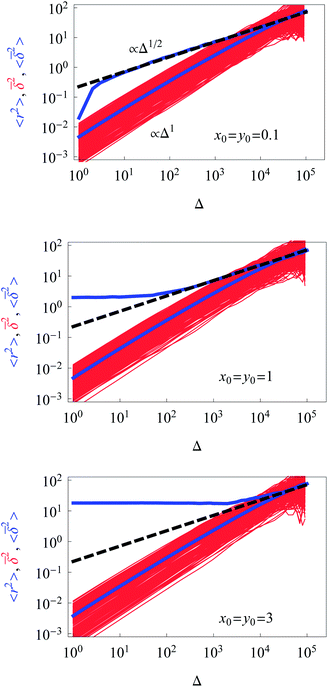 | ||
| Fig. 2 Dependence of the ensemble-averaged MSD (upper thick blue curve), the mean time averaged MSD (thick blue curve), and the time averages of the MSD for individual trajectories (red curves) for unconstrained diffusion on time t or the lag time Δ. The theoretical asymptote (9) for the ensemble-averaged MSD is represented by the dashed black line. Parameters: A = 0.01, the starting positions are x0 = y0 = 0.1, 1, and 3 in the graphs from top to bottom. The number of traces for the averaging is N = 300 and the length of each trajectory being T = 105 in units of the simulation time step. The simulation time for each choice of the starting conditions is ∼2.5 days on a standard 3 GHz working station. | ||
The time averaged MSD trajectories are linear functions of the lag time Δ, their mean scaling as
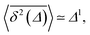 | (10) |
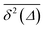 in the region of Δ/T ≪ 1 progressively decreases for larger values of the particle initial position (not shown). Here, we do not quantify the details of the distribution
in the region of Δ/T ≪ 1 progressively decreases for larger values of the particle initial position (not shown). Here, we do not quantify the details of the distribution 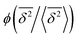 of individual traces
of individual traces 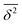 . We refer the reader to refs. 55 and 56 where this procedure is discussed in detail for the 1D HDP. In the presence of a reflecting boundary at a given outer radius R both the ensemble and time averaged MSD will saturate (not shown), similar to the effects of external confinement on Brownian motion and fractional Brownian motion.63
. We refer the reader to refs. 55 and 56 where this procedure is discussed in detail for the 1D HDP. In the presence of a reflecting boundary at a given outer radius R both the ensemble and time averaged MSD will saturate (not shown), similar to the effects of external confinement on Brownian motion and fractional Brownian motion.63
We checked that for D(x) = const we obtain the standard 2D result
| 〈rBM2(t)〉 = 4D0t, | (11) |
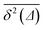 traces at Δ/T ≪ 1. Moreover, for the ergodicity breaking parameter we find that
traces at Δ/T ≪ 1. Moreover, for the ergodicity breaking parameter we find that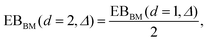 | (12) |
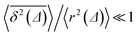 for not too small values of the initial positions {x0, y0}, see Fig. 2.
for not too small values of the initial positions {x0, y0}, see Fig. 2.
As a connection to experiments, let us define the model parameters that can describe the MSD magnitudes measured in the tracking experiments of small adeno-associated viruses,15,38,39 as mentioned in the Introduction. Specifically, for the subdiffusive population of viruses the MSD measured in the cells after the diffusion time of t ≈ 0.32 s was ≈0.4 μm2, see Fig. 3G in ref. 15. The viral diffusivity was D ∼ 0.2 μm2 s−0.6 for their subdiffusive motion with exponent β ≈ 0.6. To get the same MSD value in the same physical time t the prefactor D0 of the diffusion coefficient in our model would be D0 ≈ 10 μm4 s−1. Note that in physical units we have [D(r)] = [D0/r2] = μm2 s−1.
B. Azimuthal and radial diffusion
We project the increments of the diffusing particles at each simulation step i with the particle position ri onto the radial and azimuthal directions and compute the single-step displacements δri and riδΦi. We account for the clock- and anti-clockwise azimuthal rotation of the particle position vector ri. We then restore the corresponding average displacements after t = T/δt simulation steps, computed as the average over all the traces,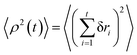 and
and 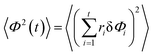 . The results of the simulations show that the growth of the radial increments, similar to the MSD in eqn (9), obeys the subdiffusive law
. The results of the simulations show that the growth of the radial increments, similar to the MSD in eqn (9), obeys the subdiffusive law| 〈ρ2(t)〉 ≃ t1/2. | (13) |
| 〈Φ2(t)〉 ≈ 4D0t. | (14) |
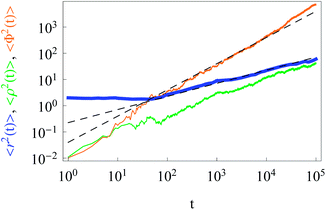 | ||
| Fig. 3 Anomalous behaviour of radial increments (orange) and Brownian diffusion of azimuthal particle increments (green line). The dashed asymptotes are given by eqn (9) and (11). The MSD corresponds to the blue line. Parameters are the same as in Fig. 2, except for x0 = y0 = 1 and N = 40. | ||
C. Ergodicity violation
The simulations show that the ergodicity breaking parameter for short lag times Δ assumes values close to those for the 1D case with analogous D(x) treated in ref. 55. The EB values at Δ/T ≪ 1 deviate from zero, indicating a weak ergodicity breaking and non-equivalence of ensemble and time averaging for this 2D diffusion process in a heterogeneous environment. Non-homogeneities in the diffusion coefficient break the ergodicity in the system, see also the discussion in ref. 64.For long lag times, when Δ → T, and for {x0, y0} values in the high-diffusivity region close to r = 0, the ergodicity breaking parameter approaches 1/2 of the value (6) of the asymptote for the 1D Brownian motion obtained in ref. 59. Such a reciprocal dependence on the space dimension d,
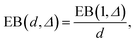 | (15) |
Clearly, in our system with an inhomogeneous diffusivity, the initial conditions of the diffusing particles affect the magnitude of the time averaged MSD traces and thus the values of the ergodicity breaking parameter. As shown in Fig. 4, this effect is quite non-trivial and corresponds to the extent to which the particles venture into areas of different diffusivities during their trajectory for a fixed trajectory length T.
 | ||
| Fig. 4 Ergodicity breaking parameter as a function of lag time Δ for different initial conditions. The Brownian asymptote (12) for the 2D case is shown by the dashed line on the right side of the plot. Parameter are the same as in Fig. 2. | ||
We performed simulations for various values of the parameter A in the diffusion coefficient D(r) of eqn (2). Variation of A regulates how strong the dependence of D(r) on the radial coordinate is. The constant A controls at what particle displacements the heterogeneity of D(r) will become pronounced, namely, for how long a nearly Brownian motion will take place before the subdiffusive regime (9) for the MSD sets in. This ‘ideal’ subdiffusive scaling given by eqn (9) is shown in Fig. 2 for a small A value (A = 0.01). We systematically explore the dependence of the ensemble and time averaged MSD on the value of A in Fig. 5: for larger A values the spread of individual time averaged trajectories decreases, eventually approaching the δ-like distribution characteristic of the Brownian motion. The Brownian diffusion law (11) is shown in Fig. 5 as the dashed-dotted line. At short diffusion times with increasing A the region of nearly normal diffusion for the MSD becomes more pronounced, and the time and ensemble averaged MSDs approach each other, see the lower panels in Fig. 5, indicating more ergodic behaviour of the system. Indeed, for this unconstrained diffusion, the EB parameter for larger A values progressively approaches the Brownian asymptote given by eqn (6), rescaled for the 2D HDP according to eqn (15). Fig. 5 shows that with increasing A the overall magnitude of the time average MSD trajectories increases, staying always linear in the regime Δ/T ≪ 1. For larger A, as the effects of the heterogeneity decrease, the computed MSD deviates progressively from the asymptote (9), shown as the dashed curve. Eventually, for very large A the ensemble and time averaged MSD coincide. The jump in the MSD at short times in Fig. 5 is due to the initial conditions x0 = y0 = 0.1.
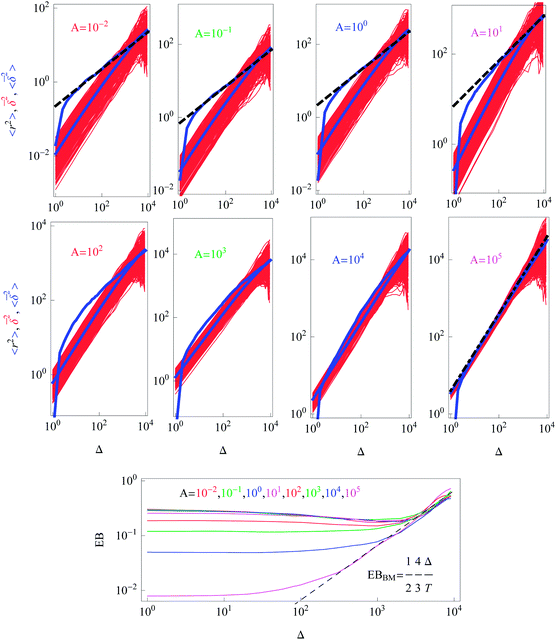 | ||
| Fig. 5 Dependence of the ensemble averaged MSD (blue), the individual time averaged MSD traces (red), and the trajectory-to-trajectory average of the time averaged MSD (lower blue) for the indicated A values. The colour coding scheme is the same as in Fig. 2. The dashed lines represent the asymptotic behaviour (9) and the dashed-dotted line in the bottom right panel corresponds to the Brownian law (11). The behaviour of the ergodicity breaking parameter EB is shown in the bottom panel, where the value of A increases from top to bottom. For all quantities the data sets were log-sampled along the x-axis. Parameters: T = 104, x0 = y0 = 0.1, and N = 300. | ||
Note here that the evaluation of the dependence EB (Δ) often requires much better statistics than that needed for the MSDs presented in Fig. 2. The reason is the large spread of 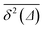 between trajectories at all lag times Δ, see the red curves in Fig. 2. This scatter has more severe implications on the ergodicity breaking parameter containing the square
between trajectories at all lag times Δ, see the red curves in Fig. 2. This scatter has more severe implications on the ergodicity breaking parameter containing the square 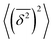 , see eqn (5), and involving the averaging over N traces.
, see eqn (5), and involving the averaging over N traces.
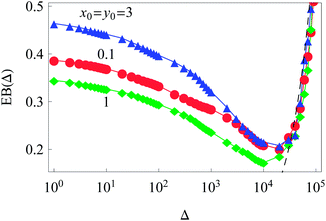
The dependence of the initial value EB (Δ = 1) on the trajectory length T for different initial conditions is illustrated in Fig. 6. Similar to the 1D situation treated in ref. 55 and 56, the variation of EB (T) depends on how far the system is away from the ergodic state for the imposed initial conditions. For instance, the ergodicity breaking parameter EB (Δ = 1) for x0 = y0 = 3 and short traces with T = 102 are quite close to the Brownian value given by eqn (12) (data not shown). Conversely, for the same initial conditions but longer trajectories, T = 103–5, the system is more non-ergodic and the corresponding EB parameter is larger than that for x0 = y0 = 0.1 or 1 (Fig. 6). This is the reason why we observe the intersection of curves for different {x0, y0} values shown in Fig. 6. At T → ∞ the ergodicity breaking parameter tends to a universal value of around 0.3–0.4.
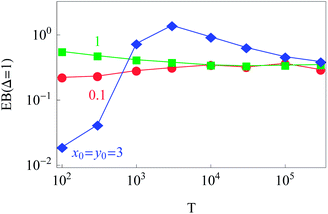 | ||
| Fig. 6 Dependence of EB (Δ = 1) on the trace length T. At least N = 300 trajectories were used to compute each point in the graph, except for the longest trajectory, for which N = 50. Parameters are the same as in Fig. 2. | ||
The data show that system heterogeneities indeed cause a weak ergodicity breaking in the 2D HDP with diffusivity (2). Due to the non-equivalence of the radial and azimuthal diffusion, we predict a direction-dependent ergodicity breaking parameter, see Fig. 7. We observe that the radial and azimuthal ergodicity breaking parameters EBρ and EBΦ become quite close in the limit Δ/T ≪ 1. In the limit of long lag times, as Δ ∼ T, the parameter EBρ behaves similarly to EB computed from r(t), compare Fig. 4 and 7. In contrast, the azimuthal parameter EBΦ does not approach the Brownian asymptote (12) at later stages of the time averaged trajectories.
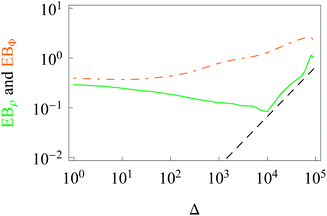 | ||
| Fig. 7 Direction-dependent ergodicity breaking parameters. The Brownian asymptote (12) is represented by the dashed line. Parameters and colour coding are the same as in Fig. 3. | ||
D. PDF and spreading of particles
Now we turn to the diffusion in a finite circular domain with a reflecting boundary placed at the outer radius R. The spreading of particles starting at the cell boundary at r = R is characterised by the PDF shown in Fig. 8. The initial accumulation of particles near the reflecting outer wall in the region of low diffusivity contributes to the enhanced azimuthal spreading. This spreading remains profound also at later times, because of the Brownian diffusive behaviour in the azimuthal direction in contrast to subdiffusive spreading in the radial direction, see Fig. 3. The overall trend is similar to the 1D case,55,56 where at long times the particles tend to accumulate in the regions of lower diffusivity. Naturally, the average effective jump length of particles diffusing near r = 0 is larger than that in the region of slow diffusion near the cell boundary. As one can see from Fig. 8, a strong azimuthal spread at t = T/30, …, T/10 turns into a pronounced invasion of particles over the entire cell at t = T (for trace length T = 105 and N = 150 analysed trajectories in this figure).The time evolution of the radial PDF shown in Fig. 9 quantifies the 2D plots in Fig. 8 when particles are initially released at the fringe of the cell. We observe that for longer trajectories the maximum of the PDF, initially localised at r = R, progressively spreads and approaches a universal scaling law given by p(r) ≃ r. We note that from visual inspection of Fig. 8 at longer times the distribution appears almost completely homogeneous. Exact information about the diffusive properties of particles thus needs to be measured locally, such as by single particle tracking, recovery of fluorescence after photobleaching, or fluorescence correlation spectroscopy, in order to grasp the inherent inhomogeneity.
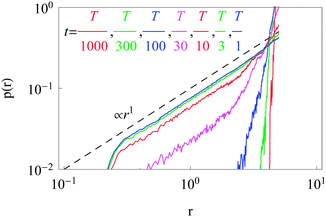 | ||
| Fig. 9 Dependence of the radial distribution function p(r) for particle invasion into a circular nucleus-free domain 0 < r < R starting from the cell boundary. Parameters are the same as in Fig. 8. | ||
We also simulated the diffusive ‘focusing’ of walkers that were initially homogeneously distributed in the cell. We find that fast-diffusing particles leave the region near the origin at r = 0 relatively quickly and progressively shift the maximum of the PDF towards the region of slow diffusion near the cell periphery, see the graphs for different times t in Fig. 10. This trend is similar to the 1D situation with power-law diffusivity.55
E. Survival probability: diffusion from the nucleus to the membrane
After starting at the cell centre and diffusion towards the cell membrane at r = R, the probability of staying in the domain of radius R is described by the survival probability S(t) as shown in Fig. 11. The simulations results obey the universal scaling| S(t) ≃ t−1/2. | (16) |
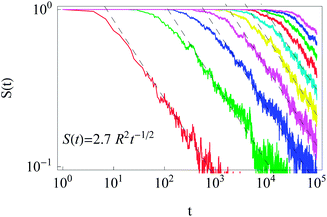 | ||
| Fig. 11 Survival probability in the domain of radius R for initial particle release near the cell centre. The universal scaling (16) is shown by the dashed lines. Parameters: R = 1,2, …, 10 for the curves from left to right, x0 = y0 = 0.1, T = 105, and N = 300. | ||
We also computed the distribution of arrival times of particles diffusing from the cell centre to the cell boundary, see Fig. 12. These distributions p(tarr) reveal a wide spread, particularly at large R values, indicating large trajectory-to-trajectory fluctuations. From these distributions we determine the threshold time t1/2 at which 50% of the fastest particles reach the outer cell boundary. Such a threshold characteristic is often important for biological problems, e.g., in the dynamics of population spreading or proliferation of viral infections.
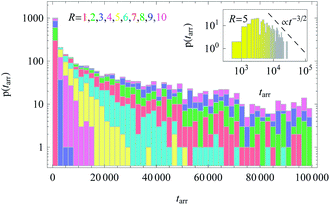 | ||
| Fig. 12 Distributions of arrival times to the cell boundary for diffusion of particles initially released near the cell centre, plotted for varying cell radius R. In the inset we demonstrate the scaling t−3/2 expected from the survival probability in Fig. 11. The stacked histograms are presented without overlap of bars. The height of the bins represents the number of particles with a given first arrival time at the boundary of radius R. While for small R all N = 300 simulated particles quickly reach the boundary, for larger R values a finite portion of the walkers still has not arrived at R after T = 105 simulation steps. This fraction amounts to approximately 0.46, 0.29, and 0.12 for R = 10, 9, and 8, respectively. The colour scheme and parameters are the same as in Fig. 11. | ||
The function t1/2(R) obtained via the analysis of the histograms presented in Fig. 12 often turns out to be bound by two asymptotes. The first one is defined via the slowest diffusivity at the cell boundary r = R. Namely, from elementary scaling arguments we can write
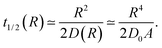 | (17) |
The second characteristic time scale is defined via the average diffusion coefficient in the domain,
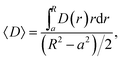 | (18) |
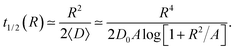 | (19) |
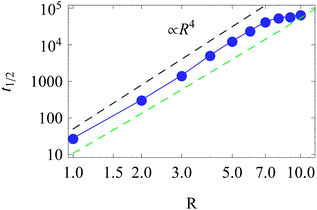 | ||
| Fig. 13 Scaling of t1/2 for diffusion from the centre to the cell boundary with cell size R. The asymptotes correspond to eqn (17) (top) and (19) (bottom line). Parameters are the same as in Fig. 12. | ||
The time t1/2 characterises the arrival of the fastest half of a population of diffusing walkers, and it can be related to the effectiveness and reliability of the target search in such a heterogeneous medium. It is particularly important as the arrival time distributions are skewed,66 compare Fig. 12. Consequently, the mean of the distribution and its width are not the best indicators of the arrival statistics,66 and instead t1/2 should be used. In our 2D bound domain the first-passage time dynamics and the histograms for p(tarr) can be fitted, e.g., by a generalised gamma distribution66,67 (not shown). Clearly, for a larger domain size R the width of the distributions of arrival times grows, because of accumulated statistical fluctuations among diffusing particles with longer trajectories, see Fig. 12 and 15.
F. Survival probability: diffusion from the cell membrane to the nucleus
The survival probability for the diffusion from the outer reflecting boundary to the absorbing cell ‘nucleus’ exhibits the exponential scaling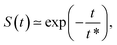 | (20) |
The characteristic time t* of the decrease of S(t) with time corresponds to the time the particles spend diffusing from the outer to the inner boundary in a medium with average diffusivity. As the radial diffusion is quasi-1D we can write
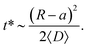 | (21) |
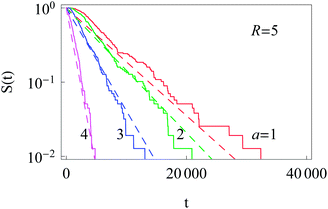 | ||
| Fig. 14 Exponential decay of the survival probability for the diffusion of particles starting at the cell membrane. The dashed lines represent eqn (20) with the decay time given by eqn (21). The radii a of the inner absorbing boundary are indicated in the graph, other parameters are the same as in Fig. 11. | ||
Similarly to the results for nucleus-to-membrane diffusion in Fig. 12, we evaluate the distribution of the arrival times from the cell periphery to the nucleus of different sizes, compare Fig. 15.
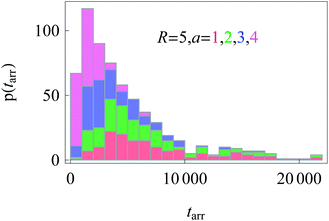 | ||
| Fig. 15 Distributions of arrival times from the cell boundary to a nucleus of radius a. Colour coding and parameters are the same as in Fig. 14. We show stacked histograms without overlap of bars. | ||
IV. Discussion and outlook
We studied the diffusion of particles in a 2D circular domain with a radially varying diffusivity D(r). We showed that the resulting HDP is weakly non-ergodic in the sense that the time and ensemble averages of physical quantities such as the MSD behave differently. This effect was shown to depend on the initial conditions of the diffusive walkers. The diffusion in the direction of the diffusivity gradient was shown to be anomalous, while the azimuthal diffusion occurs in a nearly constant environment and is Brownian. This behaviour is reminiscent of the radial and azimuthal diffusion of viral particles monitored in the bacterial cytoplasm, with radially varying diffusivity.15,27Specifically for the evaluation of single particle tracking data, our results for the non-ergodicity imply that (i) the time averages of physical quantities such as the MSD behave differently from their ensemble analogues and (ii) the individual time averages are not reproducible, i.e., there occurs a major scatter in the amplitudes of these quantities. Both need to be taken into account for a proper physical interpretation of data.
We demonstrated that the diffusion from the domain centre to its boundary (nucleus to membrane) and the reverse process obey entirely different behaviours for the respective survival probabilities. Namely, the S(t) ≃ t−1/2 scaling law was found for nucleus–membrane diffusion and the exponential S(t) ≃ e−t/t* decay was identified for membrane–nucleus diffusion. This latter fact as well as the spreading of particles according to these two scenarios can be rationalised in terms of a domain-averaged diffusion coefficient.
The quantitative understanding and the ability to tune viral diffusion in living cells have enormous potential as a tool to control and hopefully suppress the proliferation of infections. Viral gene delivery carriers37,68 with a high transfection efficiency actively transported by motors69 are nowadays extensively used for gene delivery purposes. We note that our model may also be applied to macroscopic systems. Thus, the spatial spreading of epidemics in a population of animals subject to non-homogeneous habitat or foraging conditions is another possible area for application of our model.
We mention that our HDP model may also be useful to quantitatively model the spreading of bacteria within inherently heterogeneous bacterial populations.70 Similarly, it might find application to the transport of molecules in heterogeneous and anisotropic brain tissues.71 Another field where typically diffusion is highly inhomogeneous concerns subsurface hydrology.72
In the present paper, we focus on the statistical and nonergodic properties of HDPs in circular domains. A mathematical investigation of the process of viral infection in the presence of three inter-connected diffusion pathways (anomalous diffusion, normal diffusion, and active directional transport) is currently under way.62
Acknowledgements
We thank E. Barkai, H. Büning, A. Godec, and T. Kühn for discussion. We also acknowledge funding from the Academy of Finland (FiDiPro scheme to RM), the Deutsche Forschungsgemeinschaft (Grant CH 707/5-1 to AGC), and the German Academic Exchange Service (Grant A/13/03073).References
- S. B. Zimmerman and S. O. Trach, J. Mol. Biol., 1991, 222, 599 CrossRef CAS.
- S. B. Zimmerman and A. P. Minton, Annu. Rev. Biophys. Biomol. Struct., 1993, 22, 27 CrossRef CAS PubMed.
- D. Hall and A. P. Minton, Biochim. Biophys. Acta, 2003, 1649, 127 CrossRef CAS.
- H. X. Zhou, J. Mol. Recognit., 2004, 17, 368 CrossRef CAS PubMed.
- F. Höfling and T. Franosch, Rep. Prog. Phys., 2013, 76, 046602 CrossRef PubMed.
- E. Barkai, Y. Garini and R. Metzler, Phys. Today, 2012, 65(8), 29 CrossRef CAS PubMed; I. M. Sokolov, Soft Matter, 2012, 8, 9043 RSC.
- R. Metzler and J. Klafter, Phys. Rep., 2000, 339, 1 CrossRef CAS.
- M. Wachsmuth, W. Waldeck and J. Langowski, J. Mol. Biol., 2000, 298, 677 CrossRef CAS PubMed.
- J. Vercammen, G. Martens and Y. Engelborghs, Springer Ser. Fluoresc., 2007, 4, 323 Search PubMed.
- A. Caspi, R. Granek and M. Elbaum, Phys. Rev. Lett., 2000, 85, 5655 ( Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. , 2002 , 66 , 011916 ) CrossRef CAS.
- I. M. Tolic-Nørrelykke, E. L. Munteanu, G. Thon, L. Oddershede and K. Berg-Sørensen, Phys. Rev. Lett., 2004, 93, 078102 CrossRef.
- J.-H. Jeon, V. Tejedor, S. Burov, E. Barkai, C. Selhuber-Unkel, K. Berg-Sørensen, L. Oddershede and R. Metzler, Phys. Rev. Lett., 2011, 106, 048103 CrossRef.
- S. M. A. Tabei, S. Burov, H. Y. Kim, A. Kuznetsov, T. Huynh, J. Jureller, L. H. Philipson, A. R. Dinner and N. F. Scherer, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4911 CrossRef PubMed.
- M. A. Taylor, J. Janousek, V. Daria, J. Knittel, B. Hage, H.-A. Bachor and W. P. Bowen, Nat. Photonics, 2013, 7, 229 CrossRef CAS.
- G. Seisenberger, M. U. Ried, T. Endreß, H. Büning, M. Hallek and C. Bräuchle, Science, 2001, 294, 1929 CrossRef CAS PubMed.
- G. Guigas and M. Weiss, Biophys. J., 2007, 93, 316 CrossRef CAS PubMed.
- I. Golding and E. C. Cox, Phys. Rev. Lett., 2006, 96, 098102 CrossRef PubMed; S. C. Weber, A. J. Spakowitz and J. A. Theriot, Phys. Rev. Lett., 2010, 104, 238102 CrossRef.
- I. Bronstein, Y. Israel, E. Kepten, S. Mai, Y. Shav-Tal, E. Barkai and Y. Garini, Phys. Rev. Lett., 2009, 103, 018102 CrossRef CAS.
- D. S. Banks and C. Fradin, Biophys. J., 2005, 89, 2960 CrossRef CAS PubMed.
- W. Pan, L. Filobelo, N. D. Q. Pham, O. Galkin, V. V. Uzunova and P. G. Vekilov, Phys. Rev. Lett., 2009, 102, 058101 CrossRef.
- J.-H. Jeon, N. Leijnse, L. Oddershede and R. Metzler, New J. Phys., 2013, 15, 045011 CrossRef.
- J. Szymanski and M. Weiss, Phys. Rev. Lett., 2009, 103, 038102 CrossRef.
- G. R. Kneller, K. Baczynski and M. Pasenkiewicz-Gierula, J. Chem. Phys., 2011, 135, 141105 CrossRef PubMed.
- J.-H. Jeon, H. Martinez-Seara Monne, M. Javanainen and R. Metzler, Phys. Rev. Lett., 2012, 109, 188103 CrossRef.
- T. Akimoto, E. Yamamoto, K. Yasuoka, Y. Hirano and M. Yasui, Phys. Rev. Lett., 2011, 107, 178103 CrossRef.
- B. English, V. Hauryliuk, A. Sanamrad, S. Tankov, N. Dekker and J. Elf, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, E365 CrossRef CAS PubMed.
- T. Kühn, T. O. Ihalainen, J. Hyväluoma, N. Dross, S. F. Willman, J. Langowski, M. Vihinen-Ranta and J. Timonen, PLoS One, 2011, 6, e22962 Search PubMed.
- T. Kühn, Personal communication, 2013.
- T. Kalwarczyk, N. Ziebacz, A. Bielejewska, E. Zaboklicka, K. Koynov, J. Szymanski, A. Wilk, A. Patkowski, J. Gapinski, H.-J. Butt and R. Holyst, Nano Lett., 2011, 11, 2157 CrossRef CAS PubMed.
- J. T. Mika, G. v. d. Bogaart, L. Veenhoff, V. Krasnikov and B. Poolman, Mol. Microbiol., 2010, 77, 200 CrossRef CAS PubMed.
- J. Mercer, M. Schelhaas and A. Helenius, Annu. Rev. Biochem., 2010, 79, 803 CrossRef CAS PubMed.
- B. Sodeik, M. W. Ebersold and A. Helenius, J. Cell Biol., 1997, 136, 1007 CrossRef CAS.
- K. Radtke, K. Dohner and B. Sodeik, Cell. Microbiol., 2006, 8, 387 CrossRef CAS PubMed.
- B. Brandenburg and X. Zhuang, Nat. Rev. Microbiol., 2007, 5, 197 CrossRef CAS PubMed.
- U. F. Greber and M. Way, Cell, 2006, 124, 741 CrossRef CAS PubMed.
- P. J. Xiao and R. D. Samulski, J. Virol., 2012, 86, 10462 CrossRef CAS PubMed.
- W. Ding, L. Zhang, Z. Yan and J. F. Engelhardt, Gene Ther., 2005, 12, 873 CrossRef CAS PubMed.
- G. Seisenberger, PhD thesis, LMU Munich, 2001.
- C. Bräuchle, G. Seisenberger, T. Endreß, M. U. Ried, H. Büning and M. Hallek, ChemPhysChem, 2002, 3, 299 CrossRef.
- A.-T. Dinh, T. Theofanous and S. Mitragotri, Biophys. J., 2005, 89, 1574 CrossRef CAS PubMed.
- P. C. Bressloff and J. M. Newby, Rev. Mod. Phys., 2013, 85, 135 CrossRef CAS.
- S. Soh, M. Byrska, K. Kandere-Grzybowska and B. A. Grzybowski, et al. , Angew. Chem., Int. Ed., 2010, 49, 4170 CrossRef CAS PubMed.
- C. Loverdo, O. Bénichou, M. Moreau and R. Voituriez, Nat. Phys., 2008, 4, 134 CrossRef CAS.
- J. F. Rupprecht, O. Bénichou, D. S. Grebenkov and R. Voituriez, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 041135 CrossRef.
- P. C. Bressloff and J. M. Newby, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 061139 CrossRef.
- D. A. Smith and R. M. Simons, Biophys. J., 2001, 80, 45 CrossRef CAS.
- B. Sodeik, M. W. Ebersold and A. Helenius, J. Cell Biol., 1997, 136, 1007 CrossRef CAS.
- M. Y. Nakano and U. F. Greber, J. Struct. Biol., 2000, 129, 57 CrossRef CAS PubMed.
- T. Lagache and D. Holcman, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 77, 030901(R) CrossRef.
- D. Holcman, J. Stat. Phys., 2007, 127, 471 CrossRef CAS.
- T. Lagache, E. Dauty and D. Holcman, Curr. Opin. Microbiol., 2009, 12, 439 CrossRef CAS PubMed.
- T. Lagache, E. Dauty and D. Holcman, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011921 CrossRef.
- T. Lagache, O. Danos and D. Holcman, Biophys. J., 2012, 102, 980 CrossRef CAS PubMed.
- A. Fulinski, J. Chem. Phys., 2013, 138, 021101 CrossRef CAS PubMed.
- A. G. Cherstvy, A. V. Chechkin and R. Metzler, New J. Phys., 2013, 15, 083039 CrossRef.
- A. G. Cherstvy and R. Metzler, Phys. Chem. Chem. Phys., 2013, 15, 20220 RSC.
- Y. He, S. Burov, R. Metzler and E. Barkai, Phys. Rev. Lett., 2008, 101, 058101 CrossRef CAS.
- S. Burov, J.-H. Jeon, R. Metzler and E. Barkai, Phys. Chem. Chem. Phys., 2011, 13, 1800 RSC.
- W. Deng and E. Barkai, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011112 CrossRef.
- S. M. Rytov, Y. A. Kravtsov, and V. I. Tatarskii, Principles of Statistical Radiophysics 1: Elements of Random Process Theory, Springer, Heidelberg, 1987 Search PubMed.
- Y. L. Klimontovich, Phys. A, 1990, 163, 515 CrossRef; Y. L. Klimontovich, Phys.-Usp., 1994, 37, 737 CrossRef PubMed; P. Hänggi and H. Thomas, Phys. Rep., 1982, 88, 207 CrossRef; J. Dunkel and P. Hänggi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 036106 CrossRef.
- A. G. Cherstvy, A. V. Chechkin and R. Metzler, unpublished.
- J.-H. Jeon and R. Metzler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 021103 CrossRef.
- A. Lubelski, I. M. Sokolov and J. Klafter, Phys. Rev. Lett., 2008, 100, 250602 CrossRef.
- S. Redner, A Guide to First-Passage Processes, Cambridge University Press, 2001 Search PubMed.
- T. Mattos, C. Mejía-Monasterio, R. Metzler and G. Oshanin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 031143 CrossRef.
- A. Andreanov and D. S. Grebenkov, J. Stat. Mech.: Theory Exp., 2012, p07001 Search PubMed.
- H. Büning, L. Perabo, O. Coutelle, S. Quadt-Humme and M. Hallek, J. Gene Med., 2008, 10, 717 CrossRef PubMed.
- J. Suh, D. Wirtz and J. Hanes, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 3878 CrossRef CAS PubMed.
- M. E. Lidstrom and M. C. Konopka, Nat. Chem. Biol., 2010, 6, 705 CrossRef CAS PubMed.
- C. Nicholson, Rep. Prog. Phys., 2001, 64, 815 CrossRef CAS; E. Syková and C. Nicholson, Physiol. Rev., 2008, 88, 1277 CrossRef PubMed.
- J. J. McDonnell, et al. , Water Resour. Res., 2007, 43, W07301 CrossRef.
| This journal is © The Royal Society of Chemistry 2014 |