Dynamics of confined depletion mixtures of polymers and bidispersed colloids

Abstract

We investigate the effect of confinement on solidification of mixtures of non-adsorbing polymers and bidispersed colloidal particles (size ratio a_S/a_L ≈ 0.49) in a low-dielectric-constant solvent. Holding the total volume fraction of particles fixed, the dynamics of the large particles become increasingly slow as either the volume fraction of small particles is increased or the confinement thickness is decreased. Confinement to ten large particle diameters induces gelation in all samples investigated, with the most arrested dynamics appearing when both the depletant concentration and volume fraction of small particles are large. The changes in dynamics are consistent with an increase in the effective interparticle attraction that is driven by changes in the electrostatic repulsion between particles as the suspension is confined, and thus are an indirect secondary effect of confinement.

---

I Introduction

Particle-laden complex fluids are routinely employed in confined geometries in industrial or technological applications. For example, suspensions used in complex porous media in natural resource engineering, such as drilling fluids used to lubricate the well bore¹ or viscosifiers used to enhance recovery of hydrocarbons from regions of low permeability,² frequently contain mixtures of polymers and particles of different sizes.³ Particulate inks, which are extruded through fine nozzles in inkjet printing^4–7 and three-dimensional printing,^8,9 often contain particles and polymer plasticizers to achieve both the desired flow properties during printing and the optimal mechanical properties in printed structures. Polymer nanocomposites, which contain nanoparticles dispersed in a polymer matrix, must frequently be processed as thin films for applications that exploit their exceptional mechanical, optical, or conductive properties.^10–14 Improving the design of suspensions for these and other applications thus requires understanding the influence of confinement on the structure, dynamics, and phase behavior of particle-laden complex particulate fluids.

The effects of confinement on one prototypical complex fluid, a suspension of colloidal spheres with repulsive interparticle interactions, are understood in the limit of high particle volume fraction. Suspensions of monodispersed colloidal particles solidify as crystals when confined in thin two-dimensional layers,¹⁵ driven by the formation of ordered crystalline layers at the walls.¹⁶ Increasing the dispersity in size of the particles, for example by introducing a second particle size, frustrates crystallization. Instead, bidispersed confined suspensions with repulsive interparticle interactions can solidify as a colloidal glass.¹⁷ For these concentrated suspensions, the walls again induce changes in the structure¹⁸ and dynamics^18,19 of the particles that drive the transition from liquid to solid.

In contrast to monodispersed and hard-sphere colloidal particles, the effect of confinement on suspensions in which particles exhibit attractive interactions are poorly understood. Such systems, however, may serve as better models of particle-laden complex fluids ubiquitously used in confined geometries. Towards this end, suspensions exhibiting complex interactions between monodispersed particles, including polymer-bridged spheres¹⁹ and mixtures of oppositely-charged,^20–22 charge-asymmetric,²³ or hard and sticky spheres,^24,25 have been extensively studied in bulk geometries. One particularly convenient model system for attractive complex fluids is a mixture of particles and non-adsorbing polymers,^26–31 in which the range and strength of the effective depletion attraction between particles are governed by the polymer-to-particle size ratio and the polymer concentration, respectively. Particles suspended in organic solvents may also exhibit electrostatic repulsions, and mixtures of charged particles and depleting polymers have been extensively studied as models for gelation in the presence of competing interparticle interactions.^32–39 Despite extensive research on the bulk properties of these and other model systems, how these systems solidify in confinement is poorly understood. We recently showed that depletion mixtures of monodispersed particles and polymers also solidified when confined, as indicated by transitions in both structural measures such as the cluster size distribution and dynamic measures such as the ensemble-averaged mean-squared displacement. Moreover, these transitions were not initiated by the formation of layers of particles at the walls, as expected for repulsive particles, but were instead consistent with an increase in the effective strength of attraction between the particles.^40,41

Further insight into the properties of engineering suspensions geometries requires models that incorporate additional complexity. One route to model the polydispersity of engineering suspensions is to use mixtures of particles of different sizes. Unsurprisingly, binary mixtures of particles of asymmetric size exhibit strikingly different properties than monodispersed mixtures; two examples are the dynamics⁴² and mechanical properties⁴³ of glassy bidispersed mixtures. Suspensions of attractive bi- and tridispersed particles also manifest bulk properties distinct from those of monodispersed attractive particles: for example, heteroflocculated binary latex dispersions exhibit different stability ratios⁴⁴ and aggregates of silica particles of three different sizes exhibit distinct fractal dimensions and strengths.⁴⁵

In colloid–polymer mixtures, studies incorporating particle polydispersity have largely focused on the equilibrium phase behavior. Theoretical work shows that slight polydispersity can destabilize the single-phase region compared to the gas–liquid phase separation, leading to an increase in the number of phases and in the complexity of the colloid–polymer phase diagram.⁴⁶ Experiments show that polydispersed particles indeed fractionate by size into distinct phases,⁴⁷ but separation into multiple coexisting solid phases at high particle concentrations is kinetically suppressed.⁴⁸ By contrast, the effect of particle size dispersity on the non-equilibrium phase behavior remains largely unexplored, with one report of high particle polydispersity disrupting the re-entrant glass transition seen at high particle concentrations.⁴⁹ These studies, however, concentrated on the properties of bulk suspensions, whereas applications often involve thin or confined geometries. Despite the relevance for applications, how the interplay of particle size dispersity, attractions, and confinement influences solidification of particulate suspensions remains poorly understood.

In this paper, we investigate the effects of confinement on the solidification of mixtures of bidispersed colloids with a size ratio of a_S/a_L ≈ 0.49 and depletant polymers suspended in a low-dielectric-constant solvent. We measure the dynamics of the large particles in confined geometries as a function of the volume percent of small particles using confocal microscopy and particle tracking. In bulk geometries, increasing the volume percent of small particles induces the formation of heterogeneous clusters of particles, in which small particles trap or cage the large particles. These bidispersed suspensions become increasingly more solid-like when confined between nearly parallel walls. Heterogeneous clustering and gelation of the large and small particles suppress crystallization in the large particles. The dynamics of the large particles are most arrested when both the volume fraction of the small particles is high and the sample is strongly confined. The changes in dynamics in confinement are consistent with an increase in the strength of the effective attraction between particles. This change in the interparticle interactions results from the adsorption of charge carriers from the solvent and from the particles on the walls of the chamber, which leads to a decrease in the interparticle electrostatic repulsion; this mechanism is thus a secondary indirect effect induced by the confinement. The bidispersed suspensions exhibit slower dynamics than the monodispersed suspensions, suggesting that replacing large particles with small particles further increases the effective attraction. We conclude that confinement can indirectly enhance the solidification of particulate suspensions in low-dielectric constant solvents, and that varying the size dispersity may be a simple way to further tune the solidification of attractive suspensions.

II Materials and methods

Our model binary system consisted of poly(methyl methacrylate) particles of diameters 2a_L = 1.48 μm (polydispersity ≈ 4.6%) or 2a_S = 0.73 μm (polydispersity ≈ 6%), as measured using dynamic light scattering (Brookhaven Instruments BI-200SM, equipped with an avalanche photodiode detector (BI-APD) and a BI-9000AT correlator), with a size ratio of a_S/a_L ≈ 0.49. Both sets of particles were sterically stabilized with poly(12-hydroxystearic acid).⁵⁰ The large particles (2a_L = 1.48 μm) were labeled with the fluorescent dye Rhodamine B (Sigma-Aldrich) and the small particles (2a_S = 0.73 μm) were labeled with Fluorescein 5(6)-isothiocyanate (Sigma-Aldrich).⁵¹ Particles were suspended in a solvent mixture of cyclohexylbromide (CXB, Sigma-Aldrich, grade 98%) and decahydronaphthalene (DHN, Sigma-Aldrich, grade 98%) at a weight ratio of 3.1 : 1 to match their density (ρ ≈ 1.22 g mL⁻¹) and index of refraction (n ≈ 1.49). We added 1.5 mM of tetrabutylammonium chloride salt to all solvent mixtures to partially screen the electrostatic surface charge of the particles.⁵² To controllably tune the size dispersity we fixed the total volume fraction of particles in the sample (ϕ ≈ 0.15) and varied the ratio of volume fraction of small particles to the total volume fraction r = ϕ_S/ϕ_T, where ϕ_T = ϕ_S + ϕ_L is the total volume fraction occupied by small and large particles.

We induced an entropic depletion attraction between particles by adding linear polystyrene (M_w = 333.3 kDa, M_w/M_n = 1.03, Varian) with a radius of gyration R_g = 15 nm (ref. 53) and an overlap concentration c^*_p = 3M_w/4πR_g³N_A ≈ 35 mg mL⁻¹. In a monodispersed colloid–polymer mixture, the strength and range of the depletion attraction between the particles are controlled by the concentration of polystyrene and the size ratio of the polymer and particle, respectively. In our bidispersed suspensions, the ratios of polymer-to-particle size were ξ_S = R_g/a_S ≈ 0.041 and ξ_L = R_g/a_L ≈ 0.020. We formulated suspensions at two concentrations of polymer in the free (reservoir) volume,^26,27,54,55c_p ≈ 5 mg mL⁻¹ and c_p ≈ 25 mg mL⁻¹.

The resulting interparticle potential included contributions from the depletion attraction as well as the electrostatic repulsion between particles. We used a modified Asakura–Oosawa model^27,54–56 to estimate the depletion attraction between small–small and large–large particles. We assumed that the electrostatic repulsion was described by a screened Coulomb form⁵⁷ and used an empirical rule of thumb,⁵⁸Zλ_B/2a ≈ 6, to extrapolate the charge Z on our particles from literature measurements of the charge on PMMA particles in CXB–DHN solvent mixtures.⁵⁸ (Details are given in the ESI.†) The resulting interparticle potential for a polymer concentration of c_p ≈ 5 mg mL⁻¹ indicated repulsive interactions at all separations, with a maximum repulsive barrier of 17 k_BT (small–small) or 10 k_BT (large–large). For a polymer concentration of c_p ≈ 25 mg mL⁻¹, the interparticle potential exhibited an attractive minimum at contact, with a depth of −5 k_BT (small–small) and −44 k_BT (large–large) (as shown in Fig S1 in the ESI†).

For each concentration of polymer, we prepared five different samples with values of r ranging from 0 (i.e. ϕ_S = 0) to 1 (i.e. ϕ_S = 0.15); we estimated using a modified A–O potential⁵⁹ that the magnitude of the depletion attraction between the large particles due to the small particles ranged from 0.2 k_BT (r = 0.25) to 0.5 k_BT (r = 0.75) (Fig. S2 in ESI†). After each sample was prepared, we tested the buoyancy matching by centrifuging the samples at 800 g and 25 °C for 75 min; if required, we added DHN or CXB dropwise and confirmed that both particles and clusters remained neutrally buoyant after additional centrifuging. Samples were allowed to equilibrate for 24 hours after buoyancy matching prior to loading into sample chambers. We report the polymer concentration c_p, the total volume fraction ϕ_T, and the volume percent of small particles r in Table 1.

Table 1 Polymer concentration c_p, total volume fraction ϕ_T, and volume percent of small particles r for samples

Sample	1	2	3	4	5	6	7	8	9	10
cp [mg mL^−1]	5.2	5.0	4.9	5.1	4.9	25.1	25.1	25.0	25.0	24.9
ϕT	0.147	0.146	0.152	0.151	0.149	0.152	0.150	0.154	0.148	0.151
r	1	0.75	0.51	0.26	0	1	0.75	0.49	0.25	0

---

Samples were imaged using a confocal point-scanner (VT-Eye, VisiTech International) that was attached to an inverted microscope (Leica DMI3000B). This microscope was equipped with two laser sources with emission wavelengths λ = 491 nm and λ = 561 nm. The λ = 491 nm line excited both fluorescent dyes, so that we imaged both large and small particles simultaneously without discrimination, whereas the λ = 561 nm line excited only the rhodamine dye in the large particles, so that we imaged only the large particles. For bulk measurements, samples were loaded in rectangular glass chambers of thickness 1 mm and allowed to sit undisturbed for 30 min. After this constant waiting time, we acquired multiple two-dimensional movies (x–y) using each laser source at a height z = 60 μm above the bottom surface of the chamber. To probe the effects of spatial confinement on the dynamics, samples were loaded into wedge-shaped glass chambers of varying thickness (opening angle < 0.5°). After a constant waiting time of 30 minutes, we acquired two-dimensional (x–y) movies at the midplane of different thicknesses h ranging from 7.5 to 60 μm at different positions along the length of the chamber, i.e. at distances z = h/2. Representative images from all movies are given in ESI (Fig. S3 and S4†). In a typical experiment, movies consisting of 500 8-bit images were acquired using Voxcell Scan (VisiTech International) at 1 frame per second with an image size of 512 × 512 pixels. We used standard particle-tracking algorithms⁶⁰ to locate and track the positions of the large particles in two dimensions over time (with resolution of 40 nm) in movies acquired using the λ = 561 nm laser source.

III Results

In the presence of a polymer depletant, changing the ratio of small to large particles induces changes in the structure of the particles that are consistent with more solid-like phases. When the concentration of polymer depletant is low (c_p ≈ 5 mg mL⁻¹), the particles in a suspension containing only large particles (r = 0, Fig. 1a) are mostly dispersed, consistent with the slight interparticle repulsion. Increasing the fraction of small particles while holding the total volume fraction fixed drives the formation of heterogeneous clusters containing both small and large particles (Fig. 1b–d). Similarly, when the concentration of polymer depletant is higher (c_p ≈ 25 mg mL⁻¹) increasing the fraction of small particles drives a transition from large clusters (Fig. 1e) to a connected network of particles (Fig. 1f–h).

Fig. 1 Confocal micrographs of small and large particle populations for suspensions with a constant total volume fraction ϕ_T = 0.15, concentration of depletant polymer c_p (a–d) 5 mg mL⁻¹ or (e–h) 25 mg mL⁻¹, and varying volume percent of small particles r (a and e) 0.00, (b and f) 0.50, (c and g) 0.75, and (d and h) 1.00. The scale bar is 10 μm.

We confirm the observation of solidification in the microscopy images by measuring the dynamics of the large particles. For both concentrations of polymer, we find that increasing the ratio of small particles leads to increasingly slow dynamics as quantified via the ensemble-averaged mean-squared displacement (MSD) of the large particles, as shown in Fig. 2. For a low concentration of depletant (c_p ≈ 5 mg mL⁻¹), adding a small (r = 0.25) or moderate (r = 0.50) fraction of small particles does not appreciably change the slightly subdiffusive dynamics of the large particles (Fig. 2a). A significant decrease in both the magnitude and slope of the MSD is seen only when the concentration of small particles is large (r = 0.75); the dynamics of the large particles, though, remain subdiffusive and are not fully arrested, suggesting that tuning the suspension parameters alone is insufficient to induce gelation. For a high concentration of depletant (c_p ≈ 25 mg mL⁻¹), however, even the addition of a modest fraction of small particles (r = 0.25) leads to a change in the magnitude and slope of the large-particle MSD (Fig. 2b). At the highest volume percent of small particles studied (r = 0.75), the slope of the MSD is nearly zero, indicating full dynamic arrest of the large particles; additionally, the MSD is nearly an order of magnitude smaller at long lag times than that of the monodispersed large particle suspension. The MSD decreases monotonically between r = 0 and r = 0.75 at fixed lag time, indicating that the large particles become more arrested as the volume fraction of small particles is increased. The strength of the depletion attraction from the small particles is relatively weak; the increase in arrest thus results from trapping of the large particles in clusters of small particles.

Fig. 2 Normalized mean-squared displacement 〈Δx²〉/(2a_L)² as a function of lag time τ for large particles in bulk binary suspensions with concentration of polymer c_p of (a) 5 mg mL⁻¹ and (b) 25 mg mL⁻¹. The volume percent r of small particles varies from 0 to 0.75. The dashed lines indicate a slope of 1.

We probe the effect of confinement on bidispersed systems by imaging samples at different positions along a thin wedge, as shown in Fig. 3 for two suspensions with volume percent r = 0.50. Suspensions with a low concentration of depletant polymer (c_p ≈ 5 mg mL⁻¹), and hence a weak interparticle attraction, contain nearly dispersed particles in bulk samples but a connected network of particles in the strongest confinements (Fig. 3a–d). Similarly, the large clusters of particles present in bulk suspensions with a higher concentration of depletant (c_p ≈ 25 mg mL⁻¹) form a connected network when strongly confined (Fig. 3e–h). These changes suggest that confining suspensions of bidispersed colloids and depletant polymers in a low dielectric constant solvent induces solid-like phase behavior for both weakly repulsive and weakly attractive interparticle interactions.

Fig. 3 Confocal micrographs of small and large particle populations for suspensions with a constant total volume fraction ϕ_T = 0.15, volume percent of small particles r = 0.50, concentration of depletant polymer c_p (a–d) 5 mg mL⁻¹ or (e–h) 25 mg mL⁻¹, (a and e) in bulk or (b–f and d–h) confined to a normalized height h/2a_L of (b and f) 41, (c and g) 20, or (d and h) <5.5. The scale bar is 10 μm.

To extend these qualitative observations, we again examine the behavior of the MSD of the large particles. The MSD of suspensions with a low concentration of depletant (c_p ≈ 5 mg mL⁻¹) that contain only large particles (r = 0) become arrested when the suspension is confined to a normalized thickness h/2a_L < 5.5, consistent with solidification, as shown in Fig. 4a. Increasing the volume fraction of small particles to r = 0.50 only moderately affects the dynamics of the large particles, with the onset of arrested dynamics appearing at h/2a_L = 10 (Fig. 4b). Confining a suspension with a large fraction of small particles (r = 0.75), which exhibits the slowest dynamics in bulk suspension due to the presence of large heterogeneous clusters (as can be seen by comparing images from the two laser excitations in Fig. S3 and S4†), leads to arrested dynamics at slightly weaker confinements of h/2a_L = 10 (Fig. 4c). For all nonzero values of r, arrested dynamics of large particles consistent with solidification appear only when the large particles feel the effects of the walls (i.e. at ∼10 particle diameters). Furthermore, the magnitude of the MSD for strong confinement h/2a_L < 5.5 is approximately equal for all nonzero values of r, suggesting that the presence of the small particles only weakly affects the dynamics of the large particles there. Nevertheless, the dynamics noticeably slow at more modest confinements of h/2a_L = 20, showing that confinement affects the dynamics and state of suspensions before the onset of solidification. We obtain similar results for samples that are confined for thirty days in wedge-shaped chambers prior to imaging (shown in Fig. S5 in the ESI† for a ratio of r = 0.50).

Fig. 4 Mean-squared displacement 〈Δx²〉/(2a_L)² as a function of lag time τ of large particles in binary suspensions with concentration of depletant polymer of c_p = 5 mg mL⁻¹ and varying volume percent of small particles r of (a) 0.00, (b) 0.50, and (c) 0.75. Confinement thicknesses h/2a_L: bulk (☆) >69 (○), 41 (△), 20 (◊), 10 (▽), and <5.5 (◁). The dashed lines indicate a slope of 1.

In the presence of a larger concentration of depletant polymer (c_p ≈ 25 mg mL⁻¹), confinement also induces increasingly slow dynamics, as shown in Fig. 5. Confining the samples to thicknesses of h/2a_L = 20 or below leads to fully arrested dynamics for all values of r investigated. Because the bulk dynamics of the large particles in these samples are already sub-diffusive, the change in the magnitude of the MSD of the large particles is less dramatic than seen for samples with c_p ≈ 5 mg mL⁻¹. Comparing the MSDs of confined samples with c_p ≈ 25 mg mL⁻¹ and different values of r reveals two notable features. First, the changes in dynamics with confinement are least pronounced for the sample with r = 0.50: the bulk MSD of this sample is somewhat smaller than that at r = 0, whereas the MSDs of the most-confined samples (h/2a_L < 5.5) are similar at r = 0 and r = 0.50. In high-depletant samples with the largest volume fraction of small particles (r = 0.75, Fig. 5c), however, the MSD of the large particles in strong confinements (h/2a_L ≤ 10.1) is smaller than that of similarly confined samples with r = 0 or r = 0.50. This result indicates that changing the size dispersity can lead to more solid-like behavior in confined samples with strong interparticle attractions. Furthermore, the reduction of the MSD at large thicknesses occurs at a different volume percent (r = 0.50) than that at which the magnitude of the MSD is decreased (r = 0.75), suggesting that tuning the confinement and small particle fraction separately affect solidification. Finally, our results do not significantly change if the samples are confined for long times in wedge-shaped chambers (as shown in Fig. S6† for a ratio of r = 0.50). We summarize our results by examining the MSD of the large particles at a fixed lag time of 10 seconds, corresponding approximately to the time needed for a large particle to diffuse its own diameter. The MSD of the large particles decreases by nearly two orders of magnitude as the sample is confined from bulk to h/2a_L < 5.5, as shown by the closed symbols in Fig. 6. Adding small particles allows solids to be formed at slightly weaker confinements of h/2a_L = 10, where suspensions containing only large particles (r = 0) remain fluids of clusters. Pronounced changes in the magnitude of the MSD at a fixed confinement, however, appear only when the volume percent of small particles is large (r = 0.75). When the concentration of depletant polymer is increased, confinement again slows the dynamics of the large particles at all values of r, as shown by the open symbols in Fig. 6, although the change in the magnitude of the MSD is typically less than an order of magnitude. At the highest volume percent of small particles (r = 0.75), however, the value of the MSD in the strongest confinement h/2a_L < 5.5 is smaller than that of the sample without large particles (r = 0), suggesting that the presence of the small particles enhances confinement-induced solidification for these samples.

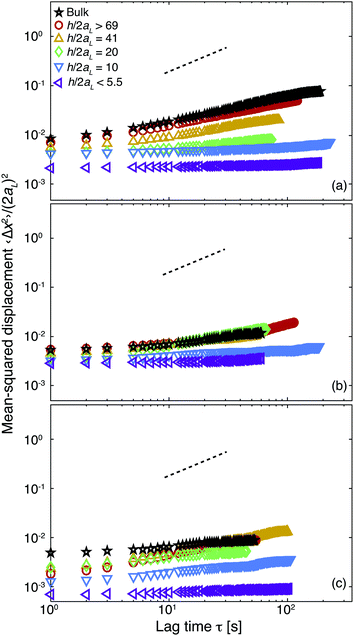Fig. 5 Normalized mean-squared displacement 〈Δx²〉/(2a_L)² as a function of lag time τ of large particles in binary suspensions with concentration of depletant polymer of c_p = 25 mg mL⁻¹ and varying volume percent of small particles r of (a) 0.00, (b) 0.50, and (c) 0.75. Confinement thicknesses h/2a_L: bulk (☆) >69 (○), 41 (△), 20 (◊), 10 (▽), and <5.5 (◁). The dashed lines indicate a slope of 1.

Fig. 6 Normalized mean-squared displacement 〈Δx²〉/(2a_L)² at a lag time τ = 10 s of large particles as a function of confinement h/2a_L for binary suspensions with concentration of depletant polymer c_p ≈ 5 mg mL⁻¹ (closed symbols) and c_p ≈ 25 mg mL⁻¹ (open symbols) for volume percent of small particles r of 0.75 (○), 0.50 (▽), and 0.00 (△).

To gain additional insight into the effect of bidispersity on solidification mechanisms, we examine the behavior of the self part of the van Hove correlation function of the large particles at a fixed lag time of τ = 10 s. We previously found for monodispersed colloid–polymer mixtures that the G_s(Δx, τ) of confined samples narrows and becomes increasingly non-Gaussian, similar to the dynamics of samples undergoing gelation.⁴⁰ For a sample with a low concentration of depletant polymer (c_p = 5 mg mL⁻¹), G_s(Δx, τ) changes from nearly Gaussian to non-Gaussian as the sample is increasingly confined, as shown in Fig. 7a–c. To highlight the change in shape of these curves we fit the function to a single Gaussian distribution, indicated as dashed lines in Fig. 7, and confirm that a Gaussian distribution cannot adequately fit the tails of G_s(Δx, τ) of a highly confined sample. The non-Gaussian distributions cannot be fit to the sum of two Gaussian functions, as found for more concentrated gels right at the solidification transition.⁶¹ We therefore interpret the highly non-Gaussian distributions as indicators of solidification via gelation.⁶² The structure of the gels in Fig. 1 and 3, and in particular the thick strands of the networks, suggest that confinement induces only a shallow quench into an arrested state.⁶³

Fig. 7 Self part of the van Hove correlation function G_s(Δx, τ) at a lag time τ = 10 s for large particles in binary suspensions with (a–c) c_p ≈ 5 mg mL⁻¹ and (d–f) and c_p ≈ 25 mg mL⁻¹. The volume percent of small particles r is (a and d) 0.00, (b and e) 0.50, (c and f) 0.75. Dashed lines indicate fits to a Gaussian distribution. Confinement thicknesses h/2a_L: >69 (○), 41 (△), 20 (◊), 10 (▽), and <5.5 (◁).

Increasing the concentration of the depletant polymer leads to a narrower distribution of particle displacements, as shown in Fig. 7d–f. The tails of G_s(Δx, τ) deviate strongly from a Gaussian function even for a bulk sample, consistent with a distribution of characteristic relaxation times in a fluid of highly bidispersed clusters as seen in the micrographs in Fig. 1. The shape of G_s(Δx, τ) does not significantly evolve upon confinement, but the widths of the distribution become increasingly narrow. The r = 0.75 sample exhibits the narrowest distribution of displacements in strong confinements, again consistent with our suggestion that the addition of small particles increases the effective caging of the large particles. We conclude from the MSD and van Hove distributions that confinement induces increasingly solid-like behavior in all samples studied. This increase is consistent with an increase in the strength of the effective interparticle attraction, which is further enhanced by bidispersity.

IV Discussion

In this paper, we show that the dynamics of bidispersed suspensions with both a weak interparticle repulsion and a weak interparticle attraction become increasingly solid-like as the suspensions are increasingly confined. We previously observed similar confinement-induced solidification in monodispersed suspensions.^40,41 In our earlier reports, we attributed this solidification to an enhanced depletion attraction due to loss of free volume for the polymer at the two walls of the chamber. Simulations of two large spheres confined between two walls, however, revealed only a very small increase in the effective strength of the depletion attraction,⁶⁴ and very recent simulations that measured the depletion attraction between two particles near a single wall found no enhanced attraction.⁶⁵ Another mechanism must therefore dominate the observed solidification in our confined colloid–polymer mixtures.

One possible alternate mechanism is a change in the electrostatic interactions between particles in confined samples. PMMA particles suspended in a CXB–DHN solvent mixture are slightly charged, with ∼150–400 charges on the surface of each particle.⁵⁸ Although earlier studies showed that electrostatic interactions between PMMA particles can vary significantly over time,⁵² our solidification transition does not depend upon the sample age or time of confinement. Instead, we considered the behavior of the counterions in the solvent. The CXB–DHN solvent mixture has a low dielectric constant (ε_r = 5.53, ESI†); nonetheless, counterions must exist in this solvent mixture to partially screen the charges on the particles. We assessed the effect of nearby surfaces on the concentration of counterions in CXB–DHN mixtures by measuring the conductivity of CXB–DHN in a bulk sample and in a sample that contained 40% v/v of powdered glass for samples at different bulk salt concentrations. The conductivity of the solvent mixture in the samples that contained powdered glass was always less than that of the bulk solvent mixture (Fig. S7 in ESI†), consistent with a decrease in the number of counterions in solution. As the samples are closed, the counterions in this experiment must adsorb onto the powdered glass surfaces or the vial surface. We posit that charge adsorption can drive confinement-induced solidification in our system: as charges from the particles and counterions in the solution adsorb onto the walls of the chamber, the interparticle repulsion is reduced. Ref. 57 reported that the zeta potential decreased and the screening length increased with increasing confinement for PMMA particles suspended in dodecane,⁵⁷ in accord with this idea. Simple calculations in ref. 58 indicate that PMMA particles with lower surface charge and longer screening lengths exhibited repulsive barriers of less than 2 k_BT in the CHB–DHN solvent mixture.⁵⁸ In our experiments, a similarly dramatic reduction in the maximum repulsion would cause the interparticle potential to develop an attractive minimum at contact (for c_p ≈ 5 mg mL⁻¹, the magnitude of the depletion attraction is 6–11 k_BT (Fig. S1†), sufficient in the absence of repulsion to gel the suspension³¹) or to deepen the minimum (for c_p ≈ 25 mg mL⁻¹). Changes in the electrostatic interactions could therefore account for the transition from a dispersed or clustered fluid in bulk to a well-connected network of particles in highly confined samples (Fig. 1). This mechanism is a secondary indirect effect of confinement, as the walls mediate the electrostatic interactions between particles. We note that this mechanism is complementary to a different mechanism proposed for electrostatically-driven gelation in small particle suspensions, in which an entropic driving force from the counterions favors gelation in certain conditions.³⁷ Although both mechanisms may be simultaneously operating here, our experimental system does not allow these mechanisms to be separately distinguished.

We find, additionally, that bidispersity enhances solidification as the samples are increasingly confined. The magnitude of the MSD of the large particles decreases for all samples as the bidispersity is increased at fixed confinement thickness (as shown in Fig. 4 and 5), consistent with clustering and gelation driven by enhanced attraction. This enhancement is somewhat counterintuitive, as the repulsive interparticle potential between the small and large particles is still significantly larger than the polymer-induced depletion attraction, but is expected based on comparisons with earlier work on monodispersed PMMA–PS depletion systems with competing long-range repulsions and short-range attractions.³⁶ In those systems, large electrostatic repulsions between particles do not prevent clustering and gelation even when the interparticle attraction is weak.^32–39 Similarly, we find that despite the large electrostatic repulsions between particles of different sizes, the addition of small particles leads to increased arrest of the large particles.

The mechanism for the increase in solid-like behavior with increased small particle volume ratio is not known, and we suggest two possibilities. First, a fixed volume of small particles has more total surface area than an equal volume of large particles. The increase in surface area may facilitate transfer of charge from the particles to the walls, so that the electrostatic repulsion between the large and small particles is reduced in the bidispersed suspensions. Second, simulations of charged binary spheres showed that electrostatic repulsions between large and small particles led to a strong attractive depletion interaction between large spheres; in this system, charge increased the free volume available to the small particles and thus enhanced the attraction.⁶⁶ This electrostatically-driven depletion interaction may also be indirectly strengthened by confinement. Either or both mechanisms would increase the effective attraction between particles and thus drive increasingly solid-like behavior in confined bidispersed systems, in agreement with our experimental observations.

V Conclusions

We investigate the effects of confinement on the solidification of mixtures of polymers and bidispersed colloidal particles in a low-dielectric constant solvent by measuring the dynamics of the large particles. We find that replacing some of the large particles with small particles leads to slowed dynamics, which reflect heterogeneous clustering and ultimately gelation when the volume percent of small particles is large. Confining these suspensions to approximately twenty large particle diameters leads to a significant slowing of the dynamics, indicating increased clustering even in relatively thick samples at low concentrations of polymer depletant. Samples that in bulk are fluids of clusters do not solidify, until confined to thicknesses of ten large particle diameters, the typical onset of geometric confinement in hard-sphere colloidal suspensions, even when the volume percent of small particles is large. For large concentrations of polymer, the combined effects of small particles and confinement lead to increased arrest of the large particles. In all samples, the increasingly solid-like behavior of confined samples is consistent with an increase in the effective interparticle attraction. The measured decrease in the conductivity of the solvent mixture in confined samples suggests that adsorption of charge carriers on nearby walls induces a reduction in the interparticle electrostatic repulsion, so that changes in the interactions are an indirect secondary effect of confinement. Increasing the bidispersity by replacing large particles with small particles may facilitate transfer of charges to the walls or may induce an additional attractive depletion interaction; both mechanisms would generate the increase in effective attraction in confined bidispersed samples that we observe in our experiments.

We note that we have studied only one size ratio of small to large colloids, a_S/a_L ≈ 0.49. Suspensions with a different size ratio exhibit different state transitions,⁶⁷ which we speculate will affect their solidification in confined geometries. Similarly, we have studied only one size of polymer, R_g ≈ 15 nm, for which ξ_S = R_g/a_S ≈ 0.041 and ξ_L = R_g/a_L ≈ 0.020. Size ratios of ξ_L > 0.08 can exhibit re-entrant melting transitions when the volume fraction of particles is very high:^68,69 tuning the size of the polymer to obtain re-entrant melting may lead to unusual phase behavior in confined geometries. In addition, we have not systematically investigated the confinement-induced solidification transition by studying the dynamics at heights h/2a_L that are very close to that at which the transition occurs. Comparing this transition to that driven by increases in r or ϕ_T is expected to generate insight into the mechanisms driving solidification in confinement, and in particular the complex role of electrostatics^66,70 in the presence of depletion interactions.⁷¹ Finally, we propose here that charge carriers in the suspension adsorb onto the surfaces of the chamber, which in our experiments were unmodified glass slides, to reduce the electrostatic repulsion between particles. Chambers with different surface chemistry may exhibit differences in charge adsorption, thereby modifying or disrupting this mechanism.

Our results suggest new ways to tailor the design of technological suspensions; examples include drilling fluids, viscosifiers, and gellants, in which suspensions must flow like fluids in bulk geometries but solidify in complex porous media, and polymer nanocomposites, which are often processed as thin films. In these examples, the presence of organic solvents and/or constituents suggests that long-range electrostatic interactions may sensitively affect the solidification of suspended particulates. We expect that confined bidispersed attractive suspensions will exhibit flow properties that differ from those of bulk monodispersed suspensions, requiring careful rheological studies across a range of confinements and interparticle potentials.

Acknowledgements

This work was supported by the American Chemical Society Petroleum Research Fund (52537-DNI). We thank J. D. Rimer for access to a dynamic light-scattering instrument for measurements of the particle sizes and a conductivity meter for measurements of solvent conductivity, C. Knutson-Huddleston for assistance with the conductivity measurements, and two anonymous referees for insightful comments.

References

1. V. Kelessidis, R. Maglione, C. Tsamantaki and Y. Aspirtakis, J. Pet. Sci. Eng., 2006, 53, 203–224.
2. R. Ponnapati, O. Karazincir, E. Dao, R. Ng, K. K. Mohanty and R. Krishnamoorti, Ind. Eng. Chem. Res., 2011, 50, 13030–13036.
3. G. C. Maitland, Curr. Opin. Colloid Interface Sci., 2000, 5, 301–311.
4. B. Derby and N. Reis, MRS Bull., 2003, 28, 815–818.
5. J. Ebert, E. Oezkol, A. Zeichner, K. Uibel, O. Weiss, U. Koops, R. Telle and H. Fischer, J. Dent. Res., 2009, 88, 673–676.
6. H. Lee, K. Chou and K. Huang, Nanotechnology, 2005, 16, 2436–2441.
7. A. M. J. van den Berg, P. J. Smith, J. Perelaer, W. Schrof, S. Koltzenburg and U. S. Schubert, Soft Matter, 2007, 3, 238–243.
8. B. Y. Ahn, E. B. Duoss, M. J. Motala, X. Guo, S.-I. Park, Y. Xiong, J. Yoon, R. G. Nuzzo, J. A. Rogers and J. A. Lewis, Science, 2009, 323, 1590–1593.
9. B. Y. Ahn, D. Shoji, C. J. Hansen, E. Hong, D. C. Dunand and J. A. Lewis, Adv. Mater., 2010, 22, 2251–2254.
10. A. Bansal, H. Yang, C. Li, K. Cho, B. Benicewicz, S. Kumar and L. Schadler, Nat. Mater., 2005, 4, 693–698.
11. Y. Liu, A. Wang and R. Claus, J. Phys. Chem. B, 1997, 101, 1385–1388.
12. A. Pasquier, H. Unalan, A. Kanwal, S. Miller and M. Chhowalla, Appl. Phys. Lett., 2005, 87, 203511.
13. B. Safadi, R. Andrews and E. Grulke, J. Appl. Polym. Sci., 2002, 84, 2660–2669.
14. A. Sellinger, P. Weiss, A. Nguyen, Y. Lu, R. Assink, W. Gong and C. Brinker, Nature, 1998, 394, 256–260.
15. P. Pieranski, L. Strzelecki and B. Pansu, Phys. Rev. Lett., 1983, 50, 900–903.
16. D. Van Winkle and C. A. Murray, J. Chem. Phys., 1988, 89, 3885–3891.
17. C. R. Nugent, K. V. Edmond, H. N. Patel and E. R. Weeks, Phys. Rev. Lett., 2007, 99, 025702.
18. K. Watanabe, T. Kawasaki and H. Tanaka, Nat. Mater., 2011, 10, 512–520.
19. K. Pickrahn, B. Rajaram and A. Mohraz, Langmuir, 2010, 26, 2392–2400.
20. E. Sanz, M. E. Leunissen, A. Fortini, A. Van Blaaderen and M. Dijkstra, J. Phys. Chem. B, 2008, 112, 10861–10872.
21. E. Sanz, C. Valeriani, T. Vissers, A. Fortini, M. E. Leunissen, A. Van Blaaderen, D. Frenkel and M. Dijkstra, J. Phys.: Condens. Matter, 2008, 20, 494247.
22. E. Russell, J. Sprakel, T. Kodger and D. A. Weitz, Soft Matter, 2012, 8, 8697–8703.
23. K. Yoshizawa, N. Wakabayashi, M. Yonese, J. Yamanaka and C. Royall, Soft Matter, 2012, 8, 11732–11736.
24. A. Mohraz, E. R. Weeks and J. A. Lewis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 060403.
25. D. C. Viehman and K. S. Schweizer, J. Chem. Phys., 2008, 128, 084509.
26. H. N. W. Lekkerkerker, W. C. K. Poon, P. N. Pusey, A. Stroobants and P. B. Warren, Europhys. Lett., 1992, 20, 559–564.
27. S. M. Ilett, A. Orrock, W. C. K. Poon and P. N. Pusey, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 1344–1352.
28. W. C. K. Poon, A. Pirie and P. N. Pusey, Faraday Discuss., 1995, 101, 65–76.
29. W. C. K. Poon, J. Phys.: Condens. Matter, 2002, 14, R859–R880.
30. P. J. Lu, J. C. Conrad, H. M. Wyss, A. B. Schofield and D. A. Weitz, Phys. Rev. Lett., 2006, 96, 028306.
31. P. J. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino and D. A. Weitz, Nature, 2008, 453, 499–504.
32. A. Stradner, H. Sedgwick, F. Cardinaux, W. C. K. Poon, S. U. Egelhaaf and P. Schurtenberger, Nature, 2004, 432, 492–495.
33. H. Sedgwick, S. U. Egelhaaf and W. C. K. Poon, J. Phys.: Condens. Matter, 2004, 16, S4913–S4922.
34. A. I. Campbell, V. Anderson, J. S. Van Duijneveldt and P. Bartlett, Phys. Rev. Lett., 2005, 94, 208301.
35. C. P. Royall, D. G. Aarts and H. Tanaka, J. Phys.: Condens. Matter, 2005, 17, S3401.
36. C. L. Klix, C. P. Royall and H. Tanaka, Phys. Rev. Lett., 2010, 104, 165702.
37. J. D. Schmit, S. Whitelam and K. Dill, J. Chem. Phys., 2011, 135, 085103.
38. T. H. Zhang, J. Klok, R. H. Tromp, J. Groenewold and W. K. Kegel, Soft Matter, 2012, 8, 667.
39. C. L. Klix, K.-i. Murata, H. Tanaka, S. R. Williams, A. Malins and C. P. Royall, Sci. Rep., 2013, 3, 2072.
40. M. Spannuth and J. C. Conrad, Phys. Rev. Lett., 2012, 109, 028301.
41. M. Spannuth and J. C. Conrad, AIP Conf. Proc., 2013, 1518, 351–356.
42. E. Flenner, M. Zhang and G. Szamel, Phys. Rev. E.: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 051501.
43. T. Sentjabrskaja, E. Babaliari, J. Hendricks, M. Laurati, G. Petekidis and S. U. Egelhaaf, Soft Matter, 2013, 9, 4524–4533.
44. S. Shenoy, R. Sadowsky, J. Mangum, L. H. Hanus and N. J. Wagner, J. Colloid Interface Sci., 2003, 268, 380–393.
45. P. Yates, G. Franks and G. Jameson, Colloids Surf., A, 2008, 326, 83–91.
46. M. Fasolo and P. Sollich, J. Chem. Phys., 2005, 122, 074904.
47. R. Evans, D. Fairhurst and W. Poon, Phys. Rev. Lett., 1998, 81, 1326–1329.
48. S. M. Liddle, T. Narayanan and W. C. K. Poon, J. Phys.: Condens. Matter, 2011, 23, 194116.
49. K. N. Pham, G. Petekidis, D. Vlassopoulos, S. U. Egelhaaf, W. C. K. Poon and P. N. Pusey, J. Rheol., 2008, 52, 649–676.
50. L. Antl, J. W. Goodwin, R. Hill, R. H. Ottewill, S. Owens, S. Papworth and J. Waters, Colloids Surf., 1986, 17, 67–78.
51. A. D. Dinsmore, E. R. Weeks, V. Prasad, A. C. Levitt and D. A. Weitz, Appl. Opt., 2001, 40, 4152–4159.
52. A. Yethiraj and A. Van Blaaderen, Nature, 2003, 421, 513–517.
53. G. Berry, J. Chem. Phys., 1966, 44, 4550–4564.
54. D. G. A. L. Aarts, R. Tuinier and H. N. W. Lekkerkerker, J. Phys.: Condens. Matter, 2002, 14, 7551–7561.
55. G. Fleer and R. Tuinier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 041802.
56. S. Asakura and F. Oosawa, J. Chem. Phys., 1954, 22, 1255–1256.
57. M. F. Hsu, E. R. Dufresne and D. A. Weitz, Langmuir, 2005, 21, 4881–4887.
58. C. P. Royall, W. C. K. Poon and E. R. Weeks, Soft Matter, 2013, 9, 17–27.
59. J. C. Crocker, J. Matteo, A. D. Dinsmore and A. G. Yodh, Phys. Rev. Lett., 1999, 82, 4352–4355.
60. J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310.
61. Y. Gao and M. L. Kilfoil, Phys. Rev. Lett., 2007, 99, 078301.
62. C. J. Dibble, M. Kogan and M. J. Solomon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 050401.
63. C. J. Dibble, M. Kogan and M. J. Solomon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 041403.
64. C. Xiao, J. Guo and P. Hu, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 061403.
65. V. Pryamitsyn and V. Ganesan, J. Chem. Phys., 2013, 138, 234905.
66. M. Peláez-Fernández, J. Callejas-Fernández and A. Moncho-Jorda, Eur. Phys. J. E, 2012, 35, 120.
67. M. Dijkstra, R. van Roij and R. Evans, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 5744–5771.
68. K. A. Dawson, G. Foffi, M. Fuchs, W. Götze, F. Sciortino, M. Sperl, P. Tartaglia, T. Voigtmann and E. Zaccarelli, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 63, 1–17.
69. K. N. Pham, S. U. Egelhaaf, P. N. Pusey and W. C. K. Poon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 011503.
70. D. Bratko, B. Jönsson and H. Wennerström, Chem. Phys. Lett., 1986, 128, 449–454.
71. A. R. Denton and M. Schmidt, J. Chem. Phys., 2005, 122, 244911.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c3sm51879e

---