Regularization of the slip length divergence in water nanoflows by inhomogeneities at the Angstrom scale

Abstract

We performed non-equilibrium Molecular Dynamics simulations of water flow in nano-channels with the aim of discriminating static from dynamic contributions of the solid surface to the slip length of the molecular flow. We show that the regularization of the slip length divergence at high shear rates, formerly attributed to the wall dynamics, is controlled instead by its static properties. Surprisingly, we find that atomic displacements at the Angstrom scale are sufficient to remove the divergence of the slip length and realize the no-slip condition. Since surface thermal fluctuations at room temperature are enough to generate these displacements, we argue that the no-slip condition for water can be achieved also for ideal surfaces, which do not present any surface roughness.

---

1 The debate about slip length divergence

In the pioneering paper,¹ it was shown that the Navier slip boundary condition u_s = [small script l]_s[small gamma, Greek, dot above] can be regarded as the low-shear limit of a universal, nonlinear relation between slip velocity u_s, the slip length [small script l]_s, and the local shear rate [small gamma, Greek, dot above] that presents a divergence of the slip length upon approaching a critical value of the shear rate. The onset of divergence is observed at [small gamma, Greek, dot above] ≃ 10¹⁰ s⁻¹, both for argon¹ and for water,² a value which has been accessible so far only to numerical simulations, although the interest in the regime of ultrahigh shear rates is rapidly growing: commercial, industrial-grade fixed-geometry fluid processors like the microfluidizer (Microfluidics Corp, MA, USA) operate at shear rates exceeding 10⁷ s⁻¹ to achieve uniform particle size reduction in emulsions and dispersions, to create nanoencapsulations or to produce cell rupture. Rheometers such as the piezoaxial vibrator³ and the torsion resonator⁴ are employed to measure the viscosity of fluids at rates up to 10⁷ s⁻¹, e.g., for the characterization of ink jet fluid rheology.^5,6 Laser-induced shock-waves in confined water,⁷ with speed up to Mach 6 in a 5 μm thick water slab yield even larger numbers, which are of the order of 10⁹ s⁻¹. A more detailed knowledge of the properties of fluids at ultrahigh shear rates has therefore become a compelling task. The issue of slip length divergence, however, is of special fundamental interest, as it provides test bed for our understanding of the fluid–solid interactions, and of the minimum requirements for the stability of the fluid slip.

In the approximately fifteen years since the publication of work, ref. 1, violations,^8–10 as well as confirmations^11–15 of the existence of a slip length divergence have been reported, preventing the emergence of a clear consensus on the dependence of fluid slippage properties not only on the imposed shear, but also on the static and dynamic surface inhomogeneities. This lack of consensus calls for further investigations, since controlling and predicting the behavior of water in nanochannels, where surface properties have a profound effect on flow dynamics, stands as a major scientific challenge with many practical applications in modern science and technology. Indeed, an accurate understanding of nanoscale friction phenomena at fluid–solid interfaces is paramount to the design of micro and nanofluidic devices aimed at optimizing mass transport against an overwhelming dissipation barrier.^16–20

The effects of static properties of the fluid–solid interface, such as the contact angle and surface roughness, on slippage phenomena have been investigated in depth in the recent past,^{1,10,14,15,21–27} not to mention the growing interest in microtextured and superhydrophobic materials.^28–37 Recent simulations, for example, suggested that the correlation between hydrophobicity and high slippage could be less stronger than expected so far, since some model hydrophilic surfaces can show slip behavior typical of hydrophobic ones.²⁵ Even though mesoscopic methods have been shown to reproduce quantitatively the results of the molecular dynamics of simple liquids,³⁸ the description at an atomistic level of both the fluid and the surface is crucial in these kinds of investigations, as even very small changes in the chemical or physical properties of the surface can result in remarkably different static and dynamic properties of the fluid, like, for example, in the case of hydroxylated surfaces.^39,40 The role of dynamic properties, such as the wall flexibility and thermal conductivity, remains, however, much less explored.^9,41,42 Most importantly, the geometric effects due to inhomogeneities of flexible walls, have never been disentangled systematically from the dynamic ones. A recent analysis pointed out that all investigations to date which report the absence of a divergent slip length under large shear were performed with flexible walls capable of exchanging momentum and energy with the fluid.⁴³ From this observation, and supported by additional numerical calculations and analytical models, the authors of ref. 43 concluded that heat and momentum transfer from the fluid to the wall are responsible for the observed saturation of the slip length at high shear rates, as opposed to the divergent behavior which takes place using rigid walls. This picture has been questioned in ref. 44 where the authors attributed the divergence to the use of a thermostat applied to the fluid molecules. Instead of a saturation of the slip length at a high shear rate, these authors report a slippage drop toward the non-slip condition due to fluid heating. With the amount of slippage at high shear rates being reported by different authors to either vanish, reach a constant finite value, or to diverge, the present picture appears rather controversial. More importantly, no clear consensus has yet emerged on the role of different physical quantities governing the transition from a finite to a divergent slip length.

We present here the results of a series of simulations performed with the aim of discriminating contributions to the slip length which are of a purely dynamical origin, from those whose origin is rooted in the surface configurational properties. To this end, we have performed simulations of water flow in channels with flexible walls varying the masses m of the wall atoms and, independently, the harmonic constant k of the potential that binds wall atoms to their lattice sites (see Fig. 1). According to our findings, this approach proves key to shed new light on the slip length behavior at high shear rates. More precisely, we report numerical evidence that it is the presence of an even extremely tiny amount of disorder in the atomic positions at the surface, rather than wall flexibility, which proves to be responsible for taming slip length divergence and making it shear-independent.

Fig. 1 Simulation snapshots of a portion of the solid surface and corresponding potential energy isosurfaces for a single water molecule at energies k_BT, 2k_BT and 3k_BT, respectively from the highest to the lowest color saturation. The vertical position of the isosurfaces is magnified by a factor 5. Panel (a), the standard surface with no atomic displacement; panel (b), random quenched functionalization with no atomic displacement and panel (c), random quenched functionalization with atomic displacement .

2 Non-equilibrium Molecular Dynamics simulations of shear flow

Using an in-house modified version of the Gromacs suite⁴⁵ in order to impose Couette flow, we simulated a slab of water molecules confined between two graphite-like walls, each consisting of three atomic layers. The water molecules are modelled using the SPC/E potential,⁴⁶ and the electrostatic interaction is calculated using the smooth particle mesh Ewald method,⁴⁷ together with Yeh–Berkowitz correction⁴⁸ to remove the contribution from periodic images along the wall normal. The distance between the two atomic planes in direct contact with water defines the channel width L = 6.306 nm, while the entire, rectangular simulation cell is 13.035 by 16.188 by 8.0 nm along x, y and z, respectively, with the wall surface normals along the z-direction. The integration time step for the equations of motion was Δt = 1 fs, and the Couette flow was realized by displacing the positions of the atomic walls every time step by a fixed amount ±u_wΔt, in addition to the usual movement arising from the integration of the equation of motion. In this way, a constant walls speed ±u_w for the upper and lower walls, respectively, is obtained. At the stationary state, the velocity profile (see Fig. 3) is linear over almost the complete extension of the channel, and deviates from it only at distances from the wall which are smaller than the size of a water molecule. By fitting the slope of the fluid velocity, i.e. the effective shear rate, [small gamma, Greek, dot above]_eff = ∂v_x/∂z it is possible to obtain the slip length from its geometrical definition of the distance from the wall at which the (extrapolated) fluid velocity |∂v_x/∂z|(L/2 + [small script l]_s) is equal to the imposed wall speed v_w,

It has to be noted that the effective shear rate γ_eff depends implicitly on the channel width L through the fluid–surface interaction properties, so that eqn (1), rather than an expression of the slip length in terms of known quantities, is merely a conversion between different ways (slip length and effective shear rate) of measuring the slippage phenomenon: if the slip length is found, e.g., to be independent of the channel width, then the effective shear rate will have to depend on it so as to satisfy eqn (1), and vice versa. Note also that in this work the symbol [small gamma, Greek, dot above] will be used to denote the imposed shear rate, [small gamma, Greek, dot above] = 2u_w/L, not to be confused with the effective shear rate [small gamma, Greek, dot above]_eff that develops in the fluid.

The viscosity and friction coefficient can be expressed in terms of the force acting on the surface atoms f as η = f/[small gamma, Greek, dot above]_eff and λ = f/u_w,²⁰ respectively, but their ratio is independent of f and equal to u_w/[small gamma, Greek, dot above]_eff, which allows us to interpret the slip length as a measure of the balance between frictional and viscous forces

[small script l]_s = η/λ − L/2, (2)

in analogy with eqn (1), where the slip length can be expressed through the ratio between imposed and effective shear rates. Likewise, the dependence on the channel width L is not as straightforward as it seems, since the friction coefficient λ depends on the number of water molecules interacting with the wall and, in turn, on the channel width.

It could be argued that the appearance of the quantity L in eqn (1) and (2) introduces an element of indetermination in the definition of the slip length if the walls are rough, as in this case the channel width (that is, the position of the hydrodynamic boundary) is not well defined. Partial solutions to these problems have been reported in the literature. For example, in a work that introduces the tunable slip length in DPD simulations,⁴⁹ and that has been successfully applied in the simulation of, e.g., nanoconfined electrophoresis⁵⁰ and electroosmotic flows,⁵¹ it was pointed out that the slip length and the position of the unknown hydrodynamic boundary can be determined by performing both a Couette and a Poiseuille experiment. In the present case, however, the situation is complicated by the fact that in a Poiseuille flow, in contrast to the Couette flow, the whole spectrum of shear rates is probed, and this would have added possibly even more detrimental indetermination, since in the present work we concentrate on the dependence of the slip length on the shear rate itself. By and large, using a fixed position for the hydrodynamic boundaries is probably the best compromise, although in this way the slip length has to be considered an effective one that incorporates a possible shift of the real hydrodynamic boundary: higher order corrections could be probably introduced by replacing the geometrical width of the channel with the effective water slab thickness obtained from the density profile, but these corrections are outside the scope of this paper.

We investigated two different setups, with respect to the wall–water interatomic interaction potential. In the first setup, hereafter identified as “standard”, the interaction between wall and the oxygen atoms in the water molecules is prescribed by a Lennard-Jones potential U(r) = C₁₂r⁻¹² − C₆r⁻⁶ with C₆ = 2.47512 × 10⁻³ (kJ nm⁻⁶) and C₁₂ = 2.836328 × 10⁻⁶ (kJ nm⁻¹²)⁵² up to an interatomic distance r of 0.9 nm. Above that distance, the potential is smoothly switched to zero at r = 1.2 nm, using a fourth order polynomial. The second setup is a random quenched functionalization of the first, realized by making 40% of wall atoms purely repulsive (C₆ = 0), and increasing the interaction strength of the remaining ones by a factor α = 1.977. This generates an intrinsic, mainly horizontal inhomogeneity of the surface, e.g. see panel (b) in Fig. 1. The value of α has been chosen such that water equally wets the surfaces of the two setups, resulting in comparable macroscopic contact angles.⁵³ Given the known dependence of the slip length on the contact angle,²⁴ equal wetting is prerequisite to compare the slip length along two microscopically different surfaces and understand to what extent the slip length is affected by different types of surface inhomogeneities, rather than by the contact angle.

For each of the surface type just described, we simulated a flexible and a rigid variant. The flexible variant is realized by tethering the atoms of each wall's outermost layer to their respective lattice sites via a harmonic potential The spring constant k defines the characteristic excursion of the tethered atoms, so that a small value of k leads to a high effective inhomogeneity. The density profiles of water molecules and surface atoms across the channel for two selected values of ξ are shown in Fig. 3. Both profiles are more sharply peaked in the small excursion case, but the effect is significant only next to the surface, and diminishes greatly by the second density peak. In both cases the flow velocity is well represented by the Couette flow solution, even in regions near the wall where the density of water becomes negligible.

The rigid variant, in contrast, is realized by freezing all surface atoms either at their lattice site positions (corresponding effectively to ξ = 0), or in a configuration taken from the equilibrium trajectory of the flexible variant with finite ξ, which we will denote by m = ∞. Both mobile and fixed wall atoms interact with water only, and not among themselves. By varying the mass m of the tethered molecules, it is possible to achieve a separate control over dynamic properties, as the value of m does not influence configurational properties (e.g.: particles distribution, free energies, contact angles), but only dynamical ones, like water–surface friction and thermal conductivity. As a result, we are able to assess the dependence of the slip length on dynamic, static and non-equilibrium properties, controlled by the mass and mean excursion of the wall atoms and by the imposed shear. While this model is surely not a completely realistic representation of a real surface, it allows us to explore in general terms the dependence of the slip length on the magnitude of surface inhomogeneities. It is worth noting that in this work we investigate fluctuations with an extension that is not large enough to model what usually goes under the name of surface roughness. Instead, we are reaching with continuity the limit of very small surface fluctuations, such as those caused by thermal motion.

Fig. 1 shows the potential energy isosurfaces for three different cases. While the spatial functionalization (b) already introduces a noticeable perturbation of the energy landscape, the addition of an even tiny spatial displacement of the surface atoms (c) generates the largest perturbation.

3 The slip length divergence and its regularization

As a first step, with the mass of surface atoms held at a constant m = 1.2 × 10³ amu (to efficiently integrate the equations of motion of the tethered atoms even with the largest spring constant) we investigated the shear rate dependence of the slip length for different displacements ξ. Providing useful information about the scales which come into play in the determination of slippage properties, we present an overview of this dependence for both the standard and randomized surfaces in Fig. 2. Five different cases were explored for the random quenched surface, between the values ξ = 0 and ξ ≃ 0.11 nm (k = 200 kJ mol⁻¹ nm⁻²), the former mimicking an infinite spring constant, and the latter corresponding to the one proposed as optimal in ref. 43. The smallest but still finite value, ξ ≃ 0.0027 nm, was chosen to model a nearly flat wall which yet retains dynamical features.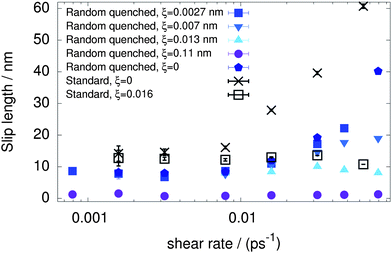

Fig. 2 Slip length as a function of the shear rate for different surface types. Very small values of excursion ξ remove the slip length divergence for both surface types. The wall atom mass is m = 1.2 × 10³ amu.

When the wall atoms are perfectly flat (ξ = 0), both surface types show a tendency towards a larger—in fact divergent—slip length at increasing shear. It takes only sub-nanoscopic excursions of wall atoms to remove the divergence and make the slip length shear independent. The slip length is shear-independent (constant) also for large values of ξ, however, the constant value does increase with the spring constant k (decreasing excursion ξ) to a limiting value of about 8 nm for the random quenched surface and a slightly larger one for the standard surface. The maximum limiting value for shear-independent slip lengths is reached at ξ_c ≃ 0.01 nm. For smaller mean excursions, the slip length is no longer shear-independent and a divergent-like behavior is observed instead. At first glance, a characteristic excursion ξ = 0.01 nm might appear to be surprisingly small, but we note that several other important scales in this system, such as the width of the 1 k_BT energy basin of a water molecule in the direction normal to the surface (see Fig. 1), and the distance δ ≃ 0.03 nm travelled by a water molecule during its translational relaxation time of τ_r ≃ 0.1 ps.⁵⁴ These, however, are only considerations about the orders of magnitude of several processes occurring in the system, and a true microscopic explanation of why a length of 0.01 nm is enough to trigger the transition from a divergent to a constant slip length is missing.

The transition from shear-independent to a divergent slip length is made even more evident by plotting the slip length as a function of ξ (Fig. 4) for two selected shear rates, [small gamma, Greek, dot above] ≃ 0.016 ps⁻¹ at the upper end of the low shear-rates plateau, and [small gamma, Greek, dot above] ≃ 0.08 ps⁻¹ well into the shear region where divergence is observed. At the lower shear rate, saturation is reached for excursions smaller than ξ_c ≃ 0.01 nm, whereas the high-shear rate slip length keeps increasing, seemingly unaffected.

Fig. 3 Left axis: the density distribution of tethered atoms (thin lines) and water molecules (thick lines) in the random quenched case at ξ ≃ 0.07 nm (solid) and ξ ≃ 0.016 nm (dashed). Right axis: water velocity profiles at the shear rate [small gamma, Greek, dot above] ≃ 0.016 ps⁻¹ (squares: ξ ≃ 0.07 nm and circles: ξ ≃ 0.016 nm).

Fig. 4 Slip length as a function of the excursion for two different values of the shear rate (squares: [small gamma, Greek, dot above] = 0.016 ps⁻¹ and circles: [small gamma, Greek, dot above] = 0.08 ps⁻¹). Tethered atoms have a mass of 1.2 × 10³ amu.

From the analysis presented thus far, the role of wall flexibility remains unclear, as this dynamical aspect was not separated out from the other features. For this reason, we selected two extreme values of excursion (ξ = 0.0027 and 0.11 nm) and calculated the slip length for several values of the tethered masses m, including the case of atoms fixed in one equilibrium configuration, m = ∞, as described before.

Results from these calculations are shown in Fig. 5. At low shear rates ([small gamma, Greek, dot above] < 10⁻² ps⁻¹) both values of ξ demonstrate marked changes to the slip length with the mass m. The small excursion case ξ = 0.0027 nm halves the slip length from the lowest mass m = 1.2 × 10³ amu to m = ∞, and in the ξ = 0.11 nm case the slip length is reduced to zero at m = ∞. The transition from thermally insulating walls (m = ∞) to conducting walls is therefore associated with a substantial increase in the slip length. In other words a flexible wall reduces friction on the fluid (therefore, increasing the slip length) by being capable of adjusting locally to the flux of water molecules. In the extreme case of m = ∞, the slip length divergence is indeed removed, provided that the excursion ξ is larger than ξ_c. This provides evidence that the flexibility cannot be responsible for the regularization of the slip length at high shear-rates, and acts instead in the opposite direction, by increasing, instead of decreasing, the slip length.

Fig. 5 Slip length as a function of the shear rate in the random quenched case, for ξ ≃ 0.0027 nm (squares: m = 1.2 × 10³ uma; circles: m = 1.2 × 10⁵ uma and upper triangles: m = ∞) and for ξ ≃ 0.11 nm (lower triangles: m = 1.2 × 10³ uma and rhombs: m = ∞). Lower panel: water viscosity as a function of the shear rate. The experimental value η_exp = 515.5 kJ mol⁻¹ ps⁻¹ nm⁻³ at 300 K has been interpolated from reference data.⁵⁵

It is important to note that these are entirely surface-related effects. The viscosity of water η is the only bulk property that appears in the definition of the slip length for a Couette flow, eqn (2), and it does not show any dependence on shear, or spring constant, as shown in Fig. 5, bottom panel. Therefore, we argue that the transition from a divergent to a shear-independent slip length is determined not by the wall flexibility, but rather by the configurational disorder induced by tiny displacements of the wall atoms in the direction normal to the flow.

For Lennard-Jones liquids, Priezjev already noticed⁹ that very small, static displacements of the atomic surface atoms (already 7% of the Lennard-Jones diameter) can have a dramatic influence on the slip length using thermal, random or periodic displacements. The systematic analysis performed here puts previous results in perspective, regarding the important case of water slippage. In particular, to get an appreciation for the physical realism of the characteristic excursion lengths discussed here, we compare them to displacements obtained from the effective spring constants of real graphite at 300 K measured by inelastic X-ray scattering,⁵⁶ which correspond to about 0.006 nm for nearest neighbors, and are much larger for second neighbors. Thermal fluctuations alone are therefore expected to be sufficient to attain a shear-independent slip length for water.

4 Conclusions

We have performed non-equilibrium Molecular Dynamics simulations of water flow in nano-channels with separate control of the flexibility and static inhomogeneity of the wall. The simulations show that the disappearance of the divergence of the slip length at high shear rates, formerly ascribed to wall flexibility, is due instead to the excursion of wall atoms from the ideal horizontal plane. Moreover, these results show that atomic displacements as small as those due to thermal motion at room temperature are sufficient to regulate the divergence of the slip length. We conclude that, even in the absence of surface imperfections such as point defects or dislocations, high-shear water flow in nanoscale channels should not exhibit any divergent slip length and that thermal motion of the wall atoms is sufficient to tame such divergence.

Acknowledgements

We acknowledge M. Chinappi & D. Lohse for useful discussions and E. M. Foard for a careful reading of the manuscript. M. Sega, M. Sbragaglia & L. Biferale kindly acknowledge funding from the European Research Council under the Europeans Community's Seventh Framework Programme (FP7/2007–2013)/ERC Grant Agreement no[279004]. M. Sega acknowledges FP7 IEF p.n. 331932 SIDIS for support.

References

1. P. A. Thompson and S. M. Troian, Nature, 1997, 389, 360–362.
2. This work.
3. J. Crassous, R. Régisser, M. Ballauff and N. Willenbacher, J. Rheol., 2005, 49, 851–863.
4. G. Fritz, W. Pechhold, N. Willenbacher and N. J. Wagner, J. Rheol., 2003, 47, 303–319.
5. M. Moseler and U. Landman, Science, 2000, 289, 1165.
6. D. C. Vadillo, T. R. Tuladhar, A. C. Mulji and M. R. Mackley, J. Rheol., 2010, 54, 781.
7. T. Pezeril, G. Saini, D. Veysset, S. Kooi, P. Fidkowski, R. Radovitzky and K. A. Nelson, Phys. Rev. Lett., 2011, 106, 214503.
8. A. Jabbarzadeh, J. Atkinson and R. Tanner, J. Non-Newtonian Fluid Mech., 1998, 77, 53–78.
9. N. V. Priezjev, J. Chem. Phys., 2007, 127, 144708.
10. A. Martini, A. Roxin, R. Snurr, Q. Wang and S. Lichter, J. Fluid Mech., 2008, 600, 257–269.
11. N. V. Priezjev and S. M. Troian, Phys. Rev. Lett., 2004, 92, 18302.
12. R. S. Voronov, D. V. Papavassiliou and L. L. Lee, J. Chem. Phys., 2006, 124, 204701.
13. Y. Chen, D. Li, K. Jiang, J. Yang, X. Wang and Y. Wang, J. Chem. Phys., 2006, 125, 084702.
14. N. V. Priezjev and S. M. Troian, J. Fluid Mech., 2006, 554, 25–46.
15. N. Priezjev, J. Chem. Phys., 2011, 135, 204704.
16. J. Eijkel and A. van den Berg, Microfluid. Nanofluid., 2005, 1, 249–267.
17. M. Sbragaglia, R. Benzi, L. Biferale, S. Succi and F. Toschi, Phys. Rev. Lett., 2006, 97, 204503.
18. R. Benzi, L. Biferale, M. Sbragaglia, S. Succi and F. Toschi, J. Fluid Mech., 2006, 548, 257.
19. R. Schoch, J. Han and P. Renaud, Rev. Mod. Phys., 2008, 80, 839.
20. L. Bocquet and E. Charlaix, Chem. Soc. Rev., 2010, 39, 1073–1095.
21. L. Bocquet and J.-L. Barrat, Soft Matter, 2007, 3, 685–693.
22. J.-L. Barrat and L. Bocquet, Phys. Rev. Lett., 1999, 82, 4671–4674.
23. J.-L. Barrat and L. Bocquet, Faraday Discuss., 1999, 112, 119–128.
24. D. M. Huang, C. Sendner, D. Horinek, R. R. Netz and L. Bocquet, Phys. Rev. Lett., 2008, 101, 226101.
25. T. A. Ho, D. V. Papavassiliou, L. L. Lee and A. Striolo, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 16170–16175.
26. O. Bäumchen and K. Jacobs, Soft Matter, 2010, 6, 6028–6035.
27. M. Chinappi and C. M. Casciola, Phys. Fluids, 2010, 22, 042003.
28. H. Y. Erbil, A. L. Demirel, Y. Avcı and O. Mert, Science, 2003, 299, 1377–1380.
29. A. Lafuma and D. Quéré, Nat. Mater., 2003, 2, 457–460.
30. C.-H. Choi and C.-J. Kim, Phys. Rev. Lett., 2006, 96, 066001.
31. M. Sbragaglia, A. M. Peters, C. Pirat, B. M. Borkent, R. G. Lammertink, M. Wessling and D. Lohse, Phys. Rev. Lett., 2007, 99, 156001.
32. M. Z. Bazant and O. I. Vinogradova, J. Fluid Mech., 2008, 613, 125–134.
33. A. Peters, C. Pirat, M. Sbragaglia, B. Borkent, M. Wessling, D. Lohse and R. Lammertink, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 29, 391–397.
34. F. Feuillebois, M. Z. Bazant and O. I. Vinogradova, Phys. Rev. Lett., 2009, 102, 026001.
35. S. Schmieschek, A. V. Belyaev, J. Harting and O. I. Vinogradova, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 016324.
36. A. Giacomello, M. Chinappi, S. Meloni and C. M. Casciola, Phys. Rev. Lett., 2012, 109, 226102.
37. A. Giacomello, S. Meloni, M. Chinappi and C. M. Casciola, Langmuir, 2012, 28, 10764–10772.
38. J. Horbach and S. Succi, Phys. Rev. Lett., 2006, 96, 224503.
39. T. A. Ho, D. Argyris, D. V. Papavassiliou and A. Striolo, Mol. Simul., 2011, 37, 172–195.
40. B.-F. Qiao, M. Sega and C. Holm, Phys. Chem. Chem. Phys., 2012, 14, 11425–11432.
41. A. Jabbarzadeh, J. Atkinson and R. Tanner, J. Chem. Phys., 1999, 110, 2612.
42. S. Hanot, M. Belushkina and G. Foffi, Soft Matter, 2013, 9, 291–296.
43. A. Martini, H.-Y. Hsu, N. A. Patankar and S. Lichter, Phys. Rev. Lett., 2008, 100, 206001.
44. A. A. Pahlavan and J. B. Freund, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 021602.
45. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
46. H. Berendsen, J. Grigera and T. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271.
47. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577.
48. I.-C. Yeh and M. L. Berkowitz, J. Chem. Phys., 1999, 111, 3155–3162.
49. J. Smiatek, M. P. Allen and F. Schmid, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 26, 115–122.
50. J. Smiatek and F. Schmid, J. Phys. Chem. B, 2010, 114, 6266–6272.
51. J. Smiatek, M. Sega, C. Holm, U. D. Schiller and F. Schmid, J. Chem. Phys., 2009, 130, 244702.
52. W. F. van Gunsteren, S. R. Billeter, A. A. Eising, P. H. Hunenberger, P. Kruger, A. E. Mark, W. R. P. Scott and I. G. Tironi, Biomolecular Simulation: The GROMOS96 Manual and User Guide, BIOMOS b.v., Groningen, 1996.
53. T. Werder, J. Walther, R. Jaffe, T. Halicioglu and P. Koumoutsakos, J. Phys. Chem. B, 2003, 107, 1345–1352.
54. K. Toukan and A. Rahman, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 2643.
55. J. Kestin, M. Sokolov and W. A. Wakeham, J. Phys. Chem. Ref. Data, 1978, 7, 941–948.
56. M. Mohr, J. Maultzsch, E. Dobardžić, S. Reich, I. Milošević, M. Damnjanović, A. Bosak, M. Krisch and C. Thomsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 035439.

---