 Open Access Article
Open Access ArticleSimulation of edge facilitated adsorption and critical concentration induced rupture of vesicles at a surface†
Pat
Plunkett
*a,
Brian A.
Camley
bc,
Kimberly L.
Weirich
d,
Jacob
Israelachvili
e and
Paul J.
Atzberger
*af
aDepartment of Mathematics, University of California, Santa Barbara, USA. E-mail: atzberg@math.ucsb.edu
bDepartment of Physics, University of California, San Diego, USA
cCenter for Theoretical Biological Physics, San Diego, USA
dDepartment of Physics, University of California, Santa Barbara, USA
eDepartment of Chemical Engineering, University of California, Santa Barbara, USA
fDepartment of Mechanical Engineering, University of California, Santa Barbara, USA
First published on 14th June 2013
Abstract
We investigate the kinetics of supported lipid bilayer formation by the adsorption and rupture of uncharged phosphatidylcholine lipid vesicles on to a solid substrate. We model the adsorption process taking into account the distinct vesicle rupture events and growth processes. This includes (i) the initial adhesion and vesicle rupture that nucleates bilayer islands, (ii) the growth and merger of bilayer islands, (iii) enhanced adhesion of vesicles to the bilayer edge, and (iv) the final desorption of excess vesicles from the substrate. These simulation studies give insight into prior experimental observations of adsorption in which an overloading of lipid on the solid substrate occurs before formation of the final supported lipid bilayer. Our model provides an explanation for the features of the interesting universal master curve that was observed for the surface fluorescence intensity in the experimental investigations of Weirich et al.
1 Introduction and background
Supported Lipid Bilayer (SLB) membranes play an important role in both biophysical studies and in biotechnology. SLBs have been used as a model system for the surface chemistry of biological cells and investigations of processes such as cell signaling and ligand–receptor interactions.1,2 In biotechnology applications SLBs are being used as a platform for the development of new sensors and drug discovery.3,4 The use of vesicle adsorption to form SLBs on a solid support is an appealing experimental approach allowing for the inclusion of membrane proteins in the bilayer, adaptability to complex surface geometries, and an overall faster construction time. However, there are many challenges in determining appropriate processing conditions to obtain reliably high quality SLBs on diverse substrates.5Important factors influencing the adsorption process include the bulk vesicle concentration, the type of solid support and surface treatments during preparation, the solvent pH and ionic concentrations, and the valence of ionic species.6–8 Variations in these factors often have a dramatic effect on the resulting surface adsorption process influencing not only the pathway but even if one achieves any adsorption at all, partial SLB coverage with isolated islands, or a supported vesicle layer (SVL) instead of SLB. Furthermore, these factors also likely strongly affect the particular pathways involved in adsorption by influencing the vesicle stability in bulk solution, the vesicle–vesicle interactions and mobility on the substrate, and the vesicle–substrate adhesion forces.5,6,9
Many experimental studies have been performed to investigate the SLB formation process and possible adsorption pathways. These studies include combined QCM-D studies to monitor surface mass content along with AFM imaging studies to investigate vesicle and bilayer morphology.5–8 Studies on the adsorption of individual GUVs have also been carried out using a two color fluorescence assay to investigate the adsorption of individual GUVs and monitor their adsorbed and ruptured states.10 As a bridge between the scales probed in these prior studies and to provide additional complimentary information about the bulk adsorption, an assay was developed that studies through fluorescence microscopy the total adsorption of lipid on the solid support during the adsorption process.11
In these studies, a regime was often observed in which the solid support appears to become “overloaded” with more lipids than are required to form a SLB before relaxing to a single supported lipid bilayer. A particularly interesting finding is that this overloading appears even when varying the bulk concentration of vesicles in the solution over many decades.11 Furthermore, during adsorption the fluorescence intensity appears to follow a universal master curve: when the fluorescence intensity I(t) for separate experiments with different bulk vesicle concentrations are plotted in terms of the rescaled time t/tmax, they collapse to a single curve. tmax is the time of peak fluorescence intensity, which is observed to be inversely proportional to the bulk vesicle concentration.11 Interesting features of this master curve include (i) an initial regime in which fluorescence increases linearly, (ii) an accelerated regime where the rate of lipid adsorption increases, (iii) a regime where the adsorption rapidly decelerates to approach an unusually sharp peak in fluorescence intensity value followed by, (iv) a rapid decay to a final value consistent with the formation of a SLB. This master curve is shown in Fig. 1.
 | ||
| Fig. 1 Experimental average fluorescence intensity of surface associated lipids. The average fluorescence intensity is shown for a typical adsorption experiment. An initial linear regime is observed for the intensity until reaching a critical value around ∼0.9ISLB. An accelerated regime is then observed for a duration. This is followed by a brief decelerating regime which results in a peak intensity value. The intensity then relaxes to a steady-state value. This fluorescence intensity data is obtained from the experiment reported in ref. 11. | ||
To investigate possible pathways and kinetics to account for these observations, we formulate a theoretical model and perform stochastic simulations of the adsorption process. We take into account the distinct vesicle rupture events and growth processes which include (i) the initial adhesion and vesicle rupture that nucleates bilayer islands, (ii) the growth and merger of bilayer islands, (iii) the hydrophobically enhanced bilayer edge interactions with vesicles, and (iv) the final desorption of excess vesicles from the substrate. Our stochastic simulation approach is based on an inhomogeneous spatial–temporal Poisson process to model the arrival location and time of adsorbed vesicles on the substrate and is based on the conservative Cahn–Hilliard equation to model the formation, evolution, and merging of lipid bilayer islands on the solid substrate. To perform simulations in practice, we have also developed numerical methods based on adaptive mesh refinement discretizations to track efficiently the geometry of the bilayer islands and their dynamics.
Using these approaches, we have found good agreement with the experimental fluorescence intensity data of ref. 11. We find that the observed acceleration in vesicle adsorption and subsequent overloading of lipid on the substrate, as well as the universality of the master curve strongly suggests that vesicles rupture only when they reach a critical local density, nucleating bilayer islands. We argue that vesicles preferentially bind to the bilayer edge, leading to the acceleration of adsorption and an overloading of lipid on the substrate. We find that the universality of the master curve scaling, even when considering very small bulk vesicle concentrations, appears to be a strong indicator against a spontaneous rupture mechanism for the physical system considered in ref. 11. Instead, the universality suggests a mechanism where rupture is initiated by high densities of vesicles on the substrate, and occurs very quickly compared with the rate of adsorption. In addition, in order to develop an overloading of lipid on the substrate, we must require that vesicles that deposit to the edge of bilayer patches are relatively stable, i.e. that edge-induced rupture is slow.
We also find from the experimental observation of overloading, along with our critical density hypothesis, that there is a rather strong constraint imposed on the largest sizes for the bilayer islands that can form by the time of the peak fluorescence intensity. This provides an indication of why in the fluorescence microscopy images no macroscopic bilayer domains appear until a rather late stage in the adsorption process. In particular, adsorption appears to occur in parallel on the substrate as opposed to through a few rather isolated nucleation events that then propagate across the entire substrate domain. These findings, along with the simulation results, provide a set of specific hypotheses for the kinetics and pathways involved in the adsorption of SLBs that we hope will be scrutinized in future experimental investigations.
2 Methodology
2.1 Overview
In experiments on SLB adsorption, a regime is observed where there is overloading of lipid on the substrate.5,11 In the fluorescence studies of ref. 11 a universal master curve is found to hold when scaling by the peak intensity time and varying the bulk vesicle concentration over a wide range, see Fig. 1.We seek to develop models to gain insights into these experimental observations. In particular, we seek to gain insights into the following features of the master curve: (i) the initial linear scaling of the lipid adsorption, (ii) the sudden on-set of acceleration in the rate of adsorption, (iii) the subsequent deceleration of adsorption as the peak intensity is approached, (iv) and the fairly rapid decay and relaxation toward steady-state. A central aim is to develop a model that not only accounts for these qualitative features of the master curve but provides an explanation and link to microscopic features of the physical system. With this aim in mind our models take into account the vesicle arrangements on the surface, the geometry and distribution of bilayer islands, kinetics of island evolution and merging, and the lipid desorption from the surface. With these processes taken into account, we show that the kinetics can exhibit a wide range of behaviors. We then identify the regime and underlying mechanisms that yield results most similar to the features observed in the experiments of ref. 11.
2.2 SLB formation pathway
The basic processes involved in the adsorption of bilayer on the substrate that we consider is as follows: (i) vesicles adsorb to the substrate, (ii) vesicles rupture to nucleate bilayer islands, (iii) vesicles can rupture to contribute to a bilayer patch, (iv) bilayer island edges can evolve in shape and interact (hydrophobically) with adsorbed vesicles or recruit vesicles from the bulk, and (v) vesicles can desorb from the substrate. Our main focus will be on the relative kinetics of these processes and the role played by the geometry of the vesicle surface arrangements and the bilayer islands during the progressive formation of the SLB.2.3 Universal scaling in bulk vesicle concentration
The universal scaling observed for the SLB formation suggests that there is only one relevant timescale for the adsorption. Because the initial adsorption rate is linearly proportional to the bulk vesicle concentration, we argue that the adsorption process is primarily diffusion limited by the time it takes for vesicles in the bulk to make encounters with the substrate surface. This suggests that each of the kinetic steps above either occurs very fast relative to the diffusion associated time-scale or the step is itself diffusion limited (or does not occur on a timescale relevant to the experiment). This places an important kinetic constraint on proposed models of the adsorption process, namely that all of the non-negligible kinetic time-scales must scale linearly with the bulk vesicle concentration.2.4 Critical intensity and acceleration
An important feature of the experimental data is that the acceleration occurs as a critical fluorescence intensity is reached for each of the bulk vesicle concentrations (on average about ∼0.9ISLB), see Fig. 1. This feature suggests that a critical density of lipid must accumulate near the substrate before acceleration arises.We interpret this in terms of a hypothesis for a critical density of intact vesicles at the surface that is required before the occurrence of rupture events that nucleate lipid bilayer islands on the substrate. We hypothesize along lines similar to prior work that the adhesion forces between a vesicle and the substrate result in a distortion that flattens the vesicle shape and stresses the vesicle bilayer.5,9,12 For sufficiently strong adhesion forces rupture of an isolated vesicle may occur, but if the adhesion forces are insufficient, additional collective effects at a critical density may be required to overcome the energy barrier for rupture of vesicles onto the substrate.
2.5 Adhesion driven jamming and vesicle rupture
In our model, we shall allow quite generally for any mechanism that depends on a critical density of vesicles to induce rupture on the substrate. For concreteness we provide a specific hypothesized mechanism. In particular, at a critical vesicle density we posit there are clustered arrangements on the substrate whereby a space surrounded by vesicles already on the substrate is large enough to accommodate the binding of a single spherical vesicle but too small to accommodate the flattened vesicle shape that is driven by the adhesion force. In such a scenario, the adhesion forces could in principle act to push this newly adhered vesicle into the neighboring vesicles, possibly driving a stressing of the bilayer or transient fusion with neighbors. The local jamming together of nearby vesicles driven by the adhesion forces is hypothesized to result in rupture of the vesicle cluster onto the substrate. We term this mechanism “adhesion jamming,” see Fig. 2. Again, in our model, we shall allow quite generally for any mechanism that depends on a critical density of vesicles to induce rupture on the substrate, but provide for concreteness the “adhesion jamming” hypothesis as one possible explanation. | ||
| Fig. 2 Pathways involved in adsorption. Adhesion may be the driving force for merging and rupture above a critical concentration of vesicles on the substrate. Our hypothesized pathway consists of four steps: (i) a vesicle from the bulk inserts at a location close to already adhered vesicles, (ii) the adhesion forces drive a flattening of the vesicle into a stressed shape that pushes its bilayer together with neighbors, (iii) interactions with neighboring vesicles drives rupture, (iv) the ruptured vesicles form a patch of supported lipid bilayer with edges having high affinity for vesicles. | ||
2.6 Preferential adhesion at edges and vesicle desorption
Once a bilayer island has been nucleated on the substrate, the edges of the island have a strong affinity for vesicles from the bulk. This is expected from the additional exposed hydrophobic area of the highly curved edge regions and has been observed in ref. 13 and 14. The sticky nature of the island edges then recruits additional vesicles to the substrate along the perimeter of the island. As islands form this results in a significant amount of high affinity edge and an acceleration in the rate that vesicles adheres to the substrate (in the form of newly recruited vesicles at domain edges). We allow for the recruitment of vesicles to the island edges to also result in additional rupture events when participating in a critical density cluster.As the bilayer islands grow and merge, the amount of substrate and high affinity edge available to vesicles decreases and the rate of lipid adsorption decreases. The many vesicles that get caught between merging bilayer patches desorb from the substrate resulting in a decrease of the fluorescence intensity. As the bilayer islands merge to form SLB and the remaining vesicles desorb, the fluorescence intensity relaxes toward its final value.
3 Model
We now give a more precise mathematical description of these processes and our overall model. The model takes into account the state of the system by using a description in terms of the two most salient features (i) the vesicle arrangement on the substrate, and (ii) the geometry of the forming supported lipid bilayer on the substrate. The vesicle locations are described by a collection of point locations xk, where the index k denotes the kth vesicle. The supported lipid bilayer on the substrate is described in terms of a phase field c(x), where c = 0 corresponds to bare substrate and c = 1 corresponds to the presence of bilayer; we often refer to c as the SLB concentration. The adsorption process can be broken down into four sub-processes that occur simultaneously (i) vesicles from the bulk diffuse to adhere to the substrate, (ii) vesicles rupture to contribute to the supported lipid bilayer, (iii) the bilayer patches evolve on the substrate to change shape and to merge with nearby patches, and (iv) vesicles that encounter merging bilayer fronts desorb from the substrate. We now discuss each of these components in more detail.3.1 Vesicle adsorption model
The vesicles adhere from the bulk by diffusion limited encounters with the substrate. To realize the adhesion distribution in practice, we algorithmically first sample the arrival time of a vesicle according to an exponentially distributed waiting time with rate λ, which is linearly proportional to the bulk vesicle concentration by our hypothesis in Section 2.3. Once an arrival event occurs, a candidate site x* is chosen uniformly across the substrate (regardless of whether that site is occupied by SLB or not). Once x* is chosen, the vesicle either adsorbs, ruptures, or diffuses back into solution. We use the following criteria to determine which outcome occurs:(1) If the average concentration of SLB in some small neighborhood B of x* is above some reference value ccutoff = 3/4, we assume x* is completely covered by the SLB, and the vesicle cannot adhere and diffuses back into solution. In our simulations, we take B to be the disc of radius r centered at x*.
(2) If the number of adsorbed vesicles in some neighborhood Brup of x* is greater than γd, then the approaching vesicle immediately ruptures, depositing SLB onto the substrate. Vesicles only partially within Brup are counted as the fraction included within Brup. In our simulations, we take Brup to be the disc of radius 3r centered at x* and γd = 2.7. See the end of Section 3.5 for details regarding how SLB is deposited after rupture events.
(3) If neither of the previous two criteria are met, the vesicle adsorbs to the substrate.
3.2 Supported lipid bilayer: geometry and dynamics
The geometry and dynamics of the forming SLB on the substrate plays a significant role in the adsorption process. To take this into account, we describe the SLB using a phase field c(x), which is proportional to the local concentration of SLB lipids on the substrate. We use the conservative Cahn–Hilliard equations to model the dynamics of the SLB | (1) |
 | (2) |
We take the state c = 1 to denote full SLB coverage, and c = 0 to denote bare substrate.
Desirable characteristics of the Cahn–Hilliard equation are that it is conservative, distinct phases remain well separated, and the phase field c evolves to minimize the arc-length of the interface between phases. A numerically challenging feature of these equations is that the fine microstructures develop on relatively short time-scale O(ε2), while the arc-length of interface layers are fully minimized on relatively long time scales  .15 This means local features in c get smoothed out very quickly, but the larger-scale shape of the bilayer patch remains relatively stable on long time-scales. In AFM studies of silica, the bilayer patch geometry was found to remain substantially stable over the time-scale to form SLB.7 From this experimental observation, ε will be chosen to be small and used primarily to control numerically the interfacial width, which is also proportional to ε. We nondimensionalize the length-scales of our simulations by the system width W; under this nondimensionalization, we pick
.15 This means local features in c get smoothed out very quickly, but the larger-scale shape of the bilayer patch remains relatively stable on long time-scales. In AFM studies of silica, the bilayer patch geometry was found to remain substantially stable over the time-scale to form SLB.7 From this experimental observation, ε will be chosen to be small and used primarily to control numerically the interfacial width, which is also proportional to ε. We nondimensionalize the length-scales of our simulations by the system width W; under this nondimensionalization, we pick  . We then nondimensionalized the time-scale of the simulation by 1/ε3 s, which we choose to ensure the stability of our numerical methods.
. We then nondimensionalized the time-scale of the simulation by 1/ε3 s, which we choose to ensure the stability of our numerical methods.
As we noted in our discussion of the universality of the master curve in Section 2.3, we expect kinetic processes involved in adsorption to be either much faster than adsorption, proportional to the adsorption rate λ, or very slow compared to adsorption. We choose our vesicle adsorption rate λ ≈ 1/221 s−1. This gives a nondimensionalized adsorption rate of ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) = λΔt = 26 so that ε2 ≪
= λΔt = 26 so that ε2 ≪ ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) −1 ≪ 1/ε, which ensures that microstructural rearrangement is much faster than adsorption, but large-scale rearrangements occur on a time scale much slower than the (nondimensional) adsorption time
−1 ≪ 1/ε, which ensures that microstructural rearrangement is much faster than adsorption, but large-scale rearrangements occur on a time scale much slower than the (nondimensional) adsorption time ![[small lambda, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0df.gif) −1. If this timescale separation is not present, our arguments of Section 2.3 no longer apply, and deviations from the master curve could occur. However, in our simulations ε is small enough that the range of applicable time-scales (i.e. between ε2 and 1/ε) is so large that the SLB rearrangement dynamics are guaranteed to occur on a separate timescale from vesicle adsorption; this should in principle ensure the experimentally observed universality of the master curve.
−1. If this timescale separation is not present, our arguments of Section 2.3 no longer apply, and deviations from the master curve could occur. However, in our simulations ε is small enough that the range of applicable time-scales (i.e. between ε2 and 1/ε) is so large that the SLB rearrangement dynamics are guaranteed to occur on a separate timescale from vesicle adsorption; this should in principle ensure the experimentally observed universality of the master curve.
3.3 Adaptive mesh refinement for bilayer edges
To capture efficiently the small interfacial width associated with the SLB domains, we use a spatial discretization mesh that is adapted to the features of the phase field c. In regions where the phase field is relatively constant having only small variations, such as within a bilayer domain, we use a spatial discretization with a large mesh for the Cahn–Hilliard eqn (1). In regions where the phase field has large variations, such as in the interfacial region at the bilayer edges, we use a spatial discretization with a much more refined mesh. As the geometry of the bilayer domains change over time, we adapt the spatial discretization mesh. The Cahn–Hilliard equations are discretized using a finite volume numerical method and evolved in time using standard time-step integrators. In Fig. 3, we show a typical spatial discretization employed during the simulations along with how data is stored and utilized to discretize the partial derivatives appearing in eqn (1). For more details see the ESI.† | ||
| Fig. 3 Numerical discretization: a typical spatial discretization employed during the simulations to resolve a bilayer domain (left). The Cahn–Hilliard equations are discretized using a finite volume numerical method with fluxes represented on the faces of the control volumes and the phase field c represented in the centers of the control volumes (right). | ||
3.4 Bilayer edge recruitment of vesicles and dynamics
During the vesicle adsorption process there is a preferential affinity for bilayer edge. We assume that this affinity is so high that the rate at which vesicles adsorb to SLB edge is orders of magnitude faster than adsorption on bare substrate. To account for this, we artificially deposit vesicles at SLB edge whenever it appears. The only time this occurs is when a vesicle ruptures on the substrate, so whenever a vesicle ruptures to produce an SLB island, we decorate the edge with vesicles. In order to ensure that SLB edge remains decorated throughout the time evolution of the bilayer, we also require that the vesicles move with the SLB edge. This is achieved by applying a c-dependent force on each vesicle of the form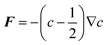 . Assuming the over-damped limit for motion of an adsorbed vesicle, the velocity of each vesicle on the substrate is proportional to F, where the proportionality constant (mobility) is chosen large enough so that the vesicles do not lag behind the SLB edge, but small enough so that vesicle motion is not the limiting timestep.
. Assuming the over-damped limit for motion of an adsorbed vesicle, the velocity of each vesicle on the substrate is proportional to F, where the proportionality constant (mobility) is chosen large enough so that the vesicles do not lag behind the SLB edge, but small enough so that vesicle motion is not the limiting timestep.
3.5 Vesicle rupture
A central feature of our model is that the rupture of a vesicle is triggered by a cluster of vesicles above a critical density. One of the ways this is captured is by performing a test immediately upon a new vesicle adhering to the substrate (see Section 3.1). Another way a rupture can occur is if a vesicle moves into a neighborhood of vesicles which are above another critical density. The check performed is almost identical to the check we perform upon vesicle adsorption, but we allow for a different parameter γm. That is, if an adsorbed vesicle moves into a neighborhood Brup with a number of vesicles greater than γm, then the vesicle ruptures. We again take Brup to be a disc of radius 3r.To account for the newly ruptured vesicle on the substrate and contribution to the SLB, we spread out the surface area of the vesicle on the substrate as a disk of radius 2r to the neighboring finite volume cells. This is done by creating a highly refined patch of finite volumes in the SLB mesh at the rupture site, and adding 1 to all cells within 2r of the rupture site. This is equivalent to an appropriate choice for the phase-field source term g discussed in Section 3.2. As can be seen in the simulation movies, the CH equations serve to rapidly equilibrate these contributions to the growing SLB (Fig. 4).
 | ||
| Fig. 4 Simulation snapshots of SLB formation, taken at times t/tmax = 0.1, 0.2, 0.6, 0.9, 1.2, 2.0. The progression of the adsorption of lipid on the substrate is shown at six different times. The substrate is populated primarily by adhering vesicles until a critical density cluster forms resulting in a rupture event (top left, top center). The ruptured vesicle forms a bilayer island with a high affinity edge that recruits additional vesicles to the surface that cause additional rupture events (top right, bottom left). As the bilayer islands grow and merge their edges evolve to carry along vesicles to interact with nearby neighbors to catalyze additional rupture events or their edges merge resulting in desorption of vesicles from the substrate (bottom center, bottom right). | ||
Another feature of our model is that vesicles do not spontaneously rupture due to interaction with the SLB edge, in contrast to the observed rupture of giant unilamellar vesicles near bilayer edges observed in ref. 16. This is quite an important feature, since without it, we were unable to produce the accelerated adsorption rate of lipid to the substrate or the lipid overloading, two of the main features observed in ref. 11. If edge-induced rupture were fast, the additional adsorption of vesicles at the bilayer edge would only lead to the formation of more bilayer, and not the vesicles on the surface needed for overloading to occur.
3.6 Bilayer island merging and vesicle desorption
As the bilayer domains grow and begin to merge, vesicles may become trapped between edges and unable to rupture because there aren't enough other vesicles nearby. In this situation, it is possible that the vesicle lies completely on top of SLB, which we assume results in the desorption of the vesicle. This is taken into account in our simulations using a similar mechanism as described in Section 3.1. That is, if at any point in the simulation, 3/4 of a vesicle lies on top of SLB, that vesicle immediately desorbs back into solution.4 Results and discussion
4.1 Comparisons to experimental data
The master curve of fluorescence intensity obtained from the experimental data provides an important test of the proposed model. Key features are the initial linear increase in fluorescence intensity during vesicle adherence to the substrate, subsequent acceleration during vesicle rupture to deposit bilayer, and the final deceleration and relaxation to the a fully formed supported lipid bilayer. As discussed in the previous sections the model includes what are thought to be key elements of the adsorption process. To understand the relative roles and contributions of these processes we have parameterized the model using as a basis for comparison the experimental master fluorescence intensity curve of Fig. 1. We find that the model agrees most closely quantitatively with the fluorescence intensity curve for the parameter values given in Table 1. For this choice, the total fluorescence intensity over time and the relative contributions arising from the lipids that are incorporated into vesicles vs. the bilayer are shown in Fig. 5.| Parameter | Value |
|---|---|
| r | 25 nm |
| λ | 2−21 s−1 |
| γ d | 1.8 |
| γ m | 3.6 |
 | ||
| Fig. 5 Fluorescence intensity: simulation results. Shown is the total fluorescence from lipids on the substrate over time (gray), calculated by integrating c over the substrate domain and adding 4πr2 per adsorbed vesicle. The model exhibits the same regimes as the universal master curve of fluorescence intensity observed in experiments, particularly the initial linear regime up to a critical fluorescence followed by a regime of accelerated adsorption. The adsorption then decelerates to a peak value that then relaxes to a steady-state value. Also shown are the contributions to the fluorescence of the lipids incorporated in vesicles (red) and lipids incorporated in the bilayer (green). The simulation parameter values for this particular profile are given in Table 1. | ||
An interesting finding when parameterizing the model was that achieving overloading of lipids on the substrate (overshoot in the fluorescence intensity curve) was not a very common behavior for the model. To achieve overshoot required a rather narrow choice of parameters to allow for an appropriate balance between the build up of vesicles on the substrate to the critical concentration followed by a significant regime of edge facilitated acceleration in adsorption. The two key parameters found to most strongly influence the appearance and magnitude of the overshoot were the critical crowding thresholds for vesicle rupture, γd and γm. The γd corresponds to the number of local vesicles that are required so a newly deposited vesicle ruptures. The γm corresponds to the number of local vesicles so that a vesicle pushed into a new region of the substrate ruptures. The model exhibits the most sensitivity to γd with γm playing a rather minor role (see Fig. 6). A relatively large critical threshold was found to be important for the appearance of an overshoot. If the critical threshold was too small the model exhibited only a saturation kinetics in the adsorption of the supported bilayer with no significant overshoot. For the initial linear regime, accelerated regime, and peak intensity, the model is found to give very good agreement with the experimental data. An overview of the range of parameters which were explored is given in the plots of Fig. 6.
 | ||
| Fig. 6 Simulated fluorescence profiles for varied parameters. γd is varied horizontally, and γm is varied vertically. The sensitivity on γd is apparent, with the greatest variation in fluorescent profile shape occurring horizontally. Note that as γd is increased, spontaneous vesicle rupture is less likely to occur, resulting in total saturation of the domain by vesicles. | ||
An important discrepancy of the model arises for the relatively slow relaxation of the fluorescence intensity of the model to the steady-state when compared to the experimental fluorescence intensity. Interestingly, the experimental data is also found to exhibit the most variation in this regime. One possible explanation in the simulation was a possible system size dependence resulting in relatively few large-scale domains that finally merge. However, upon increasing the patch size of the simulation domain this slow relaxation to steady-state still persisted. In our model the excess vesicle desorbs from the substrate only when the bilayer patch completely envelops the vesicle. Since vesicles are pushed by a moving bilayer front the desorption in our model may occur at a relatively late stage during the SLB formation, particularly only when the large-scale domains finally merge. Another possible explanation for the more rapid relaxation in the experimental data is that vesicles are able to spontaneously desorb when encountering a moving bilayer edge providing an alternative more rapid mechanism for vesicle desorption than incorporated in our model. However, the experimental data for the final relaxation to steady-state exhibits wide variation among the experiments. We think it would be difficult to distinguish with this data set between such models.
4.2 Importance of SLB geometry: lipid bilayer domain sizes
The rupture of vesicles when reaching a critical density along with an observed level of fluorescence intensity above the SLB level places some important constraints on the possible sizes that can be realized by the growing lipid bilayer domains. Let ϕT(t) = I(t)/ISLB be the total rescaled fluorescence at time t, let ϕSLB(t) be the contribution of the fluorescence from the lipid bilayer domains, and let ϕV(t) be the contribution of the fluorescence from the vesicles. This yields the decomposition ϕT = ϕSLB + ϕV. An important feature of our theory for the adsorption process is that bilayer islands have high affinity edges that are nearly fully decorated by adhering vesicles. To model the fluorescence contributions we shall consider the case where each of the bilayer domains have the largest possible area to arc-length ratio, which is given by a circular disk. This will help ensure our theory yields an upper bound on plausible domain sizes. For convenience we shall also consider the case where the domains are the same size having a radius R and that there are exactly N such domains. Under these assumptions the fluorescence intensity per unit area can be expressed as | (3) |
The A gives the total area of the substrate. The ϕSLB is given simply by the fluorescence of N disk-shaped patches. The vesicle fluorescence ϕV has contributions arising from (i) vesicles adhering at near the packing density to the high affinity edges of the bilayer domains and (ii) vesicles adhering to the glass substrate. The factor of 4 arises from the surface area of the vesicle bilayer when assuming an effective spherical shape. The r denotes the effective vesicle radius. The number of vesicles m that can be packed around the edge perimeter of a disk-shaped domain of radius R is given exactly by  , which to a good approximation can be treated as m ≈ πR/r provided R/r ≥ 2. Finally, D denotes the average number of adsorbed vesicles per unit area on the substrate (Fig. 7).
, which to a good approximation can be treated as m ≈ πR/r provided R/r ≥ 2. Finally, D denotes the average number of adsorbed vesicles per unit area on the substrate (Fig. 7).
 | ||
| Fig. 7 Bilayer domain size. The geometry of the bilayer domains play a significant role in the observed fluorescence intensity. The bilayer edges have a high affinity for vesicles which bind almost to the packing density. As a consequence, for a given area fraction covered by bilayer, having many small domains makes a larger contribution to fluorescence than an area equivalent larger domain. The edge length of the nine smaller domains (left panel) is three times larger than the edge length of the area equivalent larger domain (right panel). | ||
An important consideration is that vesicles rupture when the area coverage of adsorbed vesicles is above some critical threshold, which we describe with the dimensionless number αC. αC is closely related to our previous parameter γd: γd describes the number of adsorbed vesicles in a small neighborhood (with area |Brup|) of a depositing vesicle which induces rupture, whereas αC describes a global or averaged area coverage which would induce rupture for any vesicle. Specifically, αC can be calculated as πr2γd/|Brup|. αC places an important constraint on the absorbed vesicle density D:
| 0 ≤ πr2D ≤ αC. |
By using eqn (3), we can solve for D
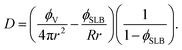 | (4) |
Since we ultimately want to consider the possible bilayer domain sizes R, we used that N = ϕSLBA/πR2. From 4.2 – (4), we have
 | (5) |
If there is overloading, i.e. if the rescaled fluorescence intensity ϕT > 1, the bilayer patch size will be strongly constrained. The peak fluorescence intensity ϕT(tmax) provides a particularly interesting case. Under the assumptions of our model we have ϕV + ϕSLB = ϕT and that ϕSLB ≤ 1. Without additional information, we can use these constraints and the extremum of the upper bound given in eqn (5). This yields a largest possible bilayer domain size bounded by
For instance, a peak fluorescence intensity of ϕT(tmax) = 3/2, as typically observed in experiments (see Fig. 1), yields an upper bound of R/r ≤ 8π ≈ 25. Our theory predicts that the domain size at such a peak fluorescence intensity can be at most 25 times the size of a vesicle. This would help to explain why in fluorescence experiments macroscopic growing bilayer domains are not seen until a rather late stage in the adsorption process well below the peak fluorescence intensity.
When more information is available beyond only the total fluorescence intensity ϕT, more stringent upper and lower bounds can be obtained on the bilayer domain sizes. Ideal experimental information would be the fluorescence contributions of the adsorbed vesicles ϕV and the supported lipid bilayer ϕSLB. While potentially difficult to obtain in experiments, in simulations this information is known and the theory can be further tested and used for analysis. In our simulations, we qualitatively observe no significant SLB domain merging until around t/tmax = 0.6. At this time, we see that ϕV ≈ 0.9, ϕSLB ≈ 0.2 using αC = 0.2. Using these values, we obtain the bounds 2.7 ≤ R/r ≤ 9.7, which means that the effective domain sizes range between 3 and 10 times as large as the vesicle radius. Qualitative analysis of a snapshot (see Fig. 8) of our simulation shows that R/r ≈ 9, which is in close agreement with our estimated bounds. Indeed, even after significant SLB domain merging, we observe that isolated islands of SLB rarely reach a size greater than 10 vesicle radii.
 | ||
| Fig. 8 Simulation snapshot at t/tmax ≈ 0.6. Some initial SLB domain merging has occurred, but individual bilayer islands are still present. We see that island sizes stay within our estimated bounds of between 3 and 10 vesicle radii. | ||
5 Summary
We have found that a combination of edge facilitated adsorption of vesicles and of critical concentration induced rupture of vesicles is important to account for the experimental observations of ref. 11. The finding of a universal master curve that describes the fluorescence intensity data over a wide range of bulk vesicle concentrations indicates that there is only one intrinsic time-scale governing the adsorption process. Our hypothesis is that this intrinsic time-scale is the delay between subsequent diffusive encounters of vesicles with the substrate. From this assumption the different regimes observed in the master curve arise from contributions of the spatial distribution of vesicle and bilayer material on the substrate. To capture the stochastic and geometric features of the adsorption process we introduced a model based on a spatial Poisson process for vesicle adherence to the substrate and a Cahn–Hilliard phase-field description of the growing and merging bilayer islands. We find that critical concentration induced rupture is an important aspect of the model to achieve a significant overloading of lipid on the substrate to account for the observed fluorescence overshoot. For the model with only edge facilitated recruitment and rupture of vesicles, we do not find significant overloading on the substrate and only observe a saturation type of kinetics. We find that the proposed model can account for the experimental fluorescence intensity curves using relatively few parameters. The most influential parameter of our model is the critical threshold for vesicle rupture. We find that an appropriate choice of this parameter can be found that closely matches the observed experimental fluorescence intensity data. In addition, in order to reproduce the observed acceleration and overloading, we must assume that edge-induced rupture observed by Hamai et al.16 is not relevant in the system we are studying. This is a generic prediction of our model that could be tested experimentally. In conclusion, our analysis indicates the importance of the critical concentration induced rupture of vesicles to achieve overloading of lipid on the substrate. We hope that our overall hypothesis of critical concentration induced rupture and the more detailed mechanisms by which vesicles rupture on the substrate can be explored in future experiments.Acknowledgements
The author PJA gratefully acknowledges support from the National Science Foundation CAREER Award 0956210. BAC acknowledges the support of the Fannie and John Hertz Foundation. For helpful suggestions, we would also like to thank Philip Pincus and Deborah Fygenson. We acknowledge support from the Center for Scientific Computing at the CNSI and MRL: an NSF MRSEC (DMR-1121053) and NSF CNS-0960316.References
- M. L. Dustin and J. T. Groves, Annu. Rev. Biophys., 2012, 41, 543–556 CrossRef CAS.
- V. Kiessling, M. K. Domanska, D. Murray, C. Wan, L. K. Tamm and T. P. Begley, Wiley Encyclopedia of Chemical Biology, John Wiley & Sons Inc., 2007 Search PubMed.
- E. T. Castellana and P. S. Cremer, Surf. Sci. Rep., 2006, 61, 429–444 CrossRef CAS.
- E. Sackmann, Science, 1996, 271, 43–48 CAS.
- R. P. Richter, R. Brat and A. R. Brisson, Langmuir, 2006, 22, 3497–3505 CrossRef CAS.
- R. P. Richter and A. R. Brisson, Biophys. J., 2005, 88, 3422–3433 CrossRef CAS.
- R. Richter, A. Mukhopadhyay and A. Brisson, Biophys. J., 2003, 85, 3035–3047 CrossRef CAS.
- C. A. Keller, K. Glasmstar, V. P. Zhdanov and B. Kasemo, Phys. Rev. Lett., 2000, 84, 5443–5446 CrossRef CAS.
- V. P. Zhdanov and B. Kasemo, Langmuir, 2001, 17, 3518–3521 CrossRef CAS.
- J. M. Johnson, T. Ha, S. Chu and S. G. Boxer, Biophys. J., 2002, 83, 3371–3379 CrossRef CAS.
- K. L. Weirich, J. N. Israelachvili and D. K. Fygenson, Biophys. J., 2010, 98, 85–92 CrossRef CAS.
- C. Lv, Y. Yin and J. Yin, Colloids Surf., B, 2009, 74, 380–388 CrossRef CAS.
- Y. Hu, I. Doudevski, D. Wood, M. Moscarello, C. Husted, C. Genain, J. A. Zasadzinski and J. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 13466–13471 CrossRef CAS.
- S. H. Donaldson, C. T. Lee, B. F. Chmelka and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2011, 15699–15704 CrossRef CAS.
- P. W. Bates and P. C. Fife, SIAM J. Appl. Math., 1993, 53, 990–1008 CrossRef.
- C. Hamai, P. Cremer and S. Musser, Biophys. J., 2007, 92, 1988 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3sm50443c |
| This journal is © The Royal Society of Chemistry 2013 |

