 Open Access Article
Open Access ArticleMonte Carlo simulations of a polymer confined within a fluid vesicle
Miha
Fošnarič
a,
Aleš
Iglič
a,
Daniel M.
Kroll
b and
Sylvio
May
*b
aLaboratory of Biophysics, Faculty of Electrical Engineering, University of Ljubljana, Tržaška 25, 1000 Ljubljana, Slovenia
bDepartment of Physics, North Dakota State University, Fargo, ND 58108-6050, USA. E-mail: sylvio.may@ndsu.edu
First published on 27th February 2013
Abstract
Monte Carlo simulations are employed to study a fluid vesicle that contains a single worm-like polymer chain. The contour length of the polymer is about five times the circumference of the nominally spherical vesicle. We vary the degree of polymer confinement in our simulations by increasing the persistence length of the polymer. The vesicle is represented by a randomly triangulated self-avoiding network that can undergo bending deformations. Upon increasing the persistence length of the polymer beyond the size of the vesicle, we observe a transition of the polymer from an isotropic disordered random conformation to an ordered toroidal coil. Concomitantly, the vesicle adopts an oblate shape to allow for some expansion of the polymer coil inside the vesicle. It is convenient to characterize both polymer and vesicle in terms of the asphericity, a quantity derived from the gyration tensor. At the onset of the polymer's ordering transition, the asphericity passes through a minimum for both polymer and vesicle. The increase in vesicle asphericity for a semi-flexible polymer can be understood in terms of ground state energy calculations, either for a simplified representation of the vesicle shape (we specifically discuss a disk shape with a semi-toroidal rim) or involving a full vesicle shape optimization. The asphericity of the polymer coil results from conformational fluctuations and can be rationalized using Odijk's deflection length of strongly curved semi-flexible polymers.
1 Introduction
Polymers are often confined to spaces much smaller then their natural size.1–3 This is routinely encountered for the packaging of nucleic acids in viruses,4 the transport of biopolymers through nanopores,5–7 or in industrial applications such as fractionation methods using microfluidic devices.8,9 The confinement boundaries are not necessarily rigid; soft boundaries may adapt their shape so as to more favorably accommodate the enclosed polymers. Such structural variability is often implied by the flexibility of cellular boundaries and sub-cellular structures.10 For example, marginal microtubule bands in some animal red blood cells help them to obtain their physiological oblate shapes,11–13 whereas sickle hemoglobin fibers rigidify human red blood cells into pathological prolate shapes.14 In artificial lipid vesicles, different types of polymers may be self-assembled,15,16 reconstituted17 or entrapped,2,18,19 strongly influencing vesicle shape and properties. Conversely, membrane properties can affect the conformation of vesicle-encapsulated biopolymers.20 Actin filaments have also been polymerized and confined into phospholipid-stabilized emulsion droplets.21Confinement of polymers within closed surfaces has been modeled extensively using both simulations and theory.22 This includes the confinement of linear or ring-like23,24 polymers into cavities25,26 (often for cavities of fixed spherical27,28 or cylindrical29,30 shape), or their surfaces.31,32 It also includes soft confining boundaries such as globular and tubular lipid membranes.33 Specifically, we mention work of Marenduzzo and Orlandini34 who simulated the growth of a self-assembling semi-flexible polymer inside a soft vesicle. It was shown (i) that very stiff polymers stall growth and lock the vesicle into a deformed prolate shape (similar to fibers in sickle red blood cells14), (ii) that polymers with intermediate stiffness form a toroidal configuration which distorts the membrane into an oblate shape (like marginal microtubule bands in growing erythrocytes11,12), and (iii) that more flexible polymers grow long inside the vesicle, forming massive spool-like condensates, inflating the vesicle isotropically (like genome packing in the cell nucleus or bacteria1).
In this work we consider a fluid-like lipid vesicle that encloses a single polymer of fixed contour length. We choose the contour length to be about five times the circumference of the vesicle if adopting a spherical shape. The vesicle represents a cavity that – unlike a rigid spherical confinement – is responsive and can adapt to the preferred shape of the polymer. Both polymer and vesicle shapes are governed by their respective bending elastic energies and entropic contributions. We model the polymer as a worm-like chain and the vesicle as a closed fluid sheet that resists bending. Our work attempts to characterize equilibrium properties of the vesicle–polymer system using phenomenological modeling and computer simulations. We are particularly interested in the question how the vesicle accommodates the polymer and how the polymer affects the vesicle shape. To this end, we systematically vary the intrinsic persistence length ξ of the polymer from values much smaller to values much larger than the vesicle size. Specifically, in Section 2 we investigate the ground state (i.e., the state of minimal energy when neglecting thermal fluctuations) of the vesicle–polymer system using approximative geometrical models and numerical vesicle shape optimization. Monte Carlo simulations are employed in Section 3 to describe thermal fluctuations of the vesicle and the polymer. In our simulations we represent the vesicle as a randomly triangulated surface.35,36 Upon increasing the stiffness of the polymer we observe a transition from an isotropic disordered random structure to an ordered toroidal coil. Concomitantly, the vesicle undergoes a transition from an (almost) spherical to an oblate disk-like shape, accommodating the toroidal coil close to its waist. We characterize the vesicle and polymer in terms of their asphericity; see Section 4. Appendices 1 and 2 contain technical details of the phenomenological models and shape optimization, respectively.
2 Ground state calculation
Consider a fluid-like lipid vesicle of fixed surface area Aves = 4πR02, where R0 is the radius of a corresponding sphere with the same area. The vesicle contains a single linear worm-like polymer chain of fixed contour length L with L ≫ R0. (In the present work we shall focus on one specific case, L/(2πR0) ≈ 5.) The elastic energy of the vesicle–polymer system,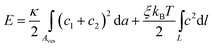 | (1) |
We first discuss the ground state and corresponding ground state energy of our vesicle–polymer system. If the polymer is infinitely rigid, ξ/R0 → ∞, the ground state must correspond to a fully stretched polymer residing within an extended, tube-like vesicle. Reducing the polymer stiffness allows the length of the extended tube to relax. This can be described phenomenologically by modeling the tube as a sphero-cylinder – a cylinder capped by two identical hemispheres – that encloses a helical polymer; see Fig. 7 in Appendix 1 or the scheme “tube” in Fig. 1 for a fully stretched polymer. Such a model introduces the tube length as single degree of freedom for given parameters ξkBT/(κR0) and L/R0. Maximal and minimal tube lengths correspond to the fully stretched polymer residing in an extended sphero-cylinder and to the polymer forming a circular ring at the equatorial region inside a spherical vesicle, respectively. Examination of the total elastic free energy as function of the tube length (see Appendix 1 for details) reveals two minima, E = Emin, corresponding to maximal and minimal tube lengths. Both minima are displayed in Fig. 1 as function of ξkBT/(κR0) for fixed L/(2πR0) = 4.9 (see the thin solid line marked “tube” and the dotted red line marked “sphere”). The constant value of Emin for the extended tube signifies the fully stretched polymer not changing its elastic energy as function of ξ. Similarly, the linear change of Emin for the spherical vesicle simply reflects the bending contribution of the polymer, with Emin ∼ ξ for all other quantities being fixed. Fig. 1 indicates that, as ξkBT/(κR0) is lowered, the energetically favorable state switches discontinuously from an almost fully extended thin tube to a spherical vesicle. However, at this point (i.e., at ξkBT/(κR0) ≈ 90 in Fig. 1) the two favorable states are separated by a large energy barrier. The height of the barrier is calculated in Appendix 1 for helical polymer conformations;34,38 allowing for other polymer conformations may somewhat lower barrier, but not remove it. Hence, if trapped in an initially spherical vesicle, the polymer will be unable to adopt its fully stretched conformation through thermal fluctuations, even if full stretching corresponds to lower elastic energy of the vesicle–polymer system.
 | ||
| Fig. 1 Minimal total elastic energy of the vesicle–polymer system as function of the scaled polymer stiffness ξkBT/(κR0). The scaled polymer length in the plot is L/(2πR0) = 4.9, corresponding to our Monte Carlo simulations in Section 3. The minimal elastic energies for various models are displayed together with an illustration of the corresponding vesicle and polymer shape: sphero-cylinder (thin solid line, marked “tube”), sphere (dotted red line, marked “sphere”), semi-toroidal disk (dashed blue line, marked “disk”), and optimized vesicle shape (thick solid line, marked “optimal shapes”). The optimal shapes are calculated as outlined in Appendix 2. They are calculated for ξkBT/(κR0) = 0, 2, 4, 6, 8 and 10, with the corresponding radii 1.0 × R0, 1.12 × R0, 1.16 × R0, 1.22 × R0 and 1.23 × R0 at the vesicle waist, respectively. | ||
Instead of forming an extended tube-like structure, the vesicle can deform into an oblate disk-like shape, with the polymer adopting a circular ring structure at the waist of the vesicle. We can phenomenologically model the vesicle as a disk with a semi-toroidal rim. This structure, to which we refer as disk model, is illustrated and marked “disk” in Fig. 1. The disk model exhibits one single degree of freedom, given the parameter LξkBT/(R02κ) is fixed. Analysis of the elastic free energy E (see Appendix 1 for details) reveals the presence of only one single minimum E = Emin. This minimum is depicted in Fig. 1 as function of ξkBT/(κR0), again for fixed L/(2πR0) = 4.9 (see the dashed blue line). It is lower than the minimum of the polymer enclosed in a sphere. Because no energy barrier resists the transformation from the spherical to the disk-like vesicle, the former is always unstable in favor of the latter.
Representing the vesicle by a flat disk with a semi-toroidal rim still overestimates the ground state energy Emin. Indeed, a full optimization of the vesicle shape (see Appendix 2 for details) reveals a further decrease of Emin. Fig. 1 displays Emin as function of ξkBT/(κR0); see the thick solid line marked “optimal shapes”. Fig. 1 also shows a sequence of optimized shapes, computed for various values of ξkBT/(κR0) ranging from 0 to 10. To go beyond ground state calculations requires us to account for fluctuations, both in vesicle shape and polymer conformations. This is achieved using Monte Carlo simulations as described in the following section.
3 Monte Carlo simulations
The fluid vesicle is represented by a set of N vertices that are linked by tethers of variable length l so as to form a closed, randomly triangulated, self-avoiding network.35,36 The lengths of the tethers can vary between a minimal value, lmin, and a maximal value, lmax. Self-avoidance of the network is ensured by choosing where s is the maximal random displacement of the vertex. In our simulations we choose s/lmin = 0.15 and lmax/lmin = 1.67. The randomly triangulated network acquires its lateral fluidity from a bond flip mechanism. A single bond flip involves the four vertices of two neighboring triangles. The tether connecting the two vertices in diagonal direction is cut and reestablished between the other two, previously unconnected, vertices.
where s is the maximal random displacement of the vertex. In our simulations we choose s/lmin = 0.15 and lmax/lmin = 1.67. The randomly triangulated network acquires its lateral fluidity from a bond flip mechanism. A single bond flip involves the four vertices of two neighboring triangles. The tether connecting the two vertices in diagonal direction is cut and reestablished between the other two, previously unconnected, vertices.
The polymer inside the vesicle is represented by M vertices that form a linear chain. The maximal vertex displacement and the maximal bond length between two neighboring vertices are chosen to be the same as for the triangulated network of the vesicle. We also introduce a minimal distance between any two polymer and vesicle vertices larger than lmin to ensure that the polymer cannot penetrate into the vesicle membrane. Most of our simulations are carried out without self-avoidance of the polymer; for some simulations (where specified explicitly) self-avoidance of the polymer is implemented by imposing a minimal distance lmin between all pairs of vertices of the polymer (and not only between neighboring vertices, as for a polymer without self-avoidance). We note that the neglect of self-avoidance renders entanglement and knot formation of the polymer irrelevant. Knots appeared sporadically in simulations with polymer self-avoidance – the corresponding runs were then discarded without further analysis.
The microstates of the vesicle–polymer system are sampled according to the Metropolis algorithm with the energy for a given microstate specified in eqn (1). The bending energy of the discretized vesicle (i.e., of the triangulated network) is calculated as described by Gompper and Kroll;35,36 for a recent review, see Ramakrishnan et al.39 The bending energy of the discretized polymer is calculated according to kBT(ξ/![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) )∑i(1 − cos θi), where θi denotes the angle between two successive bond vectors along the polymer and where the sum runs over all neighboring pairs of bond vectors; ξ/
)∑i(1 − cos θi), where θi denotes the angle between two successive bond vectors along the polymer and where the sum runs over all neighboring pairs of bond vectors; ξ/![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) is the persistence length, measured in units of the average bond length of the polymer,
is the persistence length, measured in units of the average bond length of the polymer, ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) ≈ (lmin + lmax)/2. The starting configuration in all simulations is an almost spherical vesicle with the polymer adopting a random coil inside the vesicle.
≈ (lmin + lmax)/2. The starting configuration in all simulations is an almost spherical vesicle with the polymer adopting a random coil inside the vesicle.
In all our simulations the vesicle membrane is triangulated using N = 1447 vertices, forming 2(N − 2) = 2890 triangles. Such a vesicle, if spherical, has a radius R0/lmin ≈ 13. For the bending stiffness of the vesicle we use κ = 10kBT. The polymer inside the vesicle consists of M = 300 vertices, with an average contour length, L ≈ M![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) , about 5 times longer than the circumference 2πR0 of the spherical vesicle.
, about 5 times longer than the circumference 2πR0 of the spherical vesicle.
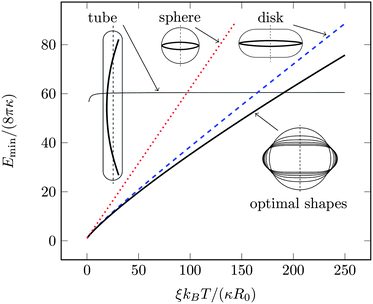
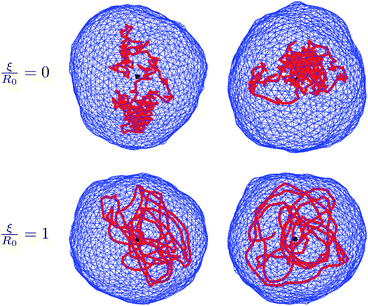
Fig. 2 shows snapshots of typical equilibrium configurations for ξ = 0 and ξ = R0. For vanishing persistence length (see the two upper images of Fig. 2) the polymer behaves almost as a random coil (although not completely, since it is still confined by the vesicle to some extent as will be discussed in Section 4). Increase of the polymer stiffness so as to match the radius R0 of the spherical vesicle results in the polymer filling the volume of the vesicle more uniformly; see the two lower images of Fig. 2. If the persistence length of the polymer increases beyond the dimensions of the vesicle, there is a transition to a more ordered structure, where the polymer forms a toroidal coil within an oblate-shaped vesicle. Corresponding snapshots are displayed in Fig. 3 for ξ = 5R0 (upper images) and ξ = 20R0 (lower images). An even further increase of the polymer's persistence length ξ/R0 leads to further flattening of the disk-like vesicle, with the polymer adopting a larger ring-like shape close to the waist of the vesicle. A snapshot for ξ = 200R0 is shown in Fig. 4. Here, the two rows refer to a polymer without (upper row of Fig. 4) and with (lower row of Fig. 4) self-avoidance. Self-avoidance of the polymer is manifested by the somewhat thicker coil structure but has little impact on the vesicle shape. We also note the non-vanishing angle the terminal segment of the polymer makes with the vesicle boundary – this angle is universal (i.e., it does not depend on the specific material properties) and adopts a value of 24.1 degrees in the ground state.40,41
 | ||
| Fig. 2 Snapshots of typical equilibrium configurations of a vesicle (blue color) containing a linear polymer (red color). Each of the two rows corresponds to a scaled persistence lengths ξ/R0 of the polymer as indicated; the two images in each row show the same system (i.e., the same microstate) from two different viewpoints. The vesicle has a bending stiffness κ = 10kBT, and the polymer has a scaled length L/(2πR0) ≈ 4.9. The polymer is modeled without accounting for self-avoidance. The black dot denotes the center of mass of the vesicle–polymer system. | ||
 | ||
| Fig. 3 Same as in Fig. 2, but for larger scaled persistence lengths ξ/R0 of the polymer as indicated. Here, the persistence lengths are larger than the diameter 2R0 of the corresponding spherical vesicle. The polymer adopts the conformation of an ordered coil within a somewhat oblate-shaped vesicle. | ||
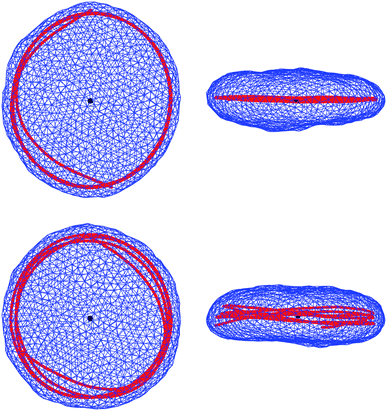 | ||
| Fig. 4 Snapshots as on Fig. 2 and 3, but for a polymer with persistence length ξ = 200R0, much larger then the lateral dimension of the vesicle. Upper and lower rows show, respectively, snapshots corresponding to the polymer without (as in Fig. 2 and 3) and with self-avoidance. | ||
For a more quantitative description of the polymer-induced shape changes, the following section introduces and analyzes the asphericity of the vesicle and polymer.
4 Asphericity
The transition of the polymer from an isotropic random conformation to an ordered coil and the subsequent flattening of the vesicle shape can be characterized conveniently in terms of the asphericity A. To this end, we make use of the Gyration tensor, whose components are defined for a discrete object through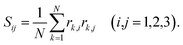 | (2) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) k of the k-th particle. The origin of the coordinate system is located at the center of mass and the sum runs over all particles of the object. From the principal moments (i.e., the eigenvalues) λ1 ≥ λ2 ≥ λ3 of Sij (calculated using the algorithm outlined by Smith42), we obtain the asphericity of the object43
k of the k-th particle. The origin of the coordinate system is located at the center of mass and the sum runs over all particles of the object. From the principal moments (i.e., the eigenvalues) λ1 ≥ λ2 ≥ λ3 of Sij (calculated using the algorithm outlined by Smith42), we obtain the asphericity of the object43 | (3) |
We separately perform the calculation of the asphericity for the vesicle and for the polymer. The ensemble averages needed to calculate A are obtained from our Monte Carlo simulations. Specifically, after an initial equilibration of the system, the averages in eqn (3) are calculated over 10 million sweeps, where one sweep consists of separate Monte Carlo attempts to displace each of the N vertices in the membrane, followed by separate N attempts to flip a randomly chosen bond within the membrane, and followed by separate attempts to displace each of the M polymer vertices. After every 2500 sweeps gyration tensors and corresponding eigenvalues are calculated.
Fig. 5 and 6 show the asphericity of the vesicle and of the polymer, respectively, as functions of the polymer persistence length ξ, measured in units of the spherical vesicle radius R0. The two datasets correspond to the polymer modeled without (filled bullets) and with (open squares) self-avoidance.
 | ||
| Fig. 5 Asphericity A of the vesicle as a function of the scaled persistence length ξ/R0 of the polymer. Bars indicate standard deviations. Filled bullets and open squares correspond to a polymer, respectively, without and with self-avoidance. Results for the disk model (dashed blue line) and for the shape-optimized ground state (dotted red line) are also shown. The inset in the lower-right corner replots the vesicle asphericity within the range 0 ≤ ξ/R0 ≤ 4. The inset in the upper-left corner shows the vesicle's waist radius Rw (scaled by R0) as function of ξ/R0. (Note that Rw is defined as the radius of the circle formed by the vesicle at its plane of up-down symmetry.) Here again, dashed blue line and dotted red line correspond to disk model and optimized vesicle shape, respectively. | ||
 | ||
| Fig. 6 Asphericity A of the polymer as a function of the scaled persistence length ξ/R0 of the polymer. Bars indicate standard deviations. Filled bullets and open squares correspond to a polymer, respectively, without and with self-avoidance. Results for the disk model (dashed blue line) and for the shape-optimized ground state (dotted red line) are also shown. The inset replots the polymer asphericity within the range 0 ≤ ξ/R0 ≤ 8. | ||
The limit ξ → 0 does not give rise to vanishing asphericity A, neither for the vesicle nor for the polymer. In the absence of the polymer, the fluctuation-driven deviation of the average vesicle shape from that of a perfect sphere has been analyzed recently by Linke et al.,45 yet not in terms of the asymmetry parameter A. Our present Monte Carlo simulations predict A = 0.0073 with a standard deviation of 0.0046 for the vesicle (with bending stiffness κ = 10kBT) in the absence of the polymer. Similarly for a bare unconstrained polymer, it is known from work by Rudnick and Gaspari43 that the asphericity A adopts a value of 0.39. Our present simulations yield a lower value of about 0.16. This is because the radius of gyration of the polymer in the limit ξ → 0 is approx.  , indicating that the polymer is confined to some extent by the vesicle and thus adopts a smaller asphericity.
, indicating that the polymer is confined to some extent by the vesicle and thus adopts a smaller asphericity.
Increasing the persistence length of the polymer from zero to about ξ/R0 ≈ 1 slightly lowers the asphericity of both the vesicle and polymer. Our simulation data clearly indicate this for the polymer, see the inset of Fig. 6, but are somewhat less conclusive for the vesicle, see the inset of Fig. 5. Upon further increasing the persistence length ξ, the asphericity A increases. This is because the polymer starts to coil into an ordered circular structure near the vesicle membrane, thus pushing the membrane outwards and deforming the vesicle into an oblate shape. For both vesicle and polymer, the increase in A starts at the same value of ξ/R0 ≈ 3, indicating that the ordering transition of the polymer and the initial shape change of the vesicle are coupled. In the limit of a very stiff polymer ξ/R0 ≫ 1 the vesicle deforms into a thin disk with the polymer adopting an almost circular shape near its waist (see Fig. 4). Here, vesicle and polymer approach the limiting values for a thin axisymmetric object, A = 1/4.
To obtain a more quantitative understanding of the behavior A = A(ξ/R0) for the vesicle (Fig. 5), we have calculated its asphericity using the phenomenological models discussed in Section 2. The simplest approximation of the vesicle shape is the disk model (introduced in Section 2 and analyzed in Appendix 1); i.e. a flat disk with semi-toroidal rim and the polymer forming a circular ring at the waist of the vesicle; see the illustration in Fig. 1. The corresponding asphericity A for the vesicle is displayed by the dashed blue line in Fig. 5. Although the disk model makes a reasonable prediction for A, it somewhat underestimates the Monte Carlo simulation values for ξ/R0 < 100 and overestimates them for ξ/R0 > 100. This, in fact, is how vesicle shape fluctuations are expected to affect the asphericity: small ξ/R0 give rise to almost spherical vesicle shapes in the ground state that fluctuations render more aspherical. Conversely, for sufficiently large ξ/R0 the ground state will be a thin disk that out-of-plane fluctuations render more spherical. We have also calculated the asphericity based on the fully optimized vesicle ground state (as outlined in Appendix 2). Results of this calculation, which was performed in the region 0 ≤ ξ/R0 ≤ 100, are displayed in Fig. 5; see the dotted red line. The bending energy of the vesicle is, of course, lower for the fully optimized vesicle ground state as compared to the disk model. (Recall that Fig. 1 explicitly compares the two elastic energies.) Hence, the polymer is able to deform the vesicle more when the ground state is fully optimized, implying that the radius Rw of the circular ring the polymer forms is larger as compared to the disk model. This is confirmed by an explicit comparison of Rw for the two models, shown in the upper-left inset of Fig. 5 (here again, the dashed blue line and the dotted red line correspond to the disk model and the fully optimized ground state, respectively). The larger waist radius Rw implies the vesicle in its fully optimized ground state to have larger asphericity – this is confirmed in Fig. 5.
We also discuss the behavior of the asphericity A = A(ξ/R0) for the polymer (Fig. 6). Ignoring fluctuations of the polymer conformation altogether would lead to a circular shaped ground state implying A = 1/4. To describe how A(ξ/R0) approaches this limiting value, polymer fluctuations must be accounted for. Based on scaling arguments, Odijk46 has introduced a deflection length lc = R2/ξ for a strongly curved semi-flexible polymer, where ξ is the polymer's persistence length and R the radius of curvature. The deflection length can be used to express the polymer's degree of orientational angular fluctuations 〈θ2〉 = δ2/lc2 as 〈θ2〉 ≃ lc/ξ, implying a “fuzziness” of δ ≃ R3/ξ2 of the strongly curved polymer.46 The “fuzziness” can also be derived from minimizing the free energy of the polymer Fp/(kBT) ≃ (L/ξ) × ln(1/δ) + ξL/(R − δ)2 with respect to δ. Here, the two contributions to Fp result, respectively, from the confinement and bending of the polymer. For R ≫ δ we obtain Odijk's result δ ≃ R3/ξ2. Let us apply this result to the polymer investigated in the present study. For large persistence length the polymer forms a ring-like structure that becomes fuzzy through in-plane and out-of-plane fluctuations. The in-plane fluctuations keep the polymer at an average distance δ ≃ R3/ξ2 away from the waist of the vesicle. Out-of-plane fluctuations will occupy the space available to the polymer in the normal direction. Assuming the vesicle forms a sphere of radius R0 = R and δ ≪ R0, the space available to the polymer in the normal direction is  (numerical prefactors are omitted). Hence, (w/R0)2 ≃ δ/R0 ≃ (R0/ξ)2. The polymer fluctuations of extension w in the normal direction give rise to a polymer asphericity
(numerical prefactors are omitted). Hence, (w/R0)2 ≃ δ/R0 ≃ (R0/ξ)2. The polymer fluctuations of extension w in the normal direction give rise to a polymer asphericity
 | (4) |
The prediction in eqn (4) is derived for a fluctuating polymer that forms a circular ring-like structure inside a spherical vesicle of radius R0. The spherical shape of the vesicle enters as an assumption that will not be fulfilled for ξ/R0 ≫ 1. We can account for shape changes based on the disk model. As discussed above, the disk model represents the vesicle by a flat disk with a semi-toroidal rim. The shape of the disk can adjust so as to best accommodate the polymer (which forms a circle at the waist of the rim). There are only two modifications that the disk model introduces as compared to representing the vesicle as a sphere. First the relation δ = R03/ξ2 is replaced by δ = Rw3/ξ2 where Rw is the optimal waist radius of the vesicle according to the disk model. Second, the relation 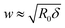 is replaced by
is replaced by 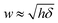 where h is the thickness of the disk. When accounting for vesicle shape changes, the thin ribbon (which represents the normal fluctuations of the polymer) is inserted into the disk instead of a sphere. The disk is able to adjust its shape as function of ξ/R0. More specifically, the two quantities Rw and h follow from minimizing the vesicle shape according to the disk model as function of ξ/R0. The elastic energy according to the disk model is specified in Appendix 1; see eqn (7). The asphericity A of the polymer with vesicle shape changes accounted for (i.e., according to the disk model) is plotted in Fig. 6; see the dotted red line. There is almost no difference, implying that vesicle shape changes have little influence on the asphericity of the polymer.
where h is the thickness of the disk. When accounting for vesicle shape changes, the thin ribbon (which represents the normal fluctuations of the polymer) is inserted into the disk instead of a sphere. The disk is able to adjust its shape as function of ξ/R0. More specifically, the two quantities Rw and h follow from minimizing the vesicle shape according to the disk model as function of ξ/R0. The elastic energy according to the disk model is specified in Appendix 1; see eqn (7). The asphericity A of the polymer with vesicle shape changes accounted for (i.e., according to the disk model) is plotted in Fig. 6; see the dotted red line. There is almost no difference, implying that vesicle shape changes have little influence on the asphericity of the polymer.
5 Conclusions
In this work we have investigated a single polymer enclosed in a fluid vesicle. Upon increasing its persistence length the polymer undergoes an ordering transition, forming a circular conformation that induces a flattening of the vesicle so as to better accommodate the polymer. Asphericity of vesicle and polymer both pass through a minimum just prior to the onset of the ordering transition; i.e., when the persistence length of the polymer is roughly equal to the vesicle size. For persistence lengths much larger than that, the vesicle adopts an increasingly more oblate shape with the polymer at its waist adopting a circular conformation. Here, ground state calculations provide reasonable estimates for the vesicle shape and asphericity. The asphericity of the polymer can be rationalized in terms of Odijk's46 deflection length. We point out that our work focuses on the simplest case, where neither interactions between membrane and polymer nor between polymer segments (other than steric) are included. For example, polymer–polymer interactions can give rise to the formation of helical structures for polymers in spherical confinement.47 Beyond that, the present model can also be extended to account for polymer networks enclosed in fluid membranes. We also point out that the present work focuses on one single contour length of the polymer, equal to roughly five times the circumference of the nominally spherical vesicle. The theoretical models employed in the present work (mostly ground state energy calculations) apply also to longer chains. We expect them to provide reasonable descriptions for vesicles with longer chains as long as self-avoidance of the polymer can be neglected. Eventually, for sufficiently long polymers steric polymer–polymer interactions and corresponding packing constraints will become relevant.34 This is another interesting extension of the present work. Even for a small contour length of the polymer i.e., when a stiff polymer is barely longer than the vesicle size, the vesicle may respond through shape changes that are worth future investigations.Appendix 1: tube model and disk model
As discussed in Section 2, we use two simplified geometric models for estimating the elastic energy of the vesicle–polymer system. The tube model consists of a cylindrical segment of length Lc and radius Rc, which contains a polymer of contour length L forming a helical conformation. The cylinder ends are covered by two hemi-spherical caps of radius Rc. The disk model consists of a flat disk of thickness h and radius Rs that is capped by an semi-toroidal segment of outer radius Rs + h. The polymer, which has a contour length L, adopts a circular conformation of radius Rw = Rs + h. Vesicle and polymer are illustrated in Fig. 7 for both the tube model (left) and disk model (right). Recall that we express the (fixed) area of the vesicle Aves = 4πR02 in terms of the radius R0 of an equivalent sphere. Also, ξkBT and κ denote the bending rigidities of the polymer and vesicle, respectively. | ||
| Fig. 7 Schematic illustration of two geometric models: the tube model (left) represents the vesicle as a sphero-cylinder of radius Rc and total length Lc + 2Rc that contains the polymer in a helical conformation. The disk model (right) represents the vesicle by a flat disk of thickness 2h and radius Rs, capped by a semi-toroidal rim. Here, the polymer adopts a circular conformation of radius Rw = Rs + h along the waist of the vesicle. The vertical broken line marks the axis of the vesicle's rotational symmetry. | ||
We first discuss the tube model. The fixed area of the sphero-cylinder provides us the relation Lc = 2Rc[(R0/Rc)2 − 1]. The helical shape of the polymer can be parameterized by the position vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) = {Rccos(ωt),Rcsin(ωt),t} with
= {Rccos(ωt),Rcsin(ωt),t} with 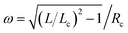 and 0 ≤ t ≤ Lc, producing a contour of length L and curvature c = [1 − (Lc/L)2]/Rc. Adding the contributions from the vesicle and the enclosed polymer and using area conservation, we express the total elastic energy E = Etube of the vesicle–polymer system (see eqn (1)) as
and 0 ≤ t ≤ Lc, producing a contour of length L and curvature c = [1 − (Lc/L)2]/Rc. Adding the contributions from the vesicle and the enclosed polymer and using area conservation, we express the total elastic energy E = Etube of the vesicle–polymer system (see eqn (1)) as
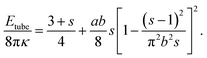 | (5) |
 | (6) |
The first term on the right-hand side of eqn (5) (i.e., (3 + s)/4) is the bending energy of the vesicle, and the second term accounts for bending the polymer. Parameters a and b describe the scaled stiffness and contour length of the polymer, respectively. Our simulations correspond to 0 ≤ a ≤ 30 and b = 4.9. Parameter s is unconstrained but must reside in the region 1 ≤ s ≤ smax. Here, s = 1 and s = smax correspond to Lc = 0 and Lc = L, respectively. Because for Lc = L the polymer is fully stretched and thus has vanishing bending energy, we obtain from eqn (5) the expression π2b2smax = (smax − 1)2 or, when solved, 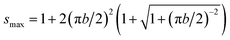 . For a long polymer b ≫ 1 and therefore smax = (πb)2 or, equivalently, A = 2πRcL. Here, the area of the two end caps becomes negligibly small as compared to the mantle of the cylinder.
. For a long polymer b ≫ 1 and therefore smax = (πb)2 or, equivalently, A = 2πRcL. Here, the area of the two end caps becomes negligibly small as compared to the mantle of the cylinder.
The elastic energy Etube(s) is plotted in Fig. 8 for b = 4.9 (i.e., corresponding to our Monte Carlo simulations). We note that Etube(s) exhibits a minimum at s = 1, indicating a spherical vesicle, and for a > 1.2 another minimum near s ≈ smax ≈ (πb)2 that corresponds to the almost fully stretched polymer. The minimum at s = 1 is lower than that at s ≈ smax as long as a < a* = 97. At a = a* both energy minima are separated by a large energy barrier (≈2100 × 8πκ for b = 4.9). The inset of Fig. 8 shows how a* depends on b.
 | ||
| Fig. 8 Elastic energy Etube(s) for the tube model, plotted according to eqn (5). Different curves correspond to different a = ξkBT/(κR0) as indicated, all derived for b = L/(2πR0) = 4.9. Generally, Etube(s) exhibits two minima, one at s = 0 and one at s ≈ smax ≈ (πb)2. At a = a* = 97 the two minima have the same magnitude as indicated by the dotted line. The inset shows how a* depends on b. Note that our simulations correspond to b = 4.9 and cover the range 0 ≤ a ≤ 30. | ||
Next, we discuss the disk model. Here, the vesicle adopts the shape of a flat disk with a semi-toroidal rim, and the polymer forms a circle at the waist of the vesicle; see Fig. 7. The area of the vesicle has contributions from the two flat circular top and bottom segments, each equal to πRs2, and from the semi-toroidal rim, which amounts to 2πh(2h + πRs). Defining the ratio s = Rs/h as a measure for the deviation of the disk shape from that of a sphere (s = 0), area conservation of the vesicle gives rise to the relation 2 + πs + s2 = 2(R0/h)2. Using this relation and calculating the bending energies for the polymer and vesicle, it is straightforward to express the elastic energy E = Edisk of the vesicle–polymer system (see eqn (1)) as
 | (7) |
Appendix 2: shape optimization
We describe the full optimization of the vesicle shape, given the vesicle has fixed area Aves = 4πR02 and the polymer adopts a circular conformation of radius Rw at the waist of the vesicle. Consider a vesicle of axial symmetry about the z-axis and mirror symmetry about the x, y-plane, where the polymer is located. (Due to the mirror symmetry, we only need to calculate the vesicle shape for z > 0.) We describe the vesicle shape as a function of the contour length l of the vesicle's cross-section using the local radial distance ρ(l) to the axis of symmetry and the angle Ψ = Ψ(l) between the normal of the vesicle surface and the axis of symmetry (i.e., the z-axis). The two functions ρ(l) and Ψ(l) depend on each other through cos Ψ = dρ/dl. The two principal curvatures of the vesicle membrane are c1 = dΨ/dl and c2 = sin Ψ/ρ. Hence, the elastic energy of the vesicle–polymer system (see eqn (1)) is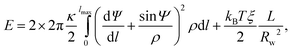 | (8) |
From the parameterization of the vesicle in terms of ρ(l) and z(l) = −sin Ψ(t) we can calculate the asphericity (as defined in eqn (3)) through
 | (9) |
Acknowledgements
The authors acknowledge the support of the Slovenian Research Agency through grant no. BI-US/12-13-049.References
- D. Marenduzzo, C. Micheletti and E. Orlandini, J. Phys.: Condens. Matter, 2010, 22, 283102 CrossRef CAS.
- V. Noireaux, Y. Maeda and A. Libchaber, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 3473–3480 CrossRef CAS.
- W. Reisner, J. N. Pedersen and R. H. Austin, Rep. Prog. Phys., 2012, 75, 106601 CrossRef.
- J. A. Speir and J. E. Johnson, Curr. Opin. Struct. Biol., 2012, 22, 65–71 CrossRef CAS.
- A. Meller, J. Phys.: Condens. Matter, 2003, 15, R581–R607 CrossRef CAS.
- D. Branton, D. W. Deamer, A. Marziali, H. Bayley, S. A. Benner, T. Butler, M. D. Ventra, S. Garaj, A. Hibbs, X. H. Huang, S. B. Jovanovich, P. S. Krstic, S. Lindsay, X. S. S. Ling, C. H. Mastrangelo, A. Meller, J. S. Oliver, Y. V. Pershin, J. M. Ramsey, R. Riehn, G. V. Soni, V. Tabard-Cossa, M. Wanunu, M. Wiggin and J. A. Schloss, Nat. Biotechnol., 2008, 26, 1146–1153 CrossRef CAS.
- H. Kumar, Y. Lansac, M. A. Glaser and P. K. Maiti, Soft Matter, 2011, 7, 5898–5907 RSC.
- R. B. Schoch, J. Y. Han and P. Renaud, Rev. Mod. Phys., 2008, 80, 839–883 CrossRef CAS.
- M. D. Graham, Annu. Rev. Fluid Mech., 2011, 43, 273–298 CrossRef.
- D. Boal, Mechanics of the Cell, Cambridge University Press, 2nd edn, 2012 Search PubMed.
- I. Nemhauser, J. Joseph-Silverstein and W. Cohen, J. Cell. Biol., 1983, 96, 979–989 CrossRef CAS.
- W. Cohen, Y. Sorokina and I. Sanchez, Cell Motil. Cytoskeleton, 1998, 40, 238–248 CrossRef CAS.
- H. Hägerstrand, M. Danieluk, M. Bobrowska-Hägerstrand, T. Holmström, V. Kralj-Iglič, C. Lindqvist and M. Nikinmaa, Mol. Membr. Biol., 1999, 16, 195–204 CrossRef.
- M. Turner, R. Briehl, F. Ferrone and R. Josephs, Phys. Rev. Lett., 2003, 90, 128103 CrossRef CAS.
- D. K. Fygenson, J. F. Marko and A. Libchaber, Phys. Rev. Lett., 1997, 79, 4497–4500 CrossRef CAS.
- L. Limozin and E. Sackmann, Phys. Rev. Lett., 2002, 89, 168103 CrossRef.
- D. Merkle, N. Kahya and P. Schwille, ChemBioChem, 2008, 9, 2673–2681 CrossRef CAS.
- A. Viallat, J. Dalous and M. Abkarian, Biophys. J., 2004, 86, 2179–2187 CrossRef CAS.
- K. Takiguchi, A. Yamada, M. Negishi, Y. Tanaka-Takiguchi and K. Yoshikawa, Langmuir, 2008, 24, 11323–11326 CrossRef CAS.
- M. Elbaum, D. K. Fygenson and A. Libchaber, Phys. Rev. Lett., 1996, 76, 4078–4081 CrossRef CAS.
- M. M. A. E. Claessens, R. Tharmann, K. Kroy and A. R. Bausch, Nat. Phys., 2006, 2, 186–189 CrossRef CAS.
- C. Micheletti, D. Marenduzzo and E. Orlandini, Phys. Rep., 2011, 504, 1–73 CrossRef CAS.
- K. Ostermeir, K. Alim and E. Frey, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 061802 CrossRef.
- M. Fritsche and D. W. Heermann, Soft Matter, 2011, 7, 6906–6913 RSC.
- P. Cifra and T. Bleha, Macromol. Theory Simul., 2012, 21, 15–23 CrossRef CAS.
- M. R. Smyda and S. C. Harvey, J. Phys. Chem. B, 2012, 116, 10928–10934 CrossRef CAS.
- A. Cacciuto and E. Luijten, Nano Lett., 2006, 6, 901–905 CrossRef CAS.
- S. Jorge and A. Rey, J. Chem. Phys., 1997, 106, 5720–5730 CrossRef CAS.
- L. Livadaru and H. J. Kreuzer, New J. Phys., 2003, 5, 95 CrossRef.
- G. Morrison and D. Thirumalai, J. Chem. Phys., 2005, 122, 194907 CrossRef CAS.
- A. J. Spakowitz and Z. G. Wang, Phys. Rev. Lett., 2003, 91, 166102 CrossRef.
- G. Morrison and D. Thirumalai, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011924 CrossRef.
- F. Brochard-Wyart, T. Tanaka, N. Borghi and P. G. de Gennes, Langmuir, 2005, 21, 4144–4148 CrossRef CAS.
- D. Marenduzzo and E. Orlandini, Europhys. Lett., 2007, 80, 48004 CrossRef.
- G. Gompper and D. M. Kroll, in Statistical Mechanics of Membranes and Surfaces, ed. D. Nelson, T. Piran and S. Weinberg, World Scientific, Singapore, 2004, pp. 359–426 Search PubMed.
- G. Gompper and D. M. Kroll, J. Phys. I, 1996, 6, 1305–1320 CrossRef.
- W. Helfrich, Z. Naturforsch., 1973, 28, 693–703 CAS.
- S. Pronk, P. Geissler and D. Fletcher, Phys. Rev. Lett., 2008, 100, 258102 CrossRef.
- N. Ramakrishnan, P. B. S. Kumar and J. H. Ipsen, Macromol. Theory Simul., 2011, 20, 446–450 CrossRef CAS.
- E. Cerda and L. Mahadevan, Proc. R. Soc. A, 2005, 461, 671–700 CrossRef.
- V. Romero, T. A. Witten and E. Cerda, Proc. R. Soc. A, 2008, 464, 2847–2866 CrossRef.
- O. K. Smith, Commun. ACM, 1961, 4, 168 CrossRef.
- J. Rudnick and G. Gaspari, Science, 1987, 237, 384–389 CAS.
- M. B. Luo, J. H. Huang and J. M. Xu, Polym. J., 1998, 30, 889–890 CrossRef CAS.
- G. T. Linke, R. Lipowsky and T. Gruhn, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 051602 CrossRef.
- T. Odijk, Macromolecules, 1993, 26, 6897–6902 CrossRef CAS.
- Z. Y. Yang, D. Zhang, L. X. Zhang, H. P. Chen, W. Ateeq-ur-Rehman and H. J. Liang, Soft Matter, 2011, 7, 6836–6843 RSC.
- M. Fošnarič, A. Iglič, D. M. Kroll and S. May, J. Chem. Phys., 2009, 131, 105103 CrossRef.
| This journal is © The Royal Society of Chemistry 2013 |
