Self-assembly of a peptide amphiphile: transition from nanotape fibrils to micelles

Abstract

A thermal transition is observed in the peptide amphiphile C₁₆-KTTKS (TFA salt) from nanotapes at 20 °C to micelles at higher temperature (the transition temperature depending on concentration). The formation of extended nanotapes by the acetate salt of this peptide amphiphile, which incorporates a pentapeptide from type I procollagen, has been studied previously [V. Castelletto et al., Chem. Commun., 2010, 46, 9185]. Here, proton NMR and SAXS provide evidence for the TFA salt spherical micelles at high temperature. The phase behavior, with a Krafft temperature separating insoluble aggregates (extended nanotapes) at low temperature from the high temperature micellar phase resembles that for conventional surfactants, however this has not previously been reported for peptide amphiphiles.

---

Introduction

Peptide amphiphiles (PAs) are attracting considerable interest as biofunctionalized self-assembling molecules in which multiple inter-molecular interactions (hydrophobic, electrostatic, van der Waals, hydrogen bonding…) can be used to tune hierarchical nanostructure formation.¹ The most common self-assembled motif is that of β-sheet based fibrils which comprise a hydrophobic core of buried alkyl chains surrounded by a corona of peptide headgroups. The presentation of bioactive peptide moieties at high density has led to important demonstrated applications of PAs in regenerative medicine where the nanofibers form a scaffold for tissue engineering.²

The β-sheet fibrillar structure is most usually observed in PA self-assemblies, these sometimes being referred to as rod- or worm-like micelles.³ The formation of spherical micelles by lipopeptide amphiphiles has been observed less commonly. A PA designed to inhibit cancer cell proliferation with a palmitoyl (hexadecyl, C₁₆) chain and a 25-residue peptide headgroup has been shown to form spherical micelles, with the peptide in an α-helical conformation.⁴ A PA with a C₁₆ tail and a 17-residue peptide designed to form α-helices was found to form spherical micelles transiently, followed by a transformation to wormlike micelles.^3c,5 Similarly, PAs with headgroups designed to form trimeric coiled coils also form spherical micelles.⁶ Templating of vesicle- or fibril-forming PAs onto dendrimers can also produce spherical micelles.⁷

The PA palmitoyl–IAAAEEEEK(DO3A:Gd)–NH₂ (where DO3A:Gd indicates a labeling moiety) exhibits a transition from fibrils to spherical micelles at high pH,⁸ however the bulky DO3A (1,4,7-tris(carboxymethylaza)cyclododecane-10-azaacetylamide) tag may influence the self-assembly. Surprisingly, a PA with a tetra C₁₈ tail and a 14-residue peptide headgroup incorporating the RGDS cell-adhesion motif has also been reported to form spherical micelles in aqueous solution.⁹ Monte Carlo simulations using bead string models indicate that directional attractive electrostatic interactions favour the formation of nanofibrils.¹⁰ A later Monte Carlo model using a coarse-grained united atom model, led to a predicted phase diagram.¹¹ This includes spherical micelles in the limit of strong hydrophobic interactions, ε_H, but weak hydrogen bonding strength, ε_β, and long cylindrical micelles for large ε_H and large ε_β. Other structures in the phase diagram include β-sheets when the hydrophobic interactions are weaker but the hydrogen bonding strength is sufficient (if ε_H is too low, free molecules are expected), and amorphous aggregates for small ε_H and large ε_β.¹¹

Designed PAs with C₉ or C₁₁ chains and pentapeptide headgroups also formed spherical micelles by adjustment of pH.¹² In the absence of such conditions, the amphiphiles self-assemble into cylindrical micelles. Modelling of small-angle neutron scattering (SANS) data indicates that the natural marinobactin lipopeptides (PAs with a C₁₆ chain and hexapeptide headgroups) form micelles (in the presence of Fe(III) a transition to vesicles was also observed).¹³ Self-assembly into spherical micelles has also been observed for the biosurfactant surfactin (a lipopeptide with a dodecyl chain and a cyclic heptapeptide-based headgroup) in D₂O¹⁴ or PBS.¹⁵ However, rod-like micelles have been reported for the same PA in a different salt solution.¹⁶

Here, we report on the temperature-dependent self-assembly of the peptide amphiphile C₁₆-KTTKS (TFA salt) which contains a pentapeptide headgroup based on a sequence from the C-terminus of the alpha-1(I) collagen propeptide.¹⁷ This PA is used commercially in formulations such as Matrixyl™ which is employed in cosmeceutical applications, in particular in anti-wrinkle creams.¹⁸

The self-assembly of C₁₆-KTTKS (acetate salt) has been discussed in previous papers from our group.¹⁹ It forms extended nanotape (tapes with >μm persistence length but nanoscale width and thickness) structures above a critical aggregation concentration. The nanotapes comprise bilayers with a spacing d = 52.5 Å.^19a Here, we present new data that shows that the TFA salt of this PA also undergoes a transition from bilayer aggregates to micelles on heating. The acetate salt was studied previously due to its improved biocompatibility compared to TFA, which is a common salt resulting from peptide synthesis and purification methods.

Experimental

Materials

Peptide amphiphile C₁₆-KTTKS, palmitoyl–Lys–Thr–Thr–Lys–Ser was purchased from CS Bio (Menlo Park, California) as the TFA salt (previously¹⁹ we have studied the acetate salt). Three different batches were used. For the first, the purity was 97.6% by analytical HPLC, M_w 802.47 (expected) 802.05 (measured), acetate content was 11% (by HPLC). For the second batch, the purity was 98.61% by analytical HPLC, molecular weight 802.2 (measured), acetate content was 11.61% (by HPLC). For the third batch, the purity was 97.1% by analytical HPLC, M_w 802.05 (measured).

Pyrene fluorescence spectroscopy

Spectra were recorded on a Varian Cary Eclipse Fluorescence Spectrometer with samples in 10 mm quartz cells. A dried film was obtained by evaporating the ethanol from a 0.2 wt% ethanol solution. The Pyr dried film was then re-suspended in water to give a 2.0 × 10⁻⁶ wt% Pyr solution. C₁₆-KTTKS solutions containing (2 × 10⁻³ to 1 × 10⁻¹) wt% PA were prepared using 2.8 × 10⁻⁶ wt% Pyr as a solvent. Pyr fluorescence emission spectra were measured from 366 to 460 nm, using λ_ex = 339 nm.

NMR

Experiments were performed using an instrument operating at 500 MHz for protons equipped with a 5 mm PFG probe. Experiments were carried out in 90 : 10 H₂O : D₂O. The samples were prepared by gentle heating (50–70 °C) of the peptide in the corresponding solvent until a solution was obtained.

Solvent signals were suppressed using PRESAT. Chemical shift assignments were obtained from 2D ¹H–¹H COSY and TOCSY experiments. Diffusion experiments were carried with the bipolar pulse pair stimulated echo sequence at 30 °C. Diffusion coefficients were calculated using the values of the intensity of the observed signal for 15 different gradient strengths in the Stejskal–Tanner equation (ln(I/I_o) = −γg²δ²(Δ − δ/3)D),²⁰ where I and I_o are the signal intensities in the presence and absence of the pulsed-field gradients respectively, γ is the gyromagnetic ratio (rad s⁻¹ G⁻¹), g is the strength of the diffusion gradients (G m⁻¹), D is the diffusion coefficient of the observed spins (m² s⁻¹), δ is the length of the diffusion gradients (s) and Δ is the time separation between the leading edges of the two diffusion pulsed gradients (s).

Small-angle X-ray scattering (SAXS)

SAXS data for 1 wt% solutions were measured using beamline BM29 at the European Synchrotron Radiation Facility, Grenoble, France. Samples were loaded in PCR tubes in a multi-well plate in a robotic sample changer and delivered automatically into a flow-through capillary tube. SAXS patterns were recorded using a Pilatus 1M detector with a sample–detector distance of 2.841 m. The X-ray wavelength was 0.99 Å. Data were reduced to one-dimensional form and background subtraction was performed using the software SAXSUtilities (http://www.sztucki.de/SAXSutilities).

FTIR

Spectra were recorded using a Nexus-FTIR spectrometer equipped with a DTGS detector. A solution of C₁₆-KTTKS in D₂O (1 wt%) was sandwiched in ring spacers between two CaF₂ plate windows (spacer 0.012 mm). All spectra were scanned 128 times over the range of 4000–950 cm⁻¹.

Fibre X-ray diffraction (XRD)

X-ray diffraction was performed on stalks prepared from a 1 wt% solution of C₁₆-KTTKS in water. The stalk was mounted (vertically) onto the four axis goniometer of a RAXIS IV++ X-ray diffractometer (Rigaku) equipped with a rotating anode generator. The XRD data was collected using a Saturn 992 CCD camera. One-dimensional profiles in the equatorial and meridional reflections (with appropriate re-alignment of images to allow for fibril orientation) were obtained using the software CLEARER²¹ which was also used to fit peak positions.

Transmission electron microscopy (TEM)

Experiments were performed using a Philips CM20 transmission electron microscope operated at 80 kV. Droplets of a 1 wt% solution were placed on Cu grids coated with a carbon film (Agar Scientific, UK), stained with uranyl acetate (1 wt%) (Agar Scientific, UK) and dried.

Results

We first determined the critical aggregation concentration (cac) of C₁₆-KTTKS in water at 20 °C via pyrene fluorescence spectroscopy. The fluorescence of pyrene is sensitive to the hydrophobicity of the environment,²² and here we analyse the concentration dependence of the first vibronic band (I₁ at 373 nm) (Fig. 1) although sometimes the ratio of vibronic band intensities I₁/I₃ is used.²² The break in the concentration dependence in Fig. 1 indicates that the cac occurs at c = 0.03 wt%. Above the cac, FTIR spectroscopy suggests the presence of β-sheet features at 20 °C in the amide I′ region (ESI Fig. 1†), i.e. the peak at 1608 cm⁻¹ which is in agreement with our previous studies on C₁₆-KTTKS (acetate salt).¹⁹ The shoulder peak near 1580 cm⁻¹ is due to asymmetrical stretching of ionised carboxylate groups (C terminus).²³ The additional peak at 1672 cm⁻¹ is due to TFA counterions bound to lysine residues.²⁴ Fibre X-ray diffraction on a dried stalk also confirms the presence of β-sheet structure in a dried sample, since a cross-β pattern is observed (ESI Fig. 2†) with peaks corresponding to the 4.87/4.55 Å β-strand spacing along with the orthogonal β-sheet spacings (23 Å and 11.7 Å), similar to our previous data on C₁₆-KTTKS (acetate salt).¹⁹ TEM confirms the presence of nanotape fibrils (ESI Fig. 3† shows a representative image) as also observed for the acetate salt.¹⁹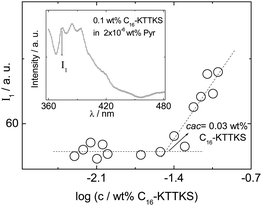

Fig. 1 Concentration dependence of pyrene fluorescence (I₁ vibronic band) at 20 °C. Inset: typical fluorescence spectrum with I₁ band indicated.

NMR spectroscopy was used to examine the aggregation of C₁₆-KTTKS in aqueous solution. Experiments were not done in buffered solutions to avoid the strong saline effect on the aggregation of amphiphiles associated, for example, with the Hofmeister effect.²⁵Scheme 1 shows the molecular structure along with assignments for ¹H NMR spectra. A representative spectrum obtained at 40 °C is shown in Fig. 2. The solubility of C₁₆-KTTKS determined by NMR experiments at different temperatures revealed a dramatic solubility increase above ca. 30 °C (Fig. 3). The representation of the logarithm of solubility vs. T⁻¹, as shown in Fig. 3, is used commonly to extract thermodynamic parameters. In our case this representation showed no dependence of the solubility with the temperature below 30 °C and a sudden exponential increase of solubility above this temperature (notice the logarithmic scale in Fig. 3). Unfortunately no thermodynamic parameters could be extracted due to the limited data available in the exponential region of the graph.

Scheme 1 Structure of PA C₁₆-KTTKS and labelling code used to identify ¹H NMR signals.

Fig. 2 ¹H NMR spectrum of C₁₆-KTTKS in H₂O : D₂O 90 : 10 (1 wt%, 40 °C).

Fig. 3 Solubility of C₁₆-KTTKS in 90 : 10 H₂O : D₂O at different temperatures determined by ¹H NMR. The solubility is plotted as log S (S = solubility in mol L⁻¹). At 35 °C the solubility is higher than 1 wt% but could not be determined exactly.

Assuming that C₁₆-KTTKS behaves as a surfactant capable of micelle formation (as demonstrated later on in this paper), the solubility graph (Fig. 3) can be transformed directly into a phase diagram which shows the presence of micelles, fibrillar aggregates or free surfactant molecules depending on the temperature and concentration (see Fig. 4). This is reminiscent of phase diagrams for surfactants in the vicinity of the Krafft temperature.²⁶ The Krafft temperature defines the temperature for the transition from soluble micelles to insoluble aggregates and can be estimated in this system to be ca. 30 °C. Below this temperature only monomers (free C₁₆-KTTKS) and insoluble aggregates (fibrillar aggregates, previously shown¹⁹ to be extended nanotapes) exist. Above the Krafft temperature an equilibrium between micelles and monomers is present.

Fig. 4 Phase diagram for C₁₆-KTTKS constructed from the solubility data from Fig. 3. T_Kr stands for Krafft temperature.

Regarding the aggregation thermodynamics, noticeably the flat solubility vs. temperature profile in the range of temperatures 5–30 °C indicates the absence of an enthalpic component in the solubilization process.²⁷ This property permits the entropy of solubilization in this temperature range to easily be estimated from the solubility data. Considering the experimental solubility of 0.2 mM, it can be calculated that the solubilization entropy is ca. −70 J K⁻¹ mol⁻¹. This negative value reflects the strong hydrophobic component of the aggregation as expected from the presence of the long aliphatic chain in the PA.

The concentration of NMR observable C₁₆-KTTKS was monitored at 30 °C for samples stabilized overnight containing different total concentrations. The behavior (Fig. 5) is similar to that for supramolecular gels²⁸ revealing that 0.06 wt% represents a critical point for the formation of fibrillar, NMR-silent aggregates (gel network).

Fig. 5 Representation of the NMR-observed vs. total concentration of C₁₆-KTTKS in 90 : 10 H₂O : D₂O at 30 °C. Samples were studied 24 h after their preparation.

Interestingly, it is possible to prepare metastable micellar solutions below the Krafft temperature. For example, a freshly prepared sample of C₁₆-KTTKS in water (1 wt%), obtained by heating the system gently and prior to stabilization at 30 °C, results in a solution where micelles coexist with monomers. The presence of micelles is confirmed by the diffusion coefficient measured for this sample which is found to be 1.5 × 10⁻¹⁰ m² s⁻¹ whereas the value measured for free monomers is 5.0 × 10⁻¹⁰ m² s⁻¹. Fig. 6 reveals that the metastable micellar solutions prepared at 30 °C evolve with time to NMR-silent insoluble aggregates, as demonstrated by the disappearance of the NMR signals.

Fig. 6 Variation of the intensity of the ¹H NMR signal with time for a sample of C₁₆-KTTKS in 90 : 10 H₂O : D₂O (1 wt%) at 30 °C.

As mentioned above, the presence of micelles is clearly shown by diffusion studies. In Fig. 7 it is shown that above 0.06 wt% a critical point is reached (critical micellar concentration, cmc) resulting in a continuous decrease of the diffusion coefficient (formation of micelles which diffuse slower than the monomer). The results in Fig. 7 correspond to freshly prepared samples at 30 °C. Similar results are obtained for the diffusion coefficients measured at 40 °C. As shown in Fig. 8, the cmc value could also be determined to be 0.06 wt% monitoring the variation with the concentration of the chemical shift of the amide signal V (see Scheme 1 for labelling). This cmc at 30 °C is a little higher than the cac at 20 °C (Fig. 1) as expected.

Fig. 7 NMR determined self-diffusion coefficients found for freshly prepared samples of C₁₆-KTTKS at 30 °C in 90 : 10 H₂O : D₂O.

Fig. 8 Concentration dependence of the chemical shift of the signal corresponding to amide V of C₁₆-KTTKS in 90 : 10 H₂O : D₂O at 40 °C (see Scheme 1 for labelling).

Regarding the ¹H NMR spectra depicted in Fig. 9, it can be noted that upon micelle formation, the signal of the NH amide groups close to the C₁₆ chain (amide V, Scheme 1) showed the most significant shift. The effect most likely should be ascribed to a desolvation of this amide unit upon micelle formation. Interestingly, a downfield shift was observed for the C-terminal NH signal (I) when the concentration was increased. This behaviour can be ascribed to the change in the ionization degree of the carboxylic acid unit with the concentration, as reported previously by us for peptide NH₂–βAβAKLVFF–COOH.²⁹

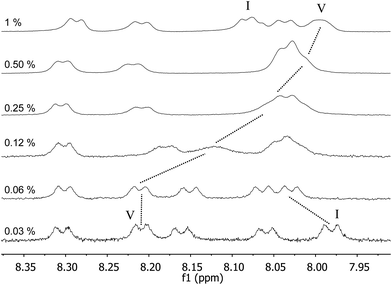Fig. 9 ¹H NMR spectra of C₁₆-KTTKS in 90 : 10 H₂O : D₂O at 40 °C for different concentration values (wt%).

Finally, comparison of the ¹H NMR spectra at 30 °C of a diluted sample (0.03 wt%) and a sample forming a gel (1 wt%) is informative (Fig. 10). Bearing in mind that the concentration of free molecules in solution in both samples is similar (0.4 mM), the rather different appearance of the spectra recorded is notable. The broad and shifted signals obtained for the gel sample reveal a fast exchange, on the NMR time scale (ms), of C₁₆-KTTKS molecules between solution and the fibrillar aggregates. This behaviour has not been observed in the case of other molecular gelators reported in the literature.²⁸

Fig. 10 ¹H NMR spectra (amide region) of C₁₆-KTTKS in 90 : 10 H₂O : D₂O at 30 °C. The samples were left to stabilize for 24 hours before measurements. Concentration units are wt%.

The transition from fibrillar tapes to micelles was confirmed by SAXS. Furthermore, SAXS confirms the reversibility of the nanotape–micelle transition (although the hysteresis of this transition was not examined). Fig. 11a shows SAXS profiles measured at 20 °C and 55 °C, the latter temperature being well above the Krafft temperature for 1 wt% C₁₆-KTTKS (cf.Fig. 3). The data at 20 °C shows three orders of Bragg reflections from a lamellar structure within the nanotapes with a d spacing 4.6 nm. This is smaller than the spacing d = 5.2 nm previously reported for the acetate salt of C₁₆-KTTKS.¹⁹ The length of a C₁₆-KTTKS molecule is estimated as 1.8 nm for the C₁₆ chain in an extended conformation plus 1.6 nm for the KTTKS headgroup, assuming a parallel β-sheet structure. The observed d = 4.6 nm spacing indicates a significantly interdigitated bilayer structure, with disorder of the alkyl chains reducing the chain length from that in the all-trans conformation and also an effect of the TFA counterions which are expected to bind to the lysine residues, hence neutralising the charge and enabling a larger headgroup area with concomitant reduction in tail length. A second order reflection with d = 2.3 nm was also observed in the XRD pattern (ESI Fig. 2†). At 55 °C, the SAXS data indicate a spherical shell structure as shown in Fig. 11b the data can be fitted (details are provided in the ESI†) with a total radius of 2.8 nm (with a Gaussian polydispersity of 8.6%) and an effective core radius 1.7 nm, the core having a relative negative electron density as expected for lipid chains.³⁰ This indicates that in the spherical micelle structure the KTTKS headgroup is not extended, which is consistent with the lack of β-sheet structure within the micellar shell. Using the molar volume of C₁₆-KTTKS (calculated using Gaussian 03 RHF/6-31G plugin in ChemBio3D Ultra 12.0) V_m = 603 cm³ mol⁻¹, together with the micellar volume, we estimate a micellar association number p ≈ 92.

Fig. 11 (a) SAXS data on heating/cooling a 1 wt% solution of C₁₆-KTTKS (temperatures indicated). (b) Model spherical micelle form factor fit (red line) to data (circles) at 55 °C (second heating).

On the other hand, the hydrodynamic radius (r_H) can be obtained from NMR diffusion experiments using the Stokes–Einstein equation: D = k_BT/6πγr_H where k_B is the Boltzmann constant and γ is the viscosity of water at 55 °C (0.504 × 10⁻³ kg m⁻¹ s⁻¹), T is the temperature (328 K) and D is the experimentally determined diffusion coefficient at that temperature for a concentrated sample (1.7 × 10⁻¹⁰ m² s⁻¹). In this way a radius of 2.8 nm is calculated which is in excellent agreement with the data obtained from SAXS mentioned above.

Summary

In water, C₁₆-KTTKS behaves as a conventional surfactant, namely, a phase diagram with three phases, monomer, insoluble aggregates (fibrous) and micelles can be drawn (Fig. 4). The Krafft temperature (T_Kr), i.e. the temperature of the transition from micelles to insoluble aggregates is found to be 30 °C. At this temperature, NMR self-diffusion experiments indicate that the critical micellar concentration is cmc = 0.06 wt%.

It was noted that the transition from micelles to insoluble aggregates is quite slow, it may take several hours. Therefore, metastable micellar solutions below the Krafft temperature can be prepared and studied in fresh samples. The exchange of monomers between solution and the fibrous aggregates is fast on the NMR time scale (ms).

NMR measurements revealed that amide units near the long alkyl chain are desolvated upon aggregation. The aggregation is driven by the hydrophobic effect as the solubilization of the fibrous solid-like material has an associated negative entropy value ΔS ≈ −70 J K⁻¹ mol⁻¹.

SAXS reveals that the nanotape–micelle transition is reversible, and modeling of the form factor provides information on the dimensions of the micelles. As far as we are aware, this is the first report on this type of transition in a peptide amphiphile system. It shows that the PA C₁₆-KTTKS has a phase diagram resembling that of conventional surfactants, although hydrogen-bonding stabilizes the low-temperature β-sheet nanotape extended fibrils. This is disrupted in the high temperature micellar phase. Although this behavior, resulting from the balance of hydrophobic interactions and hydrogen bonding has been anticipated by Monte Carlo simulations,¹¹ this is the first experimental system demonstrating a fibril–micelle transition, to our knowledge.

Acknowledgements

Financial support was granted from the Ministry of Science and Innovation of Spain (Grant CTQ2009-13961, FPU fellowship to M. T.-S.) and Universitat Jaume I (Grant P1-1B2009-42). This work was also supported by EPSRC grants EP/G026203/1 and EP/G067538/1 to I. W. H. We are grateful for access to facilities in the Chemical Analysis Facility (CAF) and the Centre for Advanced Microscopy (CfAM) at the University of Reading. Beamtime on beamline B29 at the ESRF was awarded under reference MX-1401 and we thank Louiza Zerrad for support.

References

1. (a) D. W. P. M. Löwik and J. C. M. van Hest, Chem. Soc. Rev., 2004, 33, 234–245; (b) S. Cavalli and A. Kros, Adv. Mater., 2008, 20, 627–631; (c) H. G. Cui, M. J. Webber and S. I. Stupp, Pept. Sci., 2010, 94, 1–18; (d) F. Versluis, H. R. Marsden and A. Kros, Chem. Soc. Rev., 2010, 39, 3434–3444; (e) X. B. Zhao, F. Pan, H. Xu, M. Yaseen, H. H. Shan, C. A. E. Hauser, S. G. Zhang and J. R. Lu, Chem. Soc. Rev., 2010, 39, 3480–3498; (f) I. W. Hamley, Soft Matter, 2011, 7, 4122–4138.
2. J. B. Matson, R. H. Zha and S. I. Stupp, Curr. Opin. Solid State Mater. Sci., 2011, 15, 225–235.
3. (a) D. Missirlis, H. Khant and M. Tirrell, Biochemistry, 2009, 48, 3304–3314; (b) D. Missirlis, A. Chworos, C. J. Fu, H. A. Khant, D. V. Krogstad and M. Tirrell, Langmuir, 2011, 27, 6163–6170; (c) T. Shimada, N. Sakamoto, R. Motokawa, S. Koizumi and M. Tirrell, J. Phys. Chem. B, 2012, 116, 240–243.
4. L. Aulisa, N. Forraz, C. McGuckin and J. D. Hartgerink, Acta Biomater., 2009, 5, 842–853.
5. T. Shimada, S. Lee, F. S. Bates, A. Hotta and M. Tirrell, J. Phys. Chem. B, 2009, 113, 13711–13714.
6. A. Ghasparian, T. Riedel, J. Koomullil, K. Moehle, C. Gorba, D. I. Svergun, A. W. Perriman, S. Mann, M. Tamborrini, G. Pluschke and J. A. Robinson, ChemBioChem, 2011, 12, 100–109.
7. B. F. Lin, R. S. Marullo, M. J. Robb, D. V. Krogstad, P. Antoni, C. J. Hawker, L. M. Campos and M. V. Tirrell, Nano Lett., 2011, 11, 3946–3950.
8. A. Ghosh, M. Haverick, K. Stump, X. Y. Yang, M. F. Tweedle and J. E. Goldberger, J. Am. Chem. Soc., 2012, 134, 3647–3650.
9. J. X. Chen, H. Y. Wang, C. Li, K. Han, X. Z. Zhang and R. X. Zhuo, Biomaterials, 2011, 32, 1678–1684.
10. S. Tsonchev, G. C. Schatz and M. A. Ratner, J. Phys. Chem. B, 2004, 108, 8817–8822.
11. Y. S. Velichko, S. I. Stupp and M. Olvera de la Cruz, J. Phys. Chem. B, 2008, 112, 2326–2334.
12. X. D. Xu, Y. Jin, Y. Liu, X. Z. Zhang and R. X. Zhuo, Colloids Surf., B, 2010, 81, 329–335.
13. T. Owen, R. Pynn, J. S. Martinez and A. Butler, Langmuir, 2005, 21, 12109–12114.
14. H. H. Shen, R. K. Thomas, C. Y. Chen, R. C. Darton, S. C. Baker and J. Penfold, Langmuir, 2009, 25, 4211–4218.
15. (a) A. H. Zou, J. Liu, V. M. Garamus, Y. Yang, R. Willumeit and B. Z. Mu, J. Phys. Chem. B, 2010, 114, 2712–2718; (b) J. Penfold, R. K. Thomas and H. H. Shen, Soft Matter, 2012, 8, 578–591.
16. Y. Ishigami, M. Osman, H. Nakahara, Y. Sano, R. Ishiguro and M. Matsumoto, Colloids Surf., B, 1995, 4, 341–348.
17. K. Katayama, J. Armendarizborunda, R. Raghow, A. H. Kang and J. M. Seyer, J. Biol. Chem., 1993, 268, 9941–9944.
18. (a) K. Lintner, US Pat. 6,620,419, 2003; (b) K. Lintner and O. Peschard, Int. J. Cosmet. Sci., 2000, 22, 207–218; (c) L. R. Robinson, N. C. Fitzgerald, D. G. Doughty, N. C. Dawes, C. A. Berge and D. L. Bissett, Int. J. Cosmet. Sci., 2005, 27, 155–160; (d) N. H. Abu Samah and C. M. Heard, Int. J. Cosmet. Sci., 2011, 33, 483–490.
19. (a) V. Castelletto, I. W. Hamley, J. Perez, L. Abezgauz and D. Danino, Chem. Commun., 2010, 46, 9185–9187; (b) V. Castelletto, I. W. Hamley, J. Adamcik, R. Mezzenga and J. Gummel, Soft Matter, 2012, 8, 217–226; (c) A. Dehsorkhi, V. Castelletto, I. W. Hamley and P. Lindner, Soft Matter, 2012, 8, 8608–8615.
20. E. O. Stejskal and J. E. Tanner, J. Chem. Phys., 1965, 42, 288–292.
21. O. S. Makin, P. Sikorski and L. C. Serpell, J. Appl. Crystallogr., 2007, 40, 966–972.
22. (a) K. Kalyanasundaram and J. K. Thomas, J. Am. Chem. Soc., 1977, 99, 2039–2044; (b) D. C. Dong and M. A. Winnik, Photochem. Photobiol., 1982, 35, 17–21.
23. (a) L. J. Bellamy, The Infra-red Spectra of Complex Molecules, Chapman and Hall, 1975; (b) C. Tang, R. V. Ulijn and A. Saiani, Langmuir, 2011, 27, 14438–14449.
24. (a) J. T. Pelton and L. R. McLean, Anal. Biochem., 2000, 277, 167–176; (b) H. Gaussier, H. Morency, M. C. Lavoie and M. Subirade, Appl. Environ. Microbiol., 2002, 68, 4803–4808.
25. Y. J. Zhang and P. S. Cremer, Curr. Opin. Chem. Biol., 2006, 10, 658–663.
26. D. F. Evans and H. Wennerström, The Colloidal Domain. Where Physics, Chemistry, Biology And Technology Meet, Wiley, 1999.
27. P. L. Privalov and S. J. Gill, Pure Appl. Chem., 1989, 61, 1097–1104.
28. B. Escuder, M. Llusar and J. F. Miravet, J. Org. Chem., 2006, 71, 7747–7752.
29. V. Castelletto, I. W. Hamley, C. Cenker, U. Olsson, J. Adamcik, R. Mezzenga, J. F. Miravet, B. Escuder and F. Rodriguez-Llansola, J. Phys. Chem. B, 2011, 115, 2107–2116.
30. G. Pabst, M. Rappolt, H. Amenitsch and P. Laggner, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 4000–4009.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c3sm27899a

---