Emergent colloidal dynamics in electromagnetic fields

Abstract

We present a current review of the collective dynamics that can arise in colloidal systems subjected to electromagnetic fields. The focus is on phenomena that are not simply understandable purely from a dipolar model, but instead emerge from the collective behavior of many discrete interacting components driven out of equilibrium by external forces. We examine in particular the fascinating diversity of large-scale dynamical structures that arise due to the interplay between the induced interactions, time-dependent energy injection, and coupling with the fluid flow.

---

Jure Dobnikar

Jure Dobnikar (left) received his PhD at University of Ljubljana, Slovenia (2000), worked as a postdoctoral fellow at University of Konstanz, Germany, and as a Marie Curie fellow at University of Graz, Austria. Since 2008, he is a senior researcher at University of Cambridge, UK and at Jožef Stefan Institute in Ljubljana, Slovenia. His research goal is to better understand the organization of soft and biological matter at a fundamental level. With methods of theoretical and computational physics he studies many-body colloidal interactions, self-assembly of complex colloids, collective dynamics of active colloids and bacteria. Anand Yethiraj (right) received his PhD degree at Simon Fraser University in Burnaby, Canada in 1999. He received the International Liquid Crystal Society's Glenn Brown Award for his PhD thesis. Later he was a postdoctoral fellow at the FOM Institute AMOLF, Utrecht University and at the University of British Columbia. Since 2005, he has been at Memorial University in St. John's, Canada, where he received the Presidents Award for Outstanding Research (2008) and became Associate Professor (2010). His current research combines microscopy, NMR and rheology to study colloidal self-assembly and macromolecular dynamics and to develop robust self-assembly techniques for patterned nanoscale and microscale materials.

Alexey Snezhko

Alexey Snezhko received his PhD in Physics and Materials Research from Charles University at Prague, Czech Republic in 2001. After a postdoctoral stay at University of South Carolina in Columbia, USA he joined the Materials Science Division of Argonne National Laboratory in Argonne, USA first as a postdoctoral researcher and then as a recipient of the Fermi Fellowship. Since 2008 he has been appointed as a permanent staff Physicist at Argonne National Laboratory. His recent research focuses on collective dynamics and self-assembly in out-of-equilibrium colloids with complex interactions.

Understanding the relationship between the microscopic structure and macroscopic behavior is pertinent to almost all fields of science. An understanding of this relationship is particularly relevant in the colloidal domain, which is common to soft materials and biological systems, where processes occur that have different characteristic length- and time-scales and, often, complex structures with unique properties self-assemble from “simple” building blocks. The equilibrium properties of soft materials exhibit a rich diversity of phenomena, as a result of the many-body nature of the (steric, electrostatic or magnetic) colloidal interactions. When these systems are driven out of equilibrium, the situation becomes even more interesting. The collective dynamics of such systems is governed by the interplay between such colloidal interactions, time-dependent energy injection, and hydrodynamics: the coupling of the particle dynamics to the surrounding fluid flow. Such complex systems are not only fundamentally interesting and fascinating, but also practically important. A deeper understanding of these systems could hold a key to the principles of biological organization, and could enable the design of novel responsive, smart and functional synthetic materials that exhibit multi-level functionality and hierarchical organization, both of which are typical characteristics of biological structures.

Our current understanding is limited to relatively simple colloidal systems in, or close to, equilibrium. External electromagnetic fields provide a natural way to control and tune the interaction profiles of colloidal particles, and they thus offer an additional control over self-assembly,^1–4 and lead to a greater diversity of self-assembled structures. An example of this is dipolar fluids, i.e. systems of colloidal particles with well-defined dipole moments; these dipole moments are either permanent, as in ferromagnetic and ferroelectric systems, or induced, as in paramagnetic or dielectric systems under externally imposed electromagnetic fields. In contrast to colloidal crystals nucleated utilizing capillary forces,⁵ structures formed during field-assisted assembly are usually reversible and could be melted above some critical value of the applied magnetic/electric field. Dipolar fluids have been extensively studied in the past^6–9 and it is not the purpose of this manuscript to review these studies.

In recent years, several experiments and simulations have reported novel out-of-equilibrium dynamic phenomena and coherent large-scale self-organized structures of colloidal particles subjected to time-dependent external magnetic or electric fields. Such novel emergent phenomena occur in systems where the many-body nature of the polarization interactions combines with other effects, such as particle anisotropy, geometrical constraints, the presence of interfaces, and hydrodynamic interactions. This review summarizes the main ideas, as well as recent experimental results and theoretical and simulational approaches, in this emerging research field. We start with systems close to equilibrium where structures are externally induced by time-averaged interactions. Common features, as well as important differences, between electric and magnetic systems will be discussed. Finally, we will focus on dissipative systems where the dynamic coupling between the induced polarization interactions and hydrodynamic flows governs the emergent behaviour and dynamic self-assembly.

1 Close to equilibrium: chains, clusters and open structures

External uniaxial alternating magnetic fields induce fixed dipole moments in spherical paramagnetic particles. In dilute systems the resulting dipolar interactions generally lead to the formation of chains,^6,10,11 while combined dipolar and soft isotropic potentials dictate a richer morphology of stable finite-size clusters including rings and knots.¹² Dipolar colloids geometrically confined to a quasi-planar configuration form a sequence of hexagonal, square, chainlike, labyrinthine, and honeycomb structures.¹³ This is counterintuitive because the interactions between the colloids are purely repulsive;¹⁴ however, due to geometrical constraints they experience a soft-core repulsion that favours clustering despite the lack of attractions.^15–17 Interestingly, a similar sequence of structures can be observed in hard-sphere colloids subjected to soft harmonic confinement.¹⁸

A collective assembly of paramagnetic colloidal particles driven above the periodic stripes of the domain walls by an alternating magnetic field in a uniaxial ferrimagnetic yttrium iron garnet film¹⁹ also revealed a similar sequence of self-assembled structures, shown in panel A of Fig. 1, where hexagonal (a), square (b), chainlike (c), and network structures (d) are seen. It is suggested that these different microstructures of the assembly are promoted by a mismatch between the particle size and pattern wavelength. Ensembles of ferromagnetically ordered colloidal particles subjected to external alternating fields have been investigated both experimentally²⁰ and theoretically²¹ reporting a plethora of structures including, again, chains, clusters, rings and networks. There the system dynamically selects the type of the self-assembled structures in response to parameters of the external driving excitation. Fig. 1 panel B, for example, shows clusters and rings at 20 Hz, chains and rings at 50 Hz, and chains at 100 Hz. The rich diversity of the observed patterns is attributed to the interplay between the dipolar interactions among colloids, their interaction with the alternating field resulting in mechanical agitation of particles due to magnetic torques and the friction between the colloids and the substrate. Lower excitation frequencies allow longer time for particles to adjust their position and magnetic moment orientation to effectively minimize the magnetostatic energy resulting in the formation of cluster phases. As the frequency grows, rings and chains come into play. Depending on the concentration of particles (still well below percolation) the system can undergo a phase transition to the infinite network phase (instead of the cluster phase).²⁰ The addition of a static magnetic field component that is orthogonal to the driving uniaxial alternating field resulted in the formation of complex ordered structures by paramagnetic particles.²²Fig. 1C shows self-assembled patterns of long linear clusters composed of shorter oscillating chains of particles and interconnected by T-, L- and crisscross junction forms in the plane of the excitation field. The nature of the structures (e.g.Fig. 1C, left/right are at 1 Hz/10 Hz respectively) changes with the frequency. The angles between long linear clusters can be altered by changing the ratio of the intensities of the field components. As the frequency of the oscillating field was increased, disk-like clusters started to form in some of the junctions and the number of disks increased with the frequency.

Fig. 1 Self-assembled phases in magnetic colloidal ensembles promoted by a uniaxial alternating magnetic field. Panel A: colloidal assemblies with various orders induced on a garnet film with oscillating ferromagnetic domains: (a) hexagonal, (b) square, (c) network, and (d) chain-like.¹⁹ Panel B: typical patterns formed by nickel spheres (5.3% of the surface monolayer coverage) under magnetic driving at 20 Hz (clustered phase), 50 Hz (netlike structure), and 100 Hz (chain phase).²⁰ Reproduced with the permission of the American Physical Society. Panel C: complex aggregates of paramagnetic particles formed by a combined action of a uniaxial alternating magnetic field and static field applied perpendicular to the a.c. field. Left: 1 Hz a.c. and right: 10 Hz a.c. magnetic fields result in different crisscross junctions.²² The scale bar represents 1 mm.

Alternating (a.c.) electric fields can have a range of effects on the colloidal structure and dynamics. The simplest case is high frequencies (typically in the MHz range) when the electric field oscillates too rapidly for the electric double layer to respond significantly. An external electric field induces dipole–dipole interactions between colloidal particles; in this high-frequency limit, other electrohydrodynamic interactions may be neglected. For spherical dielectric particles in a dielectric liquid medium, the structure formation has been well characterized and is essentially identical to that in magnetic dipolar colloids. In uniaxial fields, chain formation as well as further structural ordering of chains in three dimensions has been observed; this includes a body-centred tetragonal (bct) crystalline state as well as locally ordered cluster states composed of chains.^{6,8,10,11,24–26} An important difference between permanent magnetic dipoles and induced electric dipoles is that the former are only constrained to be locally aligned, while in the latter, there is global alignment, thus preventing the formation of ring-like structures.

In the presence of multiaxial fields, the structures seen with magnetic fields are well reproduced with multi-axial high-frequency electric fields.²⁷ However, unlike magnetic materials, dielectrics are transparent, and materials can be chosen to match the refractive index of the particles to the solvent, in the process also slightly reducing (although still far from eliminating) van der Waals interactions. This allows true three-dimensional structures to be determined in real space,^24,25,28 making way for a quantitative comparison with computer simulations, which have also observed chains, clusters and bct crystals.^29–32

At very low densities, however, there is experimental evidence for an unusual phase of strings that reversibly cluster laterally to form particulate networks surrounding particle-free “voids”. This phase was reported in external electric fields, first in granular spheres³³ and then in Brownian colloids,³⁴ shown in Fig. 2(a) and (b) respectively. The local structure of a single void is shown in Fig. 2(c), where each white point represents a chain along the field direction (shown in the inset) and each cell in a void is in fact a tube. Despite explicit attempts, this phase has not been found in simulations of dipolar colloids carried out by three independent groups.^23,32,35 One example of the structures seen at comparable densities in simulations²³ is shown in Fig. 2(c). This disagreement between the experiment and simulation suggests that the role of other forces could be considered: e.g. many-particle contributions to the dipolar interactions³⁶ or residual electrohydrodynamic interactions.

Fig. 2 Deviations from the dipolar model. Spheres in an a.c. electric field exhibit a cellular network-forming structure with large voids: (a) granular spheres,³³ (b) colloidal spheres,³⁴ and (c) local structure of the low-density structures is disordered, rather than microcrystalline. Field points out of the page everywhere except the inset of (c) which shows the strings along the field direction. Reproduced with the permission of the American Physical Society. (d) Simulations of dipolar spheres do not observe this low-density network-forming structure at comparable densities.²³ Reproduced with permission from ref. 23.

As illustrated by the numerous examples above, dipolar colloids at low volume fractions generally form bonds with low coordination numbers. If these bonds are strong enough (large-enough dipole moments), their lifetime increases and during the process of self-assembly structural rearrangements due to the bond breaking are rare. Under such circumstances, the systems form gel phases consisting of networks of chains—with mechanical properties that are significantly different from comparable non-percolated structures. Gels formed by charged soft dumbbells subjected to external electric fields³⁷ show a field-strength-driven transition from a network to a bundled chain phase, which in turn leads to highly non-linear dielectric susceptibility. Ferrogels, i.e., polymer networks, into which ferromagnetic nanoparticles are embedded, are characterized by the complex interplay of the mechanical polymer properties and the magnetic dipolar interactions of the embedded nanoparticles. The effect of dipolar interactions on the physical properties of 2D ferrogels has recently been examined in numerical simulations.³⁸

Electric field interactions in soft microgel colloids also result in chains and bct crystals at low and intermediate particle volume fractions. Microgel particles are compressible, however, and can be subjected to very high effective (i.e. apparent) volume fractions. Apparent volume fractions larger than 100% can occur because the volume of the compressible microgel particles decreases with the packing fraction and temperature, and all volume fractions are referenced to form factors and particle sizes at low densities. At the highest packings (ϕ_eff from 0.85 to 2.0), electric-field-induced crystal-glass transitions as well as a transition from a glassy state to what appears to be an arrested phase separated state have been observed.³⁹

A diverse set of rotationally symmetric multi-component structures have been assembled in a mixture of paramagnetic and diamagnetic colloids immersed in a magnetized ferrofluid and are subjected to external static magnetic fields.⁴⁰ Flower-shaped fluctuating clusters have also been reported in ref. 41 where it was shown that the suppression of high frequency rotational modes in such “magnetic flowers” leads to subdiffusive dynamics. A ratchet is a device that allows motion in one direction while preventing motion in the opposing direction. A magnetic ratchet effect can be produced on paramagnetic particles by an oscillating magnetic field in a uniaxial garnet film.⁴² Similar ratchet-like potentials can also be produced for non-magnetic (dielectric) particles via optical tweezers.⁴³ Directed transport of paramagnetic particles perpendicular to the stripes was achieved by externally modulating the parallel stripe domains of the garnet film with an oscillating magnetic field. It was observed that this ratchet effect triggers a giant enhancement of the diffusion of the particles transverse to the ratchet direction (and along the stripes), exceeding the zero-field diffusion by a few decades, with a pronounced peak as the oscillating frequency is varied.⁴² The data were interpreted as a signature of a field induced undulation instability in the magnetic domain structures leading to the presence of a time-dependent disordered potential landscape of the magnetic striped pattern.

2 Dynamic assembly

In dynamic self-assembly, structures are formed and continue to exist only while the system dissipates energy.⁴⁴ Alternating fields of the same frequency but with π/2 phase shift with respect to each other result in a biaxial rotating magnetic field. The dynamics of semiflexible paramagnetic chains in rotational fields has been reported and the shape evolution of chain structures due to the balance between viscous and magnetic torques has been investigated.^45,46 Biaxial fields have been effectively used to achieve dynamic self-assembly in magnetic colloidal systems. In contrast to the case of uniaxial fields where the particles assemble head-to-tail due to dipolar interactions and form chainlike structures, biaxial fields can create a net attractive interaction (inverted dipole interaction) in the plane of the field, resulting in the self-assembly of complex sheet-like structures^47–49 (Fig. 3). Athermal⁴⁹ and thermal⁵⁰ simulations of these paramagnetic colloids closely reproduced the observed phenomena. In these Langevin dynamics simulations the particles are essentially hard spheres with induced dipolar interactions, Stokes friction against a solvent, and Brownian motion. Representative simulation results for athermal simulations in biaxial fields are shown in Fig. 3(A).

Fig. 3 Panel A: dynamic self-assembly in rotational fields. Self-assembled composites of particles structured by a biaxial magnetic field. Magnetically soft Fe powder with a particle size of 4 μm and at a concentration of 2 vol% has been used in the experiments (left). Simulated structure at 5 vol% particles (right). Reproduced with permission from ref. 48. Panel B: formation of dynamic advection lattices in a suspension of magnetic platelets subjected to particular time-dependent biaxial magnetic fields.⁵¹ (a) Schematic illustrating the flow at each column tip branching to the four adjacent columns; (b) view in the plane of the magnetic field of the advection lattice for an octave field (75 and 150 Hz components with equal amplitudes); (c) view of the advection lattice normal to the field plane (the columns form a rectangular lattice).⁵¹ Reproduced with permission from ref. 51.

Unusual advection lattices have recently been reported in a suspension of magnetic platelets subjected to time-dependent, biaxial fields where the two orthogonal components have a prescribed frequency or phase relationship.⁵¹ These biaxial fields consist of two orthogonal components with relative frequencies expressed as a ratio of small integers. The observed patterns consist of a checkerboard of antiparallel flow columns that are normal to the biaxial field plane as illustrated in Fig. 3 panel B(a). Striking flow patterns that consist of 1.3 mm diameter flow columns spanning 3 cm across the cell have been observed with the biaxial field where the orthogonal components have a 45° phase difference (Fig. 3 panel B(b)). These columns pack “antiferromagnetically” into a rectangular lattice so the advection lattice can be described as a checkerboard of columns. In addition, if a strong d.c. field component is applied normal to the biaxial field plane, the advection becomes chaotic, producing extremely strong mixing.⁵¹ The effects discovered in these studies cannot be understood in terms of a magnetic force on a single particle suspended in a liquid, but are emergent collective phenomena of the ensemble.

A curious case of biaxial driving is the so-called magic angle geometry. The magic angle, θ_m ≈ 54.7° is the zero of the second Legendre polynomial (P₂(cos θ_m) = 0). At θ_m the external field precesses on a cone such that (averaged over time) the typical dipolar 1/r³ interaction terms cancel out. At the pair level the colloidal interactions (isotropic 1/r⁶ attraction) are formally equivalent to the van der Waals interactions between molecules.^53,54 However, strong many-body polarization interactions among the colloids^53,55 steer an unusual aggregation pathway: linear growth of chains, followed by branching and network formation and finally leading to the formation of thin sheets. An important detail needs to be stressed concerning these experiments:⁵³ in order to suppress the effects caused by the fluid flow, the direction of the precession of the external field has been flipped every second period. No net rotation of colloids and therefore no net flow could arise and the interactions were correctly captured in a time-averaged way. In the opposite scenario, when the external field precesses with a constant direction, the colloids follow the rotation due to the pinning defects and inherent asphericity of the particles, albeit with a lower frequency. In such cases, when colloids or their aggregates rotate, the time-averaged interactions are in principle not sufficient, which gives rise to interesting dynamic effects. For instance, viscoelastic clusters of paramagnetic colloids in a field above θ_m have been studied in ref. 52. The rotation of the clusters with a frequency proportional to the frequency of the external field has been explained by shear waves that arise due to the deformation of the effective line tension (resulting from dipolar interactions) coupled to the loss modulus of the viscoelastic clusters (see Fig. 4 (panel A)). A similar mechanism has been exploited in the experiment⁵³ in order to wrap a large 9 μm silica bead with a dynamically assembled one-particle thick membrane, comprised of 1 μm paramagnetic spheres. When rotation was allowed, the paramagnetic colloids formed rotating clusters that embedded larger spheres. The rotation was later suppressed by starting to periodically flip the direction of the external field, resulting in membranes spanned by large colloidal anchors. A free silica bead was pushed against such a membrane by means of laser tweezers to the point where the membrane was perforated. Immediately after the bead had passed through it, the membrane was spontaneously reconstituted; see the time sequence of the experiment on Fig. 4 panel B. The membrane is therefore a self-healing structure. Properties such as self-healing are usually attributed to biological systems and can emerge in colloidal suspensions when they are dynamically assembled and “live” out of equilibrium.

Fig. 4 Panel A: dynamic self-assembly of rotating clusters. Schematic of a hexagonal cluster in a precessing field H of angular frequency Ω (left). Normalized cluster rotation frequency as a function of the angular frequency of the external field for θ = 90 : 0 deg is plotted (right). Reproduced with permission from Tierno et al.⁵² Panel B: suspended colloidal membranes made of micron size superparamagnetic particles are assembled in an external magnetic field precessing at the magic angle θ_m. Physical rotation of assembled structures enables wrapping of larger particles by the thin membranes. Time-sequence micrographs of the passage of a 9 μm colloid through such a membrane are shown here. As the large colloid held by laser tweezers (marked by a red cross) is pushed against it, the membrane bends until it breaks so that the colloid can pass through it. After being punctured, the membrane self-heals spontaneously. Reproduced with permission from ref. 53.

Synchronization⁵⁶ has recently been explored as a tool towards dynamical self-assembly.⁵⁷ In the experiment, thin nickel films were directionally deposited on 3 μm spherical silica particles creating magnetic Janus particles. In precessing external fields, such particles experience torque with two orthogonal components making them spin around a precession axis, as well as oscillate perpendicular to the rotating plane. In a suspension, such Janus spheres organized into rotating microsize tubes that were dynamically synchronized with the motion of the particles in a way reminiscent of the tidal locking of the moon and earth (see Fig. 5). Synchronization-driven structural transitions reported in ref. 57 suggest a new strategy in which dynamics, rather than static energy minimization can be exploited to control the self-assembly process.

Fig. 5 Synchronization-driven self-assembly. Janus magnetic particles (shown on the schematic illustration) spin and oscillate in the precessing external field. Upon varying the field opening angle θ, due to the synchronized dynamics, structures including microtubes, zig-zag chains or hexagonal sheets are formed. (a) Phase locking of particles in a microtube at θ = 18°. (b) Order parameter defined in ref. 57 and the difference in the angular rotation frequency Δω of the constituent particles and the microtube as a function of θ. One can see that the constituent particles' dipoles are pointing in a direction different from the center of the microtube (by angle ψ). The microtube is desynchronized and unstable above the threshold value θ ≈ 25°. (c) Time evolution during the disassembly of an unstable microtube at θ = 30°. Reproduced with permission from ref. 57.

3 Coupling with the fluid flow

Theoretically, some features of the emergent dynamics of driven colloids can be understood in the framework of a Ginzburg–Landau type amplitude equation coupled to the conservation law equation describing the evolution of the particle density and the Navier–Stokes equation for hydrodynamic flows. Nevertheless, the fundamental microscopic mechanisms leading to the dynamic self-assembly and their relationship to the emergent behavior often remain unclear. Computer simulations are practically the only method to theoretically investigate such questions. However, modeling the non-equilibrium self-assembly presents a huge computational challenge due to the complex many-body interactions and collective dynamics on very different time scales. One of the main challenges is to properly account for the particle-fluid coupling, which is especially non-trivial due to the long range of the hydrodynamic interactions.

The system of colloids in an electric field is potentially richer than the magnetic system. In magnetic fields, and equivalently in the case of a.c. electric fields at very high frequencies, the external forces do not affect the solvent. Consequently, the hydrodynamic interaction is to some extent decoupled from the induced colloidal interactions. When the frequency f of the applied a.c. electric field is lowered, however, the situation becomes more interesting. At low frequencies there is no clear separation of time scales between the time constant τ_dl for the response of the double layer and the time constant of the driving field τ ∼ 1/f. Thus, in addition to the induced dipoles, there can now be ion-flow-induced fluid flows,^61–64 and a variety of new electrohydrodynamics phenomena emerge.

One such emergent phenomenon is the zig-zag instability seen in different colloidal suspensions. First shown by Hu et al.⁵⁸ in spherical colloids (shown in Fig. 6(a)), the mechanism invoked a phase lag between the applied field and polarization of the double layer, giving rise to torques. The angle between the bands and the field direction was 45°. A comprehensive experiment displaying two regimes of band formation in λ-DNA where the bands took on angles of 45° and 60° with respect to the applied field (horizontal in Fig. 6(b) where the latter case is shown) was reported by Isambert et al.⁵⁹ The main players in the electrohydrodynamics are the colloid macro-ions and the salt counter-ions in solution. Both drift electrophoretically in an oscillatory fashion (in opposite directions) as the field oscillates. Shown in Fig. 6(d) is the final state (experiment, top and simulation, bottom) in the evolution of the zig-zag state. The initial state is that of bands perpendicular to the electric field. This non-equilibrium state relaxes to a steady state of tilted bands which maximize shearing deformations. The two regimes identified are frequency dependent. At lower frequencies, the macro-ion drift is much larger than the width of the colloidal aggregate, while at high frequencies, the reverse is true. A similar zig-zag instability is also seen in a binary system of oppositely charged colloids (Fig. 6(c)).⁶⁰ There are now two species of oppositely charged macro-ions, and similar (tilted) band formation takes place.

Fig. 6 Instabilities in low-frequency a.c. electric fields. (a and b) Zig-zags and electrohydrodynamic instabilities in (a) spherical colloids (field along vertical)⁵⁸ and (b) λ-DNA⁵⁹ (field is along horizontal). (c) Zig-zags in band formation in oppositely charged colloids.⁶⁰ The field is along the horizontal direction. (d) Final stage in the evolution of experimental (top) and simulated (bottom) zig-zags. Panel (a) is reproduced with permission from ref. 58, panels (b,d), from ref. 59, and panel (c) from ref. 60.

In non-spherical colloids (viruses and other rod-like particles) one observes an anomalous Kerr effect,^66,67 with the sign of the Kerr constant switching sign as the frequency is lowered. The Kerr effect is an (electric or magnetic) field-induced anisotropy in the refractive index, whose strength is proportional to the field intensity E². While a Kerr effect is not unusual – it is seen for example in molecular liquid crystals – a frequency switchable Kerr effect is interesting. In rods synthesized so that the crystalline anisotropy is along the long axis, one observes birefringence Δn = n_‖ − n_⊥ which increases with the field intensity and saturates at Δn_max for high enough fields (Fig. 7). At high frequencies, dipolar interactions ensure that the rods align in the direction of the field. Thus, this plateau is associated with a large nematic order parameter. Measuring Δn_max as the frequency of the applied field is reduced, one finds first a positive peak, and then a region of negative Δn_max at low frequency. This has been seen for viruses (long-aspect ratio rods), as well as for short-aspect ratio rods;⁶⁷ however, the latter is only seen in the presence of nanospheres which could act as crowding agents. This anomalous sign shift in the birefringence is interpreted as a re-orientation of the rods. However, no direct real-space evidence for this sign shift is reported in the literature. In the case of fd viruses, it appears that the sign shift happens when the frequency is reduced from 1 kHz to 100 Hz.⁶⁶ No sign shift is observed by Kang and Dhont⁶⁵ above 1 kHz, where the sign of the birefringence is carefully confirmed to be consistent with homeotropic alignment. The latter study does not make any statements about rod alignment below 1 kHz; this coincides with the frequency crossover where electrode polarization becomes relevant and the situation becomes more complicated.

Fig. 7 (a) Virus suspensions.⁶⁶c^* = 0.04 mg ml⁻¹. There is a crossover from positive to an anomalous negative Kerr constant as frequency is reduced. (b) Suspensions of short-aspect-ratio rods also exhibit this anomalous Kerr effect, but only in the presence of added spheres (presumably as a kind of crowding agent).⁶⁷ (c) Virus phases.⁶⁵ As a function of field amplitude (1.0, 1.7, 2.7 and 3.4 V mm⁻¹ at 10 Hz respectively), nematic (N), chiral nematic (N^*) and nematic phases with disconnected domains (N^*_D) are observed. At the highest amplitudes, an inhomogenous dynamical state is observed whose microstructure is as yet unclear. Panel (a) is reproduced with permission from ref. 66, panels (b), from ref. 67, and panel (c) from ref. 65.

A diverse range of electrokinetic phenomena have been observed close to surfaces and in the presence of non-uniform fields. Induced-charge electro-osmosis (ICEO) is a phenomenon introduced by Bazant and Squires that utilizes both proximity to surfaces and non-uniformities in the electric field.⁶⁸ An example⁶⁸ is a cylindrical metal wire shown in Fig. 8(a), depicted as a function of time after a d.c. field is turned on. First, charge is induced in the metal wire (first panel). This induced charge in turn brings in mobile counterions in solution of opposite charge (second panel). Since these counterions are mobile, they move in the presence of the external field which is non-uniform near the metal wire, and create a flow field that is quadrupolar (third panel). Reversing the sign of E reverses the sign of the induced charge and the counterions, and the direction of the flow field is unchanged; i.e. it is a rectifying flow. Thus the ICEO mechanism is even active at relatively high frequencies.

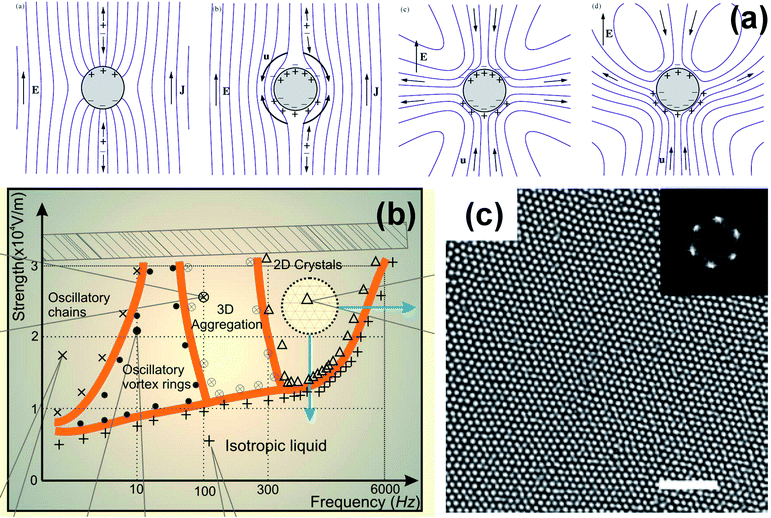Fig. 8 (a) A schematic representation of the mechanism for induced-charge electro-osmosis.⁶⁸ The first two panels show the transients to the quadrupolar flow field that result from turning on a d.c. electric field. The direction of flow is independent of the sign of the applied field, and therefore persists up to reasonably high a.c. driving fields as well. (b) Even in uniform fields, two-dimensional electrohydrodynamics can generate a rich frequency-controlled phase diagram⁷³ that includes linear and vortex-like clusters at frequencies below 100 Hz, more compressed 3-dimensional structures at intermediate frequencies (100 – 300 Hz) and (c) 2-dimensional crystals between 0.5 and 5 kHz.⁷³ The 2d crystals have been reported earlier by Trau et al.⁷² Panel (a) is reproduced with permission from ref. 68, and panels (b,c), from ref. 73.

Complex non-uniform fields can be generated from simple arrangements of micro-patterned electrodes.⁶⁹ At high frequencies, it is well known that dielectrophoretic forces guide particle transport.⁷⁰ The dielectrophoretic (DEP) force F_DEP ∼ ∇E², where E is the electric field magnitude. On the other hand, ICEO flow is linear with respect to the tangential electric field at the solid–liquid-electrolyte interface: F_ICEO ∼ E_tangential. At frequencies where ICEO is dominant, the threshold fields for particle agglomeration are seen to be around a factor of 10 lower than at high frequencies where DEP is the sole particle aggregation mechanism.

Even in uniform fields in two dimensions, particle-induced non-uniformities in the electric field play an important role. The presence of particulate obstructions induces fluid flows in the plane perpendicular to the field, and this has been shown to lead to long-range attractive interactions⁷¹ and crystallization.⁷² Further, in 2-dimensional or in 3-dimensional cells with one thin dimension, electrohydrodynamics results in a rich frequency-tunable phase diagram,⁷³ shown in Fig. 8(b). At low frequencies (f < 100 Hz), linear and vortex-like clusters are observed. More compressed 3-dimensional structures at intermediate frequencies (100 – 300 Hz). At higher frequencies (0.5 kHz < f < 5 kHz) 2-dimensional crystals are observed.⁷³

Hydrodynamics is a long-range interaction that can be attractive or repulsive, and can generate either coherent or incoherent structures. Varshney et al.⁷⁴ have demonstrated control over both the strength and lengthscale of the electrohydrodynamic interaction in a two-component oil mixture. In this mixture the majority liquid has a charge relaxation time τ_c = ε₀ε/σ (where ε and σ are the dielectric constant and conductivity of the medium) that is roughly 10 ms, making dynamics very different on frequency scales above and below f_c ∼ 1/(2πτ_c) ∼ 15 Hz. The electrohydrodynamic forces result in tangential electric stresses⁷⁵ which cause the droplets to become either oblate or prolate:^76,77 this shape transition can be frequency controlled with f_c being the crossover frequency.⁷⁴ However, the hydrodynamic effects on droplet–droplet interactions are far more complicated. The observations are summarized in Fig. 9 panel A. As a function of frequency, it is observed that a static droplet (a) breaks up in a turbulent fashion (b) giving rise to cloud-like and chaotic structures (c). At higher frequencies, but still f/f_c < 0.1, droplet deformations are observed which are non-axisymmetric with different symmetries. These deformations appear to be partly driven by spatially varying hydrodynamic flow fields, and partially from minimization of dipolar and surface energies. For f/f_c = 0.25 a regime where droplet coalescence is accelerated by ratcheting droplet motion is observed. Finally for f/f_c > 1, a droplets interact with dipolar interactions. A mechanism for producing monodisperse droplets on the 10 – 20 μm scale was reported.

Fig. 9 (A) Frequency-tunable hydrodynamic interactions in an oil-in-oil emulsion, using d.c. and a.c. electric fields.⁷⁴ A static drop (a) breaks up into tiny droplets which move in a turbulent manner at frequencies less than 2 Hz and form incoherent cloud-like structures (b and c). At intermediate frequencies (d–f: 2 to 10 Hz), droplets are stable but they pulsate in shape between spherical and oblate, with non-axisymmetric deformations in the plane perpendicular to the field. (g) At 25 Hz, droplet coalescence dominates. (h) A monodisperse droplet array is produced via a frequency quench from 1 Hz to 1 kHz. The drop shape crosses over from oblate to prolate at higher frequencies, dipolar interactions are dominant. (B) Dynamical structures in d.c. electric fields generated by electrohydrodynamic convective flows.⁷⁸ Time-lapse images of rotating toroidal vortices (left) and pulsating rings. Panels A and B are reproduced with permission from ref. 74 and 78 respectively.

Large scale dynamical structures are observed when a.c. electric fields are imposed in a suspension of metallic particles in low conductivity solvents ethanol and toluene, with f_c in the range 2 – 20 Hz.⁷⁸ The vortex (3 frames on the left) and toroidal (6 frames on the right) structures, whose time evolution is shown in Fig. 9 panel B, are proved to be formed due to electrohydrodynamic convection.

4 Out-of-equilibrium self-assembly at liquid interfaces

Nontrivial dynamics and self-assembly can be observed in ensembles of ferromagnetic particles suspended at liquid interfaces and subjected to alternating/rotational fields. Magnetized millimeter-sized disks suspended at the water–air interface and subjected to a rotating magnetic field demonstrate rich out-of-equilibrium self-assembly.⁷⁹ The disks were spinning around their axes with a frequency equal to that of the external rotating magnetic field. The fluid motion associated with disk spinning induced repulsive interactions between disks, while they got attracted towards the axis of the field rotation. The interplay between attractive and repulsive interactions gave rise to the formation of patterns with different types of ordering. Alternating magnetic fields can be effectively used to promote nontrivial dynamics in ferromagnetic colloids suspended at the liquid–air interface.^80–82 Ferromagnetic microparticles experience torques when subjected to an external magnetic field. Due to the ferromagnetic nature of particles and pinned magnetic domain walls inside them, these torques are transferred to the local excitations of the liquid–air interface through mechanical reorientation of particles. While the imposed external magnetic field is uniform across the system, the energy injection to the interface might be highly non-uniform due to the fact that it strongly depends on the positions of magnetic particles at the interface and morphology of the structures that they might have dynamically self-assembled into. Interplay between these two energy fluxes (“magnetic shaking” and the liquid interface energy injection) gives rise to novel highly nontrivial non-equilibrium phenomena and dynamic self-assembled structures.

Maintained in a state far-from-equilibrium by application of an alternating (a.c.) magnetic field applied perpendicular to the interface, a magnetic colloidal dispersion exhibits a strong tendency towards dynamic self-organization. Dynamically assembled snake-like structures emerge in the system, see Fig. 10(a), in a certain range of excitation parameters.⁸⁰ Note that the driving field is applied perpendicular to the interface so the self-assembly happens in the plane transversal to the field. Remarkable self-organized multi-segment structures emerge as a result of the collective interaction between the particles driven by an external a.c. magnetic field, interface and induced hydrodynamic flows. These structures are dynamic by nature and exist only while we supply energy by means of an external driving field. Each structure is composed of segments; each segment consists of ferromagnetically aligned chains of microparticles whose magnetic moments are aligned along the chain direction. The segments, however, are anti-ferromagnetically aligned: the total magnetic moment per segment reverses its direction from section to section as shown in Fig. 10(b). Amazingly, the long-range order has a completely unconventional origin. It is facilitated by a structure-induced surface wave. This is a first manifestation of a long-range magnetic ordering facilitated by hydrodynamic interactions.^82,83

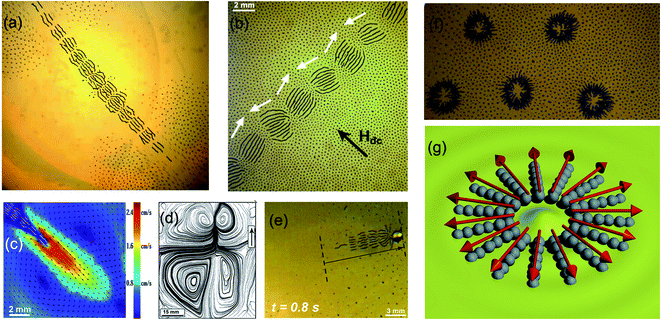Fig. 10 Dynamic self-assembly at liquid interfaces. (a) Dynamic multi-segmented pattern (snake) generated by an alternating field (110 Oe, 50 Hz) at a water–air interface;⁸⁰ (b) response of the dynamic snake structure to an in-plane magnetic field. One sees zig-zag order indicative of antiferromagnetic ordering between the segments comprising the structure;⁸² (c) surface flow velocity field in the vicinity of the snake's tail. Arrows depict the surface velocity field obtained by PIV and the background colors show magnitudes of flow velocities. (d) Self-propelled pattern-bead hybrids.⁸⁴ The arrow shows the distance travelled by the structure in 0.8 seconds. A spherical glass bead was used; (e) the asymmetric vortex structure of a self-propelled snake structure. The arrow shows the direction of swimming. (f) Self-assembled dynamic asters and (g) schematics of a magnetic ordering in asters.⁹¹ Reproduced with permission from ref. 80, 82, 84 and 91.

In the process of dynamic self-assembly, ferromagnetic suspensions at liquid–air interfaces often develop strong large-scale hydrodynamic surface flows in the vicinity of assembled structures.⁸¹ The strongest flows are concentrated at opposite ends of the dynamic pattern where the centers of the vortices are located (dark spots in Fig. 10(c)). The flow velocity can be as fast as a few centimeters per second and is controlled by the frequency of the driving magnetic field. It was demonstrated that under certain conditions⁸⁴ the reported dynamic structures spontaneously break the symmetry of self-generated surface flows and turn into self-propelled entities, see Fig. 10(d). Alternatively, another type of swimmer is realized via controlled breaking of the symmetry of surface flows. This symmetry breaking is realized by attaching a bead to one of the structure's ends (bead-snake hybrid), see Fig. 10(e). In contrast to previously reported colloidal swimmers,^85–88 both types of magnetic surface swimmers are unique due to the unusual mechanism of self-propulsion exploiting symmetry breaking of self-generated surface flows and the intrinsic antiferromagnetic nature of the swimmer's structure. In addition it was demonstrated that, when in multiple-swimmers state, dynamic self-assembled swimmers create a highly disordered and non-periodic surface velocity field⁸⁹ with Kolmogorov energy spectra that are characteristic of two-dimensional systems; this result indicates that self-generated flows are highly localized near the interface.

From the theoretical viewpoint the self-localization of the dynamic snake structures has been recovered in the framework of an amplitude equation for parametric waves (Ginzburg–Landau type equation) coupled to the conservation law equation describing the evolution of the magnetic particles and Navier–Stokes equation for large-scale mean flows.^3,80 To understand microscopic mechanisms leading to the formation of dynamic snakes a molecular dynamics approach that successfully reproduced the observed phenomenology has been developed.⁹⁰

Replacement of the liquid–air interface with a liquid–liquid one modifies the density contrast between two layers and can be used to completely eliminate the gravitational part in the dispersion relationship for the induced surface waves at the interface. In addition, the presence of a top liquid drastically changes the overall force balance and, correspondingly, the outcome of a dynamic self-assembly. Ferromagnetic dispersion at such an interface subjected to an alternating magnetic field revealed novel dynamic phases.⁹¹ Despite its apparent simplicity, the system exhibits a remarkable diversity of dynamic self-assembled structures. Localized asters (illustrated in Fig. 10(f)) emerge at the interface as a result of a dynamic self-assembly promoted by interactions between the interface's excitations and a collective response of the magnetic colloids to the external alternating field. Each aster is comprised of ferromagnetically ordered chains of microparticles. In contrast to the snakes promoting the planar surface wave at the interface, asters decorate slopes of a circular surface wave. The arrangement of chains within an aster is governed by the self-induced hydrodynamic streaming flows and dipole–dipole repulsion of chains. There are two permissible magnetic configurations for asters: magnetic moments pointing inward, towards the center of the aster, and outward (as schematically shown in Fig. 10(g)). Upon application of a small static in-plane magnetic field one can open-up and navigate asters.⁹¹ The ability to control asters' openings, speed, and direction of propulsion allows performing manipulation of nonmagnetic particles at the interface.

5 Conclusions

We have seen that the rapidly developing field of colloidal dynamics in the presence of external driving fields brings to light a plethora of novel out-of-equilibrium dynamic phenomena and self-assembled patterns. These large-scale dynamical structures are associated with the collective response of colloidal ensembles to external forcing. Seemingly simple colloidal systems demonstrate a remarkably complex dynamic behavior when driven out of equilibrium by time-dependent external fields. These phenomena seem to point us in the direction of promising functional out-of-equilibrium materials responsive to the external environment.

Acknowledgements

We acknowledge the support of CECAM and of 7th Framework Program of European Union (ITN-COMPLOIDS 234810), who co-sponsored the workshop on Emergent Dynamics in Driven Colloids held in Lausanne, 26–28.4.2012 (http://www.cecam.org/workshop-690.html). A.S. acknowledges the support of the U.S. DOE, Office of Basic Energy Sciences, Division of Materials Science and Engineering, under the Contract no. DE AC02-06CH11357. J.D. acknowledges the support of the 7th Framework Program of European Union through grants ARG-ERC-COLSTRUCTION 227758 and ITN-COMPLOIDS 234810, and by the Slovenian research agency through Grant P1-0055. A.Y. acknowledges financial support from the National Science and Engineering Research Council of Canada (NSERC) as well as the hospitality of the groups of Profs. Stefan Egelhaaf and Juergen Horbach at Heinrich Heine University, Duesseldorf.

References

1. H. Löwen, J. Phys.: Condens. Matter, 2008, 20, 400301.
2. A. van Blaaderen, MRS Bull., 2004, 29, 85–90.
3. A. Snezhko, J. Phys.: Condens. Matter, 2011, 23, 153101.
4. A. Yethiraj, Soft Matter, 2007, 3, 1099–1115.
5. N. Bowden, I. Choi, B. Grzybowski and G. Whitesides, J. Am. Chem. Soc., 1999, 121, 5373–5391.
6. T.-J. Chen, R. N. Zitter and R. Tao, Phys. Rev. Lett., 1992, 68, 2555–2558.
7. M. Parthasarathy and D. J. Klingenberg, Mater. Sci. Eng., R, 1996, 17, 57.
8. J. E. Martin, J. Odinek, T. C. Halsey and R. Kamien, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 756–775.
9. S. Klapp, J. Phys.: Condens. Matter, 2005, 17, R525–R550.
10. S. Fraden, A. J. Hurd and R. B. Meyer, Phys. Rev. Lett., 1989, 63, 2373–2378.
11. J. E. Martin, D. Adolf and T. C. Halsey, J. Colloid Interface Sci., 1994, 167, 437–452.
12. M. Miller and D. J. Wales, J. Phys. Chem. B, 2005, 109, 23109.
13. N. Osterman, D. Babić, I. Poberaj, J. Dobnikar and P. Ziherl, Phys. Rev. Lett., 2007, 99, 248301.
14. J. Dobnikar, J. Fornleitner and G. Kahl, J. Phys.: Condens. Matter, 2008, 20, 494220.
15. P. J. Camp, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 061506.
16. P. Ziherl and R. D. Kamien, J. Phys. Chem. B, 2011, 115, 7200–7205.
17. C. N. Likos, B. M. Mladek, D. Gottwald and G. Kahl, J. Chem. Phys., 2007, 126, 224502.
18. T. Curk, A. de Hoogh, F. J. Martinez-Veracoechea, E. Eiser, D. Frenkel, J. Dobnikar and M. E. Leunissen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 021502.
19. P. Tierno, T. M. Fischer, T. H. Johansen and F. Sagués, Phys. Rev. Lett., 2008, 100, 148304.
20. A. Snezhko, I. S. Aranson and W.-K. Kwok, Phys. Rev. Lett., 2005, 94, 108002.
21. G. M. Range and S. H. L. Klapp, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 031201.
22. Y. Nagaoka, H. Morimoto and T. Maekawa, Langmuir, 2011, 27, 9160–9164.
23. J. Richardi and J. J. Weis, J. Chem. Phys., 2011, 135, 124502.
24. U. Dassanayake, S. Fraden and A. van Blaaderen, J. Chem. Phys., 2000, 112, 3851–3858.
25. A. Yethiraj and A. van Blaaderen, Nature, 2003, 421, 513.
26. G. Bossis, C. Métayer and A. Zubarev, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 041401.
27. M. E. Leunissen, H. R. Vutukuri and A. van Blaaderen, Adv. Mater., 2009, 21, 0935–9648.
28. A. Yethiraj and A. van Blaaderen, Int. J. Mod. Phys. B, 2002, 16, 2328–2333.
29. R. Tao and J. M. Sun, Phys. Rev. Lett., 1991, 44, R6181–R6184.
30. A. Hynninen and M. Dijkstra, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 051402.
31. J. Richardi, M. P. Pileni and J. J. Weis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 061510.
32. A. M. Almudallal and I. Saika-Voivod, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 011402.
33. A. Kumar, B. Khusid, Z. Qiu and A. Acrivos, Phys. Rev. Lett., 2005, 95, 258301.
34. A. Agarwal and A. Yethiraj, Phys. Rev. Lett., 2009, 102, 198301.
35. J. S. Park and D. Saintillan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 041409.
36. H. J. H. Clercx and G. Bossis, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 2721–2738.
37. P. Ilg and E. Del Gado, Soft Matter, 2011, 7, 163–171.
38. R. Weeber, S. Kantorovich and C. Holm, Soft Matter, 2012, 8, 9923–9932.
39. P. S. Mohanty, A. Yethiraj and P. Schurtenberger, Soft Matter, 2012, 8, 10819.
40. R. M. Erb, H. S. Son, B. Samanta, V. M. Rotello and B. B. Yellen, Nature, 2009, 457, 999–1002.
41. A. Ray, S. Aliaskarisohi and T. M. Fischer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 031406.
42. P. Tierno, P. Reimann, T. H. Johansen and F. Sagues, Phys. Rev. Lett., 2010, 105, 230602.
43. R. D. L. Hanes, C. Dalle-Ferrier, M. Schmiedeberg, M. C. Jenkins and S. U. Egelhaaf, Soft Matter, 2012, 8, 2714–2723.
44. G. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421.
45. S. Melle, G. Fuller and M. Rubio, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 4111.
46. S. Biswal and A. Gast, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 041406.
47. J. Martin, R. Anderson and C. Tigges, J. Chem. Phys., 1999, 110, 4854–4866.
48. J. Martin, E. Venturini, J. Odinek and R. Anderson, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 2818–2830.
49. J. Martin, R. Anderson and C. Tigges, J. Chem. Phys., 1998, 108, 7887–7900.
50. J. Martin, R. Anderson and C. Tigges, J. Chem. Phys., 1999, 110, 4854–4866.
51. K. J. Solis and J. E. Martin, Appl. Phys. Lett., 2010, 97, 034101.
52. P. Tierno, R. Muruganathan and T. M. Fischer, Phys. Rev. Lett., 2007, 98, 028301.
53. N. Osterman, I. Poberaj, J. Dobnikar, D. Frenkel, P. Ziherl and D. Babić, Phys. Rev. Lett., 2009, 103, 228301.
54. J. Martin, R. Anderson and R. Williamson, J. Chem. Phys., 2003, 118, 1557–1570.
55. J. E. Martin, E. Venturini, G. L. Gulley and J. Williamson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 021508.
56. J. Kotar, M. Leoni, B. Bassetti, M. C. Lagomarsino and P. Cicuta, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 7669–7673.
57. J. Yang, M. Bloom, S. C. Bae, E. Luijten and S. Granick, Nature, 2012, 91, 578.
58. Y. Hu, J. L. Glass, A. E. Griffith and S. Fraden, J. Chem. Phys., 1994, 100, 4674–4682.
59. H. Isambert, A. Ajdari, J.-L. Viovy and J. Prost, Phys. Rev. Lett., 1997, 78, 971–974.
60. T. Vissers, A. van Blaaderen and A. Imhof, Phys. Rev. Lett., 2011, 106, 28303.
61. J. Dhont and K. Kang, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 33, 51–68.
62. I. Pagonabarraga, B. Rotenberg and D. Frenkel, Phys. Chem. Chem. Phys., 2010, 12, 9566–9580.
63. B. Rotenberg, I. Pagonabarraga and D. Frenkel, Faraday Discuss., 2010, 144, 223–243.
64. G. Giupponi and I. Pagonabarraga, Phys. Rev. Lett., 2011, 106, 248304.
65. K. Kang and J. K. G. Dhont, Soft Matter, 2010, 6, 273–286.
66. H. Kramer, C. Martin, C. Graf, M. Hagenbüchle, C. Johner and R. Weber, Prog. Colloid Polym. Sci., 1994, 97, 40–45.
67. F. Mantegazza, M. Caggioni, M. L. Jiménez and T. Bellini, Nat. Phys., 2005, 1, 103–106.
68. M. Z. Bazant and T. M. Squires, Phys. Rev. Lett., 2004, 92, 066101.
69. A. P. Bartlett, A. K. Agarwal and A. Yethiraj, Langmuir, 2011, 27, 4313–4318.
70. H. A. Pohl, Dielectrophoresis: the behavior of neutral matter in nonuniform electric fields, Cambridge University Press, Cambridge, 1978.
71. S.-R. Yeh, M. Seul and B. I. Shraiman, Nature, 1997, 386, 57–59.
72. M. Trau, D. A. Saville and I. A. Aksay, Science, 1996, 272, 706–709.
73. K.-Q. Zhang and X. Y. Liu, J. Chem. Phys., 2009, 130, 184901.
74. A. Varshney, S. Ghosh, S. Bhattacharya and A. Yethiraj, Sci. Rep., 2012, 2, 738.
75. J. Melcher and G. Taylor, Annu. Rev. Fluid Mech., 1969, 1, 111–146.
76. D. Saville, Annu. Rev. Fluid Mech., 1997, 29, 27–64.
77. J. Q. Feng, Proc. Natl. Acad. Sci. U. S. A., 1999, 455, 2245–2269.
78. M. Sapozhnikov, Y. Tolmachev, I. Aranson and W. Kwok, Phys. Rev. Lett., 2003, 90, 114301.
79. B. Grzybowski, H. Stone and G. Whitesides, Nature, 2000, 405, 1033–1036.
80. A. Snezhko, I. S. Aranson and W.-K. Kwok, Phys. Rev. Lett., 2006, 96, 078701.
81. M. Belkin, A. Snezhko, I. S. Aranson and W.-K. Kwok, Phys. Rev. Lett., 2007, 99, 158301.
82. A. Snezhko, I. S. Aranson and W.-K. Kwok, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 041306.
83. A. Snezhko and I. S. Aranson, Phys. Lett. A, 2007, 363, 337–340.
84. A. Snezhko, M. Belkin, I. S. Aranson and W.-K. Kwok, Phys. Rev. Lett., 2009, 102, 118103.
85. R. Dreyfus, J. Baudry, M. Roper, M. Fermigier, H. Stone and J. Bibette, Nature, 2005, 437, 862–865.
86. S. Gangwal, O. J. Cayre, M. Z. Bazant and O. D. Velev, Phys. Rev. Lett., 2008, 100, 058302.
87. P. Tierno, R. Golestanian, I. Pagonabarraga and F. Sagues, Phys. Rev. Lett., 2008, 101, 218304.
88. M. Vilfan, A. Potočnik, B. Kavčič, N. Osterman, I. Poberaj, A. Vilfan and D. Babić, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 1844–1847.
89. M. Belkin, A. Snezhko, I. S. Aranson and W.-K. Kwok, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 011310.
90. M. Belkin, A. Glatz, A. Snezhko and I. S. Aranson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 015301.
91. A. Snezhko and I. S. Aranson, Nat. Mater., 2011, 10, 698–703.

---