Swelling-induced deformations: a materials-defined transition from macroscale to microscale deformations

Abstract

Swelling-induced deformations are common in many biological and industrial environments, and the shapes and patterns that emerge can vary across many length scales. Here we present an experimental study of a transition between macroscopic structural bending and microscopic surface creasing in elastomeric beams swollen non-homogeneously with favorable solvents. We show that this transition is dictated by the materials and geometry of the system, and we develop a simple scaling model based on competition between bending and swelling energies that predicts if a given solvent droplet would deform a polymeric structure macroscopically or microscopically. We demonstrate how proper tuning of materials and geometry can generate instabilities at multiple length scales in a single structure.

---

Designing advanced materials to accommodate fluid–structure environments requires accurate control over the swelling-induced deformations of soft mechanical structures. The dynamics of osmotically driven movements within elastic networks, and the interplay between a structure's geometry and boundary conditions, play a crucial role in the morphology of growing tissues and tumors,^1,2 the shrinkage of mud³ and moss,⁴ and the curling of cartilage,⁵ leaves,^6–8 and pine cones.⁹ Various structural and surface instabilities can occur when a favorable solvent is introduced to a dry gel. These include buckling,^10–12 creasing,¹³ and wrinkling instabilities,^14–19 and the curling of paper and rubber.^21–24 In addition, porous thin films, such as fuel cell membranes,^25,26 are highly susceptible to swelling-induced delamination and buckling, which cripple their functionality. For materials to adequately accommodate different fluid–structure environments there must be an accurate understanding of both the global and surface-confined deformations that can occur. In this paper, we examine the transition between global structural deformations and surface patterns that occur as a function of material geometry, fluid–structure interaction, and the volume fraction of the swelling fluid.

Building on the idea that soil can be treated as a porous elastic network,²⁷ the consolidation of fluid-saturated soil was examined,²⁸ and the mathematical framework for poroelasticity that emerged^29–31 remains the dominant theory for describing the migration of fluid within gels,^32,33 tissues,^34,35 and granular media.^31,36 The fluid movement is dictated by the characteristic, or poroelastic, time required for it to move through a network. If the fluid and network are incompressible, and the fluid velocity obeys Darcy's law,²⁸ a diffusive-like time scale emerges: τ ∼ L²D⁻¹, where L is the characteristic length scale, and D is the diffusivity. The steady permeation of fluid through rigid porous networks, and the equilibrium swelling of crosslinked elastic networks are well described by these diffusion dynamics, but at early times the dynamic deformations of these soft, swelling elastomers can be highly nontrivial.

Material geometry, structural confinement, and non-homogenous exposure to fluid will all add additional complications to the swelling-induced deformations of soft mechanical structures. For instance, when the surface of a dry gel is exposed to favorable solvent, how does it accommodate the stress that develops? If a slender beam is exposed on one face to a favorable solvent the fluid will fully swell the beam at long times, and it will reach a larger equilibrium length.^32,37 At short times, the outer surface of the beam is under more stress than the bulk, and will elongate and bend into an arch.^{22–24,38,39} However, bending of the structure will only occur if the swelling stress is greater than the stress required to bend the beam.

If the material is very thick, the resistance to bending will generate a compressive stress on the surface, causing the outermost layer of the structure to crease. Biot was first to predict the presence of surface instabilities on a homogeneous elastic medium due to compressive forces.⁴⁴ Predicting and controlling these surface instabilities will impact the design of flexible electronics, soft robotics, and microfluidic devices. While most of the available literature on wrinkling and creasing deals with homogeneous swelling of confined gels submersed in solvent^13,14,40,41 or soft substrates with stiff skins,^15–17,19 understanding of the effect of elastomer geometry and fluid volume in case of the non-homogeneous swelling of gels is still lacking. We present a simple model experiment for probing this transition.

Fig. 1 illustrates the experimental procedure. We place a favorable fluid droplet of volume V_f on top surface of an elastomeric beam having undeformed length L. As the fluid swells the polymeric network, we measure the length of the beam, l(t), and surface topography, λ(t), as a function of time. The schematic in Fig. 1a shows the propagation of fluid within the crosslinked elastomer. The unswollen polymer coils within the network have an equilibrium radius of gyration, which will increase, i.e. swell, when the coil comes in contact with a solvent that has favorable enthalpic interactions (Fig. 1a(i and ii)). A balance of the enthalpic interactions between the polymer and solvent and the entropic cost of stretching the chain dictate the extent of swelling within a given material system.²⁰ This local expansion of the elastic network creates a structure analogous to a bilayer, in which the top layer wants to be longer than the bottom layer, and thus it bends (Fig. 1b). If the flexural rigidity of the beam is larger than the moment induced by swelling, then the rigid structure will impose a compressive stress on the swollen layer, analogous to a gel that is constrained at its base (Fig. 1c). If this stress creates a compressive strain that exceeds a critical value, the surface will crease.

Fig. 1 Bending and creasing of beams swollen non-homogenously. (a) A schematic showing the propagation of fluid through crosslinked polymer network. (b) A thin beam (h = 1 mm, L = 35 mm) is swollen by placing a diisopropylamine droplet of volume 5.96 μL on its top surface. As the beam is fixed at both ends, it bends out of plane to accommodate the expansion of the top surface. (c) A much thicker beam (h = 5 mm, L = 35 mm) is swollen with the same solvent and volume, but instead of bending, creases appear on the top surface.

To study this transition between bending and creasing experimentally, we prepared polydimethylsiloxane (PDMS) (Dow Corning Sylgard 184™) beams of various thicknesses (1 mm, 2 mm, 3 mm, 4 mm, 5 mm) with a width b = 2.5 mm and length L = 35 mm at a 10 : 1 (w/w) ratio of prepolymer-to-crosslinker. A droplet of fluid was deposited at the middle of the beam by a syringe pump (New Era Pump Systems Inc, Model NE-1000), and its volume was varied from 1.29 μL to 5.96 μL by appropriate choice of syringe needle diameter (Hamilton). As the beam swells, its structural deformation was captured at 30 fps using Edmund-Optics GigE camera with a Nikkor lens (35 mm f: 1–1.4), while its surface deformation were recorded at 21 fps with a Edmund-Optics GigE camera attached with an inverted Nikkor lens (35 mm f: 1–1.4) and a macro extension tube (Vivitar N-AF 36 mm). Image analysis was performed using ImageJ and Matlab to extract the macroscopic beam elongation and microscopic crease spacing as a function of time.

Fluids were chosen based on their affinity for swelling PDMS,⁴² which is comprised by similarities in both solubility δ_s and polarity μ (Table 1). The solubility and polarity of a fluid within a network combine in a nontrivial way to swell the elastic structure,⁴² therefore the measured strain at equilibrium for a beam that is fully submersed in the fluid, ε_eq, is the metric we use to differentiate swelling ability. Fig. 2a shows the swelling of PDMS beams by five different fluids. Each beam is fully submerged in a solvent and its elongation is measured as a function of time. In this figure, we highlight the elongation at short times (i.e. t ≤ 100 s) to show that the beam initially deforms faster than the diffusive dynamics that drive swelling at long times,⁴³ and that the rate of this early deformation differs for various solvents. In particular, we note that polarity differences between solvent and network may play an important role in the early time dynamics, with large deformations occurring when |Δμ| = |Δμ_s − Δμ_P| < 0.5.

Table 1 Material solubility δ_s and polarity μ obtained from Lee et al.,⁴² strain at equilibrium measured experimentally

Material	δ s (cal^1/2 cm^−3/2)	μ (D)	ε eq
PDMS	7.3	0.6–0.9	—
Diisopropylamine	7.3	1.2	1.13
Triethylamine	7.5	0.7	0.58
Hexanes	7.3	0.0	0.35
Toluene	8.9	0.4	0.31
Ethyl acetate	9.0	1.8	0.18

---

Fig. 2 Swelling dynamics of PDMS at short times. (a) Submersed swelling strain of PDMS beams by different solvents. Inset: different strain rates imparted by different solvents at short times. (b) (i) Change in macroscopic strain over a period of time when a diisopropylamine droplet of volume V_f = 5.96 μL is placed on beams of thicknesses 1 mm, 3 mm. (ii) Maximum strain developed in beams of various thicknesses due to 5.96 μL droplet of all solvents. (iii) Maximum strain in 1 mm thick beam due to different droplet volume of all solvents.

To study the transition between macroscopic structural deformation and surface deformation, we performed experiments with a finite volume of fluid. When a droplet of volume V_f is placed on the surface of a dry beam, a non-homogeneous strain field develops during swelling which propagates over time. For thin beams, a macroscopic strain is measured from the change in beam length, ε = l − L/L. Fig. 2b(i) shows a graph of ε as a function of time for two beams with different thicknesses that are exposed to 5.96 μL of diisopropylamine. This strain grows until the imbibition front reaches the centerline of the beam, and then gradually decreases as the fluid continues to propagate. At long times, the beam returns to a flat state after the fluid has evaporated from the network. We can quantify the maximum macroscopic strain ε_max that is achieved as a function of beam thickness (Fig. 2b(ii)) and fluid volume (Fig. 2b(iii)). Above a critical thickness, a particular type and volume of fluid is unable to generate enough stress to create a macroscopic deformation of the beam. We seek a reduced-order scaling analysis that will describe the material and geometric contributions to this critical threshold.

In these swelling-induced deformations, there exists an competition between the solvent's ability to swell the network, and the structure's ability to resist deformation. Since the swelling is non-homogenous, the strain variation through the thickness of the beam may induce a bending deformation. The rigidity of a structure can be quantified by the energy required to bend it, which is:

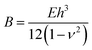where , h is the thickness of the beam, E is the elastic modulus, ν is Poisson's ratio, and θ(s) is the angle along the arc-length. Since the time scale of swelling is short, and the ratio of the fluid to the solid elastic network is very small, we assume a linear elastic behavior. If instead we allowed the swollen structures to approach chemical equilibrium, it would be necessary to consider a hyperelastic model where the elastic constants depend on the swelling strain. With these assumptions, we expect an energy due to swelling will take a similar form, with , where β is a function of the elastic properties of the network, the interaction between the polymer and solvent, and the amount of fluid, i.e. β = f(E, ε, V_f). If this takes the form of a strain energy, we may write , where V_s is the volume of the swollen region in the structure. With a finite volume of fluid, the maximum deformation will occur at short times during the swelling process, when there is a high concentration of solvent within a local region of the polymer network. If this small, but highly concentrated region is analogous to a fully swollen structure, then at short times we may assume that the strain imparted on these chains is on the order of the equilibrium swelling strain ε ≈ ε_eq, and the volume of the swollen region will be confined to the volume of the fluid V_s ≈ V_f. With these assumptions†, we expect the swelling energy to scale as:The swelling-induced deformation of these beams will be dictated by the interplay between the bending and swelling energies, such that no bending will occur when U_b ∼ U_s. Hence these competition between bending and swelling energy gives rise to a length which we call elastoswelling length scale, [small script l]_es:

[small script l]_es ∼ (ε_eq²V_f)^1/3. (3)

In the case of a transversely swollen beam, this length scale denotes a critical thickness below which bending will occur.

In Fig. 3a, we plot the experimentally observed maximum strain ε_max as a function of beam thickness normalized by this elastoswelling length, h/[small script l]_es. The critical threshold determined from the reduced-order scaling prediction describes the onset of macroscopic bending very well. We observed macroscopic deformation with beams swollen by hexane and ethyl acetate slightly above h/[small script l]_es = 1, which may be attributed to an importance of |Δμ| at short times. Further experimental studies that focus on the impact of solvent–polymer polarity will be necessary to properly account for this phenomenon.

Fig. 3 Transition between global bending to surface creasing. (a) Maximum strain in beams due to non-homogeneous swelling of different fluid droplet of different volume, as a function of beam thickness normalized by elastoswelling length. (b) Images of creases and their respective 2D FFT results. (c) Growth of crease spacing with time.

When h > [small script l]_es, the swelling-induced stress will be insufficient to macroscopically bend the structure, and the local expansion of the top surface of the beam will be restricted by the bulk PDMS network. Similar to gels that are confined to a rigid substrate, the restriction against bending will impart a compressive stress on the swelling region. If this compressive stress imparts a strain greater than ε = 0.35, a localized surface creasing instability will occur.^44–46Fig. 3b shows the development of surface creases as a thick beam (h = 5 mm) swells with diisopropylamine (V_f = 5.96 μL) such that h/[small script l]_es ≈ 1.22. Randomly oriented surface-confined deformations appear immediately after swelling begins. Following the procedure described by Ebata et al.,⁴⁷ we performed a 2D Fast Fourier Transform (FFT) on the images to get the frequency and spacing of these microstructures (Fig. 3a). At time zero, when no fluid is present, no structure is observed. On applying the fluid droplet, creases start to form across the surface, and peaks are evident on the amplitude vs. frequency plot. These peaks come closer to each other as the creases grow in length with time. Fig. 3b(ii) confirms the expected relation from Tanaka et al.⁴⁸ that the characteristic crease spacing will scale as λ ∼ t^1/2. Our experimental results suggest that macroscopic deformation (bending) will occur when the thickness is below the elastoswelling length scale, i.e. h/[small script l]_es < 1, while microscopic deformations (creases) will form when h/[small script l]_es > 1. In the region where h/[small script l]_es ≈ 1, a coexistence between both macroscale and microscopic deformations exist, suggesting that although we were unable to observe creases when h/[small script l]_es < 1, they may exist at very short times. Similarly, there will likely be an upper limit of h/[small script l]_es, dictated by the surface strain, in which no deformation occurs. Our experimental approach makes accurately quantifying the local surface strains difficult, so determining this upper threshold is beyond the scope of this paper.

Finally, we demonstrate that both macroscopic structural and microscopic surface deformation can be generated in the same material by appropriately tuning the thickness. Fig. 4 shows a beam with a variable thickness along its length. In the thin regions, macroscopic bending is observed and the surface remains smooth, while in the thick region the surface develops creases as it remains undeformed in macroscale. This represents a potential mechanism for controlling shape change and actuation across multiple length scales by generating deformation simultaneously on the microscale and the macroscale.

Fig. 4 Bending and creasing. A structure with a variable thickness, such that it exhibits both bending in the thin regions and creasing in the thick regions for the same droplet size of solvent.

In summary, we have demonstrated a materials and geometry defined transition between a swelling-induced structural deformation and surface deformation. We present a scaling model that defines a critical elastoswelling length scale based on a balance of fluid–structure interactions, fluid volume, and the bending energy of the structure. Further experimental analyses are necessary to confirm the extension of this scaling to other geometries. Additionally, while our reduced-order model accurately captures the swelling-induced deformations in this paper, a more thorough theoretical model is required to quantitatively describe the scaling presented here. We anticipate that a better understanding of the nature of swelling-induced deformations of homogeneous materials will aid in designing and controlling shape change across many structural geometries and length scales. In particular, we provide a simple means for generating both the surface patterns and global shape within a structure using a given stimulus.

Acknowledgements

Funding for this work was provided by the National Science Foundation (NSF CMMI-1300860) and the Department of Engineering Science and Mechanics at Virginia Tech. The authors acknowledge the helpful feedback from Dominic Vella and Peter Stewart.

References

1. B. Moulia, J. Plant Growth Regul., 2000, 19, 19–30.
2. M. Ben Amar and A. Goriely, J. Mech. Phys. Solids, 2005, 53, 2284–2319.
3. K. A. Shorlin, J. R. de Bruyn, M. Graham and S. W. Morris, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 6950–6957.
4. W. Arnold, Bryologist, 1899, 2, 52–55.
5. L. A. Setton, H. Tohyama and V. C. Mow, J. Biomech. Eng., 1998, 120, 355–361.
6. M. J. King, J. F. V. Vincent and W. Harris, N. Z. J. Bot., 1996, 34, 411–416.
7. S. Nechaev and R. Voituriez, J. Phys. A: Math. Gen., 2001, 34, 11069–11082.
8. M. Marder, E. Sharon, S. Smith and B. Roman, Europhys. Lett., 2003, 62, 498–504.
9. E. Reyssat and L. Mahadevan, J. R. Soc., Interface, 2009, 6, 951–957.
10. Y. Klein, E. Efrati and E. Sharon, Science, 2007, 315, 1116–1120.
11. D. P. Holmes and A. J. Crosby, Adv. Mater., 2007, 19, 3589–3593.
12. D. P. Holmes, M. Ursiny and A. J. Crosby, Soft Matter, 2008, 4, 82.
13. V. Trujillo, J. Kim and R. C. Hayward, Soft Matter, 2008, 4, 564.
14. T. Tanaka, S.-T. Sun, Y. Hirokawa, S. Katayama, J. Kucera, Y. Hirose and T. Amiya, Nature, 1987, 325, 796–798.
15. E. P. Chan and A. J. Crosby, Soft Matter, 2006, 2, 324.
16. D. Breid and A. J. Crosby, Soft Matter, 2009, 5, 425.
17. H. S. Kim and A. J. Crosby, Adv. Mater., 2011, 23, 4188–4192.
18. W. Barros, E. N. de Azevedo and M. Engelsberg, Soft Matter, 2012, 8, 8511.
19. J. Kim, J. A. Hanna, M. Byun, C. D. Santangelo and R. C. Hayward, Science, 2012, 335, 1201–1205.
20. P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, Ithaca, NY, 1953, p. 424.
21. S. Douezan, M. Wyart, F. Brochard-Wyart and D. Cuvelier, Soft Matter, 2011, 7, 1506.
22. C. Nah, G. B. Lee, C. I. Lim, J. H. Ahn and A. N. Gent, Macromolecules, 2011, 44, 1610–1614.
23. E. Reyssat and L. Mahadevan, Europhys. Lett., 2011, 93, 54001.
24. D. P. Holmes, M. Roché, T. Sinha and H. A. Stone, Soft Matter, 2011, 7, 5188.
25. Y. Tang, A. M. Karlsson, M. H. Santare, M. Gilbert, S. Cleghorn and W. B. Johnson, J. Mater. Sci. Eng. A, 2006, 425, 297–304.
26. Y. Zhou, G. Lin, A. J. Shih and S. J. Hu, J. Power Sources, 2009, 192, 544–551.
27. K. Terzaghi, Eng. News-Rec., 1925, 95, 832–836.
28. M. A. Biot, J. Appl. Phys., 1941, 12, 155–164.
29. M. J. Crochet and P. M. Naghdi, Int. J. Eng. Sci., 1966, 4, 383–401.
30. L. W. Morland, J. Geophys. Res., 1972, 77, 1–11.
31. H. F. Wang, Theory of Linear Poroelasticity with Applications to Geomechanics and Hydrogeology, Princeton University Press, Princeton, 2000.
32. T. Tanaka and D. J. Fillmore, J. Chem. Phys., 1979, 70, 1214–1218.
33. J. Dolbow, E. Fried and H. Ji, J. Mech. Phys. Solids, 2004, 52, 51–84.
34. J. M. Skotheim and L. Mahadevan, Science, 2005, 308, 1308–1310.
35. S. C. Cowin and S. B. Doty, Tissue Mechanics, Springer, 2006.
36. J. Bear, Dynamics of Fluids in Porous Media, Dover, New York, 1988.
37. Y. Li and T. Tanaka, J. Chem. Phys., 1990, 92, 1365.
38. A. Lucantonio and P. Nardinocchi, Int. J. Solids Struct., 2012, 49, 1399–1405.
39. A. Lucantonio, P. Nardinocchi and L. Teresi, J. Mech. Phys. Solids, 2013, 61, 205–218.
40. S. J. DuPont Jr, R. S. Cates, P. G. Stroot and R. Toomey, Soft Matter, 2010, 6, 3876.
41. D. Chen, S. Cai, Z. Suo and R. Hayward, Phys. Rev. Lett., 2012, 109, 1–5.
42. J. N. Lee, C. Park and G. M. Whitesides, Anal. Chem., 2003, 75, 6544–6554.
43. M. Doi, J. Phys. Soc. Jpn., 2009, 78, 052001.
44. M. A. Biot, Appl. Sci. Res., Sect. A, 1961, 12, 168–182.
45. S. Cai, D. Chen, Z. Suo and R. C. Hayward, Soft Matter, 2012, 8, 1301.
46. S. Cai, K. Bertoldi, H. Wang and Z. Suo, Soft Matter, 2010, 6, 5770.
47. Y. Ebata, A. B. Croll and A. J. Crosby, Soft Matter, 2012, 4, 564.
48. H. Tanaka, H. Tomita, a. Takasu, T. Hayashi and T. Nishi, Phys. Rev. Lett., 1992, 68, 2794–2797.

---

Footnote

† The assumption that ε ≈ ε_eq likely overestimates the local, short time strains within the polymer coils, while assuming that V_s ≈ V_f likely underestimates the volume of the swollen region at the time of maximum deformation.

---