Hybrid gelation processes in enzymatically gelled gelatin: impact on nanostructure, macroscopic properties and cellular response

Abstract

Physical, chemical and hybrid tilapia fish gelatin hydrogels were investigated by small-angle neutron scattering (SANS), molecular dynamic simulations and their biological effect in cell cultures studied; results from the different experimental techniques were then correlated and linked to the rheological properties of the gels (F. Bode et al., Biomacromolecules, 2011, 12, 3741–3752). Hydrogels were obtained by cross-linking with the microbial enzyme transglutaminase (mTGase) under two conditions: above and below gelatin physical gelation temperature (ca. 23 °C). Hydrogels cross-linked at 37 °C, from the sol-state, are referred to as ‘chemical’ gels (C); hydrogels cross-linked at 21 °C, thus with concurrent physical gelation, are referred to as ‘physical-co-chemical’ gels (PC). The SANS data were appropriately described by a combination of a Lorentzian and a power law model. For physical gels, the correlation length (ξ) obtained from the fits decreased linearly with gelatin concentration, from 42 to 26 Å for 3.5 to 10% w/w gelatin, respectively. Independently of gelation temperature, all physical gels at a given concentration showed a similar correlation length ξ (26 ± 2 Å), with no significant difference with the sol-state (23 ± 2 Å). In both C and PC gels, ξ increased with mTGase concentration over the range studied: 40 to 167 Å for 10 and 40 U mTGase per g gelatin in C gels (after 120 min cross-linking) and 40 to 82 Å for 10 and 40 U mTGase per g gelatin for PC gels. ξ reached a plateau at the highest mTGase concentration studied for both types of gels. In addition, kinetic studies on C gels revealed that ξ increased linearly with time in the first two hours and grew faster with increasing mTGase concentration. ξ values in the PC gels were smaller than in the corresponding C gels. Cell proliferation studies showed that the gels were compatible with cell growth and indicated no statistically relevant dependence on mTGase concentration for C gels. For PC gels, cell proliferation decreased with increases in mTGase concentration, by approximately 80% from 10 to 40 U mTGase per g gelatin. With the exception of the highest mTGase concentration studied, PC gels overall showed a slightly (but statistically significant) higher cell proliferation than the corresponding chemical gels.

---

Introduction

Hydrogels obtained from the chemical or physical association of macromolecules are an important subject of materials science as they offer an ample array of design possibilities and have found in particular countless applications in biomedicine; they serve for instance as skin substitutes, adhesives, or drug delivery matrices. Through the careful selection of macromolecules, the associations that maintain the hydrogels 3D network can be selected and tuned. For biological applications, the requirements are quite restraining: in particular, implantable materials and scaffolds need to be biocompatible and usually biodegradable. Thus, biopolymers, inherently more suited for such applications than their synthetic counterparts, have become a great focus of interest.¹ There is therefore a crucial need to understand the complex properties of biopolymer gels for the design of scaffolds and artificial tissues with tailored properties.

Gelatin, derived from collagen by hydrolytic degradation, provides many of the requirements for a successful biomedical application. Fish skin and bone are rich in collagen and represent up to 75% of the total fish weight that is caught.² The high availability and low cost of fish skin and bone make it an interesting source of gelatin,³ while the use of fish gelatin provides new applications because of its lower gelation temperature than mammalian gelatin.⁴ Finally, due to its origin, gelatin closely simulates the mechanical properties and composition of the extra-cellular matrix (ECM).⁵

However, the suitability of a hydrogel is more than the added properties of its components. It also requires a particular set of mechanical properties, which are, in turn, governed by its structural organisation at the nanoscopic level.⁶ Thus, a fine control of the hydrogels nanostructure is required for its successful use.

Gelatin offers the particular advantageous feature of a thermally triggered reversible sol–gel transition.⁷ Physical gels are formed through the thermally induced single-strand-to-triple-helix transition of gelatin chains. In the sol state, the single-stranded form of gelatin prevails and does not display any extensive, classical elements of secondary structure (α-helix, β-sheet or turns). During the gelation process, the gelatin single-strands self-associate to reform the original collagen triple-helix based on the left-handed, PII conformation of the individual strands. The triple-helices form the junction zones of the three-dimensional network.⁸

However, a major drawback for medical applications, such as tissue engineering, is the lack of thermal stability at physiological temperature of the physical gelatin gels, which can be addressed by adding a carefully chosen chemical cross-linker. A variety of reagents have been used to permanently cross-link gelatin chains and include synthetic cross-linkers, such as glutaraldehyde^9–13 or carbodiimide.^11,14–16 These cross-linkers improve mechanical strength and proteolytic stability, but induce cytotoxic effects or immunological responses in the body.^17,18 In contrast, naturally occurring compounds such as genipin^{10,11,13,15,19,20} or the enzyme transglutaminase^21–26 have been reported to be biocompatible and immunogenic. Microbial transglutaminase (mTGase) catalyses acyl-transferase reactions between the side chain of a glutamine residue and a primary amino group (e.g.lysine) resulting in an ε-(γ-glutamyl)lysine isopeptide bond²⁷ and show a catalytic activity independent of Ca(II) ions, differing in this way from human or animal transglutaminase. Previous studies have shown that this enzyme can covalently cross-link gelatin to create a chemical gel.^21–23 The resulting covalent gels are biocompatible, non-immunogenic and show lower cytotoxicity.¹⁷ These chemically cross-linked gelatin networks however require extensive characterisation, and little is known on their structure and properties compared to their physical counterparts.

The covalent cross-linking of gelatin, which can, by nature, also undergo physical gelation, offers the interesting opportunity of designing ‘hybrid’ gels, by using mixed gelation processes, either contemporaneous or sequential, and raise the question of the impact of each type of network (physical or chemical) on the other, both from a macroscopic viewpoint (as measured by rheology) and at the nanostructural level. This is of significance not only from a fundamental perspective, to apprehend competing mechanisms of gelation and their effect on final properties, but is also highly relevant for practical applications: by combining two simple gelation processes, sequential or simultaneous, can the final gel properties be adjusted and improved? Or, in other words, are hybrid gels synergistic? Finally, one important question to answer is to establish whether different preparation protocols, if leading to different macro- and nanoscopic properties, also induce a different biological response in cell cultures.

In previous work,²⁸ we began to address these issues and reported the effect of the physical network on the hydrogels shear modulus. We determined that in ‘physical-co-chemical’ gelatin hydrogels (where chemical cross-linking occurs in conjunction with physical gelling), the presence of the physical network increased the overall shear modulus, when compared to pure chemical gels formed from the sol state, or to pure physical gels formed in the absence of any cross-linker.²⁸ Therefore, the concomitant growth of two types of networks, chemical and physical, was found to be synergistic, in that the overall mechanical properties were improved. This was interpreted in terms of the triple-helical network being able to ‘guide’ the cross-linking process, resulting in a more ordered and efficient network, while the chemical network, lacking this guidance, resulted in more heterogeneous network.

While our previous work examined the impact of the gelation protocol on the final macroscopic properties and gelation kinetics, this work now investigates the nanostructure of the networks to rationalize the macroscopic properties previously reported,²⁸ and understand the differences between three types of networks: physical, chemical and physical-co-chemical. Furthermore, we present some initial results on the biological behaviour of the gels by assessing the cellular response in regards to viability and proliferation, and establish some correlation with the physical characteristics of the gels.

Experimental

Materials

Gelatin: fish gelatin was kindly donated by Rousselot, France (isoelectric point pI = 8–9, bloom strength 275, gelation temperature ∼23 °C). All experiments were carried out using a single batch of gelatin (obtained in 2008). The gelatin was extracted from Tilapia fish skin by an acidic process. The average molecular weight was determined to be ∼36 kDa ± 12% using GPC (Smithers Rapra). Cold-water fish gelatin was obtained from Healan Ingredients UK.

Enzyme: the cross-linker used in this study was bacterial Transglutaminase (mTGase) obtained from N-Zyme BioTec GmbH, Darmstadt Germany (specific activity 1.6 U per mg solid, molecular weight 38 kDa and purity > 80%).

Rat Bone Marrow Mesenchymal Stem Cells (MSC): were obtained from the marrow stromal of 6-week-old female rat femora and tibiae. Rats were sacrificed according to Imperial College London ethical guidelines. Their hind legs were removed, and femora and tibiae cleaned of soft tissue. Bone epiphyses were removed leaving only the diaphyses, which were flushed with alpha MEM supplemented with 10% (v/v) fetal bovine serum (FBS), 1% (v/v) penicillin/streptomycin. Marrow from two rats were pooled and passed repeatedly through a 22-gauge syringe needle and plated on TCP. Culture media was changed on days 4 and 8 after harvest. Cells were passaged starting on day 9; only cells up to passage 5 were used in experiments. All cell cultures were maintained at 37 °C in a 5% CO₂/95% air incubator with 95% humidity.

Alveolar epithelial cells (A549): human alveolar epithelial type II cell (A549) is a cell line isolated from normal human lung tissue originating from human lung carcinoma and is commercially available from ATCC. The cell line was first developed in 1972 by Giard et al.³⁰ through the removal and culturing of cancerous lung tissue in the explanted tumour of a 58-year-old Caucasian male. The cell line is widely used and well characterised. Cells were purchased from ATCC at passage 83 and were used up to passage 123. They were passaged when 80–90% confluent, approximately every 2–3 days. All cell cultures were maintained at 37 °C in a 5% CO₂/95% air incubator with 95% humidity.

Methods

Sample preparation

Preparation of the gels. Typically 15% w/w gelatin was left to swell overnight in D₂O at 4 °C. Before use, the solutions were incubated for ca. 30 min at 35 °C until transparent (slightly yellowish) solutions were obtained, and then diluted in D₂O to 10% w/w solutions.

The enzyme mTGase was also dissolved in D₂O to make up a stock solution of typically 20 mg mL⁻¹. Any undissolved particles present were separated by centrifugation (7000 rpm, 3 min) and the supernatant was stored in the fridge until needed (for a maximum of 2 days).

For cell culture assays, PBS was used instead of D₂O.

The protocols used to prepare the three different types of networks for SANS measurements are described below.

Protocol 1, physical gels: to form the physical gels, the pure 10% w/w gelatin solutions were transferred into 1 or 2 mm path length Hellma cells and cooled below their gelation temperature to 12, 18 and 21 °C. To ensure a steady state condition, the samples were left to gel overnight at the required temperature before measurement. Before the samples were transferred into the sample holder, it was ensured that the latter had equilibrated at the target temperature of 12, 18 or 21 °C.

Protocol 2, chemical gels: chemical networks were formed by action of the enzyme mTGase. Adequate volumes (around 100 μL) of enzyme stock solution giving final concentrations from 10 to 40 U mTGase per g gelatin were added to the 10% w/w gelatin samples, vortex mixed and placed into 1–2 mm Hellma cells at 37 °C (cells were preheated to prevent physical gelation). In all samples studied, the chemical cross-linking was stopped at selected times (between 0 min and 10 h) by deactivating the enzyme by heating the loaded cell to 70 °C for 5 min. For the sample at reaction time t = 0, previously deactivated mTGase was added to the 10% w/w gelatin solution.

Protocol 3, physical-co-chemical gels: chemical and physical networks were formed simultaneously at 21 °C (with 10 to 40 U mTGase per g gelatin) by adding the enzyme stock solution to the gelatin solution, transferring to a Hellma cell and leaving to gel overnight.

Small-angle neutron scattering

Small-angle neutron scattering (SANS) experiments were performed on the instrument D11 at the Institut Laue-Langevin (ILL), Grenoble, France and on KWS-1, KWS-2 at the Jülich Centre for Neutron Science (JCNS), Munich, Germany. On D11, incidental wavelengths of 4.5 and 10 Å were used with sample detector distances of 1.2, 8, and 39 m, corresponding to a total scattering vector range q of 3 × 10⁻⁴ to 1 Å⁻¹. The sample temperature was controlled by a Peltier unit. On KWS-1, an incidental wavelength of 4.486 and 18.307 Å and detector distances of 1.220, 7.720 and 19.720 m covered a total q-range of 7 × 10⁻⁴ to 5 × 10⁻¹ Å⁻¹. On KWS-2, incidental wavelengths of 4.5 and 3 Å were used with detector distances of 1.3, 2, and 8 m to cover a q-range from 4.76 × 10⁻³ to 5.30 × 10⁻¹ Å⁻¹. Both instruments were equipped with a Julabo water bath with an accuracy of ±0.5 °C to control the sample temperature.

All samples were measured in quartz cells (Hellma) with a path length of 1 or 2 mm.

Repeats were performed on one of each network type: physical (P), chemical (C) and physical-co-chemical (PC) at JCNS and ILL to ensure that the scattering pattern of each sample was satisfyingly reproducible (ESI-2†).

SANS data fitting

The scattering from the gels was fitted with a combination of a Lorentzian and power law model^29,31−34 using FISH software.³⁵ The Lorentzian model provides a characteristic correlation (ξ) length of the networks. The full model is expressed as follows:

I _L(0) is the intensity at q = 0 for the Lorentzian, A is a constant and n is the power law exponent in the low-q region.

Molecular dynamics simulations (MD)

The LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) code³⁶ was used for the molecular dynamics simulations. In our systems, ten amino acids residues are represented in one bead within the gelatin strands, which are therefore represented by 100 beads in a given chain, with approximately 3 lysine (LYS)-containing beads and 9 glutamine (GLN)-containing beads per chain. The mTransglutaminase enzyme is represented by a single bead. The simulated systems consisted of 200 gelatin strands, and the number of enzyme beads were varied (n = 10, 100, 500, 1000) in order to test the systems response. The interaction between any two beads in the system is modelled using the standard 6–12 Lennard-Jones (LJ) potential with a cut-off of 2.5σ.³⁷where r is the distance between any two beads, ε represents the LJ energy and σ represents the size of the bead. In this study, the same values of ε and σ were assigned to all of the beads in the system (ε = σ = 1.0), and all beads are given the same mass (m = 1.0).

Neighbouring beads on the same molecule are connected using bonds that are described by the finite extensible nonlinear elastic (FENE) potential,³⁸ which has the following form:

where K is the force constant of the bond and R₀ is the equilibrium distance of the bond, while the other variables are the same as defined in the LJ potential energy term. In these simulations, we use values that are typical for C–C bonds, with K = 30.0 ε/σ² and R₀ = 1.5σ.

Before starting the network formation simulations, a simulation was performed in order to remove any artefacts that might result from the initial construction of the systems and in order to allow the system to equilibrate before carrying on with the network formation simulations. In order to conduct these initial simulations, an energy minimization is performed first, which removes any atomic clashes that may result from the initial building of the configuration. The system is then simulated under the NVT conditions (constant number of beads, volume and temperature) for 100 000 time steps. For all of the simulations, the system temperature is controlled by the Langevin thermostat³⁹ with an integration time step of 0.005τ, where τ is the Lennard-Jones (LJ) time unit. The network formation simulations were conducted for 40 million time steps.

During the network simulations, the reaction kinetics have been modelled to represent what occurs in the experimental system using distance as the only criterion to whether a bond is made, which has been done in several other atomistic and coarse-grain classical simulations of cross-linked network formation.^40–42 In doing so, temporary bonds are formed between an enzyme bead and a bead representing a segment of the peptide containing a GLN residue when the distance between the two beads is no greater than 1σ. Then, if a bead containing a LYS residue is found to be less than 1.8σ away from a GLN-containing bead that is bound to an enzyme bead, a bond is formed between the LYS- and GLN-containing beads and the bond between the GLN-containing bead and enzyme bead is broken simultaneously. Additionally, 20% of the bonds formed between GLN-containing beads and enzyme beads are broken every 5000 time steps in order to allow enzymes to continue to travel throughout the system. Only one enzyme or LYS-containing bead is allowed to be bonded to a GLN-containing bead at any given time. The network formation simulations were conducted for 40 million time steps.

Cell culture

Cultivation of the cells. Rat bone-marrow mesenchymal stem cells (rBMSCs) were isolated and cultured as previously described⁴³ and human A549 lung carcinoma cells were procured from American Type Culture Collection, Manassas, Va, US. Both cell types were cultured in α-modified Eagle's medium (α-MEM) supplemented with 10% (v/v) fetal bovine serum (Invitrogen, Paisley, UK), 1% L-glutamine and 1% (v/v) antibiotic/antimycotic (A/A; Invitrogen) and cultured in 75 cm² flasks at 37 °C, 5% CO₂, 95% humidified air.

Sample preparation. 10% w/w gelatin solutions were prepared using cell culture medium as a solvent. The gelatin was left to swell overnight at 8 °C and dissolved the next day at 37 °C. The solutions were sterile filtered with a 0.22 μm sterile filter. Under sterile conditions, the sterilised mTGase stock solution (dissolved in PBS) was added to the gelatin solution. After mixing, 300 μL of the sample solution were pipetted into each well of a 48 well plate. All samples were prepared in technical triplet. For chemical network formation, the 48 well plates were left in the incubator (37 °C) for 3 hours before the enzyme was deactivated at 65 °C for 15 min. To form physical-co-chemical gels, the samples were left overnight at room temperature (constant at 21 °C) before the enzyme was again deactivated at 65 °C for 15 min and the samples placed in the incubator for 3 hours.

In preparation for viability assays, the cells were washed with calcium/magnesium free phosphate buffered saline (PBS), detached with 0.02% (v/v) EDTA/0.02% (v/v) trypsin and re-suspended in α-MEM medium. The cells were seeded at 33 000 cells per well directly on top of the gels. As a blank, three gels per plate were left without cells and only medium was added, to account for the fluorescence contribution of the gel and medium.

AlamarBlue assay. The AlamarBlue assay was used to quantitatively determine cell proliferation. Cells were washed twice with sterile PBS before adding 300 μL AlamarBlue solution (10% (v/v) AlamarBlue diluted in complete growth medium) into each well. The samples were left to incubate for 5 h during which time Resazurin is reduced to Resorufin by the living cells. The reduction causes a colour change from blue to red. 100 μL of each sample were transferred into a new 96 plate for fluorescence reading. To reduce the error of pipetting, every sample was pipetted in technical triplicates. The fluorescence excitation wavelength was set to 540 nm and emission was read at 580 nm to monitor the fluorescence of the samples. After the measurements, the AlamarBlue reagent was removed from the cells in the 48 well plates and replaced by 800 μL fresh complete growth medium, before they were returned to the incubator. The assay is non-toxic for the cells, allowing cell proliferation at different days to be determined using the same sample. The AlamarBlue assay was performed on days 1, 4, 7, 11, and 14. The measured absorbance was corrected by the blank.

MTT assay. The MTT assay was used to determine the cell viability. Living cells reduce the MTT reagent (3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyltetrazolium bromide) to purple insoluble formazan. The old cell medium was aspirated from the wells and replaced by 200 μL fresh cell culture medium and 50 μL MTT (5 mg mL⁻¹) and the plate was incubated for 4 h. The medium was then removed and the resulting intracellular formazan crystals inside the cells were dissolved over 24 h in 100 μL of 10% (v/v) SDS prepared in 1 : 1 water : DMF, after which the absorbance from the solubilized formazan was measured spectrophotometrically (SpectraMax, UK) at an absorbance wavelength of 570 nm.

Results

Physical gels

Upon cooling gelatin solutions below gelation temperature, the protein strands self-associate and partly refold the triple-helices of the native collagen structure;^8,44 these triple-helices form the junction zones of the three-dimensional network. In our previous work,²⁸ we measured the rheological properties of physical gelatin gels and correlated these to the amount of triple-helices in the networks (obtained from optical rotation measurements), confirming that the higher values of the storage modulus G′ reached with a stronger under-cooling and/or increasing gelatin concentrations are due to a higher concentration of triple-helices in the network, as demonstrated previously by Djabourov and co-workers.⁴⁵

The effect of gelatin concentration was investigated between 3.5 and 10 w/w % at 3 temperatures: 12, 18 and 21 °C. Fig. 1A shows the fitted data for 10% gelatin at various temperatures. The scattering patterns obtained (Fig. 1A) comply with the ‘s-shaped’ curves typically found for polymer gels.⁴⁶ The data were suitably fitted with a combination of a Lorentzian and power law model^31–33 (cf. Methods section). The correlation length ξ obtained from the fits decreases with increasing gelatin concentration, from 42 to 26 Å for 3.5 to 10% w/w gelatin, respectively (Fig. 1B). In previous studies, Djabourov et al.⁴⁷ reported a correlation length of 35 ± 3 Å for 5% (w/v) bovine gelatin, which correlates well with our data at the same concentration (38 ± 2 Å), despite the differences between the systems (molecular weight, and bovine gelatin versus fish gelatin). Our results also suggest that over the temperature and concentration range studied ξ decreases linearly with gelatin concentration (Fig. 1B). In physical gels, the correlation length can be interpreted as an average mesh size of the network.^48–50 As long as the system does not reach the concentrated regime, it is expected that the mesh size would decrease continuously as the density of strands increases, as indeed observed here (Fig. 1B).

Fig. 1 SANS data from 10% w/w gelatin gels and solutions, A: from bottom to top: at 12 °C (triangles), 18 °C (squares), 21 °C (circles), and a gelatin solution at 37 °C (diamonds), together with fits to the Lorentzian and power law equations. Inset: scattering from a 10% w/w gelatin solution at 37 °C (open circles) showing the two components of the model: the Lorentzian is shown in a thick, black line and the power-law in grey, while the addition of the two appears as a thin, blue line, B: correlation length ξ of physical gels as a function of gelatin concentration (10%, 7.5%, 5%, and 3.5% w/w gelatin) obtained from fits of the small-angle neutron scattering data to the Lorentzian and power law models. The gels were formed at 12 °C (triangles), 18 °C (squares), 21 °C (circles) and the solution at 37 °C (diamond) is shown as a reference.

The scattering data from 10% w/w physical tilapia gelatin in the sol state (at 37 °C and 50 °C) and from physical gels formed below the gelation temperature at 12, 18 and 21 °C do not show a significant difference (ESI-1†), whether above or below the gelation temperature. However, the shoulder in the scattering appears at a slightly lower scattering intensity for gelatin in the sol state compared to the gel state. Independently of the gelation temperature, all physical gels show a similar correlation length: 26 ± 2 Å, while a slightly smaller correlation length is obtained for the gelatin coils 23 ± 2 Å. The difference however is not statistically significant.

These results are in agreement with the literature, which reports similar values of the correlation length for gelatin gels at different temperatures, both in the sol and gel state.^51,52 A correlation length of 26 ± 2 Å for 13% bovine gelatin samples was reported in the gel (25 °C) and sol state (60 °C).⁵² The fact that the correlation length is not affected by the formation of triple-helix junction zones suggests that the transition from single strands to a helical network does not cause large enough structural changes in the overall configuration of the chains, more precisely, to their density distribution throughout the network, which is detected by neutrons. In previous studies,^28,45 the macroscopic properties (G′, G′′) were shown to directly reflect the ‘sub-nano’ structure, i.e. the ratio of amino acids in single-strand to triple-helix conformation, as demonstrated by the existence of a master curve between G′ and the density of triple-helices.^28,45 Instead, and quite surprisingly, sub-cooling does not lead to any observable nanostructural changes – as measured by SANS – while an increase in gelatin concentration leads to a decrease in mesh size, as would also be seen for a pure gelatin solution. Therefore, while the mechanical properties of the gel are clearly correlated to the triple-helical content – detected by optical rotation – they cannot be correlated to the gel architecture as measured by SANS, which ‘sees’ no difference between gels and sols.

Chemical gels

The second type of gels studied were formed by chemical cross-linking of the gelatin strands under the action of the enzyme mTransglutaminase, at a temperature above tilapia gelatin melting temperature (∼23 °C), i.e. in the absence of any triple-helices. The reaction temperature was set to physiological temperature (37 °C), as the optimum reaction temperature for mTGase²⁸ and also a relevant temperature for tissue engineering scaffolds. Two aspects were examined: the effect of the cross-linker concentration on the final gel structure and the evolution of the gels structure with reaction time. Samples at four enzyme concentrations (10, 20, 30 and 40 U g⁻¹ gelatin) were compared at two reaction times: 60 min and 10 h, in order to investigate the effect of mTGase concentration.

The scattering from the chemical gels shows a sigmoidal shape, similar to the one observed for the physical gels (Fig. 2B). A shoulder (corresponding to the plateau of the Lorentzian) in the scattering pattern is detected in the middle q-region (around 0.007 Å⁻¹), which shifts to higher scattering intensities with higher cross-linker concentration.

Fig. 2 (A) Correlation length (filled circles) obtained for tilapia gelatin chemical gels from fits of the SANS data. The right hand side y-axis shows the corresponding G′ values (open circles) for the chemical gels. The dotted line is a guide to the eye. (B) Small-angle neutron scattering patterns from tilapia gelatin chemical gels with (from bottom to top): 10 (yellow, circles), 20 (orange, triangles), 30 (red, diamonds), and 40 U mTGase per g gelatin (dark red, squares) after 60 min of cross-linking and their fits (black lines) obtained from the combination of a Lorentzian and power law model. The curves have been shifted up with respect to each other for better clarity (by 2, 30 and 100 times for 20, 30 and 40 U mTGase per g gelatin, respectively).

The intermediate cross-linking time (60 min) was chosen as a stage when the macroscopic properties (as measured by the storage modulus, G′, previously reported²⁸) have nearly stabilised. At this cross-linking time, all data curves are well described by the Lorentzian/power law model (Fig. 2B). The correlation length obtained from the fits increases with mTGase concentration over the range studied (10 to 40 mTGase per g gelatin, Fig. 2A) and seems to plateau at the highest mTGase concentration studied. This correlates well with our rheological measurements of the same gels (reproduced in Fig. 2A), which also showed that a plateau value of the storage modulus was reached at the highest cross-linker concentration studied.²⁸

This increase in correlation length with cross-linker concentration is in agreement with other studies. For instance, an increase in ξ from 45 Å to 64 Å was obtained for a ten-time increase in glutaraldehyde concentration in 5% w/v gelatin.⁵³ This observation suggests that ξ does not reflect a ‘mesh size’ (as in physical gels, see previous section), but the size of growing cross-linked aggregates, whose size correlates directly with enzyme concentration. Our molecular dynamic simulation studies also show an increase in aggregate size with increasing amounts of cross-linker (Fig. 3A), in good agreement with the structure revealed by SANS.

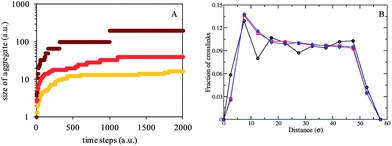Fig. 3 Results from MD simulations on the chemical gels. (A) Results of the cluster analysis showing the size of aggregates in the chemical gels formed with 100 (yellow), 500 (orange) and 1000 (red) enzyme beads, from bottom to top. (B) Fraction of cross-links as a function of distance from another crosslink. The data are determined from the MD trajectories of systems with 10 (black circles), 500 (red squares), and 1000 (blue diamonds) enzymes in the system.

The scattering data obtained from the gels after 10 h of cross-linking (taken as an infinite time of reaction) could not be fitted using the Lorentzian and power law model. The failure of this simple model at very long cross-linking times may be attributed to the presence of multiple structures formed over time, which are likely to cover a wide range of length scales, and cannot be captured by the simple combination of a Lorentzian and a power law. The combination of a Lorentzian and Debye–Bueche equations,⁵⁴ also commonly used to describe the scattering from gels,^34,47 did not provide a suitable fit either. While the data could be described by a combination of all three models (Lorentzian, Debye–Bueche and power law), the values obtained for the correlation length were extremely small and with a large error, which is expected with six unknown variables. It is likely that the correlation length ξ, reflecting the size of expanding aggregates, reaches values outside the detection limit of SANS after 10 h, as the aggregates start interpenetrating substantially. In addition, a range of large scale inhomogeneities may have formed which overshadow smaller correlation lengths, or simply structures with a large range of sizes, meaning that the system can no longer be described by a single ‘characteristic’ length, as also suggested in other studies.⁵⁵ Interestingly, only the infinite time gel with the lowest enzyme concentration studied (10 U mTGase per g gelatin) could be fitted satisfactorily. This concords with the above interpretation, since, at this low enzyme concentration, aggregates may not have grown as much as in the other gels and not be interpenetrating substantially, therefore still enabling the extraction of one characteristic aggregate size.

In addition to the structural differences caused by varying mTGase concentrations, the kinetics of the reaction were also investigated. The possibility of deactivating the enzyme at any point, and thus freezing the patterns in time, give us the unique opportunity to measure the evolving structure of the gels. High (40 U g⁻¹ gelatin, Fig. 4A) and low (10 U g⁻¹ gelatin) enzyme concentrations were investigated at selected times between 0 and 120 minutes. Fig. 4A shows the successive scattering patterns of the chemical gels cross-linked with 40 U mTGase: the shape of the scattering curves changes gradually as cross-linking proceeds. As expected, the high q-region, associated with local structure and incoherent background, does not show any changes over time. In the middle q-region instead, between 0.001 and 0.05 Å⁻¹, a shift of the shoulder towards lower q-values is observed with time, together with an increase in the scattering intensity. At q ∼ 0.0009 Å⁻¹, all data show a cross-over point followed by a power law increase in the intensity (appearing linear in a log scale). The slope seems to depend on the time of cross-linking: as the cross-linking time increases, the slope becomes less steep, with the gel at t = 10 h showing the lowest slope.

Fig. 4 (A) Kinetics of gel formation followed by SANS measurements on 10% w/w gelatin gels cross-linked with 40 U mTGase per g gelatin at 37 °C. The cross-linking reaction was stopped by deactivation of the enzyme at selected time points: 0 (dark grey), 15, 30, 60 and 120 min (increasing lighter shades of grey). The black symbols correspond to 10% w/w gelatin coils and are given as a reference. (B) Evolution of the correlation length obtained from SANS on the time of reaction, shown for 10% w/w gelatin cross-linked at 37 °C with 10, 20, 30, and 40 U mTGase per g gelatin. The increasing cross-linker concentrations are indicated by gradually darker colours (from yellow to red, and bottom to top). The dotted black lines are straight lines through the data points shown as guides to the eye.

Fig. 4B shows the correlation lengths extracted from the gels at varying reaction times up to t = 120 min: at all cross-linker concentrations, the correlation length increases linearly with time. Further, the evolution of the nanostructure within the gels proceeds at different speeds depending on cross-linker concentration: more precisely, the correlation length grows much faster at high transglutaminase concentration. The sample with the lowest amount of enzyme (10 U mTGase per g gelatin) shows almost no change in either correlation length (34 ± 2 Å) for the first 90 min of the cross-linking process, after which ξ increases slightly to 40 ± 2 Å at 120 min. Finally, ξ reaches 140 Å at ‘infinite’ time (10 h, data point not shown in Fig. 4B). Instead, the growth in ξ is much faster in gels cross-linked with 40 U mTGase per g gelatin, increasing from 30 to 167 ± 2 Å in the first 120 min. The evolution of ξ with time confirms our interpretation of a growth of aggregates, rather than a mesh size, thus differing from physical gels. The aggregates can be understood as areas highly dense in cross-links connected together, in contrast to more open and less cross-linked regions of the network.²⁹ The results from the MD simulations (Fig. 3B) corroborate this finding by showing that the density of crosslinks decreases with the distance from a given crosslink. Additionally, at the lowest enzyme concentration studied, the density of crosslinks nearest to a given crosslink is lower while at all enzyme concentrations, the density of crosslinks far away from a given crosslink remains constant. Covalent bonding is therefore a very different gelation process than triple-helix formation: in the chemical gels, network construction proceeds in a random and heterogeneous manner, with cross-links being formed in localised regions, forming aggregates, then coming together; in contrast, in physical gels, the single-strand to triple-helix transition happens throughout the solution and is homogenously spread, therefore hardly affects the distribution density of gelatin strands and preserves a homogeneous network, thus the change is not detected by neutrons.²⁹ The power law parameters, dictated by large-scale structures and caused by inhomogeneities, appear to be time- and concentration-independent, reflecting a random process in the formation of these large-scale structures. The fact that enzyme concentration determines the kinetics of the reaction concords with our rheological measurements:²⁸ we had shown that the storage modulus was mostly affected by the early stage growth of the aggregates, and although these continue to expand over the entire time of measurement, G′ remains fairly constant after ca. 1 h.

We next attempted to determine whether a correlation could be established between the size of the aggregates ξ, as measured by SANS, and the macroscopic properties, as measured by the storage modulus G′ (Fig. 5). Quite remarkably, independently of cross-linker concentration and reaction time, all data points fall into a single master curve, revealing a direct relationship between the size of the aggregates (on the nano-scale) and the storage modulus (on the macro-scale). It is reminiscent of a similar master curve established between optical rotation (OR) data and rheology for physical gels by Djabourov et al.,⁴⁵ showing a relationship between the amount of strands in triple-helix conformation and the modulus of the gels. Fig. 5 also shows that a critical value of the correlation length of ca. 30 Å is needed for gelation to occur, thus suggesting that percolation occurs only once growing aggregates have reached this critical size. Further, G′ reaches a plateau at a correlation length of around 100 Å, after which ξ growth is mostly independent of G′: while aggregates keep on expanding, they do not impact the macroscopic properties substantially, in other words, the bonds that are formed are not elastically active. A more detailed discussion of elastically active vs. inactive bonds from the rheological data can be found in our previous paper.²⁸

Fig. 5 Master curve relating the storage modulus G′ to the correlation length ξ obtained from SANS experiments at different cross-linking times for 10% w/w gelatin gels chemically cross-linked with 10 (circles), 20 (triangles), 30 (diamonds), and 40 (squares) U mTGase per g gelatin at 37 °C. The correlation length was obtained from the SANS kinetic measurements fitted with a Lorentzian and power law equation. Each point corresponds to a specific time point where ξ and G′ values have been measured. The dotted line is given as a guide to the eye.

Fig. 6 gives a schematic illustration of the networks as chemical gelation proceeds, based on these results. As the aggregates grow, they start interconnecting with each other, forming larger clusters of aggregates. However, it can be assumed that interconnections between the clusters are not many. The less well connected regions between the clusters in the network substantially affect G′, being elastically active bonds, but the growth of the aggregates inside the clusters does not generally contribute to G′, as clearly seen from the master curve in Fig. 5, which shows a near plateau for G′ (in log scale) while ξ keeps increasing.

Fig. 6 Schematic representation of the aggregates growth (red), interconnecting and forming larger clusters (green) in chemical networks.

While it is generally not expected that small changes on the nano-scale directly impact the macroscopic properties, we here demonstrate the existence of a correlation at the early stages of gelation and, at longer times, reveal that the nanostructure continues to evolve within the gels while the bulk properties have reached a quasi-equilibrium.

Physical-co-chemical gels

In this section, we investigate gels where a combination of the two gelation processes takes place simultaneously: physical-co-chemical gels are formed at 21 °C, i.e. below gelatin gelation temperature (∼23 °C) – thus enabling triple-helix formation – and also in the presence of the enzymatic cross-linker mTransglutaminase. Our previous work²⁸ showed that the concomitant formation of triple-helices and chemical junctions improved the overall mechanical properties, with respect to the pure chemical and physical gels, leading to substantially higher storage moduli. More precisely, the storage modulus of pure physical (21 °C) and chemical gels (37 °C) (10%, 40 U mTGase) were: G^′_P ∼ 3300 Pa and G^′_C,40U ∼ 7200 Pa, respectively, while the total G′ in PC gels (40 U mTGase) was G^′_PC,40U ∼ 12 800 Pa. The single-strand to triple-helix transition takes place much faster than the formation of covalent bonds;²⁸ in addition, the catalytic activity of the enzyme is reduced at 21 °C, compared to 37 °C, but still present.²⁸ Thus, it is expected that in PC gels a significant amount of physical network will already be present before the mTGase triggers any extensive cross-linking. Therefore, access of the enzyme to the binding sites will be substantially restricted compared to the pure chemical networks. On the other hand, the presence of helices may ‘direct’ the cross-linking process, leading to a more controlled distribution of the chemical junctions, for instance at the ends of helices, as suggested in other studies,⁵⁶ thus explaining the improved rheological properties.²⁸

The scattering signal from the final gel structures (10 h at 21 °C) were measured at varying enzyme concentrations (10–40 U mTGase per g gelatin) and compared to the pure physical gel at the same gelatin concentration (Fig. 7A). Clear differences are seen in the middle q-region (0.005 < q < 0.05 Å⁻¹) and the curves are adequately described by the Lorentzian and power law model. As expected from the increasing height of the shoulder, the correlation length ξ scales with cross-linker concentration, varying from 40 to 82 ± 2 Å at 10 to 40 U mTGase per g gelatin, respectively (Fig. 7B). The correlation length seems to reach a plateau value around 30–40 U mTGase per g gelatin, i.e. adding enzyme beyond this threshold value has minor effects on the cross-linking pattern and the resulting properties of the gels. This was also observed both for the macroscopic (G′)²⁸ and the nanoscopic properties (ξ), equally in the pure chemical gels. In the lower q-region (q < 0.005 Å⁻¹), the scattering curves overlay, showing a linear increase on a log scale with a similar slope for all, suggesting that the larger scale structures are of a similar nature.

Fig. 7 (A) SANS data from 10% w/w PC gels, with 0 (grey) 10, 20, 30, 40 U mTGase per g gelatin. The increasing cross-linker concentrations are indicated by a gradual colour change from light to darker shades. The gels were gelled at 21 °C for 10 h. The inset shows the fitted scattering data appropriately shifted upwards for clarity (6, 20, and 60 times) at 10, 20, 30 and 40 U mTGase per g gelatin, respectively. (B) Correlation lengths in 10% w/w physical-co-chemical gels formed at 21 °C as a function of mTGase concentration. The correlation lengths were obtained from fits of the SANS data to a combination of a Lorentzian and a power law equation. (C) Correlation of the rheology to the nanostructure (SANS) in 10% w/w pure chemical (red, lower curve) and PC gels (green, upper curve), formed at different enzyme concentrations. (D) SANS data of 10% w/w pure physical (21 °C, circles), pure chemical (37 °C, diamonds) and physical-co-chemical gels (green). The chemical and PC gels (10 h) are shown at 40 U mTGase per g gelatin (120 min).

A connection between the macro- and the nano-scale is established in Fig. 7C, which shows the final values of the overall storage modulus²⁸ as a function of the correlation length for the range of cross-linker concentrations studied, and for both types of gels: purely covalent (chemical) and physical-co-chemical. The dependence of G′ on ξ is very similar for both types of networks, however, values of the storage modulus for the PC gels show an off-set to higher G′ values, clearly attributable to the presence of the physical network. For both gels, a critical size of the aggregates (ξ) needs to be reached before gelation occurs, as detected by a sharp increase in G′. For the pure physical networks, the value of the storage modulus is dictated by the amount of triple-helices,^28,45 which are however ‘invisible’ to SANS, presumably because the spatial distribution of the gelatin coils throughout the solution is hardly altered by triple-helix formation, as discussed above. Hence, differences observed in the correlation length between the PC and C gels are unlikely to be caused by the presence of the triple-helices themselves, but rather to their effect on the spatial distribution of the covalent bonds and therefore the cross-linked chains. The shortcoming of SANS to detect the triple-helices in the PC gels may explain the off-set in G′ between the PC and C gels. The additional network junctions, created by triple-helices, improve the network elasticity (G′) but hardly cause any detectable structural change in the scattering patterns.

Fig. 7D compares the scattering from physical-co-chemical gels at 40 U mTGase per g gelatin (at 21 °C) to the pure chemical (37 °C) and the pure physical networks (21 °C). Similar observations can be made at all other enzyme concentrations (data not shown). Interestingly, the scattering curve from the PC gels appears to be an ‘intermediate’ between the pure physical and the chemical networks. In the high q-region (0.05 < q < 0.5 Å⁻¹), the scattering from the PC gel is identical to that of the pure physical gel, whereas the chemical gel shows a lower scattering intensity in this region. In the intermediate q-region, a shoulder in the scattering patterns is observed for all three networks; this shoulder shifts to lower q-values and stronger scattering intensities with increasing enzyme concentration (Fig. 7A). The correlation length in the physical gel is, at 25 Å, smaller than in the PC networks, where it ranges from 40 to 82 Å for 10 and 40 U mTGase per g gelatin. Instead, much higher values of ξ were reached in the pure chemical gels after 10 h of cross-linking for 10 U mTGase per g gelatin (140 Å), while at cross-linker concentrations higher than 10 U g⁻¹ gelatin the SANS data could not be fitted (cf. previous section), which was interpreted as a multiplicity of characteristic length scales in the networks as the aggregates grew and interpenetrated each other. The correlation length in the PC gels (at 10 h) instead compares well with the chemical gels after only 60 min cross-linking, with ξ reaching values of 35, 53, 74 and 82 Å compared to 49, 65, 79, 82 Å for the PC and C gels with 10, 20, 30, and 40 U g⁻¹ gelatin, respectively. In pure chemical gels, the binding is randomly determined by access of the mTGase to the residues on the freely diffusing single strands, without particularly favouring intra- or inter-molecular bonding. Instead, in PC gels, pre-formed triple-helices are expected to interfere with the formation of aggregates by covalent bonding. The impact of preformed triple-helices on the spatial distribution of the covalent junctions is clearly demonstrated by the small-angle scattering data: results from the fits show that ξ_PC, which describes the size of aggregates connected by covalent bonds in the PC gels, is significantly smaller than in the chemical gels, therefore the growth of the aggregates is constrained by the presence of the helices. However, we had shown previously²⁸ that G^′_C2, the covalent contribution to the storage modulus in the PC network, is larger than G^′_C, the overall storage modulus in the chemical gels, at least at low enzyme concentrations.²⁸ These differences suggest the presence of an increased number of cross-links in the PC gel and/or a more efficient spatial distribution of the chemical bonds, when ‘guided’ by the helical network. Fig. 8 schematically represents the structure of the chemical (Fig. 8A) and physical-co-chemical networks (Fig. 8B), as deduced from the SANS analysis. A more homogeneous and intermolecularly connected covalent network can be expected in the PC gels, due to the pre-formed triple helices. The physical junction zones create a relatively homogeneous network, which leads to a more uniform distribution of the cross-links and therefore of the clusters, compared to an unconstrained, and therefore more random, aggregate formation in the pure chemical networks. Further, the helices introduce some rigidity to the chains, preventing the aggregates to grow as large as in the chemical gels. In the PC gels, as well as in the pure chemical gels, the correlation length increases with mTGase concentration. However, the size of ξ is smaller in PC gels, suggesting that the triple-helices present in the PC gels restrain aggregate growth. In addition, the faster cross-linking at high enzyme concentration, and subsequent reduced number of helices, allows the formation of larger aggregates at higher enzyme concentrations (Fig. 8).

Fig. 8 Scheme representing: (A) pure chemical gels and (B) physical-co-chemical gels. In both cases, gelation proceeds through the growth of clusters (delimited in red), whose expansion is constrained by the presence of triple-helix junctions (black bars) in the physical-co-chemical gels.

Cell culture studies

In this final section, we turn to the biological response of these gels in cell culture studies, in order to (1) establish their suitability for tissue engineering applications (2) investigate whether gels created by different protocols and thus differing in their network structures (as established in the previous sections) affect cell proliferation.

Metabolic activity of rBMSCs was studied on chemical and physical-co-chemical gels made with 10% w/w tilapia gelatin gels with 10, 20, 30, and 40 U mTGase per g gelatin. We investigate the structure of the covalent networks alone, as at physiological temperature (37 °C) the triple-helices network is not present. However, as discussed above and in more detail in previous work,²⁸ the chemical networks resulting from the two fabrication processes (C vs. PC) are different, both in terms of gel strength as in the nano-scale organization. The objective of this study is to establish whether these macroscopic and nanoscale properties are reflected by a different metabolic response of the cells.

Cellular metabolic activity was assessed for both types of gels with different gelatin and cross-linker concentrations over 3 and 14 days using A549s and rBMSCs. Over this time period, no visual degradation of the gels was observed and there was no loss in cell viability over the duration of the culture period. Cellular metabolic activity was tested on chemical gels with four different gelatin concentrations (2%, 5%, 10% and 15% w/w gelatin). The correlation between cell metabolic activity and gelatin concentration for chemical gels (10 U mTGase per g gelatin) is presented in Fig. 9A and suggests that cell metabolic activity is dependent on gelatin concentration: the increase in gelatin concentration from 2% to 15% w/w gelatin gels improved cell viability five-fold. Gelatin is known to have adhesive properties,⁵⁷ thus a higher density of gelatin chains provide more adhesion sites for the cells, improving the number of cells adhering to the gel and leading to the differences observed. Similarly an increase in proliferation of rBMSCs had been observed on 1–10% w/v bovine gelatin cross-linked with mTGase,⁵⁸ attributed to a higher amount of gelatin providing proportionally more integrin binding sites for cell adherence. Collagen is known to display integrin binding sites (i.e. RGD (Arg-Gly-Asp)) – receptors of the cells that mediate attachment between the cell and its surroundings,⁵⁸ the same sequences are therefore present in gelatin. Thus, a larger number of cells can adhere to gels of higher gelatin concentration. In addition, it is generally expected that cell proliferation will vary with shear modulus, therefore both aspects may explain the results with gelatin concentration: an increased amount of cell adhesion sites and a higher shear modulus.

Fig. 9 (A) Correlation between metabolic activity (absorption) and gelatin concentration after three days of cell growth. The metabolic activity of A549 cells was determined with MTT assays. (B) Cell proliferation (tested via AlamarBlue assay) of 10% w/w chemical gels with four different enzyme concentrations (10, 20, 30, and 40 U mTGase per g gelatin). The colour change from yellow to red indicates increasing mTGase concentration from 10 to 40 U g⁻¹ gelatin. The fluorescent signal (proportional to the metabolic activity) is plotted for all cross-linker concentrations against time (day 1, 4, 7, 11, and 14). (C) Cell viability of 10% w/w physical-co-chemical gels with four different enzyme concentrations (10, 20, 30, and 40 U mTGase per g gelatin). The cell viability was determined with the AlamarBlue assay. The colour change from turquoise to blue indicates increasing mTGase concentration from 10 to 40 U g⁻¹ gelatin. The fluorescence signal (proportional to the metabolic activity) is plotted for all cross-linker concentrations against time (day 1, 4, 7, 11, and 14). (D) Metabolic activity of RBMSCs growing on 10 U (turquoise, squares) and 40 U mTGase per g gelatin (blue, diamonds) over 14 days.

Further, the effect of cross-linker was investigated with enzyme concentrations in the range 10 to 40 U mTGase per g gelatin for two weeks. Rheological measurements had shown that with 40 U mTGase per g gelatin the storage modulus approaches a plateau and does not significantly increase with further mTGase concentration increase.²⁸Fig. 9B shows the cell proliferation on chemical gels plotted from day 1 to 14 for the gels with different shear moduli (mTGase concentration), ranging from 3800 Pa to 7200 Pa. The results show a clear increase in cell proliferation for all four enzyme concentrations, with an average three-fold increase in the number of cells between day 1 and 14. More precisely, for 10, 20, 30 and 40 U mTGase per g gelatin the fluorescent signal increased by 3.8, 3.0, 3.1 and 2.7 fold (p < 0.005), respectively. For biocompatible, adhesive materials, an increase in cell viability is generally reported, and was expected for these gels. For the chemical gels, no significant effect of cross-linker concentration was determined (Fig. 9B). However, on day 7 and 11, gels formed with higher amounts of TGase show reduced cell proliferation. After 14 days in vitro, no effect of enzyme concentration was observed (p < 0.005). The fact that we do not observe a clear trend in cell metabolic activity when varying mTGase concentration, which also affects the characteristic G′ of the gels, can be ascribed to the magnitude of the changes: G′ is expected to vary substantially with large changes in gelatin concentration (2 to 15%, cf. above), while the change is smaller when varying mTGase from 10 to 40 U on a 10% gelatin gel.

Cellular metabolic activity was also determined for the physical-co-chemical gels (Fig. 9C). The fluorescence intensities measured presented a similar trend to the pure chemical gels (shown in Fig. 9B). Cell proliferation increased temporally and occurred for all four cross-linker concentrations studied. For the lowest enzyme concentration of 10 U mTGase per g gelatin, the fluorescence intensity increased approximately 4.2 folds over the 14 days. For 20, 30 and 40 U mTGase per g gelatin, the increase in cell viability over the 14 days period is 4.2, 4.2 and 3.0 fold, respectively (p > 0.005). When comparing the cellular proliferation of the physical-co-chemical gels with different enzyme concentrations (Fig. 9C), the results indicated that the cell growth was slightly affected by cross-linker concentration. On day 1, cell proliferation was not different, independent of the mTGase concentration. However, on day 4 and more so for days 7, 11, and 14, a slight decrease in cell proliferation was observed with increasing cross-linker concentration (p > 0.005 comparing the gels with 10 and 40 U mTGase per g gelatin).

To ensure that the measured metabolic activity is related to the cells growing on the gels, qualitative staining (LIVE/DEAD assay) was used to stain the living and dead cells on the different chemical and physical-co-chemical gels (SI-3) at day 14. The number of cells depicted in the microscopic images does not represent an average of cell density on the gels; the surface of the gels was convex, leading to a higher cell concentration accumulated in the centre of the gel surface.

The storage modulus of physical-co-chemical gels after melting of the helices (at 37 °C) differs from that of the pure chemical gels,²⁸ although both the chemical and the “melted” PC networks contain only covalent bonds (no triple-helices). When relating the cell proliferation to the storage modulus of each gel no (direct) relation was observed (data not shown). However, cell response confirms a different nature of the networks, since the physical-co-chemical gels overall show a slightly (but statistically significant) higher cell proliferation than the corresponding chemical gels (except for the 40 U mTGase sample). This is mostly visible after 14 days (Fig. 10). Structural (this work) and rheological (previous work²⁸) investigations both suggested that the covalent bonds in the physical-co-chemical gel are more ordered and possibly more evenly distributed, whereas the cross-links in the chemical gels are more random, resulting in larger inhomogeneities and clusters displaying a wide range of length scales, overall larger than in the PC gels (Fig. 8). Our cellular results (Fig. 10) interestingly suggest that a higher degree of order in the scaffold structure could explain the higher cell proliferation. We also note that whereas for chemical gels no statistically relevant dependence on cross-linker concentration was observed (p > 0.005), differences in cell proliferation on physical-co-chemical gels are seen (Fig. 9C and D). Cell proliferation showed a statistically significant decrease of approximately 80% from 10 to 40 U mTGase per g gelatin on PC gels, on day 14 (p < 0.005). In PC gels, the covalent network is formed after a substantial amount of helices have been created;²⁸ however, the time interval before the covalent network starts to interfere with the physical network is reduced with increasing cross-linker concentration. Therefore, PC gels cross-linked with lower amount of TGase (10 U mTGase per g gelatin) may contain a chemical network with covalent bonds more homogeneously spread than gels with higher amounts of TGase (40 U g⁻¹ gelatin), which could thus explain the differences in cell proliferation. Instead, in chemical gels, the differences observed in G′ and nanostructure with enzyme concentrations are not directly translated into a different cell behaviour.

Fig. 10 Cell proliferation of rat BMSCs grown on chemical (yellow, diamonds) and physical-co-chemical (green, squares) gels for 14 days. The gels were cross-linked with (A) 10 U mTGase per g gelatin, (B) 20 U mTGase per g gelatin, (C) 30 U mTGase per g gelatin, (D) 40 U mTGase per g gelatin.

Conclusion

In this work, we aimed to provide a detailed characterisation of the architecture of physical, chemical and hybrid gelatin hydrogels, following their rheological characterisation,²⁸ establish a connection between the macro- and the nano-scale and, finally, provide an initial evaluation of cell viability and metabolic activity on these gels and examine whether the biological response could be related to the physical characteristics.

For pure physical gelatin gels, we observed that the correlation length (ξ), obtained from fitting the SANS data to a Lorentzian and power law model, and understood as an average mesh size of the network, decreases linearly with gelatin concentration. The correlation length does not vary significantly between the sol and the gel state and is independent of gelation temperature. Thus SANS proved to be insensitive to the conformational changes undertaken by gelatin strands (strand-to-triple-helix) during the sol–gel transition.

Cross-linking was performed under two conditions: from the sol state (chemical gels, C) and from the gel state (physical-co-chemical gels, PC), or, more precisely, with contemporaneous (but faster) physical gelation occurring. In both types of gels, either pure chemical or hybrid, it was observed that ξ, in this case best understood as an average aggregate size, increases with mTGase concentration, as larger aggregates are formed with more cross-linker. The aggregation kinetics are also faster at higher enzyme concentrations. However, for C gels at very long cross-linking times, it was not possible to extract a value for ξ from the SANS curves. This was most probably due the presence of very large aggregates and/or a large and inhomogeneous aggregate size distribution, while for PC gels, the same data analysis resulted in good ξ values, reflecting not only smaller aggregates, but a more homogenous distribution of clusters and therefore a more ‘ordered’ cross-linking process. Finally, we established a connection between the macro- and the nano-scale for both network types in the form of master-curves, which correlate the measured ξ to the shear modulus measured for each gel type. They reveal the direct influence of the average aggregate size on the gel bulk mechanical strength (as measured by the shear modulus); in particular, they show that gelation only takes place beyond a critical value of ξ (ca. 30 Å).

Interestingly, the two types of chemical networks (purely covalent, C, and hybrid, PC) induce a different metabolic activity from cells. Both network types are compatible with cell growth. For chemical networks, mTGase concentration does not affect cell proliferation, while for PC gels, high amounts of mTGase lead to losses in proliferation. However, PC gels induce overall a statistically higher cell metabolic activity than their chemical counterparts; this can possibly be explained by the more ordered and mechanically stronger networks of the PC gels, where covalent cross-linking is guided by the pre-existing helical network.

The systems reported in this study, based on a widely available natural product and an enzymatic process, are attractive for biomedical applications, in particular tissue engineering. The type of multi-disciplinary approach proposed here, where the architecture of the gels on the nanoscale, their mechanical behaviour on the macroscale and their biological performance for cell regeneration are all examined and correlated is paramount – yet not often seen in the literature – to achieve a comprehensive understanding of networks properties and rationalise the design of hydrogels with controlled functional properties.

Acknowledgements

This project was funded by the EPSRC (grant EP/F037902/1). CAD and MA acknowledge the Leverhulme Trust for the provision of a research grant (F/07040/AR). Isabelle Grillo and Aurel Rădulescu are acknowledged for help with the SANS measurements at ILL (Grenoble, France) and JCNS (Münich, Germany) respectively. Richard Heenan (ISIS, UK) is thanked for his help with data fitting using the software FISH. This work is based on experiments performed on D11, KWS-1 and KWS-2 instruments operated respectively by the ILL (Grenoble, France) and by JCNS at Forschungs-Neutronenquelle Heinz Maier-Leibnitz (FRM II, Garching, Germany).

References

1. S. Van Vlierberghe, P. Dubruel and E. Schacht, Biomacromolecules, 2011, 12, 1387–1408.
2. F. Shahidi, Chemistry, processing technology and quality, Chapman & Hall, Glasgow, 1994.
3. J. H. Muyonga, C. G. B. Cole and K. G. Duodu, Food Hydrocolloids, 2004, 18, 581–592.
4. A. A. Karim and R. Bhat, Food Hydrocolloids, 2009, 23, 563–576.
5. P. B. Malafaya, G. A. Silva and R. L. Reis, Adv. Drug Delivery Rev., 2007, 59, 207–233.
6. M. M. Stevens and J. H. George, Science, 2005, 310, 1135–1138.
7. A. Veis, The Macromolecular Chemistry of Gelatin, Academic Press, London, 1964.
8. J. D. Ferry, Adv. Protein Chem., 1948, 1–78.
9. H. Akin and N. Hasirci, J. Appl. Polym. Sci., 1995, 58, 95–100.
10. H. C. Liang, W. H. Chang, K. J. Lin and H. W. Sung, J. Biomed. Mater. Res., Part A, 2003, 65, 271–282.
11. H. W. Sung, D. M. Huang, W. H. Chang, R. N. Huang and J. C. Hsu, J. Biomed. Mater. Res., 1999, 46, 520–530.
12. A. Bigi, G. Cojazzi, S. Panzavolta, K. Rubini and N. Roveri, Biomaterials, 2001, 22, 763–768.
13. B. S. Chiou, R. J. Avena-Bustillos, J. Shey, E. Yee, P. J. Bechtel, S. H. Imam, G. M. Glenn and W. J. Orts, Polymer, 2006, 47, 6379–6386.
14. C. M. Ofner and W. A. Bubnis, Pharm. Res., 1996, 13, 1821–1827.
15. H. C. Liang, W. H. Chang, H. F. Liang, M. H. Lee and H. W. Sung, J. Appl. Polym. Sci., 2004, 91, 4017–4026.
16. J. W. Mwangi and C. M. Ofner, Int. J. Pharm., 2004, 278, 319–327.
17. C. W. Yung, L. Q. Wu, J. A. Tullman, G. F. Payne, W. E. Bentley and T. A. Barbari, J. Biomed. Mater. Res., Part A, 2007, 83, 1039–1046.
18. E. Gendler, S. Gendler and M. E. Nimni, J. Biomed. Mater. Res., 1984, 18, 727–736.
19. A. Bigi, G. Cojazzi, S. Panzavolta, N. Roveri and K. Rubini, Biomaterials, 2002, 23, 4827–4832.
20. M. F. Butler, Y. F. Ng and P. D. A. Pudney, J. Polym. Sci., Part A: Polym. Chem., 2003, 41, 3941–3953.
21. H. L. Fuchsbauer, U. Gerber, J. Engelmann, T. Seeger, C. Sinks and T. Hecht, Biomaterials, 1996, 17, 1481–1488.
22. V. Crescenzi, A. Francescangeli and A. Taglienti, Biomacromolecules, 2002, 3, 1384–1391.
23. H. Babin and E. Dickinson, Food Hydrocolloids, 2001, 15, 271–276.
24. T. H. Chen, H. D. Embree, E. M. Brown, M. M. Taylor and G. F. Payne, Biomaterials, 2003, 24, 2831–2841.
25. Y. Sun, O. Giraudier and V. L. Garde, Biopolymers, 2005, 77, 257–263.
26. S. Giraudier, D. Hellio, M. Djabourov and V. Larreta-Garde, Biomacromolecules, 2004, 5, 1662–1666.
27. J. S. Finlayson and J. E. Folk, Adv. Protein Chem., 1977, 31, 1–133.
28. F. Bode, M. A. da Silva, A. F. Drake, S. B. Ross-Murphy and C. A. Dreiss, Biomacromolecules, 2011, 12, 3741–3752.
29. J. Bastide and L. Leibler, Macromolecules, 1988, 21, 2647–2649.
30. D. J. Giard, S. A. Aaronson, G. J. Todaro, P. Arnstein, J. H. Kersey, H. Dosik and W. P. Parks, J. Natl. Cancer Inst., 1973, 51, 1417–1423.
31. A. Ramzi, M. Sutter, W. E. Hennink and W. Jiskoot, J. Pharm. Sci., 2006, 95, 1703–1711.
32. F. Horkay and B. Hammouda, Colloid Polym. Sci., 2008, 286, 611–620.
33. R. A. Hule, R. P. Nagarkar, A. Altunbas, H. R. Ramay, M. C. Branco, J. P. Schneider and D. J. Pochan, Faraday Discuss., 2008, 139, 251–264.
34. F. Ramzi Zielinski, J. Bastide and F. Boue, Macromolecules, 1995, 28, 3570–3587.
35. R. K. Heenan, S. M. King, R. I. Osborn and H. B. Stanley, COLETTE Users Guide, Rutherford Appleton Laboratory Report No. RAL89-128, 1989.
36. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
37. K. Kremer and G. S. Grest, Monte Carlo and Molecular Dynamics Simulations in Polymer Science, Oxford, New York, 1995.
38. K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086.
39. T. Schneider and E. Stoll, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 17, 1302–1322.
40. D. R. Heine, G. S. Grest, C. D. Lorenz, M. Tsige and M. J. Stevens, Macromolecules, 2004, 37, 3857–3864.
41. C. D. Lorenz, M. J. Stevens and R. P. Wool, J. Polym. Sci., Part B: Polym. Phys., 2004, 42, 3333–3343.
42. M. Tsige, C. D. Lorenz and M. J. Stevens, Macromolecules, 2004, 37, 8466–8472.
43. E. Gentleman, R. J. Swain, N. D. Evans, S. Boonrungsiman, G. Jell, M. D. Ball, T. A. V. Shean, M. L. Oyen, A. Porter and M. M. Stevens, Nat. Mater., 2009, 8, 763–770.
44. M. Djabourov, Contemp. Phys., 1988, 29, 273–297.
45. C. Joly-Duhamel, D. Hellio, A. Ajdari and M. Djabourov, Langmuir, 2002, 18, 7158–7166.
46. R. A. Pethrick and J. V. Dawkins, Modern Techniques for Polymer Characterisation, Johl Wiley and Sons Ltd, New York, 1999.
47. I. Pezron, M. Djabourov and J. Leblond, Polymer, 1991, 32, 3201–3210.
48. M. Daoud, J. P. Cotton, B. Farnoux, G. Jannink, G. Sarma, H. Benoit, C. Duplessix, C. Picot and P. G. de Gennes, Macromolecules, 1975, 804–818.
49. S. F. Edwards, Theory of polymer solutions at intermediate concentration, 1966.
50. M. Daoud and J. P. Cotton, Macromolecules, 1975, 8, 804–818.
51. T. Cosgrove, S. J. White, A. Zarbakhsh, R. K. Heenan and A. M. Howe, J. Chem. Soc., Faraday Trans., 1996, 92, 595–599.
52. B. Mohanty, V. K. Aswal, J. Kohlbrecher and H. B. Bohidar, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 1653–1665.
53. J. Sharma, V. K. Aswal, P. S. Goyal and H. B. Bohidar, Macromolecules, 2001, 34, 5215–5220.
54. L. S. Ornstein and F. Zernike, Proc. K. Ned. Akad. Wet., 1914, 17, 793–806.
55. L. Benguigui and F. Boue, Eur. Phys. J. B, 1999, 11, 439–444.
56. D. Hellio-Serughetti and M. Djabourov, Langmuir, 2006, 22, 8516–8522.
57. J.-H. Yoon, J.-W. Woo, H.-J. Rho, J.-R. Ahn, S.-J. Yu, Y.-B. Lee, C.-K. Moon and S.-B. Kim, Korean J. Chem. Eng., 2008, 25, 134–138.
58. K. Kuwahara, Z. Yang, G. C. Slack, M. E. Nimni and B. Han, Tissue Eng., Part C, 2010, 16, 609–618.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c3sm00125c

---