Precise drop dispensation on superhydrophobic surfaces using acoustic nebulization

Abstract

The adhesion forces of liquid drops on superhydrophobic surfaces are typically in the nano-Newton range which presents problems in their dispensation from pipettes. Furthermore, since the liquid adheres more strongly to the pipette tip, some portion of the liquid will tend to remain on the tip, causing inaccuracy in the volume dispensed. We advance a novel approach here, in which the spray from an acoustic nebulizer is sent to a superhydrophobic receptacle and the volume ascertained precisely using a weighing scale. The superhydrophobic surface was identified to develop via a galvanic displacement mechanism in an electroless deposition process. A time dependent morphology change from granular to dendritic with longer immersion into the silver nitrate solution was found which indicated that granular growth beyond a certain size was not feasible, although granular structures were more preferentially formed just after nucleation. The dendritic structure formation was likely due to the natural tendency of the process to maintain or increase the surface area to volume ratio in order not to limit the rate of deposition. An immersion for at least 7 seconds into the silver nitrate solution, when the granular structures were predominant, was all that was needed to ensure superhydrophobicity of the surfaces. Also, the superhydrophobic state required not just significant numbers of the granular structures to be present but also interrupted coverage on the surface. On using the technique, a single drop was created by subsequently covering the receptacle with a lid and shaking it gently. The volume dispensed was found to vary linearly with the operation time of the nebulizer. We elucidated the observed increased ability of drops to reside on inclines using wetting mechanics and presented an elementary mathematical description of the extent of aerosol coverage on the surface, which has implications for the mechanics of aerosol growth into drops. The structural changes in enhanced green fluorescent protein (EGFP) observed after acoustic dispensation necessitated all samples in a fluorimetric assay to involve equal nebulized volumes of the fluorescent protein marker for measurement consistency.

---

1 Introduction

Superhydrophobic surfaces are illustrated in nature through the well-known examples of lotus leaves and the legs of water striders.^1,2 There has been a recent proliferation in methods reported to artificially mimic these surfaces.^3–7 While the original opportunity of superhydrophobicity was in self-cleaning,⁸ there is now substantial effort aimed at harnessing it for biochemical applications^9–14 since the ability to transport analytes or samples is a crucial component. This is aided by the increasing awareness that continuous and closed microfluidic flow devices are inherently difficult to integrate and scale due to the flow at any one location being dependent on the flow properties of the entire system. Discrete, independently controllable sample volumes, alternatively, permit the microfluidic function to assume a set of basic repeated operations, whereby one unit of fluid can be moved over one unit of distance, thus facilitating the use of hierarchical and cell-based approaches for microfluidic biochip designs that offer flexible and scalable system architectures as well as high fault tolerance capabilities. Moreover, because sample volumes can be controlled independently, such systems offer greater potential to be reconfigured whereby groups of unit cells in an array can be altered to change their functionality.

The adhesion forces of liquid drops on superhydrophobic surfaces are typically in the nano-Newton range.¹⁵ Hence, this presents a real problem in their dispensation from pipettes. The use of flexible pipette tips¹¹ permits drop volumes down to around 10 μL to be deposited, albeit this requires careful execution in order for them not to contact (from the tip springing back after dispensation) the surface and thus damage the nano and micro features that endow superhydrophobicity. It should also be noted that since the liquid adheres more strongly to the pipette tip, an unknown portion of the liquid will remain within the tip, causing substantial inaccuracy in the dispensed volume.

The quest to develop bioanalysis tools based on superhydrophobicity is also founded on the issues of availability and cost. Bioanalytical chemists in well endowed laboratories are often accustomed to having a plethora of convenient consumables and sophisticated instrumentation at their disposal. Many researchers in resource-limited developing countries, or field workers in remote locations far from modern conveniences, have been unable to take advantage of modern bioanalytical techniques due to a lack of infrastructure. This is unfortunate as it is these same researchers that usually have the greatest need for bioanalytical tools that will help diagnose diseases such as tuberculosis or malaria. Not surprisingly, there have been recent efforts expended to use alternative materials such as paper to serve as the analyte handling media.¹⁶ This approach, while useful for methods based on electrochemical detection, is not as effective for methods that are based on optical detection, that arguably offer the highest versatility and sensitivity. Alternative cost effective approaches have since been reported.^17,18 Despite this, paper remains indispensable as a relatively cheap, compact and robust reservoir for test samples and biochemical analytes.

In this work, we seek to develop a technique that will allow us to deliver drops of specific volumes on superhydrophobic surfaces from cost effective storage media such as paper so that they can in turn be harnessed to be developed into cost effective devices that permit transport. In the process, we will study the nature of how small aerosols form on these surfaces before evolving into single drops.

2 Materials and methods

We advance the approach depicted in Fig. 1 to circumvent this problem. A liquid supply chain was created out of a reservoir that delivers to a short capillary tube section, whose tip is placed in contact with a surface acoustic wave (SAW) nebulizer running at 30 MHz frequency using a small piece of tissue paper that constituted a capillary wick.¹⁹ The SAW device was constructed out of a low-loss piezoelectric substrate, specifically, a 127.86° Y–X-rotated single-crystal lithium niobate (LiNbO₃) substrate, with pairs of chromium–aluminum interdigital transducers fabricated on one side via standard UV photolithography. When an AC signal is supplied to the transducer at its resonant frequency, the SAW in the form of a Rayleigh wave propagates along the LiNbO₃ surface from the transducer at about 3900 m s⁻¹. Although the surface displacement amplitudes are only in the 1–10 nm range, the accelerations are extremely high (about 10⁷ m s⁻²) due to excitation at frequencies over 10 MHz. These huge surface accelerations are transmitted into the liquid placed on the substrate, inducing acoustic streaming.²⁰ When the energy is sufficient (i.e., electrical power supplied in the 1–3 W range), destabilization of the liquid's free surface occurs. This leads to a breakup of capillary waves, generating a spray of aerosol droplets through a process known as SAW atomization or nebulization.^21,22 When this spray of aerosol is channeled onto a semi-spherical superhydrophobic receptacle, larger drops develop on the receptacle surface from multiple coalescence events that are influenced by gravity (which tend to draw them towards the receptacle trough).

Fig. 1 Schematic description of the scheme to obtain precise volumes of drops on superhydrophobic surfaces. A surface acoustic wave nebulizer delivers a spray of aerosol droplets onto the receptacle in which the exact volume is determined using an accurate weighing scale. By covering with a superhydrophobic lid and gentle shaking, a single drop is created.

The receptacle was fashioned out of a copper sheet (1 mm thickness), polished earlier to remove all visible scratches using silicon carbide electro-coated waterproof abrasive paper (KMCA, WET/DRY S85 P600), by an 8.5 mm radius ball indenter. Prior to use, the receptacle surface was first cleaned using absolute ethanol, allowed to air dry, and then immersed in a 24.75 mM aqueous solution of AgNO₃ for 1 minute to form the micro and nano structures. After this, the surface was rinsed with copious amounts of distilled water followed by absolute ethanol before being allowed to air dry. Once dried, it was immersed in a 1 mM solution of the surface modifier CF₃(CF₂)₇CH₂CH₂SH in absolute ethanol for 5 minutes. After removal, it was again rinsed with copious amounts of distilled water, followed by absolute ethanol, and then air dried.

For a side experiment to study the nano and microstructures forming in relation to wetting, we created coupons 20 × 20 mm in size out of the same copper sheet (1 mm thickness) and using the same polishing and cleaning process as previously used. The coupons were then immersed in the 24.75 mM aqueous solution of AgNO₃ for selected periods ranging from 2 seconds to 120 seconds before being removed to air dry. After drying, the morphology of the superhydrophobic surface was characterized with an FEI Quanta 3D FEG scanning electron microscope (SEM). The elemental composition was characterized by an X-ray energy dispersive spectrometer (EDS) associated with the SEM. The wetting characteristics were evaluated by placing 5 μL of sessile drops of water on each surface (after immersing into the surface modifying solution) and then determining the contact angle.

In the technique, the weight of the liquid delivered to the receptacle, which could be correlated to volume, was determined using a weighing scale (A&D GR-200 with 0.0001 g precision) on which the receptacle is placed on. Once the required volume was achieved, aerosol delivery from the nebulizer was terminated, a superhydrophobic lid placed over the receptacle, and the assembly shaken gently to merge the drops together into one. Apart from ensuring that no liquid spilled out of the receptacle, the lid also served to limit the effects of evaporation, which is significant for small drop volumes. Experiments were conducted to establish the liquid (Milli-Q water) delivery characteristics when the power to the nebulizer was kept constant at 2 W.

Lastly, the effect of nebulization on the structural functionality of enhanced green fluorescent protein (EGFP) was evaluated. This C-terminally His₆-tagged fluorescent protein was isolated from genetically modified Escherichia coli and purified to near homogeneity by automated affinity chromatography using 1 mL bed volume Mini Profinity IMAC cartridges on the Profinia Protein Purification System (Bio-Rad) under the default program settings of the Native IMAC method with integrated desalting into sodium phosphate buffer (pH 7.4). The His₆-tagged EGFP was checked for purity by SDS-PAGE (see ESI†) and quantified using the BCA protein assay (Pierce, USA). Samples of the protein were nebulized at different powers, collected in capillary tubes, imaged together using a fluorescence microscope (Olympus BX61), and the intensities extracted using the ImageJ software.

3 Results and discussion

The micro- and nano-structures developed by immersing the copper coupons into the aqueous solution of AgNO₃ were formed by an electroless deposition process. This process is similar to electrolytic plating except that no external electrodes are needed.²³ In electroless deposition, the metal ions are typically reduced into metals by the introduction of a reducing agent. A variety of procedures with different reagents have been demonstrated for electroless deposition of silver.^24,25 In the process conducted here, however, the deposition was able to proceed without any external reducing agent. Rather, a galvanic displacement mechanism occurred in which the silver cations in solution were reduced just as copper from the surface was oxidized.

The SEM micrographs of structures formed in association with various immersion times of the copper coupons into the silver nitrate solution are presented in Fig. 2. The background striated structures seen at 2 seconds were formed due to the polishing process. On the substrate, very small granules started to be deposited at numerous nucleation sites. These granules grew in size with longer immersion times until about 10–20 seconds. At the 20 seconds mark, the granules appeared to shrink slightly in size whilst exhibiting greater dendritic growth from the surface of each granule. From then onwards, the dendritic structures began to proliferate on the existing granular structures, developing later into fern-like foliage. The distinct differences between these two types of structures (granular and dendritic) are shown more clearly in the higher magnification micrographs provided in Fig. 3.

Fig. 2 Scanning electron micrographs obtained from immersing the copper coupons into the silver nitrate solution for different lengths of time followed by air drying. It can be seen that granular structures developed with short period immersion, whilst dendritic structures formed with longer period immersion.

Fig. 3 Scanning electron micrographs at higher magnifications that provide a clearer picture of the (a) granular and (b) dendritic structures developed.

The time dependent morphology changes appear to indicate that granular growth beyond a certain size was not feasible, although granular structures were more preferentially formed just after nucleation. This is likely due to the natural tendency of the process to maintain or increase the surface area to volume ratio in order not to limit the rate of deposition. Taking a sphere for example, the surface area to volume ratio scales according to 3/r, where r is the radius, inferring that the surface area to volume ratio reduces as the sphere increases in size. Thus, the formation of dendritic structures offers an avenue by nature to circumvent this obstacle. This argument is supported somewhat by the XRD maps obtained that revealed no significant elemental changes in the structures.

After the surfaces were treated with the modifier, we found that immersion for at least 7 seconds into the silver nitrate solution was all that was needed to ensure superhydrophobicity of the surfaces. At this stage, the structures appeared to be predominantly granular. Previous studies have shown that granular structures alone were sufficient to cause superhydrophobicity.²⁶ Hence, we were able to conclude that the subsequent dendritic structures were not needed to maintain the non-wetting characteristic, although they seemed not to have a role in modifying it. The micrograph at 5 seconds immersion also showed significant coverage of granular structures over the substrate. This presented an interesting conundrum as to why superhydrophobicity could not be sustained at this stage. On more careful examination, we found that there were regions on the substrate surface where the granular structures were not fully developed. It appears then that the superhydrophobic state requires not just significant numbers of the granular structures to be present on the surface but also uninterrupted structure coverage.

We move now to discuss the experimentation results in obtaining the drops. During each run on liquid deposition, the nebulizer was cyclically pulsed on for 5 seconds and off for 5 seconds. This was done to accommodate the response time of the weighing scale. Fig. 4 presents results of the mass recorded in relation to time in which the nebulizer was operated for three typical runs. Highly linear trends are observed, indicating that fixed quanta of liquid were dispensed with each pulsed operation of the nebulizer for a specific run. While the data for two of the runs were almost identical, the gradient for a third run was significantly altered. This was due to the process that happens in the tissue as it served to draw liquid out from the reservoir before perturbations from the SAW device are able to dislodge it for delivery. In the course of this process, factors that affect the transfer of liquid in and out of the tissue (such as temperature and airborne particles attaching to the fibers) likely caused the flow rate to vary with each run.

Fig. 4 Plots of the readings from the weighing scale against the operation time of the nebulizer. The trends from each run are highly linear, albeit the slope variation indicates that pre-calibrated operation without the weighing scale was not feasible.

This result implied that an open-loop operation using pre-calibration without using the weighing scale was not feasible. Due to the ability of the SAW driven nebulizer to operate nearly instantly, from zero to full power and to zero power again in approximately 1 microsecond, there was no ‘lagging volume’ delivered when the nebulizer was turned off. Hence, the limiting factor for accurate volume dispensation was only that dictated by the mass resolution of the weighing scale. In the current case, the volume resolution was 1 μL based on the density of water being 1000 kg m⁻³ and the weighing scale's mass resolution being 0.0001 g. The response of the weighing scale also determined the time needed, since the off times could be shortened if it settled faster. We have also found that good isolation from draft and ambient vibrations was crucial to maintaining accuracy.

The formation of multiple drops in the receptacle (Fig. 5(a)) of up to 3 μL by volume (by estimation) before the gentle shaking operation was applied to dislodge them to form a final single drop (Fig. 5(b)) presents an interesting conundrum. Experiments with drops of this volume typically show that they move easily when dispensed on superhydrophobic surfaces. In fact, earlier dynamical studies conducted show that very small forces (in the nano-Newton range) are needed to move water drops on this surface.¹⁵ Coupled with the curvature of the receptacle, this should then result in a single drop forming all the time even when no shaking was introduced. This apparent anomalous behavior can be explained by the Cassie and Wenzel wetting states of superhydrophobic surfaces.²⁷ When a drop impinges on a wetting surface, it is known that it will first expand rapidly.²⁸ With sufficient momentum of the drop, the surface microstructures are able to impale the liquid surface. As the liquid loses kinetic energy, the drop will eventually settle into a static state, leading to the observation of stickiness. On a non-wetting surface, alternatively, stronger capillary and hydrodynamic forces develop to impede this impalement process. Consequently, the drop is able to bounce off and lose energy through a succession of bounces.

Fig. 5 Images of (a) multiple nebulized droplets formed on the surface of the receptacle and (b) a single drop that results after shaking the receptacle.

When drops of larger sizes impinge on a superhydrophobic surface, there is very high likelihood that the impalement process will not occur. Upon settlement from bouncing, they are expected to develop a high proportion of Cassie states at the three-phase contact line, facilitating easy sliding and rolling of the liquid body along the surface (Fig. 6(a)). We, of course, ignore for convenience the situation where the bouncing drops collide with each other in mid air. With individual aerosol drops (which are smaller in size) landing on the surface, however, the probability of impalement is increased since higher Laplace pressures develop on them.^27,28 The impalement process essentially develops high degrees of the Wenzel wetting state on the surface as liquid fills into the crevices between the microstructures (Fig. 6(b)). As more aerosols arrive, they either merge with those already on the surface or grow to the extent of coalescence with other surface-residing aerosols. In the absence of sufficiently large perturbations to convert the predominant Wenzel states into Cassie states,²⁹ the drop coalesced from aerosols remains adherent on the inclined surface even at larger volumes for which an equivalent volume drop deposited upon the surface would be in the predominant Cassie state from the start (Fig. 6(c)). The formation of multiple drops on the surface (Fig. 5(a)) appears to indicate some links with the process of condensation. However, previous studies conducted with condensation have shown a tendency for surfaces to lose their superhydrophobicity,³⁰ likely arising from damages to the surface structures during the process. That a single drop could be attained here (after shaking) with no apparent loss in superhydrophobic behavior (Fig. 5(b)) shows differences in the underlying mechanisms.

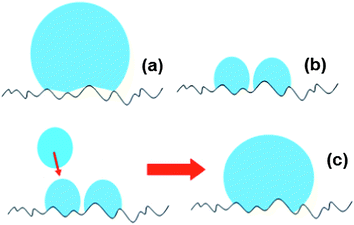Fig. 6 Illustrations depicting predominantly high (a) Cassie and (b) Wenzel wetting states of relatively larger drops and aerosols residing respectively on superhydrophobic surfaces. (c) When further aerosols arrive at the surface, they merge with existing aerosols on the surface to create larger volumes that coalescence with other surface bound aerosols. Due to the lack of a sufficiently large perturbation, the predominant Wenzel states cannot convert to Cassie states, allowing the liquid body to stay on the inclined surface with larger volumes.

While the drops are attached to the surface with a predominant Wenzel wetting state, the shaking of the receptacle imbues them with energy (see Fig. 7). With sufficient momentum, the drop will be able to dislodge from the surface to leave behind a thin film of liquid. Due to the direction of the shaking, this will occur more like a shearing operation, tearing the drop from the liquid embedded in the microstructures.¹⁵ The very small volume of the thin liquid film left behind renders it easily evaporable while the drop now functions in a predominant Cassie state. We contend that the ability of the liquid film to evaporate quickly plays a role in the conversion process, since a previous study using lotus leaves has shown that extensive pre-wetting using condensation over the surface (which creates a thin film of liquid in the Wenzel state) will cause a loss in superhydrophobic behavior of drops locating later over it.³¹ Strictly speaking then, the description of the wetting state change here does not refute the notion that the Wenzel state is strongly irreversible. Wetting state changes are often thought of as pertaining to the entire body of liquid. The ability of the liquid body to separate hence imbues the “liberated” component with the capacity to seek another predominant wetting state. Evidence of the ability of drops to separate on superhydrophobic surfaces has been reported, albeit in a different context.³²

Fig. 7 Illustrations depicting the initial predominantly high (a) Wenzel wetting state of a drop on the surface in which with sufficient momentum developed (in the direction of the arrow) will (b) cause the drop to dislodge and leave behind a thin film of liquid. The very small volume of the latter renders it easily evaporable while the former now functions as a drop in the Cassie state.

It is also apt at this point to mention that the conception of a fully Cassie state is not viable due to the heterogeneity of the microstructures developed (see Fig. 2). It has been previously established that the spacing between protruding microstructures and the height of the protruding microstructures dictate whether a droplet will assume Cassie or Wenzel states.³³ An interesting rumination relates to the interesting result of Jin et al.³⁴ that showed the possibility for superhydrophobic surfaces to possess strong adhesive forces by virtue of high van der Waals forces acting. Will it be possible to achieve the Wenzel to Cassie state changes with lowered movement of the drop during the shaking process? This has advantageous implications in terms of practical device development.

An ability to mathematically model the formation of a single drop from the spray of aerosol droplets will be instructive, although likely an involved undertaking due to the stochastic and dynamical nature of the mechanisms involved in (i) aerosols arriving at the receptacle surface, (ii) aerosols growing into drops, (iii) drops detaching from the surface under gravity, and (iv) drops coalescing. In the context of (iv), the unexpected drop–drop bouncing behavior recently uncovered on superhydrophobic surfaces³⁵ portends greater complexity in the modeling. We present here an elementary description of the extent of aerosol coverage on the surface that has implications for the mechanics of aerosols growing into drops.

A single aerosol that arrives as a sphere with radius r′ (which can be estimated to a high degree of accuracy using optical methods^36,37) on a semi-spherical surface of radius R will result in a liquid body that is governed by the equilibrium three-phase contact angle θ. This can be described using a model comprising two spheres that intersect with each other. The parameters r′, R, and θ can be related to the solid angle Ω via equations (outlined in the Appendix) that can be solved. The solid angle provides a convenient depiction of the extent of coverage taken from an assumed point source (the nebulizer). This is rather akin to the delivery of light from a point source in radiometry.³⁸

Fig. 8 presents plots of Ω against r′/R for various values of θ. As r′ and R were 5 μm and 8.5 mm, respectively, the abscissa values were normalized to O(10⁻³). The values were found using derivations given in the ESI.† The definition of superhydrophobicity is loosely correlated to a value of θ ranging from 120° to 180°. In the figure, the variations in the solid angles calculated based on this are significant. If we consider the case of θ = 120°, changing r′/R from 2 × 10⁻³ to 4 × 10⁻³ increases the solid angle by 4.2 times. An increase in the solid angle is generally favorable as it implies a greater probability for the aerosols that arrive later to impinge on those already on the surface. This improves the chance of growth towards drops and thus also the propensity for them to detach and roll towards the base of the receptacle. If the aerosol radius were to be kept constant, reducing R would achieve this. It should be noted, however, that too small a value of R will increase the chances of the spray envelope to fall outside the receptacle, thereby causing material loss. The solid angle values with θ = 170° alternatively are small, which is seemingly negative in terms of increasing the probability of aerosol coalescence on the surface. Nevertheless, the adhesion forces of drops with higher θ values are also typically smaller, enabling even a small aerosol drop to roll down to the base. In addition, the values of Ω remain relatively invariant with r′/R when θ is closer to 180°.

Fig. 8 Plots of the solid angle Ω subtended by an aerosol droplet that arrives as a sphere with radius r′ on a semi-spherical surface of radius R for various equilibrium three-phase contact angles θ. The residence of the aerosol droplet on the surface can be described using a model comprising two spheres that intersect with each other. The relevant parameters can be related, via equations that can be solved, to the solid angle.

With nebulizer powers of 1.1 W, 1.3 W, 1.52 W, and 2.05 W, the fluorescence intensity readings, normalized to the reading without nebulization, were 0.81, 0.77, 0.80, and 0.84 respectively. This indicated some expected loss in fluorescence, not inconsistent with previous results assessing post-nebulized protein viability,¹⁹ although different levels of power in the range used did not seem to have a varying effect. Samples that were nebulized also retained their fluorescence activity with no signs of any post deterioration in emission intensity after storage for a week at 4 °C. GFP fluorescence is known to be affected by pH,³⁹ dissolved oxygen,⁴⁰ and high temperatures.⁴¹ It is possible that a slight disruption of the structural integrity of EGFP, in particular its fluorophore, may have been caused by strong initial perturbations delivered to the sample. All samples in a fluorimetric assay, therefore, should comprise equal volumes of EGFP or fluorescent protein marker equivalently nebulized to ensure consistency in measurements made.

4 Conclusions

We have identified that a galvanic displacement mechanism in an electroless deposition process occurred in which the silver cations in solution were reduced just as copper from the surface was oxidized and was responsible for creating the micro- and nano-scaled structures that endow superhydrophobicity on the copper substrate. A time dependent morphology change from granular to dendritic with longer immersion into the silver nitrate solution was found. This indicated that granular growth beyond a certain size was not feasible, although granular structures were more preferentially formed just after nucleation. The dendritic structure formation was likely due to the natural tendency of the process to maintain or increase the surface area to volume ratio in order not to limit the rate of deposition. An immersion for at least 7 seconds into the silver nitrate solution was all that was needed to ensure superhydrophobicity of the surfaces. This allowed for the deduction that the dendritic structures were not needed to maintain the non-wetting characteristic, although they seemed not to have a role in modifying it. Also, the superhydrophobic state required not just significant numbers of the granular structures to be present, but also interrupted coverage on the surface. In using the proposed technique, having the nebulizer cyclically pulsed on for 5 seconds and off for 5 seconds was needed to accommodate the response time of the weighing scale. Highly linear trends were observed, indicating that fixed quanta of liquid were dispensed with each pulsed operation of the nebulizer for a specific run. However, the flow rate may be altered and this was due to factors that affected the transfer of liquid in and out of the tissue (such as temperature and airborne particles attaching to the fibers). With individual aerosols landing on the receptacle surface, the probability of impalement was increased since higher Laplace pressures developed on them. The impalement process then developed high degrees of the Wenzel state on the surface. With sufficient momentum from shaking, the drop was able to dislodge from the surface leaving behind a thin film of liquid. The very small volume of the thin liquid film rendered it easily evaporable while the drop then functioned in a predominant Cassie state. In using EGFP samples for verification, fluorescence emission could be retained to about 80% of its original level and was not affected by different levels of power used on the SAW device. In summary, we have developed a practical approach to deposit micro-liter volume drops on superhydrophobic surfaces stably and precisely. This is expected to facilitate biochemical applications using these surfaces.

Appendix

Analysis of aerosol formation on a semi-spherical surface

The residence of a single aerosol on a semi-spherical surface can be depicted by the intersection of two spheres (smaller one of the drop, and larger one of the surface) as shown in Fig. S1.† Since ∠OAB = ∠O′AB = 90°, the contact angle θ is given by

θ = 180° − ϕ. (A1)

This is related to r (radius of the drop on the surface), R (radius of the surface), and a (distance between centers) via

a² = R² + r² − 2rRcos ϕ = R² + r² + 2rRcos θ. (A2)

We next seek to establish the volume of liquid residing on the spherical surface. If the larger sphere is centered at (0,0,0) and the smaller sphere at (a,0,0) in Cartesian coordinates, we have

(x − a)² + (R² − x²) = r². (A3)

Solving for x, we have

If we apply this to the equation of the larger sphere, we have

Hence, at the point of intersection, we have a circle of radius b given by

This creates two caps of respective heights

Since the equation of volume of a spherical cap is known, we have

The extent of coverage of a single aerosol drop on the substrate surface can be conveniently depicted by the solid angle Ω in which

The maximum solid angle that can be subtended from a point source is 4π radians. If the radius r′ of aerosol delivered is known, this parameter can be related to the volume V by assuming the aerosol to be a sphere using V = 4π(r′)³/3. In (A9) then, r′ with R will relate to a and r. Using (A2) and (A10), we can then relate r′ and R instead to θ and Ω.

Verification of protein purity

The quality of C-terminal His₆-tagged EGFP purification was determined using SDS-PAGE analysis by immobilized metal affinity chromatography (IMAC). The crude bacterial lysate (CL) containing His₆-tagged EGFP (indicated by the red arrow) was loaded onto an IMAC column prepacked with UNOsphere™ beads containing the chelating ligand iminodiacetic acid charged with nickel. The strong affinity of the His₆-tag for the transition metal results in efficient binding of the recombinant EGFP onto the column resin as indicated by the loss of the EGFP band in the flow through fraction (FT). Two wash buffer cycles (W1 and W2) effectively removed most of the contaminating proteins bound on the column. Finally, purified His₆-tagged EGFP (E + D) was eluted from the IMAC column by displacement with 250 mM imidazole and desalted into sodium phosphate buffer as a near homogeneous product (indicated by the red arrow in Fig. S2†).

Acknowledgements

TW, OW and Jing F. appreciate funding support from the Australian Research Council Grant DP120100583. James F. wishes to acknowledge financial support from the Australian Research Council via grants DP120100013 and DP120100835, and the provision of facilities and equipment from the Melbourne Centre for Nanofabrication.

References

1. W. Barthlott and C. Neinhuis, Planta, 2001, 202, 1.
2. X. Gao and L. Jiang, Nature, 2004, 432, 36.
3. L. Y. L. Wu, Q. Shao, X. C. Wang, H. Y. Zheng and C. C. Wong, Soft Matter, 2012, 8, 6232.
4. Y. Lai, X. Gao, H. Zhuang, J. Huang, C. Lin and L. Jiang, Adv. Mater., 2009, 21, 3799.
5. H. Zhou, H. Wang, H. Niu, A. Gestos, X. Wang and T. Lin, Adv. Mater., 2012, 24, 2409.
6. S. M. Kang, I. You, W. K. Cho, H. K. Shon, T. G. Lee, I. S. Choi, J. M. Karp and H. Lee, Angew. Chem., Int. Ed., 2012, 49, 9401.
7. Y. Li, L. Li and J. Sun, Angew. Chem., Int. Ed., 2010, 49, 6129.
8. R. Blossey, Nat. Mater., 2003, 2, 301.
9. A. I. Neto, C. A. Custódio, W. Song and J. F. Mano, Soft Matter, 2011, 7, 4147.
10. X. Li, Y. Liu, A. Zhu, Y. Luo, Z. Deng and Y. Tian, Anal. Chem., 2010, 82, 6512.
11. F. Shao, T. W. Ng, O. W. Liew, J. Fu and T. Sridhar, Soft Matter, 2012, 8, 3563.
12. J. Ballester-Beltrán, P. Rico, D. Moratal, W. Song, J. F. Mano and M. Salmerón-Sánchez, Soft Matter, 2011, 7, 10803.
13. T. Vuong, B. H. P. Cheong, J. K. K. Lye, O. W. Liew and T. W. Ng, Anal. Biochem., 2012, 430, 53.
14. F. Gentile, G. Das, M. L. Coluccio, F. Mecarini, A. Accardo, L. Tirinato, R. Tallerico, G. Cojoc, C. Liberale, P. Candeloro, P. Decuzzi, F. De Angelis and E. Di Fabrizio, Microelectron. Eng., 2010, 87, 798.
15. T. W. Ng and Y. Panduputra, Langmuir, 2012, 28, 453.
16. E. Carrilho, S. T. Phillips, S. J. Vella, A. W. Martinez and G. M. Whitesides, Anal. Chem., 2009, 81, 5990.
17. B. H.-P. Cheong, V. Diep, T. W. Ng and O. W. Liew, Anal. Biochem., 2012, 422, 39.
18. X. Y. Li, B. H.-P. Cheong, A. Somers, O. W. Liew and T. W. Ng, Langmuir, 2013, 29, 849.
19. A. Qi, L. Yeo, J. Friend and J. Ho, Lab Chip, 2010, 10, 470.
20. J. Friend and L. Yeo, Rev. Mod. Phys., 2011, 83, 647.
21. A. Qi, L. Yeo and J. Friend, Phys. Fluids, 2008, 20, 074103.
22. L. Yeo and J. Friend, Biomicrofluidics, 2009, 3, 012002.
23. G. O. Mallory, J. B. Hajdu, Electroless Plating: Fundamentals and Applications, AESF, Orlando, FL, 1990.
24. S. G. Warrier and R. Y. Lin, J. Mater. Sci., 1993, 28, 4868.
25. H. Chang, C. H. Pitt and G. B. Alexander, J. Mater. Sci., 1993, 28, 5207.
26. J. T. Han, D. H. Lee, C. Y. Ryu and K. Cho, J. Am. Chem. Soc., 2004, 126, 4796.
27. A. Lafuma and D. Quéré, Nat. Mater., 2003, 2, 457.
28. D. Bartolo, F. Bouamrirene, E. Verneuil, A. Buguin, P. Silberzan and S. Moulinet, Europhys. Lett., 2006, 74, 299.
29. J. B. Boreyko and C.-H. Chen, Phys. Rev. Lett., 2009, 103, 174502.
30. B. Mockenhaupt, H.-J. Ensikat, M. Spaeth and W. Barthlott, Langmuir, 2008, 24, 13591.
31. Y.-T. Cheng and D. E. Rodak, Appl. Phys. Lett., 2005, 86, 144101.
32. J. W. Krumpfer, P. Bian, P. Zheng, L. Gao and T. J. McCarthy, Langmuir, 2011, 27, 2166.
33. J. B. Lee, H. R. Gwon, S. H. Lee and M. Cho, Mater. Trans., 2010, 51, 1709.
34. M. Jin, X. Feng, L. Feng, T. Sun, J. Zhai, T. Li and L. Jiang, Adv. Mater., 2005, 17, 1977.
35. H. Mertaniemi, R. Forchheimer, O. Ikkala and R. H. A. Ras, Adv. Mater., 2012, 24, 5738.
36. H. Zuo, Q. Liu, J. Wang, L. Yang and S. Luo, Opt. Lett., 2010, 35, 1380.
37. Y. Wang, S. Fan, X. Feng, G. Yan and Y. Guan, Appl. Opt., 2006, 45, 7456.
38. R. W. Boyd, Radiometry and the Detection of Optical Radiation, John Wiley & Sons, 1983.
39. S. Enoki, K. Saeki, K. Maki and K. Kuwajima, Biochemistry, 2004, 43, 14238.
40. C. Zhang, X. H. Xing and K. Lou, FEMS Microbiol. Lett., 2005, 249, 211.
41. C. Zhang, M.-S. Liu and X.-H. Xing, Appl. Microbiol. Biotechnol., 2009, 84, 511.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c3sm00016h

---