Synthesis and electronic structure of a two dimensional π-conjugated polythiophene

Abstract

We report the synthesis and first electronic characterization of an atomically thin two dimensional π-conjugated polymer. Polymerization via Ullmann coupling of a tetrabrominated tetrathienoanthracene on Ag(111) in ultra-high vacuum (UHV) produces a porous 2D polymer network that has been characterized by scanning tunnelling microscopy (STM). High-resolution X-ray photoelectron spectroscopy (HRXPS) shows that the reaction proceeds via two distinct steps: dehalogenation of the brominated precursor, which begins at room temperature (RT), and C–C coupling of the resulting Ag-bound intermediates, which requires annealing at 300 °C. The formation of the 2D conjugated network is accompanied by a shift of the occupied molecular states by 0.6 eV towards the Fermi level, as observed by UV photoelectron spectroscopy (UPS). A theoretical analysis of the electronic gap reduction in the transition from monomeric building blocks to various 1D and 2D oligomers and polymers yields important insight into the effect of topology on the electronic structure of 2D conjugated polymers.

---

Introduction

Recent interest in two-dimensional materials, most notably graphene, has spurred extensive efforts in the synthesis and isolation of such one atom-thin structures.¹ However, the applications of graphene in electronics are limited due to its lack of a band-gap, which means its conductivity cannot be switched off. A potentially limitless range of properties could be created in organic analogues of graphene, namely 2D polymers with extended π-conjugation.² In these materials, the band gap, the charge carrier mobility, the exciton diffusion length, etc. may be tuned by tailoring the structure of the molecular building block. However, while the synthesis of conjugated 1D polymers in solution is well established and is widely used in industry, classical solution polymerization cannot yield 2D extended structures except for limited size oligomers.³ The unrestricted mobility of the building blocks tends to result in kinetically “locked”, crumpled and disordered 3D networks, such as in microporous polymers,⁴ where no extended electron delocalization can be achieved.⁵ Thermodynamically-controlled polymerization under equilibrium conditions, which has been employed to generate covalent organic frameworks (COFs), is potentially a feasible route towards 2D layered structures.⁶ However, the dynamic equilibrium chemistry⁷ for reversible binding of carbon atoms in a π-conjugated chain is not established. COFs are not easily processable and obtaining 2D planar polymeric sheets would require an extra exfoliation step.

An alternative approach is to use an atomically flat substrate to confine the motion of molecular building blocks to two dimensions, thus enforcing planar growth.^8–10 The supporting surface can also act as a catalyst for polymerization, allowing control over the reaction steps and, in some cases, leading to epitaxial ordering of the polymer on the surface.^11,12 This method has also been applied to create molecularly-defined graphene nano-ribbons.¹³ Thus far, scanning tunnelling microscopy (STM) has been the primary tool for exploring these surface-confined polymerization reactions, using a variety of molecular building blocks and under different environments. Under ambient conditions, growth of monolayers of 2D polymers has been explored using 1,4-addition¹⁴ and polycondensation¹⁵ reactions. The most impressive results, however, have been obtained by performing the 2D polymerization in ultrahigh vacuum (UHV) conditions.⁹ Various flat ordered^8,16–18 and disordered^19–21 2D polymer structures were synthesized. The surface-catalyzed Ullmann coupling of halogenated aromatic building blocks has been the key reaction for the synthesis of 2D polymers in UHV, although the use of polycondensation of triboronic acid,¹⁹ and iron-catalyzed polycyclization of tetracyanobenzene¹⁶ have also been reported.

Despite this recent progress, little attention and no experimental studies have so far been devoted to studying the electronic properties of the 2D polymers. Only a few¹⁶ of these materials have a chemical structure and connectivity that could lead to significant band-gap contraction and electron confinement effects, similar to those found in graphene.¹ Although several of the reported 2D polymers possess a continuous network of sp² carbons, the electron delocalization in most of these is limited by cross-conjugation (as in meta-substituted benzene)^18,21 or by a large twist angle between the π-orbitals.⁸ Considering the paramount role of thiophene building blocks in the design of highly conjugated low band-gap 1D polymers, it is surprising that no examples of 2D polythiophene analogues are known.

We recently reported the surface-confined synthesis of epitaxially ordered 1D polythiophene (PEDOT) monolayers.¹² Here we use a similar surface-confined growth technique to synthesize monolayers of a 2D conjugated polythiophene analogue PTTA from tetrabromotetrathienoanthracene^22,23 (TBTTA, Scheme 1). The choice of TBTTA monomer was based on the expected planarity of the polymer network, the possibility of direct resonance conjugation (defined by “para” and “ortho” connectivity via the central benzene ring of TTA), and the demonstrated semiconducting properties of TTA^22,24 and other thienoacene²⁵ derivatives. The polymerization was followed by a combination of STM, high-resolution XPS, and UPS, to track the reaction path via the organometallic intermediate to the final conjugated polymer. Using DFT calculations we shed further light on the effect of topology of conjugation on the contraction of the HOMO–LUMO gap in 2D polymers.

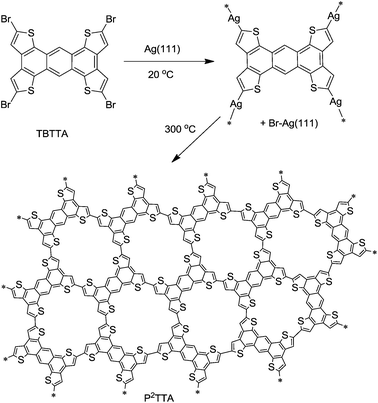Scheme 1 Ullmann polymerization of TBTTA on Ag(111).

Results and discussion

Initial polymerization attempts on Cu(111) surfaces only produced organometallic TTA intermediates which could not be transformed in a conjugated polymer, due to instability of the thiophene moiety on copper at elevated temperatures. However, sublimation of TBTTA onto Ag(111) and annealing at 300 °C for 10 min triggered the Ullmann coupling reaction, resulting in the formation of porous networks observed by STM (Fig. 1a). Although Ag is not a standard catalyst for Ullmann coupling, related polymerization of haloaromatics on Ag(111) has been reported previously.^17,18,21 As for many known 2D polymers,^19,21 the produced P²TTA networks lack long-range order. We were able to simultaneously observe the chemisorbed bromide by-product which assembles into a (√3 × √3)-R30° superstructure on Ag(111),²⁶ the organometallic intermediate, and the covalent polymer P²TTA (Fig. 1b) within the same high-resolution STM micrographs. This permitted a precise internal calibration of the images that is rarely reported in surface polymerization studies but is important for assigning the nature of bonding between the monomers. Analysis of the distances measured between the centers of mass of two adjacent building blocks shows a bimodal distribution consisting of short (1.2 ± 0.1 nm) and long (1.5 ± 0.1 nm) connections (Fig. 1c and d). The short links are in agreement with the DFT calculations for P²TTA polymer (1.21 nm) while the long ones can be reasonably attributed to an organometallic network with TTA–Ag–TTA bonding (1.48 nm).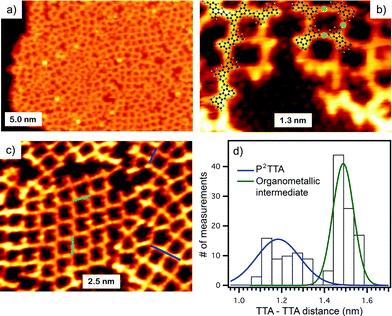

Fig. 1 (a) STM image of the P²TTA polymer on Ag(111) (U = 0.8 V, I = 0.5 nA). (b) Close-up of polymeric (left molecular model) and organometallic (right model) structures; coadsorbed atomic Br is observed in the lower portion of the image in a √3 × √3-R30° reconstruction (U = −0.8 V, I = 0.6 nA). (c) STM topograph of polymeric and organometallic structures (U = −0.7 V, I = 0.8 nA). (d) Histogram of the bond length distribution of TTA on Ag(111). Fitting of the histogram of TTA–polymer (blue) and organometallic structures (green).

HRXPS spectra are shown in Fig. 2 for the C 1s, S 2p, and Br 3d core levels, for TBTTA deposited at Ag(111) at room temperature (RT, blue) and after annealing to 300 °C (red) for 10 min. The Br 3d spectrum reveals that the first step of the reaction, dehalogenation of TBTTA, is largely complete at RT; two doublet contributions observed at RT, 3d_3/2 = 71.5 eV/3d_5/2 = 70.5 eV and 3d_3/2 = 69.0 eV/3d_5/2 = 67.9 eV originate from C–Br bonds and chemisorbed Br, respectively.²⁷ As previously demonstrated for other brominated aromatics,^17,21,28 annealing leads to the complete rupture of all C–Br bonds and the chemisorbed Br products can also be observed in STM images (Fig. 1b). As expected, the C 1s and S 2p spectra show little modification upon annealing at 300 °C. The shoulder at 285.3 eV in the C 1s spectrum can be reasonably attributed to C–Br bonds which are eliminated during annealing.

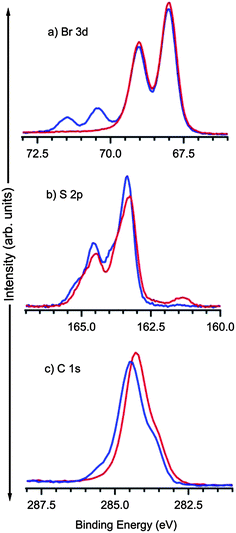Fig. 2 HRXPS spectra of Br 3d, S 2p, and C 1s core levels of TBTTA deposited on Ag(111) before (blue) and after (red) annealing at 300 °C.

The intensities of the Br, C and S core levels do not change after annealing, indicating that no desorption takes place at this temperature. The thermal stability of the thiophene unit is notable; rupture of C–S bond and subsequent chemisorption of S on silver should result in an additional doublet at lower binding energy around 161 eV to 162 eV (S 2p_3/2).²⁹ Only a very small signal (<5%) appears in this spectral region after annealing at 300 °C, indicating that almost all molecules remain intact.

The amorphous nature of P²TTA that we observe in Fig. 1 is caused by connectivity dislocations of the TTA building block (s-cis vs. s-trans, Scheme 1). These are “tolerated” due to the special symmetry of TTA connectivity (close to C₄, see ref. 30), which leads to a relatively small strain energy introduced by crystallographic defects (see ESI†).

One might expect that the observed misconnection defects in P²TTA should inhibit electronic delocalization, as is the case for 1D-conjugated systems. However, (gas phase) DFT analysis using hybrid B3LYP functional shows that even with limited order the electronic gap of P²TTA is considerably reduced. Calculations of the HOMO–LUMO gap (E_g) for various 2D oligomers of P²TTA reveal progressive reduction in the gap with increasing oligomer size (Fig. 3), a behaviour that is well established for 1D polymers,³¹ but unexplored for 2D polymers. Calculating the molecular clusters representative of the observed crystal defects shows that the topology of the connection of TTA building blocks has a minor effect on π-conjugation. All possible cyclic 2D clusters (trimers and tetramers) produce nearly the same HOMO–LUMO gap of 2.89 ± 0.05 eV (Fig. 3b and ESI†), a ∼0.6 eV reduction relative to TTA monomer.

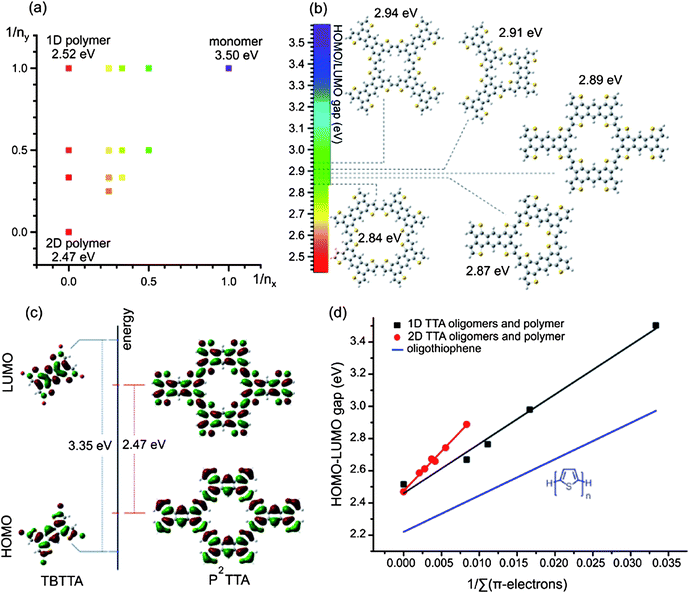Fig. 3 (a) The HOMO–LUMO gaps calculated by DFT for oligomers of different size (n_x, n_y are the number of repeat units connected along the long and short molecular axis, respectively; unsubstituted TTA was calculated as a monomer). The electronic gap for various defects is indicated in (b). (c) Topology of HOMO and LUMO for TBTTA and 2D polymer. (d) Reduction of the electronic gap in1D vs. 2D polymers as a function of inverse number of π-electrons (Σπ-electrons).

The efficiency of π-conjugation can be quantified by the rate of the decrease of the HOMO–LUMO gap with increasing number of π-electrons in the system. Such an analysis, presented in Fig. 3d, reveals that connecting TTA repeat units in 2D leads to a more efficient conjugation compared to the 1D poly-TTA and also to the parent polythiophene (Fig. 3d). The linear fit for the 1D TTA oligomers/polymer [E_g = 2.46 + 30.67/Σ(π-electrons) eV, black line] gives a similar slope to that calculated for the parent poly(2,5-thiophene) at the same level of theory [E_g = 1.82 + 29.04/Σ(π-electrons) eV, blue line³²].§ However, a ∼50% steeper slope is found for the 2D (P²TTA) case where E_g = 2.49 + 47.20/Σ(π-electrons) eV (red line). This is expected since 2D connectivity increases the number of orbital overlaps between the monomers [4 per TTA unit in P²TTA vs. 2 per TTA unit in a linearly connected poly(TTA)].

This rapid decrease of the electronic gap and the effective conjugation in the “defect clusters” suggests that the disordered P²TTA should have similar electronic state energies to those of a perfect 2D crystalline polymer. We infer that a high level of connectivity rather than long-range structural order is the necessary condition for extending conjugation and reducing electronic band gap in P²TTA. This is possible because of the design of the TTA building block, which allows for direct resonance conjugation, i.e. pathways of alternating single and double bonds,³³ in two directions (“ortho” and “para” directions vs. the central benzene ring).

To probe the occupied electronic states of the polymer overlayer we performed ultraviolet photoemission spectroscopy. Adsorption and debromination of TBTTA are accompanied by a change in the energy cut-off at high binding energy in the valence band spectra (Fig. 4a). The shift in the cut-off indicates a change of the work function of the surface, which goes from 4.9 eV for clean Ag(111) to 5.4 eV immediately after deposition of TBTTA, to 5.8 eV after annealing. This shift is largely due to charge transfer to electronegative adsorbates, as previously shown for bromine on Ag(111).²⁶ Near the Fermi level, the clean Ag surface shows the characteristic wide and flat s band and sp-derived surface state (SS) whose presence is an indicator of a pristine substrate (Fig. 4b, grey curve).³⁴

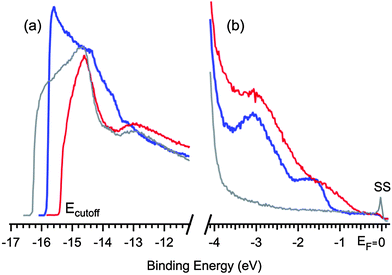Fig. 4 (a) UPS of high binding energy cut-off regions of clean Ag(111) before deposition (gray), after deposition of TBTTA (blue) and after annealing-induced polymerization (red). (b) Close up UPS of the valence bands near the Fermi level.

Immediately after the deposition of TBTTA and before annealing, new states appear at E_F −1.6 eV and E_F −3.0 eV that can be attributed to the highest occupied molecular orbitals of the (mostly) dehalogenated monomer (Fig. 4b, blue curve). Annealing the surface at 300 °C for 10 min modifies the occupied electronic states; the first peak (E_F −1.6 eV) is shifted towards the Fermi level by ≈0.6 eV, while the second peak does not significantly change its position¶ (Fig. 4b, red curve, see also ESI† for UPS at different temperatures). The magnitude of the shift towards the vacuum should be within the range 0.2–0.6 eV, depending on how the change in the work function is interpreted.|| This shift during annealing can be attributed to the polymerization, which extends the electronic π-system and reduces the electronic gap of the material and changes its interaction with the surface.

Conclusions

To conclude, we have synthesized the first two-dimensional polythiophene by surface-confined Ullmann polymerization of a tetradentate TBTTA monomer on Ag(111). High-resolution XPS analysis confirms that the reaction proceeds in two distinct steps: dehalogenation of TBTTA monomer and C–C coupling of the formed Ag-bound intermediate. While the first step is initiated upon adsorption of the monomer on the metal surface at RT, the C–C coupling forming a conjugated polymer P²TTA requires thermal activation at 300 °C. STM imaging of the annealed samples reveals extended 2D polymer networks in which the long-range order is limited by rotational disorder of the TTA unit. Interestingly, DFT predicts that the electronic gap is reduced considerably even in defective 2D polymers. The UPS measurements show that the HOMO of the molecular overlayer shifts towards the Fermi level by 0.6 eV upon polymerization. The work demonstrates that surface-confined polymerization of (hetero)aromatic building blocks is a viable route to the bottom-up synthesis of “organic graphenes” with tailored band-gaps.

Methods

Ag(111) single crystals were cleaned by repeated Ar+ sputtering and annealing cycles of 500 °C. TBTTA was synthesized as described earlier²² and purified by double sublimation in vacuum (300 °C, 10⁻¹ mbar). TBTTA was sublimed on Ag(111) from Knudsen cells (using alumina crucibles) at temperatures between 190 °C and 210 °C in UHV (p < 10⁻⁹ mbar). The sublimation temperature did not influence the experimental results. During evaporation the substrate was held at room temperature. After deposition and characterization of the room temperature TBTTA layer, the samples were annealed for 10 min to facilitate C–Br bond cleavage and subsequent polymerization. STM data were recorded using a commercial UHV system (VT-STM, Omicron GmbH) with etched tungsten and cut Pt/Ir tips, at room temperature. STM images were post-processed typically only by plane-flattening and smoothing using the free WSxM software.³⁵

High-resolution XPS measurements were performed at the Materials Science beamline at the ELETTRA synchrotron using a Phoibos 150 analyzer (SPECS GmbH). All spectra reported here were acquired in UHV with the sample held at room temperature. Photon energies of 360 eV, 250 eV and 140 eV were used to probe the C 1s, S 2p, and Br 3d core levels, respectively. The spectra were acquired after successively annealing the sample at each temperature for 10 min and are referenced to the Fermi level, which was collected after every spectrum to determine absolute binding energies. Sample degradation due to X-ray radiation was not observed. The UPS spectra were recorded with a photon energy of 21 eV with a SCIENTA 200 spectrometer (VG Scienta) in a laboratory vacuum chamber.

DFT calculations were performed on isolated molecules, small clusters, as well as polymers with periodic boundary conditions (PBC). The B3LYP functional together with the 6-31G(d) basis, as implemented in Gaussian 09 (ref. 36) set was used to optimize the geometry of the molecule/polymer. This method has proven to accurately reproduce experimental HOMO–LUMO gaps in organic semiconductors, albeit this is attributed to cancellation of errors.³¹ All atom positions were fixed in a plane and free to relax in the other two spatial dimensions. Lattice vectors were not constrained in the PBC calculations. The band gap was calculated as the difference between the HOMO and the LUMO level of the optimized structure.

Acknowledgements

This work is supported by the NSERC of Canada through Discovery Grants (FR and DFP), FQRNT through a Team Grant and the MDEIE through an international collaboration grant. We thank the Centre for Research in Molecular Modeling (CERMM) for access to computational infrastructure. LC is grateful to FRSQ for a post-doctoral fellowship. FR is grateful to the CRC program for partial salary support and acknowledges Applied Surface Science (Elsevier) for partial funding of this work. FR is grateful to the AvH Foundation for a FW Bessel Award.

Notes and references

1. K. S. Novoselov, D. Jiang, F. Schedin, T. J. Booth, V. V. Khotkevich, S. V. Morozov and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451–10453; R. Mas-Ballesté, C. Gómez-Navarro, J. Gómez-Herrero and F. Zamora, Nanoscale, 2011, 3, 20–30.
2. C. A. Palma and P. Samori, Nat. Chem., 2011, 3, 431–436.
3. J. S. Wu, W. Pisula and K. Müllen, Chem. Rev., 2007, 107, 718–747; Q. Q. Li, S. Zhang, L. M. Dai and L. S. Li, J. Am. Chem. Soc., 2012, 134, 18932–18935.
4. A. I. Cooper, Adv. Mater., 2009, 21, 1291–1295.
5. J. Sakamoto, J. Van Heijst, O. Lukin and A. D. Schlüter, Angew. Chem., Int. Ed., 2009, 48, 1030–1069; D. F. Perepichka and F. Rosei, Science, 2009, 323, 216–217.
6. A. P. Côté, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166–1170; S. Wan, F. Gandara, A. Asano, H. Furukawa, A. Saeki, S. K. Dey, L. Liao, M. W. Ambrogio, Y. Y. Botros, X. F. Duan, S. Seki, J. F. Stoddart and O. M. Yaghi, Chem. Mater., 2011, 23, 4094–4097; S. Kandambeth, A. Mallick, B. Lukose, M. V. Mane, T. Heine and R. Banerjee, J. Am. Chem. Soc., 2012, 134, 19524–19527.
7. M. E. Belowich and J. F. Stoddart, Chem. Soc. Rev., 2012, 41, 2003–2024.
8. L. Grill, M. Dyer, L. Lafferentz, M. Persson, M. V. Peters and S. Hecht, Nat. Nanotechnol., 2007, 2, 687–691; L. Lafferentz, V. Eberhardt, C. Dri, C. Africh, G. Comelli, F. Esch, S. Hecht and L. Grill, Nat. Chem., 2012, 4, 215–220.
9. G. Franc and A. Gourdon, Phys. Chem. Chem. Phys., 2011, 13, 14283–14292.
10. M. Lackinger and W. M. Heckl, J. Phys. D: Appl. Phys., 2011, 44, 464011.
11. J. A. Lipton-Duffin, O. Ivasenko, D. F. Perepichka and F. Rosei, Small, 2009, 5, 592–597.
12. J. A. Lipton-Duffin, J. A. Miwa, M. Kondratenko, F. Cicoira, B. G. Sumpter, V. Meunier, D. F. Perepichka and F. Rosei, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11200–11204.
13. J. M. Cai, P. Ruffieux, R. Jaafar, M. Bieri, T. Braun, S. Blankenburg, M. Muoth, A. P. Seitsonen, M. Saleh, X. L. Feng, K. Müllen and R. Fasel, Nature, 2010, 466, 470–473; P. Ruffieux, J. Cai, N. C. Plumb, L. Patthey, D. Prezzi, A. Ferretti, E. Molinari, X. Feng, K. Müllen, C. A. Pignedoli and R. Fasel, ACS Nano, 2012, 6, 6930–6935.
14. A. Miura, S. De Feyter, M. M. S. Abdel-Mottaleb, A. Gesquière, P. C. M. Grim, G. Moessner, M. Sieffert, M. Klapper, K. Müllen and F. C. De Schryver, Langmuir, 2003, 19, 6474–6482; Y. Okawa and M. Aono, Nature, 2001, 409, 683–684.
15. R. Tanoue, R. Higuchi, N. Enoki, Y. Miyasato, S. Uemura, N. Kimizuka, A. Z. Stieg, J. K. Gimzewski and M. Kunitake, ACS Nano, 2011, 5, 3923–3929; J. F. Dienstmaier, A. M. Gigler, A. J. Goetz, P. Knochel, T. Bein, A. Lyapin, S. Reichlmaier, W. M. Heckl and M. Lackinger, ACS Nano, 2011, 5, 9737–9745.
16. M. Abel, S. Clair, O. Ourdjini, M. Mossoyan and L. Porte, J. Am. Chem. Soc., 2011, 133, 1203–1205.
17. M. Bieri, S. Blankenburg, M. Kivala, C. A. Pignedoli, P. Ruffieux, K. Müllen and R. Fasel, Chem. Commun., 2011, 47, 10239–10241.
18. M. Bieri, M. T. Nguyen, O. Gröning, J. M. Cai, M. Treier, K. Aït-Mansour, P. Ruffieux, C. A. Pignedoli, D. Passerone, M. Kastler, K. Müllen and R. Fasel, J. Am. Chem. Soc., 2010, 132, 16669–16676.
19. N. Zwaneveld, R. Pawlak, M. Abel, D. Catalin, D. Gigmes, D. Bertin and L. Porte, J. Am. Chem. Soc., 2008, 130, 6678–6679.
20. M. O. Blunt, J. C. Russell, N. R. Champness and P. H. Beton, Chem. Commun., 2010, 46, 7157–7159.
21. R. Gutzler, H. Walch, G. Eder, S. Kloft, W. M. Heckl and M. Lackinger, Chem. Commun., 2009, 4456–4458; S. Schlögl, T. Sirtl, J. Eichhorn, W. M. Heckl and M. Lackinger, Chem. Commun., 2011, 47, 12355–12357.
22. J. L. Brusso, O. D. Hirst, A. Dadvand, S. Ganesan, F. Cicoira, C. M. Robertson, R. T. Oakley, F. Rosei and D. F. Perepichka, Chem. Mater., 2008, 20, 2484–2494.
23. W. J. Liu, Y. Zhou, Y. G. Ma, Y. Cao, J. Wang and J. Pei, Org. Lett., 2007, 9, 4187–4190.
24. F. He, W. Wang, W. Chen, T. Xu, S. B. Darling, J. Strzalka, Y. Liu and L. P. Yu, J. Am. Chem. Soc., 2011, 133, 3284–3287.
25. D. Lehnherr, A. R. Waterloo, K. P. Goetz, M. M. Payne, F. Hampel, J. E. Anthony, O. D. Jurchescu and R. R. Tykwinski, Org. Lett., 2012, 14, 3660–3663; K. Takimiya, S. Shinamura, I. Osaka and E. Miyazaki, Adv. Mater., 2011, 23, 4347–4370.
26. P. J. Goddard, K. Schwaha and R. M. Lambert, Surf. Sci., 1978, 71, 351–363.
27. M. K. Wagner, J. C. Hansen, R. Desouza-Machado, S. Liang, J. G. Tobin, M. G. Mason, S. Brandt, Y. T. Tan, A. B. Yang and F. C. Brown, Phys. Rev. B: Condens. Matter, 1991, 43, 6405–6410.
28. K.-H. Chung, B.-G. Koo, H. Kim, J. K. Yoon, J.-H. Kim, Y.-K. Kwon and S.-J. Kahng, Phys. Chem. Chem. Phys., 2012, 14, 7304–7308.
29. M. Zharnikov, J. Electron Spectrosc. Relat. Phenom., 2010, 178–179, 380–393.
30. C. Fu, F. Rosei and D. F. Perepichka, ACS Nano, 2012, 6, 7973–7980.
31. S. S. Zade, N. Zamoshchik and M. Bendikov, Acc. Chem. Res., 2011, 44, 14–24.
32. S. S. Zade and M. Bendikov, Org. Lett., 2006, 8, 5243–5246.
33. M. H. Van Der Veen, M. T. Rispens, H. T. Jonkman and J. C. Hummelen, Adv. Funct. Mater., 2004, 14, 742.
34. R. Paniago, R. Matzdorf, G. Meister and A. Goldmann, Surf. Sci., 1995, 336, 113–122.
35. I. Horcas, R. Fernández, J. M. Gómez-Rodríguez, J. Colchero, J. Gómez-Herrero and A. M. Baro, Rev. Sci. Instrum., 2007, 78, 013705.
36. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision B.01), Gaussian, Inc., Wallingford, CT, 2009.
37. T. Izumi, S. Kobashi, K. Takimiya, Y. Aso and T. Otsubo, J. Am. Chem. Soc., 2003, 125, 5286–5287.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional STM images, temperature-dependent UPS and details of DFT calculations. See DOI: 10.1039/c3sc50800e

‡ Luis Cardenas and Rico Gutzler contributed equally to this work. The authors declare no competing financial interest.

§ Experimentally determined electronic transition energies in oligothiophenes were reported to scale as hν = 2.49 + 18.84/Σ(π-electrons), hν = 2.22 + 22.56/Σ(π-electrons), hν = 2.13 + 21.84/Σ(π-electrons), depending on the substituents: ref. 37.

¶ Note that UPS peaks can incorporate more than one molecular orbital.

|| The work function varies locally across regions of P²TTA and AgBr, and the measured signal is a convolution of the entire surface. This introduces uncertainty in the alignment of the polymer vacuum level with that of the substrate. Accordingly, the HOMO in P²TTA vs. vacuum (ionization potential) is estimated to be between ∼5.9 and ∼6.8 eV. A detailed explanation of the UPS energy level alignment is provided in the ESI.†

---