A theoretical analysis of chemical bonding, vibronic coupling, and magnetic anisotropy in linear iron(II) complexes with single-molecule magnet behavior†
Mihail
Atanasov
*ab,
Joseph M.
Zadrozny
c,
Jeffrey R.
Long
c and
Frank
Neese
*a
aMax-Planck Institut fur Chemische Energiekonversion, Stifstr. 32–34, D-45470 Mulheim an der Ruhr, Germany. E-mail: mihail.atanasov@cec.mpg.de; frank.neese@cec.mpg.de
bInstitute of General and Inorganic Chemistry, Bulgarian Academy of Sciences, Acad Georgi Bontchev Str. 11, 1113 Sofia, Bulgaria
cDepartment of Chemistry, University of California, Berkeley, CA 94720, USA
First published on 25th October 2012
Abstract
The electronic structure and magnetic anisotropy of six complexes of high-spin FeII with linear FeX2 (X = C, N, O) cores, Fe[N(SiMe3)(Dipp)]2 (1), Fe[C(SiMe3)3]2 (2), Fe[N(H)Ar′]2 (3), Fe[N(H)Ar*]2 (4), Fe[O(Ar′)]2 (5), and Fe[N(t-Bu)2]2 (7) [Dipp = C6H3-2,6-Pri2; Ar′ = C6H3-2,6-(C6H3-2,6-Pri2)2; Ar* = C6H3-2,6-(C6H2-2,4,6-Pri2)2; Ar# = C6H3-2,6-(C6H2-2,4,6-Me3)2], and one bent (FeN2) complex, Fe[N(H)Ar#]2 (6), have been studied theoretically using complete active space self-consistent field (CASSCF) wavefunctions in conjunction with N-Electron Valence Perturbation Theory (NEVPT2) and quasidegenerate perturbation theory (QDPT) for the treatment of magnetic field and spin-dependent relativistic effects. Mössbauer studies on compound 2 indicate an internal magnetic field of unprecedented magnitude (151.7 T) at the FeII nucleus. This has been interpreted as arising from first order angular momentum of the 5Δ ground state of FeII center (J. Am. Chem. Soc. 2004, 126, 10206). Using geometries from X-ray structural data, ligand field parameters for the Fe-ligand bonds were extracted using a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mapping of the angular overlap model onto multireference wavefunctions. The results demonstrate that the metal–ligand bonding in these complexes is characterized by: (i) strong 3dz2–4s mixing (in all complexes), (ii) π-bonding anisotropy involving the strong π-donor amide ligands (in 1, 3–4, 6, and 7) and (iii) orbital mixings of the σ–π type for Fe–O bonds (misdirected valence in 5). The interplay of all three effects leads to an appreciable symmetry lowering and splitting of the 5Δ (3dxy, 3dx2−y2) ground state. The strengths of the effects increase in the order 1 < 5 < 7 ∼ 6. However, the differential bonding effects are largely overruled by first-order spin–orbit coupling, which leads to a nearly non-reduced orbital contribution of L = 1 to yield a net magnetic moment of about 6 μB. This unique spin–orbital driven magnetism is significantly modulated by geometric distortion effects: static distortions for the bent complex 6 and dynamic vibronic coupling effects of the Renner–Teller type of increasing strength for the series 1–5.Ab initio calculations based on geometries from X-ray data for 1 and 2 reproduce the magnetic data exceptionally well. Magnetic sublevels and wavefunctions were calculated employing a dynamic Renner–Teller vibronic coupling model with vibronic coupling parameters adjusted from the ab initio results on a small Fe(CH3)2 truncated model complex. The model reproduces the observed reduction of the orbital moments and quantitatively reproduces the magnetic susceptibility data of 3–5 after introduction of the vibronic coupling strength (f) as a single adjustable parameter. Its value varies in a narrow range (f = 0.142 ± 0.015) across the series. The results indicate that the systems are near the borderline of the transition from a static to a dynamic Renner–Teller effect. Renner–Teller vibronic activity is used to explain the large reduction of the spin-reversal barrier Ueff along the series from 1 to 5. Based upon the theoretical analysis, guidelines for generating new single-molecule magnets with enhanced magnetic anisotropies and longer relaxation times are formulated.
1 mapping of the angular overlap model onto multireference wavefunctions. The results demonstrate that the metal–ligand bonding in these complexes is characterized by: (i) strong 3dz2–4s mixing (in all complexes), (ii) π-bonding anisotropy involving the strong π-donor amide ligands (in 1, 3–4, 6, and 7) and (iii) orbital mixings of the σ–π type for Fe–O bonds (misdirected valence in 5). The interplay of all three effects leads to an appreciable symmetry lowering and splitting of the 5Δ (3dxy, 3dx2−y2) ground state. The strengths of the effects increase in the order 1 < 5 < 7 ∼ 6. However, the differential bonding effects are largely overruled by first-order spin–orbit coupling, which leads to a nearly non-reduced orbital contribution of L = 1 to yield a net magnetic moment of about 6 μB. This unique spin–orbital driven magnetism is significantly modulated by geometric distortion effects: static distortions for the bent complex 6 and dynamic vibronic coupling effects of the Renner–Teller type of increasing strength for the series 1–5.Ab initio calculations based on geometries from X-ray data for 1 and 2 reproduce the magnetic data exceptionally well. Magnetic sublevels and wavefunctions were calculated employing a dynamic Renner–Teller vibronic coupling model with vibronic coupling parameters adjusted from the ab initio results on a small Fe(CH3)2 truncated model complex. The model reproduces the observed reduction of the orbital moments and quantitatively reproduces the magnetic susceptibility data of 3–5 after introduction of the vibronic coupling strength (f) as a single adjustable parameter. Its value varies in a narrow range (f = 0.142 ± 0.015) across the series. The results indicate that the systems are near the borderline of the transition from a static to a dynamic Renner–Teller effect. Renner–Teller vibronic activity is used to explain the large reduction of the spin-reversal barrier Ueff along the series from 1 to 5. Based upon the theoretical analysis, guidelines for generating new single-molecule magnets with enhanced magnetic anisotropies and longer relaxation times are formulated.
1. Introduction
Considerable efforts have been dedicated toward the synthesis and characterization of single-molecule magnets—paramagnetic molecules displaying magnetic bistability. The motivation for these studies lies in the interest in the potential future applications for such compounds in high-density information storage,1 quantum computing,2–4 and magnetic refrigeration.5 Single-molecule magnets are open shell spin systems, which under an applied external direct current (dc) magnetic field are magnetized and remain so upon removal of the field. The phenomenon occurs at temperatures below a critical value, the blocking temperature TB. This property is intrinsically related to the existence of an energy barrier U = S2|D| for the reversal of the magnetization (D is the axial zero-field splitting parameter for the ground state of total spin S, frequently referred to as the magnetic anisotropy) by spin–phonon coupling and/or thermally assisted quantum tunneling, which usually renders the effective barrier Ueff smaller than U. The targeted large and negative quantity D implies orbital contributions to the spin from spin–orbit coupling in combination with an axial threefold or fourfold molecular symmetry (uniaxial anisotropy). Since the discovery of the effect in the celebrated Mn12 single-molecule magnet (TB ≈ 3.5 K, Ueff up to 72 K),6–8 many such systems belonging to the same family or other ones – (e.g., Mn6,9 Fe8,10 Mn4,11 and Fe4 (ref. 12–14) have been found to exhibit a similar type of magnetic behavior. It was pointed out that, with the number of spin centers being the same, since ∣D∣ ∝ 1/S2, a high value of S is not a necessary condition for large Ueff values to occur.15 It is important to note that this mathematical relationship is not a feature that arises from cluster spin coupling,16 but instead follows from the fundamental theory of the zero-field splitting interaction.17 This prediction is supported by experiment, as comparison between D values of Mnn complexes with different nuclearity (n) and variable spin-ground states (S) shows: n = 1, D = −E-mail: 2.29 cm−1, S = 2,16n = 6, D = −1.22 cm−1, S = 4 (ref. 18), n = 12, D = −0.5 cm−1, S = 10,6–8n = 6, D = −0.43 cm−1, S = 12,9 and n = 18, D = −0.13 cm−1, S = 13.19 However, in favor of systems with a large total spin, one can quote that the relaxation time (τ) for the thermally activated process is greatly enhanced by large values of S, as was pointed out on theoretical grounds (τ ∝ (S6/U3)exp(U/kBT)).20,7 It has been also shown (ref. 7, Chapter 6) that increasing total spin S leads to suppression of the quantum tunneling of the magnetization as quantified by the ground state (Landau–Zener) splitting ΔE(MS = ±S) which vanishes exponentially with ΔE (MS = ±S) ∝ [Hx/(4∣D∣S)]2S, Hx – the intrinsic transversal magnetic field.In MnIII- and FeIII-based single-molecule magnets, the magnetic anisotropy arises from favorable alignment of local D-tensors, which originate from mixing, via spin–orbit coupling, of the non-degenerate ground states of MnIII (d4, subject to static Jahn–Teller distortions) or of FeIII (d5) with excited electronic states bearing first-order orbital angular momenta. The directed, favorable alignment of local anisotropy axes in a multinuclear transition metal complex is obviously a grand synthetic challenge that cannot be considered as being solved. Hence, another strategy to achieve more negative D-values is to focus on complexes with trigonal geometries and orbitally degenerate ground states 2S+1E. Hybrid ligand scaffolds of FeII with trianionic tris(pyrrolyl-α-methyl) amines (tpa),21 for example, enforce a three-fold coordination geometry around the FeII centers, which can result in unusually large values, such as D = −40 cm−1 for [K(DME)4][Fe(tpaMes)].22 The observation of slow relaxation of the magnetization in this complex with the presence of a small dc field, with an effective relaxation barrier of Ueff = 42 cm−1, provided the first example of a mononuclear transition metal complex with single-molecule magnet-like behavior.22 Expanding on this discovery, a series of four structurally and magnetically well-documented compounds: [Fe(tpaR)]− (R = tert-butyl, mesityl, phenyl and 2,6-difluorophenyl) were reported to display similar properties tuned by a variation of the substituents R.23 In the trigonally elongated site imposed by the tpaR ligand, the (dxz,yz)1 electron configuration24 yields a contribution of ML = ±1 to the net spin moment of MS = ±2, resulting in a bistable MJ = ±3 (5/2 μB) ground state.25 The effect of the orbital moment on the magnetic anisotropy would be enhanced in hypothetical trigonally compressed tetrahedral FeX4 (5E(dx2−y2,xy)1)26 or linear FeX2 (5Δ(dx2−y2,xy)1) complexes possessing a twice larger orbital contribution to the magnetic moment of ML = ±2.27 In one complex of the latter type, Fe[C(SiMe3)3]2 (2), very large orbital momentum contributions, equivalent to adding two full S = 1/2 spins to the spin-only value of S = 2, were demonstrated by an unusually large internal hyperfine field (Hint = 151.6 T), as manifested in the Mössbauer spectra and also by dc magnetization measurement.28 A similar but less pronounced hyperfine field (Hint = 105 T) was later found in the compound Fe[N(t-Bu)2]2 (7), with the lower relative magnitude of Hint being attributed to the lower effective symmetry imposed by the non-axially symmetric ligands.29 Additionally, experimental observation of quenched orbital angular momentum induced by a bent L–Fe–L angle was shown for the two-coordinate complex Fe[N(H)Ar#]2 (Ar# = C6H3-2,6-(C6H2-2,4,6-Me3)2) (6), in contrast to the linear Fe[N(H)Ar*]2 analogue (Ar* = C6H3-2,6-(C6H2-2,4,6-Pri2)2) (4), which showed the large magnetic moment and internal hyperfine field suggestive of orbital angular momentum.30
Transition metal complexes with open d-shells have traditionally been treated by ligand field theory (LFT). As a parametrical model, LFT can only be used for the sake of interpretation, rather than for the prediction of properties. Density functional theory (DFT), being broadly used in chemistry for the prediction of ground state geometries and properties of electronic states in molecules, is well suited for systems with orbitally non-degenerate ground states (mono-determinantal wavefunctions). In contrast, the applicability of the theory is severely limited in cases where a superposition of charge distributions described by several rather than one Slater determinants (multi-determinantal wavefunctions) is mandatory for a realistic description. Systems with orbital degeneracy, which are the subject of the present study, clearly fall into this latter category. In this context, we mention, but will not further discuss, pragmatic approaches that allow one to deduce ligand field parameters from DFT calculations.31–34 Magnetic systems of the type considered here are still too large to be treated with the available implementations of variational configuration interaction (CI) type approaches that cover both static and dynamic correlation effects. Even the application of complete active space self-consistent field method (CASSCF)35 in conjunction with second-order perturbation corrections to the CASSCF energies (such as the complete active space perturbation theory, CASPT2,36–40 or the N-electron-Valence-Perturbation Theory NEVPT2 (ref. 40–44)) are very challenging to apply to systems with more than one hundred atoms in conjunction with at least triple-zeta basis sets. The potential of using such approaches to calculate spin Hamiltonian parameters of mono-15,45–47 and bi-48–50 and even trinuclear transition metal complexes51 was recently demonstrated. Additionally, a general first-principles method to calculate the spin-dependent part of the energies of ground and excited multiplets for larger polynuclear complexes was proposed.52
In this study, we apply the recent implementation of the CASSCF and NEVPT2 methods in the ORCA53,54 program package to perform large-scale correlated calculations on the electronic structure and magnetic properties of a series of complexes of high-spin FeII with linear FeX2 (1–5, 7) and bent FeN2 (6) cores (see ref. 29 and 55 for depictions of the structures of these molecules). This work was performed in parallel with an ongoing experimental study of their magnetic properties reported in the preceding companion paper.55 We use the protocol developed and applied for the interpretation, analysis, and prediction of the magnetic properties of the closely related series of [Fe(tpaR)]− compounds published recently.46 The energies of the lowest spin-levels, which govern the magnetic behavior of the complexes, and their ligand field analysis provide important insights into the respective influences of chemical bonding and static and dynamic vibronic coupling on the observed spin-reversal barriers.
This paper is divided into two parts. In the first part, the basic theory and the computational scheme are outlined. These include the ligand field background for analyzing the ab initio results and the static and dynamic vibronic coupling model employed for the interpretation of the magnetic data. In the second part, the results involving analysis of the chemical bonding, magnetic properties, and the ligand field are described.
2. Computations and theory
2.1. Computations
The electronic energy levels for the complexes were computed using geometries from the crystal structures of 1 and 3,552,564 and 6,305,57 and 7.29 The computational protocol for the calculation of CASSCF/NEVPT2 wavefunctions/energies was previously described in ref. 55. The calculation of the magnetic properties—isothermal magnetizations and magnetic susceptibilities—using these wavefunctions and energies were detailed in a recent publication.46 In order to study vibronic coupling effects, starting with complex 2, possessing trigonal symmetry and the pseudo Jahn–Teller effect in complexes 1 and 3–7, we employed the truncated model complexes Fe(CH3)2, Fe(NH2)2 and Fe(OH)2 (see Fig. 1).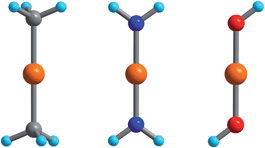 | ||
| Fig. 1 Fe(CH3)2, Fe(NH2)2, and Fe(OH)2 DFT-optimized model complexes with D3d, D2h, and C2h geometries employed in the analysis of the FeII–ligand chemical bond and the pseudo Jahn–Teller activity of the d6 configuration of FeII; Orange, gray, blue, red and cyan spheres represent Fe, C, N, O and H atoms, respectively. | ||
2.2. Ligand field considerations
The 5E ground state of FeC2 (complex 2, accounting for the trigonal symmetry due to the next-nearest neighbors) is described by a total spin S = 2 arising from two singly occupied orbitals e(dx2−y2) or e(dxy) in addition to the half-filled d5 shell. These states give rise to ML = ±2 eigenfunctions of the angular momentum operator![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) z (eqn (1)).
z (eqn (1)).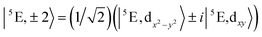 | (1) |
Note that the states ∣5E,2〉 and ∣5E,−2〉 cannot mix under the action of ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) x and
x and ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) y since ML changes by ±1 unit of angular momentum through
y since ML changes by ±1 unit of angular momentum through ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) x and
x and ![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) y. Mixing of these states with the higher-lying 5E(dxz,yz)1 (ML = ±1), levels is possible. However, the latter are much higher in energy and will be neglected here. The effects of these states on the magnetic properties will be discussed in Section 3.2.3 and 3.3. In this approximation, the spin–orbit coupling (SOC) operator ĤSOC assumes the form of eqn (2).
y. Mixing of these states with the higher-lying 5E(dxz,yz)1 (ML = ±1), levels is possible. However, the latter are much higher in energy and will be neglected here. The effects of these states on the magnetic properties will be discussed in Section 3.2.3 and 3.3. In this approximation, the spin–orbit coupling (SOC) operator ĤSOC assumes the form of eqn (2).
ĤSOC = −(ζ/4)![[L with combining circumflex]](https://www.rsc.org/images/entities/i_char_004c_0302.gif) zŜz zŜz | (2) |
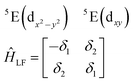 | (3) |
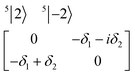 | (4) |
The physical origin of δ1 and δ2 will be subject to a thorough analysis in Sections 3.2.3 and 3.3. The Hamiltonian ĤSOC + ĤLF + ĤZ (ĤZ = the Zeeman operator) represented in the ∣ML = ±2, MS = ±2, ±1,0〉 basis, as well as energy and g-tensor expressions (normalized to a m = ±1/2 pseudo spin)25 are given in the ESI.† The [Fe(tpaR)]− single-molecule magnets from ref. 22 and 23 possess trigonally elongated geometries and a 5E(dxz,yz)1 ground state. Here, SOC leads to two lowest magnetic levels A1 and A2 which are split by the trigonal symmetry. Being an equal mixture of total angular momenta with MJ = +3 and MJ = −3, these states carry no magnetic moments. The complexes of the present study are completely different. The ground state for linear complexes FeX2 is 5E(dxy,dx2−y2)1 (complex 2, FeC2, can be ascribed as a trigonally compressed one), which under the action of SOC leads to a E(MJ = ±4) magnetic ground state. For both types of FeII-based single-molecule magnets, and within the given approximation, geometric distortions described by 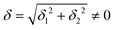 do not cause a splitting of the ±MJ(MS ≠ 0) pairs, leaving A1 and A2 in the former type of complexes accidentally degenerate. Quite differently, ±MJ levels with MS = 0 undergo a first-order splitting (2δ) depending on the magnitude of the distortion (in energetic sense,
do not cause a splitting of the ±MJ(MS ≠ 0) pairs, leaving A1 and A2 in the former type of complexes accidentally degenerate. Quite differently, ±MJ levels with MS = 0 undergo a first-order splitting (2δ) depending on the magnitude of the distortion (in energetic sense, 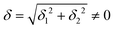 ) but not on its direction (i.e., on φ, tgφ = δ2/δ1). From eqn (1)–(4), the origin of the magnetic anisotropy arises; without off-axial distortions
) but not on its direction (i.e., on φ, tgφ = δ2/δ1). From eqn (1)–(4), the origin of the magnetic anisotropy arises; without off-axial distortions 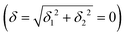 there is a 1
there is a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixing between the |dx2−y2〉1 and |dxy〉1 sublevels of the 5E term by SOC, and this leads to the addition of an orbital angular momentum of 2 μB to the net spin S = 2 moment (4 μB). Focusing on the |MJ = ±4〉 ground state magnetic pair, an Ising-type anisotropy with gz = 12 and gx,y = 0 (δ ≪ ζ) is obtained. In the limiting case of very large distortions (δ ≫ ζ), the latter reduces to the spin-only values of gz = gx = gy = 8.
1 mixing between the |dx2−y2〉1 and |dxy〉1 sublevels of the 5E term by SOC, and this leads to the addition of an orbital angular momentum of 2 μB to the net spin S = 2 moment (4 μB). Focusing on the |MJ = ±4〉 ground state magnetic pair, an Ising-type anisotropy with gz = 12 and gx,y = 0 (δ ≪ ζ) is obtained. In the limiting case of very large distortions (δ ≫ ζ), the latter reduces to the spin-only values of gz = gx = gy = 8.
2.3. The 5E⊗ε Renner–Teller effect
Unlike bent complex 6 and linear complex 7, the pseudolinear FeX2 cores in 1–5 possess inversion symmetry. Therefore, no linear vibronic coupling with the off-centric normal modes, ε, which serve to distort the linear geometry to a bent structure is possible. The energy lowering and energy splitting of the 5E(dx2−y2dxy)1 ground state of the FeII complexes due to Renner–Teller (RT) vibronic coupling is described by eqn (5),63–69 in which the nuclear coordinates Qx and Qy are components of the ε mode (eqn (6)), ρ is the RT radius (eqn (7)), and φ (eqn (8)) defines the direction of the distortion.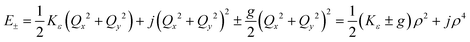 | (5) |
| Qx = ρcos φ; Qy = ρsin φ | (6) |
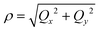 | (7) |
| tgφ = Qy/Qx = δ2/δ1 | (8) |
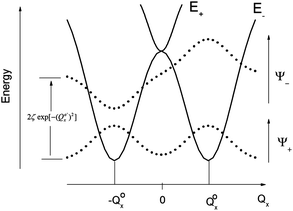
The parameters Kε and j describe the effect of the harmonicity and anharmonicity, respectively (i.e., two terms due to forces which tend to preserve the linear geometry). The g-term quantifies the vibronic force that leads to distortions and, accordingly to a splitting (g(Qx2 + Qy2)) of the 5E(dx2−y2,dxy)1 ground state (eqn (5)). Depending on whether Kε > g or Kε < g, two different situations are encountered (see Fig. 2).
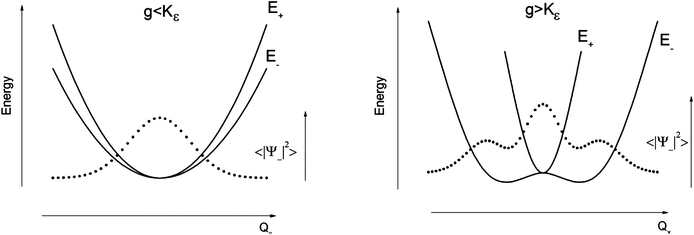 | ||
| Fig. 2 Variable adiabatic potential energy surface of a FeIIX2 complex with a doubly degenerate 5Δ ground state with respect to the off-centric displacement Qx in the case of the 5Δ⊗π Renner–Teller effect: weak coupling – term splitting without instability (left); strong coupling – dynamic instability; nuclear probability distributions 〈|ψ−|2〉 are shown with dotted lines. | ||
In the first case, no new minima in the adiabatic ground state potential energy surface (APES) arise; however, the adiabatic approximation is violated by the vibronic mixing (via a term gQxQy) between the two sublevels. The other extreme, Kε < g, leads to a negative curvature for the lower surface, and therefore to dynamical instability. As a consequence, new minima on the APES corresponding to bent structures arise. Energy expressions, derived in the ESI,† allow us to relate the parameters Kε, j, and g with the geometry of the minimum of the adiabatic ground state potential surface (APES) (ρmin), the Renner–Teller stabilization energy ERT, and the energy of the vertical Franck–Condon transition EFC from the lower to the upper sheet of the APES (at the position of the minima) in terms of g, Kε and j. In turn, using these expressions g–Kε and j have been deduced from DFT values of ρmin and ERT, obtained from a truncated FeC2 model complex (see Fig. 1). An estimate for Kε = ħωε is obtained using he corresponding Zn(CH3)2 analog, which lacks RT-activity. This leads to the parameters ħωε = 131 cm−1, g = 461 cm−1, and j = 8.2 cm−1. Energy eigenvalues and eigenfunctions of vibronic levels were calculated using a Hamiltonian of the form:
| Ĥ = Ĥvib + ĤSOC + ĤRT + ĤZ | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 and harmonic vibrational |χj(Q′x〉·|χk(Q′y〉 wavefunctions up to level nvib (see ESI† for details). Isothermal magnetic susceptibilities and magnetizations were calculated employing the representation of ĤZ in the basis ∣Ψ〉 and making explicit use of the calculated eigenvectors following procedures outlined previously.46
10 and harmonic vibrational |χj(Q′x〉·|χk(Q′y〉 wavefunctions up to level nvib (see ESI† for details). Isothermal magnetic susceptibilities and magnetizations were calculated employing the representation of ĤZ in the basis ∣Ψ〉 and making explicit use of the calculated eigenvectors following procedures outlined previously.46
2.4. Ligand field analysis of the ab initio results
Ab initio results were analyzed by mapping the ab initio multireference wavefunctions and energies onto ligand field theory in the manner developed in detail in ref. 70. In this treatment, the LF Hamiltonian is viewed as an effective Hamiltonian that acts on the subspace of states originating from a given dn-configuration of a transition metal subject to perturbations from surrounding ligands. For an FeII center without including SOC, the d6 configuration spans 5, 45 and 50 electronic states with total spins of S = 2, 1, and 0, respectively. The LF Hamiltonian within this basis is expressed in terms of a LF 5 × 5 matrix for one d-electron and atomic like parameters of interelectronic repulsion B and C. The energies of the five S = 2 states for FeII do not depend on the parameters B and C, and the LF matrix for the five S = 2 levels can be identified with the 5 × 5 LF matrix for one d-electron. From the possible parameterization offered by the LFT, the angular overlap model (AOM) finds most favor among chemists.71–73 This model expresses the matrix elements of the 5 × 5 LF matrix in terms of parameters defined for well-aligned d-orbitals of σ- and π-type, eλ (λ = σ, πc, πs) multiplied by factors Fλω(θl, φl, ψl) that depend solely on the angular geometry of the ligands (l, described by the Euler angles θl, φl, ψl). AOM energy expressions for a FeX2 complex with C2v symmetry (with a choice of Cartesian axes as shown in Fig. 3) have been derived and listed in the ESI.† The parameters eσ, eπc, and eπs quantify the energy destabilization of the FeII d-orbitals due to their negative overlap with the corresponding well-aligned ligand orbitals of σ- and π-type (see Fig. 4), where anisotropy of the interactions of π-type, eπc and eπs, is taken into account (see Fig. 3 and 4 for the definition of the angle θ and the AOM parameters, respectively). For a linear FeX2 complex (θ = 0°) with dominating ligand donor functions of eσ > eπc = eπs = eπ > 0, all parameters being positive in this case, the orbital energy order δ(dx2−y2, xy) < π(dxz,yz) < σ(dz2) results: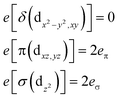 | (10) |
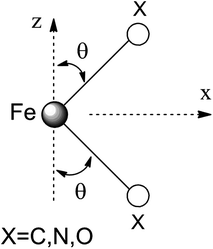 | ||
| Fig. 3 Cartesian axes choice and geometrical parameters for the FeX2 core in 1–7. | ||
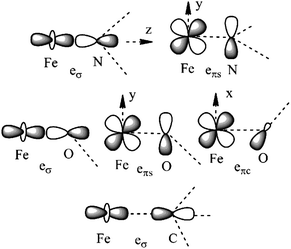 | ||
| Fig. 4 Interactions approximating the FeII–ligand bond in FeN2 complexes 1, 3–4, 6, and 7 (upper), FeO2 complex 5 (middle), and FeC2 complex 2 (lower), and their angular overlap model parameterizations. | ||
AOM parameters are traditionally deduced from a fit to electronic d–d transitions observed in absorption and emission spectra of transition metal complexes. This procedure is often (although not always) challenging, because the number of parameters is too large to allow for a unique determination. Recently, a procedure was proposed allowing one to deduce the LF parameters from ab initio calculations,70 which can be summarized as follows. First, focusing on the S = 2 states, the 5 × 5 CI matrix in the basis of the Slater Determinants (SDs) built up from the metal-3d based molecular (CASSCF) orbitals is calculated. Focusing on SDs with MS = S = 2, we note that each single SD is a spin eigenfunction (i.e., SDs and configuration state functions (CSFs) are identical in this case). With the output of the electronic structure program, the CASSCF eigenvalues (EICASSCF) and eigenfunctions CCASSCF(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, I) (I = 1
5, I) (I = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5) are directly available. Let us denote the diagonal matrix constructed from EICASSCF with ΛCASSCF(EICASSCF,I = 1
5) are directly available. Let us denote the diagonal matrix constructed from EICASSCF with ΛCASSCF(EICASSCF,I = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5). We then deduce the LF matrix HLFT = {HLFTIJ,I,J = 1
5). We then deduce the LF matrix HLFT = {HLFTIJ,I,J = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5} using the transformation:
5} using the transformation:
| HLFTCASSCF = CCASSCFΛCASSCFC†CASSCF | (11) |
Dynamic correlation effects are introduced via diagonal corrections to ΛCASSCF as provided by second-order many-body perturbation theory in form of the NEVPT2 method (ΔΛNEVPT2, eqn (13)). The AOM parameters (pλ) are then obtained by a least-squares fit based on eqn (14), where the matrices HAOM and HLFTNEVPT2 have been transformed into the traceless forms HAOMb(pλ) and HLFTNEVPT2,b, respectively.
| HLETNEVPT2 = CCASSCFΛNEVPT2C†CASSCF | (12) |
| ΛNEVPT2 = ΛCASSCF + ΔΛNEVPT2 | (13) |
| HAOMb(pλ) = HLFTNEVPT2,b | (14) |
Adopting the one-electron parameters without changes, the parameters B and C were obtained from the computed energies of the spin–forbidden transitions, which, in the present case, are the transitions from the 5E ground state to the triplet ligand field excited states. Finally, using eσ, eπ, B, and C and switching on SOC, we fix the value of ζ from the computed energies of the 5E ground state SOC split sublevels. These calculations were performed through an interface between the ORCA program and the well-established ligand field program package AOMX.74
3. Results and discussion
3.1. Chemical bonding and vibronic activity of two-coordinate complexes of FeII
It follows from X-ray data that the FeX2 cores in complexes 1–5 and 7 are linear. However, due to the nearest and next-nearest neighboring atoms of the FeII center, the electron density distribution deviates from idealized D∞h symmetry. It has been shown that the second coordination sphere affects metal–ligand bonding and results in dramatic changes to the color and magnetism of transition metals in solid matrices.75 Of immediate interest is the extent to which the next-nearest atoms in the coordination sphere of the FeII center affect the magnetic properties of complexes 1–7. Depending on the number of strong bonds formed by the donor atoms C, N, or O (see Fig. 4), these complexes can be subdivided into three classes. With the C donor involved in three strong bonds to neighboring Si atoms, and neglecting hyperconjugation, there are no ligand orbitals available for FeII–C interactions of π-type in complex 2. The local symmetry around the Fe–C bond is C3v. In complexes 1, 3, 4, 6, and 7, with N-amido donors, there is a plane defined by N and the directly connected two atoms X forming N–X bonds; here X represents C and Si (1), C and H (3, 4, and 6), or two C atoms (7). As the FeII center is located in the same plane as the N(sp2)-donor atoms and their nearest neighbors, there is a well-defined direction for the π-interactions between FeII center (according to Fig. 4, the appropriate iron orbital is dyz) and the amido π-electron pair of the same symmetry (defined here as πs type in AOM). Since the Fe–N bond can be considered as weaker than the N–X bonds, we assign the local Fe–ligand bond a pseudosymmetry of C2v. Finally, in complex 5 there are two donor lone-pairs; one of these pairs, similar to Fe–N, has the symmetry appropriate for πs-type overlap with the out-of-the Fe–O–C plane dyz orbital, while the other pair (located within the Fe–O–C plane) is available for πc-type overlap with the metal dxz orbital. This arrangement defines a local Cs pseudosymmetry.Molecular orbital energies and Fe orbital percentages, deduced from quasi restricted DFT calculations performed on truncated Fe(CH3)2, Fe(NH2)2 and Fe(OH)2 model complexes (see Fig. 1) are listed in Table 1. Focusing on Fe(CH3)2, we note that, as expected, the Fe–C bonding is solely governed by strong Fe–C σ-interactions, with the main participation coming from Fe 4s and 3dz2 orbitals; other orbitals (dxz, dyz, and dxy) are non-bonding due to a lack of ligand orbitals of appropriate symmetry. The interaction of the metal centered 3dz2 and 4s orbitals with the ligands gives rise to bonding, antibonding, and weakly antibonding MOs, as illustrated for Fe(NH2)2 at the left of Fig. 5. It is the intermixing of 4s into the nominally 3dz2 Fe-based orbital (as strong as 20% for Fe(CH3)2 and 16% for Fe(NH2)2) which converts this orbital from strongly antibonding (typical for octahedral complexes) to weakly antibonding in the FeX2 complexes 1–7.
| Fe(CH3)2 | Fe(NH2)2 | Fe(OH)2 |
|---|---|---|
| a bd – bonding; ab – antibonding; nb – non-bonding; quasi restricted orbitals from DFT optimized model complexes (see ESI† for more details regarding these calculations); orbital electron occupation numbers are given in square brackets. | ||
| σ-type orbitals | σ–πc type orbitals | σ–πc type orbitals |
| −7.45(bd): 11(4s) + 29(3dz2) [2] | −9.55(bd): 8(4s) + 20(3dz2) [2] | −11.86(bd): 5(4s) + 12(3dz2) [2] |
| −5.40(weakly ab): 20(4s) + 50(3dz2) + 16(3dx2−y2) [2] | −4.91(weakly ab): 16(4s) + 48(3dz2) + 27(3dx2−y2) [1] | −7.84(bd): 1(4s) + 6(3dz2) − 5(4s) + 13(3dxz) [2] |
| −5.37(nb): 4(4s) + 10(3dz2) + 10(3dxz) + 73(3dx2−y2) [1] | −4.06(nb): 8(4s) + 16(3dz2) + 72(3dx2−y2) [1] | −5.24(weakly ab): 17(4s) + 57(3dz2) + 16(3dxz) + 3(3dx2−y2) [1] |
| −0.32(ab): 47(4s) + 13(3dz2) [0] | −0.56(ab): 42(4s) + 15(3dz2) [0] | −4.72(weakly ab): 7(4s) + 6(3dz2) + 71(3dxz) + 2(3dx2−y2) [1] |
| −4.33(nb): 2(4s) + 3(3dz2) + 95(3dx2−y2) [2] | ||
| −1.08(ab): 49(4s) + 17(3dz2) [0] | ||
| π-type orbitals | πs-type orbitals | πs-type orbitals |
| −5.69(nb): 86(3dxz) + 10(3dx2−y2) [1] | −5.94(bd): 37(3dyz) [2] | −7.33(bd): 24(3dyz) [2] |
| −5.65(nb): 95(3dyz) [1] | −3.58(ab): 66(3dyz) [1] | −4.38(ab): 78(3dyz) [1] |
| δ-type orbital | πc-type orbital | δ-type orbital |
| −4.60(nb): 99(3dxy) [2] | −4.88(nb): 96(3dxz) [1] | −5.14(nb): 100(3dxy) [1] |
| δ-type orbital | ||
| −4.99(nb): 100(3dxy) [1] | ||
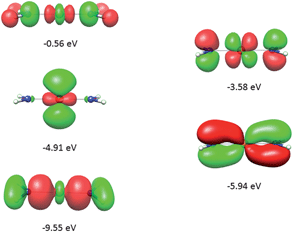 | ||
| Fig. 5 Molecular orbitals (DFT, PBE-functional) with contribution from the 3d-orbitals of FeII as exemplified using the Fe(NH2)2 model complex. From bottom to top, the σ-interactions (left) are bonding and weakly and strongly antibonding, while the πs-interactions (right) are bonding and antibonding. | ||
As will be shown below, this has an important effect on the magnetic properties. In contrast to Fe(CH3)2, the out-of-plane type of π-bonding (πs) is essential in Fe(NH2)2 and Fe(OH)2. Here, a strong mixing between the FeII(dyz) and the corresponding ligand functions takes place, giving rise to the bonding and antibonding MOs, as illustrated for Fe(NH2)2 at the right in Fig. 5. The Cs symmetry of the Fe–O–H moiety leads to a mixing of the metal-based orbitals dz2, dxz, and dx2−y2 (all behave totally symmetric with respect to the Fe–O–H symmetry plane). In a strictly linear complex, such as Cl–Fe–Cl, these orbitals would have σ, πc, and δc character, respectively (see eqn (10)). However, based on the dz2, dxz, and dx2−y2 FeII orbital percentages (57%, 71%, and 95% in the MOs with energies −5.24, −4.72 and −4.33 eV, respectively) the assignment given by the AOM (eqn (10)) is roughly correct.
Linear (D∞h) FeX2 complexes with a 5Δ(dx2−y2,xy) ground state are intrinsically unstable with respect to geometric distortions since they are Renner–Teller active. Thus, bending of these complexes can cause the strictly non-bonding dx2−y2,xy orbitals to become involved in bonding/antibonding interactions due to mixing of these orbitals with the π(dxz, yz) and σ(dz2) orbitals and their ligands counterparts. The reduction in total energy is the driving force for such distortions. Calculating geometries from first principles for such complexes is still far from trivial. First, at the point of orbital degeneracy and close to it, DFT is not applicable, while CASSCF is usually not accurate enough and many body perturbation approaches, such as NEVPT2, suffer from a lack of availability of analytic gradients, at least for larger molecules. Second, a ground state APES with two minima at distorted geometries is stationary at the point of degeneracy, implying that the energy gradient at that point is zero. Therefore, while keeping to DFT, use of a distorted structure as the starting geometry in a geometry optimization is advisable. Third, the APES is highly anharmonic, implying the requirement of higher-order polynomials (up to order 8 for the cases studied below) in the Herzberg–Teller series66 expansion to model the energy of the 5Δ(dx2−y2,xy) APES.
DFT geometry optimizations of FeX2 (X = CH3−, NH2−, and OH−) starting from bent geometries resulted in a bent structure for Fe(CH3)2 with an X–Fe–X angle of 144.5°, but resulted in linear structures for Fe(NH2)2 and Fe(OH)2 (see Table 2). Based on a normal mode analysis, all geometrically optimized structures with linear FeX2 cores were calculated to be stable with respect to X–Fe–X bending. For the reasons stated previously (breakdown of the adiabatic approximation for closely-lying electronic levels), numerical values of the harmonic X–Fe–X frequencies are questionable. However, based on the very low values of these frequencies (see Table 2), they are still strongly indicative of soft mode behavior. The quantification of the effect of the latter on the magnetic properties will be analyzed below (see Section 3.2.2). A scan of the ground state energy versus the X–Fe–X angle for Fe(CH3)2 and the analogous Mn(CH3)2 and Zn(CH3)2 complexes with half filled (d5) and closed shell (d10) electronic configurations for the MII center, respectively, is shown in Fig. 6. To avoid the point of degeneracy, in these calculations X–M–X angles higher than 170° were excluded.
| R | 2(90°−θ) | E − | ρ min | ν[δ(X–Fe–X)] (cm−1) | |
|---|---|---|---|---|---|
| Zn(CH3)2 | 1.952 | 180 | 0 | 0 | 136 |
| Mn(CH3)2 | 2.064 | 158.3 | −233 | 1.80 | 124 |
| Fe(CH3)2 | 2.006 | 144.5 | −964 | 2.50 | 134 |
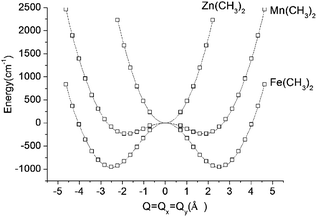 | ||
| Fig. 6 Adiabatic potential energy (in cm−1) surfaces (APES) for M(CH3)2 (M = Mn, Fe, Zn) model complexes, illustrating dynamical instabilities in the cases of Mn(CH3)2 (3d–4p pseudo Jahn–Teller coupling) and Fe(CH3)2 (3d–4p pseudo Jahn–Teller coupling superimposed by a (stronger) 5E⊗ε Renner–Teller effect). DFT optimized M–ligand bond distances are almost unchanged along the distortion path and have been fixed at their values at the minimum of the APES (see Table 2). The APES has been constructed by varying the angle θ (see Fig. 3 for its definition) between 45° and 80° in steps. Solid lines reproduce the data in terms of a polynomial of the degree 8: P(1)·Q8 + P(3)·Q6 + P(5)·Q4 + P(7)·Q2 + P(9) with the following values of the coefficients P(1), P(3), P(5), P(7), and P(9): 0.0288, −1.7513, 43.0557, −362.0133, and 953 for Fe(CH3)2; 0.0181, −1.1037, 27.7868, −150.9680, and 232.8404 for Mn(CH3)2; 0.0514, −0.6800, 1.0285, 459.3716, and −234.2324 for Zn(CH3)2. Here, Q is expressed by the variable angle θ at fixed values of the metal–ligand bond distance R (from Table 2) according to Q = 2R(90° − θ)(π/180). | ||
A least-squares fit to the data with a polynomial of degree 8 (solid lines in Fig. 6) allows one to deduce the energy of the linear geometry via interpolation. Remarkably, not only Fe(CH3)2 but also Mn(CH3)2 is stabilized by bending. It is interesting to note, that [FeCl2]+ (which is isoelectronic with Mn(CH3)2) is calculated by DFT to be distorted as well, with an X–Fe–X angle of 132.2° and with an appreciably large stabilization energy of 1250 cm−1. The origin of this effect is found in the different roles played by the 4px,y valence orbitals of FeII in the linear and bent configurations, respectively (see ESI†). Being non-bonding (due to their high energy separations from the ligand orbitals) and of different parity (compared to 3d), the 4px,y AOs are essentially non-bonding in linear Mn(CH3)2. As illustrated in the ESI,† bending leads to a considerable mixing of 4px,y into 3dyz,xz, because both orbitals transform under the same irreducible representation in C2v. This mixing, or partial hybridization, leads to an increase of both σ- and, to a lesser extent, π-type metal–ligand overlap. The effect can be considered to be analogous to 3d–4s mixing for linear geometries but is energetically less pronounced. The extra electron in the dx2−y2,xy orbital pair leads to an enhancement of the distortion (ρmin) and an additional energy stabilization (E−) as the comparison between Mn(CH3)2 (ρmin = 1.80 Å, E− = −233 cm−1) and Fe(CH3)2 (ρmin = 2.50 Å, E− = −964 cm−1) shows (see Fig. 6 and Table 2). Using data in Table 2, parameters of the vibronic coupling model were derived as specified in Section 2.3.
3.2. Electronic (vibronic) levels and magnetic properties
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200–20
200–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1 than that of the lowest triplet state.
600 cm−1 than that of the lowest triplet state.
| Electronic statea | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| a Experimental transition energies from near-IR d–d spectra of 1 are listed in square brackets. | |||||||
| 5E(dxy)1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| (dx2−y2)1 | 164 | 92 | 241 | 381 | 222 | 1246 | 766 |
| 5E(dxz)1 | 3726 | 4760 | 2080 | 2372 | 5004 | 8829 | 6820 |
| (dyz)1 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 468 [9400] 468 [9400] |
4799 | 8156 | 8057 | 7124 | 2409 | 7649 |
| 5A(dz2)1 | 7068 [7700] | 5087 | 9190 | 9623 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 002 002 |
9907 | 8409 |
| 3A | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 023 023 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 622 622 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 944 944 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 826 826 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 813 813 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 176 176 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 947 947 |
| E(1) | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.002 | 0.001 | 0.013 | 0.022 | 0.004 | 0.078 | 0.020 | |
| A1,A2(1) | 189.8 | 195.2 | 176.4 | 158.4 | 183.9 | 78.1 | 122.3 |
| 190.4 | 195.3 | 179.8 | 163.2 | 185.6 | 84.9 | 123.3 | |
| E(2) | 322.8 | 353.0 | 286.6 | 242.7 | 300.9 | 111.2 | 172.2 |
| 485.8 | 444.6 | 529.1 | 624.6 | 521.4 | 1347.5 | 937.6 | |
| E(3) | 612.8 | 602.0 | 632.0 | 704.4 | 632.8 | 1373.2 | 985.7 |
| 625.0 | 603.8 | 646.6 | 710.1 | 641.5 | 1384.4 | 986.8 | |
| A1,A2(2) | 810.1 | 799.7 | 822.0 | 870.4 | 820.4 | 1464.7 | 1106.7 |
| 810.3 | 800.0 | 822.5 | 870.7 | 820.5 | 1464.8 | 1106.8 | |
The electronic absorption spectrum of 1 in 2-methyltetrahydrofuran consists of a broad asymmetric band centered at 8500 cm−1 (see ESI†). Its simulation with two Gaussian envelopes led to the identification of the energies of the two expected d–d transitions centered at 7700 and 9400 cm−1, respectively. These numbers compare well with the calculated CASSCF/NEVPT2 transition energies (6936 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 062 cm−1). We accordingly assign these as electronic transitions from 5E(dx2−y2,xy)1 to 5A1(dz2)1 and the 5E(dyz)1 split component of the 5E(dyz,xz)1 state, with the lower energy transitions assigned to the 5E(dxz1) component and the even lower transitions within the 5E(dx2−y2,xy)1 SOC sublevels manifold lying outside the spectrally accessible energy range. Deviations from axial symmetry (see Section 3.1) lead to a non-relativistic ground state splitting that is lowest for 2 (92 cm−1) and increases from 4 (381 cm−1) to 7 (766 cm−1) and 6 (1246 cm−1). The 5E ground state splitting for complexes 1, 3, and 5 (164, 241, and 222 cm−1, respectively) are intermediate between those of 2 and 4 and thus lie outside the observed trend. This behavior will be analyzed below. The magnetic sublevels (classified according to the D3 symmetry encountered in complex 2) arising from the 5E ground state after SOC are also included in Table 3. The ordering of these sublevels and their relative energy separations closely follows the energy expressions derived from a simplified treatment (see ESI†) in which only the in-state 5E SOC is considered. This behavior reflects the dominant role of SOC, which widely suppresses low-symmetry splitting of all sublevels pairs with non-zero ML. In particular, splitting of the ground state magnetic sublevels |ML = +2, MS = +2〉 and |ML = −2, MS = −2〉, through mixing with the topmost state |ML = −2, MS = +2〉 and |ML = +2, MS = −2〉, respectively, is prevented by the large energy gap (2ζ ≈ 800 cm−1) between the two sublevels. This splitting is more pronounced for the first excited states |ML = +2, MS = +1〉 and |ML = −2, MS = −1〉, which interact with their respective |ML = −2, MS = +1〉 and |ML = +2, MS = −1〉 counterparts, because the former states are separated by a twofold smaller energy (ζ ≈ 400 cm−1). Being not affected by SOC, the state E |ML = ±2, MS = 0〉 is the only one that is strongly influenced by off-axial distortions; its splitting is identical to that of non-relativistic 5E ground state (see Table 3).
062 cm−1). We accordingly assign these as electronic transitions from 5E(dx2−y2,xy)1 to 5A1(dz2)1 and the 5E(dyz)1 split component of the 5E(dyz,xz)1 state, with the lower energy transitions assigned to the 5E(dxz1) component and the even lower transitions within the 5E(dx2−y2,xy)1 SOC sublevels manifold lying outside the spectrally accessible energy range. Deviations from axial symmetry (see Section 3.1) lead to a non-relativistic ground state splitting that is lowest for 2 (92 cm−1) and increases from 4 (381 cm−1) to 7 (766 cm−1) and 6 (1246 cm−1). The 5E ground state splitting for complexes 1, 3, and 5 (164, 241, and 222 cm−1, respectively) are intermediate between those of 2 and 4 and thus lie outside the observed trend. This behavior will be analyzed below. The magnetic sublevels (classified according to the D3 symmetry encountered in complex 2) arising from the 5E ground state after SOC are also included in Table 3. The ordering of these sublevels and their relative energy separations closely follows the energy expressions derived from a simplified treatment (see ESI†) in which only the in-state 5E SOC is considered. This behavior reflects the dominant role of SOC, which widely suppresses low-symmetry splitting of all sublevels pairs with non-zero ML. In particular, splitting of the ground state magnetic sublevels |ML = +2, MS = +2〉 and |ML = −2, MS = −2〉, through mixing with the topmost state |ML = −2, MS = +2〉 and |ML = +2, MS = −2〉, respectively, is prevented by the large energy gap (2ζ ≈ 800 cm−1) between the two sublevels. This splitting is more pronounced for the first excited states |ML = +2, MS = +1〉 and |ML = −2, MS = −1〉, which interact with their respective |ML = −2, MS = +1〉 and |ML = +2, MS = −1〉 counterparts, because the former states are separated by a twofold smaller energy (ζ ≈ 400 cm−1). Being not affected by SOC, the state E |ML = ±2, MS = 0〉 is the only one that is strongly influenced by off-axial distortions; its splitting is identical to that of non-relativistic 5E ground state (see Table 3).
Using all of the SOC split sublevels of 5E ground state parentage and their associated wavefunctions, magnetizations (M) and susceptibilities (χT) were calculated for 1–6. NEVPT2 values for χT and M for complexes 1 and 2 are both in good agreement with experimental data (see Fig. 7 and ESI†). The direct-current magnetization measurement at 1.85 K of the same crystalline sample as used for the Mössbauer study28 yielded Mz = 5.82 μB, which is very close to the NEVPT2 result (5.98 μB) for a sample of crystallites fully aligned with the applied magnetic field. The experimental data given in ref. 55 are also in good agreement with the NEVPT2 result; however, here the NEVPT2 results have been converted to a powder average. The error for the data in ref. 28 is less than 3% away from the maximal achievable magnetic moment of 6 μB (gM′J, g = 2, M′J = 3).
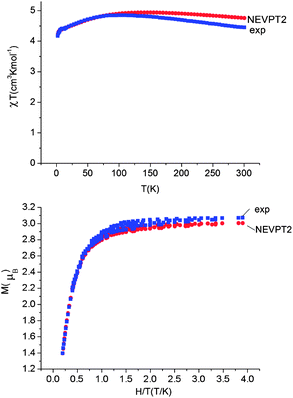 | ||
| Fig. 7 Upper: experimental (blue squares) and calculated (NEVPT2, red circles) magnetic susceptibility data for complex 1 in the temperature range from 2 to 300 K under a static applied dc field of 1000 Oe. Lower: experimental (squares) and calculated (NEVPT2, red circles) isothermal magnetization M vs. H/T for complex 1. | ||
The situation changes for complexes 3–5 and 6. Here, the comparison between theory and experiment for χT and M (see Table 4 and ESI†) shows that the calculated values are systematically larger than the experimental ones. The same complexes 3–5 display a drastic reduction (by as much as two to three orders of magnitude) in their relaxation times, as compared to 1 and 2.55 One could speculate that spin–orbit coupling (ζ), which is usually slightly overestimated in post Hartree–Fock calculations,46 might be responsible for the observed deviations. However, using empirically reduced values of ζ (accounting for the relativistic nephelauxetic effect17 in the crudest possible way with an orbital reduction factor k) does not alleviate the problems. Thus, focusing on complex 3, both χT and M can only be brought into agreement with experiment by using an anomalously low orbital reduction factor k = 0.6 (see ESI†). Hence, the deviations between theory and experiment must have a different origin, as will be discussed in detail below.
| Complex | 1 Exp(calc.) | 2 Exp(calc.) | 3 Exp(calc.) | 4 Exp(calc.) | 5 Exp(calc.) | 6 Exp(calc.) |
|---|---|---|---|---|---|---|
| a M HTLF (high-temperature low-field): T = 5 K, H = 1 T. b M LTHF (low-temperature high-field): T = 1.8 K, H = 7 T. c Marks the appearance of a static limit corresponding to a value of f close to 0. | ||||||
| (χT)300K | 4.45(4.76) | 4.78(4.82) | 3.35(4.35) | 3.37(4.76) | 3.19(4.87) | 2.87(3.99) |
| f 300K | 0c | 0c | 0.133 | 0.132 | 0.162 | |
| (χT)2K | 4.17(4.22) | 4.33(4.30) | 3.73(4.80) | 2.88(4.30) | 2.87(4.46) | 2.03(3.44) |
| f 2K | 0c | 0c | 0.082 | 0.099 | 0.099 | |
| M HTLF | 2.47(2.48) | 1.50(1.42) | 1.23(1.44) | 0.96(1.43) | 0.92(1.47) | 0.74(1.17) |
| M LTHF | 3.00(3.00) | 3.24(3.04) | 2.74(3.10) | 2.14(3.11) | 2.06(3.15) | 1.93(2.88) |
| E(MJ = ML + MS,k, l) = −(ζ/4)MLMS + (k + l + 1)ħω | (15) |
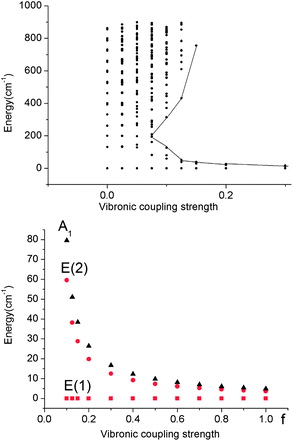 | ||
| Fig. 8 Upper: vibronic energy levels from calculations on a Fe(CH3)2 model complex in the energy range below 900 cm−1versus the vibronic coupling strength parameter f scaling the vibronic parameters g = 461 cm−1 and j = 8.19 cm−1 of eqn (5). Lower: low energy range of the five lowest vibronic states responsible for the magnetic behavior (ℏωε = 131 cm−1). The ground state E(1) and the lowest excited state E(2) responsible for the energy barrier Ueff of the Orbach relaxation mechanism are depicted in red. | ||
A mixing of these wavefunctions for non-zero f leads to the opening of a gap between the five lowest levels and the other excited states (see Fig. 8, upper) and this gap increases with f. Thus, at values of f close to 0.1, a discontinuity in the spectrum of the magnetic excitations is predicted to occur.
As illustrated by the dependence of the z-components of the g-tensor (see Fig. 9), the opening of the gap leads to a dramatic decrease in the orbital contributions to the net magnetic moment and a concomitant change in the magnetic properties. From the energies and term assignments of the five lowest magnetic levels (see Fig. 8, lower), we deduce that the level ordering (E < E < A1) in a dynamic Renner–Teller regime is completely different than the one that applies in the static limit. In both cases the lowest sublevels remain doubly degenerate. Thus, the main difference is that the electronic degeneracy gives way to a vibronic one. One can qualitatively understand this behavior
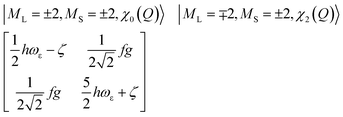 | (16) |
 , Fig. 2, left).
, Fig. 2, left).
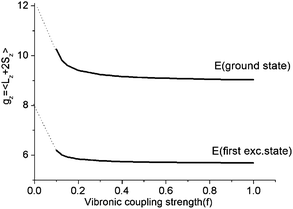 | ||
| Fig. 9 Dependence of the z-components of the g-tensor in the lowest five thermally accessible magnetic states on the vibronic coupling strength parameter f. | ||
Thus, there are negligible contributions of the ML = ∓2 orbital moments of opposite sign to the ground state magnetic pair ML = ±2. The probability distribution for the nuclear motion is close to Gaussian type |χo(Q′)|2 (see Fig. 2, left) with a maximum at the undistorted (linear) nuclear configuration. Let us now assume the other extreme: the strong Renner–Teller coupling limit of f = 1. Here, there is nearly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixing between the orbital moments ML = +2 and ML = −2, which are now better approximated by the |dx2−y21〉 and |dxy1〉 spatial components and ground vibronic state described by two ground state harmonic oscillator wavefunctions, displaced by 2Q′o in configurational space relative to the undistorted geometry,
1 mixing between the orbital moments ML = +2 and ML = −2, which are now better approximated by the |dx2−y21〉 and |dxy1〉 spatial components and ground vibronic state described by two ground state harmonic oscillator wavefunctions, displaced by 2Q′o in configurational space relative to the undistorted geometry,
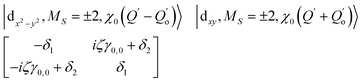 | (17) |
 | ||
| Fig. 10 Adiabatic potential energy surface in the strong coupling limit (f = 1). The inversion splitting of spin–orbit vibronic levels rationalizing the reduction of the orbital magnetic moments is schematically presented. | ||
As illustrated by the dependence of χT on f (see Fig. 11, as well as the ESI† for a similar but less monotonic effect on the magnetization), for intermediate Renner–Teller couplings, which imply 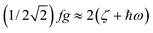 , Fig. 2, right), a discontinuous change of the vibronic wavefunction and reduction of the orbital momenta takes place. Under these conditions, the nominal ground ∣ML = ±2,MS = ±2, χ0(Q′)〉 and excited ∣ML = ±2,MS = ±2, χ2(Q)〉 wavefunctions start to mix strongly, thus leading to large reductions of the orbital moments. Nuclear probability distributions also imply superposition between ground state harmonic wavefunctions (χ0(Q′)) with higher excited vibrational states (in the given illustration with the second harmonic χ2(Q′), Fig. 2). This induces large amplitude motions and dynamic distortions. Such a behavior may not apply to the situation in the solid state where, due to crystal packing forces (δ1, δ2 in eq. 17 ≠ 0), transitions from dynamically averaged distorted configurations to statically distorted structures can take place. This point of view is supported by the observation that the FeC2 core in complex 2 was reported to be linear, while a derivative with a bent FeC2 geometry in Fe(Ar)2 (C–Fe–C = 159.34(6)°) has also been reported.57 Likewise, while a distorted X-ray structure of 6 was reported, the EPR spectrum of the same compound in solution is only compatible with a more linear complex.30 It is remarkable that by using this dynamic Renner–Teller coupling model, room temperature values of χT for complexes 2–5 could be fitted with a single adjustable parameter f that is confined to the narrow range between f = 0.142 ± 0.015 (see Table 4). At lower temperatures, however, smaller values of f (0.082–0.099) were required to fit the susceptibility. One would expect the influence of vibronic coupling to scale with temperature, and therefore f should increase with increasing T. Likewise, at lower temperatures, one would expect the value of f to decrease in concert with the increasing influence of the spin–orbit coupling, which attempts to mitigate the vibronic effects in order to sustain the orbital angular momentum, a so-called inverse Jahn–Teller effect.58–60
, Fig. 2, right), a discontinuous change of the vibronic wavefunction and reduction of the orbital momenta takes place. Under these conditions, the nominal ground ∣ML = ±2,MS = ±2, χ0(Q′)〉 and excited ∣ML = ±2,MS = ±2, χ2(Q)〉 wavefunctions start to mix strongly, thus leading to large reductions of the orbital moments. Nuclear probability distributions also imply superposition between ground state harmonic wavefunctions (χ0(Q′)) with higher excited vibrational states (in the given illustration with the second harmonic χ2(Q′), Fig. 2). This induces large amplitude motions and dynamic distortions. Such a behavior may not apply to the situation in the solid state where, due to crystal packing forces (δ1, δ2 in eq. 17 ≠ 0), transitions from dynamically averaged distorted configurations to statically distorted structures can take place. This point of view is supported by the observation that the FeC2 core in complex 2 was reported to be linear, while a derivative with a bent FeC2 geometry in Fe(Ar)2 (C–Fe–C = 159.34(6)°) has also been reported.57 Likewise, while a distorted X-ray structure of 6 was reported, the EPR spectrum of the same compound in solution is only compatible with a more linear complex.30 It is remarkable that by using this dynamic Renner–Teller coupling model, room temperature values of χT for complexes 2–5 could be fitted with a single adjustable parameter f that is confined to the narrow range between f = 0.142 ± 0.015 (see Table 4). At lower temperatures, however, smaller values of f (0.082–0.099) were required to fit the susceptibility. One would expect the influence of vibronic coupling to scale with temperature, and therefore f should increase with increasing T. Likewise, at lower temperatures, one would expect the value of f to decrease in concert with the increasing influence of the spin–orbit coupling, which attempts to mitigate the vibronic effects in order to sustain the orbital angular momentum, a so-called inverse Jahn–Teller effect.58–60
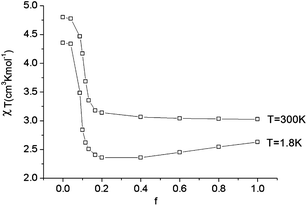 | ||
| Fig. 11 Calculated values of χT (H = 1000 Oe) at 1.8 and 300 K as a function of the vibronic coupling parameter f. | ||
The proposed underlying nuclear dynamics of these linear X–Fe–X complexes would be expected to show up in the ellipsoids of thermal motion.76–79 An inspection of the low-temperature (T = 90(2) K for 1 and 3–7 and 100(2) K for 2) structures of complexes 1–6 indeed lends support the notion of vibronic activity in the first coordination sphere of the FeII centers. Temperature- and field-dependent structural studies should give more detailed information about this interesting phenomenon.
Two critical remarks should be made regarding the quantitative aspects of the Renner–Teller model presented in Sections 2.3 and 3.2.2. First, as has been stated in Section 3.1, the actual symmetry of all complexes 1–7 is not D∞h but lower, generally C1, and the electronic ground state, assumed to be electronically doubly degenerate (5E) is actually split. Thus, any vibronic activity of the kind discussed in Section 3.2.2 should be viewed as being of the pseudo Jahn–Teller type. Second, the actual molecular complexes are large and possess a huge number of degrees of freedom. Thus, many vibrations of ε-type may be involved in vibronic coupling, which leads to an unapproachable multimode dynamic pseudo Jahn–Teller coupling problem.
Employing complex 6 as a model and following the general theory of Ham,80,81 the effect of the static distortion on the magnetic properties can be accounted for by considering vibronic coupling and lower symmetry ligand fields (strain) as independent perturbations. The latter is quantified by the strain energy matrix Hstrain deduced here directly from the mapping of the NEVPT2 results for the quintet state manifold onto ligand field theory (see ESI†). The dependence of the magnetic susceptibility on the vibronic coupling strength under the strain influence for complex 6 is depicted in Fig. 12. It follows from these results that the combined action of lowered symmetry and vibronic coupling have a crucial effect in reducing the magnetic susceptibility from its static limit (with a calculated room temperature value of χT ≈ 3.95 cm3K mol−1 for f = 0) to values closer (χT = 3.05 cm3K mol−1 for f = 1) to the experimentally reported value of χT = 2.87 cm3K mol−1.55 The observed (and calculated) Curie–Weiss behavior of 6 results from the even population of the lowest lying vibronic energy levels (at 0.0, 0.051, 2.32, 3.05, and 3.61 cm−1), which are well-separated from other excited vibronic spin states.
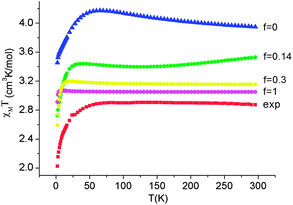 | ||
| Fig. 12 Experimental χT data (H = 1000 Oe) for complex 6 (red squares) and theoretical values calculated using a model80,81 accounting for the simultaneous presence of the low-symmetry ligand field (strain) and vibronic coupling of variable strength f (where f = 0 corresponds to the static limit of no vibronic coupling). | ||
The combination of reduced symmetry and vibronic coupling also has a crucial effect on the magnetic relaxation time, τ. Low-temperature (T = 2 K) field-dependent magnetic relaxation data have been used to quantify contributions to τ from quantum tunneling (τt) and direct relaxation (τd) mechanisms according to eqn (18) (ref. 55) (see Table 3 for a list of B1, B2, and AH2 deduced from a least square fit to such data). Expressions connecting B1, B2, and A with tunnel-splitting of the ground state magnetic pair ΔE, the effective g-tensor value along the easy direction (gz), and the
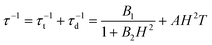 | (18) |
| B1 = ΔE2τ1/2 | (19) |
| B2 = (βgzτ1/2)2 | (20) |
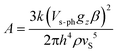 | (21) |
Adopting a realistic value of 1.20 km s−1 for vS,83 the mass density ρ from X-ray structures and the ab initio values of gz (static, 1–2, or vibronic, 3–5), τ1/2, ΔE and Vs–ph were deduced (see Table 5) using the reported values B1, B2, and A (Table 3).55 There is no clear trend for the changes of τ1/2 across the series 1–6, which also differ from the lifetimes τo due to the thermally activated Orbach relaxation mechanism.
| τ 1/2 (s) | ΔE (cm−1) | V s–ph (cm−1) | τ o (s)1 | U eff(cm−1)1 | |
|---|---|---|---|---|---|
| a g z = 11.66, computed from CASSCF + NEVPT2 using the X-ray geometry and ρ = 1.149 g cm−3. b g z = 11.95, computed from CASSCF + NEVPT2 using the X-ray geometry and ρ = 1.118 g cm−3. c g z = 9.60, calculated with a dynamic vibronic coupling model using f = 0.15 and ρ = 1.182 g cm−3. d g z = 9.60, calculated with a dynamic vibronic coupling model using f = 0.15 and ρ = 1.127 g cm−3. e g z = 9.60, calculated with a dynamic vibronic coupling model using f = 0.15 and ρ = 1.203 g cm−3. | |||||
| 1 | 1.48 × 10−10 | 6.93 × 10−7 | 0.017 | 1 × 10−11 | 181 |
| 2 | 2.27 × 10−11 | 5.10 × 10−7 | 0.024 | 4 × 10−9 | 146 |
| 3 | 4.93 × 10−6 | 0.002 | 0.045 | 5 × 10−9 | 109 |
| 4 | 4.27 × 10−11 | 2.85 × 10−6 | 0.078 | 4 × 10−8 | 104 |
| 5 | 7.43 × 10−7 | 0.003 | 0.133 | 3 × 10−7 | 43 |
Impressively, there is clear trend of the spin–phonon coupling parameter Vs–ph, which increases from 1 to 5 (see Fig. 13). With one exception, complex 4, the tunnel-splitting energy ΔE follows the same trend. It increases dramatically ongoing from 1 and 2 to complexes 3 and 5. Not unexpectedly, no relaxation time data could be recorded for complex 6. The low-symmetry ligand field in this complex leads to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixing (via the matrix element of 475 cm−1) between the |ML = +2> and |ML = −2> electronic levels, in addition to a mixing of |ML = 0> in the |ML = ±2> pair due to mixing via the off-diagonal matrix element of 1602 cm−1. Both effects reduce the orbital moments and facilitate quantum tunneling of the magnetization. Similar effects on the relaxation times for complexes 1–5 emerge from the plots of the corresponding matrix elements (see ESI†). A second effect on the relaxation time at elevated temperature is due to the narrowing of the energy gap between the ground and the excited magnetic sublevels (see experimentally deduced values of Ueff included in Table 5 in comparison with the energy gap between the energy levels marked with red circles in Fig. 8, lower). The anisotropy-reducing effect of the low symmetry decreases on further symmetry lowering from nearly C2v (in 1, 3, and 4 with one lone pair) to C1 (in 5 with two lone pairs) and can be ascribed to bonding effects arising from the next-nearest neighboring atoms of the FeII centers (see Section 3.3).
1 mixing (via the matrix element of 475 cm−1) between the |ML = +2> and |ML = −2> electronic levels, in addition to a mixing of |ML = 0> in the |ML = ±2> pair due to mixing via the off-diagonal matrix element of 1602 cm−1. Both effects reduce the orbital moments and facilitate quantum tunneling of the magnetization. Similar effects on the relaxation times for complexes 1–5 emerge from the plots of the corresponding matrix elements (see ESI†). A second effect on the relaxation time at elevated temperature is due to the narrowing of the energy gap between the ground and the excited magnetic sublevels (see experimentally deduced values of Ueff included in Table 5 in comparison with the energy gap between the energy levels marked with red circles in Fig. 8, lower). The anisotropy-reducing effect of the low symmetry decreases on further symmetry lowering from nearly C2v (in 1, 3, and 4 with one lone pair) to C1 (in 5 with two lone pairs) and can be ascribed to bonding effects arising from the next-nearest neighboring atoms of the FeII centers (see Section 3.3).
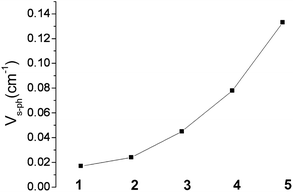 | ||
| Fig. 13 Variation of the spin–phonon coupling parameter Vs–ph across the series from 1 to 5. | ||
We note, however, that the changes of these matrix elements across 1–6 are not monotonic and do not follow the observed trend in τ across the series.55 The reasons for such differences may be twofold: (i) thermal ellipsoids of the L–Fe–L moieties (see Fig. S1† in ref. 55) show that contributions from vibronic coupling may be present in all complexes, and (ii) secondary interactions of the FeII center with next nearest neighboring C atoms might be important. This is particularly relevant in 3–6, where π-electron lobes due to C(sp2) atoms from the phenyl substituents make relatively short contacts providing σ/π overlap to the FeII centers (Fe⋯C = 2.588, 2.765, 2.792, and 2.817 Å, decreasing from 6 to 5 to 4 to 3, respectively). Such interactions are absent in 1 and 2 where Fe–C(sp3) contacts occur at much longer distances (2 × 3.621, 2 × 3.587 Å in 1 and 2 × 3.275, 2 × 3.369, and 2 × 3.504 Å in 2).
3.3. Ligand field analysis of the ab initio results
The AOM parameters eσ, eπc, and eπs derived from the CASSCF + NEVPT2 results are listed in Table 6. Compared to other studies,70 standard deviations between LF (calculated using the AOM parameter set) and ab initio matrix elements here are in the expected range and show the adequacy of the LF approach for the studied complexes. The AOM parameters are consistent with values resulting from the fit of the spectrum of the linear complex FeCl2 (eσ = 3500 cm−1, eπ = 2300 cm−1).84| Parameter | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Fe(CH3)2 | Fe(NH2)2 | Fe(OH)2 |
|---|---|---|---|---|---|---|---|---|---|---|
| a Standard deviations between calculated (using the listed set of AOM parameters) and NEVPT2 matrix elements within the quintet state manifold. | ||||||||||
| e σ | 3351 | 2513 | 4418 | 4512 | 5255 | 5291 | 3977 | 1799 | 2478 | 3560 |
| e πs | 5137 | 2364 | 3973 | 3860 | 3397 | 3414 | 4530 | 1757 | 5354 | 4478 |
| e πc | 1828 | 2364 | 932 | 1018 | 2439 | 884 | 2321 | 1757 | 1454 | 2921 |
| σ(AOM)a | 349 | 68 | 344 | 464 | 493 | 794 | 189 | 431 | 223 | 136 |
| ΔE(5A1–5B1) | 442 | 18 | 373 | 346 | 108 | 308 | 291 | 15 | 519 | 221 |
| E(5A1) σ, πc | 660 | 310 | 512 | 497 | 444 | 440 | 607 | 236 | 717 | 599 |
| E(5B1) πs | 248 | 292 | 139 | 151 | 336 | 132 | 316 | 221 | 198 | 378 |
The origin of the anomalously low calculated values of the parameter eσ (in particular for the FeC2 complex 2) originates from the stabilizing effect of 4s–3d mixing, which reduces largely the Fe–X σ-antibonding interactions in the nominally dz2 type MO (see Section 3.1). Because of this stabilizing effect (and in contrast to the results obtained for the series of [Fe(tpaR)]− complexes),22,23 a correlation between eσ and the Lewis ligand basicity is not observed (see ESI†). Thus, the lowest value of eσ in complex 2 (see Table 6) correlates with the greatest Lewis basicity for the C ligator. Table 6 also reports AOM parameters for the truncated model complexes Fe(CH3)2, Fe(NH2)2 and Fe(OH)2. From a comparison between the sets of parameters of the model complexes with those of 1–7, we can conclude that there is a significant tuning of the ligand field strength for each type of donor, C, N, and O, by the structure (substituents) of the extended ligand framework. As follows from the parameter ratio eπs/eπc ≫1, there is a large π-bonding anisotropy for the amido ligands in 1, 3, 4, 6, and 7, and the large values of eπs characterize the amido ligands as strong π-donors. For N being involved in two strong bonds to neighbor atoms, there are no orbitals for π bonding in the Fe–NR2 plane. One should therefore expect eπc to be zero. That this is not the case implies that there are large electrostatic contributions to the LF parameters for FeN2 complexes 1, 3, 4, 6, and 7. A similar conclusion can be made based on the non-zero eπs = eπc = eπ parameters deduced from the ab initio results for complex 2 (compare with the zero overlap due to such kind of interaction emerging from Table 1). It was pointed out in Section 3.1 that bonding anisotropy reduces the symmetry from approximately C3v (for 2 and Fe(CH3)2) to approximately C2v in the FeN2 cores of 1, 3, 4, 6, and 7. Values of the energy Δ(5A1–5B1) – the splitting between the upper and lower components of the 5E ground terms, were computed with AOM parameters (see Table 6) assuming an arbitrary but fixed value of the angle θ = 15°. This energy correlates directly with the term g(Qx2 + Qy2) (see eqn (5)) and thus with the effect of vibronic pseudo Jahn–Teller coupling on the magnetic anisotropy (Section 3.2). This can be seen in Fig. 14, which shows that the energies of 5A1 and 5B1 increase upon bending because the two states are being destabilized by σ, πc, and πs antibonding interactions, respectively. Thus, the splitting Δ(5A1–5B1) appears as a combination of the effects of σ, πc, and πs antibonding interactions. Distortions also lead to a lowering of the orbital moments because of mixing of the 5A1(dz2 ∼ |2,0>) state into the 5A1 dx2−y2 ∼ |2,2>+|2,−2> state. In addition, s–d mixing further lowers 5A1(dz2) and contributes to the reduction of the orbital angular momentum. Finally, at acute values of the angle θ, an avoided crossing leads to a switch from a 5A1(dx2−y2) to a 5A1(dz2) electronic ground state. This switch quenches the orbital angular momentum (Table 7).
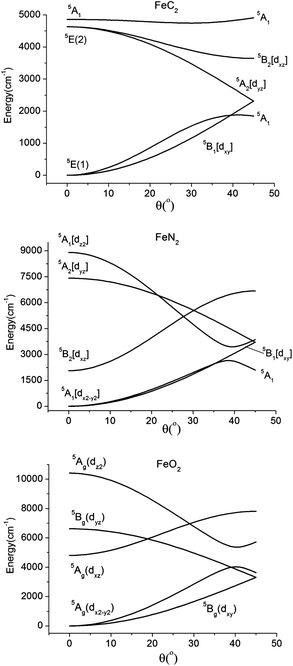 | ||
| Fig. 14 Dependence of the quintet term energies on the distortion angle θ (see Fig. 3) for linear complexes with FeC2 (C2v, top), FeN2 (C2v, middle), and FeO2 (C2h, lower) cores, as obtained using the set of parameters for complexes 2, 4, and 5, respectively (see Table 6). | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| a Standard deviations σ between the energies of electronic multiplets, calculated using the given set of parameters B, C (deduced from a least squares fit to energies of the ground state quintet to triplet excited states transitions) and ζ (from a least squares fit to the spin–orbit split terms of the 5E ground state) and the NEVPT2 (B and C) and NEVPT2 + SOC (ζ) results. | |||||||
| B | 1512 | 1418 | 970 | 822 | 1090 | 602 | 1833 |
| C | 3245 | 3564 | 3782 | 3965 | 3734 | 4364 | 3030 |
| σ(B, C) | 1012 | 402 | 1003 | 1072 | 952 | 746 | 325 |
| ζ | 413 | 407 | 426 | 459 | 420 | 822 | 591 |
| σ(ζ) | 44 | 2 | 66 | 114 | 60 | 274 | 225 |
The parameterization given by the AOM with diagonal energy terms described by σ (for M(dz2)–X(pz)), in-plane (πc for M(dxz)–X(px)), and out-of-plane (πs for M(dyz)–X(py)) antibonding interactions between M and X, is only justified in complexes with strictly linear (eπc = eπs = eπ) or two-fold (C2v) symmetry for each Fe–X fragment. This situation can change in complexes with composite ligands, where, say, carbon atoms attached to a given sp2-type N donor atom can affect its lone pair from being optimally aligned for σ-bonding with the metal. The physical implications of such bent bonds (or “misdirected valence”) have been discussed by Liehr in relation to the optical rotatory power in tri- and digonal dihedral compounds.85,86 As judged by the standard deviations in Table 6, the overall success of the standard LF model (where misdirected valence is neglected) with AOM parameters eσ, eπs, and eπc is quite high. Yet, as expected for complexes 5, 4, and the bent complex 6, all possessing Cs or even lower (C1) Fe–X pseudosymmetries, standard deviations (493, 464, and 794 cm−1, respectively) are larger than for the complexes with the more regular structures: FeC2 (C3v, σ = 68 cm−1) and, to a lesser extent, the FeN2 complexes 1, 3, and 7 (C2v, σ = 349, 344, and 189 cm−1, respectively). The extra lone pair located in the Fe–O–R plane of the FeO2 complex 5 (see Fig. 4) has the proper symmetry for both σ and πc overlap. Keeping to the linear O–Fe–O geometry, this is expected to create an off-diagonal matrix element 〈dz2∣Vlone_pair∣dxz〉 = 2eσπc and to affect the nominal values of eσ and eπc. As has been pointed out by Gerloch et al.,87,88 in the general case of a Fe–X bond with pseudosymmetry C1, up to six AOM parameters for a given ligand have to be introduced (extended AOM, diagonal eσ, eπs, eπc and off-diagonal eσπc, eσπc, eπcs).
While there is little hope in obtaining much insight from such an over-parameterized model (the data base from optical spectroscopy is too limited in order to unambiguously extract the model parameters; see ref. 87 and 88 for attempts to do this), it is worthwhile to reconsider the more complete ab initio results in the light of this concept. Numerical data (see ESI†) given by the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mapping of the ab initio NEVPT2 data onto LFT for complex 5 leads to the following conclusions:
1 mapping of the ab initio NEVPT2 data onto LFT for complex 5 leads to the following conclusions:
(i) There is full support from ab initio theory for the expected σ–π mixing between the ∣ddz2〉 and ∣ddxz〉 orbitals. The energetic effect of the C2v to the Cs symmetry lowering is calculated not to be very large (eσπc = 420 cm−1) but comparable to that of the symmetry lowering from Cs to C1 (∣ddxz〉–∣ddyz〉, eπcs = 409 cm−1).
(ii) Bonding anisotropy implicated by a lowered actual symmetry causes 5E(dx2−y2, dxy) in-state mixing (eδπc = 217 cm−1) and first-order splitting (eδc − eδs = 138 cm−1), effects that are ignored in conventional AOM modeling. Such mixings are counterintuitive and must be electrostatic in origin.
(iii) The largest off-diagonal terms are calculated between 5E(dx2−y2, dxy) and 5A1(dz2) (eσδc = −1302 cm−1, eσδs = −828 cm−1), but are ignored in the extended AOM. These terms lead to a mixing of 5A1 into 5E(dx2−y2, dxy) and thus reduce the orbital momenta (see above). However, the 5A1(dz2)–5E(dx2−y2, dxy) energy separation is relatively large (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 483 cm−1), which somewhat lessens this effect.
483 cm−1), which somewhat lessens this effect.
While not being favorable for the single-molecule magnet behavior of the considered complexes, spatial asymmetries leading to matrix elements of the type 〈dz2∣Vlone_pair∣dxz〉 = 2eσπc are responsible for chirality leading to natural circular dichroism (NCD) in chelate complexes with highly-symmetric MXn (n = 2–6) cores. The combination of this property with that of a high-spin FeII center, providing coexistence of spatial asymmetry (chirality leading to a parity break) and magnetization (causing a break of time reversal symmetry) can lead to optically active magnets (or magneto-chirality) and to magneto-chiral dichroism with non-polarized light.89 As magnetic chiral media are intrinsically magnetoelectric, electrical reading/writing in the magnetic state is possible, a feature that is currently being pursued in the rising field of molecular multiferroic materials. With a bistable ground magnetic state E and A1 and A2 excited states, as found in complexes 1–7, a combination with chirality in properly selected enantiopure derivatives seems a very promising direction for further exploration.
4. Conclusions
(1) CASSCF/NEVPT2 calculations of the electronic multiplets of two-coordinate FeII complexes with C, N, and O donor ligands have been used to analyze the bonding within complexes 1–7 and to trace the effects of the next-nearest atoms to the metal center on the Fe-ligand bonds. Angular overlap model parameters deduced from ab initio data, along with DFT calculations performed on linear Fe(CH3)2, Fe(NH2)2, and Fe(OH)2 model complexes, demonstrate that the respective properties are strongly affected by the supporting ligand scaffold (N(CSi) in 1, C(Si)3 in 2, N(HC) in 3, 4, and 6, O(C) in 5, and N(C)2 in 7). Due to these bonds, the approximate local Fe–X pseudosymmetry is lowered from C3v for Fe–C(sp2) to C2v for Fe–N(sp2) to Cs for Fe–O(sp), leaving one, two and three ligand lone pairs for bonding to FeII, respectively. The bonding anisotropy, increasing in this sequence, causes a splitting of the doubly degenerate ground and excited state levels assumed respectively as 5Δ(dx2−y2, dxy) and 5Π(dxz, dyz) for linear FeX2 complexes.(2) Spin orbit coupling, here accounted for by quasidegenerate perturbation theory (QDPT) in the basis of the non-relativistic CASSCF wavefunctions and diagonal NEVPT2 corrections to the CASSCF energies, leads to magnetic sublevels of 5E parentage. Low symmetry splitting of the doubly degenerate E ground state magnetic sublevel pair, caused by the bonding anisotropy, is strongly suppressed by SOC, but shows up to the full extent in the second doubly degenerate excited magnetic sublevel pair. Using static geometries taken from the crystal structures, low-temperature (T = 1.8–5 K) isothermal magnetization data and magnetic susceptibilities (for 1 and 2) could be reasonably well reproduced.
(3) A dynamic 5E⊗ε vibronic coupling model of the Renner–Teller type has been employed to explain why the experimentally determined magnetization and susceptibility data for complexes 3–6 are systematically lower than the theoretically predicted results, assuming only static geometric distortions. The model incorporates three model parameters (g, j, and ħωε, corresponding to the Renner–Teller vibronic coupling constant, anharmonicity, and harmonic energy parameters, respectively) that were adjusted to the adiabatic ground state potential of a distorted Fe(CH3)2 model complex. Vibronic reductions of orbital contributions to the net magnetic moment exceed by far the orbital moment quenching induced by covalency. Following this model, it was possible to fit the low (T = 2 K) and room (T = 300 K) temperature magnetic susceptibility data for complexes 2–6 in terms of a single parameter f, the vibronic coupling strength, which can vary between 0 (no vibronic coupling) and 1 (strong vibronic coupling). The best fit values for f fall into a narrow range at 0.142 ± 0.015. The given range of f nearly coincides with borderline of a discontinuous change from weak (f < 0.1) to strongly (f > 0.1) coupled electronic and nuclear motions, where vibronic coupling is being quenched by SOC (f < 0.1) or vice versa (f > 0.1). It is conceivable that in a solid, large amplitude movements will readily drive the system from a dynamically averaged into a static distorted nuclear configuration. The very different magnetic behaviors reported for complexes 1–2 and 3–6 are a clear manifestation of such behavior, and should be the subject of more detailed structural, magnetic, and spectroscopic studies.
(4) A general method allowing a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mapping of the ligand field matrix, as deduced from ab initio CASSCF + NEVPT2 calculations, onto corresponding AOM energy expressions was used to obtain values of the antibonding energies of σ (eσ), the in- (eπc) and out-of- (eπs) plane π-type. The parameters show: (i) a large reduction of eσ due to 3dz2–4s mixing (hybridization) typical for linear X–M–X transition metal complexes, (ii) π-bonding anisotropy reflected in eπs > eπc for the Fe–N(sp2) and Fe–O(sp) type complexes, and (iii) framework hyperconjugative effects manifested in values of eπ assumed otherwise to be zero (eπ for C(sp3) and eπc for N(sp2)). In the same context, ligand field matrix elements neglected in common AOM parameterization schemes, but accounted for by its extended versions (such as σ–π mixings and misdirected valence) could be traced back and verified. Other couplings (dx2−y2–dz2, dxy–dz2, and dxy–dx2−y2), which, due to the high level of over-parameterization have not been discussed before, emerged from our analysis.
1 mapping of the ligand field matrix, as deduced from ab initio CASSCF + NEVPT2 calculations, onto corresponding AOM energy expressions was used to obtain values of the antibonding energies of σ (eσ), the in- (eπc) and out-of- (eπs) plane π-type. The parameters show: (i) a large reduction of eσ due to 3dz2–4s mixing (hybridization) typical for linear X–M–X transition metal complexes, (ii) π-bonding anisotropy reflected in eπs > eπc for the Fe–N(sp2) and Fe–O(sp) type complexes, and (iii) framework hyperconjugative effects manifested in values of eπ assumed otherwise to be zero (eπ for C(sp3) and eπc for N(sp2)). In the same context, ligand field matrix elements neglected in common AOM parameterization schemes, but accounted for by its extended versions (such as σ–π mixings and misdirected valence) could be traced back and verified. Other couplings (dx2−y2–dz2, dxy–dz2, and dxy–dx2−y2), which, due to the high level of over-parameterization have not been discussed before, emerged from our analysis.
(5) Based on the theoretical analysis, the following guidelines for generating new single-molecule magnets with improved magnetic anisotropies and relaxation times can be formulated:
(i) enhancement of the spin–orbit coupling and concomitant suppression of the vibronic coupling is predicted to improve the anisotropy barrier Ueff (see Fig. 8). Both features can be met by replacing the C, N, or O donor atoms with their heavier analogues, such as Si, P, or S. Indeed, some FeS2 moieties have already been reported.90 Ligand spin–orbit coupling, increasing in this direction may add to the metal one, thus compensating for the enhanced metal–ligand covalence, which tends to act in the opposite direction (relativistic nephelauxetic effect). Such an increase in molecular magnetic anisotropy as a result of the coordination of increasingly heavier ligand atoms has been demonstrated recently in octahedral complexes of CrIII.91 Additionally, vibronic coupling, which decreases with increasing metal–ligand covalency, is expected to support a larger Ueff. A nice manifestation of such an effect is a recently reported CoS4 single-molecule magnet, the first example of a transition metal complex exhibiting slow magnetic relaxation under zero applied dc magnetic field.92
(ii) Metal–ligand bonds with C3v and C2v local pseudosymmetries, enforced by the next-nearest metal neighbors (C(sp3) and N(sp2)), are preferable to lower symmetry ones (O(sp2)), which create large matrix elements between the ground state MJ sublevels.
(iii) Avoiding secondary metal–ligand interactions through the use of sterically encumbering ligands with aliphatic (1, 2) rather than aromatic substituents (3–5) has a favorable effect on the relaxation time. Along the same line, bulky ligands of the former type tend to support linear FeX2 cores and thus oppose in an indirect way unfavorable vibronic coupling.
(iv) Suppression of dipolar spin–spin interactions between magnetic centers in the solid will increase the relaxation time for the direct process. It is this kind of interaction which shows the expected trend of relaxation times (see Fig. 13) across the series. Thus decoupling of the molecule from the lattice is an important goal. Aside from the usual approaches used to achieve this (e.g., dilution of the single-molecule magnets by substitution in a diamagnetic isomorphic compound or in frozen solution), stabilization of the molecules on a metal (usually gold) surface provides a modern way of approaching this. One possibility of doing this is given by using appropriately chosen spacer molecules that can “wire” a single-molecule magnet to a gold surface.1 Another method, involving vapor deposition, should be facile for certain mononuclear transition metal complexes that are neutral and can sublime. For example, complex 2 is easily sublimable.93 In the context of the FeX2 single-molecule magnets, a possible target would be an – AuS3C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–Fe–C
C–Fe–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–CS3Au – structure. Unfavorable vibronic coupling which tends to stabilize bent structures will be suppressed within the constraints given above.
C–CS3Au – structure. Unfavorable vibronic coupling which tends to stabilize bent structures will be suppressed within the constraints given above.
(6) The large magnetic anisotropy due to unquenched first order orbital momentum in the 5E ground states of the considered FeX2 complexes leads to large anisotropy barriers. However, quantum tunneling of the magnetization is particularly efficient owing to the small value of S = 2 and the low-symmetry perturbations of the kind discussed in Sections 3.2.3 and 3.3. Thus, the search for better single-molecule magnets that stay magnetized at elevated temperatures requires a combination of a large Ueff and a small quantum tunneling rate. This goal is only partly (due to intrinsic transversal magnetic fields stemming from dipole–dipole interactions which cannot be avoided in a solid) achieved by choosing Kramers rather than non-Kramers Fe(II) (S = 2) ions, as was shown in the recently reported [Co(SPh)4]2− (S = 3/2) complex.92 The condition of larger Ueff (large/small spin–orbit/vibronic coupling) and a small quantum tunneling of the magnetization (large total moments MJ) seems to be ideally met in complexes of rare earths such as phthalocyanine (pc) double decker complexes, e.g. (pc)2TbIII.94 A similar possibility for complexes of 3d metals employs low-coordinate Fe(II) (introducing large Ueff) ferromagnetically coupled with several MnII (S = 5/2, introducing a large spin). Such a synthetic strategy has yet to be explored.
Acknowledgements
This research was supported by NSF grant CHE-1111900. We thank Tyco Electronics for fellowship support of J.M.Z.Notes and references
- M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194 CrossRef CAS.
- M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789 CrossRef CAS.
- A. Ardavan, O. Rival, J. J. L. Morton, S. J. Blundell, A. M. Tyryshkin, G. A. Timco and R. E. P. Winpenny, Phys. Rev. Lett., 2007, 98, 057201 CrossRef.
- P. C. E. Stamp and A. Gaita-Ariño, J. Mater. Chem., 2009, 19, 1718 RSC.
- F. Torres, J. M. Hernández, X. Bohigas and J. Tejada, Appl. Phys. Lett., 2000, 77, 3248 CrossRef CAS.
- R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141 CrossRef CAS.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, New York, 2006 and references therein Search PubMed.
- N. E. Chakov, S.-C. Lee, A. G. Harter, P. L. Kuhns, A. P. Reyes, S. O. Hill, N. S. Dalal, W. Wernsdorfer, K. Abboud and G. Christou, J. Am. Chem. Soc., 2006, 128, 6975 CrossRef CAS.
- C. J. Milios, A. Vinslava, W. Wernsdorfer, S. Moggach, S. Parsons, S. P. Perlepes, G. Christou and E. K. Brechin, J. Am. Chem. Soc., 2007, 129, 2754 CrossRef CAS.
- C. Sangregorio, T. Ohm, C. Paulsen, R. Sessoli and D. Gatteschi, Phys. Rev. Lett., 1997, 78, 4645 CrossRef CAS.
- S. M. J. Aubin, N. R. Dilley, L. Pardi, J. Krzystek, M. W. Wemple, L.-C. Brunel, M. B. Maple, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1998, 120, 4991 CrossRef CAS.
- A.-L. Barra, A. Canneschi, A. Cornia, F. Fabrizi de Biani, D. Gatteschi, C. Sangregorio, R. Sessoli and L. Sorace, J. Am. Chem. Soc., 1999, 121, 5302 CrossRef CAS.
- S. Accorsi, A. L. Barra, A. Caneschi, G. Chastanet, A. Cornia, A. C. Fabretti, D. Gatteschi, C. Mortalò, E. Olvieri, F. Parenti, R. Sessoli, L. Sorace, W. Wernsdorfer and L. Zobbi, J. Am. Chem. Soc., 2006, 128, 4742 CrossRef CAS.
- L. Gregoli, C. Danieli, A.-L. Barra, P. Neugebauer, G. Pellegrino, G. Poneti, R. Sessoli and A. Cornia, Chem.–Eur. J., 2009, 15, 6456 CrossRef CAS.
- F. Neese and D. A. Pantazis, Faraday Discuss., 2011, 148, 229 RSC.
- O. Waldmann, Inorg. Chem., 2007, 46, 10035 CrossRef CAS.
- F. Neese and E. I. Solomon, Inorg. Chem., 1998, 37, 6568 CrossRef CAS.
- C. J. Milios, C. P. Raptopoulou, A. Terzis, F. Lloret, R. Vincente, S. P. Perlepes and A. Escuer, Angew. Chem., Int. Ed., 2004, 43, 210 CrossRef CAS.
- E. K. Brechin, C. Boskovic, W. Wernsdorfer, J. Yoo, A. Yamaguchi, E. C. Sañudo, T. R. Concolino, A. L. Rheingold, H. Ishimoto, D. N. Hendrickson and G. Christou, J. Am. Chem. Soc., 2002, 124, 9710 CrossRef CAS.
- J. Villain, F. Hartman-Boutron, R. Sessoli and A. Rettori, Europhys. Lett., 1994, 27, 159 CrossRef.
- W. H. Harman and C. J. Chang, J. Am. Chem. Soc., 2007, 129, 15128 CrossRef CAS.
- D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, J. Am. Chem. Soc., 2010, 132, 1224 CrossRef CAS.
- W. H. Harman, T. D. Harris, D. E. Freedman, H. Fong, A. Chang, J. D. Rinehart, A. Ozarowski, M. T. Sougrati, F. Grandjean, G. J. Long, J. R. Long and C. J. Chang, J. Am. Chem. Soc., 2010, 132, 18115 CrossRef CAS.
- Throughout this work electron configurations due to the high-spin Fe(II) d6 subshell will be denoted by orbitals which carry the extra electron in addition to the half-filled d5 shell.
- A different definition of M′J = MS + ML/2, used to directly relate the magnetic moment with the free electron go = 2 value (M = μBgoM′JH), was employed in ref. 46. Here, we return to the usual definition of MJ = MS + ML which also correctly reflects the transformation symmetry of the wavefunction. Another definition treating the total moment in a S = 1/2 pseudospin approach (used by the ESR community) defines the magnetic moment as M = μBmgeffH (geff = goSM′J, m = ±1/2).
- B. R. McGarvey and J. Telser, Inorg. Chem., 2012, 51, 6000 Search PubMed.
- D. Dai and M.-H. Whangbo, Inorg. Chem., 2005, 44, 4407 CrossRef CAS.
- W. M. Reiff, A. M. LaPointe and E. H. Witten, J. Am. Chem. Soc., 2004, 126, 10206 CrossRef CAS.
- W. M. Reiff, C. E. Schulz, M.-H. Whangbo, J. I. Seo, Y. S. Lee, G. R. Potratz, C. W. Spicer and G. S. Girolami, J. Am. Chem. Soc., 2009, 131, 404 CrossRef CAS.
- W. A. Merrill, T. A. Stich, M. Brynda, G. J. Yeagle, J. C. Fettinger, R. De Hont, W. M. Reiff, C. E. Schulz, R. D. Britt and P. P. Power, J. Am. Chem. Soc., 2009, 131, 12693 CrossRef.
- M. Atanasov, P. Comba and C. A. Daul, Inorg. Chem., 2008, 47, 2449 CrossRef CAS.
- M. Atanasov, C. A. Daul and C. Rauzy, Struct. Bonding, 2004, 106, 97 CAS.
- M. Atanasov, C. A. Daul and C. Rauzy, Chem. Phys. Lett., 2003, 367, 737 CrossRef CAS.
- M. Atanasov and P. Comba, in The Jahn-Teller Effect: Fundamentals and Implications for Physics and Chemistry, ed. H. Köppel, H. Barentzen and D. R. Yarkony, Springer Series in Chemical Physics, Berlin, 2009, p. 97 Search PubMed.
- P.-Å. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189 CrossRef CAS.
- K. Wolinski and P. Pulay, J. Chem. Phys., 1989, 90, 3647 CrossRef CAS.
- K. Andersson, P.-Å. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483 CrossRef CAS.
- K. Andersson, P.-Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218 CrossRef CAS.
- B. O. Roos, M. P. Fülscher, P.-Å. Malmqvist, P. L. Serrano-Andrés, and M. Merchán, Theoretical Studies of the Electronic Spectra of Organic Molecules, in Quantum Mechanical Electronic Structure Calculations with Chemical Accuracy, ed. S. R. Langhoff, Kluwer, Dordrecht, 1994 Search PubMed.
- B. O. Roos and P.-Å. Malmqvist, Phys. Chem. Chem. Phys., 2004, 6, 2919 RSC.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138 CrossRef CAS.
- C. Angeli, B. Bories, A. Cavallini and R. Cimiraglia, J. Chem. Phys., 2006, 124, 054108 CrossRef.
- R. Maurice, C. de Graaf and N. Guihéry, J. Chem. Phys., 2010, 133, 084307 Search PubMed.
- M. Atanasov, D. Ganyushin, D. A. Pantazis, K. Sivalingam and F. Neese, Inorg. Chem., 2011, 50, 7640 Search PubMed.
- D. Maganas, S. Sottini, P. Kyritsis, E. J. J. Groenen and F. Neese, Inorg. Chem., 2011, 50, 8741 CrossRef CAS.
- R. Maurice, R. Bastardis, C. de Graaf, N. Suaud, T. Mallah and N. Guihéry, J. Chem. Theory Comput., 2009, 5, 2977 CrossRef CAS.
- R. Maurice, N. Guihéry and C. de Graaf, J. Chem. Theory Comput., 2010, 6, 55 CrossRef CAS.
- R. Maurice, A. M. Pradipto, N. Guihéry, R. Broer and C. de Graaf, J. Chem. Theory Comput., 2010, 6, 3092 CrossRef CAS.
- S. Vancoillie, J. Chalupský, U. Ryde, E. I. Solomon, K. Pierloot, F. Neese and L. Rulȋšek, J. Phys. Chem. B, 2010, 114, 7692 CrossRef.
- M. Atanasov and P. Comba, in Structure and Function, ed. P. Comba, Springer, 2010, pp. 74–79 Search PubMed.
- F. Neese, WIREs Comput. Mol. Sci., 2012, 2, 73 Search PubMed.
- ORCA, An ab initio, DFT and Semiempirical SCF-MO Package – Version 2.8, 20 September 2010by F. Neese, F. Wennmohs, with contributions from U. Becker, D. Bykov, D. Ganyushin, A. Hansen, R. Izsak, D. G. Liakos, C. Kollmar, S. Kossmann, D. A. Pantazis, T. Petrenko, C. Reimann, C. Riplinger, M. Roemelt, B. Sandhöfer, I. Schapiro, K. Sivalingam, E. Valeev and B. Wezisla, Max-Planck Institut für Chemische Energiekonversion, http://www.mpibac.mpg.de/bac/index_en.php Search PubMed.
- J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2012 10.1039/c2sc20801f.
- T. Viefhaus, W. Schwarz, K. Hübler, K. Locke and J. Weidlein, Z. Anorg. Allg. Chem., 2001, 627, 715 CrossRef CAS.
- C. Ni and P. P. Power, Chem. Commun., 2009, 5543 RSC.
- R. S. Fishman and F. A. Reboredo, Phys. Rev. Lett., 2007, 99, 217203-1 Search PubMed.
- R. S. Fishman, S. Okamoto and F. A. Reboredo, Phys. Rev. Lett., 2008, 101, 116402-1 Search PubMed.
- R. S. Fishman and F. A. Reboredo, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 144421 Search PubMed.
- P. Reis, R. S. Fishman, F. A. Reboredo and J. Moreno, Phys. Rev. B, 2008, 77, 174433 Search PubMed.
- F. Neese and E. I. Solomon, in Magnetism: Molecules to Materials, ed. J. S. Miller and M. Drillon, Wiley-VCH, Weinheim, 2003, vol. IV, pp. 345–466 Search PubMed.
- I. B. Bersuker, The Jahn–Teller Effect and Vibronic Interactions in Modern Chemistry, Plenum Press, New York and London, 1984 Search PubMed.
- I. B. Bersuker, The Jahn–Teller Effect, University Press, Cambridge, 2006 Search PubMed.
- E. Renner, Z. Phys., 1934, 92, 172 Search PubMed.
- G. Herzberg and E. Teller, Z. Phys. Chem., Abt. B, 1933, 21, 410.
- J. A. Pople and H. C. Longuet-Higgins, Mol. Phys., 1958, 1, 372 CAS.
- R. N. Dixon, Mol. Phys., 1965, 9, 357 CAS.
- A. A. Petelin, Int. J. Quantum Chem., 1972, 6, 701 CAS.
- M. Atanasov, D. Ganyushin, K. Sivalingam and F. Neese, Struct. Bonding, 2012, 143, 149 Search PubMed.
- C. K. Jørgensen, R. Pappalardo and H.-H. Schmidtke, J. Chem. Phys., 1963, 39, 1422 CrossRef.
- C. E. Schäffer and C. K. Jørgensen, Mol. Phys., 1965, 9, 401.
- B. N. Figgis and M. A. Hitchman, Ligand Field Theory and Its Applications, Wiley-VCH, NewYork, 2000 Search PubMed.
- H. Adamsky, with contributions from P. E. Hoggard, M. Atanasov and K. Eifert, AOMX, http://www.aomx.de Search PubMed.
- D. Reinen, M. Atanasov and S.-L. Lee, Coord. Chem. Rev., 1998, 175, 91 CrossRef CAS.
- J. D. Dunitz and D. N. J. White, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1973, A29, 93 CrossRef.
- J. D. Dunitz, E. F. Maverick and K. N. Trueblood, Angew. Chem., 1988, 100, 910 Search PubMed.
- J. H. Ammeter, H. B. Bürgi, E. Gamp, V. Meyer-Sandrin and W. P. Jensen, Inorg. Chem., 1979, 18, 733 CrossRef CAS.
- M. Atanasov, W. König, H. Craubner and D. Reinen, New. J. Chem., 1993, 17, 115 Search PubMed.
- F. S. Ham, in Electron Paramagnetic Resonance, ed. S. Geschwind, Plenum Press, New York, 1972, p. 1 Search PubMed.
- F. S. Ham, Phys. Rev., 1965, 138, 1727 Search PubMed.
-
V
s–ph is related with the magnetogyric ratio for electrons, γ = −e/mc, the parameter
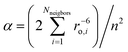 – a constant somewhat greater than unity, the magnetic moment per ion
– a constant somewhat greater than unity, the magnetic moment per ion 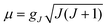 (in Bohr magnetons) and n –the number of magnetic ions per 1 volume as Vs–ph2 = (3α/8)γ2n2μ2ℏ2,
A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Clarendon Press, Oxford, 1970 Search PubMed.
(in Bohr magnetons) and n –the number of magnetic ions per 1 volume as Vs–ph2 = (3α/8)γ2n2μ2ℏ2,
A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Clarendon Press, Oxford, 1970 Search PubMed. - V. Starovoitova, G. R. A. Wyllie, W. R. Scheidt, W. Sturhan, E. Ercan Alp and S. M. Durbin, J. Phys. Chem. B, 2008, 112, 12661 Search PubMed.
- C. W. DeKock and D. M. Gruen, J. Chem. Phys., 1966, 44, 4383 Search PubMed.
- A. D. Liehr, J. Phys. Chem., 1964, 68, 665 Search PubMed.
- A. D. Liehr, J. Phys. Chem., 1964, 68, 3629 Search PubMed.
- M. Gerloch, J. H. Harding and G. G. Woolley, Struct. Bonding, 1981, 46, 1 CAS.
- A. J. Bridgeman and M. Gerloch, Prog. Inorg. Chem., 1997, 45, 179–281 CAS , p. 238, Table III.
- C. Train, R. Gheorghe, V. Krstic, L.-M. Chamoreau, N. S. Ovanesyan, G. L. J. A. Rikken, M. Gruselle and M. Verdaguer, Nat. Mater., 2008, 7, 729 CrossRef CAS.
- T. Nguyen, A. Panda, M. M. Olmstead, A. F. Richards, M. Stender, M. Brynda and P. P. Power, J. Am. Chem. Soc., 2005, 127, 8545 CrossRef CAS.
- H. I. Karunadasa, K. D. Arquero, L. A. Berben and J. R. Long, Inorg. Chem., 2010, 49, 4738 Search PubMed.
- J. M. Zadrozny and J. R. Long, J. Am. Chem. Soc., 2011, 133, 20732 CrossRef CAS.
- A. M. LaPointe, Inorg. Chim. Acta, 2003, 345, 359 CrossRef CAS.
- N. Ishikawa, Struct. Bonding, 2010, 135, 211 CAS and references therein.
Footnote |
| † Electronic supplementary information (ESI) available: Full computational details, results, and formulae. Calculated molar dc susceptibility and magnetization data for 2–5 and NIR d–d absorption spectrum of 1. See DOI: 10.1039/c2sc21394j |
| This journal is © The Royal Society of Chemistry 2013 |
